burger矢量
- 格式:doc
- 大小:23.00 KB
- 文档页数:2

《材料科学基础》名词解释AOrowan mechanism (奥罗万机制)位错绕过第二相粒子,形成包围第二相粒子的位错环的机制。
Austenite(奥氏体)碳在γ-Fe中形成的间隙固溶体称为奥氏体。
B布拉菲点阵除考虑晶胞外形外,还考虑阵点位置所构成的点阵。
Half-coherent interface(半共格相界)两相邻晶体在相界面处的晶面间距相差较大,则在相界面上不可能做到完全一一对应,于是在界面上将产生一些位错,以降低界面弹性应变能。
这时两相原子部分保持匹配,这样的界面称为半共格界面。
Sheet texture(板织构)轧板时形成的组织的择优取向。
Peritectic reaction(包晶反应)固相和液相生成另一成分的固溶体的反应Peritectic segregation(包晶偏析)新生成的固相的芯部保留残余的原有固相,新相本身成分也不均匀。
Peritectic phase diagram(包晶相图)具有包晶反应的相图Peritectoid reaction(包析反应)由两个固相反应得到一个固相的过程为包析反应。
Cellular structure(胞状结构)成分过冷区很小时,固相突出部分局限在很小区域内,不生成侧向枝晶。
Intrinstic diffusion coefficient(本征扩散系数)依赖热缺陷进行的扩散的扩散系数。
Transformed ledeburite(变态莱氏体)渗碳体和奥氏体组成的莱氏体冷却至727℃时奥氏体发生共析反应转变为珠光体,此时称变态莱氏体。
Deformation twins(变形孪晶)晶体通过孪生方式发生塑性变形时产生的孪晶(BCC,HCP)Chill zone(表层细晶区)和低温铸模模壁接触,强烈过冷形成的细小的方向杂乱的等轴晶粒细晶区。
Burger’s vector(柏氏矢量)表征位错引起的晶格点阵畸变大小和方向的物理量。
Asymmetric tilt boundary(不对称倾斜晶界)晶界两侧晶粒不对称的小角度晶界,界面含两套垂直的刃型位错。
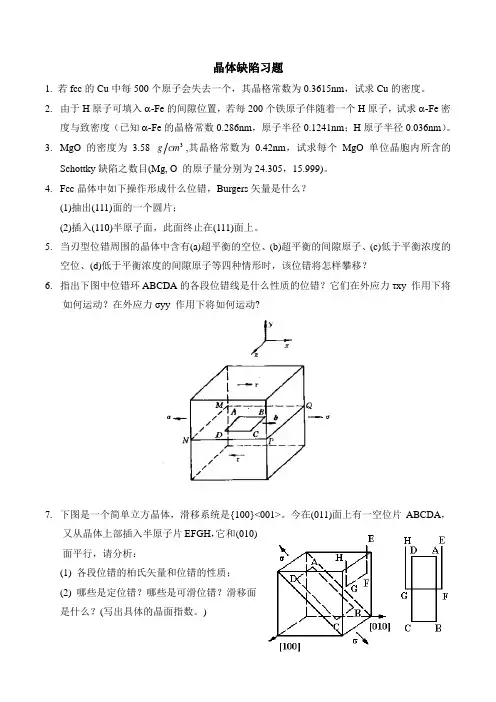
晶体缺陷习题1. 若fcc的Cu中每500个原子会失去一个,其晶格常数为0.3615nm,试求Cu的密度。
2.由于H原子可填入α-Fe的间隙位置,若每200个铁原子伴随着一个H原子,试求α-Fe密度与致密度(已知α-Fe的晶格常数0.286nm,原子半径0.1241nm;H原子半径0.036nm)。
3.MgO的密度为3.58 3g cm,其晶格常数为0.42nm,试求每个MgO单位晶胞内所含的Schottky缺陷之数目(Mg, O 的原子量分别为24.305,15.999)。
4.Fcc晶体中如下操作形成什么位错,Burgers矢量是什么?(1)抽出(111)面的一个圆片;(2)插入(110)半原子面,此面终止在(111)面上。
5.当刃型位错周围的晶体中含有(a)超平衡的空位、(b)超平衡的间隙原子、(c)低于平衡浓度的空位、(d)低于平衡浓度的间隙原子等四种情形时,该位错将怎样攀移?6.指出下图中位错环ABCDA的各段位错线是什么性质的位错?它们在外应力τxy 作用下将如何运动?在外应力σyy 作用下将如何运动?7.下图是一个简单立方晶体,滑移系统是{100}<001>。
今在(011)面上有一空位片ABCDA,又从晶体上部插入半原子片EFGH,它和(010)面平行,请分析:(1) 各段位错的柏氏矢量和位错的性质;(2) 哪些是定位错?哪些是可滑位错?滑移面是什么?(写出具体的晶面指数。
)(3) 如果沿[01]方向拉伸,各位错将如何运动?(4) 画出在位错运动过程中各位错线形状的变化,指出割阶、弯折和位错偶的位置。
(5)画出晶体最后的形状和滑移线的位置。
8. 晶体滑移面,有一圆形位错环如图所示。
问:(1) 晶体滑移面的上部晶体外加切应力方向和Burgers 矢量 同向或反向时,位错环向外滑移?(2) 位错环平衡半径和外加切应力的关系式。
9. 同一滑移面上有二段Burgers 矢量相同异号刃型位错(AB ,CD 位错线方向相反),位错线处在同一直线上,每段位错线长度x, 相距x 。


burgers方程的应用场景
Burgers方程是一种非线性偏微分方程,最初用于描述气体或
液体中的冲击波和涡旋。
然而,随着时间的推移,Burgers方
程的应用领域逐渐扩展到其他科学和工程领域。
以下是一些Burgers方程的应用场景:
1. 冲击波传播:Burgers方程可以描述气体或液体中的冲击波
传播现象。
这种应用常见于研究爆炸物理学、声波传播和空气动力学等领域。
2. 流体动力学:Burgers方程可以用来描述流体力学中的非线
性粘性流动,例如在河流、海洋和大气环流中的应用。
3. 交通流量模型:Burgers方程可以用于描述交通流量模型中
的非平衡流动现象。
通过将Burgers方程应用于交通流量模型,可以预测交通流量的变化和拥堵情况。
4. 经济学:Burgers方程也被用于经济学中的某些模型,例如
描述市场供求关系中的非线性效应。
5. 物理模拟:Burgers方程可以用于模拟和预测涡旋、湍流、
非线性波等物理现象。
它在计算物理、计算流体力学和声学等领域中有着广泛的应用。
总之,Burgers方程在许多领域中被广泛应用,其中包括流体
力学、声学、气象学、经济学和物理学等。
尽管最初是为了描
述液体和气体中的特定现象而提出的,但此方程的应用范围现在已经远远超出了原始的领域。


Chapter 1.Introduction1.What are electronic materials?电子材料是用在电子电气工厂的材料,它们是电子器件和集成电路制造的基础。
2.What are the functional electronic materials?功能电子材料是指除强度性能外,还有特殊功能,或能实现光电磁热力等不同形式的交互作用和转换的非结构材料。
3.What are the basic requirements of modern society to electronic materials?1.高纯度与完美的晶体结构。
2.先进的制造技术。
3.大尺寸。
4.寿命长且可控。
5.具有优异结构与功能特性。
6.减少污染节约能源。
4.What is the future direction for the development of advanced electronicmaterials?先进复合材料有机电子材料电子薄膜材料5.What is Moore’s law?集成电路上可容纳的晶体管数目将在每三年变成原来的4倍。
Chapter 2. Elementary materials science concepts1.Please explain the shell model of atomic structure and sketch that for sodium.壳模型是基于波尔模型的。
原子核:带正电的质子与中性的中子。
原子序数:核电荷数。
电子:质量极小,带负电,在原子中绕电子核旋转。
核外电子排布:泡利不相容定理、能量最低原理、洪特定理。
2.What’s the force between the two atoms when their separation is above the bond length, equal to the bond length and below the bond length? What are the net force and potential energy in bonding between two atoms?距离大于键长时合力为吸引力,等于键长时合力为0,小于键长时合力为斥力。



晶格参数为2.5a0 的立方金属刃型位错的burgers 矢量的miller 指数及其长度。
1. 引言1.1 概述本文主要探究晶格参数为2.5a0的立方金属刃型位错的Burgers矢量以及Milller指数,并对其长度进行研究和分析。
位错是材料中常见的缺陷,它的存在对材料的性能和力学行为有着重要影响。
了解和研究位错在晶体中的特征和行为对我们深入理解材料性质具有重要意义。
1.2 文章结构本文分为引言、正文和结论部分。
引言部分将介绍本篇文章的背景和目的,正文部分将详细介绍立方金属刃型位错以及与之相关的Burgers矢量和Milller指数,结合实例进行具体分析。
最后,在结论部分对本文进行总结,并讨论立方金属刃型位错的Burgers矢量和Miller指数在研究中的重要性。
1.3 目的本文旨在深入了解立方金属刃型位错的特征,探讨Burgers矢量与Milller指数之间关系,并提供相应计算方法与应用案例。
通过这些内容的讨论,希望能够增进对晶体缺陷与位错行为的理解,为材料研究和工程应用提供有价值的参考和指导。
2. 正文:2.1 立方金属刃型位错概述立方金属刃型位错是一种晶体缺陷,它在晶格中形成了沿特定方向和平面的错配。
此类位错通常发生在金属材料中,并且对材料的力学性能和电子性质产生重要影响。
立方金属刃型位错可以通过其生成机制进行分类,如排列型、夹杂型和膨胀型等。
2.2 晶格参数为2.5a0 的立方金属刃型位错特征分析2.2.1 Milller指数的概念解释Milller指数是描述结晶面在晶格中位置的一种方式。
它用一组整数(hkl)来表示一个结晶面相对于基准晶面(通常为晶体表面)的斜率。
例如,(100)代表着平行于x轴、y轴和z轴的结晶面。
2.2.2 立方金属刃型位错中的Burgers矢量与Milller指数关系分析与推导在立方金属刃型位错中,Burgers矢量是描述两个部分之间相互滑移所需原子距离的矢量。

1.1模型参数代码可参考manual中各个章节的command命令及说明,注意单位。
用prop 赋值。
16 ttable 塑性拉应变-抗拉强度的表号下列参数可以显示、绘图和通过fish访问1 es_plastic 塑性切应变2 et_plastic 塑性拉应变3 ff_count 检测切应变反向的数4 ff_cvd 体应变,εvd经典粘弹性模型的材料参数(Classical Viscoelastic (Maxwell Substance)–MODEL mechanical viscous)1 bulk 弹性体积模量,K2 shear 弹性剪切模量,G3 viscosity 动力粘度,η粘弹性模型的材料参数(Burgers Model –MODEL mechanical burgers)1 bulk 弹性体积模量,K2 kshear Kelvin弹性剪切模量,G K3 kviscosity Kelvin动力粘度,ηK4 mkshear Maxwell切边模量,G M5 mviscosity Maxwell动力粘度,ηM二分幂律模型的材料参数(Power Law –MODEL mechanical power)1 a_1 常数,A12 a_2 常数,A23 bulk 弹性体积模量,K4 n_1 指数,n15 n_2 指数,n26 rs_1 参考应力,σ1ref7 rs_2 参考应力,σ2ref8 shear 弹性剪切模量,G蠕变模型材料参数(WIPP Model –MODEL mechanical wipp)1 act_energy 活化能,Q2 a_wipp 常数,A3 b_wipp 常数,B4 bulk 弹性体积模量,K5 d_wipp 常数,D6 e_dot_star临界稳定状态蠕变率,7 gas_c 气体常数,R8 n_wipp 指数,n9 shear 弹性剪切模量,G10 temp 温度,T下列参数可以显示、绘图和通过fish访问1 e_prime 累积主蠕变应变2 e_rate 累积主蠕变应变率Burger、蠕变组合材料模型的材料参数(Burgers-Creep Viscoplastic Model –MODEL mechanical cvisc)1 bulk 弹性体积模量,K2 cohesion 聚力,c3 density 密度,ρ4 dilation 剪胀角,Ψ5 friction 摩擦角,Φ6 kshear Kelvin弹性剪切模量,G K7 kviscosity Kelvin粘度,ηK8 shear 弹性剪切模量,G9 tension 抗拉强度,σt10 mviscosity Maxwell动力粘度,ηM下列计算参数可以显示、绘图和通过fish访问1 es_plastic 累积塑性切应变2 et_plastic 累积塑性拉应变幂律模型的材料参数(Power-Law Viscoplastic Model –MODEL mechanical cpower)1 a_1 常数,A12 a_2 常数,A23 bulk 弹性体积模量,K4 cohesion 聚力,c5 dilation 剪胀角,Ψ6 friction 摩擦角,Φ7 n_1 指数,n18 n_2 指数,n29 rs_1 参考应力,σ1ref10 rs_2 参考应力,σ2ref11 shear 弹性剪切模量,G12 tension 抗拉强度,σt粘塑形模型的材料参数(WIPP-Creep Viscoplastic Model –MODEL mechanical pwipp)1 act_energy 活化能,Q2 a_wipp 常数,A3 b_wipp 常数,B4 bulk 弹性体积模量,K5 d_wipp 常数,D6 e_dot_star临界稳定状态蠕变率,7 gas_c 气体常数,R8 kshear 材料参数,KΦ9 n_wipp 指数,n10 kdil 材料参数,q k11 kvol 材料参数,qΦ12 shear 弹性切变模量,G13 temp 温度,T14 tension 抗拉强度,σt以下计算参数可以显示、绘图和通过fish访问1 e_prime 累积主蠕变应变2 e_rate 累积主蠕变应变率3 es_plastic 累积塑性切应变4 et_plastic 累积塑性拉应变碎盐变形模型的材料参数(Crushed-Salt Model –MODEL mechanical cwipp)1 act_energy 活化能,Q2 a_wipp 常数,A3 b_f 最终体积模量,K f4 b_wipp 常数,B5 b0 蠕变压实系数,B06 b1 蠕变压实系数,B17 b2 蠕变压实系数,B28 bulk 弹性体积模量,K9 d_f 最终密度,ρf10 d_wipp 常数,D11 e_dot_star临界稳定状态蠕变率,12 gas_c 气体常数,R13 n_wipp 指数,n14 rho 密度,ρ15 s_f 最终切变模量,G f16 shear 弹性切变模量,G17 temp 温度,T以下计算参数可以显示、绘图和通过fish访问1 frac_d 当前碎片密度,ρd2 s_g1 蠕变压实参数,G3 s_k1 蠕变压实参数,K均质流体模型的材料参数1 permeability 等方向渗透性,k2 porosity 孔隙率,n(默认时,n=0.5)各向异性流体模型的材料参数1 fdd k1-k2的平面倾向2 fdip k1-k2的平面倾角1.2模型适用说明遍布节理模型适用于Mohr-Coulomb材料来明确显示力在各个方向上的差异性。
burgers方程的新的精确解
Burgers方程是一种物理方程,它描述的是一类非线性的相移二维流动的数学
模型。
Burgers方程由荷兰物理学家J.M. Burgers于1920年提出,他证明Burgers方程可以通过有限差分方法得到精确解。
但是,Burgers方程后来被发现有一些其他解法更优越,能够带来更高的精度。
近年来,新一代计算机科学研究者们对Burgers方程进行了研究,通过将高精
度算法和Matlab处理器结合起来,实现了一种新的精确解,能更加有效地解读Burgers方程。
与此同时,一些先进的数学模型也被应用用来替代Burgers方程
的数学形式,使得Burgers方程的求解变得更加容易和准确。
要充分发挥新解法的优势,必须对现有的非线性参数方程组进行多方面的探讨。
首先,可以利用小改变现有方程组参数,来拓展解的存在范围,进而大大提高Burgers方程的精确度。
另外,利用多层次及理论上的分析,将帮助研究者们改
进已经存在的非线性参数方程组,改善Burgers方程的运算效率,且在计算机上取得更好的精确解。
总之,Burgers方程的新的精确解取得了值得称赞的进步,它有助于促进研究
者们对复杂问题的深入研究,同时也有助于解决实际应用中科学家面临的许多问题。
因此,未来,将会有更多的研究朝着寻找Burgers方程更准确、更高效的解法而开展,以期更好地解释和应用该方程。
求解burgers方程
求解Burgers方程是一个非常复杂的问题,因为Burgers方程是一个非线性偏微分方程,具有许多不同的解法和技巧。
Burgers 方程是描述粘性流体力学中的非线性现象的方程,通常写作ut + uux νuxx = 0,其中u是速度场,t是时间,x是空间变量,ν是粘性系数。
对于Burgers方程的求解,可以采用多种方法。
一种常见的方法是使用特征线方法,即将方程转化为特征方程,然后求解特征方程得到通解。
另一种方法是使用变换法,例如通过变量代换将Burgers方程转化为更容易求解的形式。
还可以尝试使用分离变量法、级数展开法、变分法等数学工具来求解Burgers方程。
另外,Burgers方程也可以通过数值方法进行求解,如有限差分法、有限元法、谱方法等。
这些数值方法可以通过离散化空间和时间变量来近似求解Burgers方程,得到数值解。
总之,求解Burgers方程是一个复杂而丰富的领域,涉及到多种数学方法和物理理论。
针对具体的问题和条件,选择合适的方法
进行求解是非常重要的。
希望这个回答能够帮助你对Burgers方程的求解有一个初步的了解。
铝的伯氏矢矢量大小铝的伯氏矢量大小,这听起来是不是有点儿头疼的感觉?别担心,今天我来给你讲讲这个看似高大上的话题,保证你听得懂,也能听得开心。
要知道,铝这种金属咱们生活中几乎随处可见,铝箔、铝罐、铝合金车身……它们就像是咱们生活中的隐形大英雄,虽然默默无闻,但其实每天都在为咱们提供便利。
你可能会好奇,既然它这么常见,怎么还跟“伯氏矢量”挂钩了?别急,咱慢慢聊。
首先啊,咱得搞清楚什么是“伯氏矢量”。
说白了,它就是用来描述一个粒子在磁场中运动状态的一个数学工具。
好比你在骑自行车,如果你想知道风吹得有多强、车速有多快,那你就得用一堆公式来算一算。
伯氏矢量就是这个“公式”的一部分。
它和磁场、速度什么的密切相关,能帮助咱们知道磁场对铝原子产生了什么样的影响。
嗯,听起来是不是还是有点抽象?别着急,咱们举个例子再说。
想象一下,你拿着一块铝板,突然把它放到一个磁场里去。
铝板里面的那些小原子就开始在磁场的影响下“跳舞”了。
磁场让这些原子产生了什么变化呢?它们的运动方向发生了改变,速度变了,甚至位置也被调整了。
这些变化就是伯氏矢量的作用。
而你说,这个伯氏矢量到底多大呢?它的大小就取决于铝的某些特性,比如温度、磁场的强度、原子的排列方式……看吧,问题又来了,这个矢量到底有多大?伯氏矢量的大小和铝的电子密切相关。
它和铝原子里的电子运动模式紧密挂钩。
铝的电子比较“机灵”,它们运动起来像是个小精灵,不停地在原子核周围晃悠。
当咱们加一个磁场进去,这些电子就开始受到磁场的“指挥”,它们的运动会有一定的规律性。
伯氏矢量就是用来量化这个规律的。
你可以把它想象成一个“力矩”,它的大小代表了磁场对铝电子的影响程度,方向则告诉你这些小家伙运动的方向。
那为什么我们要关心这个东西呢?听着好像有点儿枯燥对吧?但伯氏矢量的研究对咱们有着很大的意义。
你想啊,铝作为一种广泛应用的金属,它的导电性能、磁性、甚至温度变化时的行为,都和它内部原子的运动状态密切相关。
隆格楞次矢量的物理意义布隆格楞次向量(Bloch Wave Vector)是用来描述物质波动在物质晶格中的空间分布的一个重要的概念。
它是一种数量,表示波在晶格中传输的方向,描述了晶格能带的“结构”。
在实际情况中,由于晶格的存在,材料的特性取决于物质波的传播方向。
因此,了解布隆格楞次矢量的物理意义,对于研究材料的性能具有重要的意义。
布隆格楞次矢量的物理意义主要体现在四个方面:第一,它表示物质波动在晶格中的传播方向。
物质波动能在晶格中被完美叠加和平均分布,并以一定的特定波形在晶格间传播。
物质波在晶格中传播的方向取决于晶格的结构特征,晶体结构存在特定的传播方向,直接决定了物质波传播的路径,其方向由布隆格楞次矢量来表示。
第二,它表示晶体中物质波的波向。
对于晶格中的物质波,它的波向由它的静止矢量决定,而布隆格楞次矢量是物质波传播的量子态,只有它在晶格中的传播方向可以确定其物质波的波向,惯性动力学定律才能指导物质波在晶格中传播。
第三,它反映了晶体能带的“结构”。
能带是晶体中电子运动的波状,不同的能带实际上是由物质波共同形成的,布隆格楞次的数量是物质波传播的量子态,它反映了晶体能带的“结构”,即晶体能带在晶体中的波向及波数范围。
最后,它描述了晶体的散射行为。
由于布隆格楞次矢量能够反映晶体中物质波的波向,因此它也是一种定义晶体散射行为的最佳参数。
在反射、衍射和散射实验中,物质波会受到晶体特定波向和波数范围的局域结构的影响,因此可以去研究晶体的散射行为。
综上所述,布隆格楞次向量是反映晶体中物质波在晶格结构中传播方向,以及描述晶体能带结构和晶体的散射行为的重要参数。
它是定量学习和研究晶体物性的关键,对于更好地理解和提高晶体的性能,有着重要的意义。
柏氏矢量用来描述位错区域原子的畸变特征(包括畸变发生在什么晶向以及畸变有多大)的物理参量,称为柏氏矢量(Burgers vector)。
它是一个矢量,1939年由柏格斯(J.M.Burgers)率先提出。
3.2.3.1柏氏矢量的确定:
柏氏矢量可通过柏氏回路(Burgers circuit)来确定。
在含有位错的实际晶体中作一个包含位错发生畸变的回路,然后将这同样大小的回路置于理想晶体中,此时回路将不能封闭,需引一个额外的矢量b连接回路,才能使回路闭合,这个矢量b就是实际晶体中位错的柏氏矢量。
如图所示。
刃型位错柏氏矢量的确定
a)实际晶体b) 完整晶体
1. 右手法则
刃型位错的柏氏矢量与位错线垂直,其正负可用右手法则确定,如图3-22所示。
(通常先人为地规定位错线的方向,然后用右手食指表示位错线的方向,中指表示柏氏矢量的方向,当拇指向上是为正刃型位错,向下时为负刃型位错。
)
螺型位错的柏氏矢量与位错线平行,且规定柏氏矢量与位错线正向平行的为右旋;反向平行的为左旋。
2. 三种类型位错的矢量图解法,如图3-23所示。
3.2.3.2柏氏矢量的特征:
●用柏氏矢量可判断位错的类型。
柏氏矢量与位错线垂直者为刃型位错,平行者为螺型位错,既不垂直又不平行者为混合位错。
●柏氏矢量反映位错区域点阵畸变总累积的大小。
柏氏矢量越大,位错周围晶体畸变越严重。
●用柏氏矢量可以表示晶体滑移的方向和大小。
位错运动导致晶体滑移时,滑移量大小即柏氏矢量b,滑移方向即为柏氏矢量的方向。
●一条位错线具有唯一的柏氏矢量。
它与柏氏回路的大小和回路在位错线上的位置无关,位错在晶体中运动或改变方向时,其柏氏矢量不变。
●若位错可分解,则分解后各分位错的柏氏矢量之和等于原位错的柏氏矢量。
●位错可定义为柏氏矢量不为零的晶体缺陷,它具有连续性,不能中断于晶体内部。
其存在形态可形成一个闭合的位错环,或连接于其他位错,或终止在晶界,或露头于晶体表面。