模式识别聚类分析

化学模式识别在生药鉴别和质量评价中的应用摘要：化学模式识别是物以类聚,同类或相似的样本间的距离较近,不同类的/样本间的距离应较远。

这样可以根据各样本的距离或距离的函数来判别、分类,并利用分类的结果预报未知。

模式识别属于多变量数值分析方法,它是借助于计算机来揭示隐含于事物内部规律的一种综合技术，是用现代分离分析检测方法对中药材或药品样本中的有机或无机的药用化学成分进行检测,用化学计量学方法关联检测数据阵,确定可用于样品质量控制的模式,通过上述方法进行整体分析、分类和描述来对未知样本进行识别。

关键词:聚类分析法、主成分分析法、矩阵、空间模式识别(pattern recognition)是一门用机器代替人对模式即所研究的事物进行分析、描述、判断和识别的技术[1]。

它的中心任务就是要识别出某个样本与哪一种模式(样本)相同或相近,即在一定的度量和观测的基础上把待识别的模式划分到各自模式类中。

模式识别可分为基于统计学习理论的统计模式识别和基于语法的结构模式识别。

统计模式识别是目前最成熟也是应用最广泛的方法。

以完成识别过程的方式而论,模式识别又可分为两个系统:有监督学习系统和无监督学习系统。

有监督学习系统要运用一组已知其类别的样本进行训练(或学习)获得分类准则,再利用准则来判别未知模式所属的类别。

常用的方法有: SIMCA法(Simple classification algorithm,简单分类法)、Bayes判别、逐步判别分析(Step-wise discriminate analysis, STEPDA)、人工神经网络(Artificial neural networks,ANN)等。

而无监督学习系统则是把模式划分到目前为止仍然未知的类别中,即无须预先知道模式所属的类别。

其中最重要的一种就是聚类分析的方法。

如系统聚类分析(Hierarchical clustering analysis)、模糊聚类分析(Fuzzy clustering analysis)等。

模式识别中的聚类分析方法聚类分析是一种常用的机器学习方法，用于将大量数据分为不同的类别或群组，并在其中寻找共性和差异性。

在模式识别中，聚类分析可以帮助我们理解数据集中不同对象之间的关系，以及它们之间的相似性和差异性。

本文将介绍聚类分析的基本概念、算法和应用，以及一些实用的技巧和方法，以帮助读者更好地理解和应用这一方法。

一、聚类分析的基础概念在聚类分析中，我们通常会面对一个数据点集合，其特征被表示为$n$个$d$维向量$x_{i}=(x_{i1},x_{i2},…,x_{id})$。

聚类分析的目标是将这些数据点划分为$k$个不同的类别或群组$G_{1},G_{2},…,G_{k}$，并使得同一类别中的数据点相似性较高，不同类别之间的相似性较低。

为了完成这个任务，我们需要先定义一个相似性度量方法，用于计算数据点之间的距离或相似度。

常用的相似性度量方法包括欧式距离、余弦相似度、Jaccard相似度和曼哈顿距离等，具体选择哪一种方法取决于我们要研究的数据类型和应用要求。

定义了相似性度量方法后，我们可以使用聚类算法将数据点分成不同的类别。

聚类算法的主要分类包括层次聚类和基于中心点的聚类。

层次聚类是通过自下而上的方法将数据点归属到不同的类别中，以便于构建聚类树或聚类图。

基于中心点的聚类则是通过不断地计算每个数据点离其所属类别的中心点的距离来更新类别簇，直到收敛为止。

通常来说，基于中心点的聚类算法更快且更易于应用，因此被广泛应用于实际问题中。

二、聚类分析的主要算法1. K-means 聚类算法K-means 聚类算法是一种基于中心点的聚类算法，其核心思想是通过不断更新每个数据点所属的类别，同时更新该类别的中心点，直到找到最优的聚类结果。

具体而言，K-means 聚类算法首先需要预设$k$个初始的聚类中心点，然后计算每个数据点与这$k$个聚类中心的距离，并将其分配到最近的一个聚类中心点所代表的类别中。

完成初始聚类后，算法会重新计算每个类别的中心点，并根据新的中心点重新分配所有数据点，直到所有数据点都不再变换为止。

机器学习中的聚类分析方法机器学习中的聚类分析是一种数据挖掘技术，该技术可以将大量的数据集按照特定的规则进行分类和分组。

聚类分析主要用于数据分析、分类、数据挖掘和模式识别等领域，该技术的应用范围非常广泛，包括自然语言处理、图像识别、推荐系统等领域。

在聚类分析中，数据集合被分为不同的类别，每个类别都有相似的属性、特征或属性。

聚类分析方法可以通过设置聚类算法的参数来对数据进行分组，对于同一类别的数据，聚类算法能够产生一个类别标签。

聚类分析方法的优点在于能够将大量不同的数据进行有意义的分类，从而可以实现多种应用。

聚类分析方法的类型在机器学习中，聚类分析方法主要分为以下几种类型：1. 划分式聚类：这种方法通过将数据集分成互不重叠的子集来实现聚类。

在划分式聚类中，每个数据点只属于一个簇。

这种方法适合于数据集中每个数据点都属于同一个类别的情况。

划分式聚类算法包括K-Means算法等。

2. 层次式聚类：这种方法通过渐进地将数据点分成更多的子集来实现聚类。

在层次式聚类中，每个数据点都可以被分配到多个簇中。

这种方法适合于数据集中数据点属于多个类别的情况。

层次式聚类算法包括凝聚层次聚类、分裂式层次聚类等。

3. 密度式聚类：这种方法通过密度划分数据簇来实现聚类。

密度式聚类算法包括DBSCAN、OPTICS等。

4. 模型式聚类：这种方法通过使用统计学模型来实现聚类。

模型式聚类算法包括高斯混合模型等。

其中，划分式聚类和层次式聚类是常用的聚类分析方法。

K-Means聚类算法K-Means算法是目前应用最多的划分式聚类算法之一，其主要思想是将输入数据分成K个簇，每个簇有一个中心点，根据输入数据与各个簇的中心距离进行分类。

K-Means算法通过多次更新簇中心点和分类，来达到最终的聚类结果。

K-Means算法的优点在于其算法简单、时间复杂度较低，同时也适合于大规模数据和高维数据的处理。

但是，K-Means算法也存在着一些问题。

首先，初始点的随机性可能会对聚类结果产生较大的影响。

聚类分析方法及其应用条件扩展研究聚类分析是一种将数据根据其相似性进行自动分类的方法，具有广泛的应用领域，包括数据挖掘、模式识别、信息检索等。

本文将介绍聚类分析的基本概念和常用方法，并探讨其在不同应用场景下的扩展研究。

一、聚类分析基本概念和常用方法聚类分析是一种无监督学习的方法，它试图将数据集划分为若干个类别，使得同一类别内的数据相似性最大，不同类别之间的相似性最小。

聚类分析的基本概念包括距离度量和聚类准则。

1.1 距离度量距离度量是聚类分析的基础，常用的距离度量方法有欧氏距离、曼哈顿距离和闵可夫斯基距离等。

欧氏距离是最常用的距离度量方法，它基于向量空间中的欧氏距离定义。

曼哈顿距离是城市街区距离的度量方法，它在计算距离时只考虑了水平和垂直方向上的位移。

闵可夫斯基距离是欧氏距离和曼哈顿距离的一种推广，当参数取不同的值时可以得到不同的距离度量。

1.2 聚类准则聚类准则用于评估数据集划分的好坏程度，常用的聚类准则有最小平方误差准则、最大间隔准则和最大密度准则等。

最小平方误差准则试图将同一类别内的数据点尽可能的靠近，不同类别之间的距离尽可能的大。

最大间隔准则则是通过最大化同一类别内部的相似度，同时最小化不同类别之间的相似度来进行数据集划分。

最大密度准则是通过计算数据点的密度来进行聚类分析，将密度较大的数据点划分到同一类别中。

二、经典聚类分析方法经典聚类分析方法包括层次聚类分析和划分聚类分析，它们使用不同的算法来进行数据集的划分。

2.1 层次聚类分析层次聚类分析是一种自底向上或自顶向下的聚类方法，它根据数据点之间的相似性建立一个层次结构，从而得到不同层次的聚类结果。

自底向上的层次聚类方法将每个数据点作为一个初始聚类，然后通过计算两个聚类之间的相似度来合并聚类，直到达到聚类的最终结果。

自顶向下的层次聚类方法则是从一个包含所有数据点的初始聚类开始，然后通过分裂聚类来得到最终的聚类结果。

2.2 划分聚类分析划分聚类分析是一种将数据集划分为不相交的子集的方法，最常用的划分聚类算法是k-means算法。

模式识别试题及总结一、填空与选择填空（本题答案写在此试卷上，30分）1、模式识别系统的基本构成单元包括：模式采集、特征提取与选择和模式分类。

2、统计模式识别中描述模式的方法一般使用特真矢量；句法模式识别中模式描述方法一般有串、树、网。

3、聚类分析算法属于（1）；判别域代数界面方程法属于（3）。

（1）无监督分类 (2)有监督分类（3）统计模式识别方法（4）句法模式识别方法4、若描述模式的特征量为0-1二值特征量，则一般采用（4）进行相似性度量。

（1）距离测度（2）模糊测度（3）相似测度（4）匹配测度5、下列函数可以作为聚类分析中的准则函数的有（1）（3）（4）。

（1）（2） (3) (4)6、Fisher线性判别函数的求解过程是将N维特征矢量投影在（2）中进行。

（1）二维空间（2）一维空间（3）N-1维空间7、下列判别域界面方程法中只适用于线性可分情况的算法有（1）；线性可分、不可分都适用的有（3）。

（1）感知器算法（2）H-K算法（3）积累位势函数法8、下列四元组中满足文法定义的有（1）（2）（4）。

（1）({A, B}, {0, 1}, {A?01, A ? 0A1 , A ? 1A0 , B ? BA , B ? 0}, A) （2）({A}, {0, 1}, {A?0, A ? 0A}, A)（3）({S}, {a, b}, {S ? 00S, S ? 11S, S ? 00, S ? 11}, S)（4）({A}, {0, 1}, {A?01, A ? 0A1, A ? 1A0}, A)9、影响层次聚类算法结果的主要因素有（计算模式距离的测度、（聚类准则、类间距离门限、预定的类别数目））。

10、欧式距离具有（ 1、2 ）；马式距离具有（1、2、3、4 ）。

（1）平移不变性（2）旋转不变性（3）尺度缩放不变性（4）不受量纲影响的特性11、线性判别函数的正负和数值大小的几何意义是（正（负）表示样本点位于判别界面法向量指向的正（负）半空间中；绝对值正比于样本点到判别界面的距离。

如何进行分类与聚类分析分类与聚类分析是数据挖掘中常用的技术手段，通过对数据进行不同属性的划分和聚合，能够帮助我们洞察数据的内部规律和特征。

本文将介绍分类与聚类分析的基本概念和方法，并提供一些实际案例进行说明。

I. 分类分析分类分析是对数据进行归类的过程，将具有相似性质的数据归为一类。

分类分析的基本思想是通过特征提取和模式识别，将数据分为预先定义的类别，以便进一步理解和解释数据。

1. 数据准备在进行分类分析前，需要准备好适合分析的数据集。

数据集一般包含多个样本和多个属性，其中样本是指具体的数据实例，属性是指样本所具有的特征。

2. 特征选择特征选择是分类分析的重要步骤，其目的是从给定的属性中选择出最能代表数据特征的属性。

特征选择需要根据实际问题和数据集的特点来进行，通常可以采用统计学方法或信息论方法来评估属性的重要性。

3. 模型构建在分类分析中，需要选择适当的分类模型来对数据进行分类。

常见的分类模型包括决策树、朴素贝叶斯、支持向量机等。

模型的选择需要考虑数据的性质和问题的要求。

4. 分类效果评估在进行分类分析后，需要对分类结果进行评估。

常用的评估指标有准确率、召回率、精确率等。

评估结果可以反映分类模型的性能，并帮助我们判断模型的优劣。

II. 聚类分析聚类分析是对数据进行聚合的过程，将具有相似性质的数据聚为一类。

聚类分析的目的是发现数据的内部结构，揭示数据的潜在规律和关系。

1. 数据准备聚类分析前，需要准备好适合分析的数据集。

数据集包含多个样本和多个属性，其中样本是指具体的数据实例，属性是指样本所具有的特征。

2. 相似性度量在聚类分析中，需要选择合适的相似性度量来衡量数据之间的相似程度。

常用的相似性度量有欧氏距离、余弦相似度等。

3. 聚类算法聚类分析需要选择合适的聚类算法来对数据进行聚类。

常见的聚类算法有K均值聚类、层次聚类、密度聚类等。

选择聚类算法需要考虑数据的性质和问题的要求。

4. 聚类结果评估在进行聚类分析后，需要对聚类结果进行评估。

一、信息融合技术分类：多源信息融合技术分为假设检验型信息融合技术、滤波跟踪型信息融合技术、聚类分析型信息融合技术、模式识别型信息融合技术、人工智能型信息融合技术等。

1、假设检验型信息融合技术假设检验型信息融合技术是以统计假设检验原理为基础，信息融合中心选择某种最优化假设检验判决准则执行多传感器数据假设检验处理，获取综合相关结论。

2、滤波跟踪型信息融合技术滤波跟踪型信息融合技术是将卡尔曼滤波(或其他滤波)航迹相关技术由单一传感器扩展到多个传感器组成的探测网，用联合卡尔曼滤波相关算法执行多传感器滤波跟踪相关处理。

3、聚类分析型信息融合技术聚类分析型信息融合技术是以统计聚类分析或模糊聚类分析原理为基础，在多目标、多传感器大量观测数据样本的情况下，使来自同一目标的数据样本自然聚集、来自不同目标的数据样本自然隔离，从而实现多目标信息融合。

4、模式识别型信息融合技术模式识别型信息融合技术是以统计模式识别或模糊模式识别原理为基础，在通常的单一传感器模式识别准则基础上建立最小风险多目标多传感器模式识别判决准则，通过信息融合处理自然实现目标分类和识别。

5、人工智能信息融合技术人工智能信息融合技术将人工智能技术应用于多传感器信息融合，对于解决信息融合中的不精确、不确定信息有着很大优势，因此成为信息融合的发展方向。

智能融合方法可分为：基于专家系统的融合方法；基于神经网络的融合方法；基于生物基础的融合方法；基于模糊逻辑的融合方法等。

二、按融合判决方式分类：多源信息融合的融合判决方式分为硬判决方式和软判决方式。

所谓硬判决或软判决指的是数据处理活动中用于信号检测、目标识别的判决方式。

每个传感器内部或信息融合中心都既可选用硬判决方式，也可选用软判决方式。

1、硬判决方式硬判决方式设置有确定的预置判决门限。

只有当数据样本特征量达到或超过预置门限时，系统才做出判决断言；只有当系统做出了确定的断言时，系统才向更高层次系统传送”确定无疑”的判决结论。

模式识别摘要：本文简单介绍了模式识别，主要讲述了模式识别常用的方法：神经网络、模糊诊断、支持向量机、聚类分析的定义及各自有缺点。

关键字：模式识别；神经网络；模糊诊；、支持向量机；聚类分析ABSTRACT：This paper briefly introduced the pattern recognition, mainly tells the story of pattern recognition commonly used method: neural network and fuzzy diagnosis, support vector machine, clustering analysis of the definition and have their own shortcomings.Key words: Pattern recognition; Neural network; Fuzzy diagnosis; And support vector machine (SVM); Clustering analysis一、模式识别我们知道，被识对象都具有一些属性、状态或者特征。

而对象之间的差异也就表现在这些特征的差异上。

因此可以用对象的特征来表征对象。

另一方面，从结构来看，有些被识对象可以看作是由若干基本成分按一定的规则组合而成。

因此，可以用一些基本元素的某种组合来刻画对象。

广义地说，存在于时间和空间中可观察的物体，如果我们可以区别它们是否相似，都可以称之为模式。

模式所指的不是事物本身，而是从事物获得的信息，能够表征或刻画被识对象类属特征的信息模型成为对象的模式。

有了模式，对实体对象的识别就转化为对其模式的识别。

识别其实就是分类，即辨识或判别被识对象的类属。

模式识别就是确定一个样本的类别属性（模式类）的过程，即把某一样本归属于多个类型中的某个类型。

模式识别的三大任务：模式采集、特征提取和特征选择、类型判别。

针对聚类分析的具体描述摘要：本文简单介绍了模式识别中的聚类分析法的基本概念，各种聚类分析方法，及各种方法的具体应用，其中，重点讲述了层次聚类法和动态聚类法。

1. 聚类分析概述聚类分析又叫群分析、点群分析或者簇分析，是直接比较各事物之间的性质，将性质相近的归为一类，将性质差别较大的归入不同的类。

聚类分析方法根据分类对象的不同可以分为两类：一类是对样品所作的分类，即Q-型聚类，一类是对变量所作的分类，即R-型聚类。

聚类分析的基本思想是，对于位置类别的样本或变量，依据相应的定义把它们分为若干类，分类过程是一个逐步减少类别的过程，在每一个聚类层次，必须满足“类内差异小，类间差异大”原则，直至归为一类。

评价聚类效果的指标一般是方差，距离小的样品所组成的类方差较小。

2. 聚类分析的定义聚类分析是将样品或变量按照它们性质上的亲疏程度进行分类的多元统计分析方法。

进行聚类分析时，用来描述物品或变量的亲疏程度通常有两个途径，一个是把每个样品或变量看成是多维空间上的一个点，在多维坐标中，定义点与点，类与类之间的距离，用点与点间距离来描述作品或变量之间的亲疏程度；二是计算样品或变量的相似系数，用相似系数来描述样品或变量之间的亲疏程度。

3. 层次聚类（系统聚类）法3.1基本思想系统聚类分析的基本思想是，把n个样品看成p维（p个指标）空间的点，而把每个变量看成p维空间的坐标轴，根据空间上点与点的距离来进行分类。

3. 2系统聚类分析的一般步骤1) 对数据进行变换处理；2) 计算各样品之间的距离，并将距离最近的两个样品合并成一类；3) 选择并计算类与类之间的距离，并将距离最近的两类合并，如果累的个数大于1，则继续并类，直至所有样品归为一类为止；4) 最后绘制系统聚类谱系图，按不同的分类标准，得出不同的分类结果。

3.3常用层次聚类分析方法1）最短距离法聚类和之间的最短距离定义为（3-1）2）最长距离法聚类和之间的最长距离定义为（3-2）3）中间距离法设聚类到的距离分别为和，到的距离为，如图3.1所示，中间距离定义为（3-3）图3.1 中间距离法4）重心法从物理的观点看，若要用一个点表示一个类的空间位置，那么类的重心较为合理。

一、概念解释：监督模式识别与非监督模式识别 1.监督模式识别：有一个已知样本集（集合中每个样本的类别已知，）作为训练样本集，通过挖掘先验已知信息来指导设计分类器，这种情况下建立分类器的问题属于监督学习问题，称作监督模式识别。

2.非监督模式识别：没有已知类别标签的训练数据可用，通过挖掘样本中潜在的相似性分类。

这种学习过程称为非监督模式识别。

在统计中常被称作聚类，所得到的类别也称作聚类。

由于没有已知类别标签的训练数据，在没有额外信息的情况下，采用不同的方法或不同的假定可能得到不同的结果，聚类结果仅是数学上的划分，对应的实际问题要结合更多专业知识进行解释。

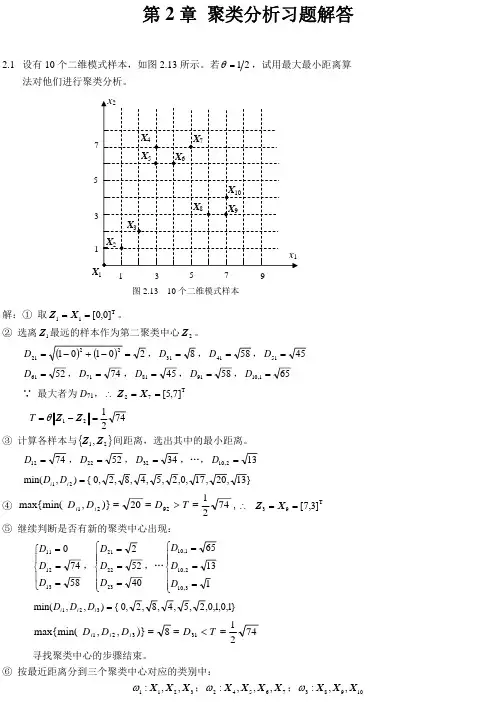
二、聚类分析的基本思想；C-均值动态聚类算法的思想及步骤。

1.聚类分析的基本思想：聚类分析为无监督分类。

1>假设：对象集客观存在着若干个自然类；每个自然类中个体的某些属性具有较强的相似性。

2>原理：将给定模式分成若干组，组内的模式是相似的；组间各模式差别较大。

3>方法：a.根据待分类模式的属性或特征的相似程度进行分类，相似的模式归为一类，不相似的模式划到不同的类中，将待分类的模式或集分成若干个互不重叠的子集。

b.定义适当的准则函数、运用有关的数学工具、或利用有关统计的概念和原理进行分类。

2.C-均值思想：1>条件及约定：设待分类模式的特征矢量集为{},,.....12x x x N ，类的数目C 是事先取定的。

2>算法思想：取定C 个类别、选取C 个初始聚类中心，按最少距离原则，将各模式分配到C 类中的某一类，之后不断地计算类心和调整各模式的类别，最终使各模式到其判属类别中心的距离平方之和最小。

3.原理步骤：a.任选c 个模式的特征矢量作为初始聚类中心：()()()00012,,.....,,k =0C Z Z Z 令。

b.将待分类模式的特征矢量集{},,.....12x x x N 中的模式，逐个按最小距离原则分化给c 类中的某一类，即若()()()min ,1,2,...,k k dd i N ij ilj ==⎡⎤⎢⎥⎣⎦,则()1x i k l ω∈+，式中，()k d ij表示xi 和()k j ω的中心()k Z j 的距离。

用户行为分析中的模式识别方法随着互联网的发展和普及，大量的数据不断被积累，其中蕴含着用户行为的信息。

通过对用户行为的分析和挖掘，可以发现很多有价值的信息，比如用户爱好、购买意向、活跃度等等。

而模式识别方法是用户行为分析的重要手段之一，可以对海量的用户数据进行分类、聚类、预测等操作，从而揭示出数据背后的规律和模式。

下面将介绍一些常见的模式识别方法及其应用。

一、聚类分析聚类分析是将一组数据分成多个类别（cluster）的方法，每个类别内的数据具有相似的特征，而不同类别之间的数据则具有较大的差异。

聚类分析的目的是在不事先知道类别的情况下，发现潜在的类别结构。

聚类分析通常有两种方法：基于距离的聚类和基于密度的聚类。

基于距离的聚类可以将数据点根据他们之间的距离分成不同的类别，而基于密度的聚类是区分数据点所处的密度区域。

聚类分析在电商领域的应用非常广泛，可以根据用户的购买行为、搜索行为等对用户进行分类，提供个性化的推荐和服务，从而提升用户满意度和粘性。

二、分类分析分类分析是将一组数据分为多个已知的类别（class）的方法，分类分析通常由两个步骤构成：建立分类模型和用模型对数据进行分类。

分类模型可以使用多种算法，如决策树、神经网络、朴素贝叶斯等。

分类分析的应用场景也非常广泛，例如通过对用户行为数据进行分类，可以识别出哪些用户属于流失用户、哪些用户属于高价值用户，以便采取针对性的策略来提升用户留存和增加用户价值。

三、关联规则挖掘关联规则挖掘是发现数据中蕴含的关联性的过程，通过发现事物之间的关联，可以从数据中推断出潜在的规律和模式。

关联规则挖掘通常包括两个步骤：频繁项集生成和关联规则产生。

频繁项集生成是指在数据集中发现频繁出现的项集，而关联规则产生则是从这些频繁项集中找出规律性的关联规则。

在电商领域，关联规则挖掘可以用来发现哪些商品经常被一起购买，从而提供以套餐为基础的促销策略。

四、时间序列分析时间序列分析是一种基于时间序列数据的分析方法，它研究的是同一变量在不同时间点上的表现，并且假设它们之间存在一定的因果关系。

聚类分析（英语：Cluster analysis，亦称为群集分析）是对于静态数据分析的一门技术，在许多领域受到广泛应用，包括机器学习，数据挖掘，模式识别，图像分析以及生物信息。

聚类是把相似的对象通过静态分类的方法分成不同的组别或者更多的子集（subset），这样让在同一个子集中的成员对象都有相似的一些属性，常见的包括在坐标系中更加短的空间距离等。

一般把数据聚类归纳为一种非监督式学习。

聚类类型数据聚类算法可以分为结构性或者分散性。

结构性算法利用以前成功使用过的聚类器进行分类，而分散型算法则是一次确定所有分类。

结构性算法可以从上至下或者从下至上双向进行计算。

从下至上算法从每个对象作为单独分类开始，不断融合其中相近的对象。

而从上至下算法则是把所有对象作为一个整体分类，然后逐渐分小。

分割式聚类算法，是一次性确定要产生的类别，这种算法也已应用于从下至上聚类算法。

基于密度的聚类算法，是为了挖掘有任意形状特性的类别而发明的。

此算法把一个类别视为数据集中大于某阈值的一个区域。

DBSCAN和OPTICS是两个典型的算法。

许多聚类算法在执行之前，需要指定从输入数据集中产生的分类个数。

除非事先准备好一个合适的值，否则必须决定一个大概值，关于这个问题已经有一些现成的技术。

距离测量在结构性聚类中，关键性的一步就是要选择测量的距离。

一个简单的测量就是使用曼哈顿距离，它相当于每个变量的绝对差值之和。

该名字的由来起源于在纽约市区测量街道之间的距离就是由人步行的步数来确定的。

一个更为常见的测量是欧式空间距离，他的算法是找到一个空间，来计算每个空间中点到原点的距离，然后对所有距离进行换算。

常用的几个距离计算方法：•欧式距离（2-norm距离）•曼哈顿距离（Manhattan distance, 1-norm距离）•infinity norm•马氏距离•余弦相似性•汉明距离结构性聚类在已经得到距离值之后，元素间可以被联系起来。

通过分离和融合可以构建一个结构。

数据分析中的模式识别和异常检测方法数据分析已经成为当今社会中不可或缺的重要工具，它可以被应用于各个领域，例如金融、医学、交通、能源等等。

而在进行数据分析的过程中，模式识别和异常检测方法则成为了常用的两种技术，因为它们可以帮助分析人员更加深入地了解数据的本质和规律。

下面我们将分别介绍这两种方法。

一、模式识别方法模式识别方法是一种用于分类和预测的技术，它的基本思想是将数据根据某种特定的标准分为不同的类别，或者通过数据中的分布规律来预测未来的趋势。

其中常用的方法有K-Means、K-NN、SVM、决策树等。

下面我们详细介绍其中的两种方法。

1.1 K-MeansK-Means是一种聚类算法，它主要是通过将数据分为不同的组来发现潜在的模式。

这种算法首先需要确定聚类的数量，然后将数据中的每个点分配到最近的聚类中心，然后重新计算每个聚类中心的位置，重复以上步骤，直到找到最佳的聚类中心和聚类数量。

K-Means的优点是运算速度快，可以处理大量的数据，并且可以将数据有效地划分为不同的类别。

缺点是对初值敏感，需要多次运算来寻找最佳的聚类中心，而且聚类数量需要提前确定。

1.2 SVMSVM（Support Vector Machine）是一种具有二分类和多分类能力的监督学习算法，它可以通过寻找最优的超平面来对数据进行分类。

在SVM中，数据被映射到高维空间，然后用一个超平面将不同的类别分开，从而实现分类的目的。

SVM的优点是可以处理线性和非线性问题，并且在处理高维数据时效果较好。

另外，在训练过程中可以调整惩罚参数和核函数等参数来获得更好的分类效果。

缺点是对数据中的异常点比较敏感，对于数据量较大的情况可能存在运算速度较慢的问题。

二、异常检测方法异常检测方法是一种通过分析数据中的偏差和异常值来识别可能存在的异常情况的技术。

常见的方法有统计学方法、机器学习方法和地理信息系统方法等。

下面我们简要介绍其中的两种方法。

2.1 统计学方法统计学方法是一种使用统计模型来识别异常值的方法。