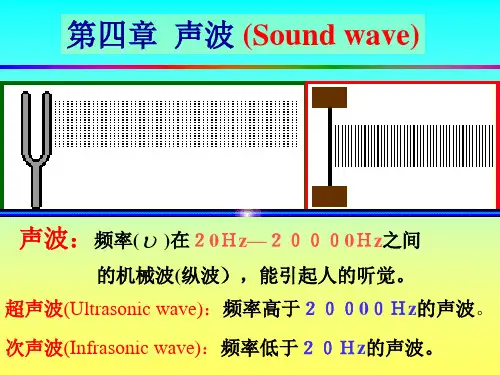
第4章 声波3

第四章 海洋中的声传播理论水声传播常用的方法：波动理论（简正波方法）——研究声信号的振幅和相位在声场中的变化；射线理论（射线声学）——研究声场中声强随射线束的变化，它是近似处理方法，且适用于高频，但它能有效、清晰地解决海洋中地声场问题。

4.1 波动方程和定解条件1、波动方程当介质声学特性是空间坐标的函数，则可得小振幅波的运动方程、连续性方程和状态方程：p t u -∇=∂∂ρ 0=⋅∇+∂∂u tρρρd c dp 2= 状态方程可写为：tc t p ∂∂=∂∂ρ2由状态方程和连续性方程可得：012=⋅∇+∂∂u tp c ρ 利用运动方程从上式中消去u可得0112222=∇⋅∇-∂∂-∇ρρp tp c p当介质密度是空间坐标的函数时，波动方程的形式和密度均匀介质中波动方程的形式不同。

引入新的从变量：ρϕp=，则可得0432********=⎥⎥⎦⎤⎢⎢⎣⎡⎪⎪⎭⎫ ⎝⎛∇-∇+∂∂-∇ρρρρϕϕt c 对于简谐波，222ω-=∂∂t ，则上式可写为：()0,,22=+∇ϕϕz y x K式中，2224321⎪⎪⎭⎫⎝⎛∇-∇+=ρρρρk K 。

ϕ不是声场势函数，K 也不是波数。

在海水中，与声速相比密度变化很小，可将其视为常数，则()z y x c k K ,,ω==，于是()0,,22=+∇ϕϕz y x k ()0,,22=+∇p z y x k p如果介质中有外力作用F，例如有声源情况，则有()ρϕϕFz y x K ⋅∇=+∇,,22在密度等于常数时，有()ρϕϕFz y x k ⋅∇=+∇,,22()F p z y x k p⋅∇=+∇,,22上述赫姆霍茨方程是变系数的偏微分方程——泛定方程。

2、定解条件满足物理问题的具体条件——定解条件。

物理量在介质边界上必须满足的条件。

（1）绝对软边界绝对软边界条件：声压为零界面方程表示为()t y x z ,,η=，()()0,,,,,==t y x z t y x p ηη——不平整海面 也称为第一类齐次边界条件如果已知边界面上的压力分布，则()()s t y x z p t y x p ==,,,,,ηη，称为第一类非齐次边界条件。

八年级第4章物理知识点
在八年级的第4章中，我们学习了物理方面的知识。

这些知识点可以让我们更好地理解物理学的基本规律，为将来的学习打下坚实的基础。

以下是本章的几个重要知识点：
1. 声音的产生
声音是由物体振动产生的，也就是说，当物体振动时，周围的空气密度也随之变化，形成了声波。

这些振动会以一定的频率传播，我们所听到的声音的音高与这些频率有关。

2. 声的特性
声音在传播过程中具有一些特殊的物理特性，例如声波的振动方向与振动方向相同，声音的速度随着媒介的变化而变化，音量与声波的振幅有关等等。

3. 火的产生
火的产生是物理学中一个很基本的问题。

我们知道，火需要氧气、燃料和一定的温度才能产生。

当这三个条件都满足时，就会
产生火焰。

在物理学中，火的产生可以从化学反应角度来加以理解。

4. 感应电流
感应电流是指当电磁场线穿过一定面积时，在这个面积内就会
产生感应电流的现象。

这种电流可以用来实现电磁感应、发电等
重要应用。

在实际应用中，感应电流被广泛用于生产和科研领域。

5. 气体压强及其应用
气体压强是指气体分子对物体单位面积施加的压力。

气体压强
的大小受到气体分子总数、气体温度等因素的影响。

在实际生活中，我们可以用气体压强来进行一些测量或者进行压力的调节。

以上是本章中的几个重要知识点。

这些知识可以帮助我们更好
地理解物理学中常见问题的原理和规律，同时也能够启发我们进
行创新和实践应用。

第四章 海洋中的声传播理论水声传播常用的方法：波动理论（简正波方法）——研究声信号的振幅和相位在声场中的变化；射线理论（射线声学）——研究声场中声强随射线束的变化，它是近似处理方法，且适用于高频，但它能有效、清晰地解决海洋中地声场问题。

4.1 波动方程和定解条件1、波动方程当介质声学特性是空间坐标的函数，则可得小振幅波的运动方程、连续性方程和状态方程：p t u -∇=∂∂ρ 0=⋅∇+∂∂u tρρρd c dp 2= 状态方程可写为：tc t p ∂∂=∂∂ρ2由状态方程和连续性方程可得：012=⋅∇+∂∂u tp c ρ 利用运动方程从上式中消去u可得0112222=∇⋅∇-∂∂-∇ρρp tp c p当介质密度是空间坐标的函数时，波动方程的形式和密度均匀介质中波动方程的形式不同。

引入新的从变量：ρϕp=，则可得0432********=⎥⎥⎦⎤⎢⎢⎣⎡⎪⎪⎭⎫ ⎝⎛∇-∇+∂∂-∇ρρρρϕϕt c 对于简谐波，222ω-=∂∂t ，则上式可写为：()0,,22=+∇ϕϕz y x K式中，2224321⎪⎪⎭⎫⎝⎛∇-∇+=ρρρρk K 。

ϕ不是声场势函数，K 也不是波数。

在海水中，与声速相比密度变化很小，可将其视为常数，则()z y x c k K ,,ω==，于是()0,,22=+∇ϕϕz y x k ()0,,22=+∇p z y x k p如果介质中有外力作用F，例如有声源情况，则有()ρϕϕFz y x K ⋅∇=+∇,,22在密度等于常数时，有()ρϕϕFz y x k ⋅∇=+∇,,22()F p z y x k p⋅∇=+∇,,22上述赫姆霍茨方程是变系数的偏微分方程——泛定方程。

2、定解条件满足物理问题的具体条件——定解条件。

物理量在介质边界上必须满足的条件。

（1）绝对软边界绝对软边界条件：声压为零界面方程表示为()t y x z ,,η=，()()0,,,,,==t y x z t y x p ηη——不平整海面 也称为第一类齐次边界条件如果已知边界面上的压力分布，则()()s t y x z p t y x p ==,,,,,ηη，称为第一类非齐次边界条件。

雷达原理简介首先，大家必须先了解雷达的基本原理，因为雷达仍是目前用来侦测移动物体最普遍的方法．雷达英文为RADAR,是Radio Detection And Ranging的缩写．所有利用雷达波来侦测移动物体速度的原理，其理论基础皆源自于“多谱勒效应”,其应该也是一般常见的多谱勒雷达(Doppler Radar），此原理是在19世纪一位澳地利物理学家所发现的物理现像，后来世人为了纪念他的贡献，就以他的名字来为该原理命名．都卜勒的理论基础为时间．波是由频率及振幅所构成，而无线电波是随着波而前进的．当无线电波在行进的过程中，碰到物体时,该无线电波会被反弹，而且其反弹回来的波，其频率及振幅都会随着所碰到的物体的移动状态而改变．若无线电波所碰到的物体是固定不动的，那么所反弹回来的无线电波其频率是不会改变的．然而，若物体是朝着无线电线发射的方向前进时，此时所反弹回来的无线电波会被压缩，因此该电波的率频会随之增加；反之，若物体是朝着远离无线电波方向行进时,则反弹回来的无线电波，其频率则会随之减小．速度侦测装置（即台湾警方所使用的测速雷达)所应用的原理，就是可以侦测到发射出现的无线电波,及反弹回来的无浅电波其间的频率变化．由这两个不同频率的差值,便可以依特定的比例关系，而计算是该波所碰撞到物体的速度．当然，此种速度侦测装置可以将所侦测到的速度，转换为「公里/小时」或是「英哩/小时」．也许大家还是无法体会什么是「都卜勒效应」，但每个人在日常生活中应该都有「听」过「都卜勒效应」．例如：当火车鸣笛或救护车的警报声一直朝着你接近时，会发现声音会一直在变化,这就是所谓的「都卜勒效应」，此例子是生活中最常见的例子，因为当声波一直朝着你接近时，该声波的频率会一直增加，所以听到的声音才会一直变．这跟测速雷达所用到的原理是一样的,只不过测速雷达所使用的不是声波，而是无线电波．由于警方的测速雷达总是侦测到一个较强的反单电波后，才决定该移动物体(车子)的速度;而通常体积较大的物体其反弹的电波也较强；另外，离发射电波较近的物体，其所反弹的电波也会较强．根据这个原理，若有两辆大小相同的车子，同样都是超速时，测速雷达只会侦测到开在较前面车子的速度；若有一辆未超速的大卡车开在前方，而另一辆已超速的小客车开在后方时，测速雷达是无法侦测出该小客车已超速，除非该小客车已经超越了大卡车而继续超速．这告诉我们,利用雷达波来侦测车速时,是无法在车阵中，侦测到特定车辆的速度，而只能侦测到开在车阵最前面，且体积较大的车子的速度．雷达（radar)原是“无线电探测与定位”的英文缩写。

北师大版八年级物理上册导学案第4章《声现象》第四章声现象第一节声音的产生与传播【学习目标】1．通过观察和实验初步认识声音产生的条件。

知道声音是由物体振动发生的。

2．知道声音传播需要介质。

声音在不同介质中传播的速度不同。

【重点与难点】1．声音的产生和传播的条件2．声音在不同介质中的传播速度不同。

3．解释一些声现象。

【设问导读】1．观察与思考在一次风较大的时候，观察旗杆上的国旗，当你听到国旗在风中发出“噼啪噼啪”的声音的时候，你可以看到国旗在不停地_____________；当风停了以后，国旗不再发声，这时国旗在旗杆上不再________。

2．动手做一做横线上要求:使刻度尺2/3伸出桌边,一只手将其另1/3紧压在桌边上,另一只手拨动伸出端,观察尺子①能听到声音吗此时尺子处于什么状态②当尺子停止振动的时候,还能听到声音吗结论:声音是由产生的,振动停止,物体发声.3．先实验，再思考，然后填空①一个同学把耳朵贴在桌子一端，另一个同学轻敲桌子另一端，能听到声音吗？②玻璃缸中盛有金鱼，用细棍轻轻敲击鱼缸上沿，金鱼还呆在原地吗？③正播放音乐的录音机，离开一段距离欣赏音乐，能听到吗？结论：声音可以在、和中传播。

4．仔细观察并感受实验，思考后回答问题①在玻璃罩内放一个小电铃，接通电源，此时你能听到电铃声吗？②用抽气机抽取罩内的空气，在抽气的过程中，你听到铃声有什么变化？③猜想：如果把钟罩中的空气完全抽出，还能听到声音吗？结论：声音的传播需要，不能传播声音。

5．声传播的快慢用描述，15℃时空气中的声速是声速大小跟有关,还跟有关,一般情况下,中的声速最大(填“固体”、“液体”、“气体”)【自学检测】1．声音是由物体的________产生的，_________停止，声音就消失。

2．“风在吼,马在叫,黄河在咆哮”分别是由、、的振动而发出声音的。

3.声音靠_______传播的，______、______、______都是能传播声音的介质，由于_______中什么都没有，所以它不能传声。

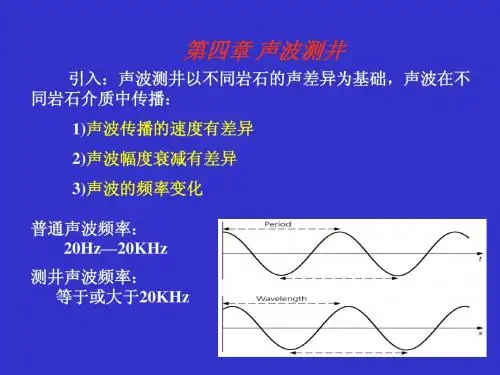
第四章声波的衰减§4.1概述到目前为止，我们讨论的声波一直是在理想介质中传播，即声波在传播过程中不存在任何形式的能量耗损。

实际上，严格的理想介质是不存在的，声波在介质中传播的过程总会伴随不同程度、不同形式的能量损耗，声衰减就是声波在介质中传播时其强度随传播距离的增加而逐渐减弱的现象。

声衰减具体表现主要有：随着声波在介质中传播距离的增加，声波动的振幅减小；声强或（平均）声能密度下降；色（频）散或声速变化等，其实色（频）散程度本身就反映声传播能耗的大小。

声波衰减的程度不仅与声波动的物理量（如频率、波矢等）有关，还与介质的特性（如均匀程度、完整程度、连续程度、介质微观粒子的质量密度和弹性性质等）密切相关。

同时还严重依赖声波长与介质内不均匀区域尺度的相对大小。

根据引起声衰减的原因或微观机制的不同，可以把声衰减划分为①几何衰减；②散射衰减；③吸收衰减。

几何衰减主要考虑声波传播中因波阵面的面积扩大而导致的声强（或声能密度）减弱。

它仅取决于声源辐射的波形及声束状况，而与介质特性无关，如球面波的声强反比于传播距离的平方。

声波的扩散衰减因其不符合指数衰减规律而无法纳入衰减系数中，因此在讨论与介质特性相关的声波衰减问题时，通常不考虑扩散衰减。

对扩散衰减的分析只能根据具体波型及其相应的指向特性单独来进行估算。

另外从能量的角度看，扩散衰减过程声源辐射声波的总能量并未变化，只不过因声扰动体积的扩大而使声能密度减小，即使在理想介质中，扩散衰减也照样可以发生。

散射衰减是指声波在介质中传播时，因碰到由另外一种介质组成的障碍物而使部分声波偏离原方向，从而导致原方向声波减弱的现象。

因此广义的散射可以认为是声传播过程中，由于遇到各种散射体而发生的反射、折射和衍射的总效应。

所谓的散射波是指在声传播方向有散射时实际接收到的波与假设无散射时应收到的波之差。

散射衰减不仅与介质的性质、状况有关，还与障碍物的性质、形状、尺寸、分布和数量有关。