SAS讲义 第三十四课非线性回归分析
- 格式：doc
- 大小：386.00 KB
- 文档页数：10
下载文档原格式
合集下载
《非线性回归分析》课件
• 常用的过滤方法包括皮 尔逊相关系数、方差分 析和卡方检验等。
封装式
• 基于模型的错误率和复 杂性进行特征选择。
• 常用的封装方法包括递 归特征消除法和遗传算 法等。
嵌入式
• 特征选择和模型训练同 时进行。
• 与算法结合在一起的特 征选择方法，例如正则 化（Lasso、Ridge）。
数据处理方法：缺失值填充、异常值 处理等
1
网格搜索
通过预定义的参数空间中的方格进行搜
随机搜索
2
索。
在预定义的参数空间中进行随机搜索。
3
贝叶斯调参
使用贝叶斯优化方法对超参数进行优化。
集成学习在非线性回归中的应用
集成学习是一种将若干个基学习器集成在一起以获得更好分类效果的方法，也可以用于非线性回归建模中。
1 堆叠
使用多层模型来组成一个 超级学习器，每个模型继 承前一模型的输出做为自 己的输入。
不可避免地存在数据缺失、异常值等问题，需要使用相应的方法对其进行处理。这是非线性回归 分析中至关重要的一环。
1 缺失值填充
常见的方法包括插值法、代入法和主成分分析等。
2 异常值处理
常见的方法包括删除、截尾、平滑等。
3 特征缩放和标准化
为了提高模型的计算速度和准确性，需要对特征进行缩放和标准化。
偏差-方差平衡与模型复杂度
一种广泛用于图像识别和计算机 视觉领域的神经网络。
循环神经网络
一种用于处理序列数据的神经网 络，如自然语言处理。
sklearn库在非线性回归中的应用
scikit-learn是Python中最受欢迎的机器学习库之一，可以用于非线性回归的建模、评估和调参。
1 模型建立
scikit-learn提供各种非线 性回归算法的实现，如 KNN回归、决策树回归和 支持向量机回归等。
封装式
• 基于模型的错误率和复 杂性进行特征选择。
• 常用的封装方法包括递 归特征消除法和遗传算 法等。
嵌入式
• 特征选择和模型训练同 时进行。
• 与算法结合在一起的特 征选择方法，例如正则 化（Lasso、Ridge）。
数据处理方法：缺失值填充、异常值 处理等
1
网格搜索
通过预定义的参数空间中的方格进行搜
随机搜索
2
索。
在预定义的参数空间中进行随机搜索。
3
贝叶斯调参
使用贝叶斯优化方法对超参数进行优化。
集成学习在非线性回归中的应用
集成学习是一种将若干个基学习器集成在一起以获得更好分类效果的方法，也可以用于非线性回归建模中。
1 堆叠
使用多层模型来组成一个 超级学习器，每个模型继 承前一模型的输出做为自 己的输入。
不可避免地存在数据缺失、异常值等问题，需要使用相应的方法对其进行处理。这是非线性回归 分析中至关重要的一环。
1 缺失值填充
常见的方法包括插值法、代入法和主成分分析等。
2 异常值处理
常见的方法包括删除、截尾、平滑等。
3 特征缩放和标准化
为了提高模型的计算速度和准确性，需要对特征进行缩放和标准化。
偏差-方差平衡与模型复杂度
一种广泛用于图像识别和计算机 视觉领域的神经网络。
循环神经网络
一种用于处理序列数据的神经网 络，如自然语言处理。
sklearn库在非线性回归中的应用
scikit-learn是Python中最受欢迎的机器学习库之一，可以用于非线性回归的建模、评估和调参。
1 模型建立
scikit-learn提供各种非线 性回归算法的实现，如 KNN回归、决策树回归和 支持向量机回归等。
SPSS—非线性回归（模型表达式）案例解析
SPSS—非线性回归（模型表达式）案例解析SPSS—非线性回归(模型表达式)案例解析2011-11-16 10:56由简单到复杂，人生有下坡就必有上坡，有低潮就必有高潮的迭起，随着SPSS 的深入学习，已经逐渐开始走向复杂，今天跟大家交流一下，SPSS非线性回归，希望大家能够指点一二！非线性回归过程是用来建立因变量与一组自变量之间的非线性关系，它不像线性模型那样有众多的假设条件，可以在自变量和因变量之间建立任何形式的模型非线性，能够通过变量转换成为线性模型——称之为本质线性模型，转换后的模型，用线性回归的方式处理转换后的模型，有的非线性模型并不能够通过变量转换为线性模型，我们称之为：本质非线性模型还是以“销售量”和“广告费用”这个样本为例，进行研究，前面已经研究得出：“二次曲线模型”比“线性模型”能够更好的拟合“销售量随着广告费用的增加而呈现的趋势变化”，那么“二次曲线”会不会是最佳模型呢？答案是否定的，因为“非线性模型”能够更好的拟合“销售量随着广告费用的增加而呈现的变化趋势” 下面我们开始研究：第一步：非线性模型那么多，我们应该选择“哪一个模型呢？”1：绘制图形，根据图形的变化趋势结合自己的经验判断，选择合适的模型点击“图形”—图表构建程序—进入如下所示界面：点击确定按钮，得到如下结果：放眼望去, 图形的变化趋势，其实是一条曲线，这条曲线更倾向于"S" 型曲线，我们来验证一下，看“二次曲线”和“S曲线”相比，两者哪一个的拟合度更高！点击“分析—回归—曲线估计——进入如下界面在“模型”选项中，勾选”二次项“和”S"两个模型，点击确定，得到如下结果：通过“二次”和“S“ 两个模型的对比，可以看出S 模型的拟合度明显高于“二次”模型的拟合度（0.912 >0.900）不过，几乎接近接着，我们采用S 模型，得到如下所示的结果：结果分析：1：从ANOVA表中可以看出：总体误差= 回归平方和+ 残差平方和（共计：0.782）F统计量为（240.216）显著性SIG为（0.000）由于0.000<0.01 （所以具备显著性，方差齐性相等）2：从“系数”表中可以看出：在未标准化的情况下，系数为（-0.986）常数项为2.672所以S 型曲线的表达式为：Y（销售量）=e^(b0+b1/t) = e^(2.672-0.986/广告费用）当数据通过标准化处理后，常数项被剔除了，所以标准化的S型表达式为：Y(销售量） = e^(-0.957/广告费用）下面，我们直接采用“非线性”模型来进行操作第一步：确定“非线性模型”从绘图中可以看出：广告费用在1千万——4千多万的时候，销售量增加的跨度较大，当广告费用超过“4千多万"的时候，增加幅度较小，在达到6千多万”达到顶峰，之后呈现下降趋势。
SAS学习系列25.-非线性回归
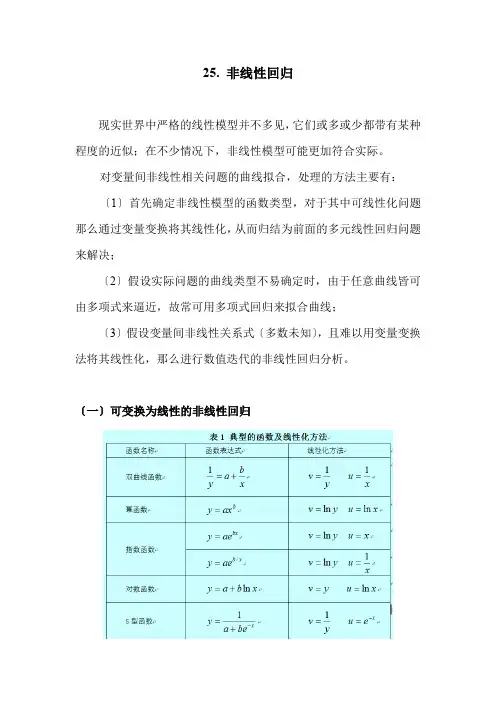
25. 非线性回归现实世界中严格的线性模型并不多见，它们或多或少都带有某种程度的近似；在不少情况下，非线性模型可能更加符合实际。
对变量间非线性相关问题的曲线拟合，处理的方法主要有：〔1〕首先确定非线性模型的函数类型，对于其中可线性化问题那么通过变量变换将其线性化，从而归结为前面的多元线性回归问题来解决；〔2〕假设实际问题的曲线类型不易确定时，由于任意曲线皆可由多项式来逼近，故常可用多项式回归来拟合曲线；〔3〕假设变量间非线性关系式〔多数未知〕，且难以用变量变换法将其线性化，那么进行数值迭代的非线性回归分析。
〔一〕可变换为线性的非线性回归在很多场合，可以对非线性模型进行线性化处理，尤其是可变换为线性的非线性回归，运用最小二乘法进行推断，对线性化后的线性模型，可以应用REG过程步进行计算。
例1 有实验数据如下：试分别采用指数回归〔y =ae bx〕方法进行回归分析。
代码：data exam25_1;input x y;cards;1.1 109.951.2 40.451.3 20.091.4 24.531.5 11.021.6 7.391.7 4.951.82.721.9 1.822 1.492.1 0.822.2 0.32.3 0.22.4 0.22;run;proc sgplot data = exam25_1;scatter x = x y = y;run;proc corr data = exam25_1;var x y;run;data new1;set exam25_1;v = log(y);run;proc sgplot data = new1;scatter x = x y = v;title'变量代换后数据';run;proc reg data = new1;var x v;model v = x;print cli;title'残差图';plot residual. * predicted.;run;data new2;set exam25_1;y1 = 14530.28*exp(-4.73895*x);run;proc gplot data = new2;plot y*x=1 y1*x=2 /overlay;symbol v=dot i=none cv=red;symbol2i=sm color=blue;title'指数回归图';运行结果：程序说明：〔1〕调整后的R 2=0.9831，说明拟合程度很好；F 检验的P 值=0.0001<α=0.05，拒绝原假设，故直线回归的斜率不为0；〔2〕将线性回归系数代入，得到原回归方程y =14530.28*e −4.73895x〔3〕残差图趋势，符合残差随机正态分布的假设〔不带其它明显趋势〕。
spss-非线性回归分析
实验三非线性回归分析（2学时）一、实验重点掌握非线性回归分析的方法。
二、实验难点模型的选择及对SPSS软件的输出结果进行分析和整理。
三、实验举例例1、对GDP（国内生产总值）的拟合。
选取GDP指标为因变量，单位为亿元，拟合GDP关于时间t的趋势曲线。
以1981年为基准年，取值为t=1,1998年t=18,1991-1998年的数据如下：解：分析过程（一）画散点图图3.1：Y 与t 的散点图图3.2：Ln Y 与t 的散点图（二）根据画散点图，及经济背景可选用模型 复合函数：01t y b b = （也称增长模型或半对数模型）同时，做简单线性回归 01y b b t =+ 以作比较。
（三）模型求解直接用SPSS 软件的Curve Estimation 命令计算。
（也可以用线性化的方法求解，结果基本一致。
） 运行结果如下：（四）结果分析线性回归方程：2ˆ133754417.520.856y t R =-+=复合函数回归方程：ˆ3603.06(1.1924)t y= ………（*）2ˆln 8.190.1760.992y t R =+=注意：不能直接比较两模型的拟合优度，需要对复合函数模型处理，利用(*)式，得到复合函数的残差，计算该模型的残差平方和RSS=2.1696×108 ，并计算y 的离差平方和TSS=1.1×1010 ，得到非线性回归的相关指数82102.169610110.981.110RSS R TSS ⨯=-=-≈⨯ 由于该相关指数大于线性回归的拟合优度，所以可以判断复合函数模型比线性回归模型要好。
例2 、一位药物学家是用下面的非线性模型对药物反应拟合回归模型1021()i i c i c y c u c =-++ 其中，自变量x 为药剂量，用级别表示； 因变量y 为药物反应程度，用百分数表示。
三个参数c 0 ,c 1 ,c 2都是非负的, c 0 的上限是100%，三个参数的初始值取为c 0 =100,c 1=5 ,c 2=4.8.测得9个数据如下表：解：分析过程：（一）画散点图从图形上看，y 与x 确实呈非线性关系！ （二）模型求解用SPSS 软件的Nonlinear 命令计算，具体操作如下： （1）建立数据集；（2）在数据窗口点击：Analyze → Regression → Nonlinear …,出现窗口在将y 点入Dependent 框中，在Model Expression 框中输入表达式：c0-c0/(1+(x/c2)**c1)（3） 点击Parametere …, 出现下图：在Name 框中输入: c0Starting Value 框中输入：100点击add,即可得到参数c0的初始赋值，类似的方法可以得到c1和c2参数的初始赋值，Continue 。
《非线性回归》课件
灵活性高
非线性回归模型形式多样，可以根据 实际数据和问题选择合适的模型，能 够更好地适应数据变化。
解释性强
非线性回归模型可以提供直观和易于 理解的解释结果，有助于更好地理解 数据和现象。
预测准确
非线性回归模型在某些情况下可以提 供更准确的预测结果，尤其是在数据 存在非线性关系的情况下。
缺点
模型选择主观性
势。
政策制定依据
政府和决策者可以利用非线性回归模型来评估不同政策方案的影响，从而制定更符合实 际情况的政策。例如，通过分析税收政策和经济增长之间的关系，可以制定更合理的税
收政策。
生物学领域
生态学研究
在生态学研究中，非线性回归模型被广 泛应用于分析物种数量变化、种群动态 和生态系统稳定性等方面。通过建立非 线性回归模型，可以揭示生态系统中物 种之间的相互作用和环境因素对种群变 化的影响。
模型诊断与检验
诊断图
通过绘制诊断图，可以直观地观察模型是否满足回归分析的假设条件，如线性关系、误差同方差性等 。
显著性检验
通过显著性检验，如F检验、t检验等，可以检验模型中各个参数的显著性水平，从而判断模型是否具 有统计意义。
04
非线性回归在实践中的应用
经济学领域
描述经济现象
非线性回归模型可以用来描述和解释经济现象，例如消费行为、投资回报、经济增长等 。通过建立非线性回归模型，可以分析影响经济指标的各种因素，并预测未来的发展趋
VS
生物医学研究
在生物医学研究中，非线性回归模型被用 于分析药物疗效、疾病传播和生理过程等 方面。例如，通过分析药物浓度与治疗效 果之间的关系，可以制定更有效的治疗方 案。
医学领域
流行病学研究
在流行病学研究中，非线性回归模型被用于 分析疾病发病率和死亡率与各种因素之间的 关系。通过建立非线性回归模型，可以揭示 环境因素、生活方式和遗传因素对健康的影 响。
《非线性回归》课件
• 金融市场预测 • 生物医学领域 • 工业控制 展示非线性回归在实际领域中的应用案例，并探索其作用和贡献。
挑战与未来发展趋势
• 数据收集和质量 • 参数估计和模型拟合 • 算法选择和性能评估 总结当前非线性回归面临的挑战，并展望其未来发展的趋势和应用前景。
3
Dropout
解释dropout技术如何防止过拟合，并提升模型的泛化能力。
4
Early Stopping
介绍early stopping方法来优化非线性回归模型的训练过程。
实例分析：Pytho n 实现
通过Python编程语言示例，演示如何使用非线性回归模型来解决实际问题。
非线性回归的应用案例
指数回归
1 背景
探索指数回归模型在描述 增长趋势时的优势。
2 应用
介绍指数回归在经济、生 物、市场等领域的实际应 用案例。
3 模型拟合
讨论如何通过最小二乘法 获取指数回归模型的参数。
对数回归
数学基础
介绍对数函数和对数回归模型的 数学原理。
金Байду номын сангаас市场预测
探索对数回归在金融市场预测中 的应用案例。
生物医学领域
非线性回归
探索非线性回归的概念、应用场景和解决方案。比较线性回归与非线性回归 的区别，并介绍求解非线性回归模型的最小二乘法。
多项式回归
1
简介
利用多项式函数逼近非线性关系，探索多项式回归的应用和优缺点。
2
示例
通过案例研究，展示如何使用多项式回归模型来拟合实际数据。
3
拟合度
介绍如何选择合适的多项式阶数以获得最佳拟合度。
展示对数回归在生物医学领域中 用于研究和分析的实际应用。
挑战与未来发展趋势
• 数据收集和质量 • 参数估计和模型拟合 • 算法选择和性能评估 总结当前非线性回归面临的挑战，并展望其未来发展的趋势和应用前景。
3
Dropout
解释dropout技术如何防止过拟合，并提升模型的泛化能力。
4
Early Stopping
介绍early stopping方法来优化非线性回归模型的训练过程。
实例分析：Pytho n 实现
通过Python编程语言示例，演示如何使用非线性回归模型来解决实际问题。
非线性回归的应用案例
指数回归
1 背景
探索指数回归模型在描述 增长趋势时的优势。
2 应用
介绍指数回归在经济、生 物、市场等领域的实际应 用案例。
3 模型拟合
讨论如何通过最小二乘法 获取指数回归模型的参数。
对数回归
数学基础
介绍对数函数和对数回归模型的 数学原理。
金Байду номын сангаас市场预测
探索对数回归在金融市场预测中 的应用案例。
生物医学领域
非线性回归
探索非线性回归的概念、应用场景和解决方案。比较线性回归与非线性回归 的区别，并介绍求解非线性回归模型的最小二乘法。
多项式回归
1
简介
利用多项式函数逼近非线性关系，探索多项式回归的应用和优缺点。
2
示例
通过案例研究，展示如何使用多项式回归模型来拟合实际数据。
3
拟合度
介绍如何选择合适的多项式阶数以获得最佳拟合度。
展示对数回归在生物医学领域中 用于研究和分析的实际应用。
数据预测—非线性回归
数据预测—非线性回归非线性回归是一种在数据预测中常用的方法，它适用于无法通过线性关系来准确预测的场景。
通过寻找非线性模型中的最佳拟合曲线，非线性回归可以帮助我们预测未来的数据趋势。
什么是非线性回归回归分析是一种统计方法，用于确定自变量与因变量之间的关系。
线性回归假设自变量与因变量之间存在线性关系，但在某些情况下，真实的关系可能是非线性的。
这时，我们就需要使用非线性回归来更准确地建立模型。
非线性回归用曲线来描述自变量与因变量的关系，常见的非线性模型包括指数模型、多项式模型、对数模型等。
通过调整非线性模型的参数，我们可以找到最佳的拟合曲线，从而预测未来的数据。
如何进行非线性回归进行非线性回归的一般步骤如下：1. 收集数据：首先，我们需要收集自变量与因变量之间的样本数据。
2. 选择合适的模型：根据数据的特点，选择适合的非线性模型来描述自变量与因变量之间的关系。
3. 参数估计：使用统计方法，估计非线性模型中的参数值，找到最佳的拟合曲线。
4. 模型评估：通过评估模型的拟合程度，确定模型的可靠性和预测能力。
5. 预测未来数据：使用已建立的非线性模型，预测未来的数据趋势。
非线性回归的优势和应用非线性回归相比线性回归具有以下优势：- 更准确的预测能力：非线性回归可以更好地拟合真实的数据模式，提供更准确的预测结果。
- 更强的灵活性：非线性回归可以适应各种复杂的数据模式和关系，允许我们探索更多的可能性。
非线性回归在各个领域都有广泛的应用，例如金融、医学、经济学等。
在金融领域，非线性回归可以用于股票价格预测和风险评估；在医学领域，非线性回归可以用于疾病发展趋势预测和药物效果评估。
总结非线性回归是一种在数据预测中常用的方法，适用于无法通过线性关系进行准确预测的场景。
通过寻找非线性模型中的最佳拟合曲线，非线性回归可以帮助我们更准确地预测未来的数据趋势。
非线性回归具有更准确的预测能力和更强的灵活性，在各个领域都有广泛的应用。
非线性回归分析(教案)
非线性回归分析(教案)第一章：非线性回归分析简介1.1 非线性回归的定义与意义1.2 非线性回归与线性回归的比较1.3 非线性回归分析的应用领域1.4 本章小结第二章：非线性回归模型建立2.1 非线性回归模型的形式2.2 非线性回归模型的建立方法2.3 非线性回归模型的参数估计2.4 模型检验与优化2.5 本章小结第三章：非线性回归分析软件介绍3.1 非线性回归分析软件的选择3.2 非线性回归分析软件的操作步骤3.3 非线性回归分析软件的应用案例3.4 本章小结第四章：非线性回归在实际问题中的应用4.1 非线性回归在生物医学领域的应用4.2 非线性回归在经济学领域的应用4.3 非线性回归在环境科学领域的应用4.4 本章小结第五章：非线性回归分析的扩展与改进5.1 非线性回归模型的扩展5.2 非线性回归分析方法的改进5.3 非线性回归分析的发展趋势5.4 本章小结第六章：非线性回归模型的选择与评估6.1 模型选择的原则与方法6.2 模型评估指标6.3 模型选择的实际案例6.4 本章小结第七章：非线性回归分析的编程实现7.1 非线性回归分析的编程基础7.2 常见非线性回归模型的编程实现7.3 非线性回归分析的编程实践7.4 本章小结第八章：非线性回归分析在数据挖掘中的应用8.1 数据挖掘与非线性回归分析8.2 非线性回归分析在数据挖掘中的案例分析8.3 非线性回归分析在数据挖掘中的挑战与应对8.4 本章小结第九章：非线性回归分析在多变量分析中的应用9.1 多变量分析与非线性回归分析9.2 非线性回归分析在多变量数据分析中的方法与应用9.3 非线性回归分析在多变量分析中的案例研究9.4 本章小结第十章：非线性回归分析的未来展望10.1 非线性回归分析的发展趋势10.2 非线性回归分析在科学研究中的潜在应用10.3 非线性回归分析的教育与培训10.4 本章小结重点和难点解析一、非线性回归的定义与意义：理解非线性回归的基本概念，掌握非线性回归与线性回归的本质区别，以及非线性回归在实际问题中的应用场景。
非线性回归分析简介
非线性回归分析简介在统计学和机器学习领域，回归分析是一种重要的数据分析方法，用于研究自变量和因变量之间的关系。
在实际问题中，很多情况下自变量和因变量之间的关系并不是简单的线性关系，而是呈现出一种复杂的非线性关系。
因此，非线性回归分析应运而生，用于描述和预测这种非线性关系。
本文将介绍非线性回归分析的基本概念、方法和应用。
一、非线性回归分析概述1.1 非线性回归模型在回归分析中，最简单的模型是线性回归模型，即因变量和自变量之间的关系可以用一个线性方程来描述。
但是在实际问题中，很多情况下因变量和自变量之间的关系并不是线性的，而是呈现出曲线、指数、对数等非线性形式。
这时就需要使用非线性回归模型来拟合数据，通常非线性回归模型可以表示为：$$y = f(x, \beta) + \varepsilon$$其中，$y$为因变量，$x$为自变量，$f(x, \beta)$为非线性函数，$\beta$为参数向量，$\varepsilon$为误差项。
1.2 非线性回归分析的优势与线性回归相比，非线性回归分析具有更强的灵活性和适用性。
通过使用适当的非线性函数，可以更好地拟合实际数据，提高模型的预测能力。
非线性回归分析还可以揭示数据中潜在的复杂关系，帮助研究人员更好地理解数据背后的规律。
1.3 非线性回归分析的挑战然而，非线性回归分析也面临一些挑战。
首先，选择合适的非线性函数是一个关键问题，需要根据实际问题和数据特点进行合理选择。
其次，非线性回归模型的参数估计通常比线性回归模型更复杂，需要使用更为复杂的优化算法进行求解。
因此，在进行非线性回归分析时，需要谨慎选择模型和方法，以确保结果的准确性和可靠性。
二、非线性回归分析方法2.1 常见的非线性回归模型在实际应用中，有许多常见的非线性回归模型，常用的包括多项式回归模型、指数回归模型、对数回归模型、幂函数回归模型等。
这些模型可以根据实际问题的特点进行选择，用于描述和预测自变量和因变量之间的非线性关系。
非线性回归分析(教案)
非线性回归分析(教案)第一章：非线性回归分析简介1.1 非线性回归的定义与意义1.2 非线性回归与线性回归的比较1.3 非线性回归分析的应用领域1.4 本章概要第二章：非线性模型的选择2.1 常见非线性模型介绍2.2 模型选择的方法与原则2.3 利用软件选择非线性模型2.4 本章概要第三章：非线性回归的计算方法3.1 数值解法简介3.2 梯度下降法3.3 牛顿法3.4 拟牛顿法3.5 本章概要第四章：非线性回归的参数估计与检验4.1 参数估计的原理与方法4.2 参数估计的算法实现4.3 参数检验的方法与准则4.4 模型诊断与改进4.5 本章概要第五章：非线性回归在实际问题中的应用5.1 实例一：人口增长模型5.2 实例二：药物动力学模型5.3 实例三：经济预测模型5.4 实例四：生物医学信号处理模型5.5 本章概要第六章：非线性回归软件的使用6.1 常见非线性回归软件介绍6.2 非线性回归软件的使用方法6.3 利用软件进行非线性回归分析的步骤6.4 本章概要第七章：非线性回归在生物学中的应用7.1 生物学中常见非线性模型介绍7.2 非线性回归在生物学研究中的应用案例7.3 生物学数据处理与非线性回归分析7.4 本章概要第八章：非线性回归在经济与管理科学中的应用8.1 经济与管理科学中的非线性模型介绍8.2 非线性回归在经济预测中的应用案例8.3 非线性回归在管理决策中的应用案例8.4 本章概要第九章：非线性回归在工程与应用科学中的应用9.1 工程与应用科学中的非线性模型介绍9.2 非线性回归在工程设计中的应用案例9.3 非线性回归在应用科学研究中的应用案例9.4 本章概要第十章：非线性回归分析的扩展与前沿10.1 非线性回归分析的局限性与改进10.2 非线性回归分析的新方法与发展趋势10.3 非线性回归分析与其他统计方法的结合10.4 本章概要第十一章：非线性回归的优化策略11.1 优化算法概述11.2 常见优化算法介绍11.3 非线性回归的优化策略11.4 本章概要第十二章：非线性回归在医学中的应用12.1 医学中的非线性模型介绍12.2 非线性回归在医学诊断中的应用案例12.3 非线性回归在医学治疗方案设计中的应用案例12.4 本章概要第十三章：非线性回归在地球科学中的应用13.1 地球科学中的非线性模型介绍13.2 非线性回归在地球物理勘探中的应用案例13.3 非线性回归在气候学研究中的应用案例13.4 本章概要第十四章：非线性回归在化学与材料科学中的应用14.1 化学与材料科学中的非线性模型介绍14.2 非线性回归在化学反应动力学分析中的应用案例14.3 非线性回归在材料性能预测中的应用案例14.4 本章概要第十五章：非线性回归分析的实践与挑战15.1 非线性回归分析的实际操作技巧15.2 非线性回归分析面临的挑战与问题15.3 未来非线性回归分析的发展方向15.4 本章概要重点和难点解析第一章：非线性回归分析简介重点：非线性回归的定义与意义，非线性回归与线性回归的比较。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第三十四课 非线性回归分析现实世界中严格的线性模型并不多见，它们或多或少都带有某种程度的近似；在不少情况下，非线性模型可能更加符合实际。
由于人们在传统上常把“非线性”视为畏途，非线性回归的应用在国内还不够普及。
事实上，在计算机与统计软件十分发达的令天，非线性回归的基本统计分析已经与线性回归一样切实可行。
在常见的软件包中（诸如SAS 、SPSS 等等），人们已经可以像线性回归一样，方便的对非线性回归进行统计分析。
因此，在国内回归分析方法的应用中，已经到了“更上一层楼”，线性回归与非线性回归同时并重的时候。
对变量间非线性相关问题的曲线拟合，处理的方法主要有：● 首先决定非线性模型的函数类型，对于其中可线性化问题则通过变量变换将其线性化，从而归结为前面的多元线性回归问题来解决。
● 若实际问题的曲线类型不易确定时，由于任意曲线皆可由多项式来逼近，故常可用多项式回归来拟合曲线。
● 若变量间非线性关系式已知（多数未知），且难以用变量变换法将其线性化，则进行数值迭代的非线性回归分析。
一、 可变换成线性的非线性回归在实际问题中一些非线性回归模型可通过变量变换的方法化为线性回归问题。
例如，对非线性回归模型()t i t i t i t ix b ix a y εα+++=∑=210sin cos(34.1)即可作变换t t t t t t t t x x x x x x x x 2sin ,2cos ,sin ,cos 4321====将其化为多元线性回归模型。
一般地，若非线性模型的表达式为()()()t m m t t t x g b x g b x g b b y ++++= 22110(34.2)则可作变量变换()()()t m m t t t t t x g x x g x x g x ===*2*21*1,,, (34.3)将其化为线性回归模型的表达式，从而用前面线性模型的方法来解决，其中(34.3)中的x t 也可为自变量构成的向量。
这种变量变换法也适用于因变量和待定参数 b i 。
如()[]1exp 2132211-++=t t t t t x x b x b x b a y(34.4)时上式两边取对数得()1ln ln 2132211-+++=t t t t t x x b x b x b a y(34.5)现作变换1,ln ,ln 2130*-===t t t t t x x x a b y y(34.6)则可得线性表达式t t t t x b x b x b b y 3322110*+++=(34.7)利用前面方法确定了3,2,1,0,ˆ=i b i ，并由)ˆexp(ˆ0b a =得到a ˆ 的值。
变量变换的线性化方法可推广到下列形式的非线性模型()()t m m m t t x g b c x g b c b c y h )()()()(11100+++=(34.8)其中x =（x 1,x 2, ,x p ），而h （y t ）、c i （b i ）、g i （x t ）则分别化为新的因变量、线性回归参数和自变量，即可归结为线性回归模型来解。
见表34.1所示给出了一些常见的可线性化的非线性模型。
表34.1 典型的函数及线性化方法函数名称函数表达式线性化方法双曲线函数xb a y +=1 yv 1=xu 1=幂函数b ax y =y v ln = x u ln = 指数函数bx ae y =y v ln = x u = x b ae y /=y v ln = xu 1=对数函数x b a y ln += y v = x u ln =S 型函数 xbe a y -+=1yv 1=x e u-=当曲线的函数类型未确定时，我们常采用上述非线性模型作为其拟合曲线，即将自变量的各种初等函数的组合作为新自变量，用逐步回归法（或正交筛选法等）对新变量进行筛选，以确定一个项数不多的线性函数表达式。
该方法对表达式形式没限制且精度要求不高的问题颇为有效。
二、 多项式回归分析在式(34.2)中，若取()i i x x g =，则为多项式回归模型。
由数学分析知识可知，一般函数都可用多项式来逼近，故多项式回归分析可用来处理相当广泛的非线性问题。
对观测数据（x t ，y t ）（t = 1，…，N ），多项式回归模型为t m t m t t t x b x b x b b y ε+++++= 2210，t =1,2, ,N令⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=N y y y Y 21，⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡=m N NNm m x x x x x x x x x X 222221211111，⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=m b b b B 10，⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=N εεεε 21 则模型可表示为ε+=XB Y当X 列满秩时，由前面的讨论知，其最小二乘估计为()Y X X X B ''=-1ˆ由此即可求得其多项式回归方程。
但由于()1-'X X 的计算既复杂又不稳定，故我们一般采用正交多项式法来进行多项式回归。
三、 不可变换成线性的非线性回归分析假设因变量y 与自变量（x 1，x 2,…，x p ）之间满足非线性模型()εβ+=;,,,21p x x x F y(34.9)其中()'=m ββββ,,,21 为未知参数，F 为已知表达式，仅β未知的非线性函数，ε 为误差项。
现将观察数据()pt t t t x x x y ,,,,21 ， t =1,2, ,N代人上式(34.9)得非线性回归模型()t pt t t t x x x F y εβ+=;,,,21 ， t =1,2, ,N常记为E F Y +=)(β其中()'=N y y y Y ,,,21 为y 的观察向量，()'=m βββ,,1 为非线性回归系数，E =()'N εεε,,,21 为观察误差向量，F 为未知参数β的函数向量。
非线性回归分析就是利用最小二乘准则来估计回归系数β，即求βˆ 使得残差平方和()()()()()βββF Y F Y E E Q -'-='=2121 在ββˆ= 处达到最小。
非线性回归分析一般来用数值迭代法来进行，其共同特点是：由选定β的初值0β出发，通过逐步迭代∆⋅+=t 0ββ(34.10)即选择适当的步长t ( >0 ) 及确定搜索方向向量∆＝（∆1，∆2，…，∆m ），使得()()0ββQ Q <(5.4.11)再β由取代0β，重复上述迭代过程，直至 Q (β)可认为达到最小值为止，即可将所得的β作为其最小二乘估计βˆ，从而得到非线性回归方程()βˆ;,,,ˆ21p x x x F y= 1. 下降方向和步长的选择首先考察()()()()()βββF Y F Y E E Q -'-='=2121的梯度向量（即导数）()()()()ββββF Y G F Y F Q-'-=-'⎪⎪⎭⎫ ⎝⎛∂∂-=∂∂ 其中'⎪⎪⎭⎫⎝⎛∂∂∂∂=∂∂=m F F F G βββ,,1 为F 的梯度矩阵。
为使0β迭代收敛到βˆ，其迭代公式应满足下降性质(5.4.11)。
现考虑一元函数()()∆⋅+=t Q t 0βϕ，它从0β出发以 ∆为方向的射线上取值。
由复合求导公式得()()()∆⋅'--=∆⋅'⎪⎪⎭⎫ ⎝⎛∂∂='==G F Y Q t d t ββϕ0可以证明，当 d <0 时，在以 ∆为方向向量的射线上可以找到∆⋅+=t 0ββ，使得()()0ββQ Q <。
我们将满足 d <0 的∆称为下降方向，Bard 于1974年给出了∆为下降方向的充要条件为()()βF Y G P -'=∆其中P 为对称正定阵，由此我们可得下降算法的迭代公式为()()βββF Y G tP -'+=0(34.12)其中P 为任意正定阵，G 为F 的梯度，t 为满足()()0ββQQ <的正实数，即步长。
如何计算∆以便修改参数向量β有五种常用的非线性回归迭代方法：高斯-牛顿法（Gauss-Newton ）、最速下降法（梯度法，Gradient ）、牛顿法（Newton ）、麦夸特法（Marquardt ）、正割法（DUD ）。
以下我们介绍其中高斯-牛顿法。
2. Gauss －Newton 法首先选取β的一切初始近似值0β，令0ββ-=∆，则只要确定∆的值即可确定β。
为此，考虑)(βF 在0β处的Taylor 展开式，并略去二次以上的项得()()()()∆⋅'+=∆⋅'⎪⎪⎭⎫ ⎝⎛∂∂+=∆+==G F F F F F 00βββββββ 其中0βββ=∂∂=F G 为F 的梯度。
此时其残差平方和()()()()∆'--'∆'--=G F Y G F Y Q 0021ββ 由0=∆∂∂Q，得其∆的正则方程为 ()()()0βF Y G G G -'=∆'(34.13)故()()()01βF Y G G G -''=∆-(34.14)由此即可用前面线性回归法求∆，只需将G 、)(0βF Y -视为前面（5.2.1）式中的X 、Y即可。
此时，对给定精度1ε、2ε ，当{}1max ε<∆i i或()20εβ<∆+Q 时，即得的β最小二乘法估计∆+=0ˆββ；否则用所得的βˆ代替0β，重复上述步骤，直至i∆或Q (β)满足精度要求为止。
该法称为Gauss －Newton 法，其一般迭代公式为∆+=+i i i t ββ1(34.15)其中：∆为()()()()()iiiiF YG G G ββββ-'=∆'的解，t i为()()∆⋅+=t Q t iβϕ的最小值点。
Gauss-Newton 法在初值0β选取适当，且G G '可逆时非常有效，但在其他情形，其求解 较为困难，对此，Marguardt 对(34.14)中∆的正则系数阵作适当修正，得到了改进算法。
四、 nlin 非线性回归过程在很多场合，可以对非线性模型进行线性化处理，尤其是关于变量非线性的模型，以运用OLS 进行推断。
对线性化后的线性模型，可以应用SAS 的reg 过程进行计算。
多项式模型可以直接应用glm （广义线性模型）求解。
对于不能线性化的非线性模型。
其估计不能直接运用经典的最小二乘法，而需要运用其他估计方法，如直接搜索法、直接最优法与Taylor 级数展开法进行线性逼近。
此时，可以利用SAS/STA T 的nlin 过程实现相应的计算。