二次函数综合(动点)问题——平行四边形存在问题培优学案(横版)
- 格式:docx
- 大小:258.67 KB
- 文档页数:33

二次函数中的平行四边形的存在性问题一、已知三个定点,再找一个定点构成平行四边形(平面内有三个点满足)在总角处标平而内确定点M,使得以点M、4、B、C为顶点的四边形是平行四边形,请写出点M的坐标。
1.已知抛物线=-ax2+ 2cix + b与兀轴的一•个交点为水-1,0),与y轴的正半轴交于点C.⑴直接写出抛物线的对称轴,及抛物线与x轴的另一个交点〃的坐标;⑵当点Q在以ABM径的0P上时,求抛物线的解析式;⑶处标平面内是否存在点M ,使得以点弭和⑵屮抛物线上的三点A. B、C为顶点的四边形是平行四边形?若存在,请求出点M的处标;若不存在,请说明理由.解:⑴对称轴是直线:x = l,点〃的坐标是(3,0)・……2分(2)如图,连接%・・•点久〃的坐标分别是辰-1,0)、B (3,0),;・AB=A. :. pc = -AB = -x4 = 2.2 2在RtZlPOC中,9:6P=PA-0A=2-l = l t:.oc = Q PC?_ PO? = V22-i2 = Va・・・b=Vi ............................. 3分当x = —1, y = 0 R寸,—ci —2a + V3 = 0,⑶存在.理由:如图,连接化、BC.设点財的坐标为M(x,y).①当以M或%为对角线时,点於在左轴上方,此时CM//AB,且CM=AB.y由(2)知,AB=4,・・・|”=4, y = OC =相.・・・x=±4.・・・点妙的处标为M(4,、/§)或(―4,、庁).・・・9分说明:少求一个点的坐标扣1分.②当以昇〃为对角线时,点M在X轴下方.过必作MNLAB于皿则ZMNB= ZAOC=90° .•・•四边形舷%、是平行四边形,:・AC=MB,吐AC// MB.:,ACAO=AMBN. :.AAOC^ABML :・BN=AO=\, MN=CO=晶.•:0B=3,—3 — 1 = 2.・•・点必的坐标为M(2,—巧). ..................... 12分说明:求点"的坐标时,用解直角三角形的方法或用先求直线解析式,然后求交点〃的坐标的方法均可,请参照给分.综上所述,坐标平面内存在点M ,使得以点久B、G 〃为顶点的四边形是平行四边形.其坐标为M](4, V3),“2(-4, V3), (2,-希).说明:①综上所述不写不扣分;②如果开头“存在”二字没写,但最后解答全部正确,不扣分。

教学过程一、课堂导入1、在平面直角坐标系中,已知点A(4,4)、B(-4,4),试在x轴上找出点P,使△APB为直角三角形,请直接写出所有符合条件的P点的坐标2、在平面直角坐标系中找出所有的点C,使得△ABC是以AB为腰的等腰三角形,且C点的横坐标与纵坐标为自然数.画出C点的位置并写出C点的坐标.问题:这是我们在平面直角坐标系那章学习的容,如果我们将二次函数容纳其中,在抛物线上求作一点,使得三角形是等腰三角形(等边三角形、直角三角形等)并求出该点坐标时,又该如何解答呢?二、复习预习根据实际问题列二次函数关系式:1、列二次函数解应用题与列整式方程解应用题的思路和方法是一致的,不同的是,学习了二次函数后,表示量与量的关系的代数式是含有两个变量的等式.对于应用题要注意以下步骤:(1)审清题意,弄清题中涉及哪些量,已知量有几个,已知量与变量之间的基本关系是什么,找出等量关系(即函数关系).(2)设出两个变量,注意分清自变量和因变量,同时还要注意所设变量的单位要准确.(3)列函数表达式,抓住题中含有等量关系的语句,将此语句抽象为含变量的等式,这就是二次函数.(4)按题目要求,结合二次函数的性质解答相应的问题。
(5)检验所得解是否符合实际:即是否为所提问题的答案.(6)写出答案.2、常见题目类型(1)几何类(三角形、四边形、圆等)一般问题是求图形的面积,首先可以根据特殊图形的面积公式来求解,这时关键是表示出公式里各个部分的代数式;其次,如果不是特殊的图形,可以通过特殊图形的面积相加减来表示;最后,还可以通过构造特殊图形来进行表示求解;总之,要根据题目给的条件实际运用。
(2)桥梁问题这类题型是出现较多的类型,首先应该建立适当的直角坐标系,将桥梁的拱形转化为二次函数来进行求解,强调的是特殊点的表示与运用。
(3)销售问题这类题型会在考试中频繁出现,解题的方法就是:围绕总利润=(售价-进价)×数量这个公式去进行,难度大一点的就是会涉及提价跟降价两种情况,关键是要根据题意分别表示出降价或者提价后商品的售价、数量(进价一般不变),然后再通过公式将各个部分组合在一起就可以了。

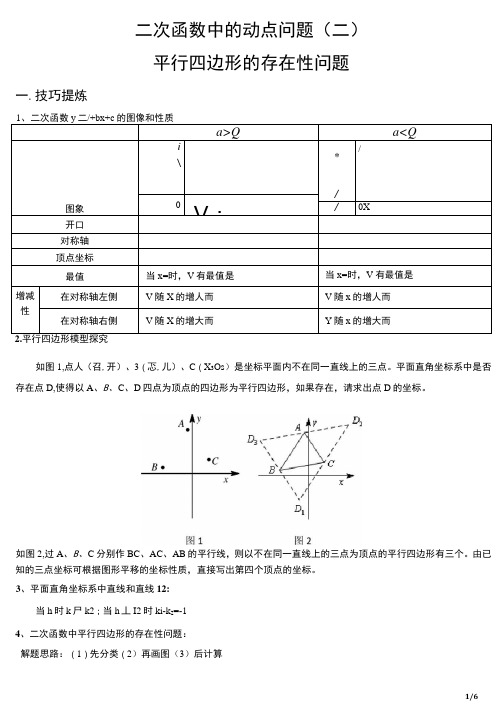
二次函数中的动点问题(二)平行四边形的存在性问题一.技巧提炼如图1,点人(召,开)、3(忑,儿)、C(X3Os)是坐标平面内不在同一直线上的三点。
平面直角坐标系中是否存在点D,使得以A、B、C、D四点为顶点的四边形为平行四边形,如果存在,请求出点D的坐标。
如图2,过A、B、C分别作BC、AC、AB的平行线,则以不在同一直线上的三点为顶点的平行四边形有三个。
由已知的三点坐标可根据图形平移的坐标性质,直接写出第四个顶点的坐标。
3、平面直角坐标系中直线和直线12:当h时k尸k2;当h丄I2时ki-k2=-14、二次函数中平行四边形的存在性问题:解题思路:(1)先分类(2)再画图(3)后计算二、精讲精练1、已知抛物线y=ax-+bx+c与x轴相交于A、E两点(A、B分别在原点的左右两侧),与y轴正半轴相交于C点,且OA:OB:OC=1:3:3,AABC的面积为6,(如图1)(1)求抛物线的解析式:(2)坐标平面内是否存在点M,使得以点M、A、B、C为顶点四边形是平行四边形?若存在,请求出点M的坐标;若不存在,请说明理由;(3)如图2,在直线BC±方的抛物线上是否存在一动点P,ABCP面枳最大?如果存在,求出最人面积,2、如图,己知抛物线经过A(-2,0),B(・3,3)及原点6顶点为C(1)求抛物线的函数解析式:(2)设点D在抛物线上,点E在抛物线的对称轴上,且以AO为边的四边形AODE是平行四边形,求点D的坐标。
【变式练习】7如图,对称轴为直线x二一的抛物线经过点A(6,0)和B(0,4)・2(1)求抛物线解析式及顶点坐标;(2)设点E(x,y)是抛物线上一动点,且位于第四彖限,四边形0EAF是以0A为对角线的平行四边形, 求平行四边形OEAF的面积S与x之间的函数关系式,并写出自变量x的取值范围;①当平行四边形OEAF的面积为24时,请判断平行四边形0EAF是否为菱形?②是否存在点E,使平行四边形0EAF为正方形?若存在,求出点E的坐标;若不存在,请说明理由.、方法规律1、平行四边形模型探究如图1,点&(內,开)、3(七,儿)、C(X3,”)是坐标平面内不在同一直线上的三点。
《平行四边形存在性问题》教学设计执教者学情分析本节课是在已经进行过一轮复习,也适当做了一些往年的中考试卷,对于基础知识学生掌握的还是不错的,但对于综合性的题目却感觉困难,特别是动点问题。
对于这类问题存在以下几种情况:1、这类问题无论教师做了多大的努力,对学生来说都比较困难,所以一部分学生放弃作答。
2、一部分学生对动点问题从根本上不理解,勉强照猫画虎,写了不少但不得分。
3、学生对动点问题有一定认识,对分类能进行简单尝试, 但不完整。
针对以上情况,我希望通过本节课的学习,一方面帮助学生树立信心,让他们明白所谓的综合题都是由诸多小知识点组成的,所谓的动态问题可以变为“静”来解决,通过代数解决几何问题另一方面通过例题讲解让学生掌握解决这类题目的解题策略。
效果分析针对学生面临的困难:首先,我在教学时注意层次性,讲究循序渐进,由浅入深,由易到难,不要一步到位,逐步过渡。
其次,注意所选例题的典型性,选了最具代表性的两类动点问题产生的平行四边形形存在性问题,一类一个例题,这样就可由一题推及一类,让学生可触类旁通,达到举一反三的效果。
教学时注重这几个方面:1、利用几何画板动态画图,让学生体会点在运动过程中,图形会跟着发生变化。
在变化的过程中抓住某一瞬间,化“动”为“静”,使其构成平行四边形,再利用所学知识解决问题。
2、注重板书。
通过清晰的板书让学生一目明了如何分析平行四边形存在性问题。
3、注重数学思想方法的渗透。
数学思想方法是数学学科的精髓,是数学素养的重要内容之一,在数学教学和探究活动中始终体现这些数学思想方法,动点问题也不例外,因此,在数学教学中应特别注重这些思想方法的渗透,因为只有让学生充分掌握领会这种思维,才能更有效地运用所学知识,形成求解动点问题的能力。
动点问题中主要体现方程思想,数形结合思想,分类讨论思想等。
方程思想,大多数动点问题到最后都转化为方程形式,然后利用方程来求解。
数形结合思想,动点问题中,所研究的量的几何特征与数量特征紧密结合,体现了数形结合的特征与方法。

学习过程一、复习预习(一)利用待定系数法求抛物线解析式的三种常用形式: (1)【一般式】已知抛物线上任意三点时,通常设解析式为 ,然后解三元方程组求解; (2)【顶点式】已知抛物线的顶点坐标和抛物线上另一点时,通常设解析式为 求解; (3)【交点式】已知抛物线与轴的交点的坐标时,通常设解析式为 。
(二)抛物线上两个点A (x 1,y ),B (x 2,y )之间的关系: (1)如果两点关于对称轴对称,则有对称轴2x 21x x +=;(2)两点之间距离公式:已知两点()()2211y ,x Q ,y ,x P ,则由勾股定理可得:221221)()(y y x x PQ -+-=练一练:已知A (0,5)和B (-2,3),则AB = 。
(3)中点公式:已知两点()()2211y ,x Q ,y ,x P ,则线段PQ 的中点M 为⎪⎭⎫⎝⎛++222121y y ,x x 。
练一练:已知A (0,5)和B (-2,3),则线段AB 的中点坐标是(4)如图:PG ∥X 轴,QG ∥Y 轴,P 点的横坐标为,G 点的横坐标为,纵坐标为,Q 点的纵坐标为,则线段PG=,QG=。
(三)求三角形的面积: (1)直接用面积公式计算;(2)割补法;(3)铅垂高法; 如图,过△ABC 的三个顶点分别作出与水平线垂直的三条直线,外侧两条直线之间的距离叫△ABC 的“水平宽”(a ),中间的这条直线在△ABC 内部线段的长度叫△ABC 的“铅垂高”(h ).我们可得出一种计算三角形面积的新方法:S △ABC =12ah ,即三角形面积等于水平宽与铅垂高乘积的一半。
B 铅垂高 水平宽haA(四)二次函数中三角形面积、周长的存在性问题解题思路:(1)如果是一个三角形面积为一个三角形面积的多少倍,则分别表示出每个三角形的面积去求解;如果是一个三角形面积为固定值,则用含有未知数的式子去表示面积去求解;如果是三角形周长最小,则做对称点去求解;如果是三角形面积最大,则划归为二次函数最值问题去求解。
有关平行四边形的存在性问题一.知识与方法积累:1.已知三个定点,一个动点的情况在直角坐标平面内确定点M ,使得以点M 、A 、B 、C 为顶点的四边形是平行四边形, 请直接写出点M 的坐标。
2.已知两个定点,两个动点的情况已知点C(0,2), B(4,0),点A 为X 轴上一个动点,试在直角坐标平面内确定点M ,使得以点M 、A 、B 、C 为顶点的四边形是平行四边形(画出草图即可)分以下几种情况:(1)以BC 为对角线,BE 为边;(2)以CE 为对角线,BC 为边; (3)以BE 为对角线,BC 为边;3. 方法归纳: 先分类;(按对角线和边)再画图;(画草图,确定目标点的大概位置)后计算。
(可利用三角形全等性质和平行四边形性质,准确求点的坐标)3211234224OBC321123422468OBC3211234224OBC二.例题解析:如图,抛物线32++=bx ax y 与y 轴交于点C ,与x 轴交于A 、B 两点,31tan =∠OCA ,6=∆ABC S .(1)求点B 的坐标; (2)求抛物线的解析式及顶点坐标;(3)设点E 在x 轴上,点F 在抛物线上,如果A 、C 、E 、F 构成平行四边形,请求出点E 的坐标.巩固练习:1. 已知抛物线322++-=x x y 与x 轴的一个交点为 A(-1,0),与y 轴的正半轴交于点C . 问坐标平面内是否存在点M ,使得以点M 和抛物线上的三点A 、B 、C 为顶点的四边形是平行四边形?若存在,请求出点M 的坐标;若不存在,请说明理由.2. 若点P 是x 轴上一点,以P 、A 、D 为顶点作平行四边形,该平行四边形的另一顶点E 在y 轴上,写出点P 的坐标.CAB Oyx3.如图,抛物线223y x x =-++与x 轴相交于A 、B 两点(点A 在点B 的左侧),与y 轴相交于点C ,顶点为D .(1)直接写出A 、B 、C 三点的坐标和抛物线的对称轴;(2)连接BC,与抛物线的对称轴交于点E ,点P 为线段BC 上的一个动点,过点P 作PF DE ∥交抛物线于点F ,设点P 的横坐标为m ;并求出当m 为何值时,四边形PEDF 为平行四边形?4. 已知抛物线22y x x a =-+(0a <)与y 轴相交于点A ,顶点为M .直线12y x a =-分别与x 轴,y 轴相交于B C ,两点,并且与直线AM 相交于点N .在抛物线22y x x a =-+(0a <)上是否存在一点P ,使得以P A C N ,,,为顶点的四边形是平行四边形?若存在,求出P 点的坐标;若不存在,试说明理由.43211242246Dy = x ∙x + 2∙x + 3CBA5.如图,已知抛物线)0(2≠++=a c bx ax y 的顶点坐标为Q ()1,2-,且与y 轴交于点C ()3,0,与x 轴交于A 、B 两点(点A 在点B 的右侧),点P 是该抛物线上一动点,从点C 沿抛物线向点A 运动(点P 与A 不重合),过点P 作PD ∥y 轴,交AC 于点D . (1)求该抛物线的函数关系式;(2)当△ADP 是直角三角形时,求点P 的坐标;(3)在问题(2)的结论下,若点E 在x 轴上,点F 在抛物线上, 问是否存在以A 、P 、E 、F 为顶点的平行四边形?若存在, 求点F 的坐标;若不存在,请说明理由.6. 如图,抛物线21y ax bx =++与x 轴交于两点A (-1,0),B (1,0),与y 轴交于点C .(1)求抛物线的解析式;(12+-=x y )(2)过点B 作BD ∥CA 与抛物线交于点D ,求四边形ACBD 的面积;四边形ACBD 的面积S =12AB •OC +12AB •DE 112123422=⨯⨯+⨯⨯= (也可直接求直角梯形ACBD 的面积为4)(3)在x 轴下方的抛物线上是否存在一点M ,过M 作MN ⊥x 轴于点N ,使以A 、M 、N 为顶点的三角形与△BCD 相似?若存在,则求出点M 的坐标;若不存在,请说明理由.。
教学过程一、课堂导入二次函数的综合问题是中考压轴题常考题型之一,考点分值12分,难度较大。
主要考查形式为二次函数与一些简单几何图形的点存在性问题,既考查了学生的数形结合能力,又考查学生的计算能力。
此类问题出现后,大多学生都无从下手,主要是学生的综合能力、解题技巧及实战经验不足所致。
就本节二次函数与平行四边形的点存在性问题,主要考查了学生能否将平行四边形的性质与判定融入到二次函数,在函数图像中构造题意所需图形的能力。
二、复习预习平行四边形的判定与性质1. 定义:两组对边分别平行的四边形叫做平行四边形。
2. 性质:①平行四边形两组对边分别平行;②平行四边形两组对边分别相等;③平行四边形两组对角分别相等;④平行四边形的对角线互相平分;3. 判定:①两组对边分别平行的四边形是平行四边形;②两组对边分别相等的四边形是平行四边形;③两组对角分别相等的四边形是平行四边形;④对角线互相平分的四边形是平行四边形;⑤一组对边平行且相等的四边形是平行四边形;三、知识讲解考点1 二次函数的基础知识1.一般地,如果y=ax 2+bx+c (a ,b ,c 是常数且a ≠0),那么y 叫做x 的二次函数,它是关于自变量的二次式,二次项系数必须是非零实数时才是二次函数,这也是判断函数是不是二次函数的重要依据.当b=c=0时,二次函数y=ax 2是最简单的二次函数.2.二次函数y=ax 2+bx+c (a ,b ,c 是常数,a ≠0)的三种表达形式分别为:一般式:y=ax 2+bx+c ,通常要知道图像上的三个点的坐标才能得出此解析式;顶点式:y=a (x -h )2+k ,通常要知道顶点坐标或对称轴才能求出此解析式;交点式:y=a (x -x 1)(x -x 2),通常要知道图像与x 轴的两个交点坐标x 1,x 2才能求出此解析式;对于y=ax 2+bx+c 而言,其顶点坐标为(-2b a ,244ac b a ).对于y=a (x -h )2+k 而言其顶点坐标为(h ,k ),•由于二次函数的图像为抛物线,因此关键要抓住抛物线的三要素:开口方向,对称轴,顶点.考点2 探究平行四边形的一般思路在探究平行四边形的存在性问题时,具体方法如下:(1)假设结论成立;(2)探究平行四边形存在问题一般是已知平行四边形的3个顶点,再去求另外一个顶点,具体方法有两种:第一种是:①从给定的3个顶点中任选2个定点确定的线段作为探究平行四边形的边或对角线分别作出平行四边形;②根据题干要求找出符合条件的平行四边形;第二种是:①以给定的3个定点两两组合成3条线段,分别以这3条线段为对角线作出平行四边形;②根据题干要求找出符合条件的平行四边形;(3)建立关系式,并计算;根据以上分类方法画出所有的符合条件的图形后,可以利用平行四边形的性质进行计算,也可以利用全等三角形、相似三角形或直角三角形的性质进行计算,要具体情况具体分析,有时也可以利用直线的解析式联立方程组,由方程组的解为交点坐标的方法求解。
广东省中考数学疑难问题教学设计:二次函数中的动点问题之平行四边形一、教学内容的确定及前期思考:二次函数中的动点问题无疑会成为压轴题三位主角中的一个,而动点产生平行四边形的问题也经常出现,本人发现:无论是各种复习资料对这类题给出的解答方法,还是我听公开课时发现很多老师给出的解决方式都将简单问题复杂化了,而我们数学老师的任务应该是化繁为简,找出各个知识点之间的联系,充分利用我们熟悉的数学方法和数学思想去解决压轴题中的疑难问题,由此产生了将此类问题形成一篇教学设计的想法,并已长达两年之久。
二、教学目标分析:(一)通性通法:1、通过知识转化、类比、迁移的方式学会观察分析并找出线段的平移和点的坐标之间的关系,再利用形成平行四边形的动点的位置的特殊性(在抛物线上或在抛物线的对称轴上等),求出动点的坐标。
2、熟练掌握和应用函数模型、数形结合、分类讨论与整合、化归与转化等数学思想和方法。
(二)情感教育:能通过本节课化繁为简、化难为易的学习过程克服对压轴题的恐惧心理,增强学生解决压轴题的信心和勇气。
三、教学重点与难点分析:重点:掌握根据平移与点的坐标之间的关系规律来解决二次函数中动点产生平行四边形的问题。
1难点:首先是能利用平移画出大致图形,其次是能充分利用隐含的条件(如点在对称轴上就意味着已知横坐标等)来求出动点的坐标。
四、教学过程设计总流程如下:具体教学过程如下:(一)观看旧解,提出问题:环节一:展示疑难题图,引出课题设计意图:展示三道平行四边形和二次函数结合的题图,冲击学生的视觉,让学生的注意力一下子就集中到本节课要学习的题目类型上。
开场白设计:在压轴题中,我们经常会见到平行四边形和二次函数相依相伴的身影,这节课我们就一起来研究二次函数和平行四边形的那些事儿。
环节二:探讨平行四边形中暗含的平移知识(聊天引入)让我们先把平行四边形请过来做客吧!下面,给你们展示一道题以及这道题的解题过程,你知道答案是怎么做的吗?辅例 1、(选自练习册中的练习题)在直角坐标系中,已知: A(-1,0),B(3,0),C(0,2).以A、B、C、D 为顶点的四边形是平行四边形,求 D 点的坐标。
学习过程一、复习预习(一)二次函数y=ax2+bx+c的图像和性质:(二)相似三角形的性质:(1)相似三角形的对应角相等。
(2)相似三角形的对应边成比例。
(3)相似三角形的对应高线的比,对应中线的比和对应角平分线的比都等于相似比。
(4)相似三角形的周长比等于相似比。
(5)相似三角形的面积比等于相似比的平方。
(三)相似三角形模型探究与解题技巧:1、课堂导入题解如图,在平面直角坐标系中有两点A(4,0)、B(0,2),如果点C在x轴上(C与A不重合),当点C的坐标为_________________时,使得由点B、O、C组成的三角形与△AOB相似(至少找出两个满足条件的点的坐标).解:∵点C在x轴上,∴点C的纵坐标是0,且当∠BOC=90°时,由点B、O、C组成的三角形与△AOB 相似,即∠BOC应该与∠BOA=90°对应,①当△AOB∽△COB,即OC与OA相对应时,则OC=OA=4,C(-4,0);②当△AOB∽△BOC,即OC与OB对应,则OC=1,C(-1,0)或者(1,0).故答案可以是:(-1,0);(1,0).解析:分类讨论:①当△AOB∽△COB时,求点C的坐标;②当△AOB∽△BOC时,求点C的坐标;如果非直角三角形也要分类讨论,对应边不一样就得到不同的结果。
2、几种常见的相似三角形模型①直角三角形相似的几种常见模型②非直角三角形相似的几种常见模型3、解题技巧函数中因动点产生的相似三角形问题一般有三个解题途径。
①求相似三角形的第三个顶点时,先要分析已知三角形的边和角的特点,进而得出已知三角形是否为特殊三角形。
根据未知三角形中已知边与已知三角形可能对应边成比例进行分类讨论。
②或利用已知三角形中对应角,在未知三角形中利用勾股定理、三角函数、对称、旋转等知识来推导边的大小。
③若两个三角形的各边均未给出,则应先设所求点的坐标进而用函数解析式来表示各边的长度,之后利用相似来列方程。