信号与系统习题解
- 格式:doc
- 大小:918.00 KB
- 文档页数:20

信号系统(第3版)习题解答《信号与系统》(第3版)习题解析高等教育出版社目录第1章习题解析 (2)第2章习题解析 (6)第3章习题解析 (16)第4章习题解析 (23)第5章习题解析 (31)第6章习题解析 (41)第7章习题解析 (49)第8章习题解析 (55)第1章习题解析1-1 题1-1图示信号中,哪些是连续信号?哪些是离散信号?哪些是周期信号?哪些是非周期信号?哪些是有始信号?(c) (d)题1-1图解 (a)、(c)、(d)为连续信号;(b)为离散信号;(d)为周期信号;其余为非周期信号;(a)、(b)、(c)为有始(因果)信号。
1-2 给定题1-2图示信号f ( t ),试画出下列信号的波形。
[提示:f ( 2t )表示将f ( t )波形压缩,f (2t )表示将f ( t )波形展宽。
] (a) 2 f ( t - 2 )(b) f ( 2t )(c) f ( 2t ) (d) f ( -t +1 )题1-2图解 以上各函数的波形如图p1-2所示。
图p1-21-3 如图1-3图示,R 、L 、C 元件可以看成以电流为输入,电压为响应的简单线性系统S R 、S L 、S C ,试写出各系统响应电压与激励电流函数关系的表达式。
题1-3图解 各系统响应与输入的关系可分别表示为)()(t i R t u R R ⋅= tt i L t u L L d )(d )(= ⎰∞-=t C C i Ct u ττd )(1)(1-4 如题1-4图示系统由加法器、积分器和放大量为-a 的放大器三个子系统组成,系统属于何种联接形式?试写出该系统的微分方程。
S R S L S C题1-4图解 系统为反馈联接形式。
设加法器的输出为x ( t ),由于)()()()(t y a t f t x -+=且)()(,d )()(t y t x t t x t y '==⎰故有 )()()(t ay t f t y -='即)()()(t f t ay t y =+'1-5 已知某系统的输入f ( t )与输出y ( t )的关系为y ( t ) = | f ( t )|,试判定该系统是否为线性时不变系统?解 设T 为系统的运算子,则可以表示为)()]([)(t f t f T t y ==不失一般性,设f ( t ) = f 1( t ) + f 2( t ),则)()()]([111t y t f t f T ==)()()]([222t y t f t f T ==故有)()()()]([21t y t f t f t f T =+=显然)()()()(2121t f t f t f t f +≠+即不满足可加性,故为非线性时不变系统。


1试分别指出以下波形是属于哪种信号?题图1-11-2 试写出题1-1 图中信号的函数表达式。
1-3 已知信号x1(t)与x2(t)波形如题图1-3 中所示,试作出下列各信号的波形图,并加以标注。
题图1-3⑴x1(t2)⑵ x1(1 t)⑶ x1(2t 2)⑷ x2(t 3)⑸ x2(t 2) ⑹x2(1 2t)2⑺x1(t) x2( t)⑻x1(1 t)x2(t 1)⑼x1(2 t) x2(t 4)21- 4 已知信号x1(n)与x2 (n)波形如题图1-4中所示,试作出下列各信号的波形图,并加以标注。
题图1-4⑴x1(2n 1) ⑵ x1(4 n)⑶ x1(n)2⑷ x2 (2 n)⑸ x2(n 2) ⑹ x2(n 2) x2( n 1)⑺x1(n 2) x2(1 2n)⑻x1(1 n) x2(n 4)⑼ x1(n 1) x2(n 3)1- 5 已知信号x(5 2t )的波形如题图1-5 所示,试作出信号x(t)的波形图,并加以标注。
题图1-51- 6 试画出下列信号的波形图:1⑴ x(t) sin( t) sin(8 t)⑵ x(t) [1 sin( t )] sin(8 t)21⑶x(t) [1 sin( t)] sin(8 t)⑷ x(t) sin( 2t )1-7 试画出下列信号的波形图:⑴ x(t)1 e t u(t) ⑵ x(t) e t cos10 t[u(t 1) u(t 2)]⑶ x(t)(2 e t)u(t)⑷ x(t) e (t 1)u(t)⑸ x(t)u(t22 9) ⑹ x(t)(t2 4)1-8 试求出以下复变函数的模与幅角,并画出模与幅角的波形图1j2 ⑴ X (j ) (1 e j2)⑵ X( j1 e j4⑶ X (j ) 11 ee j ⑷ X( j )试作出下列波形的奇分量、偶分量和非零区间上的平均分量与交流分量。
题图 1-10形图。
题图 1-141-15 已知系统的信号流图如下,试写出各自系统的输入输出方程。

习 题 一 第一章习题解答基本练习题1-1 解 (a) 基频 =0f GCD (15,6)=3 Hz 。
因此,公共周期3110==f T s 。
(b) )30cos 10(cos 5.0)20cos()10cos()(t t t t t f ππππ+==基频 =0f GCD (5, 15)=5 Hz 。
因此,公共周期5110==f T s 。
(c) 由于两个分量的频率1ω=10π rad/s 、1ω=20 rad/s 的比值是无理数,因此无法找出公共周期。
所以是非周期的。
(d) 两个分量是同频率的,基频 =0f 1/π Hz 。
因此,公共周期π==01f T s 。
1-2 解 (a) 波形如图1-2(a)所示。
显然是功率信号。
t d t f TP T TT ⎰-∞→=2)(21lim16163611lim 22110=⎥⎦⎤⎢⎣⎡++=⎰⎰⎰∞→t d t d t d T T T W(b) 波形如图1.2(b)所示。
显然是能量信号。
3716112=⨯+⨯=E J (c) 能量信号 1.0101)(lim101025=-===⎰⎰∞∞---∞→T t ttT e dt edt eE J(d) 功率信号,显然有 1=P W1-3 解 周期T=7 ,一个周期的能量为 5624316=⨯+⨯=E J 信号的功率为 8756===T E P W 1-5 解 (a) )(4)2()23(2t tt δδ=+; (b) )5.2(5.0)5.2(5.0)25(5.733-=-=----t e t e t et tδδδ(c) )2(23)2()3sin()2()32sin(πδπδπππδπ+-=++-=++t t t t 题解图1-2(a) 21题解图1-2(b) 21(d) )3()3()(1)2(-=----t e t t et δδε。
1-6 解 (a) 5)3()94()3()4(2-=+-=+-⎰⎰∞∞-∞∞-dt t dt t t δδ(b) 0)4()4(632=+-⎰-dt t t δ(c) 2)]2(2)4(10[)]42(2)4()[6(63632=+++-=+++-⎰⎰--dt t t dt t t t δδδδ(d)3)3(3)(3sin )(1010=⋅=⎰⎰∞-∞-dt t Sa t dt ttt δδ。
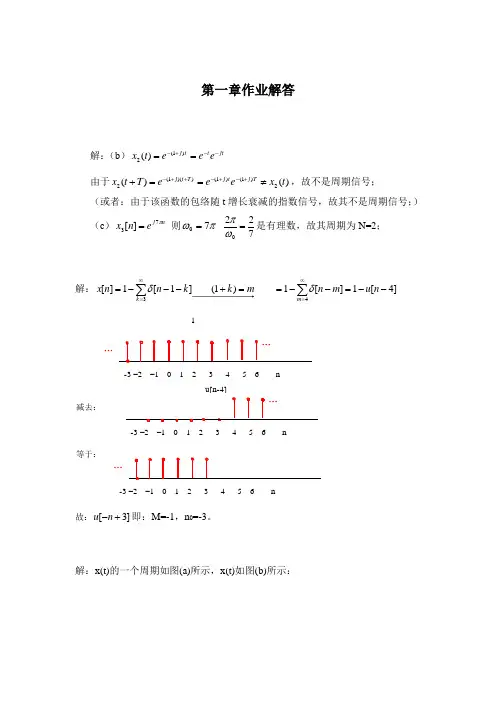
第一章作业解答解:(b )jt t t j e e e t x --+-==)1(2)(由于)()(2)1()1())(1(2t x e e e T t x T j t j T t j ≠==++-+-++-,故不是周期信号;(或者:由于该函数的包络随t 增长衰减的指数信号,故其不是周期信号;) (c )n j e n x π73][= 则πω70= 7220=ωπ是有理数,故其周期为N=2;解:]4[1][1)1(]1[1][43--=--==+---=∑∑∞=∞=n u m n mk k n n x m k δδ-3 –2 –1 0 1 2 3 4 5 6 n1…减去:-3 –2 –1 0 1 2 3 4 5 6 nu[n-4]等于:-3 –2 –1 0 1 2 34 5 6 n…故:]3[+-n u 即:M=-1,n 0=-3。
解:x(t)的一个周期如图(a)所示,x(t)如图(b)所示:而:g(t)如图(c)所示……dtt dx )(如图(d )所示:……故:)1(3)(3)(--=t g t g dtt dx 则:1t ,0t 3,32121==-==;A A 1.15解:该系统如下图所示: 2[n](1)]4[2]3[5]2[2]}4[4]3[2{21]}3[4]2[2{]3[21]2[][][1111111222-+-+-=-+-+-+-=-+-==n x n x n x n x n x n x n x n x n x n y n y即:]4[2]3[5]2[2][-+-+-=n x n x n x n y(2)若系统级联顺序改变,该系统不会改变,因为该系统是线性时不变系统。
(也可以通过改变顺序求取输入、输出关系,与前面做对比)。
解:(a )因果性:)(sin )(t x t y =举一反例:当)0()y(,0int s x t =-=-=ππ则时输出与以后的输入有关,不是因果的;(b )线性:按照线性的证明过程(这里略),该系统是线性的。



第2章 习 题2-1 求下列齐次微分方程在给定起始状态条件下的零输入响应(1)0)(2)(3)(22=++t y t y dt d t y dt d ;给定:2)0(,3)0(==--y dt dy ; (2)0)(4)(22=+t y t y dt d ;给定:1)0(,1)0(==--y dtd y ;(3)0)(2)(2)(22=++t y t y dt d t y dt d ;给定:2)0(,1)0(==--y dt dy ; (4)0)()(2)(22=++t y t y dt d t y dt d ;给定:2)0(,1)0(==--y dtdy ; (5)0)()(2)(2233=++t y dt d t y dt d t y dt d ;给定:2)0(,1)0(,1)0(22===---y dt d y dt d y 。
(6)0)(4)(22=+t y dt d t y dt d ;给定:2)0(,1)0(==--y dtdy 。
解:(1)微分方程的特征方程为:2320λλ++=,解得特征根:121, 2.λλ=-=- 因此该方程的齐次解为:2()t th y t Ae Be --=+.由(0)3,(0)2dy y dt--==得:3,2 2.A B A B +=--=解得:8, 5.A B ==- 所以此齐次方程的零输入响应为:2()85tty t e e--=-.(2)微分方程的特征方程为:240λ+=,解得特征根:1,22i λ=±.因此该方程的齐次解为:()cos(2)sin(2)h y t A t B t =+.由(0)1,(0)1d y y dx --==得:1A =,21B =,解得:11,2A B ==. 所以此齐次方程的零输入响应为:1()cos(2)sin(2)2y t t t =+.(3)微分方程的特征方程为:2220λλ++=,解得特征根:1,21i λ=-± 因此该方程的齐次解为:()(cos()sin())th y t e A t B t -=+.由(0)1,(0)2dy y dx--==得:1,2,A B A =-= 解得:1,3A B ==.所以齐次方程的零输入响应为:()(cos()3sin())ty t e t t -=+.(4)微分方程的特征方程为:2210λλ++=,解得二重根:1,21λ=-.因此该方程的齐次解为:()()th y t At B e -=+. 由(0)1,(0)2dy y dx--==得:1,2,B A B =-=解得:3, 1.A B == 所以该方程的零输入响应为:()(31)ty t t e -=+.(5)微分方程的特征方程为:3220λλλ++=,解得特征根: 1,21λ=-,30λ=. 因此该方程的齐次解为:()()th y t A Bt C e -=++.由22(0)1,(0)1,(0)2d d y y y dx dt---===得:1,1,22A C B C C B +=-=-=. 解得:5,3,4A B C ==-=-.所以方程的零输入响应为:()5(34)ty t t e -=-+.(6)微分方程的特征方程为:240λλ+=,解得特征根:120,4λλ==-. 因此该方程的齐次解为:4()th y t A Be -=+.由(0)1,(0)2d y y dx --==得:1,42A B B +=-=.解得:31,22A B ==-. 所以此齐次方程的零输入响应为:431()22ty t e -=-.2-2 已知系统的微分方程和激励信号,求系统的零状态响应。


第一章1.8 系统的数学模型如下,试判断其线性、时不变性和因果性。
其中X (0-)为系统的初始状态。
(2)()()2f t y t e= (5)()()cos2y t f t t= (8)()()2y t f t =解:(2)()()2f t y t e=① 线性: 设()()()()1122,f t y t f t y t →→,则()()()()122212,f t f t y t ey t e==那么()()()()()()()112211222221122a f t a f t a f t a f t a f t a f t y t ee e +⎡⎤⎣⎦+→==,显然,()()()1122y t a y t a y t ≠+,所以是非线性的。
② 时不变性 设()()11,f t y t →则()()()()10122110,f t t f t y t ey t t e-=-=设()()102,f t t y t -→则()()()102210f t t y t ey t t -==-,所以是时不变的。
③ 因果性因为对任意时刻 t1,()()121f t y t e=,即输出由当前时刻的输入决定,所以系统是因果的。
(5)()()cos2y t f t t=① 线性: 设()()()()1122,f t y t f t y t →→,则()()()()1122cos2,cos2y t f t t y t f t t==那么()()()()()()()112211221122cos 2cos 2cos 2a f t a f t y t a f t a f t t a f t t a f t t+→=+=+⎡⎤⎣⎦,显然()()()1122y t a y t a y t =+,所以系统是线性的。
② 时不变性 设()()11,f t y t →则()()()()()1110100cos2,cos2y t f t t y t t f t t t t =-=--设()()102,f t t y t -→则()()()21010cos2y t f t t t y t t =-≠-,所以是时变的。
《信号与系统》(第3版)习题解析高等教育目录第1章习题解析 (2)第2章习题解析 (6)第3章习题解析 (16)第4章习题解析 (23)第5章习题解析 (31)第6章习题解析 (41)第7章习题解析 (49)第8章习题解析 (55)第1章习题解析1-1 题1-1图示信号中,哪些是连续信号?哪些是离散信号?哪些是周期信号?哪些是非周期信号?哪些是有始信号?(c) (d)题1-1图解 (a)、(c)、(d)为连续信号;(b)为离散信号;(d)为周期信号;其余为非周期信号;(a)、(b)、(c)为有始(因果)信号。
1-2 给定题1-2图示信号f ( t ),试画出下列信号的波形。
[提示:f ( 2t )表示将f ( t )波形压缩,f (2t)表示将f ( t )波形展宽。
](a) 2 f ( t - 2 ) (b) f ( 2t )(c) f ( 2t)(d) f ( -t +1 )题1-2图解 以上各函数的波形如图p1-2所示。
图p1-21-3 如图1-3图示,R 、L 、C 元件可以看成以电流为输入,电压为响应的简单线性系统S R 、S L 、S C ,试写出各系统响应电压与激励电流函数关系的表达式。
题1-3图解 各系统响应与输入的关系可分别表示为)()(t i R t u R R ⋅= tt i Lt u L L d )(d )(= ⎰∞-=tC C i Ct u ττd )(1)(1-4 如题1-4图示系统由加法器、积分器和放大量为-a 的放大器三个子系统组成,系统属于何种联接形式?试写出该系统的微分方程。
S RS LS C题1-4图解 系统为反馈联接形式。
设加法器的输出为x ( t ),由于)()()()(t y a t f t x -+=且)()(,d )()(t y t x t t x t y '==⎰故有)()()(t ay t f t y -='即)()()(t f t ay t y =+'1-5 已知某系统的输入f ( t )与输出y ( t )的关系为y ( t ) = | f ( t )|,试判定该系统是否为线性时不变系统?解 设T 为系统的运算子,则可以表示为)()]([)(t f t f T t y ==不失一般性,设f ( t ) = f 1( t ) + f 2( t ),则)()()]([111t y t f t f T == )()()]([222t y t f t f T ==故有)()()()]([21t y t f t f t f T =+=显然)()()()(2121t f t f t f t f +≠+即不满足可加性,故为非线性时不变系统。
《信号与系统》课程习题与解答第二章习题(教材上册第二章p81-p87)2-1,2-4~2-10,2-12~2-15,2-17~2-21,2-23,2-24第二章习题解答2-1 对下图所示电路图分别列写求电压的微分方程表示。
图(a):微分方程:11222012()2()1()()()2()()()()2()()()c cc di t i t u t e t dtdi t i t u t dtdi t u t dt du t i t i t dt ⎧+*+=⎪⎪⎪+=⎪⇒⎨⎪=⎪⎪⎪=-⎩图(b ):微分方程:⎪⎪⎪⎩⎪⎪⎪⎨⎧-==+++=+++⎰⎰2021'2'21'2'11)(01)(1Ri t v Ri Mi Li dt i Ct e Ri Mi Li dt i C)()(1)(2)()2()(2)()(33020022203304422t e dtd MR t v C t v dt d C R t v dt d C L R t v dt d RL t v dt d M L =+++++-⇒ 图(c)微分方程:dt i C i L t v ⎰==211'101)(⎪⎪⎪⎩⎪⎪⎪⎨⎧===⇒⎰dt t v L i t v L i dtdt v L i dt d)(1)(1)(10110'1122011∵ )(122111213t i dt d L C i i i i +=+=)(0(1]1[][101011022110331t e dt dR t v RL v dt d RR L C v dt d R C R C v dt d CC μ=+++++⇒图(d)微分方程:⎪⎩⎪⎨⎧+-=++=⎰)()()()()(1)()(11111t e t Ri t v t v dt t i C t Ri t e μRC v dt d 1)1(1+-⇒μ)(11t e V = ∵)()(10t v t v μ=)()(1)1(0'0t e R v t v R Cv v =+-⇒2-4 已知系统相应的其次方程及其对应的0+状态条件,求系统的零输入响应。
1-1 分别判断图1-1所示各波形是连续时间信号还是离散时间信号,若是离散时间信号是否为数字信号?图1-1图1-2解 信号分类如下:⎪⎪⎩⎪⎪⎨⎧⎩⎨⎧--⎩⎨⎧--))(散(例见图数字:幅值、时间均离))(连续(例见图抽样:时间离散,幅值离散))(连续(例见图量化:幅值离散,时间))(续(例见图模拟:幅值、时间均连连续信号d 21c 21b 21a 21图1-1所示信号分别为 (a )连续信号(模拟信号); (b )连续(量化)信号; (c )离散信号,数字信号; (d )离散信号;(e )离散信号,数字信号; (f )离散信号,数字信号。
1-2 分别判断下列各函数式属于何种信号?(重复1-1题所示问) (1))sin(t e at ω-; (2)nT e -; (3))cos(πn ;(4)为任意值)(00)sin(ωωn ;(5)221⎪⎭⎫⎝⎛。
解由1-1题的分析可知: (1)连续信号; (2)离散信号;(3)离散信号,数字信号; (4)离散信号; (5)离散信号。
1-3 分别求下列各周期信号的周期T : (1))30t (cos )10t (cos -; (2)j10t e ;(3)2)]8t (5sin [;(4)[]为整数)(n )T nT t (u )nT t (u )1(0n n ∑∞=-----。
解 判断一个包含有多个不同频率分量的复合信号是否为一个周期信号,需要考察各分量信号的周期是否存在公倍数,若存在,则该复合信号的周期极为此公倍数;若不存在,则该复合信号为非周期信号。
(1)对于分量cos (10t )其周期5T 1π=;对于分量cos (30t ),其周期15T 2π=。
由于5π为21T T 、的最小公倍数,所以此信号的周期5T π=。
(2)由欧拉公式)t (jsin )t (cos e t j ωωω+= 即)10t (jsin )10t (cos e j10t +=得周期5102T ππ==。
《信号与系统》课程习题与解答第三章习题(教材上册第三章p160-p172)3-1~3-3,3-5,3-9,3-12,3-13,3-15~3-17,3-19,3-22,3-24,3-25,3-29,3-32第三章习题解答3-2 周期矩形信号如题图3-2所示。
若:求直流分量大小以及基波、二次和三次谐波的有效值。
解:直流分量⎰⎰--=⨯==2222301105)(1ττv Edt dt t f T a TTf(t)为偶函数,∴0=n b)(2cos )(222T n Sa T E tdt n t f T a n πττωττ⎰-==)(21T n Sa T E a F n n πςτ== 基波 =1a )1.0s i n (20)(2πππττ=T Sa T E有效值 39.11.0sin 22021≈=ππa二次谐波有效值 32.122≈a三次谐波有效值 21.123≈a3-3 若周期矩形信号)(1t f 和 )(2t f 波形如题图3-2所示,)(1t f 的参数为s μτ5.0=,s T μ1=,E=1V ;)(2t f 的参数为s μτ5.1=,s T μ3=,E=3V ,分别求:(1))(1t f 的谱线间隔和带宽(第一零点位置),频率单位以kHz 表示; (2))(2t f 的谱线间隔和带宽; (3) )(1t f 和 )(2t f 的基波幅度之比; (4) )(1t f 基波与)(2t f 三次谐波幅度之比。
解:(1))(1t f s μτ5.0= s T μ1= E=1V 谱线间隔:khZ T 10001==∆带宽:KHzB f 20001==τ(2) )(2t f s μτ5.1= s T μ3= E=3V间隔:khZ T 310001==∆谱线带宽:KHzB f 320001==τ(3) )(1t f 基波幅度:ππτ2)2cos(4201==⎰dt t T E T a )(2t f 基波幅度:ππτ6)2cos(4201==⎰dt t T E T a幅度比:1:3(4) )(2t f 三次谐波幅度:ππτ2)23cos(4203-=⨯=⎰dt t T E T a 幅度比:1:13-5 求题图3-5所示半波余弦信号的傅立叶级数。
1-4 分析过程:(1)例1-1的方法:()()()()23232f t f t f t f t →−→−→−− (2)方法二:()()()233323f t f t f t f t ⎡⎤⎛⎞→→−→−−⎜⎟⎢⎥⎝⎠⎣⎦(3)方法三:()()()()232f t f t f t f t →−→−+→−−⎡⎤⎣⎦ 解题过程:(1)方法一:方法二:(1)()−f at 左移0t :()()()000−+=−−≠−⎡⎤⎣⎦f a t t f at at f t at (2)()f at 右移0t :()()()000−=−≠−⎡⎤⎣⎦f a t t f at at f t at (3)()f at 左移0t a :()()000⎡⎤⎛⎞+=+≠−⎜⎟⎢⎥⎝⎠⎣⎦t f a t f at t f t at a (4)()f at 右移0t a :()()000⎡⎤⎛⎞−−=−+=−⎜⎟⎢⎥⎝⎠⎣⎦t f a t f at t f t at a 故(4)运算可以得到正确结果。
注:1-4、1-5题考察信号时域运算:1-4题说明采用不同的运算次序可以得到一致的结果;1-5题提醒所有的运算是针对自变量t 进行的。
如果先进行尺度变换或者反转变换,再进行移位变换,一定要注意移位量和移位的方向。
1-9 解题过程: (1)()()()2tf t eu t −=− (2)()()()232tt f t ee u t −−=+(3)()()()255ttf t e eu t −−=− (4)()()()()cos 1012tf t et u t u t π−=−−−⎡⎤⎣⎦1-12 解题过程:((((注:1-9、1-12题中的时域信号均为实因果信号,即()()()=f t f t u t 1-18 分析过程:任何信号均可分解为奇分量与偶分量之和的形式,即()()()()1e o f t f t f t =+其中,()e f t 为偶分量,()o f t 为奇分量,二者性质如下:()()()()()()23e e o o f t f t f t f t =−=−−()()13∼式联立得()()()12e f t f t f t =+−⎡⎤⎣⎦ ()()()12o f t f t f t =−−⎡⎤⎣⎦ 解题过程:(a-1) (a-2)(a-3)(a-4)f t为偶函数,故只有偶分量,为其本身(b) ()(c-1)(c-2)(c-3)(c-4)(d-1)(d-2)(d-3)(d-4)1-20 分析过程:本题为判断系统性质:线性、时不变性、因果性(1)线性(Linearity):基本含义为叠加性和均匀性即输入()1x t ,()2x t 得到的输出分别为()1y t ,()2y t ,()()11T x t y t =⎡⎤⎣⎦,()()22T x t y t =⎡⎤⎣⎦,则()()()()11221122T c x t c x t c y t c y t +=+⎡⎤⎣⎦(1c ,2c 为常数)。
信号与系统习题解第二章1.从本章所讲的各讲中挑出你认为比较新的概念。
2.若物理信号()x t 的频谱存在,记为()X f ,考虑截断信号(),||()20,T T x t t x t ⎧≤⎪=⎨⎪⎩其它,1,||()20,T T t R t ⎧≤⎪=⎨⎪⎩其它在如下情况下的频谱(1)将截断信号()T x t 视为非周期模拟信号求其频谱()T X f ; (2)将截断信号()T x t 视为周期为T 的模拟信号求其频谱()T X n ;(3)将截断信号()T x t 视为)()()(t R t x t x T T =,求其频谱的解析表达式,并由此推出积分变换sin ()()()()()f s TKX f X s dsf s ππ+∞-∞-=-⎰的性质。
由此讨论各种观点下的频谱的表现形式以及内在规律。
解: (1)2222)(()()T T T T j ftj ft f X x t edt x t e dt ππ+∞---∞-==⎰⎰(2)2222()1()jnt TT nn T jn tTT n T x t C eC x t e dtTππ+∞=-∞--==∑⎰(3)2()2()22ˆ()()*()ˆ()()()()()sin ()()()T TTj f s t T T j f s t T X f X f R f X s R f s ds X s R t e dtds X s e dtds f s TX s dsf s ππππ+∞-∞∞+∞---∞-∞+∞---∞-+∞-∞==-==-=-⎰⎰⎰⎰⎰⎰积分变换sin ()()()()()f s TKX f X s ds f s ππ+∞-∞-=-⎰将信号()x t 的频谱化为截断信号()T x t 的频谱。
当视信号为非周期的模拟信号时,其频谱是模拟的;当视信号为周期的模拟信号时,其频谱是离散的;并且二者有如下关系1()n n C X T T=当视信号为两个信号的乘积时,其频谱为这两个信号频谱的卷积;利用这三种观点求出的频谱,在本质上是一致的。
3.给出帕色伐尔定理的不同表示形式(周期信号与非周期信号)。
解:(1)非周期信号 记()[()],()[()]X f FT x t Y f FT x t ==则()()()()x t y t dt X f Y f df +∞+∞-∞-∞=⎰⎰(2)周期信号指数表示设()T x t 和()T y t 为周期为T 的周期函数且22(1)(2)(),()n n j t j t TTT nT nn n x t Cey t Ceππ+∞+∞=-∞=-∞==∑∑则22(1)(2)222222(1)(2)222(1)(2)22(1)(2)()()11T T nm j t jt TTT T T T nmn m T n m j t j t T T T n m n m T n m j t T T nmn m nnn x t y t dt CeCedtT C e C e dtT T C Ce dt T TCC πππππ+∞+∞--=-∞=-∞+∞+∞-=-∞=-∞-+∞+∞-=-∞=-∞+∞=-∞====∑∑⎰⎰∑∑⎰∑∑⎰∑(3)周期信号正余弦表示设()T x t 和()T y t 为周期为T 的周期函数且(1)(1)(1)01(2)(2)(2)0122()cos sin222()cos sin2T k k k T k k k a kx kx x t a b T T a kx kx y t a b T T ππππ∞=∞==++=++∑∑ 则22(1)(2)(1)(1)(2)(2)002112(1)(2)(1)(2)(1)(2)00(1)(2)(1)(2)(1)(2)00()()2222cos sin cos sin 224222TT T T T T k k k kk k k k k k k k k k k k x t y t dta a kx kx kx kx ab a b dt T T T T a a T T a a b b a a T a a b b ππππ-∞∞-==+∞=-∞=-⎛⎫⎛⎫=++++ ⎪⎪⎝⎭⎝⎭=++=++⎰∑∑⎰∑+∞∞⎛⎫ ⎪⎝⎭∑4.给出图解法的实施步骤、数学证明中的辅助函数及其任意阶广义导函数。
见讲义5.证明以下普通函数的广义极限均为()t δ()10e erf λπ设()f t 是任意实的连续可积函数,则(1)()1()()()21()2 () [,]0,()()()(0)()()()()g t f t dt f t dt f dtf g t f t dt f f t f t dtg t t λλλλλλλλξλξξλλλξδδ+∞-∞--+∞+∞-∞-∞===∈-∴→=→=∴→⎰⎰⎰⎰⎰(2)()1||()()(1)()1|| ()(1) () [,]0,()()()(0)()()()()t g t f t dt f t dt t f dtf g t f t dt f f t f t dtg t t λλλλλλλλλξλλξξλλλξδδ+∞-∞--+∞+∞-∞-∞=-=-=∈-∴→=→=∴→⎰⎰⎰⎰⎰(3)()||1||11()()()2(1)1()2(1)() [,]0,()()()(0)()()()()t t g t f t dt e f t dt e f e dt e f g t f t dt f f t f t dtg t t λλλλλλλλλλξλξξλλλξδδ-+∞--∞----+∞+∞-∞-∞=-=-=∈-∴→=→=∴→⎰⎰⎰⎰⎰(4)()22()()1()()()()1()()() [,]0,()()()(0)()()()()t t g t f t dt e f t dterf f e dterf f g t f t dt f f t f t dtg t t πλλλλπλλλλλλπξλπξξλλλξδδ-+∞-∞---+∞+∞-∞-∞===∈-∴→=→=∴→⎰⎰⎰⎰⎰6.利用傅立叶正反变换可以导出一种非常广义的导数,其定义为()(){2()},()(())defDx t IFT j fX f X f FT x t π==因为傅立叶变换存在的条件相当低,所以很多不一定连续的函数也都存在如此定义的广义导数。
请模仿经典导数,列出该广义导数的性质。
解: 1.()()()()()()Dx y t Dx t Dy t +=+证明:()(){2(()())}{2()}{2()}()()()()Dx y t IFT j f X f Y f IFT j fX f IFT j f Y f Dx t Dy t πππ+=+=++=+2. ()()()()D x t D x t αα=3.()()()()()()()()D xy t x t D y t D x t y t =+证明:()(){2(()*())}D xy t IFT j f X f Y f π=而2(()*())2()()2()()2()()()2()()2()*(())2(())*()j f X f Y f j f X Y f d j X fY f d j X f Y f d j X Y f d j X f fY f j fX f Y f ππτττπτττπττττπττττππ+∞-∞+∞-∞+∞+∞-∞-∞=-=-=--+-=+⎰⎰⎰⎰所以()(){()*(2())(2())*()}(){2()}{2()}()()()()()()()D xy t IFT X f j fY f j fX f Y f x t IFT j fY f IFT j fX f y t x t D y t D x t y t ππππ=+=+=+…… 第三章1. 在一般情况下,按L ∞-范数收敛强于按2L -范数收敛,但在特殊情况下,按2L -范数收敛也能推出按L ∞-范数收敛。
比如令2L σ为所有能量有限且其频谱()X f 满足()||()0X f f X f σ<⎧=⎨⎩其它 的信号(),(,)x t t ∈-∞+∞组成的线性空间(按照通常的加法和数乘),按内积(,)()()x y x t y t dt +∞-∞=⎰诱导的范数12||||(,)x x x =成为一个Hilbert 空间。
它与有限区间(,)σσ-+上的一切平方可积函数构成的Hilbert 空间2(,)L σσ-+等距同构。
证明2()x t L σ∀∈,当2|()()|0,()n x t x t dt n +∞-∞-→→∞⎰时,必有(,)sup |()()|0,()t n x t x t n ∈-∞+∞-→→∞。
证明: 由于221222|()()||(()())||(()())||()()||()()||()()||()()|j ft n n j ft n n n Schwarts n Paserval equalityn x t x t X f X f e df X f X f e dfX f X f dfX f X f dfX f X f df x t x t dt ππσσσσ+∞-∞+∞-∞+∞-∞+-+-+∞-∞-=-≤-=-=-⎤≤-⎥⎦⎤=-⎰⎰⎰⎰⎰⎰122()()||n x t x t ⎥⎦=-从而(,)2sup |()()|()()||t n n x t x t x t x t ∈-∞+∞--因此当2|()()|0n x t x t dt +∞-∞-→⎰时,必有(,)sup |()()|0t n x t x t ∈-∞+∞-→。
2. 设()X f 为信号()x t 的频谱,{}()x n ∆为信号()x t 的采样序列,记0()()n nX f X f +∞=-∞=+∆∑,2()()j fn n X f x n e π+∞∆∆=-∞=∆∆∑,证明0()()X f X f ∆=。
证明:由于∑+∞-∞=∆+=n nf X f X )()(0是以∆1为周期的函数,即)()1(00f X f X =∆+,设20()j fm mm X f Ce π+∞-∆=-∞=∑ 为)(0f X Fourier 级数展开式, 其中122102122121221212()212122122()()()()()()(j fm m j fm n j fm n n nj m n n nj m n n j fm C X f e df n X f e df nX f e dfX ed Xe d Xf e dfx m ππππθπθπθθθθ∆∆-∆+∞∆∆-=-∞∆+∞∆∆-=-∞∆+∞+-∆∆∆∆-+=-∞∆∆+∞+∆∆∆-+=-∞∆∆+∞∆-∞=∆⎛⎫=∆+ ⎪∆⎝⎭=∆+∆=∆=∆=∆=∆⎰∑⎰∑⎰∑⎰∑⎰⎰)∆从而得到220()()()()j fm j fn m n X f x m ex n e X f ππ+∞+∞-∆-∆∆=-∞=-∞=∆∆=∆∆=∑∑3. 设{}()x n ∆为信号()x t 的采样序列,如果再以1μ∆=∆(2μ≥为正整数)抽出子列1{()}x m ∆,证明111111sin()()()()m t m x t x m t m ππ+∞=-∞-∆∆=∆-∆∆∑与sin()()()()n t n x t x n t n ππ+∞=-∞-∆∆=∆-∆∆∑满足 12111|2()()2|()|f x t x t X f df >∆-≤⎰,其中()X f 是()x t 的频谱。