统计(5)：茎叶图与直方图的比较

3。

５。

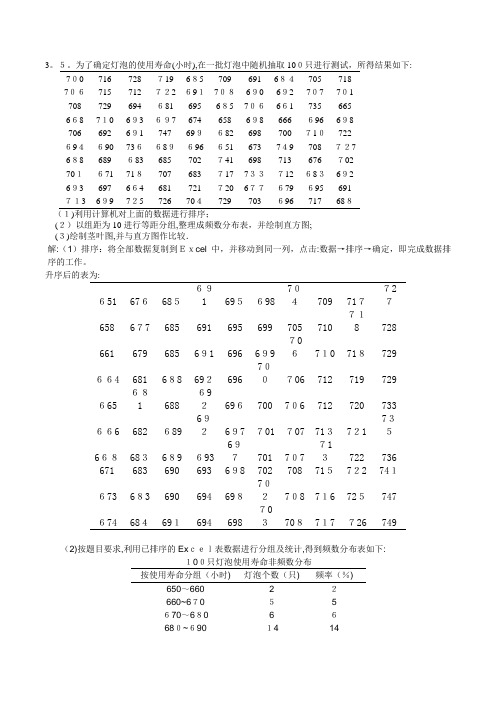
为了确定灯泡的使用寿命(小时),在一批灯泡中随机抽取10０只进行测试，所得结果如下: 7０0 716 728 ７19 6８5 709 691 6８４705 7187０６715 712 ７２2 ６9１7０８6９0 6９2 7０7 7０1708 729 694 ６81 695 6８5 7０６6６1 735 6656６8 7１0 6９3 ６９7 674 658 6９8 666 ６96 6９8706 692 6９1 747 69９６82 698 700 ７1０722６9４６90 73６６8９６96 ６51 673 7４9 708 ７２76８8 689 ６83 685 702 ７41 698 713 676 ７0270１６71 71８707 683 ７17 7３３７12 ６8３6９26９3 697 6６4 681 721 ７20 6７７６79 ６95 691７１3 6９9 7２5 726 70４729 703 ６96 717 68８（１)利用计算机对上面的数据进行排序；(２）以组距为10进行等距分组,整理成频数分布表，并绘制直方图;(３)绘制茎叶图,并与直方图作比较．解:（1）排序：将全部数据复制到Ｅｘcel中，并移动到同一列，点击:数据→排序→确定，即完成数据排序的工作。

升序后的表为:６51 67６68５６９1 69５６987０４709 71７７2７658 6７7 685 691 695 699 705 710 ７１8 728661 679 685 6９1 696 6９9 ７0６7１0 71８729６６4 681 6８8 69２696 7００７06 712 719 729６65 ６８1 688６9２69６700 7０6 712 720 733６６6 682 ６89 6９２6９7 ７01 ７07 71３7２17３５6６８68３6８9 ６93 6９７701 7０7７1３722 736671 683 690 693 6９8 702 708 71５7２2 74１６73 6８3 690 694 69８7０２7０8 7１6 72５747６74 68４69１694 698 ７0３70８7１7 ７26 749（2)按题目要求,利用已排序的Exｃｅｌ表数据进行分组及统计,得到频数分布表如下:１0０只灯泡使用寿命非频数分布按使用寿命分组（小时) 灯泡个数（只) 频率（％)650～660 2 ２660~6７0 ５ 5６70～6８0 6 ６68０~６90 １4 1469０~7０0 ２６２6700~71０1８１8710~720 1３１3720~73０1０10730~7４0 3 3７40～7５0 3 3合计10０１0０(3)制作直方图:将上表(包含总标题,去掉合计栏)复制到Exｃel表中，选择全表后,点击：图表向导→柱形图→选择子图表类型→完成。

统计学基础（贾俊平）课后简答题第一章1．什么是统计学？统计方法可以分为哪两大类？统计学是收集、处理、分析、解释数据并从数据中得出结论的科学。

统计方法可以分为描述统计和分类统计。

2、统计数据可分为哪几种类型？不同类型的数据各有什么特点？按照所采用的计量尺度不同，分为分类数据、顺序数据和数值型数据；按照统计数据的收集方法，分为观测的数据和实验的数据；按照被描述的对象与时间的关系，分为截面数据和时间序列数据。

按计量尺度分时：分类数据中各类别之间是平等的并列关系，各类别之间的顺序是可以任意改变的；顺序数据的类别之间是可以比较顺序的；数值型数据其结果表现为具体的数值。

按收集方法分时：观测数据是在没有对事物进行人为控制的条件下等到的；实验数据的在实验中控制实验对象而收集到的数据。

按被描述的对象与时间关系分时：截面数据所描述的是现象在某一时刻的变化情况；时间序列数据所描述的是现象随时间而变化的情况。

3．举例说明总体、样本、参数、统计量、变量这几个概念。

总体是包含所研究的全部个体（数据）的集合样本是从总体中抽取的一部分元素的集合参数是用来描述总体特征的概括性数字度量统计量是用来描述样本特征的概括性数字度量变量是说明现象某种特征的概念。

对一千灯泡进行寿命测试，那么这千个灯泡就是总体，从中抽取一百个进行检测，这一百个灯泡的集合就是样本，这一千个灯泡的寿命的平均值和标准差还有合格率等描述特征的数值就是参数，这一百个灯泡的寿命的平均值和标准差还有合格率等描述特征的数值就是统计量，变量就是说明现象某种特征的概念，比如说灯泡的寿命。

4．什么是有限总体和无限总体？举例说明。

根据总体所包含的单位数目是否可数可以分为有限总体和无限总体。

总体的范围能够明确确定，而且元素的数目是有限可数的。

比如，由若干个企业构成的总体就是有限总体，一批待检验的灯泡也是有限总体。

无限总体是指总体所包括的元素是无限的，不可数的。

例如，在科学试验中，每一个试验数据可以看作是一个总体的一个元素，而试验可以无限地进行下去，因此由试验数据构成的总体就是一个无限总体。

《统计学》分章习题及答案（贾俊平，第五版）主编：杨群目录习题部分 (2)第1章导论 (3)第2章数据的搜集 (4)第3章数据的整理与显示 (5)第4章数据的概括性度量 (6)第5章概率与概率分布 (10)第6章统计量及其抽样分布 (11)第7章参数估计 (11)第8章假设检验 (13)第9章分类数据分析 (14)第10章方差分析 (16)第11章一元线性回归 (17)第12章多元线性回归 (19)第13章时间序列分析和预测 (22)第14章指数 (25)答案部分 (30)第1章导论 (30)第2章数据的搜集 (30)第3章数据的图表展示 (30)第4章数据的概括性度量 (31)第5章概率与概率分布 (32)第6章统计量及其抽样分布 (33)第7章参数估计 (33)第8章假设检验 (34)第9章分类数据分析 (34)第10章方差分析 (36)第11章一元线性回归 (37)第12章多元线性回归 (38)第13章时间序列分析和预测 (40)第14章指数 (41)习题部分第1章导论一、单项选择题1．指出下面的数据哪一个属于分类数据（）A.年龄B.工资C.汽车产量D.购买商品的支付方式（现金、信用卡、支票）2.指出下面的数据哪一个属于顺序数据（）A.年龄B.工资C.汽车产量D.员工对企业某项制度改革措施的态度（赞成、中立、反对）3.某研究部门准备在全市200万个家庭中抽取2000个家庭，据此推断该城市所有职工家庭的年人均收入，这项研究的统计量是（）A.2000个家庭B.200万个家庭C.2000个家庭的人均收入D.200万个家庭的人均收入4.了解居民的消费支出情况，则（）A.居民的消费支出情况是总体B.所有居民是总体C.居民的消费支出情况是总体单位D.所有居民是总体单位5.统计学研究的基本特点是（）A.从数量上认识总体单位的特征和规律B.从数量上认识总体的特征和规律C.从性质上认识总体单位的特征和规律D.从性质上认识总体的特征和规律6.一家研究机构从IT从业者中随机抽取500人作为样本进行调查，其中60%的人回答他们的月收入在5000元以上，50%的回答他们的消费支付方式是使用信用卡。

简答题：1.简述直方图和茎叶图的区别：直：用于展示分组数据分布的一种图形。

茎：用于反映原始数据分布的图像。

茎叶图类似于横置的直方图，与直方图相比，茎叶图既能给出数据的分布状况，又能给出每一个原始数值，即保留了原始数据的信息。

而直方图虽然能很好的显示数据的分布，但不能保留原有的数据。

在应用方面，直方图通常适用于大批量数据，茎叶图适用于小批量数据。

2.回归分析主要解决那几个方面的问题:3.简述概率抽样的定义及特点：定义；遵循随机原则进行的抽样，总体中的每个单位都有一定的机会被选入样本。

特点;4.简述评价估计量好坏的标准:无偏性：估计量抽样分布的数学期望等于被估计的总体参数；有效性：对同一总体参数的两个无偏估计量，有更小的标准差的估计量更有效；一致性：随着样本量的增大，点估计量的值越来越接近被估计总体的参数。

5.简述直方图与条形图的不同点：①条形图是用条形的长度（横置时）表示各类别频数的多少，其宽度（表示类别）则是固定的；②直方图是用面积表示各组频数的多少，矩形的高度表示每一组的频数或频率，宽度表示各组的组距，因此其高度与宽度都有意义。

③由于分组数据具有连续性，直方图的各矩形通常是连续排列，而条形图则是分开排列。

条形图主要用于展示分类数据，直方图则主要用于展示数值型数据。

6.简述一张好的图形应具有的特征：①显示数据；②让读者把注意力集中在图形的内容上，而不是制作图形的程序上；③避免歪曲；④强调数据之间的比较；⑤服务于一个明确的目标；⑥有对图形的统计描述和文字说明。

7.简述众数、中位数、平均数的关系：从分布的角度，众数始终是一组数据分布的最高峰值，中位数是处于一组数据中间位置上的值，平均数是全部数据的算术平均。

因此，对于具有单峰分布的大多数数据而言，众数、中位数、平均数之间具有以下关系;若数据的分布是对称的，众数、中位数、平均数必定相等，若数据是左偏分布，说明数据存在极小值，必然拉动平均数向极小值一方靠，而众数和中位数由于是位值代表值，不受极值的影响；若数据是右偏分布，说明数据存在极大值，必然拉动平均数向极大值一方靠。

第一章统计和统计数据名词解释1.统计学：收集处理分析解释数据并从数据中得出结论的科学。

2.描述统计：研究数据收集处理汇总图表描述概括与分析等统计方法。

3.推断统计：研究如何利用样本数据来推断总体特征的统计方法。

4.分类数据：只能归于某一类别的非数字型数据。

5.顺序数据：只能归于某一有序类别的非数字型数据。

6.数值型数据：按数字尺度测量的观察值。

7.总体：包含所研究的全部个体（数据）的集合。

8.样本：从总体中抽取的一部分元素的集合。

9.参数：用来描述总体特征的概括性数字度量。

10.变量：说明现象某种特征的概念。

11.分类变量：说明事物类别的一个名称。

12.顺序变量：说明事物有序类别的一个名称。

13.数值型变量：说明事物数字特征的一个名称。

14.概率抽样：随机抽样，遵循随机原则进行的抽样，总体中每个单位都有一定的机会被选入样本。

15.非概率抽样：不随机，根据研究目的对数据的要求，采用某种方式从总体中抽出部分单位对其实施调查。

16.简单随机抽样：从包括总体的N个单位的抽样框中随机，一个个抽取n个单位作为样本，每单位等概论。

17.分层抽样：将抽样单位按某种特征或某种规则划分为不同的层，然后从不同层中独立、随机地抽取样本。

18.整群抽样：总体中若干单位合并为组，群，抽样时直接抽取群，然后对中选群中的所有单位全部实施调查。

19.系统抽样：总体中所有单位按顺序排列，在规定范围内随机抽取一单位作为初始单位，然后按事先规则确定其它样本单位。

20. 抽样误差：由于抽样的随机性引起的样本结果与总体真值之的误差简答题。

1.概率抽样与非概率抽样比较：性质不同，非概不依据随机原则选样本，样本统计量分布不确切，无法使用样本的结果对总体相应参数进行推断。

操作简便，时效快，成本低，专业要求不很高。

概率抽样依据随机原则抽选样本，理论分布存在，对总体有关参数可进行估计，计算估计误差，得到总体参数的置信区间。

提出精度要求。

2.数据收集方法的选择：抽样框中有关信息，目标总体特征，调查问题的内容，有形辅助物的使用，实施调查的资源，管理与控制，质量要求3.误差的控制：抽样误差是抽样随机性带来的，不可避免可以计算，改大样本量。

第二章习题与答案同学们根据自己作答的实际情况，并结合总正误率和单个题目正误统计以及答案解析来总结和分析习题！！！标红表示正确答案标蓝表示解析1、为掌握商品销售情况，对占该地区商品销售额60%的10家大型商场进行调查，这种调查方式属于( )。

A普查B抽样调查【解析：抽取一部分单位进行调查；习惯上将概率抽样（根据随机原则来抽取样本）称为抽样调查】C重点调查【解析：在调查对象中选择一部分重点单位进行调查的一种非全面调查】D统计报表2、人口普查规定标准时间是为了（）。

A确定调查对象和调查单位B避免资料的重复和遗漏。

C使不同时间的资料具有可比性D便于登记资料【解析：规定时间只是为了统计该时间段内的人口数据，没有不同时间数据对比的需要】3、对一批灯泡的使用寿命进行调查，应该采用( )。

A普查 B重点调查 C典型调查D抽样调查4、分布数列反映( )。

A总体单位标志值在各组的分布状况B总体单位在各组的分布状况【解析：课本30页1.分布数列的概念一段最后一句】C总体单位标志值的差异情况D总体单位的差异情况5、与直方图比较，茎叶图( )。

A没有保留原始数据的信息B保留了原始数据的信息【解析：直方图展示了总体数据的主要分布特征，但它掩盖了各组内数据的具体差异。

为了弥补这一局限，对于未分组的原始数据则可以用茎叶图来观察其分布。

课本P38】C更适合描述分类数据D不能很好反映数据的分布特征6、在累计次数分布中，某组的向上累计次数表明( )。

A大于该组上限的次数是多少B大于该组下限的次数是多少C小于该组上限的次数是多少【解析：向上累计是由变量值小的组向变量值大的组累计各组的次数或频率，各组的累计次数表明小于该组上限的次数或百分数共有多少。

课本P33】D小于该组下限的次数是多少7、对某连续变量编制组距数列，第一组上限为500，第二组组中值是750，则第一组组中值为 ( )。

A. 200B. 250C. 500D. 300【解析：组中值=下限+组距/2=上限+组距/2】8、下列图形中最适合描述一组定量数据分布的是( )。

1. 分类数据是只能归于某一类别的非数字型数据，(1分)它是对事物进行分类的结果，(1分)数据表现为类别，使用文字来表述的。

(1分)2. 四分位数(quartile)也称四分位点，他是一组数据排序后处于25%和75%位置上的值。

(1分)四分位数是通过3个点将全部数据等分为4部分，(1分)其中每部分包括25%的数据。

(1分)3. 方差分析（analysis of variance, ANOVA）就是通过检验各总体的均值是否相等，(1分)来判断分类型自变量对数值型因变量是否有显著影响。

(2分)4. 相关系数（correlation coefficient）是根据样本数据计算的，(1分)度量两个变量之间线性关系强度的统计量。

(2分)5. 居民消费价格指数（consumer price index， CPI）是度量居民消费品和服务项目价格水平随时间变动的相对数，(1分)反映居民家庭购买的消费品和服务价格水平的变动情况。

(2分)五、简答题6. 简述直方图和茎叶图的区别。

答：（1）直方图虽然能很好地显示数据的分布，但不能保留原始的数值；茎叶图类似于横置的直方图，与直方图相比，茎叶图既能给出数据的分布状况，又能给出每一个原始数值，即保留了原始数据的信息。

（3分）（2）在应用方面，直方图通常用于大批量数据，茎叶图通常适用于小批量数据。

（2分）7. 回归分析主要解决那几个方面的问题？答：（1）从一组样本数据出发，确定出变量之间的数学关系式；（1分）（2）对这些关系式的可信程度进行各种统计检验，并从中影响某一特定变量的诸多变量中找出哪些变量的影响是显著的，哪些是不显著的；（2分）（3）利用这些所求的关系式，根据一个或几个变量的取值来估计或预测另一个特定变量的取值，并给出这种估计或预测的可靠程度。

（2分8. 简述概率抽样的定义及特点。

答：概率抽样（probability sampling）也称随机抽样，是指遵循随机原则进行的抽样，总体中每个单位都有一定的机会被选入样本。

第一章：1、什么是统计学？统计学是一门收集、分析、表述、解释数据的科学和艺术。

2、描述统计:研究的是数据收集、汇总、处理、图表描述、概括与分析等统计方法。

推断统计：研究的是如何利用样本数据来推断总体特征。

3、统计学据可以分成哪几种类型，个有什么特点？按照计量尺度不同,分为：分类数据、顺序数据、数值型数据。

分类数据:只能归于某一类别的，非数字型数据。

顺序数据:只能归于某一有序类别的，非数字型数据。

数值型数据：按数字尺度测量的观察值,结果表现为数值。

按收集方法不同。

分为：观测数据、和实验数据观测数据：通过调查或观测而收集到的数据；不控制条件；社会经济领域实验数据：在试验中收集到的数据；控制条件；自然科学领域。

按时间不同,分为：截面数据、时间序列数据截面数据：在相同或近似相同的时间点上收集的数据。

时间序列数据:在不同时间收集的数据。

4、举例说明总体、样本、参数、统计量、变量这几个概念.总体:是包含全部研究个体的集合,包括有限总体和无限总体(范围、数目判定）样本：从总体中抽取的一部分元素的集合.参数：用来描述总体特征的概括性数字度量。

（平均数、标准差、比例等）统计量：用来描述样本特征的概括性数字度量。

(平均数、标准差、比例等）变量：是说明样本某种特征的概念，其特点：从一次观察到下一次观察结果会呈现出差别或变化。

(商品销售额、受教育程度、产品质量等级等)（对一千灯泡进行寿命测试，那么这千个灯泡就是总体，从中抽取一百个进行检测,这一百个灯泡的集合就是样本，这一千个灯泡的寿命的平均值和标准差还有合格率等描述特征的数值就是参数，这一百个灯泡的寿命的平均值和标准差还有合格率等描述特征的数值就是统计量，变量就是说明现象某种特征的概念,比如说灯泡的寿命。

)5、变量可以分为哪几类？分类变量：说明事物类别；取值是分类数据.顺序变量：说明事物有序类别；取值是顺序数据数值型变量：说明事物数字特征；取值是数值型数据。

变量也可以分为:随机变量和非随机变量;经验变量和理论变量6、举例说明离散型变量和连续型变量。