6.1.2平面直角坐标系(一)

6.1.2平面直角坐标系第一课时编写：衡帅杰审核：衡帅杰复审：蔡俊豪审批：刘俊华一、学习目标：1.认识平面直角坐标系，了解点与坐标的对应关系；2.在给定的直角坐标系中，能由点的位置写出点的坐标（坐标为整数），能根据坐标（坐标为整数）描出点的位置。

3.掌握特殊点的坐标的特征。

二、学习重难点：认识平面直角坐标系，根据点的位置写出点的坐标。

三、学习过程：（一）情景引入1、请画一条数轴，并指出它的三要素。

2、说出下列数轴上的点所表示的数。

A B-23、说出下列各点的坐标：A B C-2（二）探索新知①独立探索1、刚才是利用数轴确定点在直线上的位置，能否找到一种方法来确定平面内点的位置呢？（例如课本41页图6.1-3中的A、B、C、D的各点）2、平面直角坐标系的概念（认真阅读课本41页中间一段，理解平面直角坐标系及横轴、纵轴、原点、正方向等概念，并画个平面直角坐标系，标出X轴和Y轴，原点等）注意：在一般情况下，两条坐标轴所取的单位长度是一致的．3、点的坐标（认真阅读41页最后一段话）尝试：请在图6中写出点A 、B、C、D的坐标。

注意：表示点的坐标时，必须横坐标在前，纵坐标在后，中间用逗号隔开。

②合作探究（一）根据图6完成下列各题：1.上题中，点A到X轴的距离是_____。

到Y轴的距离是_____。

点C呢？2.对任意点Ｐ（X1，Y1）到X轴的距离为_____。

到Y轴的距离为_____。

3.你能在图6中描出点P（4,2）和Q（-3，-4）的坐标吗？说说你的方法。

（二）根据图7完成下列各题：4.（1）在图7的平面直角坐标系中，你能分别说出点A，B，C，D的坐标是什么吗？（2）从上面的练习中你有什么发现？原点O的坐标是什么？x轴和y轴上的点的坐标有什么特点？（三）学以致用（3-6题为宜）1、教材第43页“练习”第1，2题。

2、点A（2，-7）到x轴的距离为______，到Y轴的距离为______。

为。

4、如图，在直角坐标系中，画出点A（-3，4），B（-1，-2），O为原点，求三角形AOB的面积．（四）课堂小结本节课你学到了什么？（五）检测反馈1.在平面直角坐标系中描出下列各点的坐标：A（-5，3）、B（0，-4）、C（-3，-5）、D（4，-2）。

平面直角坐标系练习题及答案6.1.2 平面直角坐标系基础过关作业1.点 P(3,2) 在第一象限。

2.如图，矩形 ABCD 中，A(-4,1)，B(2,1)，C(2,3)，则点D 的坐标为(-4,3)。

3.以点 M(-3,0) 为圆心，以5为半径画圆，分别交 x 轴的正半轴，负半轴于 P、Q 两点，则点 P 的坐标为(4,0)，点 Q 的坐标为(-2,0)。

4.点 M(-3,5) 关于 x 轴的对称点 M1 的坐标是(-3,-5)；关于y 轴的对称点 M2 的坐标是(3,5)。

5.已知 x 轴上的点 P 到 y 轴的距离为3，则点 P 的坐标为(C) (0,3) 或 (0,-3)。

6.在平面直角坐标系中，点(-1,m2+1) 一定在第二象限。

7.在直角坐标系中，点 P(2x-6,x-5) 在第四象限中，则 x 的取值范围是(B) -3<x<5.8.如图，在所给的坐标系中描出下列各点的位置：A(-4,4)、B(-2,2)、C(3,-3)、D(5,-5)、E(-3,3)、F(0,0)。

这些点没有明显的关系。

综合创新作业9.(综合题) 在如图所示的平面直角坐标系中描出 A(2,3)、B(-3,-2)、C(4,1) 三点，并用线段将 A、B、C 三点依次连接起来，其面积为 12.5.10.如图，是儿童乐园平面图。

建立适当的平面直角坐标系，各娱乐设施的坐标为：滑梯(5,5)、秋千(2,2)、跷跷板(-3,-3)、摇摆(0,0)。

11.(创新题) 在平面直角坐标系中，画出点 A(0,2)、B(-1,0)，过点 A 作直线 L1 ∥x轴，过点 B 作 L2 ∥y轴，分析 L1、L2上点的坐标特点，由此，可以总结出在平面直角坐标系中，如果一条直线平行于 x 轴，那么这条直线上的点的 y 坐标相等；如果一条直线平行于 y 轴，那么这条直线上的点的 x 坐标相等。

12.(1) 已知点 P1(a,3) 与 P2(-2,-3) 关于原点对称，则a=2.(2) 在一次科学探测活动中，探测人员发现一目标在如图所示的阴影区域内，则目标的坐标可能是(D) (-2,-800)。

本节知识要点
1认识平面直角坐标系，了解点与坐标的对应关系
2在给定的直角坐标系中能根据坐标描出点，能由点的位置写出其坐标。

能力测试：
1．在直角坐标系中，坐标轴上到点P（－3，－4）的距离等于5的点共有（）
A．1个B．2个C．3个D．4个2．若点A（a，b）在第四象限，则点B（－a－2，b＋5）在（）A．第一象限B．第二象限C．第三象限D．第四象限3．已知A（a，b），A关于一、三象限平分线对称点为B．B与点C关于y 轴对称，点C与D关于x轴对称．则B与D关于（）对称．
A．x轴B．y轴C．原点D．都不是
答案：
1．C 设坐标轴上的点为M（x，0）或M（0，y）．由题意，得()5
4
32
2＝
＋
＋
x
或
()5
4
32
2＝
＋
＋y．解得x
1
＝0，x2＝－6，或y1＝0，y2＝－8．∴M的坐标是（0，
0），或（－6，0），或（0，－8）．
2．B 此题考查的是点的坐标及对称点的概念．若已知A（a，b）在第四象限，就相当于已知a＞0，b＜0；要判断B点在第几象限，就要判定－a－2与｜b｜＋5的符号．
∵点A（a，b）在第四象限，
∴a＞0，b＜0．∴－a－2＜0．
∵｜b｜＋5＞0，∴点B（－a－2，｜b｜＋5）在第二象限，故应选B．3．C 数形结合易知：B与D关于原点对称．。

第六章 6.1.2平面直角坐标系
大连市实验学校刘佳妮
教学过程设计
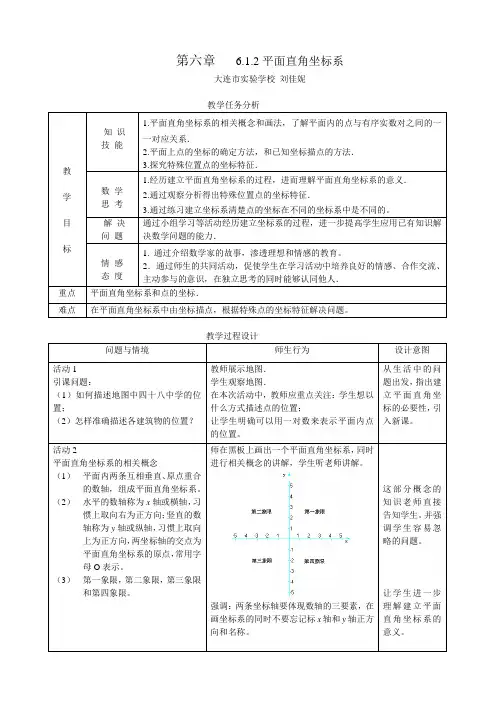
强调：两条坐标轴要体现数轴的三要素，
画坐标系的同时不要忘记标x轴和y轴正方
向和名称。

y
x -1
-21
23
4
-1-2-3-4-56543
21O
A(4,5)
B(-2,3)C(-4,-1)
D(2.5,-2)
师在屏幕上出示问题，找同学回答。

2.已知P点坐标为（a-1，a-5）：
①点P在x轴上，a= ；
②点P在y轴上，a= ；
③若a=-3，则P在第象限内；
（2）动手实践：如图，这是一所学校的平面示意图，建立适当的
平面直角坐标系，并用坐标表
示教学楼、图书馆、校门、实
验楼、国旗杆的位置。

思考：点的坐标是唯一的吗？
（3）发散思维。

联系生活，谈一谈利用平面直角坐标系可以解决那些问题？。

§6.1.2平面直角坐标系北京市永丰中学 钱健教学任务分析教学目标：1、知识与技能：了解平面直角坐标系的产生过程及其应用，熟练掌握由点确定坐标,根据坐标描出点的位置的方法；能利用坐标的符号特征解决相应问题；培养数形结合能力，小组合作交流能力，以及应用数学的能力.2、过程与方法：基本方法：问题式教学, 互动式教学、开放式教学、情境式教学.分别引导学生学会探究、学会合作、学会学习、学会体验.分别包含在情境引入、探索性质、变式训练；动手实践与思考相结合法鼓励学生动手操作.在操作过程中，启发学生思考，使学生操作与思考相结合.3、情感态度价值观：由平面直角坐标系的有关内容，以及由点找坐标，反映平面直角坐标系与现实世界的密切联系，让学生认识数学与人类生活的密切联系和对人类历史发展的作用，提高学生参加数学学习活动的积极性和好奇.重点：根据坐标描出点的位置；由点的位置写出点的坐标；不同位置点的坐标的符号特征.难点：根据要求合理建立平面直角坐标系，确定点的坐标；利用坐标的符号特征解决相应问题.教学活动设计【活动一】复习引入：请回答：1、数轴的三要素；2、请画一条数轴，在上面分别标出3和-1.5的点；3、分别写出数轴点A 、B 、C 、D 表示的数.【活动二】明确概念“思考：类似于利用数轴确定直线上点的位置，能不能找到一种方法来确定平面内的点的位置呢？（例如如图中，A 、B 、C 、D 个点？）提示：我们可以仿照用数轴表示直线上一个点的方式，构造两条数轴组成的工具，来表示平 AB D面上的一个点，这个工具叫做——平面直角坐标系.概念：1、平面直角坐标系；2、横轴、纵轴、原点；3、坐标；4、象限.【学生活动】写出P42/填空【活动三】实际应用例题1：在平面直角坐标系中，描出下列各点：A（4,5）、B（-2,3）、C（-4，-1），D（2.5，-2），E（0，-4）.探究：如图，正方形ABCD的边长为6，如果以点A为原点，AB所在直线为x轴，建立平面直角坐标系，那么y轴式哪条直线？写出正方形的顶点A、B、C、D的坐标.请另建立一个平面直角坐标系，这时正方形的顶点A、B、C、D的坐标又分别是多少？与同学交流一下.【活动四】自主探究1、原点的坐标有什么特点？2、任意在x轴，y轴上各找一个点，观察点的坐标有何特点？3、任意在四个象限内各找一个点，观察点的坐标的符号有何特点？总结：各象限内的点的坐标的符号是：第一象限：（+，+）；第二象限：（-，+）；第三象限（-，-）；第四象限：（+，-）.【注意】：当平面直角坐标系中的一个点的坐标位置确定后，它的坐标的符号也就确定了，反之，当一个点的坐标的符号确定了，它的位置也就确定了.【学生活动】填表P44/2例题2：指出下列各点所在的象限或坐标轴A（-2,0），B（2，-0.5），C（0，0），D（0，-3.3），E（5,5），F（-2，-4）例题3：已知x、y为实数，且P（x、y）的坐标满足x²+y²=0，则点p必在____________.例题4：在平面直角坐标系中，适合条件8y x 5x =-=，的点P （x ，y ）的个数为_______.s【活动五】课堂练习：书P43/练习，P44/1，P45/3，P46/7.【活动六】作业：P45/4、5、6.。