模拟电路第八章
- 格式:doc
- 大小:187.50 KB
- 文档页数:4






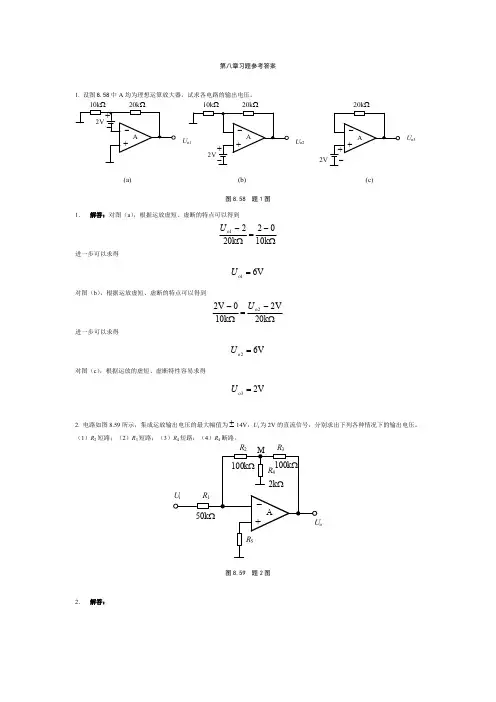
第八章习题参考答案1. 设图8.58中A 均为理想运算放大器,试求各电路的输出电压。
Ωk 10Ωk 20(a)U o2(b)Ωk 202V(c)U o3图8.58 题1图1.解答:对图(a ),根据运放虚短、虚断的特点可以得到Ω-=Ω-k 1002k 2021o U 进一步可以求得V61o =U 对图(b ),根据运放虚短、虚断的特点可以得到Ω-=Ω-k 20V2k 100V 22o U 进一步可以求得V62o =U 对图(c ),根据运放的虚短、虚断特性容易求得V2o3=U 2. 电路如图8.59所示,集成运放输出电压的最大幅值为14V,U i 为2V 的直流信号,分别求出下列各种情况下的输出电压。
±(1)R 2短路;(2)R 3短路;(3)R 4短路;(4)R 4断路。
o图8.59 题2图2.解答:(1)时可以得到,求得02=R ⎪⎩⎪⎨⎧-==1i3o M 0R U R U U V4o-=U (2)时可以得到03=R ⎪⎩⎪⎨⎧=-=-=M oi 12M V4UU U R R U (3)时支路无电流,放大电路相当于开环应用, 04=R 2R V14o -=U (4)时可以得到∞=4R V 8i 132o -=+-=U R R R U 3. 如图8.60所示电路,设A 为理想集成运算放大器。
(1)写出U o 的表达式;(2)若R f =3k ,R 1=1.5k ,R 2=1k ,稳压管VZ 的稳定电压值U Z =1.5V ,求U o 的值。
ΩΩΩ图8.60 题3图3.解答:(1)图中的集成运算放大器组成了同相比例运算电路,其输出电压表达式为P 1f N 1f o 11U R R U R R U ⎪⎪⎭⎫ ⎝⎛+=⎪⎪⎭⎫ ⎝⎛+=当稳压管VZ 的稳定电压值时,,输出电压表达式为V 10Z<U Z P U U =Z 1f o 1U R R U ⎪⎪⎭⎫⎝⎛+=当稳压管VZ 的稳定电压值时,,输出电压表达式为V 10Z>U k P U U =k1f o 1U R R U ⎪⎪⎭⎫⎝⎛+=(2),故输出电压表达式为V 10V 5.1Z<=U Z 1f o 1U R R U ⎪⎪⎭⎫⎝⎛+=将,,代入上式得Ω=k 3fR Ω=k 5.11R V 5.1Z =U V5.4V 5.1k 5.1k 31o =⨯⎪⎭⎫ ⎝⎛ΩΩ+=U 4. 如图8.61所示电路中,A 为理想运算放大器,已知R 1=R w =10k ,R 2=20k ,U i =1V ,输出电压的最大值为12V ,试分ΩΩ±别求出当电位器R w 的滑动端移到最上端、中间位置和最小端时的输出电压U o 的值。

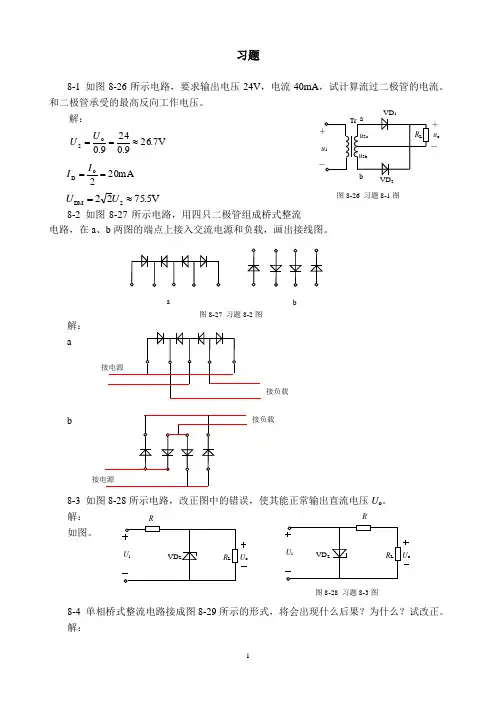
习题8-1 如图8-26所示电路,要求输出电压24V ,电流40mA ,试计算流过二极管的电流。
和二极管承受的最高反向工作电压。
解:V 7.269.0249.0o 2≈==U U mA 202oD ==I IV 5.75222D M ≈=U U8-2 如图8-27所示电路,用四只二极管组成桥式整流电路,在a 、b 两图的端点上接入交流电源和负载,画出接线图。
解: ab 8-3 如图8-28所示电路,改正图中的错误,使其能正常输出直流电压U o 。
解: 如图。
8-4 单相桥式整流电路接成图8-29所示的形式,将会出现什么后果?为什么?试改正。
解:图8-26 习题8-1图2图8-27 习题8-2图ab接负载接负载R图8-28 习题8-3图R变压器副边短路。
因为当u 2为负半周,即b 端为正, a 端为负时,VD 2、VD 1导通,VD 3、VD 4导通。
将VD 1及VD 3正负极换方向。
8-5 在图8-6所示单相桥式整流电路中,试分析产生下列故障时的后果。
(1)VD 1正负极接反。
(2)VD 2击穿。
(3)负载R L 短路。
(4)任一只二极管开路或脱焊。
解:(1)变压器副边短路。
(2)变压器副边短路。
(3)变压器副边短路。
(4)桥式整流电路变半波整流电路。
8-6 如图8-30所示电路,计算U 21= U 22= 24V 时,负载R L1和R L2上输出的电压? 解:U L1= U L2=0.9U 21=21.6V8-7 一桥式整流电容滤波电路,已知变压器二次侧电压频率50Hz ,负载电阻50Ω,要求负载电压为20V ,试选择整流二极管型号,并选择滤波电容。
解:V 7.162.1202.1o 2===U U A 4.0Loo ==R U I A 2.02oD ==I I V 6.2322D M ==U U查半导体手册可以选择2CZ55B ,其最大整流电流为1A ,最高反向工作电压为50V 。

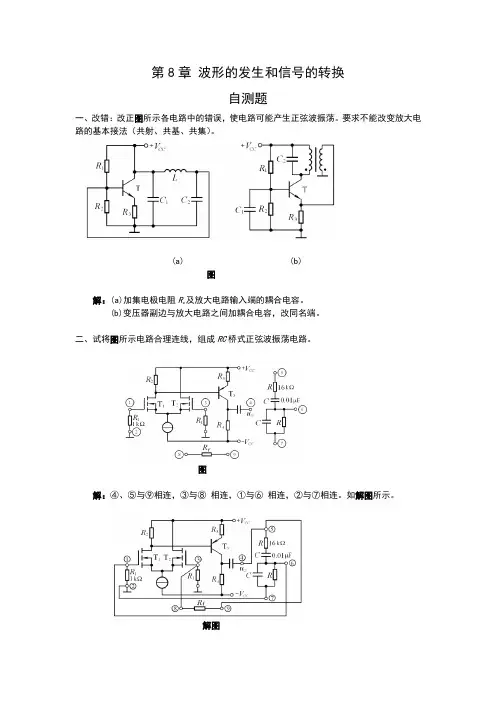
第8章波形的发生和信号的转换自测题一、改错:改正图所示各电路中的错误,使电路可能产生正弦波振荡。
要求不能改变放大电路的基本接法(共射、共基、共集)。
(a) (b)图解:(a)加集电极电阻R c及放大电路输入端的耦合电容。
(b)变压器副边与放大电路之间加耦合电容,改同名端。
二、试将图所示电路合理连线,组成RC桥式正弦波振荡电路。
图解:④、⑤与⑨相连,③与⑧ 相连,①与⑥ 相连,②与⑦相连。
如解图所示。
解图三、已知图(a)所示方框图各点的波形如图(b)所示,填写各电路的名称。
电路1为正弦波振荡电路,电路2为同相输入过零比较器,电路3为反相输入积分运算电路,电路4 为同相输入滞回比较器。
(a)(b)图四、试分别求出图所示各电路的电压传输特性。
(a) (b)图解:图(a)所示电路为同相输入的过零比较器;图(b)所示电路为同相输入的滞回比较器,两个阈值电压为±U T =±U Z。
两个电路的电压传输特性如解图所示。
解图五、电路如图所示。
图(1)分别说明A 1和A 2各构成哪种基本电路; (2)求出u O1与u O 的关系曲线u O1=f (u O ); (3)求出u O 与u O1的运算关系式u O =f (u O1); (4)定性画出u O1与u O 的波形;(5)说明若要提高振荡频率,则可以改变哪些电路参数,如何改变?解:(1)A 1:滞回比较器;A 2:积分运算电路。
(2)根据12111112121()02P O O O O N R R u u u u u u R R R R =⋅+⋅=+==++可得:8T U V ±=±u O1与u O 的关系曲线如解图 (a)所示。
(3) u O 与u O1的运算关系式1211121141()()2000()()O O O O O u u t t u t u t t u t R C=--+=--+ (4) u O1与u O 的波形如解图(b)所示。
第八章
8.1、试将下列二进制数转换为十进制数。
10
2431010111)())((= 10
2625.13101.11012)())((= 1026875.01011.03)())((=
8.2、试将下列十进制数转换为二进制数。
2
101001011751)())((= 210110101.11100183.573)())((=
8.3、试将下列二进制数转换为十六进制数及八进制数。
8
16266.08.011011.01)()())((==D 8
162275101111012)()())((==BD 8
16236.6778.3701111.1101113)()())((== 8.5试将下列十进制数表示为8421BCD 码。
BCD 8421100001.1010010011001.9321)())((=
BCD
84211001011000.0110011158.672)())((=
8.7、用真值表证明下列各式相等。
)()()(2AC AB C B A ⊕=⊕)(
C B A C B A )(3+=+)(
8.8、写出下列逻辑函数的对偶式'F 和反函数F 。
G E D C B A F ])[(2++=)(
解:G E D C B A F +++=])[('
G E D C B A F +++=])[(
BC A C B A F +++=)3(
解:C B A C B A F +∙+=)('
C B A C B A F +∙+=)(
8.10、用逻辑代数公式将下列逻辑函数化成最简与或表达式。
B C D C A ABD AB F +++=)(
1 解: BCD C A ABD AB F +++=
C A AB BCD
C A AB +=++=
D C B BC C A B A C B D C B A F ++++++=)(3)( 解: D C B BC C A B A C B D C B A F ++++++=)(
1=++++=++++=+++++=+++++=++++++=D
C A B
D C D
C A B A
D AC C
A D C A
B D B A
C B A C
A B A D C B D B A C B A BC
C A B A
D C C B D B A C B A
C B B A C B A F ++++=)(5
解: C B B A C B A F ++++=
1
))((=+++=+++=++++++=+++++=++∙=C B C A C
B C B A C B C B C A AB B A A C
B B A
C B A C
B B A
C B A
8.11、用卡诺图将下列逻辑函数化成最简与或表达式。
D C A C B A D C ABD ABC F ++++=)(1
))((3C B BCD CD A D C B A D B C A AB F +++++=)(
D B A C B A CD F ++=
)15,14,13,12,10,9,7,4(),,,(6m D C B A F ∑=)(
D AC BCD D C A D C B F +++=
)12109876543210(),,,(7,,,,,,,,,,,)(m D C B A F ∑=
D B C B D C A F +++=
8.12、用卡诺图将下列逻辑函数化成最简与或表达式。
)11,5,4,3,2()10,8,1,0(),,,(1d m D C B A F ∑+∑=)(
D B C A F += 0)11,5,4,3,2(=∑d
)15121098()141311421(),,,(3,,,,,,,,,)(d m D C B A F ∑+∑=
D C B D C B D C
B A F +++= 0)15121098(=∑,,,,d
C B A
D C A D C A D B A F +++=)(5
0=+CD AC
D B B A D A C F +
++=
0=+CD AC。