结构化学第5章例题与习题
- 格式:ppt
- 大小:764.50 KB
- 文档页数:18

目录第一章答案----------------------------------------------------------------------------1 第二章答案---------------------------------------------------------------------------26 第三章答案---------------------------------------------------------------------------47 第四章答案---------------------------------------------------------------------------63 第五章答案---------------------------------------------------------------------------711《结构化学》第一章习题答案1001 (D) 1002 E =h ν p =h /λ 1003,mvh p h ==λ 小 1004 电子概率密度 1005 1-241-9--34s kg m 10626.6s kg m 100.1106.626⋅⋅⨯=⋅⋅⨯⨯==-λhp T = m p 22 = 3123410109.92)10626.6(--⨯⨯⨯ J = 2.410×10-17J 1006 T = h ν- h ν0=λhc -0λhcT = (1/2) mv 2 v =)11(20λλ-m hc = 6.03×105 m ·s -11007 (1/2)mv 2= h ν - W 0 = hc /λ - W 0 = 2.06×10-19 J v = 6.73×105 m/s 1008 λ = 1.226×10-9m/10000= 1.226×10-11 m 1009 (B) 1010 A,B 两步都是对的, A 中v 是自由粒子的运动速率, 它不等于实物波的传播速率u , C 中用了λ= v /ν,这就错了。

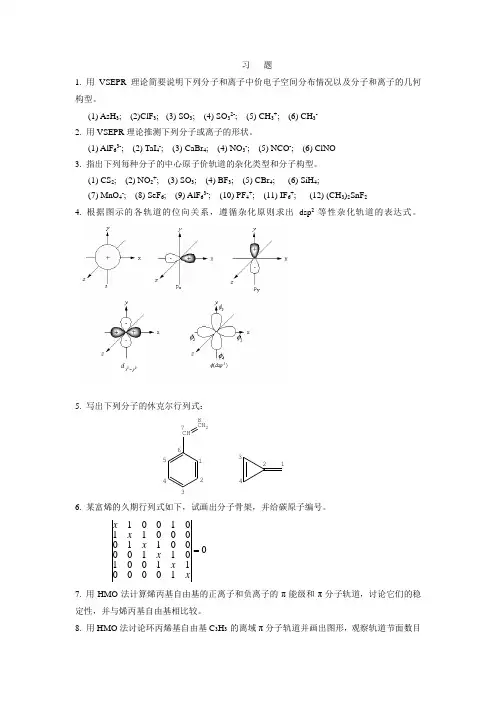
习 题1. 用VSEPR 理论简要说明下列分子和离子中价电子空间分布情况以及分子和离子的几何构型。
(1) AsH 3; (2)ClF 3; (3) SO 3; (4) SO 32-; (5) CH 3+; (6) CH 3- 2. 用VSEPR 理论推测下列分子或离子的形状。
(1) AlF 63-; (2) TaI 4-; (3) CaBr 4; (4) NO 3-; (5) NCO -; (6) ClNO 3. 指出下列每种分子的中心原子价轨道的杂化类型和分子构型。
(1) CS 2; (2) NO 2+; (3) SO 3; (4) BF 3; (5) CBr 4; (6) SiH 4;(7) MnO 4-; (8) SeF 6; (9) AlF 63-; (10) PF 4+; (11) IF 6+; (12) (CH 3)2SnF 24. 根据图示的各轨道的位向关系,遵循杂化原则求出dsp 2等性杂化轨道的表达式。
5. 写出下列分子的休克尔行列式:CH CH 21234567812346. 某富烯的久期行列式如下,试画出分子骨架,并给碳原子编号。
0100001100101100001100001101001 xx x x x x 7. 用HMO 法计算烯丙基自由基的正离子和负离子的π能级和π分子轨道,讨论它们的稳定性,并与烯丙基自由基相比较。
8. 用HMO 法讨论环丙烯基自由基C 3H 3·的离域π分子轨道并画出图形,观察轨道节面数目和分布特点;计算各碳原子的π电荷密度,键级和自由价,画出分子图。
9. 判断下列分子中的离域π键类型:(1) CO2(2) BF3(3) C6H6(4) CH2=CH-CH=O(5) NO3-(6) C6H5COO-(7) O3(8) C6H5NO2(9) CH2=CH-O-CH=CH2(10) CH2=C=CH210. 比较CO2, CO和丙酮中C—O键的相对长度,并说明理由。

第一章 量子理论1. 说明⎥⎦⎤⎢⎣⎡-=) (2cos ),(0t x a t x a νλπ及⎥⎦⎤⎢⎣⎡-=) (2sin ),(0t x a t x a νλπ都是波动方程22222),(1),(t t x a c x t x a ∂∂=∂∂的解。
提示:将),(t x a 代入方程式两端,经过运算后,视其是否相同。
解:利用三角函数的微分公式)cos()sin(ax a ax x=∂∂和)sin()cos(ax a ax x -=∂∂,将⎥⎦⎤⎢⎣⎡-=) (2c o s ),(0t x a t x a νλπ代入方程:⎥⎦⎤⎢⎣⎡-⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫⎝⎛⎥⎦⎤⎢⎣⎡--∂∂=⎭⎬⎫⎩⎨⎧⎥⎦⎤⎢⎣⎡-∂∂∂∂=⎥⎦⎤⎢⎣⎡-∂∂=) (2cos 2 ) (2sin 2 ) (2cos ) (2cos 2000022t x a t x x a t x x x a t x a x νλπλπνλπλπνλπνλπ左边 ()⎥⎦⎤⎢⎣⎡--=⎪⎪⎭⎫⎝⎛⎥⎦⎤⎢⎣⎡-∂∂=⎭⎬⎫⎩⎨⎧⎥⎦⎤⎢⎣⎡-∂∂∂∂=⎥⎦⎤⎢⎣⎡-∂∂=) (2cos 2 ) (2sin 2 ) (2cos ) (2cos 122020200222t x c a t x x c a t x t t c a t x a t c νλππννλππννλπνλπ右边 对于电磁波νλ=c ,所以⎥⎦⎤⎢⎣⎡-=) (2cos ),(0t x a t x a νλπ是波动方程的一个解。
对于⎥⎦⎤⎢⎣⎡-=) (2sin ),(0t x a t x a νλπ,可以通过类似的计算而加以证明:⎥⎦⎤⎢⎣⎡-⎪⎭⎫ ⎝⎛-=⎥⎦⎤⎢⎣⎡-∂∂=) (2sin 2) (2sin 20022t x a t x a x νλπλπνλπ左边()⎥⎦⎤⎢⎣⎡--=⎥⎦⎤⎢⎣⎡-∂∂=) (2sin 2) (2sin 12200222t x c a t x a t c νλππννλπ右边2. 试根据Planck 黑体辐射公式,推证Stefan 定律:4 T I σ=,给出σ的表示式,并计算它的数值。



第五章 多原子分子1. 试给出等键长弯曲构型分子H 3的分子轨道和能级图; 随着键角的增大(线形化), 能级图会产生什么变化? 根据能级图, 你认为稳定的实体是H 3, 还是H 3+或H 3-?解: 与水分子相同, H 3 分子属于点群C 2v , 参加成建的原子轨道涉及三个H 原子的1s 轨道容易验证, 中间的H 原子的1s 轨道属于恒等表示A 1, 而边上的两个H 原子的1s 轨道可重新组合成分别属于A 1和 B 2的两个基函数:)11(211b a a s s +=φ )11(212b a b s s -=φ21b a E E φφ<二中间原子的1s 轨道能量介于两者之间.按照对称性原理, 属于A 1的中间原子的1s 轨道与2b φ之间无相互作用, 但与1a φ有作用. 得到两个A 1对称性的分子轨道1a 1, 2a 1. 从能级图中可以看出, B 2对称性分子轨道的能量介于两个A 1对称性的分子轨道之间.当键角增大时, 1s a 和1s b 的重叠减小, 1a φ和2b φ能量差减小, 导致B 2对称性分子轨道的能量降低.由能级图可知, B 2对称性分子轨道为HOMO 轨道, 在H 3分子中, 其上填充有一个电子, 为不稳定电子结构, H 3+才是稳定的结构.2. 若H 4具有BH 3的几何构型, 请给出分子轨道和能级图、基组态及多重度(自旋单态、三态等), 由此判断它的稳定性如何?解: 与BH 3分子相同, H 4 分子属于点群D 3h , 由于所有原子都在同一个平面内, σh 是一个平庸的对称操作, 可以直接考虑在其子群D 3下讨这一体系. 参加成建的原子轨道涉及四个H 原子的1s 轨道容易验证, 中间的H 原子的1s 轨道属于恒等表示A 1, 周围的三个H 原子的1s 轨道可重新组合成分别属于A 1和E 的两个基函数:⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛---=⎪⎪⎪⎭⎫ ⎝⎛c b a e e a y x 616162212103131311 按照对称性原理, 属于A 1的中间原子的1s 轨道与e x , e y 轨道之间无相互作用, 但与上述a 1轨道有作用. 得到两个A 1对称性的分子轨道1a 1, 2a 1.能级图如下:HH 43H基组态为 (1a 1)2(e x )1(e y )1, 多重度为3, 为不稳定电子构型, 倾向于失去两个电子而成为H 42+.3.若H 4具有正四面体构型, 请给出分子轨道和能级图、基组态及多重度; 你认为稳定的实体是H 4, H 4+, H 42+, H 4-, H 42-中的哪一个?解: 若H 4具有正四面体构型, 则属于T d 对称性, 四个1s 轨道重新组合成一个a 1轨道和三个t 2轨道. 若按如图所示的坐标, 容易得到所有分子轨道:⎪⎪⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛------=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛d c b a t t t a z y x 212121212121212121212121212121212221 能级图如下:基组态为 (a 1)2(t 2)2, 多重度为3, 为不稳定电子构型, 倾向于失去两个电子而成为H 42+.4. 对CH 4, 若选择一个三重轴(C -H)为z 轴, xz 平面上有两个H, 原点在C 上, 试造出分子轨道和能级图.解: 若选择一个三重轴(C -H)为z 轴, xz 平面上有两个H, 原点在C 上, 原子坐标如图所示为碳原子坐标为(0, 0, 0), 四个氢原子坐标为a(0, 0, 1), b(322, 0, -31),c(-32,36,-31), d(-32,-36,-31). 四个H 原子在组合成a 1轨道时仍然取全对称组合, 在组合成t 2轨道时, 参照第114页NH 3群轨道的构造方法, 每一原子的轨道系数各取其对应的坐标. 例如, 在构造t 2x 时,各原子轨道的系数为坐标的x 分量.d c b t x 32323222--=, 归一化后为,d c b t x 6161622--=.同理可得 t 2y , t 2z 的群轨道. 归结为1t 24HH 4⎪⎪⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛------=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛d c b at t t a z y x 1211211211232121006161620212121212221 上述群轨道分别与C 原子的2s , 2p x , 2p y , 2p z 组合成分子轨道. 能级图如下:5. 根据题二与题三的结果, 画出Walsh 相关图,讨论H 4的几何构型(C 3v 与T d )与电子数的关系.解: 在画出Walsh 图之前, 我们先对两种结构的分子轨道的能量逐一加以比较,1a 1: 在C 3v 构型中, 周围三个H 原子的距离较远,重叠较之T d 构型要小, 故T d 构型1a 1轨道能量较低.C 3v 下的1e 和2a 1相当于T d 下的t 2轨道在子群下的分裂的结果. 显然, 1e 的能量低于t 2的能量2a 1的能量高于t 2的能量. 据此可画出Walsh 图:由上述相关图可知, H 4+, H 4取C 3v 构型, 其余取T d 构型.6. 请补充画出AH 2能级-键角相关图5.13中未画出的两条相关线: 3σg -4a 1与2σu -2b 2,预测H 2O 的激发组态(2a 1)2(1b 2)2(3a 1)2(1b 1)1(4a 1)1与(2a 1)2(1b 2)2(3a 1)2(1b 1)1(2b 2)1的几何构型:线性还是弯曲?(提示:根据反键轨道4a 1与2b 2的位相, 可以推知E 3σg (线形)>E 4a 1(弯曲), E 2σu <E 2b 2).解: 3σg , 2σu 轨道的示意图分别为:4H2t 2CCH41a 1C 3vTd显然, 当分子采取弯曲构型时, 对于3σg 轨道, 两个同位相的氢原子相互靠近, 使轨道能量下降,故E 3σg (线形)>E 4a1(弯曲);而对于2σu 轨道, 两个反位相的氢原子相互靠近, 使轨道能量升高, 故E 2σu <E 2b2. 据此可补充画出AH 2能级-键角相关图5.13中未画出的两条相关线.由上述能级相关图容易判断, H 2O 的两个激发组态的构型为: (1b 1)1(4a 1)1取弯曲结构, (1b 1)1(2b 2)1取线形结构.7. 对于CH 4, 当一个C -H 键不断缩短,直至H 与C 成为联合原子N,就得到了NH 3, 请给出CH 4与NH 3的能级相关图。



第五章 多原子分子的化学键1. (东北师大98)离域π键有几种类型? (三种) 正常离域π键,多电子离域π键,缺电子离域π键2. 用HMO 法计算环丙烯基π体系能量。
1 11 10 1 1 x x x=展开x 3-3x+2=0 (x-1)2(x+2)=0 解得 x 1=-2,x 2=x 3=1E 1=α+2β E 2= E 3=α-β E D π=2E 1+E 2=3α+3β3. NO 2+为直线型, NO 3-为平面三角型,指出它们中心原子杂化类型,成键情况和所属分子点群。
..4.3O-N-O : 2 D h O N N SP π+⎡⎤∞⎣⎦.杂化 2643h N SP D O O π⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦: 4. (东北师大99)推出y 轴的等性sp 2杂化轨道波函数 解: 等性杂化:c 112=c 212=c 312=1/3, Ψ1中只有py 成分:c 112+c 122=1 1s py ψ 123k k s k px k pyc c c ψφφφ=++11c =12c2s py px 3s py px ψψ5. (东北师大2000)乙烯中∠HCH=116.6。
,其中含-C-H 键指向x 轴的正向,试求形成该键的杂化轨道波函数和杂化指数。
解:x两个C -H 键夹角为116.6。
cos 0.3091kl αθαα==-=-p 成分/s 成分=(1- α)/α=2.236所以在C-H 方向上的杂化轨道为:sp 2.2361111222122233313233=c =c =c s pxs px py s px pyc c c c c ψφφψφφφψφφφ+++++22213123y 232222233323332333222221222322220.309, p , =1 +=1 0.191 c c c c c c c c c c c c c αψψψψ====++==等价,轨道对有相同的贡献231s px py s px py s pxψψψ+- 6. (东北师大2000) 分子离域π键的符号和久期行列式CH 2CH 2CH 2123456解:∏66x 1 0 0 0 0 1 x 1 0 1 0 0 1 x 1 1 0 0 0 1 x 0 0 0 1 1 0 x 1 0 0 0 0 1 x7. (北师大96)名词解释: 休克尔近似8. (北师大96)用HMO 法处理环丙烯基正离子C 3H 3+,计算该体系的π电子离域能。

《结构化学》第五章习题答案5001 (a) 小;(b) F的电负性比N高, NF3和NH3相比, NF3中电子离N远, 互斥作用小。
5002 (1) 两四面体共边连接;(2) 三个N原子呈直线型;(3) 四个配体近似四面体排列;(4) 四方锥形;(5) 平面四方形。
5003 NH35004 (a) 四面体形;(b) sp3;(c) 平面四方形;(d) sp3d2。
5005HgCl2: sp, 直线形; Co(CO)4-: sp3, 正四面体;ψ13/1φs+3/2φxpψ23/1φs-6/1φxp+2/1φypψ33/1φs-6/1φxp- 2/1φyp5005HgCl2: sp, 直线形; Co(CO)4-: sp3, 正四面体;ψ13/1φs+3/2φxpψ23/1φs-6/1φxp+2/1φypψ33/1φs-6/1φxp- 2/1φyp5007(1) c12= -c22cos116.8°= 0.4509c22由归一化条件c12+ c22= 1, 解得c1= 0.557, c2= 0.830;(2) ψ= 0.557ψ2s+ 0.830ψ2p在杂化轨道ψ中, ψ2s所占的比重为c12= 0.31,ψ2p所占的比重为c22= 0.69。
5008 (B) 5009ψ1= 0.617ψ2s+0.787ψ2xp;ψ2= 0.557ψ2s-0.436ψ2xp+0.707ψ2yp;ψ3= 0.557ψ2s-0.436ψ2xp-0.707ψ2yp。
5011 不对。
5012 不正确。
5013 (A)5015 (D)5016 不正确。
5018 (略去答案)5019 (B)5020 (C)5021分子中有两个垂直的∏33(1) 对每一个∏33E1= α + 2β, E2= α, E3= α - 2β;(2) 分子总离域能为1.65614;(3) 对每一个∏33ψ1= (1/2)φ1+ (2/2)φ2+(1/2)φ3 ,ψ2= (2/2)φ1- (2/2)φ3,ψ3= (1/2)φ1- (2/2)φ2+(1/2)φ3;(4) 分子总的π键键级P12= 1.414P23= 1.4145022采用HMO法, 中心C原子编号定为1, 得久期行列式│x 1 1 1 ││1 x 0 0 ││1 0 x 0 │= 0 ,│1 0 0 x│得x1= -3, x2= x3= 0, x4= 3,E1= α + 3β, E2= E3=α, E4= α -3β,以x1= -3代入久期方程可得ψ1= (1/2)φ1+( 1/6) (φ2+φ3+φ4)x = 0 代入久期方程可得c2+ c3+ c4= 0, c1= 0 ,c1= 0, 意味着在ψ2和ψ3中, 中心C原子的原子轨道没有参加, 中心C原子的π键级决定于ψ1, 其值为:P12=P13=P14=2×(1/2)×(1/6)=1/3中心C原子的成键度N=3+3×1/3=4.7325024依题意: │x 1 1 ││1 x 1 │=0│1 1 x │E1= α + 2β, E2= α - β, E3= α - βψ1= (1/ 3) (φ1+φ2+φ3)ψ2= (1/2)(φ2-φ3)ψ3= (1/6)(-2φ1+φ2+φ3)5025分子有两个垂直的∏33共轭体系,对每一个∏33为│x 1 0 ││1 x 1 │= 0, x=0,±2│0 1 x│E1= α + 2β, ψ1=(1/2)(φ1+ 2φ2+ φ3)E2= α, ψ2= (1/2) (φ1- φ3)E3= α - 2β, ψ3= (1/2)(φ1-2φ2+ φ3)1.318 0.096 1.318↑1.414 ↑1.414 ↑对整个分子C───C───C2.0 2.0 2.05026│x 1 0 1 ││1 x 1 0 ││0 1 x 1 │= 0 , x = 2,0,0,-2│1 0 1 x│E1= α + 2βE2= E3= αE4= α- 2βψ1=( 1/2)(φ1+ φ2+ φ3+ φ4)5027(1) E1= α + 2βE2= E3= αE4= α - 2β共轭能∆E = 2(2β) - 4β = 0(2) 由于共轭能为0 , 基态为双自由基, 稳定性差, 基态为三重态。
结构化学练习(4-7章)第四章练习(1)I3和I6不是独立的对称元素,因为I3= ,I6= 。
(2)下列等式成立的是A S3=C3+B S3=C6+σhC S3=C3+iD S3=C6+i(3)如果图形中有对称元素S6,那么该图形中必然包含A C6, σhB C3,C C3,iD C6,i(4)下列说法错误的是A 分子中有S n轴,则此分子必然同时存在C n轴和σh。
B 反映面σd一定也是反映面。
C I4是个独立的对称元素。
D 分子既有C n轴又有垂直于C n轴的σh,此分子必有Sn轴。
(5)对称元素C2与σh组合得到,C n轴与垂直于它的C2轴组合可得到。
(6)写出如下点群所具有的全部对称元素及其对称操作:(1)C2h (2)D3 (3)C3i(7)已知配合物MA2B4的中心原子M是d2sp3杂化,该分子中有多少种构造异构体,这些异构体各属于什么点群。
(8)下列说法正确的是A 凡是八面体配合物一定属于Oh点群B 异核双原子分子一定没有对称中心C 凡是四面体构型分子一定属于Td点群D 在分子点群中,对称性最低的是C1,对称性最高的是Oh(9)下列分子具有偶极矩,而不属于C nv群的是A H2O2B NH3C CH2Cl2D H2C=CH2(10)下列各组分子中有极性,但无旋光性的是(1)N3- (2)I3- (3)O3A (1),(2)B (2),(3)C (1),(2),(3)D (3)(11)下列具有相同阶的分子是(1)B2H6 (2)BrCl5 (3)SiF4A (1),(2)B (2),(3) B (1),(3) D 都不同(12)下列分子的点群不是16个群元素的是A CCl4B XeO4C S8D Ni(CN)4(13)(1)SO42- (2)PO43- (3)ClO4-三者中不是T d点群的是A (1)B (2)C (3)D 都是T d点群(14)下列空格中打上“+”或“-”分别表示对与错。
第五章题目1、三种原子○,◎,●排列成按虚线单位重复的点阵结构,试画出点阵素单位,写出结构基元。
●┄┄┄○┄┄┄●|◎●|○●○|●◎|●┄┄┄○┄┄┄●2、根据划分点阵正当单位的基本原则,试证平面点阵的四种类型中只有矩形单位可以有带心和不带心两种型式,而其它均无带心的型式。
3、根据划分点阵正当单位的基本原则,试说明为什么四方晶系中没有四方F和四方C。
4、有一AB2型立方面心晶体,问一个晶胞中可能含有多少个A和多少个B。
5、已知黄铁矿(FeS2,即“愚人金”)属立方晶系,请作图(取c与纸面垂直)示出其晶面(100)、(010)、(110)、(210)取向,并由图中计算出各晶面间距相应的晶面交角。
6、给出在三个坐标轴上之截距分别为(2a,3b,c) ,(a,b,c) ,(6a,3b,3c) ,(2a,-3b,-3c)的点阵面的指标。
7、论证在晶体结构中不可能存在五重旋转轴。
8、有一AB4型晶体,属立方晶系,每个晶胞中有1个A和4个B,1个A的坐标是(1/2,1/2,1/2),4个B的坐标分别是(0,0,0);(1/2,1/2,0);(1/2,0,1/2);(0,1/2,1/2),试确定此晶体的点阵类型。
9、请在一正八面体的明矾晶体上确定立方晶胞a、b、c的取向,并在立方晶系国际记号三个位相应的方向上找出正八面体的对称元素,写出正八面体点群的国际记号。
10、 -SiC为立方晶系晶体,晶胞参数a=435.8pm,晶胞中原子的分数坐标为C:0,0,0;1/2,1/2,0;1/2,0,1/2;0,1/2,1/2Si:1/4,1/4,1/4;1/4,3/4,3/4;3/4,1/4,3/4;3/4,3/4,1/4(1)确定该晶体的结构基元和点阵型式;(2)说明碳原子和硅原子的配位数各是多少;(3)计算晶体密度;(4)计算晶体中C —Si 键长和Si 原子的共价半径(C 原子的共价半径为77pm)(5)求d 100;1112、求算A 2型密堆积结构中圆球的空间占有率。