2018届中考数学复习第二部分空间与图形第二十五课时圆的有关概念和性质练习

《圆》章节知识点复习一、圆的概念集合形式的概念： 1、圆可以看作是到定点的距离等于定长的点的集合；2、圆的外部：可以看作是到定点的距离大于定长的点的集合；3、圆的内部：可以看作是到定点的距离小于定长的点的集合轨迹形式的概念：1、圆：到定点的距离等于定长的点的轨迹就是以定点为圆心，定长为半径的圆；（补充）2、垂直平分线：到线段两端距离相等的点的轨迹是这条线段的垂直平分线（也叫中垂线）；3、角的平分线：到角两边距离相等的点的轨迹是这个角的平分线；4、到直线的距离相等的点的轨迹是：平行于这条直线且到这条直线的距离等于定长的两条直线；5、到两条平行线距离相等的点的轨迹是：平行于这两条平行线且到两条直线距离都相等的一条直线。

二、点与圆的位置关系1、点在圆内⇒d r<⇒点C在圆内；2、点在圆上⇒d r=⇒点B在圆上；3、点在圆外⇒d r>⇒点A在圆外；三、直线与圆的位置关系1、直线与圆相离⇒d r>⇒无交点；2、直线与圆相切⇒d r=⇒有一个交点；3、直线与圆相交⇒d r<⇒有两个交点；A四、圆与圆的位置关系外离（图1）⇒ 无交点 ⇒ d R r >+； 外切（图2）⇒ 有一个交点 ⇒ d R r =+； 相交（图3）⇒ 有两个交点 ⇒ R r d R r -<<+； 内切（图4）⇒ 有一个交点 ⇒ d R r =-； 内含（图5）⇒ 无交点 ⇒ d R r <-；图1五、垂径定理垂径定理：垂直于弦的直径平分弦且平分弦所对的弧。

推论1：（1）平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧； （2）弦的垂直平分线经过圆心，并且平分弦所对的两条弧；（3）平分弦所对的一条弧的直径，垂直平分弦，并且平分弦所对的另一条弧 以上共4个定理，简称2推3定理：此定理中共5个结论中，只要知道其中2个即可推出其它3个结论，即：①AB 是直径 ②AB CD ⊥ ③CE DE = ④ 弧BC =弧BD ⑤ 弧AC =弧AD 中任意2个条件推出其他3个结论。

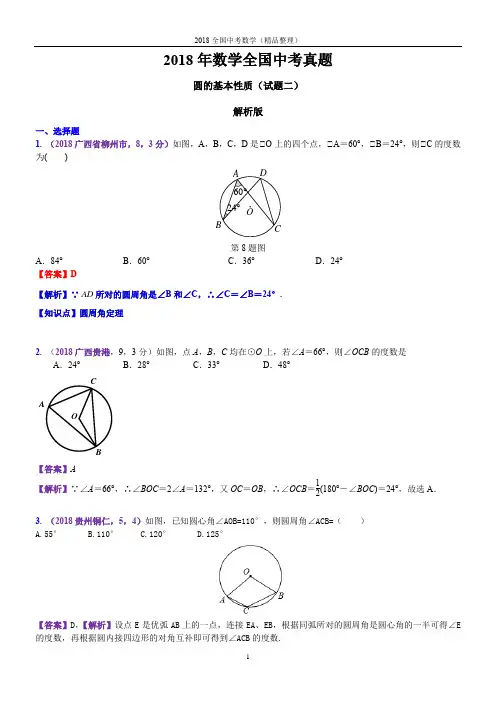
2018年数学全国中考真题圆的基本性质（试题二）解析版一、选择题1. （2018广西省柳州市，8，3分）如图，A ，B ，C ，D 是⊙O 上的四个点，⊙A ＝60°，⊙B ＝24°，则⊙C 的度数为( )第8题图 A ．84° B．60°C ．36°D ．24°【答案】D【解析】∵AD 所对的圆周角是∠B 和∠C ，∴∠C ＝∠B ＝24°.【知识点】圆周角定理2. （2018广西贵港，9，3分）如图，点A ，B ，C 均在⊙O 上，若∠A ＝66°，则∠OCB 的度数是 A ．24° B ．28° C ．33° D ．48°【答案】A【解析】∵∠A ＝66°，∴∠BOC ＝2∠A ＝132°，又OC ＝OB ，∴∠OCB ＝12(180°－∠BOC )＝24°，故选A ．3. （2018贵州铜仁，5，4）如图，已知圆心角∠AOB=110°，则圆周角∠ACB=（ ） A.55° B.110° C.120° D.125°【答案】D ，【解析】设点E 是优弧AB 上的一点，连接EA 、EB ，根据同弧所对的圆周角是圆心角的一半可得∠E 的度数，再根据圆内接四边形的对角互补即可得到∠ACB 的度数.【解答过程】设点E 是优弧AB 上的一点，连接EA 、EB ，如图， ∵∠AOB=110°，∴∠AEB=12∠AOB=55°，∴∠ACB=180°-∠E=125°.4. （2018江苏苏州，7，3分）如图，AB 是半圆的直径，O 为圆心，C 是半圆上的点，D 是AC 上的点．若∠BOC＝40°，则∠D 的度数为 A ．100° B ．110°C ．120°D ．130°【答案】B【解析】 本题解答时要利用等腰三角形的性质和圆的内接四边形的对角互补的性质进行计算.∵OC =OB ，∠BOC =40゜，∴∠B =70゜，∴∠D =180゜-70゜=110゜，故选B .5. （2018内蒙古通辽，7，3分）已知⊙O 的半径为10，圆心O 到弦AB 的距离为5，则弦AB 所对圆周角的度数是 A ．30° B ．60° C ．30°或150° D ．60°或120° 【答案】D【解析】如答图，连接OA 、OB ，∵OC ⊥AB ，∴OC ＝5，OA ＝OB ＝10，又OC ＝12OA ，∴cos ∠AOC ＝12，∴∠AOC ＝60°∴∠AOB ＝120°，∴弦AB 所对的圆周角的度数是60°或120°． 故选D ．6.（湖北省咸宁市，7，3）如图，已知⊙O 的半径为5，弦AB ，CD 所对的圆心角分别为∠AOB ，∠COD ，若∠AOB 与∠COD 互补，弦CD =6，则弦AB 的长为( )A ．6B ．8 C． D．【答案】【解析】解：作OF ⊥AB 于F ，作直径BE ，连接AE ，如图， ∵∠AOB+∠COD=180°， 而∠AOE+∠AOB=180°， ∴∠AOE=∠COD ， ∴AE DC ，∴AE=DC=6，∵OF ⊥AB ， ∴BF=AF ， 而OB=OE ，∴OF 为△ABE 的中位线， 由勾股定理可得AF=4，∴AB=8，故选择B ．【知识点】圆周角定理；垂径定理；三角形中位线性质7. (2018湖北黄石，8，3分)如图，AB 是⊙O 的直径，点D 为⊙O 上一点，且∠ABD ＝30°，BO ＝4，则BD 的长为( )第8题图A ．23πB ．43πC ．2πD ．83π FE【答案】D 【解析】连接OD ，则∠AOD ＝2∠B ＝60°，∴∠BOD ＝120°.∴l BD ＝120180π×4＝83π.8. (2018湖南邵阳，6，3分)如图(二)所示，四边形ABCD 为⊙O 的内接四边形，∠BCD ＝120°，则∠BOD 的大小是( )A ．80°B ．120°C ．100°D ．90°图(二)【答案】B ，【解析】根据“圆内接四边形的对角互补”可得∠BCD ＋∠A ＝180°，因为∠BCD ＝120°所以∠A ＝60°．又根据“在同圆中，同弧所对的圆心角等于圆周角的2倍”，所以∠BOD ＝2∠A ＝120°．故选B ．9.（2018四川眉山，6，3分）如图所示，AB 是⊙O 的直径，P A 切⊙O 于点A ，线段PO 交⊙O 于点C ，连结BC ，若∠P ＝36°，则∠B 等于（ ）A ．27°B ．32°C ．36°D ．54°【答案】A ，【解析】由P A 是⊙O 的切线，可得⊙OAP ＝90°，∴∠AOP ＝54°，根据同弧所对的圆周角等于圆心角的一半，可得∠B ＝27°10. （2018辽宁锦州，7，3分）如图：在△ABC 中，∠ACB=90°，过B 、C 两点的⊙O 交AC 于点D ，交AB 于点E ，连接EO 并延长交⊙O 于点F ，连接BF 、CF ，若∠EDC=135°，CF=22，则AE 2+BE 2的值为A 、8B 、12C 、16D 、20D【答案】C，【解析】：如图，∠EDC=1350，∠ACB=90°，得△ACB是等腰直角三角形，ECF是等腰直角三角形，得△AEC与△BFC是全等三角形，AE=BF,△EBF是直角三角形，AE2+BE2=FE2=2FC2.二、填空题100，则弧AB所对的圆周角是°.1.（2018广东省，11，3）同圆中，已知弧AB所对的圆心角是【答案】50°【解析】同弧所对的圆周角是圆心角的一半，圆心角为100°，所以圆周角为50°.【知识点】圆周角、圆心角关系2. （2018海南省，18，4分）如图，在平面直角坐标系中，点A 的坐标是（20，0），点B 的坐标是（16，0），点C ， D 在以OA 为直径的半圆M 上，且四边形OCDB 是平行四边形，则点C 的坐标为________．【答案】（2，6）【思路分析】过点M 作MN ⊥CD ，垂足为点N ，连接CM ，过点C 作CE ⊥OA ，垂足为点E ，由题意可知OB 及圆的半径长，OB =CD ，由垂径定理可求得MN 的长，CN =EM ，从而求出OE 的长，进而得到点C 的坐标．【解题过程】过点M 作MN ⊥CD ，垂足为点N ，连接CM ，过点C 作CE ⊥OA ，垂足为点E ，点A 的坐标是（20，0），所以CM =OM =10，点B 的坐标是（16，0），所以CD =OB =16，由垂径定理可知，821==CD CN ，在Rt⊙CMN 中，CM =10，CN =8，由勾股定理可知MN =6，所以CE =MN =6，OE =OM ﹣EM =10﹣8=2，所以点C 的坐标为（2，6）．【知识点】垂径定理，勾股定理，平行四边形的性质3. （2018黑龙江省龙东地区，6，3分）如图，AB 为⊙O 的直径，弦CD ⊥AB 于点E ，已知CD ＝6，EB ＝＝1，则⊙O 的半径为________．【答案】5【解析】连接OC ，∵AB 是⊙O 的直径，CD ⊥AB ，∴CE ＝12CD ，∵CD ＝6，∴CE ＝3．设⊙O 的半径为r ，则OC ＝r ，∵EB ＝1，∴OE ＝4，在Rt △OCE 中，由勾股定理得OE 2＋CE 2＝OC 2，∴（r －1）2＋32＝r 2，解得r ＝5，∴⊙O 的半径为5．D【知识点】垂径定理；勾股定理4.（2018黑龙江绥化，16，3分）如图，△ABC是半径为2的圆内接正三角形，则图中阴影部分的面积是．（结果用含π的式子表示）【答案】4π-.【解析】解：连接OA，OB，OC，过O点作OD⊥BC于点D.∵△ABC为等边三角形，∴∠OBD=30°.∵⊙O的半径为2，∴OB=2，∴OD=1，∴∴S△ABC=3S△OBC=3×12BC·OD=D∴S阴影=4π-故答案为：4π-【知识点】含30°角的直角三角形的性质，垂径定理，三角形面积计算，圆的面积计算5.（2018黑龙江绥化，20，3分）如图，一下水管道横截面为圆形，直径为100cm，下雨前水面宽为60cm，一场大雨过后，水面宽为80cm，则水位上升 cm【答案】10或70.【解析】解：作半径OD⊥AB于C，连接OB，由垂径定理得：BC=12AB=30，在Rt△OBC中，当水位上升到圆心以下时水面宽80 cm则OC′，水面上升的高度为：40-30=10cm；当水位上升到圆心以上时，水面上升的高度为：40+30=70cm，综上可得，水面上升的高度为10cm或70cm．故答案为10或70.【知识点】垂径定理，勾股定理6.7.（2018浙江嘉兴，14，4）如图，量角器的O度刻度线为AB．将一矩形直尺与量角器部分重叠，使直尺一边与量角器相切于点C，直尺另一边交量角器于点A、D，量得AD＝10cm，点D在量角器上的读数为60°．则该直尺的宽度为cm．【解析】根据题意，抽象出数学图形根据题意可知：AD ＝10，∠AOD ＝120°，由OA ＝OD ，∴∠DAO ＝30°，设OE ＝x ，则OA ＝2x ，∵OE ⊥AD ，∴AE ＝DE ＝5，在Rt △AOE 中，x 2+52＝（2x ）2，解得：xCE ＝OE8. （2018贵州省毕节市，19，3分）如图,AB 是⊙O 的直径，C 、D 为半圆的三等分点，CE ⊥AB 于点E ， ∠ACE 的度数为______.【答案】30°．【解题过程】∵AB 是⊙O 的直径,C 、D 为半圆的三等分点，∴∠A ＝∠BOD ＝13×180°＝60°，又∵CE ⊥AB ，∴∠ACE ＝90°－60°＝30°．【知识点】圆的性质；直角三角形的性质9.（2018吉林省，13, 2分）如图，A ，B ，C ，D 是⊙O 上的四个点，=⌒BC ，，若∠AOB=58°，则∠BDC=___ 度．BO【答案】29【解析】连接CO，根据同圆中，等弧所对圆心角相等，则∠COB=∠AOB=58°，∴∠BDC=29°【知识点】圆周角定理，圆心角、弧、弦之间的关系10.（2018江苏扬州，15，3）如图，已知⊙O的半径为2，△ABC内接于⊙O，∠ACB=135°，则AB= ．2【答案】2【思路分析】根据圆内接四边形对边互补和同弧所对的圆心角是圆周角的2倍，可以求得∠AOB的度数，然后根据勾股定理即可求得AB的长．【解题过程】连接AD、AE、OA、OB，∵⊙O的半径为2，△ABC内接于⊙O，∠ACB=135°，∴∠ADB=45°，∴∠AOB=90°，∵OA=OB=2，∴2，故答案为2．【知识点】三角形的外接圆和外心，圆内接四边形对边互补，圆周角的性质11.（2018青海，9，2分）如图5，A、B、C是⊙O上的三点，若∠AOC=110°,则∠ABC= . 【答案】125°．【解析】如图所示：优弧AC上任取一点D，连接AD、CD，∵∠AOC=110°，∴∠ADC=∠AOC=×110°=55°，∵四边形ABCD内接与⊙O，∴∠ABC=180°﹣∠ADC=180°﹣55°=125°．【知识点】圆内接四边形的性质，圆周角的性质12. （2018江苏镇江，9，2分）如图，AD 为△ABC 的外接圆⊙O 的直径，若∠BAD ＝50°，则∠ACD ＝________°．【答案】40°．【解析】如答图所示，连接B C ． ∵AB 是⊙O 的直径， ∴∠ACB ＝90°．∵∠BCD ＝∠BAD ＝50°，∴∠ACD ＝∠ACB －∠BCD ＝90°－50°＝40°．13. （2018内蒙古通辽，17，3分）如图，在平面直角坐标系中，反比例函数y ＝kx （k ＞0）的图象与半径为5的⊙O 相交于M 、N 两点，△MON 的面积为3.5，若动点P 在x 轴上，则PM ＋PN 的最小值是 ．【答案】52【解析】设M （a ，b ），则N （b ，a ），依题意，得：a 2＋b 2＝52……①（第9题答图）（第9题图）a 2－ab －12（a －b ）2＝3.5……②①、②联立解得a ＝572，b ＝432所以M 、N 的坐标分别为（572，432），（432，572） 作M 关于x 轴的对称点M ′，则M ′的坐标为（572，－432）， 则M ′N 的距离即为PM ＋PN 的最小值．由于M ′N 2＝（572－432）2＋（－432－572）2＝50， 所以M ′N ＝52，故应填：52．14. （2018山东莱芜，16，3分）如图，正方形ABCD 的边长为2a ，E 为BC 边的中点，⌒AE 、⌒DE 的圆心分别在边AB 、CD 上，这两段圆弧在正方形内交于点F ，则E 、F 间的距离为_______．【答案】32a【思路分析】先用勾股定理求出⌒DFE 的所在圆的半径，再由垂径定理求出EF 的长．【解题过程】解：如图，设⌒DFE 的圆心为G ，作GH ⊥EF 于H ，连接EG ．设⌒DFE 所在圆的半径为x ，在Rt △CEG 中，EG 2＝CG 2＋CE 2，则x 2＝(2a －x )2＋a 2，解得x ＝54a ；由垂径定理，得EF ＝2EH ＝2⎝ ⎛⎭⎪⎫54a 2－a 2＝32a ．故答案为32a ．【知识点】正方形的性质；勾股定理；垂径定理；15. （2018湖北随州12，3分）如图，点A ，B ，C 在⊙O 上，∠A ＝40度，∠C ＝20度，则∠B ＝______度．EEA D【答案】60．【解析】如图，连接OA ，根据“同圆的半径相等”可得OA ＝OC ＝OB ，所以∠C ＝∠OAC ，∠OAB ＝∠B ，故∠B ＝∠OAB ＝∠OAC ＋∠BAC ＝∠C ＋∠BAC ＝20°＋40°＝60°．16.（2018湖北随州16，3分）如图，在四边形ABCD 中，AB ＝AD ＝5，BC ＝CD 且BC ＞AB ，BD ＝8．给出下列判断：①AC 垂直平分BD ；②四边形ABCD 的面积S ＝AC ·BD ；③顺次连接四边形ABCD 的四边中点得到的四边形可能是正方形；④当A 、B 、C 、D 四点在同一个圆上时，该圆的半径为256； ⑤将△ABD 沿直线BD 对折，点A 落在点E 处，连接BE 并延长交CD 于点F ，当BF ⊥CD 时，点F 到直线AB 的距离为678125．其中正确的是______________．（写出所有正确判断的序号）【答案】①③④．【解析】根据“到线段两个端点的距离相等的点在这条线段的垂直平分线上”可知，A ，C 两点都在线段BD 的垂直平分线上，又“两点确定一条直线”，所以AC 垂直平分BD ，故①正确； 如图1，取AC ，BD 的交点为点O ，则由①知OB ⊥AC ，OD ⊥AC ，所以S 四边形ABCD ＝S △ABC ＋S △ADC ＝12AC ·OB ＋12AC ·OD ＝12AC ·(OB ＋OD )＝ 12AC ·BD ，故②错误； 如图2，取AB ，BC ，CD ，AD 四边的中点分别为P ，Q ，M ，N ，则由三角形的中位线定理得PQ ∥AC ∥MN ，PQ ＝MN ＝12AC ，PN ∥BD ∥QM ，PN ＝QM ＝12BD ，于是知四边形PQMN 及阴影四边形都是平行四边形．又由①知AC ⊥BC ，所以可证∠AOB ＝∠QPN ＝90°，故四边形PQMN 为矩形．若AC ＝BD ，则有PQ ＝PN ，四边O ABCCBAO ABDC形PQMN 是正方形，所以顺次连接四边形ABCD 的四边中点得到的四边形可能是正方形，故③正确；当A 、B 、C 、D 四点在同一个圆上时，四边形ABCD 是这个圆的内接四边形，则∠ABC ＋∠ADC ＝180°．根据“SSS ”可证△ABC ≌△ADC ，所以∠ABC ＝∠ADC ＝90°，则AC 是这个圆的直径．由①知BO ＝OD ＝12BD ＝4，在Rt △AOB 中，根据勾股定理，求得AO＝3．然后，证明△AOB ∽△ABC ，得到AB 2＝AO ·AC ，所以AC ＝253，该圆的半径为256，故④正确； 如图1，过点F 作FG ⊥AB 于点G ，过点E 作EH ⊥AB 于点H ，由折叠知，AE ＝2AO ＝6，BE ＝BA ＝5．由于BF ⊥CD ，AE ⊥BD ，可证得△BOE ∽△BFD ，所以BO BF ＝BE BD ，即4BF ＝58，BF ＝325．因为S △ABE ＝12AB ·EH＝12AE ·BO ，所以EH ＝645⨯＝245．又可证△BEH ∽△BFG ，所以EH FG ＝BE BF ，即245FG ＝5325，FG ＝768125，故⑤错误．17. （2018云南曲靖，10，3分）如图，四边形ABCD 内接于⊙O ，E 为BC 延长线上一点，若∠A ＝n °，则∠DCE ＝_________【答案】n °【解析】圆内接四边形的对角互补，所以∠BCD ＝180°－∠A ，而三点BCD 在一条直线上，则∠DCE ＝180°－∠BCD ，所以∠DCE ＝∠A ＝n °.18. （2018年浙江省义乌市，13，5）如图，公园内有一个半径为20米的圆形草坪，A ，B 是圆上的点，O 为圆心，∠AOB =120°，从A 到B 只有路AB ，一部分市民为走“捷径”，踩坏了花草，走出了一条小路AB ．通过计算可知，这些市民其实仅仅少B 走了_________步（假设1步为0.5米，结果保留整数）．（参考数据：图1GFEH OABDC 图21.732，π取3.142）【答案】15【解析】作OC⊥AB于C，如图，则AC=BC，∵OA=OB，∴∠A=∠B=12（180°﹣∠AOB）=12（180°﹣120°）=30°，在Rt△AOC中，OC=12OA=10，，∴69（步）；而AB的长=12020180π⨯≈84（步），AB的长与AB的长多15步．所以这些市民其实仅仅少B走了15步．故答案为15．【知识点】垂径定理；勾股定理19.（2018浙江舟山，14，4）如图，量角器的O度刻度线为AB．将一矩形直尺与量角器部分重叠，使直尺一边与量角器相切于点C，直尺另一边交量角器于点A、D，量得AD＝10cm，点D在量角器上的读数为60°．则该直尺的宽度为cm．BC【解析】根据题意，抽象出数学图形根据题意可知：AD ＝10，∠AOD ＝120°，由OA ＝OD ，∴∠DAO ＝30°，设OE ＝x ，则OA ＝2x ，∵OE ⊥AD ，∴AE ＝DE ＝5，在Rt △AOE 中，x 2+52＝（2x ）2，解得：x ，∴CE ＝OE．三、解答题1. （2018年江苏省南京市，26，8分）如图，在正方形ABCD 中，E 是AB 上一点，连接DE .过点A 作AF DE ⊥，垂足为F .⊙O 经过点C 、D 、F ，与AD 相交于点G .（1）求证AFG DFC ∽△△；（2）若正方形ABCD 的边长为4，1AE =，求O 的半径.【思路分析】（1）欲证明△AFG ∽△DFC ，只要证明∠FAG=∠FDC ，∠AGF=∠FCD ； （2）首先证明CG 是直径，求出CG 即可解决问题；【解题过程】（1）证明：在正方形ABCD 中，90ADC ∠=. ∴90CDF ADF ∠+∠=. ∵AF DE ⊥. ∴90AFD ∠=.∴90DAF ADF ∠+∠=. ∴DAF CDF ∠=∠.∵四边形GFCD 是⊙O 的内接四边形， ∴180FCD DGF ∠+∠=. 又180FGA DGF ∠+∠=，O∴FGA FCD ∠=∠. ∴AFG DFC ∽△△. （2）解：如图，连接CG .∵90EAD AFD ∠=∠=，EDA ADF ∠=∠， ∴EDA ADF ∽△△. ∴EA DA AF DF =，即EA AFDA DF=. ∵AFG DFC ∽△△， ∴AG AFDC DF =. ∴AG EADC DA=. 在正方形ABCD 中，DA DC =，∴1AG EA ==，413DG DA AG =-=-=.∴5CG ===.∵90CDG ∠=， ∴CG 是⊙O 的直径. ∴⊙O 的半径为52.【知识点】相似三角形的判定和性质 正方形的性质 圆周角定理及推论2. （2018江苏徐州，28，10分） 如图，将等腰直角三角形ABC 对折，折痕为CD ．展平后，再将点B 折叠再边AC 上，（不与A 、C 重合）折痕为EF ，点B 在AC 上的对应点为M ，设C D 与EM 交于点P ，连接PF ．已知BC ＝4．（1）若点M 为AC 的中点，求CF 的长；（2）随着点M 在边AC 上取不同的位置．①△PFM 的形状是否发生变化？请说明理由； ②求△PFM 的周长的取值范围.第28题图【解答过程】 解：（1）根据题意，设BF ＝FM ＝x ，则CF ＝4－x ，∵M 为AC 中点，AC ＝BC ＝4，∴ CM ＝12AC ＝2，∵∠ACB ＝90°，∴CF 2+CM 2＝FM 2，∴(4－x )2+22＝x 2，解得x ＝52，∴CF ＝4－52＝32； （2）①△PFM 的形状不变，始终是以PM 、PF 为腰的等腰直角三角形，理由如下：∵等腰直角三角形ABC 中，CD ⊥AB ，∴AD ＝DB ，CD ＝12AB ＝DB ，∴∠B ＝∠DCB ＝45°，由折叠可得∠PMF ＝∠B ＝45°，∴∠PMF ＝∠DCB ，∴P 、M 、F 、C 四点共圆，∴∠FPM +∠FCM ＝180°，∴∠FPM ＝180°－∠FCM ＝90°，∠PFM ＝90°－∠PMF ＝45°＝∠PMF ，∴△PFM 的形状不变，始终是以PM 、PF 为腰的等腰直角三角形； ②当M 与C 重合时，F 为BC 中点，CF ＝12BC ＝2，PM ＝PF ＝cos 45CF=︒此时△PFM 的周长为2＋当M 与A 重合时，F 于C 重合，E 与D 重合，FM ＝AC ＝4，PM ＝PF ＝ACcos45°＝，此时△PFM 的周长为4＋B 不与A 、C 重合，所以△PFM 的周长的取值范围是大于2＋且小于4＋.3. (2018辽宁葫芦岛，25，12分)在△ABC 中，AB ＝BC ，点O 是AC 的中点，点P 是AC 上的一个动点(点P 不与点A ，O ，C 重合)．过点A ，点C 作直线BP 的垂线，垂足分别为点E 和点F ，连接OE ，OF ． （1）如图1，请直接写出线段OE 与OF 的数量关系；（2）如图2，当∠ABC ＝90°时，请判断线段OE 与OF 之间的数量关系和位置关系，并说明理由； （3）若｜CF －AE ｜＝2，EF ＝POF 为等腰三角形时，请直接写出线段OP 的长．【思路分析】（1）连接OB ，则OB ⊥AC ，进而得A 、E 、O 、B 四点共圆，B 、F 、O 、C 四点共圆．由同弧所对的圆周角相等得∠OEB ＝∠OAB ，∠OFC ＝∠OBC ．又因为∠OFE ＝90°－∠OFC ，∠ACB ＝90°－∠OBC ，所以∠OFE ＝∠OCB ，又因为∠OAB ＝∠OCB ，所以∠OE B ＝∠OFE ，所以OE ＝OF ；（2）类比（1）可得OE ＝OF ；由∠ABC ＝90°，AB ＝BC ，可得∠OAB ＝∠OCB ＝∠OEB ＝∠OFE ＝45°，所以OE ⊥OF ．（3）取EF的中点为M，则EM＝FMAM并延长交CF于D，连接OM．由△AME≌△DMF，｜CF－AE｜＝2，得OM＝1．进而得OF＝2．由sin∠OFM＝12，得∠OFM＝30°．因为点P在EF上，所以OP＜OE＝OF；因为AE⊥EF，∠APE、∠OPF均为锐角，故PF≠PO．当PF＝OF＝2时，PM＝2理得OP＝【解答过程】（1）OE＝OF；（2）OE＝OF，OE⊥OF．理由：连接OB，则OB⊥AC．∵∠AEB＝∠AOB＝90°，∴进而得A、E、O、B四点共圆，∴∠OEB＝∠OAB．∵∠BFC＝∠BOC＝90°，∴B、F、O、C四点共圆．∴∠OFC＝∠OBC．又∵∠OFE＝90°－∠OFC，∠ACB＝90°－∠OBC，∴∠OFE＝∠OCB，又∵∠ABC＝90°，AB＝BC，∴∠OAB＝∠OCB＝45°．∴∠OE B＝∠OFE＝45°．∴OE＝OF，OE⊥OF．（3）OP＝223．4.（2018上海，25，14分）已知圆O的直径AB=2，弦AC与弦BD，交于点E，且OD⊥AC，垂足为点F．(1)图11，如果AC=BD，求弦AC的长；(2)如图12，如果E为BD的中点，求∠ABD的余切值(3)联结BC、CD、DA，如果BC是圆O的内接正n边形的一边，CD是的内接正(n+4)边形的一边，求△ACD的面积．【思路分析】(1)连结CB．可以证明弧AD、弧DC、弧CB相等，从而得到∠ABC=60°．在△ABC中求出AC长．(2)运用中位线及全等转化求出CB长，再把直角三角形OBE中的两个直角边求出，即可∠ABD的余切值．(3)根据“BC是圆O的内接正n边形的一边，CD是的内接正(n+4)边形的一边”求出n值，从而求出∠AOD=45°，可得各线段长，再求△ACD的面积．【解答过程】（1）连结CB．∵AC=BD，∴弧AC=弧BD，∵OD⊥AC，∴弧AD=弧DC=12弧AC，∴弧AD=弧DC=弧CB，∴∠ABC=60°在Rt△ABC中, ∠ABC=60°，AB=2，∴AC=3（2）∵OD⊥AC，∴∠AFO=90°，AF=FC∵AO=OB，∴FO∥CB，FO=12 CB∵E为BD的中点，∴DE=EB∵FO∥CB，∴△DEF≌△BEC，∴DF=CB=2FO∴FO=13，CB=23在Rt △ABC 中，AB =2，CB =23，∴AC ，∴EC ∴EB ，∵E 为BD 的中点，OD =OB ，∴∠OEB =90°，∴EO cot ∠ABD =EB EO ． （3）∵BC 是圆O 的内接正n 边形的一边，∴∠COB =360n° ∵CD 是的内接正(n +4)边形的一边，∴∠COD =3604n +° ∵弧AD =弧DC ，∴∠AOD =3604n +° ∵∠COB +∠COD +∠AOD =180°，∴360n +3604n ++3604n +=180，解得n =4 ∴∠AOD =∠COD =3604n +°=45°∵OD =OA =OC =1，∴AC ，OF ，DF =1，∴S △ACD =12×AC ×DF =2－12．5. （2018黑龙江哈尔滨，26，10）已知:⊙O 是正方形ABCD 的外接圆，点E 在弧AB 上，连接BE 、DE ，点F 在弧AD 上，连接BF 、DF 、BF 与DE 、DA 分别交于点G 、点H ，且DA 平分∠EDF ．(1)如图1，求证:∠CBE ＝∠DHG ;(2)如图2，在线段AH 上取一点N (点N 不与点A 、点H 重合)，连接BN 交DE 于点L ，过点H 作HK //BN 交DE 于点K ，过点E 作EP ⊥BN ，垂足为点P ，当BP ＝HF 时，求证:BE ＝HK ;(3)如图3，在(2)的条件下，当3HF ＝2DF 时，延长EP 交⊙O 于点R ，连接BR ，若△BER 的面积与△DHK 的面积的差为47，求线段BR 的长．图1 图2 图3【思路分析】（1）问利用同弧和等弧所对圆周角等与三角形外角性质易证的结论．（2）过H 作HM ⊥KD ，易证得HM ＝BP ，加上直角条件，可导出第三个全等条件，得到△BEP ≌△HKM ，所以BE ＝HK ．（3）连接BD 后根据条件3HF ＝2DF 可得到tan ∠ABH ＝tan ∠ADE ＝ABAH ＝32，过点H 作HS ⊥BD 后再设边计算就能求出tan ∠BDE ＝tan ∠DBF ＝BSHS ＝51，在ER 上截取ET ＝DK ，连接BT 易证得△BET ≌△HKD ，这时21BP ·ER 21-HM ·DK ＝21BP (ER －DK )＝21BP (ER －ET )＝47，易求得BP ＝1，PR ＝5，BR ＝22RP BP +＝2251+＝26【解答过程】（1）证明:∵四边形ABCD 是正方形∴∠A ＝∠ABC ＝90°∵∠F ＝∠A ＝90°∴∠F ＝∠ABC∵DA 平分∠EDF ∴∠ADE ＝∠ADF ∵∠ABE ＝∠ADE ∴∠ABE ＝∠ADF又∵∠CBE ＝∠ABC ＋∠ABE ，∠DHG ＝∠F ＋∠ADF ∴∠CBE ＝∠DHG（2）证明:过H 作HM ⊥KD 垂足为点M ∵∠F ＝90°∴HF ⊥FD 又∵DA 平分∠EDF ∴HM ＝FH∵FH ＝BP ∴HM ＝BP ∵KH ∥BN ∴∠DKH ＝∠DLN ∵∠ELP ＝∠DLN ∴∠DKH ＝∠ELP∵∠BED ＝∠A ＝90°∴∠BEP ＋∠LEP ＝90°∵EP ⊥BN ∴∠BPE ＝∠EPL ＝90°∴∠LEP ＋∠ELP ＝90°∴∠BEP ＝∠ELP ＝∠DKH ∵HM ⊥KD ∴∠KMH ＝∠BPE ＝90°∴△BEP ≌△HKM ∴BE ＝HK(3)解:连接BD ∵3HF ＝2DF ，BP ＝FH ∴设HF ＝2a ，DF ＝3a ∴BP ＝FH ＝2a由(2)得HM ＝BP ，∠HMD ＝90°∵∠F ＝∠A ＝90°∴tan ∠HDM ＝tan ∠FDH ∴DM HM ＝DF FH ＝32 ∴DM ＝3a ∴四边形ABCD 是正方形∴AB ＝AD ∴∠ABD ＝∠ADB ＝45°∵∠ABF ＝∠ADF ＝∠ADE ，∠DBF ＝45°－∠ABF ，∠BDE ＝45°－∠ADE ∴∠DBF ＝∠BDE ∵∠BED ＝∠F ，BD ＝BD ∴△BED ≌△DFB ∴BE ＝FD ＝3a 过点H 作HS ⊥BD 垂足为点S ∵tan ∠ABH ＝tan ∠ADE ＝ABAH ＝32 ∴设AB ＝32m ，AH ＝22m ∴BD ＝2AB ＝6m DH ＝AD －AH ＝2m sin ∠ADB ＝DHHS ＝22 ∴HS ＝m ∴ DS ＝22HS DH -＝m ∴BS ＝BD －DS ＝5m ∴tan ∠BDE ＝tan ∠DBF ＝BS HS ＝51 ∵∠BDE ＝∠BRE ∵tan ∠BRE ＝PR BP ＝51∵BP ＝FH ＝2a ∴RP ＝10a 在ER 上截取ET ＝DK ，连接BT 由(2)得∠BEP ＝∠HKD ∴△BET ≌△HKD ∴∠BTE ＝∠KDH ∴tan ∠BTE ＝tan ∠KDH ∴PT BP ＝32 ∴PT ＝3a ∴TR ＝RP －PT ＝7a ∵S △BER －S △KDH ＝47∴21BP ·ER 21-HM ·DK ＝47 ∴21BP (ER －DK )＝21BP (ER －ET )＝47∴21×2a ×7a ＝47 ∴a 2＝41，a 1＝21，a 2＝21-(舍去)∴BP ＝1，PR ＝5 ∴BR ＝22RP BP +＝2251+＝26。

例题
1：圆的性质应用
例 1 如图，CD 是⊙O 的直径，BE 是⊙O 的弦，DC、EB 的延长线相交于点 A．若∠A＝25°， AB＝OC，求∠EOD 的度数．
2：利用圆的性质进行证明
例1如图，⊙O 的半径OA、OB 分别交弦C D 于点E、F，且CE＝DF．试说明∠OEF 与∠OFE 的关系．
例 2 如图，O为AB所在圆的圆心，已知OA⊥OB，M为弦AB的中点，且MC∥OB交AB于点C．求AC的度数．60
延长CM交OA于E,OE=1/2 OA=1/2 OC
3：圆的性质和矩形性质综合
例 1 如图，点 A、D、G、M 在半圆 O 上，四边形 ABOC、DEOF、HMNO 为矩形，设 BC＝a，EF＝b，NH＝c．则下列各式正确的是( )
A．a>b>c B．a＝b＝c C．c>a>b D．b>c>a
4：点与圆的位置关系中分类讨论思想
例1若⊙O 所在平面上的一点P到⊙O 上的点的最大距离是10，最小距离是2，则此圆的半径为
5：利用圆的定义与直角三角形的性质综合进行证明
例1、已知：如图，BD、CE 是△ABC 的高，M 为B C 的中点，试说明点B、C、D、E 在以点M为圆心的同一个圆上．
例2、如图，在□ABCD 中，∠BAD 为钝角，且A E⊥BC，AF⊥CD． (1)求证：A、E、C、F 四点共圆；
(2)设线段B D 与(1)中的圆交于点M、N．求证：BM＝ND．。

中考数学《圆的有关概念及性质》专题复习【基础知识回顾】一、圆的定义：1、⑴形成性定义：在一个平面内，线段OA绕它固定的一个端点O旋转一周，另一个端点A随之旋转形成的图形叫做圆，固定的端点叫线段OA叫做⑵描述性定义：圆是到定点的距离等于的点的集合【名师提醒：1、在一个圆中，圆心决定圆的半径决定圆的2、直径是圆中的弦，弦不一定是直径】3、弦与弧：弦：连接圆上任意两点的叫做弦弧：圆上任意两点间的叫做弧，弧可分为、、三类4、圆的对称性：⑴轴对称性：圆是轴对称图形，有条对称轴的直线都是它的对称轴.⑵中心对称性：圆是中心对称图形，对称中心是【名师提醒：圆不仅是中心对称图形，而且具有旋转性，即绕圆心旋转任意角度都被与原来的图形重合】5、垂径定理及推论：（1）垂径定理：垂直于弦的直径，并且平分弦所对的几何语言：∵CD过圆心, 且___________∴ , , .（2）推论：平分弦（）的直径，并且平分弦所对的几何语言：∵CD过圆心, 且___________∴ , , .【名师提醒：1、垂径定理及其推论实质是指一条直线满足：⑴过圆心⑵垂直于弦⑶平分弦⑷平分弦所对的优弧⑸平分弦所对的劣弧五个条件中的两个，那么可推出其中三个，注意解题过程中的灵活运用2、圆中常作的辅助线是过圆心作弦的线3、垂径定理常用作计算，在半径r弦a弦心d和弦h中已知两个可求另外两个】三、圆心角、弧、弦之间的关系：1、圆心角定义：顶点在的角叫做圆心角2、定理：在中，两个圆心角、两条弧、两条弦中有一组量它们所对应的其余各组量也分别几何语言：∵在圆O中，_______∴ , .∵在圆O中，________∴ , .∵在圆O中，________∴ , .【名师提醒：注意：该定理的前提条件是“在同圆或等圆中”】四、圆周角定理及其推论：1、圆周角定义：顶点在并且两边都和圆的角叫圆周角2、圆周角定理：在同圆或等圆中，圆弧或等弧所对的圆周角都等于这条弧所对的圆心角的推论1、在同圆或等圆中，如果两个圆周角那么它们所对的弧推论2、半圆（或直弦）所对的圆周角是 900的圆周角所对的弦是【名师提醒：1、在圆中，一条弦所对的圆心角只有一个，而它所对的圆周角有个，它们的关系是2、作直弦所对的圆周角是圆中常作的辅助线】3、圆内接四边形定义：如果一个多边形的所有顶点都在圆上，这个多边形叫做这个圆叫做性质：圆内接四边形的对角【名师提醒：圆内接平行四边形是圆内接梯形是】考点一：垂径定理例1、一条排水管的截面如图所示，已知排水管的半径OB=10，水面宽AB=16，则截面圆心O到水面的距离OC是A. 4B. 5C. 6D. 8例2、绍兴市著名的桥乡，如图，石拱桥的桥顶到水面的距离CD为8m，桥拱半径OC为5m，则水面宽AB 为_________考点二：圆心角定理例3、如图，DC 是⊙O直径，弦AB⊥CD于F，连接BC，DB，则下列结论错误的是（）A．B．AF=BF C．OF=CF D．∠DBC=90°例4、如图，半圆O的直径AB=10cm，弦AC=6cm，AD平分∠BAC，则AD的长为____________对应训练2．如图，AB是半圆的直径，点D是弧AC的中点，∠ABC＝50°，则∠DAB等于（）．A．55° B．60°C．65° D．70°考点三：圆周角定理例5、如图，将直角三角板60°角的顶点放在圆心O上，斜边和一直角边分别与⊙O相交于A、B两点，P 是优弧AB上任意一点（与A、B不重合），则∠APB= ．例6、如图，已知⊙O是△ABD的外接圆，AB是⊙O的直径，CD是⊙O的弦，∠ABD=58°，则∠BCD等于_____________对应训练6、△ABC为⊙O的内接三角形，若∠AOC=160°，则∠ABC的度数是（）A．80° B．160° C．100° D．80°或100°7、如图，AB是⊙O的直径，弦CD⊥AB于点N，点M在⊙O上，∠1=∠C（1）求证：CB∥MD；（2）若BC=4，sinM= ，求⊙O的直径．考点四：圆内接四边形的性质例3 如图，⊙C过原点，且与两坐标轴分别交于点A、点B，点A的坐标为（0，3），M是第三象限内上一点，∠BMO=120°，则⊙C的半径长为（）A．6 B．5 C．3 D．3对应训练【聚焦中考】1．如图，AB是的直径，C是上一点，AB=10，AC=6，，垂足为D，则BD的长为（A）2 （B）3 （C）4 （D）62．如图，⊙O的直径AB＝12，CD是⊙O的弦，CD⊥AB，垂足为P，且BP：AP＝1：5，则CD的长为（）． A． B． C． D．3．如图，在⊙O中，∠CBO=45°，∠CAO=15°，则∠AOB的度数是(A)75°. (B)60°. (C)45°. (D)30°.4．如图，已知圆心角∠BOC=78°，则圆周角∠BAC的度数是（）A．156°B．78°C．39°D．12°5．如图，点A，B，C，在⊙O上，∠ABO=32°，∠ACO=38°，则∠BOC等于（）A．60° B．70° C．120° D．140°6．如图，AB是⊙O的直径，，AB=5，BD=4，则sin∠ECB=______7．如图，在⊙O中，已知∠OAB=22.5°，则∠C的度数为（）A. 135°B. 122.5°C. 115.5°D.112.5°8．如图，在△ABC中，以BC为直径的圆分别交边AC、AB于D、E两点，连接BD、DE．若BD平分∠ABC，则下列结论不一定成立的是A.BD⊥ACB.AC2=2AB·AEC.△ADE是等腰三角形D. BC＝2AD.9．如图(b)，已知，⊙O的直径CD为4，点A 在⊙O 上，∠ACD=30°，B 为弧AD 的中点，P为直径CD上一动点，则BP+AP的最小值为__________．10．如图，CD为⊙O的直径，CD⊥AB，垂足为点F，AO⊥BC，垂足为点E，AO=1．（1）求∠C的大小；（2）求阴影部分的面积．11．AB是圆O的直径,BC是圆O的切线,连接AC交圆O于点D,E为弧AD上一点,连接AE、BE，BE交AC于点F，且AF²=EF.EB（1）求证：CB=CF （2）若点E到弦AD的距离为1，cos角C=3/5，求圆O的半径12．某施工工地安放了一个圆柱形饮水桶的木制支架（如图1），若不计木条的厚度，其俯视图如图2所示，已知AD垂直平分BC，AD=BC=48cm，则圆柱形饮水桶的底面半径的最大值是 cm．【备考真题过关】一、选择题1．如图，⊙O的半径OD⊥弦AB于点C，连结AO并延长交⊙O于点E，连结EC．若AB=8，CD=2，则EC的长为__________2．如图，以M（-5，0）为圆心、4为半径的圆与x轴交于A、B两点，P是⊙M上异于A、B的一动点，直线PA、PB分别交y轴于C、D，以CD为直径的⊙N与x轴交于E、F，则EF的长（）A．等于4 B．等于4 C．等于6 D．随P点位置的变化而变化3．如图，在半径为5的⊙O中，AB、CD是互相垂直的两条弦，垂足为P，且AB=CD=8，则OP的长为（）A．3 B．4 C．3 D．44．如图，AB为⊙O的直径，弦CD⊥AB于E，已知CD=12，BE=2，则⊙O的直径为（）A．8 B．10 C．16 D．205．如图，CD是⊙O的直径，AB是弦（不是直径），AB⊥CD于点E，则下列结论正确的是（）A．AE＞BE B．C．∠D=∠AEC D．△ADE∽△CBE6．△ABC为⊙O的内接三角形，若∠AOC=160°，则∠ABC的度数是（）A．80° B．160° C．100° D．80°或100°7．如图，在△ABC中，AB为⊙O的直径，∠B=60°，∠BOD=100°，则∠C的度数为（）A．50° B．60° C．70° D．80°二、填空题8．如图，AB为⊙O的直径，CD为⊙O的一条弦，CD⊥AB，垂足为E，已知CD=6，AE=1，则⊙0的半径为．9．如图，AB是⊙O的弦，OC⊥AB于C．若AB=2，0C=1，则半径OB的长为．10．如图，在⊙O中，直径AB丄弦CD于点M，AM=18，BM=8，则CD的长为．111314．如图，已知点A（0，2）、B（2，2）、C（0，4），过点C向右作平行于x轴的射线，点P是射线上的动点，连接AP，以AP为边在其左侧作等边△APQ，连接PB、BA．若四边形ABPQ为梯形，则：（1）当AB为梯形的底时，点P的横坐标是；15．如图，△ABC内接于⊙O，AB、CD为⊙O直径，DE⊥AB于点E，sinA=，则∠D的度数是．三、解答题16．如图所示为圆柱形大型储油罐固定在U型槽上的横截面图．已知图中ABCD为等腰梯形（AB∥DC），支点A与B相距8m，罐底最低点到地面CD距离为1m．设油罐横截面圆心为O，半径为5m，∠D=56°，求：U 型槽的横截面（阴影部分）的面积．（参考数据：sin53°≈0.8，tan56°≈1.5，π≈3，结果保留整数）17．如图，⊙O的半径为17cm，弦AB∥CD，AB=30cm，CD=16cm，圆心O位于AB，CD的上方，求AB和CD的距离．18．在⊙O中，直径AB⊥CD于点E，连接CO并延长交AD于点F，且CF⊥AD．求∠D的度数．19．如图，A，P，B，C是半径为8的⊙O上的四点，且满足∠BAC=∠APC=60°，（1）求证：△ABC是等边三角形；（2）求圆心O到BC的距离OD．20．如图△ABC中，BC=3，以BC为直径的⊙O交AC于点D，若D是AC中点，∠ABC=120°．（1）求∠ACB的大小；（2）求点A到直线BC的距离．21．如图，已知AB是⊙O的弦，OB=4，∠OBC=30°，点C是弦AB上任意一点（不与点A、B重合），连接CO并延长CO交⊙O于点D，连接AD、DB．（1）当∠ADC=18°时，求∠DOB的度数；（2）若AC=2，求证：△ACD∽△OCB．。

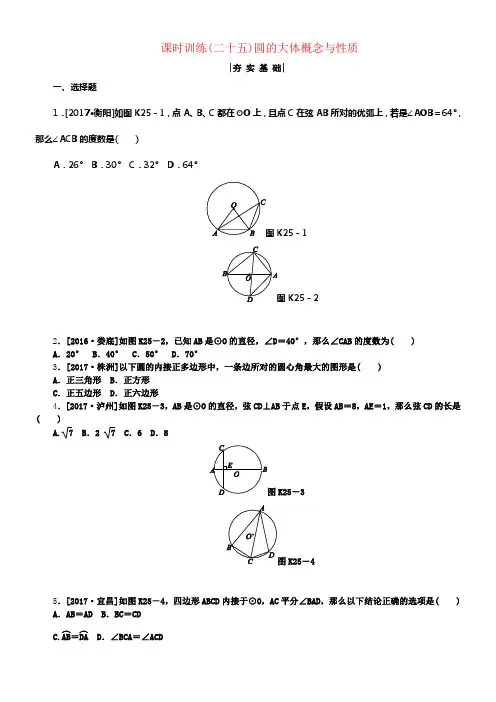
课时训练(二十五)圆的大体概念与性质|夯 实 基 础|一、选择题1．[2017·衡阳]如图K25－1，点A 、B 、C 都在⊙O 上，且点C 在弦AB 所对的优弧上，若是∠AOB＝64°，那么∠ACB 的度数是( )A ．26°B ．30°C ．32°D ．64°K25－1K25－22．[2016·娄底]如图K25－2，已知AB 是⊙O 的直径，∠D ＝40°，那么∠CAB 的度数为( ) A ．20° B ．40° C ．50° D ．70°3．[2017·株洲]以下圆的内接正多边形中，一条边所对的圆心角最大的图形是( ) A ．正三角形 B ．正方形 C ．正五边形 D ．正六边形4．[2017·泸州]如图K25－3，AB 是⊙O 的直径，弦CD⊥AB 于点E ，假设AB ＝8，AE ＝1，那么弦CD 的长是( )A.7 B ．2 7 C ．6 D ．8K25－3K25－45．[2017·宜昌]如图K25－4，四边形ABCD 内接于⊙O，AC 平分∠BAD，那么以下结论正确的选项是( ) A ．AB ＝AD B ．BC ＝CD C.AB ︵＝DA ︵D ．∠BCA ＝∠ACD图K25－56．[2017·陕西]如图K25－5，△ABC 是⊙O 的内接三角形，∠C ＝30°，⊙O 的半径为5，假设点P 是⊙O 上的一点，在△ABP 中，PB ＝AB ，那么PA 的长为( )A ．5 B.5 32C ．5 2D ．5 37．[2017·西宁]如图K25－6，AB 是⊙O 的直径，弦CD 交AB 于点P ，AP ＝2，BP ＝6，∠APC ＝30°.那么CD 的长为( )A.15 B ．2 5 C ．2 15 D ．8K25－6K25－78．[2016·连云港]如图K25－7，在网格中(每一个小正方形的边长均为1个单位)选取9个格点(格线的交点称为格点)．若是以A 为圆心，r 为半径画圆，选取的格点中除点A 外恰好有3个在圆内，那么r 的取值范围为( )A ．2 2＜r ＜17 B.17＜r ＜3 2 C.17＜r ＜5 D ．5＜r ＜29二、填空题9．[2016·岳阳]如图K25－8，四边形ABCD 为⊙O 的内接四边形，已知∠BCD＝110°，那么∠BAD＝________°.K25－8K25－910．[2017·义乌]如图K25－9，一块含45°角的直角三角板，它的一个锐角极点A在⊙O上，边AB，AC别离与⊙O交于点D，E，那么∠EOD的度数为________．11．[2017·庆阳]如图K25－10，△ABC内接于⊙O，假设∠OAB＝32°，那么∠C＝________．图K25－1012．如图K25－11所示，工程上经常使用钢珠来测量零件上小圆孔的宽口，假设钢珠的直径是10 mm，测得钢珠顶端离零件表面的距离为8 mm，那么那个小圆孔的宽口AB的长度为________mm.K25－11K25－1213．[2017·十堰]如图K25－12，△ABC内接于⊙O，∠ACB＝90°，∠ACB的角平分线交⊙O于D，假设AC ＝6，BD＝5 2，那么BC的长为________．三、解答题14．[2016·宁夏]如图K25－13，已知△ABC，以AB为直径的⊙O别离交AC于D，BC于E，连接ED，假设ED＝EC.(1)求证：AB＝AC；(2)假设AB＝4，BC＝2 3，求CD的长．图K25－1315．[2017·安徽]如图K25－14，在四边形ABCD中，AD＝BC，∠B＝∠D，AD不平行于BC，过点C作CE∥AD 交△ABC的外接圆O于点E，连接AE.(1)求证：四边形AECD为平行四边形；(2)连接CO，求证：CO平分∠BCE.图K25－14|拓展提升|图K25－1516．如图K25－15，AB是⊙O的直径，弦BC＝4 cm，F是弦BC的中点，∠ABC＝60°.假设动点E以1 cm/s 的速度从点A动身在AB上沿着A→B→A运动，设运动时刻为t s(0≤t＜16)，连接EF，当△BEF是直角三角形时，t的值为________．(填出一个正确的即可)17．在⊙O中，直径AB＝6，BC是弦，∠ABC＝30°，点P在BC上，点Q在⊙O上，且OP⊥PQ.(1)如图K25－16①，当PQ∥AB时，求PQ的长度；(2)如图K25－16②，当点P在BC上移动时，求PQ长的最大值．图K25－16参考答案1．C2．C [解析] ∠D＝40°，依照圆周角性质那么有∠B＝∠D＝40°.又AB是⊙O的直径，∴∠ACB＝90°，∴∠CAB＝90°－40°＝50°.3．A [解析] 正三角形的边所对的圆心角是120°；正方形的边所对的圆心角是90°；正五边形的边所对的圆心角是72°；正六边形的边所对的圆心角是60°.应选A.4．B [解析] 连接OC ，那么OC ＝4，OE ＝3，在Rt △OCE 中，CE ＝OC 2－OE 2＝42－32＝7.因为AB⊥CD，因此CD ＝2CE ＝2 7.5．B [解析] 依照弦、弧、圆周角之间的关系，由相等的圆周角取得所对的弧、弦相等，可知选项B 正确． 6．D [解析] 连接OB ，OA ，OP ，设OB 与AP 交于点D ，由题意可知OB⊥AP；易知△OAB 为等边三角形，再运用解直角三角形的知识可求出AP 的长为5 3.7．C [解析] 作OH⊥PD 于H ，AP ＝2，BP ＝4，那么PO ＝2，又∠HPO＝∠APC＝30°，∴OH ＝1，OD ＝OB ＝4，在Rt △HOD 中，HD ＝OD 2－OH 2＝15，∴CD ＝2HD ＝2 15.8．B [解析] 依照图形中网格与勾股定理可知，AD ＝2 2，AE ＝AF ＝17，AB ＝3 2，∴AB ＞AE ＞AD.以A 为圆心，r 为半径画圆，选取的格点中除点A 外恰好有3个在圆内，那么必需知足17＜r ＜3 2.9．70 10．90° [解析] 依照一条弧所对的圆周角是它所对的圆心角的一半，取得∠EOD＝2∠A＝2×45°＝90°. 11．58° [解析] 连接OB.在△OAB 中，OA ＝OB ，∴∠OAB ＝∠OBA.又∵∠OAB＝32°，∴∠OBA ＝32°.∴∠AOB ＝180°－2×32°＝116°.而∠C＝12∠AOB，∴∠C ＝58°.12．8 [解析] 设钢珠的圆心为O ，连接OA ，过点O 作OD ⊥AB 于点D ，那么AB ＝2AD.在Rt △AOD 中，利用勾股定理得AD ＝OA 2－OD 2＝52－32＝4(mm)，因此AB ＝2AD ＝2×4＝8(mm)．13．8 [解析] 连接DA ，因为∠ACB＝90°，因此AB 为直径，因此∠ADB＝90°，因为CD 平分∠ACB，因此BD ＝AD ，在△ABD 中AB ＝AD 2＋BD 2＝（5 2）2＋（5 2）2＝10，在△ABC 中BC ＝AB 2－AC 2＝102－62＝8.14．解：(1)证明：∵ED＝EC ，∴∠CDE ＝∠C. 又∵四边形ABED 是⊙O 的内接四边形， ∴∠CDE ＝∠B， ∴∠B ＝∠C， ∴AB ＝AC.(2)连接AE ，那么AE⊥BC，∴BE ＝EC ＝12BC.在△ABC 与△EDC 中，∵∠C ＝∠C，∠CDE ＝∠B， ∴△ABC ∽△EDC ，∴AB DE ＝BC DC ，∴DC ＝BC·DE AB ＝BC 22AB. 由AB ＝4，BC ＝2 3，∴DC ＝（2 3）22×4＝32.15．证明：(1)依照圆周角定理知∠E＝∠B， 又∵∠B＝∠D， ∴∠E ＝∠D， 又∵AD∥CE，∴∠D ＋∠DCE＝180°， ∴∠E ＋∠DCE＝180°， ∴AE ∥DC ，∴四边形AECD 为平行四边形．(2)如图，连接OE ，OB ，由(1)得四边形AECD 为平行四边形， ∴AD ＝EC ，∵AD ＝BC ，∴EC ＝BC ，∵OC ＝OC ，OB ＝OE ，∴△OCE ≌△OCB(SSS)， ∴∠ECO ＝∠BCO，即CO 平分∠ECB.16．答案不唯一，如4 [解析] ∵AB是⊙O ∴∠C＝90°.∵∠ABC＝60°，BC＝4 cm，∴AB＝2BC＝8 cm.∵F是弦BC的中点，∴当EF∥AC时，△BEF是直角三角形，现在E为AB的中点，即AE＝AO＝4 cm，∴t＝4÷1＝4(s)，或t＝4＋81＝12(s)．当FE⊥AB时，∵FB＝12BC＝2(cm)，∠B＝60°，∴BE＝12FB＝1(cm)，∴AE＝AB－BE＝8－1＝7(cm)，∴t＝71＝7(s)．或t＝7＋1＋11＝9(s)．17．解：(1)如图①，连接OQ，∵PQ∥AB，PQ⊥OP，∴OP⊥AB，∵tan30°＝OPOB，∴OP＝3×33＝3，由勾股定理得PQ＝32－（3）2＝ 6.(2)如图②，连接OQ取最大值，需OP取最小值，现在OP⊥BC，∵∠ABC＝30°，∴OP＝12OB＝32，现在。

第五章 圆§5.1 圆的有关概念与性质一、选择题1. (2014·浙江杭州朝晖中学三模，7，3分)如图，AB 是⊙O 的直径，C ，D 为圆上两点，∠AOC ＝130°，则∠D 等于( )A ．25°B ．30°C ．35°D ．50°解析 ∵∠AOC ＝130°，∴∠BOC ＝180°－∠AOC ＝180°－130°＝50°.∵∠BOC 和∠D 分别是BC ︵所对的圆心角和圆周角，∴∠D ＝12∠BOC ＝12×50°＝25°.故选A. 答案 A2．(2015·浙江湖州模拟(17)，5，3分)如图，已知⊙O 的两条弦AC ，BD 相交于点E ，∠A ＝75°，∠C ＝45°，那么sin ∠AEB 的值为( )A.12B.33C.22D.32解析 ∵∠B 和∠C 是同弧对应的圆周角，∴∠B ＝∠C .∵∠A ＝75°，∠C ＝45°， ∴∠B ＝∠C ＝45°，∠AEB ＝180°－∠A －∠B ＝60°，∴sin∠AEB＝32.答案 D3．(2015·浙江模拟，8，3分)如图，已知⊙O的直径AB⊥弦CD于点E，下列结论中一定正确的是()A．AE＝OE B．CE＝DEC．OE＝12CE D．∠AOC＝60°解析根据直径AB⊥弦CD于点E，由垂径定理求出，CE＝DE，即可得出答案．根据⊙O的直径AB⊥弦CD于点E，∴CE＝DE.答案 B4．(2014·浙江杭州江干一模，9，3分)已知⊙O半径为3 cm，下列与⊙O不是．．等圆的是()A．⊙O1中，120°圆心角所对弦长为3 3 cmB．⊙O2中，45°圆周角所对弦长为32cmC．⊙O3中，90°圆周角所对弧长为32πcmD．⊙O4中，圆心角为60°的扇形面积为32πcm解析A中，如图1，作O1D⊥AB，则AD＝332，cos 30°＝ADAO1，AO1＝3，与⊙O是等圆，故A不符合要求；B中，如图2，∠B＝45°，则∠AO2C＝90°，AO2＝32sin 45°＝32×22＝3，与⊙O是等圆，故B不符合要求；C中，设半径为r，90°圆周角所对弧长为32πcm，可得πr＝32π，r＝32，与⊙O的半径不等，不是等圆，故C符合要求；D中，设半径为r，则60πr2360＝3π2，解得r＝3，与⊙O是等圆，故D不符合要求．故选C.答案 C5．(2013·浙江湖州中考模拟试卷一，10，3分)如图，AB 为⊙O 的直径，AC 交⊙O 于E 点，BC 交⊙O 于D 点，CD ＝BD ，∠C ＝70°，现给出以下四个结论：①∠A ＝45°；②AC ＝AB ；③AE ︵＝BE ︵；④CE ·AB ＝2BD 2.其中正确结论的个数为( )A ．1个B ．2个C ．3个D ．4个解析 连结AD ，ED ，OE ，∵AB 为圆O 的直径，∴∠ADB ＝90°，∴AD ⊥BC .∵CD ＝BD ，∴AD 垂直平分BC ，∴AC ＝AB ，故②正确；∵∠B ＝∠C ＝70°，∴∠BAC ＝180°－70°－70°＝40°，故①错误；∵四边形AEDB 为圆O 的∽△CAB ，∴CD CA ＝CECB ，内接四边形，∴∠CED ＝∠B ，∠CDE ＝∠BAC ，∴△CDE即CA ·CE ＝CD ·CB ，又CA ＝AB ，CD ＝BD ＝12BC ，则CE ·AB ＝2BD 2，故④正确；∵OE ＝OA ，∴∠OEA ＝∠OAE ＝40°，∴∠EOB ＝80°，∠EOA ＝100°，∴AE ︵≠BE ︵.故③错误，则其中正确的有2个．故选B. 答案 B 二、填空题6．(2013·浙江湖州中考模拟八，14，4分)如图，点A ，B ，C 在圆O 上，且∠BAC＝40°，则∠BOC ＝________．解析∠BAC与∠BOC分别是BC︵所对的圆周角与圆心角，∴∠BOC＝2∠BAC＝80°.答案80°7．(2014·浙江杭州朝晖中学三模，14，4分)如图，⊙O的直径AB＝12，CD 是⊙O的弦，CD⊥AB，垂足为P，且BP∶AP＝1∶5，则CD的长为__________．CP＝OC2－OP2＝解析连结OC，由题意可得OC＝6，OP＝4，∴62－42＝25，∴CD＝2CP＝4 5.答案4 58．(2015·浙江宁波北仑区一模，16，4分)如图，AB是⊙O的直径，∠C＝30°，则∠ABD等于________．解析连结AD，∵AB是⊙O的直径，∴∠ADB＝90°.∵∠A＝∠C＝30°，∴∠ABD＝90°－∠A＝60°.答案60°9．(2013·浙江湖州中考模拟七，11，3分)一条弦把圆分成2∶3两部分，那么这条弦所对的圆周角的度数为________．解析如图，∠AOB＝25×360°＝144°，∴∠ACB＝72°.由圆内接四边形的对角互补可得∠ADB＝108°.∵∠ACB和∠ADB都是弦AB所对的圆周角，∴这条弦所对的圆周角为72°或108°.答案72°或108°三、解答题10．(2015·浙江温州模拟(2)，19，8分)如图，四边形ABCD内接于⊙O，并且AD是⊙O的直径，C是弧BD的中点，AB和DC的延长线交⊙O外一点E.求证：BC＝EC.证明连结AC.∵AD是⊙O的直径，∴∠ACD ＝∠ACE ＝90°. ∵四边形ABCD 内接于⊙O ， ∴∠D ＋∠ABC ＝180°. 又∠ABC ＋∠EBC ＝180°， ∴∠EBC ＝∠D . ∵C 是弧BD 的中点， ∴∠1＝∠2，∴∠1＋∠E ＝∠2＋∠D ＝90°， ∴∠E ＝∠D ，∴∠EBC ＝∠E ， ∴BC ＝EC .11．(2015·浙江衢州一模，19，6分)如图，AB 是⊙O 的直径，弦CD ⊥AB 于点E ，点P 在⊙O 上，∠1＝∠C . (1)求证：CB ∥PD ；(2)若BC ＝3，sin ∠P ＝35，求⊙O 的直径． (1)证明 ∵∠C ＝∠P ，又∵∠1＝∠C ， ∴∠1＝∠P ，∴CB ∥PD . (2)解 连结AC . ∵AB 为⊙O 的直径，∴∠ACB ＝90°.又∵CD ⊥AB ， ∴BC ︵＝BD ︵，∴∠P ＝∠CAB . 又∵sin ∠P ＝35， ∴sin ∠CAB ＝35， 即BC AB ＝35， 又知，BC ＝3， ∴AB ＝5， ∴⊙O 的直径为5.。

《圆》专题复习第一讲圆的有关概念及性质【基础知识回顾】一、圆的定义及性质：1、圆的定义：⑴形成性定义：在一个平面内，线段0A绕它固定的一个端点0旋转一周，另一个端点A随之旋转形成的图形叫做圆，固定的端点叫_____ 线段0A叫做__________⑵描述性定义：圆是到定点的距离等于__________ 的点的集合2、弦与弧：弦：连接圆上任意两点的________ 叫做弦弧：圆上任意两点间的________ 叫做弧，弧可分为 ____ 、_______ 、 _____ 三类3、圆的对称性：⑴轴对称性：圆是轴对称图形，有 ______ 条对称轴， ________________ 的直线都是它的对称轴⑵中心对称性：圆是中心对称图形，对称中心是 _________【名师提醒：1、在一个圆中，圆心决定圆的 _________ 半径决定圆的________2、直径是圆中 _____ 的弦，弦不-3、圆不仅是中心对称图形，而且具有旋转_________ 性，即绕圆心旋转任意角度都被与原来的图形重合】二、垂径定理及推论：1、垂径定理：垂直于弦的直径___________ ，并且平分弦所对的______________ 。

2、推论：平分弦（ _______ ）的直径___________ ，并且平分弦所对的______________ 。

【名师提醒：1、垂径定理及其推论实质是指一条直线满足：⑴过圆心⑵垂直于弦⑶平分弦⑷平分弦所对的优弧⑸平分弦所对的劣弧五个条件中的两个，那么可推出其余三个，注意解题过程中的灵活运用2、圆中常作的辅助线是过圆心作弦的_______ 线（即弦心距）。

3、垂径定理常用作计算，在半径r、弦a、弦心d和弓高h中已知其中两个量可求另外两个量。

】三、圆心角、弧、弦之间的关系：1、圆心角定义：顶点在 _________ 的角叫做圆心角2、定理：在 _______ 中，两个圆心角、两条弧、两条弦中有一组量___________ 它们所对应的其余各组量也分别一【名师提醒：注意：该定理的前提条件是在同圆或等圆中”四、圆周角定理及其推论：1、圆周角定义：顶点在 _______ 并且两边都和圆 ______ 的角叫圆周角2、圆周角定理：在同圆或等圆中，圆弧或等弧所对的圆周角都等于这条弧所对的圆心角的_____________ 推论1、在同圆或等圆中，如果两个圆周角 __________ 那么它们所对的弧 ___________推论2、半圆（或直弦）所对的圆周角是 _________ ，90°的圆周角所对的弦是 ____________【名师提醒：1、在圆中，一条弦所对的圆心角只有一个，而它所对的圆周角有_________ 个，是____ 类，它们的关系是_________ ，2、作直径所对的圆周角是圆中常作的辅助线】五、圆内接四边形：定义：如果一个多边形的所有顶点都在圆上，这个多边形叫做_______________ ，这个圆叫做_____________________ 性质：圆内接四边形的对角____________ 。

圆专题一、圆的相关概念1.圆的定义（1）描述性定义：在一个平面内，线段OA绕它固定的一个端点O旋转一周，另一个端点A随之旋转所形成的图形叫做圆，其中固定端点O叫做圆心，OA叫做半径．（2）集合性定义：平面内到定点的距离等于定长的点的集合叫做圆，顶点叫做圆心，定长叫做半径．（3）圆的表示方法：通常用符号⊙表示圆，定义中以O为圆心，OA为半径的圆记作”O⊙“，读作”圆O“．（4）同圆、同心圆、等圆：圆心相同且半径相等的圆叫同圆；圆心相同，半径不相等的两个圆叫做同心圆；能够重合的两个圆叫做等圆．注意：注意：同圆或等圆的半径相等．2.弦和弧（1）弦：连结圆上任意两点的线段叫做弦．（2）直径：经过圆心的弦叫做圆的直径，直径等于半径的2倍．（3）弦心距：从圆心到弦的距离叫做弦心距．、为端点的圆弧记作AB，读作弧AB．（4）弧：圆上任意两点间的部分叫做圆弧，简称弧．以A B（5）等弧：在同圆或等圆中，能够互相重合的弧叫做等弧．（6）半圆：圆的任意一条直径的两个端点分圆成两条弧，每一条弧都叫做半圆．（7）优弧、劣弧：大于半圆的弧叫做优弧，小于半圆的弧叫做劣弧．（8）弓形：由弦及其所对的弧组成的图形叫做弓形．3.圆心角和圆周角（1）圆心角：顶点在圆心的角叫做圆心角．将整个圆分为360等份，每一份的弧对应1︒的圆心角，我们也称这样的弧为1︒的弧．圆心角的度数和它所对的弧的度数相等．（2）圆周角：顶点在圆上，并且两边都和圆相交的角叫做圆周角．二、圆的对称性1.旋转对称性（1）圆是中心对称图形，对称中心是圆心；圆是旋转对称图形，无论绕圆心旋转多少度角，总能与自身重合．（2）圆的旋转对称性⇒圆心角、弧、弦、弦心距之间的关系．2.轴对称性（1）圆是轴对称图形，经过圆心的任一条直线是它的对称轴．（2）圆的轴对称性⇒垂径定理．三、圆的性质定理1.圆周角定理（1） 定理：一条弧所对的圆周角等于它所对的圆心角的一半． （2） 推论：推论1：同弧或等弧所对的圆周角相等；同圆或等圆中，相等的圆周角所对的弧相等． 推论2：半圆(或直径)所对的圆周角是直角，90︒的圆周角所对的弦是直径．推论3：如果三角形一边上的中线等于这边的一半，那么这个三角形是直角三角形．2. 圆心角、弧、弦、弦心距之间的关系（1） 定理：在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦相等，所对的弦的弦心距相等．（2） 推论：在同圆或等圆中，如果两个圆心角、两条弧、两条弦或两条弦的弦心距中有一组量相等，那么它们所对应的其余各组量分别相等．注意：①前提条件是在同圆或等圆中；②在由等弦推出等弧时应注意：优弧与优弧相等；劣弧与劣弧相等．3. 垂径定理（1） 定理：垂直于弦的直径平分这条弦，并且平分弦所对的两条弧． （2） 推论1：①平分弦（非直径）的直径，垂直于弦，并且平分弦所对的两条弧．②弦的垂直平分线经过圆心，并且平分弦所对的两条弧．③平分弦所对的一条弧的直径，垂直平分弦，并且平分弦所对的另一条弧． （3） 推论2：圆的两条平行线所夹的弧相等．注意：若“过圆心的直线”、“垂直于弦”、“平分弦（非直径）”、“平分弦所对的优弧”、“平分弦所对的劣弧”中的任意两个成立，则另外三个都成立．注意：应用垂径定理与推论进行计算时，往往要构造如右图所示的直角三角形，根据垂径定理与勾股定理有：222()2ar d =+，根据此公式，在a ，r ，d 三个量中知道任何两个量就可以求出第三个量．F EBA CDOr a 2d O CBA所对的两圆心角相等所对的两条弦相等 所对的两条弧相等所对的两条弦的弦心距相等EO D B A【例1】 如图，点A D G M 、、、在半圆O 上，四边形ABOC DEOF HMNO 、、均为矩形，设BC a =，EF b =，NH c =则下列格式中正确的是( )A ．a b c >>B ．a b c ==C ．c a b >>D ．b c a >>【例2】 如图，两正方形彼此相邻且内接于半圆，若小正方形的面积为216cm ，则该半圆的半径为______．二、圆的性质定理1. 圆周角定理【例3】 如图，量角器外沿上有A B 、两点，它们的度数分别是7040︒︒、，则1∠的度数为_________．【例4】 如图，量角器外缘边上有A P Q ，，三点，它们所表示的读数分别是180︒，70︒，30︒，则PAQ ∠的大小为（ ）A ．10︒B ．20︒C ．30︒D ．40︒【例5】 如图，O ⊙是ABC ∆的外接圆，已知60B ∠=︒，则CAO ∠的度数是（ ）A ．15︒B ．30︒C ．45︒D ．60︒【例6】 如图，已知O 的弦AB CD ，相交于点E ，AC 的度数为60︒，BD 的度数为100︒，则AEC ∠等于ON MHG FE DC BA（ ） A ．60°B ．100°C ．80°D ．130°【例7】 如图所示的半圆中，AD 是直径，且32AD AC ==，，则sin B 的值是________．【例8】 如图，已知AB 为⊙O 的直径，20E ∠=︒，50DBC ∠=︒，则CBE ∠=______．【例9】 如图，在O ⊙中，AOB ∠的度数为m ，C 是ACB 上一点，D E 、是AB 上不同的两点(不与A B 、两点重合)，则D E ∠+∠的度数为____________．【例10】 如图，AB 是O 的直径，点C ，D ，E 都在O 上，若C D E ==∠∠∠，求A B +∠∠．DCA BBA【例11】 如图，有一圆形展厅，在其圆形边缘上的点A 处安装了一台监视器，它的监控角度是65︒．为了监控整个展厅，最少需在圆形边缘上共安装．．．这样的监视器 台．【例12】 如图所示，在ABC ∆中，45C ∠=︒，4AB =，则O ⊙的半径为( )B.4D.5【例13】 如图AB 是半圆O 的直径，点C D 、在弧AB 上，且AD 平分CAB ∠，已知106AB AC ==，，求AD的长．【例14】 如图，半圆的直径10AB =，点C 在半圆上，6BC =．（1）求弦AC 的长；（2）若P 为AB 的中点，PE AB ⊥交AC 于点E ，求PE 的长．2. 圆内接四边形【例15】 如图，O ⊙外接于正方形ABCD ，P 为弧AD 上一点，且1AP =，PB =PC 的长．【例16】 如图，已知四边形ABCD 内接于直径为3的圆O ，对角线AC 是直径，对角线AC 和BD 的交点P ，BAPEC BAP DCBAAB BD =，且0.6PC =，求四边形ABCD 的周长．【例17】 如图，AB CD ，是O ⊙的两条弦，它们相交于点P ，连结AD BD 、，已知4AD BD ==，6PC =，求CD 的长．一、点与圆的位置关系4. 确定圆的条件（5） 圆心(定点)，确定圆的位置； （6）半径(定长)，确定圆的大小．注意：只有当圆心和半径都确定时，圆才能确定． 5. 点与圆的位置关系（7） 点与圆的位置关系有：点在圆上、点在圆内、点在圆外三种，这三种关系由这个点到圆心的距离与半径的大小关系决定． （8） 设O ⊙的半径为r ，点P 到圆心O 的距离为d ，则有：点在圆外⇔d r >；点在圆上⇔d r =；点在圆内⇔d r <.如下表所示：C二、过已知点的圆1. 过已知点的圆（1） 经过点A 的圆：以点A 以外的任意一点O 为圆心，以OA 的长为半径，即可作出过点A 的圆，这样的圆有无数个． （2） 经过两点A B 、的圆：以线段AB 中垂线上任意一点O 作为圆心，以OA 的长为半径，即可作出过点A B 、的圆，这样的圆也有无数个． （3） 过三点的圆：若这三点A B C 、、共线时，过三点的圆不存在；若A B C 、、三点不共线时，圆心是线段AB 与BC 的中垂线的交点，而这个交点O 是唯一存在的，这样的圆有唯一一个． （4） 过n ()4n ≥个点的圆：只可以作0个或1个，当只可作一个时，其圆心是其中不共线三点确定的圆的圆心．2. 定理：不在同一直线上的三点确定一个圆（1） “不在同一直线上”这个条件不可忽视，换句话说，在同一直线上的三点不能作圆； （2） “确定”一词的含义是”有且只有”，即”唯一存在”．三、三角形的外接圆及外心1. 三角形的外接圆（1） 经过三角形三个顶点的圆叫做三角形的外接圆，外接圆的圆心是三角形三条边垂直平分线的交点，叫做三角形的外心，这个三角形叫做这个圆的内接三角形． （2） 锐角三角形外接圆的圆心在它的内部；直角三角形外接圆的圆心在斜边中点处(即直角三角形外接圆半径等于斜边的一半)；钝角三角形外接圆的圆心在它的外部. 2. 三角形外心的性质（1） 三角形的外心是指外接圆的圆心，它是三角形三边垂直平分线的交点，它到三角形各顶点的距离相等； （2） 三角形的外接圆有且只有一个，即对于给定的三角形，其外心是唯一的，但一个圆的内接三角形却有无数个，这些三角形的外心重合.一、点与圆的位置关系【例18】 已知圆内一点到圆周上的点的最大距离是7，最小距离是5，则该圆的半径是( )A ．2B ．6C ．12D ．7二、过三点的圆【例19】 如图，四边形ABCD 中，AB AC AD ==，若7613CAD BDC ∠=︒∠=︒，，则CBD ∠=_________，BAC ∠=__________．DCBA【例20】 如图，直角坐标系中一条圆弧经过网格点A B C ，，，其中B 点的坐标为()44，，则该圆弧所在圆的圆心的坐标为 ．三、三角形的外接圆及外心【例21】 如图，ABC ∆内接于O ⊙，120BAC ∠=︒，AB AC =，BD 为O ⊙的直径，6AD =，则BC = .【例22】 等边三角形的外接圆的半径等于边长的( )倍． ABCD ．12【例23】 ABC ∆中，10AB AC ==，12BC =，求其外接圆的半径．【例24】 已知如图，ACD ∆的外角平分线CB 交其外接圆于B ，连接BA 、BD ，求证：BA BD =．N【例25】 已知∆ABC 中，=AB AC ，D 是∆ABC 外接圆劣弧AC 上的点(不与点A C ，重合)，延长BD 至E ． ⑴ 求证：AD 的延长线平分∠CDE ；⑴ 若30∠=︒BAC ，∆ABC 中BC边上的高为2+∆ABC 外接圆的面积．直线与圆的位置关系设O ⊙的半径为r ，圆心O 到直线l 的距离为d ，则直线和圆的位置关系如下表：6. 切线的性质（9） 定理：圆的切线垂直于过切点的半径．推论1：经过圆心且垂直于切线的直线必经过切点． 推论2：经过切点且垂直于切线的直线必经过圆心．（10） 注意：这个定理共有三个条件，即一条直线满足：①垂直于切线②过切点③过圆心①过圆心，过切点⇒垂直于切线．AB 过圆心，AB 过切点M ，则AB l ⊥． ②过圆心，垂直于切线⇒过切点．AB 过圆心，AB l ⊥，则AB 过切点M ． ③过切点，垂直于切线⇒过圆心．AB l ⊥，AB 过切点M ，则AB 过圆心．7. 切线的判定（1） 定义法：和圆只有一个公共点的直线是圆的切线； （2） 距离法：和圆心距离等于半径的直线是圆的切线； （3） 定理：经过半径的外端并且垂直于这条半径的直线是圆的切线．注意：定理的题设是①“经过半径外端”，②“垂直于半径”，两个条件缺一不可；定理的结论是“直线是圆的切线”．因此，证明一条直线是圆的切线有两个思路：①连接半径，证直线与此半径垂直；②作垂直，证垂直在圆上．AB CD El8. 切线长和切线长定理（1） 切线长：在经过圆外一点的圆的切线上，这点和切点之间的线段的长，叫做这点到圆的切线长． （2） 切线长定理：从圆外一点引圆的两条切线，它们的切线长相等，圆心和这一点的连线平分两条切线的夹角．三、三角形的内切圆1. 三角形的内切圆：和三角形各边都相切的圆叫做三角形的内切圆，内切圆的圆心叫做三角形的内心，这个三角形叫做圆的外切三角形．2. 多边形的内切圆：和多边形的各边都相切的圆叫做多边形的内切圆，这个多边形叫做圆的外切多边形．3. 直角三角形内切圆的半径与三边的关系设a 、b 、c 分别为ABC △中A ∠、B ∠、C ∠的对边，面积为S ，则内切圆半径为sr p=，其中()12p a b c =++．若90C ∠=︒，则()12r a b c =+-．二、切线的性质及判定【例1】 如图，ABC ∆为等腰三角形，AB AC =，O 是底边BC 的中点，O ⊙与腰AB 相切于点D ，求证AC 与O ⊙相切．lcb acbaO F ED CACBAB A【例2】 已知：如图，ABC ∆内接于O ，AD 是过A 的一条射线，且B CAD ∠=∠．求证：AD 是O 的切线．【例3】 已知：如图，AB 是O ⊙的直径，C 为O ⊙上一点，MN 过C 点，AD MN ⊥于D ，AC 平分DAB ∠．求证：MN 为O ⊙的切线．【例4】 如图，已知OA 是O ⊙的半径，B 是OA 中点，BC OA ⊥，P 是OA 延长线上一点，且PA AC =．求证：PC 是O ⊙的切线．【例5】 已知：如图，C 为O ⊙上一点，DA 交O ⊙于B ，连结AC BC 、，且DCB CAB ∠=∠DC 为O ⊙的切线；（2）2CD AD BD =⋅．【例6】 如图，以等腰ABC ∆中的腰AB 为直径作O ，交BC 于点D ．过点D 作DE AC ⊥，垂足为E ．（1）求证：DE 为O 的切线；（2）若O 的半径为5，60BAC ∠=︒，求DE 的长．C【例7】 如图，已知AB 为⑴O 的弦，C 为⑴O 上一点，⑴C =⑴BAD ，且BD ⑴AB 于B ．（1）求证：AD 是⑴O 的切线．（2）若⑴O 的半径为3，AB =4，求AD 的长．【例8】 如图，Rt ABC ∆中，90ABC ∠=︒，以AB 为直径作O ⊙交AC 边于点D ，E 是边BC 的中点，连接DE ．（1）求证：直线DE 是O ⊙的切线；（2）连接OC 交DE 于点F ，若OF CF =，求tan ACO ∠的值．【例9】 如图，AB 是O ⊙的的直径，BC AB ⊥于点B ，连接OC 交O ⊙于点E ，弦AD OC ∥，弦DF AB⊥于点G ．（1）求证：点E 是BD 的中点； （2）求证：CD 是O ⊙的切线；（3）若4sin 5BAD ∠=，O ⊙的半径为5，求DF 的长．【例10】 如图，等腰三角形ABC 中，10AC BC ==，12AB =．以BC 为直径作O ⊙交AB 于点D ，交AC于点G ，DF AC ⊥，垂足为F ，交CB 的延长线于点E ． （1）求证：直线EF 是O ⊙的切线； （2）求sin E ∠的值．一、切线长定理1.如图，PA PB ，分别是O 的切线，A B ，为切点，AC 是O 的直径，已知35BAC ∠=︒，P ∠的度数为（ ） A ．35︒ B ．45︒ C ．60︒ D ．70︒2.如图，PA PB 、分别切O ⊙于A B ，两点，PC 满足AB PB AC PC AB PC AC PB ⋅-⋅=⋅-⋅，且AP PC ⊥，2PAB BPC ∠=∠，求ACB ∠的度数．3.如图，从圆O 外一点P 引圆O 的两条切线PA PB ，，切点分别为A B ，．如果60APB ∠=，8PA =，那么弦AB 的长是（ ）A ．4B ．8C．D．P则OP =（ ）A ．50cm B．cm Ccm D．cm5.如图，已知以直角梯形ABCD 的腰CD 为直径的半圆O 与梯形上底AD 、下底BC 以及腰AB 均相切，切点分别是D C E ，，．若半圆O 的半径为2，梯形的腰AB 为5，则该梯形的周长是（ ）A ．9B ．10C ．12D ．146.等腰梯形ABCD 外切于圆，且中位线MN 的长为10，那么这个等腰梯形的周长是________．7.如图，PA PB DE 、、分别切O ⊙于A B C 、、，若10PO =，PDE ∆周长为16，求O ⊙的半径．8.如图，PA PB ，切O 于AB ，，MN 切O 于C ，交PA PB ，于M N ，两点，已知8PA =，求PMN ∆的周长．PB P于G，交AB AC、于MN，则BMN∆的周长为______________．10.如图，已知AB是O⊙的直径，BC是和O⊙相切于点B的切线，O⊙的弦AD平行于OC，若2OA=，且6AD OC+=，求CD的长．补充讲义两圆的公切线（选讲自己了解）9.两圆的外公切线（11）求两圆外公切线长：构造外公切线、圆心距、大圆与小圆半径的差为边的特征直角三角形．如图，设大圆的半径为R，小圆的半径为r，两圆的圆心距为d，两外公切线的夹角为α，则两圆的外公切线长为：l=，sin2R rdα-=（12）求两圆内公切线长：构造外公切线、圆心距、大圆与小圆半径的和为边的特征直角三角形．10.两圆的内公切线如图，设大圆的半径为R，小圆的半径为r，两圆的圆心距为d，两外公切线的夹角为α，则两圆的内公切线长l=，sin2R r dα+ =CB AP圆与相似三角形经典证明题1.如图，A、B、C、D依次为一直线上4个点，BC=2，△BCE为等边三角形，⊙O过A、D、E3 点，且∠AOD=120°．设AB=x，CD=y，则y与x的函数关系为．2．如图，在△ABC中，AB=AC，AE是∠BAC的平分线，∠ABC的平分线BM交AE于点M，点O在AB上，以点O为圆心，OB的长为半径的圆经过点M，交BC于点G，交AB于点F．（1）求证：AE为⊙O的切线．（2）当BC=8，AC=12时，求⊙O的半径．（3）在（2）的条件下，求线段BG的长．3．如图，在△ABC中，AB=AC，以AC为直径的⊙O交BC于点D，交AB于点E，过点D作DF⊥AB，垂足为F，连接DE．（1）求证：直线DF与⊙O相切；（2）若AE=7，BC=6，求AC的长．4．．Rt．ABC．．．ACB=90°．D．AB．．．．．．．BD．．．．．O．AC．．E．．．DE．．．．．BC．．．．．．．F．．BD=BF．．1．．．．AC．．O．．．．2．．BC=6．AB=12．．．O．．．．5．．．．AB．．O．．．．．．A．．O．．．．．．．．．．C．．．OC．．O．．D．BD．．．．．AC．E．．．AD．．1．．．．．CDE．．CAD．．2．．AB=2．AC=2．．AE．．．6. 已知在△ABC中，∠B=90°，以AB上的一点O为圆心，以OA为半径的圆交AC于点D，交AB 于点E．．1．．．．AC•AD=AB•AE．．2．．．BD．⊙O．．．．D．．．．E．OB．．．．．BC=2．．．AC．．．7．如图所示，⊙O是Rt△ABC的外接圆，∠ABC=90°，弦BD=BA，AB=12，BC=5，BE⊥DC交DC的延长线于点E.（1）求证：∠BCA=∠BAD；（2）求DE的长；（3）求证：BE是⊙O的切线.8. 如图，已知在△ABC中，AD是BC边上的中线，以AB为直径的⊙O交BC于点D，过D作MN⊥AC于点M，交AB的延长线于点N，过点B作BG⊥MN于G．（1）求证：△BGD∽△DMA；（2）求证：直线MN是⊙O的切线．9. 如图的⊙O中，AB为直径，OC⊥AB，弦CD与OB交于点F，过点D、A分别作⊙O的切线交于点G，并与AB延长线交于点E．（1）求证：∠1=∠2．（2）已知：OF：OB=1：3，⊙O的半径为3，求AG的长．10.．．．．．O．．AB．．．．OC．AB．．CD．OB．．．F．．AB．．．．．．．E．．EF=ED．．1．．．．DE．．O．．．．．2．．OF．OB=1．3．．O．．．R=3．．．．．11．．．．AB ．⊙O ．．．．．D ．．．．．．∠BDE =∠CBE ．BD ．AE ．．．F ．（1）求证：BC 是⊙O 的切线；（2）若BD 平分∠ABE ，求证：DE 2=DF •DB ；（3）在（2）的条件下，延长ED ，BA 交于点P ，若PA =AO ，DE =2，求PD 的长和⊙O 的半径．12．如图，AB 是⊙O 的直径，点C 为⊙O 上一点，AE 和过点C 的切线互相垂直，垂足为E ，AE 交⊙O 于点D ，直线EC 交AB 的延长线于点P ，连接AC ，BC ，PB ：PC =1：2． （1）求证：AC 平分∠BAD ；（2）探究线段PB ，AB 之间的数量关系，并说明理由； （3）若AD =3，求△ABC 的面积．13．已知，如图，AB 是⊙O 的直径，点C 为⊙O 上一点，OF ⊥BC 于点F ，交⊙O 于点E ，AE 与BC 交于点H ，点D 为OE 的延长线上一点，且∠ODB =∠AEC . （1）求证：BD 是⊙O 的切线； （2）求证：2CE EH EA =⋅； （3）若⊙O 的半径为5，3sin 5A =，求BH 的长.第13题图FH EOC B A。

中考总复习：圆的有关概念、性质与圆有关的位置关系—巩固练习（基础）【巩固练习】一、选择题1. 已知⊙1O 与⊙2O 的半径分别为3 cm 和4 cm ，若12O O =7 cm ，则⊙1O 与⊙2O 的位置关系是（ ）A ．相交B ．相离C ．内切D ．外切2．如图，AB 是⊙O 的直径，点C 、D 在⊙O 上 ，∠BOD=110°，AC∥OD，则∠AOC 的度数 （ ）A. 70°B. 60°C. 50°D. 40°3．如图所示，AB 是⊙O 的直径，CD 为弦，CD ⊥AB 于点E ，则下列结论中不成立的是( )A ．∠COE ＝∠DOEB ．CE ＝DEC ．OE ＝BED ．»»BDBC第2题 第3题 第5题 第6题4．（2015•黑龙江）如图，⊙O 的半径是2，AB 是⊙O 的弦，点P 是弦AB 上的动点，且1≤OP≤2，则弦AB 所对的圆周角的度数是（ ）A ．60°B ．120°C ．60°或120°D ．30°或150°5．如图所示，△ABC 内接于圆O ，∠A ＝50°；∠ABC ＝60°，BD 是圆O 的直径，BD 交AC 于点E ，连接DC ，则∠AEB 等于( )A ．70°B ．110°C ．90°D ．120°6．小明不慎把家里的圆形玻璃打碎了，其中四块碎片如图所示，为配成与原来大小一样的圆形玻璃，小明带到商店去的一块玻璃碎片应该是( )A ．第①块B ．第②块C ．第③块D ．第④块二、填空题7．（2015•雁江区模拟）如图，MN 是半径为2的⊙O 的直径，点A 在⊙O 上，∠AMN=30°，B 为弧AN 的中点，P 是直径MN 上一动点，则PA+PB 的最小值为 .8．如图所示，⊙O的直径AC＝8 cm，C为⊙O上一点，∠BAC＝30°，则BC＝________cm．第8题第9题9．两圆有多种位置关系，图中(如图所示)不存在的位置关系是__________．10．如图所示，AB与⊙O相切于点B，AO的延长线交⊙O于点C，连接BC．若∠A＝36°，则∠C＝______．11．如图，直线PA过半圆的圆心O，交半圆于A，B两点，PC切半圆与点C，已知PC=3，PB=1，则该半圆的半径为　．第10题第11题第12题12．如图所示．B是线段AC上的一点，且AB:AC＝2:5．分别以AB、AC为直径画圆，则小圆的面积与大圆的面积之比为________．三、解答题13．已知AB与⊙O相切于点C，OA=OB．OA、OB与⊙O分别交于点D、E.(1) 如图①，若⊙O的直径为8，AB=10，求OA的长(结果保留根号)；(2)如图②，连接CD、CE，若四边形ODCE为菱形．求ODOA的值．14. 如图所示，在Rt△ABC中，∠C＝90°，O为直角边BC上一点，以O为圆心、OC为半径的圆恰好与斜边AB相切于点D，与BC交于另一点E．(1)求证：△AOC≌△AOD；(2)若BE＝1，BD＝3，求⊙O的半径及图中阴影部分的面积S．15．（2015•上城区二模）如图，已知四边形ABCD内接于圆，对角线AC与BD相交于点E，F在AC上，AB=AD，∠BFC=∠BAD=2∠DFC．（1）若∠DFC=40°，求∠CBF的度数；（2）求证：CD⊥DF．l16. 如图，已知∠ABC=90°，AB=BC．直线与以BC为直径的圆O相切于点C．点F是圆O上异于B、Cl的动点，直线BF与相交于点E，过点F作AF的垂线交直线BC与点D．（1）如果BE=15，CE=9，求EF的长；（2）证明：①△CDF∽△BAF；②CD=CE；（3）探求动点F在什么位置时，相应的点D位于线段BC的延长线上，且使CD，请说明你的理由．【答案与解析】一、选择题1.【答案】D；O O=7，根据圆与圆位置关系的判定可知两圆外切.【解析】两圆半径之和3+4=7，等于两圆圆心距122.【答案】D；【解析】由AB是⊙O的直径，点C、D在⊙O上，知OA＝OC，根据等腰三角形等边对等角的性质和三角形内角和定理，得∠AOC＝180°－2∠OAC.由AC∥OD，根据两直线平行，内错角相等的性质，得∠OAC＝∠AOD.由AB是⊙O的直径，∠BOD=110°，根据平角的定义，得∠AOD＝180°－∠BOD=70°.∴∠AOC＝180°－2×70°＝40°.故选D.3.【答案】C；【解析】由垂径定理知A、B、D都正确．4.【答案】C；【解析】作OD⊥AB，如图，∵点P是弦AB上的动点，且1≤OP≤2，∴OD=1，∴∠OAB=30°，∴∠AOB=120°，∴∠AEB=∠AOB=60°，∵∠E+∠F=180°，∴∠F=120°，即弦AB所对的圆周角的度数为60°或120°．故选C．5.【答案】B；【解析】∵∠A=50°，∴∠D=50°，又∵BD是直径，∴∠BCD=90°，∴∠DBC=90°-50°=40°，∠ABD=60°-40°=20°，∴∠BEC=50°+20°=70°，∴∠AEB=180°-70°=110°.6.【答案】B；【解析】因为第②块含有圆周的一部分，可以找到圆心，量出半径.其他块都不行.二、填空题7．【答案】2；【解析】如图，作点B关于MN的对称点B′，连接OA、OB′、AB′，由轴对称确定最短路线问题可知，AB′与M的交点即为所求的使PA+PB的值最小的点，∵∠AMN=30°，∴∠AON=2∠AMN=2×30°=60°，∵B为弧AN的中点，∴∠NOB′=×60°=30°，∴∠AOB′=90°，∴△AOB′是等腰直角三角形，∵⊙O的半径为2，∴AB′=2，即PA+PB的最小值为为2．8．【答案】4；【解析】因为AC为直径，根据直径所对的圆周角为直角，得∠ABC＝90°，则BC＝AC·sin∠BAC＝4(am)．9．【答案】相交；【解析】认真观察、判断可发现每两圆间不存在的位置关系是：相交．10．【答案】27°；【解析】如图，连结OB，由AB与⊙O相切于点B，得∠ABO＝90°，因为∠A＝36°，所以∠AOB＝54°，所以∠C＝27°.11．【答案】4；【解析】连接OC，则由直线PC是圆的切线，得OC⊥PC.设圆的半径为x，则在Rt△OPC中，PC=3，OC= x，OP=1＋x，根据地勾股定理，得OP2=OC2＋PC2，即（1＋x）2= x2＋32，解得x=4.即该半圆的半径为4.12．【答案】4:25；三、解答题13.【答案与解析】(1) 如图①，连接OC ，则OC=4.∵AB 与⊙O 相切于点C ，∴OC⊥AB. ∴在△OAB 中，由OA=OB ，AB=10得1AC AB 52==.∴ 在△RtOAB 中，OA ===.(2)如图②，连接OC ，则OC=OD.∵四边形ODCE 为菱形，∴OD=DC.∴△ODC 为等边三角形.∴∠AOC=60°.∴∠A=30°.∴1OC 1OD 1OC OA 2OA 2OA 2===，，即.14.【答案与解析】解：（1）∵ AB 切⊙O 于D ，∴OD ⊥AB ．在Rt △AOC 和Rt △AOD 中，,.OC OD AO AO =⎧⎨=⎩ ∴Rt △AOC ≌Rt △AOD(HL)．(2)设半径为r ，在Rt △ODB 中，，解得r ＝4．2223(1)r r +=+ 由(1)有AC ＝AD ，∴，2229(3)AC AC +=+ 解得AC ＝12，∴．22111112945482222S AC BC r πππ=-=⨯⨯-⨯=-g 15.【答案与解析】解：（1）∵∠ADB=∠ACB ，∠BAD=∠BFC ，∴∠ABD=∠FBC ，又∵AB=AD ，∴∠ABD=∠ADB ，∴∠CBF=∠BCF ，∵∠BFC=2∠DFC=80°，∴∠CBF==50°；（2）令∠CFD=α，则∠BAD=∠BFC=2α，∵四边形ABCD 是圆的内接四边形，∴∠BAD+∠BCD=180°，即∠BCD=180°﹣2α，又∵AB=AD ，∴∠ACD=∠ACB ，∴∠ACD=∠ACB=90°﹣α，∴∠CFD+∠FCD=α+（90°﹣α）=90°，∴∠CDF=90°，即CD ⊥DF ．16.【答案与解析】解：（1）∵直线与以BC 为直径的圆O 相切于点C ，l ∴∠BCE=90°，又∵BC 为直径，∴∠BFC=∠CFE=90°.∴∠CFE=∠BCE.∵∠FEC=∠CEB，∴△CEF∽△BEC.∴CE EF BE EC =.∵BE=15，CE=9，即：9EF 159=，解得：EF=275.（2）证明：①∵∠FCD+∠FBC=90°，∠ABF+∠FBC=90°，∴∠ABF=∠FCD.同理：∠AFB=∠CFD.∴△CDF∽△BAF.②∵△CDF∽△BAF，∴CF CD BF BA =.又∵△CEF∽△BCF，∴CF CE BF BC =.∴CD CE BA BC=.又∵AB=BC，∴CE=CD.（3）当F 在⊙O 的下半圆上，且»»2BF BC 3=时，相应的点D 位于线段BC 的延长线上，且使CD.理由如下：CE.在Rt△BCE 中，tan∠CBE=CEBC =，∴∠CBE=30°，∴»CF所对圆心角为60°.∴F 在⊙O 的下半圆上，且»»2BF BC 3=.。