下载文档原格式
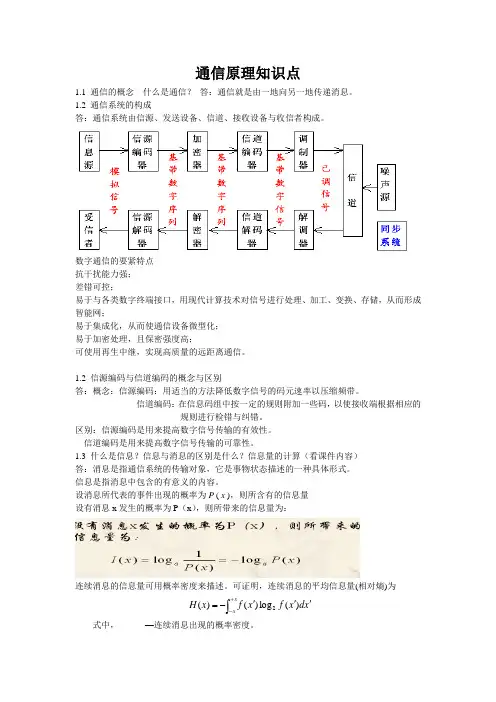
通信原理知识点1.1 通信的概念什么是通信？答：通信就是由一地向另一地传递消息。
1.2 通信系统的构成答：通信系统由信源、发送设备、信道、接收设备与收信者构成。
数字通信的要紧特点抗干扰能力强；差错可控；易于与各类数字终端接口，用现代计算技术对信号进行处理、加工、变换、存储，从而形成智能网；易于集成化，从而使通信设备微型化；易于加密处理，且保密强度高；可使用再生中继，实现高质量的远距离通信。
1.2 信源编码与信道编码的概念与区别答：概念：信源编码：用适当的方法降低数字信号的码元速率以压缩频带。
信道编码：在信息码组中按一定的规则附加一些码，以使接收端根据相应的规则进行检错与纠错。
区别：信源编码是用来提高数字信号传输的有效性。
信道编码是用来提高数字信号传输的可靠性。
1.3 什么是信息？信息与消息的区别是什么？信息量的计算（看课件内容）答：消息是指通信系统的传输对象，它是事物状态描述的一种具体形式。
信息是指消息中包含的有意义的内容。
设消息所代表的事件出现的概率为P ( x )，则所含有的信息量设有消息x发生的概率为P（x），则所带来的信息量为：连续消息的信息量可用概率密度来描述。
可证明，连续消息的平均信息量(相对熵)为式中，—连续消息出现的概率密度。
x d xfxfxH xx'''-=⎰+-)(log)()(2若a = 2，则信息量的单位为比特(bit ），它代表出现概率为1/2的消息所含有的信息量。
当两个消息等概率时，任一消息所含有的信息量为1比特。
一位二进制数称之1比特，而不管这两个符号是否相等概率。
1.4 衡量通信系统的性能指标有效性、可靠性、安全性、保密性。
1.4 什么是传码率、误码率与传信率？答：码元传输速率是传码率；在传输中出现错误码元的概率叫误码率；信息传输速率叫传信率。
1.5 通信方式单工通信，是指消息只能在一个方向传输的工作方式。
如广播、电视、遥控等。
所谓半双工通信，是指信号能够在两个方向上传输，但不能同时传输，务必是交替进行，一个时间只能同意向一个方向传送。
扩频通信一、简介扩频通信是一种通过同时传输多个频带信号以提高通信效率和抗干扰能力的通信技术。
扩频通信技术在军事通信、卫星通信、移动通信等领域得到广泛应用。
本文将介绍扩频通信的原理、应用和发展趋势。
二、扩频通信原理扩频通信利用码分多址技术，通过同时使用多个频带信号的方式来传输信息。
在发送端，数据会被编码成高频率的扩频码序列，然后与载波信号相乘，形成一个带有更宽频率的信号。
接收端利用相同的扩频码序列进行解码，将多个频带信号分离出来还原成原始数据。
这种方法可以提高数据传输速率和保护通信安全。
三、扩频通信应用1.军事通信：扩频通信技术可以有效保护通信数据的安全性，提高抗干扰能力，广泛应用于军事通信系统中。
2.卫星通信：卫星通信需要长距离传输数据，扩频通信技术可以提高通信质量和覆盖范围，是卫星通信的重要技术支持。
3.移动通信：3G、4G、5G等移动通信标准中都采用了扩频通信技术，以提高数据传输速率、提高通话质量和减少信号干扰。
四、扩频通信发展趋势1.多载波扩频技术：通过同时使用多个载波信号，提高通信吞吐量和频谱利用率。
2.混合码扩频技术：结合不同类型的扩频码序列，进一步提高通信系统的性能和安全性。
3.飞跃式发展：未来扩频通信技术将朝着更高速率、更低功耗和更广覆盖等方向发展，为5G、IoT和智能网联汽车等新兴应用提供支持。
五、总结扩频通信技术作为一种高效的通信方法，已在各个领域得到广泛应用。
随着通信技术的不断进步，扩频通信将继续发挥重要作用，推动通信行业的发展。
希望本文对您对扩频通信有更深入的了解，并对其未来发展趋势有所启示。
初级认证大纲知识点●扩频通信：指将信号扩展至一很宽频带后进行传送的通信系统。
●扩频通信系统有多种实现方法，CDMA系统采用直接序列调制的方式实现扩频。
●直接序列调制见下图，将原始信号编码和一比特率远大于它的扩频序列想乘（求异或）之后去调制载波得到扩频信号，此种扩频方式称为直接序列调制。
3、相关性和正交相关性：指两个信号的相似程度。
相关性使用相关系数来衡量，当两个信号完全相同时的相关系数为1，当两个信号的相关系数为0时称两个信号正交。
如果两个二进制数字编码序列相关系数为0，称两者为正交序列。
多个两两正交的二进制数字编码序列构成的码组称为正交码组。
4、系统框图5、常用名词●比特（bit）、符号（Symbol）与码片（Chip）→纯信息数据称为比特（bit）→在经过卷积编码器、符号重复与交织后的数据被称为符号（symbol）→经过最终扩频后得到的数据被称为码片（chip）●处理增益（Processing Gain）→理解为最终扩频速率与信息速率的比；在IS-95中处理增益为128，即21dB●前向（Forward）：从基站到移动台●反向（Reverse）：从移动台到基站信道编码采用卷积码（语音）或者TURBO（数据）码。
约束长度：移位寄存器数+1。
编码效率：输入bit数 / 输出bit数。
6、扩频和Walsh码●前向信道：采用Walsh码扩频区分信道。
●反向信道：IS95A/B和CDMA2000的RC1、RC2中，Walsh码用于正交调制。
CDMA2000的其他RC用Walsh码区分信道类型。
●区分信道：编码器输出数据的每1个比特与一个2n阶Walsh码相乘（1符号变换到2n个码片）。
●正交调制：编码器输出数据每6个比特变换为一个64阶Walsh码（6符号变换到64个码片）。
7、m序列●m序列是最长线形反馈寄存器序列的简称。
●m序列重要性质：→输出序列Ck和C（k+t）模2相加后的序列仍然是序列Ck的一个时延序列→不同相位的m序列的相关值近似为0（-1/m）●输出序列周期为2n -1 （没有全0状态，n为寄存器个数）8、短码、长码●CDMA系统中使用了两种m序列，其中一个周期为215 (m序列是15位的）称为短码，另一个周期为242称为长码（增加了全0状态）。
移动通信复习资料移动通信原理与系统复习资料第⼀章：1.在4G系统中，⽹元间的协议是基于IP的，每⼀个MT（移动终端）都有各⾃的IP地址。
2.IP核⼼⽹：它不是专门⽤作移动通信，⽽是作为⼀种统⼀的⽹络，⽀持有线和⽆线接⼊。
主要功能是：完成位置管理和控制、呼叫控制和业务控制。
3.4G⽹络应该是⼀个⽆缝连接的⽹络，也就是说各种有线和⽆线⽹都能以IP协议为基础连接到IP核⼼⽹。
当然为了与传统的⽹络互联则需要⽤⽹关建⽴⽹络的互联，所以将来的4G⽹络将是⼀个复杂的多协议的⽹络。
4.移动通信的定义：指通信双⽅或⾄少有⼀⽅处于运动中进⾏信息交换的通信⽅式。
5.移动通信系统包括：⽆绳电话、⽆线寻呼、陆地蜂窝移动通信、卫星移动通信等。
6.⽆线通信是移动通信的基础。
7.移动通信所受⼲扰种类：（1）：互调⼲扰：指两个或多个信号作⽤在通信设备的⾮线性器件上，产⽣与有⽤信号频率相近的组合频率。
从⽽对通信系统构成⼲扰的现象。
（2）：邻道⼲扰：指相邻或邻近的信道之间的⼲扰，是由于⼀个强信号串扰弱信号⽽造成的⼲扰。
（3）：同频⼲扰：指相同频率电台之间的⼲扰。
8.移动通信的⼯作⽅式：（1）：单⼯通信：指通信双⽅电台交替地进⾏收信和发信。
它常⽤于点到点通信。
（2）双⼯通信：指通信双⽅。
收发信机均同时⼯作。
即任⼀⽅讲话时都可以听到对⽅的话⾳，没有“按-讲”开关。
（3）半双⼯通信第⼆章：1. 移动通信的信道：指基站天线、移动⽤户天线和两幅天线之间的传播路径。
2. 从某种意义上来说，对移动⽆线电波传播特性的研究就是对移动信道的研究。
（判断）3. 移动信道的基本特性就是衰落特性。
4. ⽆线电波的传播⽅式：直射、反射、绕射和散射以及它们的合成。
5. 移动信道是⼀种时变信道。
在这种信道中传播表现出来的衰落⼀般为：随信号传播距离变化⽽导致的传播损耗和弥散。
6. （1）阴影衰落：由于传播环境中的地形起伏、建筑物及其它障碍物对电磁波的遮蔽所引起的衰落。
无线扩频集成电路开发中信道编解码技术研究与FPGA实现本论文主要对无线扩频集成电路设计中的信道编解码算法进行研究并对其FPGA实现思路和方法进行相关研究。
近年来无线局域网IEEE802.11b标准建议物理层采用无线扩频技术,所以开发一套扩频通信芯片具有重大的现实意义。
无线扩频通信系统与常规通信相比,具有很强的抗干扰能力,并具有信息荫蔽、多址保密通信等特点。
无线信道的特性较复杂,因此在无线扩频集成电路设计中,加入信道编码是提高芯片稳定性的重要方法。
在了解扩频通信基本原理的基础上,本文提出了“串联级联码+两次交织”的信道编码方案。
串联的级联码由外码——(15,9,4)里德-所罗门(Reed-Solomon)码,和内码——(2,1,3)卷积码构成,交织则采用交织深度为4的块交织。
重点对RS码的时域迭代译码算法和卷积码的维特比译码算法进行了详细的讨论,并完成信道编译码方案的性能仿真及用FPGA实现的方法。
计算机仿真的结果表明,采用此信道编码方案可以较好的改善现有仿真系统的误符号率。
本论文的内容安排如下:第一章介绍了无线扩频通信技术的发展状态以及国内外开发扩频通信芯片的现状,并给出了本论文的研究内容和安排。
第二章主要介绍了扩频通信的基本原理,主要包括扩频通信的定义、理论基础和分类,直接序列扩频通信方式的数学模型。
第三章介绍了基本的信道编码原理,信道编码的分类和各自的特点。
第四章给出了本课题选择的信道编码方案——“串联级联码+两次交织”,详细讨论了方案中里德-所罗门(Reed-Solomon)码和卷积码的基本原理、编码算法和译码算法。
最后给出编码方案的实际参数。
第五章对第四章提出的编码方案进行了性能仿真。
第六章结合项目实际,讨论了FPGA开发基带扩频通信系统的设计思路和方法。
首先对FPGA开发流程以及实际开发的工具进行了简要的介绍,然后给出了扩频通信系统的总体设计。
对发射和接收子系统中信道编码、解码等相关功能模块的实现原理和方法进行分析。
PN 码（gold 码） 同步序列发生器信道编码与扩频通信直接扩频技术是二十一世纪通信的主要潮流之一。
特别是在移动通信领域，码分多址已经成为公 认的二十一世纪蜂窝式移动通信基本特征。
故而通过仿真手段讨论扩频通信与信道编码的关系，具有 相当重要的现实意义。
从某种意义上说，直接扩频技术也可以看作一种信道编码的分组编码形式，编 译码都是通过码序列分组和同一个 PN 码的乘运算实现。
应用这一思想，可以进行二进制双极性扩频通信系统的蒙特卡罗仿真。
二进制双极性扩频通信系统的蒙特卡罗仿真双用户二进制双极性扩频通信系统的蒙特卡罗仿真模型输出数据1E +-高斯随机数发生器均匀随机数发生器比较差错计数器2双用户二进制双极性扩频通信系统的蒙特卡罗仿真流程图初始化变量：信噪比、双用户发送接收信号变量数组、噪声变量数组、 仿真序列长度、循环步长、数据块长、临时变量 清零： 循环计数器和差错计数器、数据块长计数器A sin (wn )正弦干扰 序列发生器±EPN 码 2（ gold 码） 同步序列发生器累加判决器输出数据2循环计数器加1生成叠加噪声与人为正弦干扰信号模块循环计数器置1生成发送用户1数据块模块生成发送用户2数据块模块发送用户1数据块扩频模块发送用户2数据块扩频模块解扩判决接收用户1数据块模块—解扩判决接收用户2数据块模块接收用户1数据块差错计数模块接收用户2数据块差错计数模块显示：接收用户1差错计数器数值、接收用户2差错计数器数值,为了简化二进制双极性扩频通信系统的蒙特卡罗仿真模型，使我们把主要精力真正集中于编码仿真本身，本次仿真用户数为2，PN码采用长度为30的gold码。
如上图所示，双用户二进制双极性扩频通信系统的蒙特卡罗仿真模型中还加入了正弦干扰序列发生器，以用来测试扩频技术对人为正弦干扰的抑制作用。
在双用户二进制双极性扩频通信系统的蒙特卡罗仿真流程图中，正弦干扰被视做噪声的一部分置于叠加噪声模块。
无线通信中的信道编码技术在当今高度互联的世界中，无线通信已经成为我们生活中不可或缺的一部分。
从手机通话、无线网络到卫星通信，无线通信技术的发展极大地改变了我们的生活方式和工作方式。
而在无线通信中，信道编码技术是确保信息准确、可靠传输的关键技术之一。
信道编码技术的核心目标是在存在噪声和干扰的无线信道中，提高数据传输的可靠性和有效性。
简单来说，就是在发送端对原始数据进行编码处理，使得接收端能够更好地从受到干扰的信号中恢复出原始数据。
为了更好地理解信道编码技术，我们先来了解一下无线信道的特点。
无线信道是一个充满不确定性和干扰的环境。
信号在传输过程中会受到多径衰落、阴影效应、噪声干扰等多种因素的影响，导致信号失真、误码等问题。
这些问题就像是在信息传递的道路上设置了重重障碍，而信道编码技术就是要帮助信息“突破”这些障碍。
在众多的信道编码技术中，卷积码是一种被广泛应用的编码方式。
卷积码通过将输入的信息序列与编码器的生成多项式进行卷积运算，生成编码后的输出序列。
这种编码方式具有较强的纠错能力，而且编码和解码的复杂度相对较低，因此在许多无线通信系统中得到了应用。
另一种重要的信道编码技术是Turbo 码。
Turbo 码的出现是信道编码领域的一个重大突破。
它采用了迭代译码的思想，通过多次迭代来提高译码的准确性。
Turbo 码在接近香农极限的情况下，仍能保持良好的性能，因此在 3G、4G 等移动通信系统中发挥了重要作用。
除了卷积码和 Turbo 码，低密度奇偶校验码（LDPC 码）也是一种性能优异的信道编码技术。
LDPC 码基于稀疏矩阵的校验关系，具有接近香农极限的纠错性能，同时在硬件实现上也具有一定的优势。
信道编码技术的性能评估通常通过一些关键指标来衡量，比如码率、纠错能力和译码复杂度等。
码率是指编码后的数据量与原始数据量的比值，它反映了编码的效率。
纠错能力则表示编码能够纠正的错误位数，纠错能力越强，意味着在恶劣的信道条件下仍能保证数据的可靠传输。
信道编码与扩频通信直接扩频技术是二十一世纪通信的主要潮流之一。
特别是在移动通信领域，码分多址已经成为公认的二十一世纪蜂窝式移动通信基本特征。
故而通过仿真手段讨论扩频通信与信道编码的关系，具有相当重要的现实意义。
从某种意义上说，直接扩频技术也可以看作一种信道编码的分组编码形式，编译码都是通过码序列分组和同一个PN码的乘运算实现。
应用这一思想，可以进行二进制双极性扩频通信系统的蒙特卡罗仿真。
二进制双极性扩频通信系统的蒙特卡罗仿真双用户二进制双极性扩频通信系统的蒙特卡罗仿真模型双用户二进制双极性扩频通信系统的蒙特卡罗仿真流程图为了简化二进制双极性扩频通信系统的蒙特卡罗仿真模型，使我们把主要精力真正集中于编码仿真本身，本次仿真用户数为2，PN码采用长度为30的gold码。
如上图所示，双用户二进制双极性扩频通信系统的蒙特卡罗仿真模型中还加入了正弦干扰序列发生器，以用来测试扩频技术对人为正弦干扰的抑制作用。
在双用户二进制双极性扩频通信系统的蒙特卡罗仿真流程图中，正弦干扰被视做噪声的一部分置于叠加噪声模块。
MATLAB源程序function [p1,p2]=ss_Pe94_2105(snr_in_dB,A,w)%ss_Pe94_2105.m 双用户二进制双极性扩频通信系统的蒙特卡罗仿真%snr_in_dB 信噪比%p 误码率%A 正弦干扰幅度%w 正弦干扰角频率%PN码采用长度Lc为30的gold码,Lc=length(gold)=30snr=10^(snr_in_dB/10);sgma=1;Eb=2*sgma^2*snr;N=10^5; %仿真序列长度10^5，运行时间约3分钟p1=0;p2=0;gold1=[0 1 1 1 0 0 0 0 1 0 0 0 0 1 1 0 0 1 0 0 1 0 1 1 1 1 0 0 0 0 0];gold2=[0 1 0 1 1 0 1 1 1 0 0 0 1 0 0 0 0 0 1 0 0 1 0 0 0 1 1 0 0 0 1];Lc=length(gold1); %Lc=30;pn_seq1=2*gold1-1;pn_seq2=2*gold2-1;E_chip=Eb/Lc;temp=0;data1=0;data2=0;repeated_data1=zeros(1,Lc);repeated_data2=zeros(1,Lc);trans_sig1=zeros(1,Lc);trans_sig2=zeros(1,Lc);noise=zeros(1,Lc);n=1:Lc;interference=zeros(1,Lc);rec_sig=zeros(1,Lc);temp1=zeros(1,Lc);temp2=zeros(1,Lc);decision_variable1=0;decision_variable2=0;decision1=0;decision2=0;num_of_err_1=0;num_of_err_2=0;time=0;for i=1:Ntemp=rand;if (temp<0.5)data1=-1;elsedata1=1;endfor j=1:Lcrepeated_data1(j)=data1;endtrans_sig1=sqrt(E_chip)*repeated_data1.*pn_seq1;temp=rand;if (temp<0.5)data2=-1;elsedata2=1;endfor j=1:Lcrepeated_data2(j)=data2;endtrans_sig2=sqrt(E_chip)*repeated_data2.*pn_seq2; noise=sgma*randn(1,Lc);time=time+1,n=(time-1)*Lc+1:time*Lc;interference=A*sin(w*n);rec_sig=trans_sig1+trans_sig2+noise+interference; temp1=rec_sig.*pn_seq1;decision_variable1=sum(temp1);if (decision_variable1<0)decision1=-1;elsedecision1=1;endif (decision1~=data1)num_of_err_1=num_of_err_1+1;endtemp2=rec_sig.*pn_seq2;decision_variable2=sum(temp2);if (decision_variable2<0)decision2=-1;elsedecision2=1;endif (decision2~=data2)num_of_err_2=num_of_err_2+1;endendnum_of_err_1,num_of_err_2,p1=num_of_err_1/N;p2=num_of_err_2/N;%ss_Pe94_2105.m 双用户二进制双极性扩频通信系统的蒙特卡罗仿真echo on%cd94_2_030_105.m 双用户二进制双极性扩频通信系统的蒙特卡罗仿真绘图%PN码采用长度Lc为30的gold码,Lc=length(gold)=30%仿真序列长度10^5，运行时间约1小时A1=3;A2=7;A3=12;A4=0;%A1 A2 A3 A4 正弦干扰幅度w0=1;%w0 正弦干扰角频率SNRindB=0:2:30;for i=1:length(SNRindB)[smld_err_prb11(i),smld_err_prb12(i)]=ss_Pe94_2105(SNRindB(i),A1,w0);[smld_err_prb21(i),smld_err_prb22(i)]=ss_Pe94_2105(SNRindB(i),A2,w0);[smld_err_prb31(i),smld_err_prb32(i)]=ss_Pe94_2105(SNRindB(i),A3,w0);[smld_err_prb41(i),smld_err_prb42(i)]=ss_Pe94_2105(SNRindB(i),A4,w0);end;%绘图函数semilogy(SNRindB,smld_err_prb11,'mx-');title('双用户二进制双极性扩频通信系统的蒙特卡罗仿真')axis([0,30,10^(-5),1])hold onsemilogy(SNRindB,smld_err_prb12,'mo-');semilogy(SNRindB,smld_err_prb21,'gx-');semilogy(SNRindB,smld_err_prb22,'go-');semilogy(SNRindB,smld_err_prb31,'kx-');semilogy(SNRindB,smld_err_prb32,'ko-');semilogy(SNRindB,smld_err_prb41,'rx-');semilogy(SNRindB,smld_err_prb42,'ro-');%绘图函数SNRindB2=0:0.1:30;theo_err_prb=zeros(1,length(SNRindB2));for i=1:length(SNRindB2)SNR=exp(SNRindB2(i)*log(10)/10);theo_err_prb(i)=Qfunct(sqrt(2*SNR));%Qfunct y=(1/2)*erfc(x/sqrt(2)); 理论误码率公式endsemilogy(SNRindB2,theo_err_prb,'b:'); %绘图函数%cd94_2_030_105.m 双用户二进制双极性扩频通信系统的蒙特卡罗仿真绘图运行结果下图（cd94_2_030_105的运行结果）给出了不同信噪比条件（0dB-30dB）和不同幅度（A1=3、A2=7、A3=12、A4=0）正弦干扰下，发送100000比特的双用户二进制双极性扩频通信系统的蒙特卡罗仿真结果以及理论值曲线。
从仿真结果来看，无正弦干扰下的蒙特卡罗仿真结果与理论值曲线吻合程度好的令人惊叹，仿真中两用户在同一信道真正实现了和平共处，因此用蒙特卡罗仿真模型来模拟实际双用户二进制双极性扩频通信系统，是可以被接受的；同时可以看出，扩频技术对人为的正弦干扰具有抑制能力，并且对于同样的人为正弦干扰，不同gold码的抑制干扰能力相对来说也有高下之分，在本次仿真中，用户1使用的gold码抑制正弦干扰能力更强。
级联码对双用户二进制双极性扩频系统误码性能的改善无正弦干扰下的仿真结果和扩频理论都已经说明，从单个用户角度来看，双用户二进制双极性扩频通信系统和原来的单用户二进制双极性通信系统是相同的。
于是我们可以推论，在双用户二进制双极性扩频通信系统中对上文各种信道编码性能测试结果，也将和前面的测试结果相同，即按照误码率性能指标，信道编码的最好方案是级联码。
另外，考虑到实际应用信道编码时通常采用级联码，本次双用户二进制双极性扩频通信系统中的信道编码仿真采用了级联码。
在双用户二进制双极性扩频通信系统的蒙特卡罗仿真模型框图中加入级联码的编译码器，就构成了测试级联码对双用户二进制双极性扩频通信系统误码性能改善的蒙特卡罗仿真模型，系统框图如下：双用户二进制双极性扩频级联码通信系统的蒙特卡罗仿真模型双用户二进制双极性扩频级联码通信系统的蒙特卡罗仿真流程图MATLAB源程序function [p1,p2]=ss_Pe94_2(snr_in_dB,A,w)%ss_Pe94_2.m 双用户二进制双极性扩频通信系统的蒙特卡罗仿真函数%snr_in_dB 信噪比%p 误码率%A 正弦干扰幅度%w 正弦干扰角频率%PN码采用长度Lc为30的gold码,Lc=length(gold)=30snr=10^(snr_in_dB/10);sgma=1;Eb=2*sgma^2*snr;N=16; %Nloop=10^4; %loopNs=N*loop1*loop2; %仿真序列长度loop*N=16*10^4，运行时间约5分钟p1=0;p2=0;gold1=[0 1 1 1 0 0 0 0 1 0 0 0 0 1 1 0 0 1 0 0 1 0 1 1 1 1 0 0 0 0 0]; gold2=[0 1 0 1 1 0 1 1 1 0 0 0 1 0 0 0 0 0 1 0 0 1 0 0 0 1 1 0 0 0 1]; Lc=length(gold1); %Lc=30;pn_seq1=2*gold1-1;pn_seq2=2*gold2-1;E_chip=Eb/Lc;temp=0;data1=0;data2=0;repeated_data1=zeros(1,Lc);repeated_data2=zeros(1,Lc);trans_sig1=zeros(1,Lc);trans_sig2=zeros(1,Lc);noise=zeros(1,Lc);n=1:Lc;interference=zeros(1,Lc);rec_sig=zeros(1,Lc);temp1=zeros(1,Lc);temp2=zeros(1,Lc);decision_variable1=0;decision_variable2=0;decision1=0;decision2=0;num_of_err_1=0;num_of_err_2=0;time=0;for h=1:loopfor i=1:Ntemp=rand;if (temp<0.5)data1=-1;elsedata1=1;endfor j=1:Lcrepeated_data1(j)=data1;endtrans_sig1=sqrt(E_chip)*repeated_data1.*pn_seq1; temp=rand;if (temp<0.5)data2=-1;elsedata2=1;endfor j=1:Lcrepeated_data2(j)=data2;endtrans_sig2=sqrt(E_chip)*repeated_data2.*pn_seq2; noise=sgma*randn(1,Lc);time=time+1,n=(time-1)*Lc+1:time*Lc;interference=A*sin(w*n);rec_sig=trans_sig1+trans_sig2+noise+interference;temp1=rec_sig.*pn_seq1;decision_variable1=sum(temp1);if (decision_variable1<0)decision1=-1;elsedecision1=1;endif (decision1~=data1)num_of_err_1=num_of_err_1+1;endtemp2=rec_sig.*pn_seq2;decision_variable2=sum(temp2);if (decision_variable2<0)decision2=-1;elsedecision2=1;endif (decision2~=data2)num_of_err_2=num_of_err_2+1;endendendnum_of_err_1,num_of_err_2,p1=num_of_err_1/Ns;p2=num_of_err_2/Ns;%ss_Pe94_2.m 双用户二进制双极性扩频通信系统的蒙特卡罗仿真函数function [p1,p2]=ss_Pe94_2_cnv_jz_74(snr_in_dB,A,w)%ss_Pe94_2_cnv_jz_74.m 双用户二进制双极性扩频通信系统的蒙特卡罗仿真函数%snr_in_dB 信噪比%p 误码率%A 正弦干扰幅度%w 正弦干扰角频率%PN码采用长度Lc为30的gold码,Lc=length(gold)=30snr=10^(snr_in_dB/10);sgma=1;Eb=2*sgma^2*snr;N=16; %Nloop=10^4; %loopNs=N*loop; %仿真序列长度Ns=loop*N=16*10^4，运行时间约15分钟dsource1=zeros(1,N); dsource2=zeros(1,N);output1_h74=hamming74(dsource1);output2_h74=hamming74(dsource2);G=[1 0 1 1 ; 1 1 1 1 ];k=1;output_cnv_encd1=cnv_encd(G,k,output1_h74);output_cnv_encd2=cnv_encd(G,k,output2_h74);channel_output1=zeros(1,length(output_cnv_encd2));channel_output2=zeros(1,length(output_cnv_encd2));[decoder_output1,survivor_state1,cumulated_metric1]=viterbi(G,k,channel_output1) ;[decoder_output2,survivor_state2,cumulated_metric2]=viterbi(G,k,channel_output2) ;[h4output1,h7output1]=h47(decoder_output1);[h4output2,h7output2]=h47(decoder_output2);p1=0;p2=0;numoferr1=0;numoferr2=0;num_of_err_1=0;num_of_err_2=0;cnv_jz_74_time=0;gold1=[0 1 1 1 0 0 0 0 1 0 0 0 0 1 1 0 0 1 0 0 1 0 1 1 1 1 0 0 0 0 0];gold2=[0 1 0 1 1 0 1 1 1 0 0 0 1 0 0 0 0 0 1 0 0 1 0 0 0 1 1 0 0 0 1];Lc=length(gold1); %Lc=30;pn_seq1=2*gold1-1;pn_seq2=2*gold2-1;E_chip=Eb/Lc;temp=0;data1=0;data2=0;repeated_data1=zeros(1,Lc);repeated_data2=zeros(1,Lc);trans_sig1=zeros(1,Lc);trans_sig2=zeros(1,Lc);noise=zeros(1,Lc);n=1:Lc;interference=zeros(1,Lc);rec_sig=zeros(1,Lc);temp1=zeros(1,Lc);temp2=zeros(1,Lc);decision_variable1=0;decision_variable2=0;decision1=0;decision2=0;for h=1:loopfor i=1:Ntemp=rand;if (temp<0.5)dsource1(i)=0;elsedsource1(i)=1;endtemp=rand;if (temp<0.5)dsource2(i)=0;elsedsource2(i)=1;endend%length(dsource) 28output1_h74=hamming74(dsource1);output2_h74=hamming74(dsource2);output1_jz28=jiaozhi(output1_h74,28);output2_jz28=jiaozhi(output2_h74,28);output_cnv_encd1=cnv_encd(G,k,output1_jz28);output_cnv_encd2=cnv_encd(G,k,output2_jz28);%length(output_cnv_encd),pausefor m=1:length(output_cnv_encd1)%=length(output_cnv_encd2) data1=2*output_cnv_encd1(m)-1;data2=2*output_cnv_encd2(m)-1;for j=1:Lcrepeated_data1(j)=data1;repeated_data2(j)=data2;endtrans_sig1=sqrt(E_chip)*repeated_data1.*pn_seq1;trans_sig2=sqrt(E_chip)*repeated_data2.*pn_seq2;noise=sgma*randn(1,Lc);cnv_jz_74_time=cnv_jz_74_time+1;n=(cnv_jz_74_time-1)*Lc+1:cnv_jz_74_time*Lc;interference=A*sin(w*n);rec_sig=trans_sig1+trans_sig2+noise+interference;%temp1=rec_sig.*pn_seq1;decision_variable1=sum(temp1);if (decision_variable1<0)decision1=-1;elsedecision1=1;endif (decision1~=data1)num_of_err_1=num_of_err_1+1;end%temp2=rec_sig.*pn_seq2;decision_variable2=sum(temp2);if (decision_variable2<0)decision2=-1;elsedecision2=1;endif (decision2~=data2)num_of_err_2=num_of_err_2+1;end%channel_output1(m)=(decision1+1)/2;channel_output2(m)=(decision2+1)/2;%end[decoder_output1,survivor_state1,cumulated_metric1]=viterbi(G,k,channel_output1) ;[decoder_output2,survivor_state2,cumulated_metric2]=viterbi(G,k,channel_output2) ;[decoder_output1_jjz28]=jiejiaozhi(decoder_output1,28);[decoder_output2_jjz28]=jiejiaozhi(decoder_output2,28);[h4output1,h7output1]=h47(decoder_output1_jjz28);[h4output2,h7output2]=h47(decoder_output2_jjz28);for i=1:N%=length(dsource1)=length(dsource2)if(h4output1(i)~=dsource1(i))numoferr1=numoferr1+1;endif(h4output2(i)~=dsource2(i))numoferr2=numoferr2+1;endendendnum_of_err_1,numoferr1,num_of_err_1-numoferr1,num_of_err_2,numoferr2,num_of_err_2-numoferr2,p1=numoferr1/Ns;p2=numoferr2/Ns;%ss_Pe94_2_cnv_jz_74.m 双用户二进制双极性扩频通信系统的蒙特卡罗仿真函数echo on%cd94_2_0216_jz.m 双用户二进制双极性扩频通信系统的蒙特卡罗仿真绘图%仿真序列长度Ns=loop*N=16*10^4，运行时间约12小时A1=3;A2=7;A3=12;A4=0;%A1 A2 A3 A4 正弦干扰幅度w0=1;%w0 正弦干扰角频率SNRindB=0:2:16;smld_err_prb110=zeros(1,length(SNRindB));smld_err_prb120=zeros(1,length(SNRindB));smld_err_prb210=zeros(1,length(SNRindB));smld_err_prb220=zeros(1,length(SNRindB));smld_err_prb310=zeros(1,length(SNRindB));smld_err_prb320=zeros(1,length(SNRindB));smld_err_prb410=zeros(1,length(SNRindB));smld_err_prb420=zeros(1,length(SNRindB));smld_err_jz_prb11=zeros(1,length(SNRindB));smld_err_jz_prb12=zeros(1,length(SNRindB));smld_err_jz_prb21=zeros(1,length(SNRindB));smld_err_jz_prb22=zeros(1,length(SNRindB));smld_err_jz_prb31=zeros(1,length(SNRindB));smld_err_jz_prb32=zeros(1,length(SNRindB));smld_err_jz_prb41=zeros(1,length(SNRindB));smld_err_jz_prb42=zeros(1,length(SNRindB));for i=1:length(SNRindB)i,SNRindB(i),[smld_err_prb110(i),smld_err_prb120(i)]=ss_Pe94_2(SNRindB(i),A1,w0);[smld_err_prb210(i),smld_err_prb220(i)]=ss_Pe94_2(SNRindB(i),A2,w0);[smld_err_prb310(i),smld_err_prb320(i)]=ss_Pe94_2(SNRindB(i),A3,w0);[smld_err_prb410(i),smld_err_prb420(i)]=ss_Pe94_2(SNRindB(i),A4,w0);end;for i=1:length(SNRindB)i,SNRindB(i),[smld_err_jz_prb11(i),smld_err_jz_prb12(i)]=ss_Pe94_2_cnv_jz_74(SNRindB(i),A1,w0 );[smld_err_jz_prb21(i),smld_err_jz_prb22(i)]=ss_Pe94_2_cnv_jz_74(SNRindB(i),A2,w0 );[smld_err_jz_prb31(i),smld_err_jz_prb32(i)]=ss_Pe94_2_cnv_jz_74(SNRindB(i),A3,w0 );[smld_err_jz_prb41(i),smld_err_jz_prb42(i)]=ss_Pe94_2_cnv_jz_74(SNRindB(i),A4,w0 );end;%绘图函数figure;semilogy(SNRindB,smld_err_jz_prb42,'r>:');axis([0,16,1e-5,1]);xlabel('Eb/N0 in dB');ylabel('Pe');title('双用户级联编码及未编码扩频系统仿真误比特率曲线比较');hold onsemilogy(SNRindB,smld_err_jz_prb11,'m<:');semilogy(SNRindB,smld_err_jz_prb12,'m>:');semilogy(SNRindB,smld_err_jz_prb21,'g<:');semilogy(SNRindB,smld_err_jz_prb22,'g>:');semilogy(SNRindB,smld_err_jz_prb31,'k<:');semilogy(SNRindB,smld_err_jz_prb32,'k>:');semilogy(SNRindB,smld_err_jz_prb41,'r<:');semilogy(SNRindB,smld_err_jz_prb42,'r>:');semilogy(SNRindB,smld_err_prb110,'mx-');semilogy(SNRindB,smld_err_prb120,'mo-');semilogy(SNRindB,smld_err_prb210,'gx-');semilogy(SNRindB,smld_err_prb220,'go-');semilogy(SNRindB,smld_err_prb310,'kx-');semilogy(SNRindB,smld_err_prb320,'ko-');semilogy(SNRindB,smld_err_prb410,'rx-');semilogy(SNRindB,smld_err_prb420,'ro-');%绘图函数SNRindB2=0:0.1:16;theo_err_prb=zeros(1,length(SNRindB2));for i=1:length(SNRindB2)SNR=exp(SNRindB2(i)*log(10)/10);theo_err_prb(i)=Qfunct(sqrt(2*SNR));%Qfunct y=(1/2)*erfc(x/sqrt(2)); 理论误码率公式endhold onsemilogy(SNRindB2,theo_err_prb,'b:'); %绘图函数%cd94_2_0216_jz.m 双用户二进制双极性扩频通信系统的蒙特卡罗仿真绘图运行结果下图（cd94_2_0216_jz的运行结果）给出了不同信噪比条件（0dB-16dB）和不同幅度（A1=3、A2=7、A3=12、A4=0）正弦干扰下，发送160000比特的双用户二进制双极性扩频级联码( 外编码采用（7，4）HAMMING码，交织编码采用（7，4）卷积交织编码，内编码采用（2，1，3）卷积码) 通信系统和未编码的双用户二进制双极性扩频通信系统蒙特卡罗仿真结果以及理论值曲线。
