选修5-第4节-高考真题重组

2021年高考化学大一轮复习 第5节 高考真题重组 鲁科版选修51．(xx·海南高考卷)下列化合物在核磁共振氢谱中能出现两组峰，且峰面积之比为3∶1的有( )A ．乙酸异丙酯B ．乙酸叔丁酯C ．对二甲苯D ．均三甲苯解析：A 选项有三种氢；B 选项有两种氢，个数比为9∶3；C 选项有两种氢，个数比为6∶4，D 选项有两种氢，个数比为9∶3。

答案：BD2．(xx·全国卷新课标Ⅰ)[化学－选修5：有机化学基础]查尔酮类化合物G 是黄酮类药物的主要合成中间体，其中一种合成路线如下：已知以下信息：①芳香烃A 的相对分子质量在100～110之间，1 mol A 充分燃烧可生成72 g 水。

②C 不能发生银镜反应。

③D 能发生银镜反应、可溶于饱和Na 2CO 3溶液、核磁共振氢谱显示其有4种氢。

④⑤RCOCH 3＋R′CHO ――→一定条件RCOCH===CHR′回答下列问题：(1)A 的化学名称为________________。

(2)由B 生成C 的化学方程式为___________________________________________________________________。

(3)E的分子式为______________，由E生成F的反应类型为_________。

(4)G的结构简式为___________________________________________________________________。

(5)D的芳香同分异构体H既能发生银镜反应，又能发生水解反应，H在酸催化下发生水解反应的化学方程式为___________________________________________________________________。

(6)F的同分异构体中，既能发生银镜反应，又能与FeCl3溶液发生显色反应的共有________种，其中核磁共振氢谱比为5组峰，且峰面积比为2∶2∶2∶1∶1的为________________(写结构简式)。

冲刺2024年高考语文真题重组卷（新高考七省专用）真题重组卷05（参考答案）（考试时间：150分钟试卷满分：150分）1．（3分）D2．（3分）B3．（3分）C4．（4分）①“己所不欲，勿施于人”出自《论语》，意思是以对待自身的行为为参照物来对待他人，在关注自身的同时还要关注他人，体现了理性思辨换位思考的古代哲学大智慧。

②“现已成为国际社会公认的处理人际关系和国际关系的黄金准则”体现与时俱进、推陈出新。

③要加强对中华优秀传统文化的挖掘与阐发，使民族性更符合当代中国和当今世界的发展，为解决世界性问题提供思路和方法，体现了特殊到普遍的发展规律。

（每点2分，答出任意2点得满分）5．（6分）①复兴中华传统文化。

建立强大的中华文化传统，固本健体才可以消化吸收了四方异域的文化，借以繁荣本民族文化。

②与时俱进。

当代社会让世界村的居民们多少都进入了一个更复杂的感性与知性世界，中国诗歌也相应地在寻找与之相当的艺术形式，主要是诗歌语言、内在结构、外在形态。

③借鉴世界优秀文化，外为中用。

（每点2分）6．（3分）B7．（3分）D8．（4分）①具有渲染效果，把故事描述得更充分；②具有延宕效果，迟迟不讲下文，引发听众的好奇与追问。

（每点2分）9．（6分）①现实生活中的门是木头门，洪子店村民以砖头堵门；②在王木匠的故事加工中，砖头门变成了“石头门”，战斗故事随之变成了传奇的“石门阵”；③王木匠从现实中明白了“守住了大门，不用关二门”的道理，即只有保卫国门，才能守护家门，才有实现“夜不闭户”的希望。

（每点2分）10．（3分）CEG11．（3分）B12．（3分）C13．（8分，每小题4分）（1）我的大臣们都对我有高傲轻慢的意思，只有高赫没有失掉君臣之间的礼节，所以先奖赏他。

（“骄侮”，高傲轻慢；“唯”，副词，只有；“先”，动词，以……为先、放在前面。

每点1分，句意1分。

）（2）请允许我简略地说其中的一小部分，您来仔细考察它真实与否。

2021届高考化学一轮温习辅导与测试第4节醛羧酸酯高考真题重组鲁科版选修51．(2021·上海高考卷)过量的以下溶液与水杨酸()反映能取得化学式为C7H5O3Na的是A．NaHCO3溶液B．Na2CO3溶液C．NaOH溶液D．NaCl溶液解析：此题考查有机化学知识，意在考查考生对羧酸、酚和碳酸酸性强弱的判定。

由于酸性：>可知水杨酸与NaHCO3溶液反映时只与—COOH作用转化为—COONa，产物的分子式为C7H5O3Na，A项正确；水杨酸与Na2CO3溶液反映时—COOH、—OH均反映，生成产物的分子式为C7H4O3Na2，B项错误；水杨酸与NaOH溶液反映时—COOH、—OH均反映，生成产物的分子式为C7H4O3Na2，C项错误；与NaCl溶液不反映，D项错误。

答案：A2．(2021·重庆高考卷)萤火虫发光原理如下：关于荧光素及氧化荧光素的表达，正确的选项是( )A．互为同系物B．都可发生硝化反映C．都可与碳酸氢钠反映D．均最多有7个碳原子共平面解析：两分子中均最少有7个碳原子共平面。

答案：B3．(2021·高考上海卷)以下关于实验室制备乙酸乙酯和乙酸丁酯的描述正确的选项是( )A．均采纳水浴加热B．制备乙酸乙酯时正丁醇过量C．均采纳边反映边蒸馏的方式D．制备乙酸乙酯时乙醇过量解析：制备乙酸丁酯和乙酸乙酯均是采取用酒精灯直接加热法制取，A项错误；制备乙酸丁酯时采纳容易取得的乙酸过量、以提高丁醇的利用率的做法，B项错误；制备乙酸乙酯采取边反映边蒸馏的方式、制备乙酸丁酯那么采取直接回流的方式，待反映后再提取产物，C项错误；制备乙酸乙酯时，为提高乙酸的利用率，采取乙醇过量的方式，D项正确。

答案：D4．(2021·高考江苏卷) 药物贝诺酯可由乙酰水杨酸和对乙酰氨基酚在必然条件下反映制得：以下有关表达正确的选项是A．贝诺酯分子中有三种含氧官能团B．可用FeCl3溶液区别乙酰水杨酸和对乙酰氨基酚C．乙酰水杨酸和对乙酰氨基酚均能与NaHCO3溶液反映D．贝诺酯与足量NaOH 溶液共热，最终生成乙酰水杨酸钠和对乙酰氨基酚钠解析：结合三种有机物的结构确信含有的官能团及具有的性质。

冲刺2024年高考语文真题重组卷（全国甲卷、乙卷通用）真题重组卷01（考试时间：150分钟试卷满分：150分）一、现代文阅读（39分）（一）（2021·全国乙卷）论述类文本阅读（本题共3小题，9分）阅读下面的文字，完成下面小题。

对于人文研究来说，计算方法以往只是作为辅助手段而存在的，而今天已取得了不可替代的地位。

一种新的人文研究形态应运而生，这就是“数字人文”。

学者莫莱蒂曾设想一种建立在全部文学文本之上的世界文学研究，人们必须借助计算机对大规模的文学文本集合进行采样、统计、图绘，分类，描述文学史的总体特征，然后再做文学评论式的解读。

为此，他提出了与“细读”相对的“远读”作为方法论。

弄清计算机的远读与人的细读之间的差别，不仅能使我们清晰地界定计算方法在人文研究中的作用，而且可以帮助我们重新确立人的阅读的价值。

计算机是为科学计算而创造出来的，擅长的是“计数”，而非理解。

要处理自然语言文本，计算机必须先将文本置换成便于计数的词汇集合，或者用更复杂的代数模型和概率模型来表示文本，这一过程被称为“数据化”。

数据化之后所得到的文本替代物（集合、向量、概率）虽然损失了原始文本的丰富语义，但终究是可以计算的了。

不过，尽管计算机能处理海量的语料，执行复杂的统计、分类、查询等任务，但它并不能理解文本的内容。

远读是数字人文的基石。

大规模的文本集合上的远读，基本上可以归为两类：一是对文本集合整体统计特征的描述，一是对文本集合内在结构特征的揭示。

例如，数字人文学者米歇尔等人对数百万册数字化图书进行多种词汇和词频统计，以分析英语世界的语言演变，这属于前者；莫莱蒂用地图、树结构来分别展示文学作品的地理特征和侦探故事的类型结构，这属于后者。

无论是宏观统计描述还是内在结构揭示，都是超越文本具体内容的抽象表示，所得结果都是需要解读的。

正如米歇尔所说，在巨量文本集合上得到的统计分析结果，为人文材料的宏观研究提供了证据；但是要解读这些证据，就像分析古代生物化石一样，是有挑战性的。

重组卷05-冲刺2021年高考数学（理）之精选真题+模拟重组卷（新课标卷）1．（2020.全国1卷）若1i z =+，则2|2|z z -=A ．0B ．1C D ．2【解析】由1i z =+得，22i z =，222i z =+，所以2|2||2i (22i)|2z z -=-+=．故选：D 2．（2020.浙江卷）已知集合{}14P x x =<<，{}23Q x x =<<，则P Q = A ．{}12x x < B ．{}23x x <<C ．{}34x x <D ．{}14x x <<【解析】B3．（2020.全国3卷）在新冠肺炎疫情防控期间，某超市开通网上销售业务，每天能完成1200份订单的配货，由于订单量大幅增加，导致订单积压，为解决困难，许多志愿者踊跃报名参加配货工作.已知该超市某日积压500份订单未配货，预计第二天新订单超过1600份的概率为0.05.志愿者每人每天能完成50份订单的配货，为使第二天完成积压订单及当日订单配货的概率不小于0.95，则至少需要志愿者 A ．10名B ．18名C ．24名D ．32名【解析】：因为公司可以完成配货1200份订单，则至少需要志愿者为160050012001850+-=名.故选：B4．（2020.全国2卷）北京天坛的圜丘坛为古代祭天的场所，分上、中、下三层，上层中心有一块圆形石板（称为天心石），环绕天心石砌9块扇面形石板构成第一环，向外每环依次增加9块，下一层的第一环比上一层的最后一环多9块，向外每环依次也增加9块，已知每层环数相同，且下层比中层多729块，则三层共有扇形面形石板（不含天心石） A ．3699块B ．3474块C ．3402块D ．3339块【解析】：设每一层有n 环，由题可知从内到外每环之间构成等差数列，公差9d =，19a =，由等差数列性质知232,,n n n n n S S S S S --成等差数列，且2322()()n n n n S S S S n d ---=，则29729n =，得9n =，则三层共有扇形面石板为3271272627934022n S S a ⨯==+⨯=块.故选：C5．（2020.浙江卷）某几何体的三视图（单位：cm ）如图所示，则该几何体的体积（单位：3cm ）是A ．73B ．143C ．3D ．6【解析】：还原图，上方为一个高为1三棱锥，下方是一个高为2三棱柱，其体积为11172112123223⨯⨯⨯⨯+⨯⨯⨯=．故选A ． 6．（2020.北京卷）已知函数()21x f x x =--，则不等式()0f x ＞的解集是 A ．(1,1)- B ．(,1)(1,)-∞-+∞ C ．(0,1)D ．(,0)(1,)-∞+∞【解析】：不等式()0f x ＞等价于21x x --＞0，即21x x +＞，令12x y =，21y x =+，由初等函数图像可知，不等式的解集为(,0)(1,)-∞+∞．故选D ．7．（2020.山东卷）已知P 是边长为2的正六边形ABCDEF 内的一点，则AP AB ⋅的取值范围是 A ．(2,6)-B ．(6,2)-C ．(2,4)-D ．(4,6)-【解析】：如图，以A 为坐标原点建立平面直角坐标系，则(0,0)A ，B(2,0)，，D，E，(1F -，设(,)P x y ，则13x -<<，由(,)AP x y =，(2,0)AB =，所以2(2,6)AP AB x ⋅=∈-． 故选：A8．（2020.全国2卷）设O 为坐标原点，直线x a =与双曲线()2222:10,0x y C a b a b-=>>的两条渐近线分别交于D ，E 两点.若ODE △的面积为8，则C 的焦距的最小值为 A ．4B ．8C ．16D ．32【解析】：易知(,),(,)D a b E a b -，则1282ABC S a b ∆=⋅=，所以8ab =，所以焦距为2248c =⨯=，当且仅当a =时，等号成立， 故选B.9．（2020.全国1卷）52)(y x xy x ++）（的展开式中33y x 的系数为 A ．5B ．10C ．15D ． 20【解析】：5)(y x +的通项公式为)5,4,3,2,1,0(55=-r y xC r rr ，所以1=r 时，3341525y x y x C xy =，3r =时 33323510y x y x xC =，所以33y x 的系数为15.故选：C 10．（2018.全国1卷）下图来自古希腊数学家希波克拉底所研究的几何图形．此图由三个半圆构成，三个半圆的直径分别为直角三角形ABC 的斜边BC ，直角边AB ，AC ．△ABC 的三边所围成的区域记为I ，黑色部分记为II ，其余部分记为III ．在整个图形中随机取一点，此点取自I ，II ，III 的概率分别记为p1，p2，p3，则A ．p1=p2B ．p1=p3C ．p2=p3D ．p1=p2+p3【解析】： △AC=3，AB=4，△BC=5AB=2 , 12BC=52×π×(32)2+12×π×22=258π×π×(52)2- 12-6；-(258π-6)=6=ΔABC 面积△p1=p2.故选A11．（2020.全国1卷）已知22:2220M x y x y +---=，直线:220l x y ++=，P 为l 上的动点，过点P 作M 的切线PA ,PB ,且切点为,A B ，当||||PM AB ⋅最小时，直线AB 的方程为A ．210x y --=B ．210x y +-=C ．210x y -+=D ．210x y ++=【解析】：22:(1)(1)4M x y -+-=,因为1||||2||||2||2PAMB PAM S PM AB S PA AM PA ∆==== 所以||||PM AB ⋅最小，即||PM 最小，此时PM 与直线l 垂直，11:22PM y x =+， 直线PM 与直线l 的交点(1,0)P -，过直线外一点P 作M 的切线所得切点弦所在直线方程为：210x y ++=，故选D.12．（2020.上海卷）在棱长为10的正方体1111D C B A ABCD -中，P 为左侧面11A ADD 上一点，已知点P 到11D A 的距离为3，点P 到1AA 的距离为2，则过点P 且与C A 1平行的直线交正方体于Q P ,两点，则Q 点所在的平面是 A ．B B AA 11B ．C C BB 11 C ．D D CC 11 D ．ABCD【解析】如图由条件可知直线1A P 交线段AD 于点M ，连接MC ，过点P 作1AC 的平行线，必与MC 相交，那么也与平面ABCD 相交，故选D ．二、填空题：本题共4小题，每小题5分，共20分.13．（2020.全国1卷）若x ，y 满足约束条件22010,10,x y x y y +-⎧⎪--⎨⎪+⎩，则7z x y =+的最大值为．【解析】：如图，当直线7z x y =+经过(10)A ，时z 取到最大值1.故填：114．（2020.全国2卷）4名同学到3个小区参加垃圾分类宣传活动，每名同学只去1个小区，每个小区至少安排1名学生，则不同的安排方法有 种．【解析】：2343C A ＝36．故填：3615．（2020.江苏卷）设{}n a 是公差为d 的等差数列，{}n b 是公比为q 的等比数列．已知{}n n a b +的前n 项和2*21()n n S n n n =-+-∈N ，则d q +的值是 ． 【解析】：因为{}n n a b +的前n 项和2*21()n n S n n n =-+-∈N ， 当1n =时，111a b +=，当2n 时，11222n n n n n a b S S n --+=-=-+， 由题意知22n a n =-，12n n b -=，从而有4d q +=． 故填：416．（2020.全国2卷）设有下列四个命题：1p ：两两相交且不过同一点的三条直线必在同一平面内. 2p ：过空间中任意三点有且仅有一个平面. 3p ：若空间两条直线不相交，则这两条直线平行. 4p ：若直线l ⊂平面α，直线m ⊥平面α，则m l ⊥. 则下列命题中所有真命题的序号是_________ △14p p ∧△12p p ∧△23p p ⌝∨△34p p ⌝∨⌝【解析】：对于1p ：可设1l 与2l 相交，所得平面为α.若3l 与1l 相交，则交点A 必在α内，同理，3l 与2l 交点B 在α内，故AB 直线在α内，即3l 在α内，故1p 为真命题. 对于2p ：过空间中任意三点，若三点共线，可形成无数多平面，故2p 为假命题. 对于3p ：空间中两条直线的位置关系有相交、平行、异面，故3p 为假命题. 对于4p ：若m α⊥，则m 垂直于平面α内的所有直线，故m l ⊥，故4p 为真命题. 综上可知：14p p ∧为真命题，23p p ⌝∨为真命题，34p p ⌝∨⌝为真命题. 故正确的有：△△△.三、解答题：共70分。

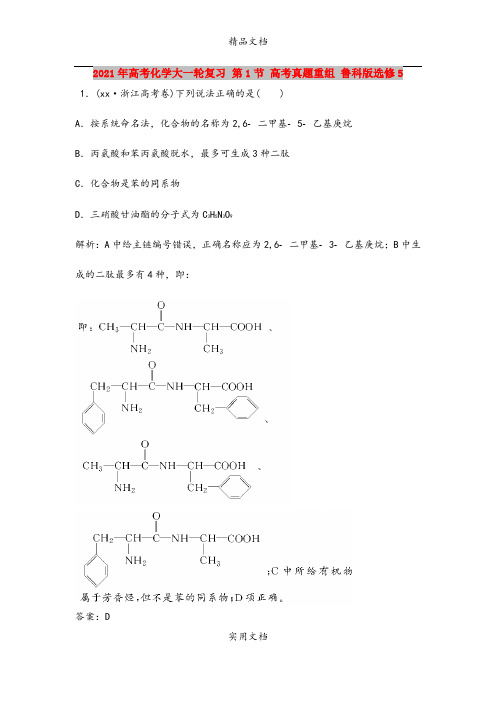
2021年高考化学大一轮复习第1节高考真题重组鲁科版选修5 1．(xx·浙江高考卷)下列说法正确的是( )A．按系统命名法，化合物的名称为2,6­二甲基­5­乙基庚烷B．丙氨酸和苯丙氨酸脱水，最多可生成3种二肽C．化合物是苯的同系物D．三硝酸甘油酯的分子式为C3H5N3O9解析：A中给主链编号错误，正确名称应为2,6­二甲基­3­乙基庚烷；B中生成的二肽最多有4种，即：答案：D2．(xx·高考新课标卷Ⅰ)分子式为C5H10O2的有机物在酸性条件下可水解为酸和醇，若不考虑立体异构，这些醇和酸重新组合可形成的酯共有( ) A．15种B．28种C．32种D．40种解析：从有机化学反应判断酸、醇种类，结合数学思维解决问题。

由分子式C5H10O2分析，酯类：HCOO—类酯，醇为4个C原子的醇，同分异构体有4种；CH3COO—类酯，醇为3个C原子的醇，同分异构体有2种；CH3CH2COO—类酯，醇为乙醇；CH3CH2CH2COO—类酯，其中丙基CH3CH2CH2—(有正丙基和异丙基)2种，醇为甲醇；故羧酸5种，醇8种。

从5种羧酸中任取一种，8种醇中任取一种反应生成酯，共有5×8＝40种。

答案：D3．(双选)(xx·高考海南卷)下列化合物中，同分异构体数目超过7个的有( ) A．已烷B．已烯C．1,2－二溴丙烷D．乙酸乙酯答案：BD4．(xx·高考大纲全国卷)某单官能团有机化合物，只含碳、氢、氧三种元素，相对分子质量为58，完全燃烧时产生等物质的量的CO2和H2O。

它可能的结构共有(不考虑立体异构)( )A．4种B．5种C．6种D．7种解析：根据有机物的结构特征分析其可能的结构。

根据燃烧产物CO2和H2O的物质的量相等可知C、H原子个数比为1∶2，分子式可设为(CH2)m O n，利用讨论法得出分子式为C3H6O，其可能的结构有丙醛CH3CH2CHO，丙酮CH3COCH3，环丙醇，环醚、，共5种。

冲刺2024年高考※※真题重组卷（湖南专用）真题重组卷05•参考答案【答案】 （1）1.02（2分）；（5）（3分）； 0.342（2分）12. （9分） 【答案】 （1）右（1分）；（2）② 断开（1分）； 40.0（2分） ；③ 闭合（1分）； 60.0（2分）；（3） 100（2分）13. （10分）【答案】 （1）00101p V p V V =+；（2）0001[1()]n V F p S V V ∆=-+ 【解析】（1）以助力气室内的气体为研究对象，则初态压强p 0，体积V 0，第一次抽气后，气体体积 01V V V =+（1分）根据玻意耳定律001p V p V =（2分）解得00101p V p V V =+（2分）（2）同理第二次抽气102p V p V =（1分）解得2100200101p V V p p V V V V ⎛⎫== ⎪++⎝⎭（1分） 以此类推……则当n 次抽气后助力气室内的气体压强0001nn V p p V V ⎛⎫= ⎪+⎝⎭（1分） 则刹车助力系统为驾驶员省力大小为00001()[1]nn V F p p S p S V V ⎛⎫∆=-=- ⎪+⎝⎭（2分） 14. （14分）【答案】 （1）0222sin mgR v B L θ=；（2）2sin a g θ=；（3）022sin sin mgR v g t B L θθ=⋅+，22442sin m R g x B L θ∆=【解析】（1）a 导体棒在运动过程中重力沿斜面的分力和a 棒的安培力相等时做匀速运动，由法拉第电磁感应定律可得0E BLv =（1分）有闭合电路欧姆定律及安培力公式可得2EI R =，F BIL =（1分）a 棒受力平衡可得sin mg BIL θ=（1分）联立记得0222sin mgR v B L θ=（1分）（2）由右手定则可知导体棒b 中电流向里，b 棒 沿斜面向下的安培力，此时电路中电流不变，则b 棒牛顿第二定律可得sin mg BIL ma θ+=（2分）解得2sin a g θ=（2分）（3）释放b 棒后a 棒受到沿斜面向上的安培力，在到达共速时对a 棒动量定理000sin mg t BILt mv mv θ-=-（1分）b 棒受到向下的安培力，对b 棒动量定理00sin mg t BILt mv θ+=（1分）联立解得00022sin sin sin 2v mgR v g t g t B L θθθ=⋅+=⋅+（1分）此过程流过b 棒的电荷量为q ，则有0q It =（1分）由法拉第电磁感应定律可得0122E BL x I R R t ∆==（1分）联立b 棒动量定理可得22022442sin mv R m R g x B L B L θ∆==（1分）15. （16分）【答案】 （1）k （2）002(1)()=mg H h F h h λ---；（3）I =【解析】（1）篮球下降过程中根据牛顿第二定律有mg mg ma λ-=下（1分）再根据匀变速直线运动的公式，下落的过程中有22v a H =下下（1分）篮球反弹后上升过程中根据牛顿第二定律有mg mg ma λ+=上（1分）再根据匀变速直线运动的公式，上升的过程中有22v a h =上上（1分）则篮球与地面碰撞的碰后速率与碰前速率之比v k v =上下1分）（2）若篮球反弹至最高处h 时，运动员对篮球施加一个向下的压力F ，则篮球下落过程中根据动能定理有 200122h h mgh F mgh mv λ-'+-=下（1分）篮球反弹后上升过程中根据动能定理有210(2mgh mgh m kv λ'--=-下）（1分）联立解得002(1)()=mg H h F h h λ---（2分）（3）方法一：由（1）问可知篮球上升和下降过程中的加速度分别为()1a g λ=-下（方向向下）()1a gλ=+上（方向向下）（1分）由题知运动员拍击一次篮球（拍击时间极短），瞬间给其一个竖直向下、大小相等的冲量I ，由于拍击时间极短，则重力的冲量可忽略不计，则根据动量定理有I mv =（1分）即每拍击一次篮球将给它一个速度v 。

冲刺2024年高考真题重组卷（全国甲卷、乙卷通用）真题重组卷（文）01（考试时间：120分钟 试卷满分：150分）第I 卷（选择题）一、选择题：本题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合要求的。

1．（2023·全国·统考高考真题）设全集{}0,1,2,4,6,8U =，集合{}{}0,4,6,0,1,6M N ==，则U M N ⋃=（ ）A ．{}0,2,4,6,8B ．{}0,1,4,6,8C ．{}1,2,4,6,8D ．U 2．（2023·全国·统考高考真题）在复平面内，()()13i 3i +-对应的点位于（ ）．A ．第一象限B ．第二象限C ．第三象限D ．第四象限3．（2023·北京·统考高考真题）已知向量a b ，满足(2,3),(2,1)a b a b +=-=-，则22||||a b -=（ ） A ．2- B ．1- C ．0 D ．14．（2023·全国·统考高考真题）某学校举办作文比赛，共6个主题，每位参赛同学从中随机抽取一个主题准5．（2023·天津·统考高考真题）已知{}n a 为等比数列，n S 为数列{}n a 的前n 项和，122n n a S +=+，则4a 的值为（ ）A ．3B ．18C ．54D ．152 6．（2023·全国·统考高考真题）执行下面的程序框图，输出的B =（ ）A ．21B ．34C ．55D ．898．（2019·全国·高考真题）已知曲线e ln x y a x x =+在点()1,ae 处的切线方程为2y x b =+，则10．（2022·浙江·统考高考真题）某几何体的三视图如图所示（单位：cm ），则该几何体的体积（单位：3cm ）221611．（2023·全国·统考高考真题）设函数()()2x x a f x -=在区间()0,1上单调递减，则a 的取值范围是（ ）C ，若C 关于y 轴对称，则ω的最小值是（ ）第II卷（非选择题）二、填空题：本题共4小题，每小题5分，共20分。

重组十九 选修4－5测试时间：120分钟满分：150分解答题(本题共15小题，每小题10分，共150分，解答应写出文字说明、证明过程或演算步骤)1．已知函数f (x )＝|x ＋1|－|2x －3|.(1)画出y ＝f (x )的图象； (2)求不等式|f (x )|>1的解集．解 (1)f (x )＝⎩⎪⎨⎪⎧x －4，x ≤－1，3x －2，－1<x ≤32，－x ＋4，x >32，(2分)y ＝f (x )的图象如图所示．(5分)(2)由f (x )的表达式及图象知，当f (x )＝1时，可得x ＝1或x ＝3； 当f (x )＝－1时，可得x ＝13或x ＝5.(7分)故f (x )>1的解集为{x |1<x <3}；f (x )<－1的解集为⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪x <13或x >5.(8分)所以|f (x )|>1的解集为⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪x <13或1<x <3或x >5.(10分) 2．已知关于x 的不等式m －|x －2|≥1，其解集为x ∈． (1)求m 的值；(2)若a ，b 均为正实数，且满足a ＋b ＝m ，求a 2＋b 2的最小值． 解 (1)不等式m －|x －2|≥1可化为|x －2|≤m －1， ∴1－m ≤x －2≤m －1，即3－m ≤x ≤m ＋1.(3分) ∵其解集为，∴⎩⎪⎨⎪⎧3－m ＝0，m ＋1＝4，∴m ＝3.(5分)(2)由(1)知a ＋b ＝3，∵(a ＋b )2＝a 2＋b 2＋2ab ≤(a 2＋b 2)＋(a 2＋b 2)＝2(a 2＋b 2)， ∴a 2＋b 2≥92，(8分)∴当且仅当a ＝b ＝32时，a 2＋b 2取最小值为92.(10分)3．已知f (x )＝|x ＋2|－|2x －1|，M 为不等式f (x )>0的解集． (1)求M ；(2)求证：当x ，y ∈M 时，|x ＋y ＋xy |<15.解 (1)f (x )＝⎩⎪⎨⎪⎧x －3，x <－2，3x ＋1，－2≤x ≤12，－x ＋3，x >12，(2分)当x <－2时，由x －3>0，得x >3，舍去；(3分)当－2≤x ≤12时，由3x ＋1>0，得x >－13，即－13<x ≤12；(4分)当x >12时，由－x ＋3>0，得x <3，即12<x <3.(5分)综上，M ＝⎝ ⎛⎭⎪⎫－13，3.(6分)(2)证明：∵x ，y ∈M ，∴|x |<3，|y |<3，∴|x ＋y ＋xy |≤|x ＋y |＋|xy |≤|x |＋|y |＋|xy |＝|x |＋|y |＋|x |·|y |<3＋3＋3×3＝15.(10分)4．已知定义在R上的函数f(x)＝|x－m|＋|x|，m∈N*，存在实数x使f(x)<2成立．(1)求实数m的值；(2)若α，β>1，f(α)＋f(β)＝4，求证：4α＋1β>3.解(1)因为|x－m|＋|x|≥|(x－m)－x|＝|m|，(2分)要使不等式|x－m|＋|x|<2有解，则|m|<2，解得－2<m<2，(4分)因为m∈N*，所以m＝1.(5分)(2)证明：因为α，β>1，所以f(α)＋f(β)＝2α－1＋2β－1＝4，可得α＋β＝3，(6分)所以4α＋1β＝13⎝⎛⎭⎪⎫4α＋1β(α＋β)＝13⎝⎛⎭⎪⎫5＋4βα＋αβ≥13⎝⎛⎭⎪⎫5＋24βα·αβ＝3( 当且仅当4βα＝αβ，即α＝2，β＝1时取等号 )，(9分)又因为α，β>1，所以4α＋1β>3恒成立，故4α＋1β>3.(10分)5．设函数f(x)＝|2x＋3|＋|x－1|.(1)解不等式f(x)>4；(2)若存在x∈⎣⎢⎡⎦⎥⎤－32，1使不等式a＋1>f(x)成立，求实数a的取值范围．解(1)∵f(x)＝|2x＋3|＋|x－1|.∴f(x)＝⎩⎪⎨⎪⎧－3x－2，x<－32，x＋4，－32≤x≤1，3x＋2，x>1，(2分)∴f(x)>4⇔⎩⎪⎨⎪⎧x<－32，－3x－2>4或⎩⎪⎨⎪⎧－32≤x≤1，x＋4>4或⎩⎪⎨⎪⎧x>1，3x＋2>4.(4分) ⇔x<－2或0<x≤1或x>1.(5分)综上，不等式f(x)>4的解集为(－∞，－2)∪(0，＋∞)．(6分) (2)存在x∈⎣⎢⎡⎦⎥⎤－32，1使不等式a＋1>f(x)成立⇔a＋1>f(x)min，(7分)由(1)知，x∈⎣⎢⎡⎦⎥⎤－32，1时，f(x)＝x＋4，∴x ＝－32时，f (x )min ＝52，(8分)∴a ＋1>52⇔a >32.(9分)∴实数a 的取值范围为⎝ ⎛⎭⎪⎫32，＋∞.(10分)6．已知函数f (x )＝|x －m |－|x －2|. (1)若函数f (x )的值域为，求实数m 的值；(2)若不等式f (x )≥|x －4|的解集为M ，且⊆M ，求实数m 的取值范围． 解 (1)由不等式的性质得：||x －m |－|x －2||≤|x －m －x ＋2|＝|m －2|.(2分) 因为函数f (x )的值域为，所以|m －2|＝4，即m －2＝－4或m －2＝4，所以实数m ＝－2或6.(5分) (2)f (x )≥|x －4|，即|x －m |－|x －2|≥|x －4|，当2≤x ≤4时，|x －m |≥|x －4|＋|x －2|⇔|x －m |≥－x ＋4＋x －2＝2，|x －m |≥2， 解得x ≤m －2或x ≥m ＋2，即解集为(－∞，m －2]∪∪已知a >0，b >0，记A ＝a ＋b ，B ＝a ＋b .(1)求2A －B 的最大值；(2)若ab ＝4，是否存在a ，b ，使得A ＋B ＝6？并说明理由． 解 (1)2A －B ＝2a －a ＋2b －b ＝－⎝ ⎛⎭⎪⎫a －222－⎝ ⎛⎭⎪⎫b －222＋1≤1，等号在a ＝b ＝12时取得，即2A －B 的最大值为1.(5分) (2)A ＋B ＝a ＋b ＋a ＋b ≥2ab ＋2ab ，因为ab ＝4，所以A ＋B ≥4＋22>6，所以不存在这样的a ，b ，使得A ＋B ＝6.(10分) 8．已知函数f (x )＝|x －2|. (1)解不等式f (x ＋1)＋f (x ＋2)<4；(2)已知a >2，求证：∀x ∈R ，f (ax )＋af (x )>2恒成立． 解 (1)f (x ＋1)＋f (x ＋2)<4，即|x －1|＋|x |<4，(1分) ①当x ≤0时，不等式为1－x －x <4，即x >－32，∴－32<x ≤0是不等式的解；(2分)②当0<x ≤1时，不等式为1－x ＋x <4，即1<4恒成立，∴0<x ≤1是不等式的解；(3分) ③当x >1时，不等式为x －1＋x <4，即x <52，∴1<x <52是不等式的解．(4分)综上所述，不等式的解集为⎝ ⎛⎭⎪⎫－32，52.(5分) (2)证明：∵a >2，∴f (ax )＋af (x )＝|ax －2|＋a |x －2|＝|ax －2|＋|ax －2a |＝|ax －2|＋|2a －ax |≥|ax －2＋2a －ax |＝|2a －2|>2，(8分) ∴∀x ∈R ，f (ax )＋af (x )>2恒成立．(10分) 9．已知函数f (x )＝|x ＋1|－a |x －1|. (1)当a ＝－2时，解不等式f (x )>5； (2)若f (x )≤a |x ＋3|，求a 的最小值．解 (1)当a ＝－2时，f (x )＝⎩⎪⎨⎪⎧1－3x ，x <－1，3－x ，－1≤x ≤1，3x －1，x >1.(2分)由f (x )的单调性及f ⎝ ⎛⎭⎪⎫－43＝f (2)＝5，得f (x )>5的解集为⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪x <－43或x >2.(5分) (2)由f (x )≤a |x ＋3|，得a ≥|x ＋1||x －1|＋|x ＋3|，由|x －1|＋|x ＋3|≥2|x ＋1|， 得|x ＋1||x －1|＋|x ＋3|≤12，得a ≥12(当且仅当x ≤－3或x ≥1时等号成立)．故a 的最小值为12.(10分)10．已知函数f (x )＝|2x －1|＋|x －a |. (1)当a ＝1时，解不等式f (x )≥2； (2)若f (x )＝|x －1＋a |，求x 的取值范围． 解 (1)当a ＝1时，f (x )＝|2x －1|＋|x －1|＝⎩⎪⎨⎪⎧3x －2 x ≥1 ，x ⎝ ⎛⎭⎪⎫12≤x <1，2－3x ⎝ ⎛⎭⎪⎫x <12，(2分)当x ≥1时，x ≥43，当12≤x <1时，x 无解，当x <12时，x ≤0，综上不等式的解集为⎩⎨⎧⎭⎬⎫x |x ≤0或x ≥43.(5分)(2)因为|2x －1|＋|x －a |≥|(2x －1)－(x －a )|＝|x －1＋a |，(7分)由绝对值不等式成立条件可知：当且仅当(2x －1)(x －a )≤0时成立．(8分) 当a >12时，12≤x ≤a ，当a ＝12时，x ＝12，当a <12时，a ≤x ≤12.(10分)11．已知函数f (x )＝|2x －a |＋|2x ＋3|，g (x )＝|x －1|＋2. (1)解不等式|g (x )|<5；(2)若对任意x 1∈R ，都有x 2∈R ，使得f (x 1)＝g (x 2)成立，求实数a 的取值范围． 解 (1)由||x －1|＋2|<5，得－5<|x －1|＋2<5，(2分) 所以－7<|x －1|<3， 解得－2<x <4.所以不等式的解集为{x |－2<x <4}．(4分)(2)因为对任意x 1∈R ，都有x 2∈R ，使得f (x 1)＝g (x 2)成立，所以{y |y ＝f (x )}⊆{y |y ＝g (x )}，(6分)又f (x )＝|2x －a |＋|2x ＋3|≥|(2x －a )－(2x ＋3)|＝|a ＋3|.(8分)g (x )＝|x －1|＋2≥2，所以|a ＋3|≥2，解得a ≥－1或a ≤－5，所以实数a 的取值范围为a ≥－1或a ≤－5.(10分) 12．已知函数f (x )＝|x －3|.(1)若不等式f (x －1)＋f (x )<a 的解集为空集，求实数a 的取值范围； (2)若|a |<1，|b |<3，且a ≠0，判断f ab |a |与f ⎝ ⎛⎭⎪⎫b a 的大小，并说明理由．解 (1)f (x －1)＋f (x )＝|x －4|＋|x －3|≥|(x －4)－(x －3)|＝1，因为f (x －1)＋f (x )<a 的解集为空集，故只需令a 不大于f (x －1)＋f (x )的最小值即可，所以实数a 的取值范围是(－∞，1]．(5分)(2)f ab |a |>f ⎝ ⎛⎭⎪⎫b a ，要证f ab |a |>f ⎝ ⎛⎭⎪⎫b a ，只需证|ab －3|>|b －3a |，即证(ab －3)2>(b －3a )2，又(ab －3)2－(b －3a )2＝a 2b 2－9a 2－b 2＋9＝(a 2－1)(b 2－9)，因为|a |<1，|b |<3，所以(ab －3)2－(b －3a )2>0，所以原不等式成立．(10分)13．已知函数f (x )＝|x －a |＋|x －2|，a >0. (1)当a ＝3时，解不等式f (x )<4；(2)若正实数b ，c 满足a ＋b ＋c ＝1，且不等式f (x )≥a 2＋b 2＋c 2b ＋c对任意实数x 都成立，求a 的取值范围．解 (1)当a ＝3时，函数f (x )＝|x －3|＋|x －2|表示数轴上的x 对应点到2、3对应点的距离之和，(2分)而12和92对应点到2、3对应点的距离之和正好等于4， 故不等式f (x )<4的解集为⎝ ⎛⎭⎪⎫12，92.(5分) (2)因为a ＋b ＋c ＝1，a >0，b 、c 为正实数，所以0<a <1，f (x )＝|x －a |＋|x －2|≥|a －2|＝2－a ， 结合题意可得2－a ≥a 2＋b 2＋c 2b ＋c，即(2－a )(1－a )≥a 2＋b 2＋c 2.①(6分) 又因为a ＋b ＋c ＝1，a ，b ，c 为正实数， 所以(1－a )2＝(b ＋c )2≤2(b 2＋c 2)， 所以 1－a 22≤b 2＋c 2.②(8分)结合①②可得(1－a )(2－a )≥a 2＋ 1－a 22，即a 2＋4a －3≤0，再结合0<a <1，解得0<a ≤7－2.(10分)14．已知a >b >c >d >0，ad ＝bc . (1)证明：a ＋d >b ＋c ；(2)比较a a b b c d d c 与a b b a c c d d的大小．解 (1)证明：由a ＞b ＞c ＞d ＞0，得a －d ＞b －c ＞0，即(a －d )2＞(b －c )2，(2分) 由ad ＝bc ，得(a －d )2＋4ad ＞(b －c )2＋4bc ，即(a ＋d )2＞(b ＋c )2，故a ＋d ＞b ＋c .(5分)(2)a a b b c d d c a b b a c c d d ＝⎝ ⎛⎭⎪⎫a b a －b ⎝ ⎛⎭⎪⎫c d d －c ＝⎝ ⎛⎭⎪⎫a b a －b ⎝ ⎛⎭⎪⎫d c c －d，(7分) 由(1)得，a －b ＞c －d ，又ab＞1，所以⎝ ⎛⎭⎪⎫a b a －b ＞⎝ ⎛⎭⎪⎫a b c －d ，即⎝ ⎛⎭⎪⎫a b a －b ⎝ ⎛⎭⎪⎫d c c －d >⎝ ⎛⎭⎪⎫a b c －d ⎝ ⎛⎭⎪⎫d c c －d ＝⎝ ⎛⎭⎪⎫ad bc c －d ＝1，(9分)故a a b b c d d c＞a b b a c c d d.(10分) 15．已知命题“∀a >b >c ，1a －b ＋1b －c ≥ta －c”是真命题，记t 的最大值为m ，命题“∀n ∈R ，|n ＋sin γ|－|n －cos γ|<m14 ”是假命题，其中γ∈⎝⎛⎭⎪⎫0，π2.(1)求m 的值； (2)求n 的取值范围．解 (1)因为“∀a >b >c ，1a －b ＋1b －c ≥t a －c”是真命题， 所以∀a >b >c ，1a －b ＋1b －c ≥t a －c恒成立， 又a >b >c ，所以t ≤(a －c )·⎝ ⎛⎭⎪⎫1a －b ＋1b －c 恒成立，所以，t ≤⎣⎢⎡⎦⎥⎤ a －c ·⎝ ⎛⎭⎪⎫1a －b ＋1b －c min.(2分)又因为(a －c )·⎝⎛⎭⎪⎫1a －b ＋1b －c ＝(a －b ＋b －c )·⎝ ⎛⎭⎪⎫1a －b ＋1b －c ＝2＋b －c a －b ＋a －b b －c ≥4，当且仅当b －c ＝a －b 时“＝”成立． 因此，t ≤4，于是m ＝4.(5分)(2)由(1)得，因为“∀n ∈R ，|n ＋sin γ|－|n －cos γ|<m 14”是假命题，所以“∃n ∈R ，|n ＋sin γ|－|n －cos γ|≥2”是真命题．因为|n ＋sin γ|－|n －cos γ|＝|n ＋sin γ|－|cos r －n |≤|sin γ＋cos γ|≤2⎝ ⎛⎭⎪⎫γ∈⎝⎛⎭⎪⎫0，π2，(7分) 因此|n ＋sin γ|－|n －cos γ|＝2，此时|sin γ＋cos γ|＝2，即γ＝π4时，(9分)即⎪⎪⎪⎪⎪⎪n ＋22－⎪⎪⎪⎪⎪⎪n －22＝2，由绝对值的意义可知，n ≥22.(10分)。

冲刺2024年高考物理真题重组卷（辽宁专用）真题重组卷05（参考答案）（考试时间：75分钟 试卷满分：100分）一、选择题：本题共10小题，共46分。

在每小题给出的四个选项中，第1~7题只有一项符合题目要求，每小题4分，第8~10题有多项符合题目要求。

每小题6分，全部选对的得6分，选对但不全的得3分，有选错或不答的得0分。

11.【答案】（1）正极（1分）；（2）C （2分）；（3）R 2（2分）；电荷量（1分）12.【答案】（1）dΔt （2分）；（2）m 1gl （2分）；12(m 1+m 2)(dΔt )2（2分）；（3）2m 1gm1+m 2（2分）13.【答案】（1）解：小物块C 运动至刚要与物块B 相碰过程，根据动能定理可得 −μmgs 0=12mv 12−12mv 02（1分） 解得C 在碰撞前瞬间的速度大小为 v 1=√v 02−2μgs 0（1分）（2）解：物块B 、C 碰撞过程，根据动量守恒可得 mv 1=2mv 2（1分）解得物块B 与物块C 碰后一起运动的速度大小为 v 2=12√v 02−2μgs 0（1分） 故C 与B 碰撞过程中损失的机械能为 ΔE =12mv 12−12×2mv 22=14m(v 02−2μgs 0)（1分） （3）解：滑板A 刚要滑动时，对滑板A ，由受力平衡可得 kΔx +2μmg =3μmg （1分） 解得弹簧的压缩量，即滑板A 开始运动前物块B 和物块C 一起运动的位移大小为 Δx =μmg k（1分）从C 与B 相碰后到A 开始运动的过程中，C 和B 克服摩擦力所做的功为 W =2μmg ⋅Δx =2μ2m 2g 2k（1分）14.【答案】（1）已知小球P与Q碰撞之前的向心加速度，由向心力公式可得：F向=mv2L=ma（1分）代入数据解得：v≈1.29m/s（1分）又因为碰撞前后P的速度之比为5：1，所以碰后P的速度：v P=15v≅0.28m s⁄（1分）P与Q碰撞时间极端，系统内力远大于外力，动量守恒得：m P v=m P v P+m Q v Q（1分）代入数据解得：v Q≅1.67m s⁄方向水平向右；（1分）（2）由于L=1.2m远大于小球直径，碰后速度小上升高度小，根据简谐运动单摆周期公式：T=2π√Lg ；小球碰后再次到平衡位置的时间：t=T2，（2分）联立解得：t=2.20s（1分）碰后Q做匀减速直线运动，由牛顿第二定律得：μm Q g=m Q a（1分）速度减为零所需时间，由速度公式得：0=v Q−at′（1分）代入数据联立解得：t′=0.16s得：t>t′（1分）由速度位移公式可得：s=v Q 22a代入数据解得：s=0.51m（1分）15.【答案】（1）解：当电流从M流向N时，由左手定则可判断安培力向右，故加速度方向向右。