下载文档原格式
习 题 解 答第一章 质点运动学1-1 (1) 质点t 时刻位矢为：j t t i t r⎪⎭⎫ ⎝⎛-+++=4321)53(2(m)(2) 第一秒内位移j y y i x x r)()(01011-+-=∆)101(3)01(21)01(32ji ⎥⎦⎤⎢⎣⎡-+--=(3) (4) (5) (6) 1-2 =v c t t t c t v x x +++=+==⎰⎰241d d 34当t =2时x =4代入求证 c =－12 即1224134-++=t t t xtt tv a t t v 63d d 23223+==++=将t =3s 代入证)sm (45)sm (56)(414123133--⋅=⋅==a v m x1-3 (1) 由运动方程⎩⎨⎧+==ty t x 2342消去t 得轨迹方程0)3(2=--y x(2) 1秒时间坐标和位矢方向为 m y m x 5411==[4,5]m: ︒===3.51,25.1ααx y tg(3) 第1秒内的位移和平均速度分别为)m (24)35()04(1j i j i r+=-+-=∆(4) 1-41-5 g)(25m/s1047.280.13600101600223≈⨯=⨯⨯==t v a基本上未超过25g.1.80s 内实验车跑的距离为）（m 40080.13600210160023=⨯⨯⨯==t v s1-6 (1)设第一块石头扔出后t 秒未被第二块击中，则2021gt t v h -=代入已知数得28.9211511t t ⨯-=解此方程，可得二解为s 22.1s,84.111='=t t第一块石头上升到顶点所用的时间为s 53.18.9/15/10===g v t m由于m t t >1,这对应于第一块石头回落时与第二块相碰；又由于m t t <'1这对应于第一块石头上升时被第二块赶上击中.以20v 和'20v 分别对应于在t 1和'1t 时刻两石块相碰时第二石块的初速度，则由于2111120)(21)(t t g t t v h ∆∆---=(2) .对应于t 13.184.122212120-=-="t t v ∆m /s )(0.23=1-7 以l 表示从船到定滑轮的绳长，则t l v d /d 0-=.由图可知22h l s -=于是得船的速度为02222d d d d v sh s tl hl l ts v +-=-==负号表示船在水面上向岸靠近. 船的加速度为3202022d d d dd d s v h t l v hl l lt va -=⎥⎥⎦⎤⎢⎢⎣⎡⎪⎪⎭⎫ ⎝⎛--== 负号表示a 的方向指向岸边，因而船向岸边加速运动. 1-8 所求位数为522422221048.9601.0)106(44⨯=⨯⨯⨯==ππωgr n gr1-9 物体A 下降的加速度(如图所示)为222m/s 2.04.022=⨯==h a在1-10 2m /s 2.1=a ,s 5.00=t ,m 5.10=h .如图所示，相对南面，小球开始下落时，它和电梯的速度为m/s)(6.05.02.100=⨯==at v以t 表示此后小球落至底板所需时间，则在这段时间内，小球下落的距离为2021gt t v h +=电梯下降的距离为习题1-9图 习题1-10图2021at t v h +='又20)(21t a g h h h -='-=由此得s 59.02.18.95.1220=-⨯=-=ag h t而小球相对地面下落的距离为2021gt t v h +=259.08.92159.06.0⨯⨯+⨯=m 06.2= 1-11风地vb ）两图中风地v应是同一矢量.1-12 (1) vLv L t 22==(2) 22212uv vL uv L uv L t t t -=++-=+=1212-⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛-=v u v L(3) v L v L t t t '+'=+=21,如图所示风速u 由东向西，由速度合成可得飞机对地速度v u v+=',则22uv V -='.习题1-12图习题1-11图2221222⎪⎭⎫ ⎝⎛-=--='=v u v L uv L v L t 证毕1-13 （1）设船相对岸的速度为V '(如图所示),由速度合成得V u V +='V 的大小由图1.7示可得αβcos cos u V V +'=即332323cos cos -=⨯-=-='αβu V V而1212sin sin =⨯=='αβu V船达到BD OB AB 将式（1） (2) 由t =即 c o s α故船头应与岸垂直，航时最短.将α值代入（3）式得最短航时为s)(500105.021012/sin 101333min =⨯=⨯=⨯=s u t π(3) 设l OB =,则ααββsin cos 2sin sin 22u uV Vu D V D V D l -+=''==欲使l 最短，应满足极值条件.习题1-13图a a uV Vu u D l'⎢⎢⎣⎡''-+-='cos sin cos 2d d 22αα0c o s 2s i n s i n 2222=⎥⎦⎤'-+''+αuV Vu a a uV简化后可得01cos cos 222=+'+-'αuVV u a即 01c o s 613c o s 2=+'-'αa解此方程得32cos ='α︒=='-2.4832cos1α将α'AB。
第一章质点运动学单元测验题一、选择题1.一质点沿x 轴运动，加速度与位置的关系为a (x )=2x +4x 2(SI 单位).已知质点在x =0处的速度为2m/s ，则质点在x =3m 处的速度为A.42m/s; B.26m/s ; C.94m/s ; D.34m/s .答案：C 解：根据题意：224dv a x x dt ==+，两边同乘dx 有：2(24)dv dx x x dx dt ⋅=+⋅由dx v dt=,上式化为:2(24)v dv x x dx ⋅=+对上式两边积分得到：223423v x x c =++由x =0，v =2m/s ，确定c =2.则当x =3m 时，解得：v =94m/s.2.一质点沿x 轴做直线运动，其速度v 随时间t 的变化关系如图所示.则下列哪个图可表示质点加速度a 随时间t 变化关系？2-•/s m a 2-•/s m a AB C答案：B 解：依据质点在一维运动时，速度-时间曲线的斜率对应加速度可知B 为加速度曲线.3.质点的运动学方程为33(21)t t =++r i j (SI 单位).则t =1s 时质点的速度为(SI单位)A.ji 6+3; B.j i 3+3; C.j i 6+6; D.j i 3+6.答案：A解：根据题意：33(21)t t =++r i j ，微分得：236d t dt ==+r v i j ，()136=+v i j 4.质点运动学方程为：kbt j t a i t a r +sin +cos =ωω，其中a 、b 、ω均为正的常数.问质点作什么运动？A.平面圆周运动；B.平面椭圆运动；C.螺旋运动；D.三维空间的直线运动.答案：C解：把质点的运动分解到三个方向上：cos sin x a t y a t z bt ωω===，，整理可知：222x y a z bt+==，则质点是以z 5.如图所示，在桌面的一边，—小球作斜抛运动，初速度v 0=4.7m/s.已知桌面宽a =2.0m.欲使小球能从桌面的另—边切过，小球的抛射角θ为A.30°;B.38°;C.50°;D.58°.答案：D 解：根据题意，小球沿x 和y 方向的运动方程为：t v x ⋅=θcos 0，201sin 2y v t gt θ=⋅-由x =2.0m 时，y =0，解得：o 58θ=.6.如图，有一半径为R 的定滑轮，沿轮周绕着一根绳子，悬在绳子一端的物体按s =(1/2)bt 2的规律向下运动.若绳子与轮周间没有相对滑动，轮周上一点A 在任一时刻t 的总加速度大为A.2t b a ;B.222/=R t b a ；C.b a =;D.R t b b a /+=22.答案：A 解：已知221bt s =，微分可得速度大小：t b dtds v ⋅==切向加速度大小：b dt dv a ==τ;法向加速度大小：Rt b R v a n 222==总加速度大小：a ==.7.当蒸汽船以15km/h 的速度向正北方向航行时，船上的人观察到船上的烟囱里冒出的烟飘向正东方向.过一会儿，船以24km/h 的速度向正东方向航行，船上的人则观察到烟飘向正西北方向.若在这两次航行期间风速不变，则风速的大小为A.9km/h; B.17.5km/h ; C.26.9km/h ; D.41km/h.答案：B解：地面为静系，船为动系，风为研究对象，则风对地的速度为绝对速度：风v v =船对地的速度为牵连速度：船牵连v v =风对船的速度为相对速度：风对船牵连v v =由绝对速度、牵连速度和相对速度的关系可得v v v =+船风对船，其矢量几何关系如图所示由此几何关系可得：1cos v v θ=船风，o 2145sin v v ctg v θ-=风船船联立解得：o 31θ=，5.17=v km /h .8.一个自由落体在它运动的最后一秒内所通过的路程等于全程的1/3.则物体通过全程所需的时间为A.3s ;B.6-3s ;C.6+3s ;D.6s答案：C解：设自由落体的全程下落时间和下落的高度分别为t 、S t 。
第一章质点运动学一选择题1．以下说法中，正确的选项是：（）A.一物体若拥有恒定的速率，则没有变化的速度；B.一物体拥有恒定的速度，但仍有变化的速率；C.一物体拥有恒定的加快度，则其速度不行能为零；D. 一物体拥有沿x 轴正方向的加快度而有沿x 轴负方向的速度。
解：答案是 D。
2.长度不变的杆 AB，其端点 A 以 v0匀速沿 y 轴向下滑动， B 点沿 x 轴挪动，则 B 点的速率为：（）A . v0 sinB .v0 cos C.v0 tan D.v0 / cos解：答案是 C。
简要提示：设 B 点的坐标为 x， A 点的坐标为 y，杆的长度为l，则x2y2l 2对上式两边关于时间求导：dx dy0，因dxv，dyv0，所以2 x 2 ydtdt dt dt2xv2yv0 = 0即v=v0 y/x =v0tan所以答案是 C。
3.如图示，路灯距地面高为 H，行人身高为 h，若人以匀速 v 背向路灯行走，灯y人头A H vv0hθvx影sB选择题 3图选择题 2图则人头影子挪动的速度u 为（）H h Hv h HA.vB.H H h H h 解：答案是 B 。
简要提示：设人头影子到灯杆的距离为 x ，则x s h ， x Hs ， x H H hdx H ds HvuH h dt Hdt h所以答案是 B 。
4. 某质点作直线运动的运动学方程为x ＝ 3t-5t 3 + 6 (SI)，则该质点作A. 匀加快直线运动，加快度沿 x 轴正方向．B. 匀加快直线运动，加快度沿 x 轴负方向．C. 变加快直线运动，加快度沿 x 轴正方向．D. 变加快直线运动，加快度沿x 轴负方向．()解： 答案是 D5. 一物体从某一确立高度以v 0 的初速度水平抛出，已知它落地时的速度为v t ，那么它的运动时间是： （）v t - v 0v t v 0v t2 22v v 0 v t A.B.C.gD.2 gg2 g解：答案是 C 。
第一章 质点运动学一、简答题1、运动质点的路程和位移有何区别?答：路程是标量，位移是矢量；路程表示质点实际运动轨迹的长度，而位移表示始点指向终点的有向线段。
2、质点运动方程为()()()()k t z j t y i t x t r ++=，其位置矢量的大小、速度及加速度如何表示? 答：()()()t z t y t x r 222r ++==()()()k t z j t y i t xv ++= ()()()k t z j t y i t x a ++=3、质点做曲线运动在t t t ∆+→时间内速度从1v 变为到2v ，则平均加速度和t时刻的瞬时加速度各为多少? 答：平均加速度 t v v a ∆-=12 ，瞬时加速度()()dt v d t v v a t t lim t 120 =∆-=→∆4、画出示意图说明什么是伽利略速度变换公式? 其适用条件是什么?答：牵连相对绝对U V +=V ，适用条件宏观低速5、什么质点? 一个物体具备哪些条件时才可以被看作质点?答：质点是一个理想化的模型,它是实际物体在一定条件下的科学抽象。
条件：只要物体的形状和大小在所研究的问题中属于无关因素或次要因素,物体就能被看作质点。
二、选择题1、关于运动和静止的说法中正确的是 ( C )A 、我们看到的物体的位置没有变化，物体一定处于静止状态B 、两物体间的距离没有变化，两物体就一定都静止C 、自然界中找不到不运动的物体，运动是绝对的，静止是相对的D 、为了研究物体的运动，必须先选参考系，平时说的运动和静止是相对地球而言的2、下列说法中正确的是 ( D )A 、物体运动的速度越大，加速度也一定越大B 、物体的加速度越大，它的速度一定越大C 、加速度就是“加出来的速度”D 、加速度反映速度变化的快慢，与速度大小无关3、质点沿x 轴作直线运动，其t v-曲线如图所示，如s t 0=时，质点位于坐标原点，则s .t 54=时，质点在x 轴的位置为 ( B )A 、5 mB 、2 mC 、0 mD 、-2 m4、质点作匀速率圆周运动，则 ( B )A 、线速度不变B 、角速度不变C 、法向加速度不变D 、加速度不变5、质点作直线运动，某时刻的瞬时速度为s /m v 2=，瞬时加速度为22s /m a -=，则一秒钟后质点的速度 ( D )A 、等于0B 、等于s /m 2-C 、等于s /m 2D 、不能确定6、质点作曲线运动，r 表示位置矢量的大小，s 表示路程，z a 表示切向加速度的大小，v 表示速度的大小。
第一章质点运动学1-1质点作曲线运动，在时刻 t 质点的位失为r ，速度为v ,速率为v , t 至（t t 路程为 s ，位失大小的变化量为 r （或称 r ），平均速度为v ,平均速率为v 。
（1）根据上述情况，则必有（ B ） 时间内的位移为 r ，(A) r s r (B) r s r ，当 t 0时有 dr ds dr (C ) r r s ，当 t 0时有 dr dr ds (D)r s r ，当 t 0时有 dr dr ds （2）根据上述情况,则必有 （ C )(A) v vj 7 v (B) v vj v v(C ) v v 侗 v (D) v vj v v1-2 一运动质点在某瞬时位于位失 r （x, y ）的端点处，对其速度的大小有四种意见，即 dr （1）巴；（2） dr ；（3） ds . (4) J (dx )2 (dy ) dt dt dtXdt dt下述判断正确的是 :（ D )（A ）只有（1） (2) 正确； (A ) 只有 ( 2）正确（A ）只有（2） (3) 正确； (A ) 只有 ( 3) (4) 正确 1-3质点作曲线运动, r 表示位置矢量，v 表示速度，a 表示加速度，s 表示路程，a t 表示切向加速度。
/、 dv/、 dr / 、ds v ； (4) dv (1) 一a ； (2)— v ； (3)— dt dt dt dt对下列表达式，即 a t 下述判断正确的是（ D ） （A ）只有（1）（ 4 ）是对的；（A ）只有（2）（ 4）是对的 （A ）只有（2 ）是对的；（A ）只有（3）是对的 1-4 一个质点在做圆周运动时，则有（ B ） （A ）切向加速度一定改变，法向加速度也改变 （B ） 切向加速度可能不变，法向加速度一定改变 （C ） 切向加速度可能不变，法向加速度不变 （D ） 切向加速度一定改变，法向加速度不变 1-5有一质点作直线运动，其运动方程为 x =6t -2t （SI 制），试求: （1） 第二秒内的平均速度； （2） 第三秒末的速度； （3） 第一秒末的加速度；（4） 质点作什么类型的运动？(5 0解：⑴ 先求出质点在第二秒内的位移。
第一章 质点运动学1-1 一质点在平面上运动，已知质点位置矢量的表示式为j i r 22bt at += （其中b a ,为常量） 则该质点作（A ）匀速直线运动 （B ）变速直线运动（C ）抛物线运动 （D ）一般曲线运动 [B]解：由j i rv bt at t 22d d +==知 v 随t 变化，质点作变速运动。
又由x aby bt y at x =⎪⎭⎪⎬⎫==22 知质点轨迹为一直线。
故该质点作变速直线运动。
1-2 质点作曲线运动，r 表示位置矢量，s 表示路程，t a 表示切向加速度，下列表达式中，① a t v =d ② v t r =d ③ v t s =d d ④ t a t =d d v （A ）只有（1）、（4）是对的。
（B ）只有（2）、（4）是对的。
（C ）只有（2）是对的。
（D ）只有（3）是对的。
[D]解：由定义：t vt a d d d d ≠=v ； t r t s t v d d d d d d ≠==r ； t t v a d d d d v ≠=τ只有③正确。
1-3 在相对地面静止的坐标系内，A 、B 二船都以21s m -⋅的速率匀速行驶，A 船沿x 轴正向，B 船沿y 轴正向。
今在A 船上设置与静止坐标系方向相同的坐标系（x ，y 方向单位矢用j i ,表示），那么在A 船上的坐标系中，B 船的速度（以1s m -⋅为单位）为（A ）j i 22+ （B ）j i 22+-（C ）j i 22-- （D ）j i 22- [B]解：由i v 2=对地A ，j v 2=对地B 可得 A B A B 地对对地对v v v +=⎰对地对地A B v v -=i j 22-=j i 22+-= （1s m -⋅）1-4 一质点沿x 方向运动，其加速度随时间变化关系为)SI (23t a +=如果初始时质点的速度0v 为51s m -⋅，则当t 为3s 时，质点的速度1s m 23-⋅=v解：⎰+=tta v v 00d13s m 23d )23(5-⋅=++=⎰tt1-5 一质点的运动方程为SI)(62t t x -=，则在t 由0至4s 的时间间隔内，质点的位移大小为 8m ，在t 由0到4s 的时间间隔内质点走过的路程为 10m 。
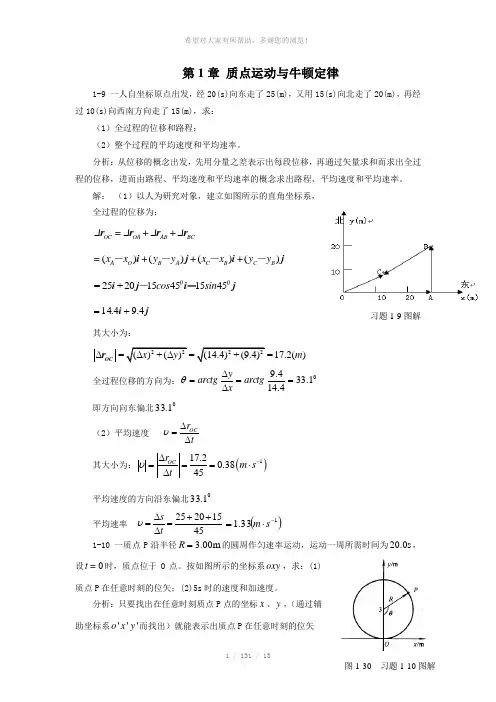
第1章 质点运动与牛顿定律1-9 一人自坐标原点出发，经20(s)向东走了25(m)，又用15(s)向北走了20(m)，再经过10(s)向西南方向走了15(m)，求：（1）全过程的位移和路程；（2）整个过程的平均速度和平均速率。
分析：从位移的概念出发，先用分量之差表示出每段位移，再通过矢量求和而求出全过程的位移，进而由路程、平均速度和平均速率的概念求出路程、平均速度和平均速率。
解： （1）以人为研究对象，建立如图所示的直角坐标系， 全过程的位移为：r r r r OC OA AB BC Δ=Δ+Δ+Δ()()()()A O B A C B C B =x x +y y +x x +y y －－－－i j i j =25+2015451545i j i j 00cos sin －－j i 4.94.14+=其大小为：2222Δ=(Δ)+(Δ)=(14.4)+(9.4)=17.2()OC r x y m全过程位移的方向为：01.334.144.9==∆∆=arctg x y arctg θ 即方向向东偏北01.33 （2）平均速度 OCr tυ∆=∆ 其大小为：()117.20.3845OC r m s t υ-∆===⋅∆ 平均速度的方向沿东偏北01.33平均速率 25201545s t υ∆++==∆()133.1-⋅=s m 1-10 一质点P 沿半径 3.00m R =的圆周作匀速率运动，运动一周所需时间为20.0s ，设0t =时，质点位于O 点。
按如图所示的坐标系oxy ，求：(1)质点P 在任意时刻的位矢；(2)5s 时的速度和加速度。
分析：只要找出在任意时刻质点P 点的坐标x 、y ，（通过辅助坐标系'''o x y 而找出）就能表示出质点P 在任意时刻的位矢习题1-9图解x y =+r i j ，进而由r 对时间求导求出速度υ和加速度a 。
解：如图所示，在'''o x y 坐标系中，因t Tπθ2=，则质点P 的参数方程为： 22`,`x Rsint y Rcos t T Tππ==- 坐标变换后，在oxy 坐标系中有：2`x x Rsint T π==，02`y y y Rcos t R Tπ=+=-+ 则质点P 的位矢方程为： 22ππ=Rsint +Rcos t +R T T ⎛⎫ ⎪⎝⎭－r i j ()()=30.1310.1i j sin t cos t ππ+⎡⎤⎣⎦－ 5s 时的速度和加速度分别为 ：22220.3r i j j υd R cos t R sin t dt T T T Tπππππ==+=2222222=()+()(0.03)22d =R sin t R cos t =dt T T T Tπππππ－－r a i j j1-11 已知一质点的运动方程为2362x t t =-(单位为SI 制)，求：(1)第2秒内的平均速度；(2)第3秒末的速度；(3)第一秒末的加速度；(4)物体运动的类型。
第一章质点运动学单元测验题一、选择题1.一质点沿x 轴运动，加速度与位置的关系为a (x )=2x +4x 2(SI 单位).已知质点在x =0处的速度为2m/s ，则质点在x =3m 处的速度为A.42m/s; B.26m/s ; C.94m/s ; D.34m/s .答案：C 解：根据题意：224dv a x x dt ==+，两边同乘dx 有：2(24)dv dx x x dx dt ⋅=+⋅由dx v dt=,上式化为:2(24)v dv x x dx ⋅=+对上式两边积分得到：223423v x x c =++由x =0，v =2m/s ，确定c =2.则当x =3m 时，解得：v =94m/s.2.一质点沿x 轴做直线运动，其速度v 随时间t 的变化关系如图所示.则下列哪个图可表示质点加速度a 随时间t 变化关系？2-•/s m a 2-•/s m a AB C答案：B 解：依据质点在一维运动时，速度-时间曲线的斜率对应加速度可知B 为加速度曲线.3.质点的运动学方程为33(21)t t =++r i j (SI 单位).则t =1s 时质点的速度为(SI单位)A.ji 6+3; B.j i 3+3; C.j i 6+6; D.j i 3+6.答案：A解：根据题意：33(21)t t =++r i j ，微分得：236d t dt ==+r v i j ，()136=+v i j 4.质点运动学方程为：kbt j t a i t a r +sin +cos =ωω，其中a 、b 、ω均为正的常数.问质点作什么运动？A.平面圆周运动；B.平面椭圆运动；C.螺旋运动；D.三维空间的直线运动.答案：C解：把质点的运动分解到三个方向上：cos sin x a t y a t z bt ωω===，，整理可知：222x y a z bt+==，则质点是以z 5.如图所示，在桌面的一边，—小球作斜抛运动，初速度v 0=4.7m/s.已知桌面宽a =2.0m.欲使小球能从桌面的另—边切过，小球的抛射角θ为A.30°;B.38°;C.50°;D.58°.答案：D 解：根据题意，小球沿x 和y 方向的运动方程为：t v x ⋅=θcos 0，201sin 2y v t gt θ=⋅-由x =2.0m 时，y =0，解得：o 58θ=.6.如图，有一半径为R 的定滑轮，沿轮周绕着一根绳子，悬在绳子一端的物体按s =(1/2)bt 2的规律向下运动.若绳子与轮周间没有相对滑动，轮周上一点A 在任一时刻t 的总加速度大为A.2t b a ;B.222/=R t b a ；C.b a =;D.R t b b a /+=22.答案：A 解：已知221bt s =，微分可得速度大小：t b dtds v ⋅==切向加速度大小：b dt dv a ==τ;法向加速度大小：Rt b R v a n 222==总加速度大小：a ==.7.当蒸汽船以15km/h 的速度向正北方向航行时，船上的人观察到船上的烟囱里冒出的烟飘向正东方向.过一会儿，船以24km/h 的速度向正东方向航行，船上的人则观察到烟飘向正西北方向.若在这两次航行期间风速不变，则风速的大小为A.9km/h; B.17.5km/h ; C.26.9km/h ; D.41km/h.答案：B解：地面为静系，船为动系，风为研究对象，则风对地的速度为绝对速度：风v v =船对地的速度为牵连速度：船牵连v v =风对船的速度为相对速度：风对船牵连v v =由绝对速度、牵连速度和相对速度的关系可得v v v =+船风对船，其矢量几何关系如图所示由此几何关系可得：1cos v v θ=船风，o 2145sin v v ctg v θ-=风船船联立解得：o 31θ=，5.17=v km /h .8.一个自由落体在它运动的最后一秒内所通过的路程等于全程的1/3.则物体通过全程所需的时间为A.3s ;B.6-3s ;C.6+3s ;D.6s答案：C解：设自由落体的全程下落时间和下落的高度分别为t 、S t 。
第一章质点运动学习题答案1-1 质点做直线运动，运动方程为其中以s为单位，以m为单位，求：(1)＝4s时，质点的位置、速度和加速度；(2)质点通过原点时的速度；(3)质点速度为零时的位置；(4) 做出-t图、-t图、-t图.解：(1) 根据直线运动情况下的定义，可得质点的位置、速度和加速度分别为（1）（2）（3）当＝4s时，代入数字得：mm/sm/s（2）当质点通过原点时，＝0，代入运动方程得：＝0解得：，代入（2）式得：m/s=－12m/s(3) 将代入（2）式，得解得：s代入（1）式得：12m－6m=6m1.2一质点在平面上运动，运动方程为=3+5,=2+3-4.式中以 s计，,以m计．(1)以时间为变量，写出质点位置矢量的表示式；(2)求出=1 s 时刻和＝2s 时刻的位置矢量，计算这1秒内质点的位移；(3)计算＝0s时刻到＝4s时刻内的平均速度；(4)求出质点速度矢量表示式，计算＝4s 时质点的速度；(5)计算＝0s 到＝4s 内质点的平均加速度；(6)求出质点加速度矢量的表示式，计算＝4s 时质点的加速度.解：（1）(2)将,代入上式即有(3)∵∴(4)则(5)∵(6)这说明该点只有方向的加速度，且为恒量.1-4 一质点沿一直线运动，其加速度为，式中的单位为m，的单位为m/s,试求该质点的速度与位置坐标之间的关系.设时，＝4m/s解：依题意积分得1-5质点沿直线运动，加速度，如果当＝3时，，，求质点的运动方程. (其中以m/s为单位，以s为单位，以m为单位，以m/s为单位)解：加速度表示式对积分，得将＝3s，＝9m，m/s代入以上二式，得积分常数m/s，＝0.75m，则1-6 当物体以非常高的速度穿过空气时，由空气阻力产生的反向加速度大小与物体速度的平方成反比，即，其中为常量. 若物体不受其他力作用沿方向运动，通过原点时的速度为，试证明在此后的任意位置处其速度为.解：根据加速度定义得：，因，代入上式，分离变量，整理后得：，应用初始条件，两边积分得得即有：1-7试写出以矢量形式表示的质点做匀速圆周运动的运动学方程，并证明做匀速圆周运动质点的速度矢量和加速度矢量的标积等于零，即解：以直角坐标表示的质点运动学方程为以矢量形式表示的指点运动学方程为速度和加速度分别为所以1-8一质点在平面内运动，其运动方程为，其中均为大于零的常量.(1)试求质点在任意时刻的速度；(2)证明质点运动的轨道为椭圆；(3)证明质点的加速度恒指向椭圆的中心.解：（1）质点在任意时刻的速度（2）由消去，可得轨道方程可见是椭圆方程，表明质点作椭圆运动（3）加速度因为>0，所以的方向恒与反向，即恒指向椭圆中心.1-9路灯离地面高度为，一个身高为的人，在灯下水平路面上以匀速度步行. 如图所示，求当人与灯的水平距离为时，他的头顶在地面上的影子移动的速度的大小.解：建立如图所示的坐标，时刻头顶影子的坐标为，设头顶影子的移动速度为，则由图中可看出有，则有所以有1-10 1.10质点沿半径为的圆周按＝的规律运动，式中为质点离圆周上某点的弧长,，都是常量，求：(1)时刻质点的加速度；(2)为何值时，加速度在数值上等于．解：（1）则加速度与半径的夹角为(2)由题意应有即∴当时，1-11质点做半径为20cm的圆周运动，其切向加速度恒为5cm/s，若该质点由静止开始运动，需要多少时间：(1)它的法向加速度等于切向加速度；(2)法向加速度等于切向加速度的二倍.解：质点圆周运动半径＝20cm，切向加速度＝5cm/s，时刻速度为，法向加速度为，因此有（1）当时，s（2）当时，s1-12 (1)地球的半径为6.37m，求地球赤道表面上一点相对于地球中心的向心加速度. (2)地球绕太阳运行的轨道半径为1.5m，求地球相对于太阳的向心加速度. (3)天文测量表明，太阳系以近似圆形的轨道绕银河系中心运动，半径为2.8m，速率为2.5m/s，求太阳系相对于银河系的向心加速度.解：（1）地球赤道表面一点相对于地球中心的向心角速度为m/s（2）地球相对太阳的向心加速度为m/s（3）太阳系相对银河系的向心加速度m/s1-13 以初速度＝20抛出一小球，抛出方向与水平面成60°的夹角，求：(1)球轨道最高点的曲率半径；(2)落地处的曲率半径．解：设小球所作抛物线轨道如题1-13图所示．题1-13图(1)在最高点，又∵∴(2)在落地点，,而∴1-14一架飞机在水平地面的上方，以174m/s的速率垂直俯冲，假定飞机以圆形路径脱离俯冲，而飞机可以承受的最大加速度为78.4m/s，为了避免飞机撞到地面，求飞机开始脱离俯冲的最低高度. 假定整个运动中速率恒定.解：设飞机以半径为圆形路径俯冲，其加速度为当为飞机所能承受的最大加速度时，即为最小，所以m1-15一飞轮以速度rev/min转动，受制动而均匀减速，经s 静止，求(1) 角加速度和从制动开始到静止飞轮转过的转数；(2) 求制动开始后，s时飞轮的角速度；(3) 设飞轮半径=1m，求s时，飞轮边缘上一点的速度和加速度.解：（1）飞轮的初角速度，当s时，；代入得从开始到静止，飞轮转过的角度及其转数为：radrev（2）s 时，飞轮的角速度为rad/s（3）s 时，飞轮边缘上一点的速度为m/s相应的切线和法线加速度为m/sm/s1-16一质点沿半径为1m的圆周运动，运动方程为，式中以弧度计，以秒计，求：(1)＝2s时，质点的切向和法向加速度；(2)当加速度的方向和半径成角时，其角位移是多少？解：(1)时，(2)当加速度方向与半径成角时，有即亦即则解得于是角位移为1-17一圆盘半径为3m，它的角速度在＝0时为3.33rad/s，以后均匀地减小，到＝4s时角速度变为零. 试计算圆盘边缘上一点在＝2s时的切向加速度和法向加速度的大小.解：角速度均匀减小，因此，角加速度为rad/s圆盘做匀角加速度，故有当s时，rad/s法向和切向加速度分别为m/s＝－7.8 m/s1-18某雷达站对一个飞行中的炮弹进行观测，发现炮弹达最高点时，正好位于雷达站的上方，且速率为，高度为，求在炮弹此后的飞行过程中，在(以s为单位)时刻雷达的观测方向与铅垂直方向之间的夹角及其变化率(雷达的转动角速度)解：以雷达位置为坐标原点，取坐标系如图所示，根据题意，炮弹的运动方程为可解得：（1）则将（1）式两边对求导数，得则有1-19 汽车在大雨中行驶，车速为80km/h，车中乘客看见侧面的玻璃上雨滴和铅垂线成角，当车停下来时，他发现雨滴是垂直下落的，求雨滴下落的速度.解：取车为运动参考系，雨滴相对于车的速度为，雨滴对地速度为，车对地的速度为，相对运动速度合成定理为见如图所示的速度合成图，则有m/s1-20一升降机以加速度1.22m/s上升，当上升速度为2.44 m/s时，有一螺帽自升降机的天花板松落，天花板与升降机底面相距 2.74m，计算：(1)螺帽从天花板落到底面所需的时间；(2)螺帽相对于升降机外固定柱子的下降距离.解：以升降机外固定柱子为参考系，竖直向上为坐标轴正向，螺帽松落时升降机底面位置为原点. 螺帽从＝2.74m处松落，以初速度＝2.44m/s做竖直上抛运动，升降机底面则从原点以同样的初速度做向上的加速运动，加速度＝1.22m/s，它们的运动方程分别为螺帽：底面：螺帽落到底面上时，，由以上两式得＝0.705s（2）螺帽相对于升降机外固定柱子的下降距离为m1-21某人骑自行车以速率向西行使，北风以速率吹来（对地面），问骑车者遇到风速及风向如何？解：地为静系E，人为动系M。
