2016—2020近五年高考数学全国卷(1)考点分布分析
- 格式:docx
- 大小:23.89 KB
- 文档页数:3

2020年数学新高考i卷考点分布摘要:1.2020年数学新高考I卷概述2.高考数学考点分布a.集合与不等式b.复数与向量c.立体几何d.排列组合、概率与统计e.三角函数与解三角形f.函数与导数3.应对高考数学策略正文:【1】2020年数学新高考I卷概述2020年数学新高考I卷涵盖了全国多个省份,包括山东、广东、湖北、河北、福建、湖南、江苏和浙江等地。
该卷结合了各地教育特点,充分体现了数学知识的广泛性和实用性。
【2】高考数学考点分布2.1 集合与不等式集合的交集、并集、补集等概念,以及不等式的解法和不等式恒成立问题等。
2.2 复数与向量复数的概念、运算、模以及向量的线性运算、平行向量、向量数量积等。
2.3 立体几何空间几何体的性质、几何体的表面积和体积计算、空间直线与平面的位置关系、空间角、空间距离等。
2.4 排列组合、概率与统计排列组合的计算、概率的求解、离散型随机变量、统计量、参数估计等。
2.5 三角函数与解三角形三角函数的定义、性质、图象和周期性、三角函数的求值、解三角形等。
2.6 函数与导数函数的性质、函数的图像、导数的计算、导数的应用、高阶导数等。
【3】应对高考数学策略1.扎实掌握基本概念和基本运算,强化基本功。
2.注重解题方法和技巧,提高解题效率。
3.培养自己的逻辑思维能力和分析问题的能力。
4.多做真题,积累经验,了解高考命题趋势。
5.及时复习,查漏补缺,确保知识体系的完整性。
通过以上分析,我们可以对2020年数学新高考I卷的考点有一个全面的了解,从而为未来的高考数学复习和备考提供有益的参考。

成语小故事成语小故事(通用18篇)小故事是一种篇幅短小,故事情节简单而又富于哲理的故事,因其每个故事都能给人以启迪,成功做人之道而受到广大读者特别是在校学生的喜爱。
下面是小编整理的成语小故事,一起来看看吧。
成语小故事篇1(一)井底之蛙【典故】《庄子秋水篇》讲了一个浅井的虾蟆和东海之鳖的故事。
一日,一只浅井的青蛙见到一只东海大鳖,便兴致勃勃地对它说:“我可快乐啦!出来就在井栏边跳来跳去,进去就在井壁砖缝中休息;跳入井中,水就泡着我的两腋和腮;游到浅处,泥汤就没了我的脚。
我独占一井之水,螃蟹和蝌蚪都没法跟我相比,你何不也下来看看?”东海之鳖来到井边,左脚还没进去,石膝已经被卡住了。
东海之鳖慢慢退了出去,然后对这只浅井青蛙讲述了大海的样子:“用千里之遥这样的字眼儿,不足以说明大海的广阔;用千仞之高这样的词,不足以量尽它的深度。
大禹时十年九涝,海水没显出增加了多少;商汤时八年七早,海水也并不见减少多少……”浅井的青蛙听得目瞪口呆,惊恐万分,茫茫然若有所失,它何尝想到还有比它的一方水井更大的世界呢!【出处】《庄子·秋水》:“井蛙不可以语于海者,拘于虚也。
”【释读】井底的蛙只能看到井口那么大的一块天。
比喻见识狭窄的人。
(二)叶公好龙【典故】鲁哀公经常向别人说自己是多么地渴望人才,多么喜欢有知识才干的人。
有个叫子张的人听说鲁哀公这么欢迎贤才,便从很远的地方风尘仆仆地来到鲁国,请求拜见鲁哀公。
子张在鲁国一直住了七天,也没等到鲁哀公的影子。
原来鲁哀公说自己喜欢有知识的人只是赶时髦,学着别的国君说说而已,对前来求见的子张根本没当一回事,早已忘到脑后去了。
子张很是失望,也十分生气。
他给鲁哀公的车夫讲了一个故事,并让车夫把这个故事转述给鲁哀公听。
然后,子张悄然离去了。
终于有一天,鲁哀公记起子张求见的事情,准备叫自己的车夫去把子张请来。
车夫对鲁哀公说:“他早已走了。
”鲁哀公很是不明白,他问车夫道:“他不是投奔我而来的吗?为什么又走掉了呢?”于是,车夫向鲁哀公转述了子张留下的故事。

近五年高考文科数学试卷及答案解析(全国1卷)(2016年—2020年)说明:含有2016年—2020年的全国1卷高考文科数学试题以及答案详细解析(客观题也有答案详解)目录2020年普通高等学校招生全国统一考试文科数学(I卷)答案详解 (3)2020年普通高等学校招生全国统一考试文科数学(I卷) (19)2019年普通高等学校招生全国统一考试文科数学1卷 (29)2019年普通高等学校招生全国统一考试文科数学1卷答案详解 (39)2018年普通高等学校招生全国统一考试文科数学1卷 (50)2018年普通高等学校招生全国统一考试文科数学1卷答案详解 (60)2017年普通高等学校招生全国统一考试文科数学1卷 (71)2017年普通高等学校招生全国统一考试文科数学I卷答案详解 (81)2016年普通高等学校招生全国统一考试文科数学1卷 (93)2016年普通高等学校招生全国统一考试文科数学1卷答案详解 (103)2020年普通高等学校招生全国统一考试文科数学(I 卷)答案详解一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.(集合)已知合集{}2340A x x x =--<,{}4,1,3,5B =-,则A B = A.{}4,1- B.{}1,5C.{}3,5 D.{}1,3【解析】∵{}14A x x =-<<,∴{1,3}A B = .【答案】D2.(复数)若312z i i =++,则z =A.0 B.1C. D.2【解析】∵3i i =-,∴1z i =+,∴z 【答案】C3.(立体几何)埃及胡夫金字塔是古代世界建筑奇迹之一,它的形状可视为一个正四棱锥,以该四棱锥的高为边长的正方形面积等于该四棱锥一个侧面三角形的面积,则其侧面三角形底边上的高与底面正方形的边长的比值为A.514- B.512C.514+ D.512【解析】如图A3所示,设正四棱锥底面的边长为a ,则有22221212h am a h m ⎧=⎪⎪⎨⎛⎫⎪+= ⎪⎪⎝⎭⎩整理得22420m am a --=,令mt a=,则有24210t t --=,∴114t +=,214t -=(舍去),即14m a +=.图A3【答案】C4.(概率统计)设O 为正方形ABCD 的中心,在O,A ,B,C,D 中任取3点,则取到的3点共线的概率为A.15B.25C.12D.45【解析】如图A4所示,从O,A ,B,C,D 中任取3点的所有情况数为35C =10,取到的3点共线的情况有:AOC 、BOD ,共2种情况,所以所求的概率为51102==P.图A4【答案】A5.(概率统计)某校一个课外学习小组为研究某作物种子的发芽率y 和温度x (单位:C )的关系,在20个不同的温度条件下进行种子的发芽实验,由实验数据,)(i i x y i =(1,2,…,20)得到下面的散点图:由此散点图,在10C 至40C 之间,下面四个回归方程类型中最适宜作为发芽率y 和温度x 的回归方程类型的是A.y a bx=+ B.2y a bx =+ C.xy a be =+ D.ln y a b x=+【解析】根据散点图的趋势和已学函数图象可知,本题的回归方程类型为对数函数,故选D选项.【答案】D6.(解析几何)已知圆2260x y x +-=,过点(1,2)的直线被该圆所截得的弦的长度的最小值为A.1B.2C.3D.4【解析】222(3)3x y -+=,设直线方程为2(1)y k x -=-,∴20kx y k -+-=,∴圆心(3,0)到该直线的距离为d ==,∴2max 8d =,故弦的长度的最小值为2==.【答案】B7.(三角函数)设函数()cos()6f x x πω=+在[]ππ-,的图像大致如下图,则()f x 的最小正周期为A.109π B.76π C.43π D.32π【解析】∵函数过点4π,09⎛⎫- ⎪⎝⎭,∴4ππcos()=096x ω-+,∴4πππ=962x ω-+-,解得23=ω,∴()f x 的最小正周期为3π4π2==ωT .【答案】C8.(函数)设3log 42a =,则4a -A.116B.19C.18D.16【解析】∵33log 4log 42a a ==,∴2439a ==,∴11449a a -==.【答案】B9.(算法框图)执行右面的程序框图,则输出的n =A.17B.19C.21D.23【解析】①输入10n S ==,,得1S S n =+=,100S ≤成立,继续;②输入31n S ==,,得4S S n =+=,100S ≤成立,继续;③输入54n S ==,,得9S S n =+=,100S ≤成立,继续;……由上述规律可以看出,S 是一个以a 1=1为首项,d =2为公差的等差数列的前m 项和,且21n m =-,故有21(1)2m m m S ma d m -=+=.当2100m S m =>,即11n >时,程序退出循环,此时2121n m =-=.【答案】C10.(数列)设{}n a 是等比数列,且123+1a a a +=,2342a a a ++=,则678+a a a +=A.12B.24C.30D.32【解析】设{}n a 的公比为q ,∵234123(+)2a a a q a a a ++=+=,∴2q =,∴55678123+(+)232a a a q a a a +=+==.【答案】D11.(解析几何)设1F ,2F 是双曲线22:13y C x -=的两个焦点,O 为坐标原点,点P 在C 上且|OP |=2,则∆12PF F 的面积为A.72B.3C.52D.2【解析】由题可知1,2a b c ===,12(2,0),(2,0)F F -,解法一:设(,)P m n ,∵||2OP =,故有224m n +=,又∵点P 在C 上,故有2213n m -=,联立方程2222413m n n m ⎧+=⎪⎨-=⎪⎩,解得3||2n =,故∆12PF F 的面积为12113||||43222n F F ⋅=⨯⨯=.解法二:∵||2OP =,故点P 在以F 1、F 2为直径的圆上,故PF 1⊥PF 2,则22212||||(2)16PF PF c +==,又∵12||||22PF PF a -==,即222121212||||||||2||||4PF PF PF PF PF PF -=+-=,∴12||||6PF PF =,∴∆12PF F 的面积为1211||||6322PF PF =⨯=.图A11【答案】B12.(立体几何)已知A ,B ,C 为球O 的球面上的三个点, 1O 为△ABC 的外接圆.若 1O 的面积为4π,1AB BC AC OO ===,则球O 的表面积为A .64πB .48πC .36πD .32π【解析】由题意可知, 1O 为的半径r =2,由正弦定理可知,2sin =ABr C,则12sin 2sin 6023==== OO AB r C r O 的半径2214R r OO =+=,∴球O 的表面积为24π64πR =.图A12【答案】A二、填空题:本题共4小题,每小题5分,共20分。


近五年高考文科数学试卷及答案解析(全国1卷)(2016年—2020年)说明:含有2016年—2020年的全国1卷高考文科数学试题以及答案详细解析(客观题也有答案详解)目录2020年普通高等学校招生全国统一考试文科数学(I卷)答案详解 (3)2020年普通高等学校招生全国统一考试文科数学(I卷) (19)2019年普通高等学校招生全国统一考试文科数学1卷 (29)2019年普通高等学校招生全国统一考试文科数学1卷答案详解 (39)2018年普通高等学校招生全国统一考试文科数学1卷 (50)2018年普通高等学校招生全国统一考试文科数学1卷答案详解 (60)2017年普通高等学校招生全国统一考试文科数学1卷 (71)2017年普通高等学校招生全国统一考试文科数学I卷答案详解 (81)2016年普通高等学校招生全国统一考试文科数学1卷 (93)2016年普通高等学校招生全国统一考试文科数学1卷答案详解 (103)2020年普通高等学校招生全国统一考试文科数学(I 卷)答案详解一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.(集合)已知合集{}2340A x x x =--<,{}4,1,3,5B =-,则A B = A.{}4,1- B.{}1,5C.{}3,5 D.{}1,3【解析】∵{}14A x x =-<<,∴{1,3}A B = .【答案】D2.(复数)若312z i i =++,则z =A.0 B.1C. D.2【解析】∵3i i =-,∴1z i =+,∴z 【答案】C3.(立体几何)埃及胡夫金字塔是古代世界建筑奇迹之一,它的形状可视为一个正四棱锥,以该四棱锥的高为边长的正方形面积等于该四棱锥一个侧面三角形的面积,则其侧面三角形底边上的高与底面正方形的边长的比值为A.514- B.512C.514+ D.512【解析】如图A3所示,设正四棱锥底面的边长为a ,则有22221212h am a h m ⎧=⎪⎪⎨⎛⎫⎪+= ⎪⎪⎝⎭⎩整理得22420m am a --=,令mt a=,则有24210t t --=,∴114t +=,214t -=(舍去),即14m a +=.图A3【答案】C4.(概率统计)设O 为正方形ABCD 的中心,在O,A ,B,C,D 中任取3点,则取到的3点共线的概率为A.15B.25C.12D.45【解析】如图A4所示,从O,A ,B,C,D 中任取3点的所有情况数为35C =10,取到的3点共线的情况有:AOC 、BOD ,共2种情况,所以所求的概率为51102==P.图A4【答案】A5.(概率统计)某校一个课外学习小组为研究某作物种子的发芽率y 和温度x (单位:C )的关系,在20个不同的温度条件下进行种子的发芽实验,由实验数据,)(i i x y i =(1,2,…,20)得到下面的散点图:由此散点图,在10C 至40C 之间,下面四个回归方程类型中最适宜作为发芽率y 和温度x 的回归方程类型的是A.y a bx=+ B.2y a bx =+ C.xy a be =+ D.ln y a b x=+【解析】根据散点图的趋势和已学函数图象可知,本题的回归方程类型为对数函数,故选D选项.【答案】D6.(解析几何)已知圆2260x y x +-=,过点(1,2)的直线被该圆所截得的弦的长度的最小值为A.1B.2C.3D.4【解析】222(3)3x y -+=,设直线方程为2(1)y k x -=-,∴20kx y k -+-=,∴圆心(3,0)到该直线的距离为d ==,∴2max 8d =,故弦的长度的最小值为2==.【答案】B7.(三角函数)设函数()cos()6f x x πω=+在[]ππ-,的图像大致如下图,则()f x 的最小正周期为A.109π B.76π C.43π D.32π【解析】∵函数过点4π,09⎛⎫- ⎪⎝⎭,∴4ππcos()=096x ω-+,∴4πππ=962x ω-+-,解得23=ω,∴()f x 的最小正周期为3π4π2==ωT .【答案】C8.(函数)设3log 42a =,则4a -A.116B.19C.18D.16【解析】∵33log 4log 42a a ==,∴2439a ==,∴11449a a -==.【答案】B9.(算法框图)执行右面的程序框图,则输出的n =A.17B.19C.21D.23【解析】①输入10n S ==,,得1S S n =+=,100S ≤成立,继续;②输入31n S ==,,得4S S n =+=,100S ≤成立,继续;③输入54n S ==,,得9S S n =+=,100S ≤成立,继续;……由上述规律可以看出,S 是一个以a 1=1为首项,d =2为公差的等差数列的前m 项和,且21n m =-,故有21(1)2m m m S ma d m -=+=.当2100m S m =>,即11n >时,程序退出循环,此时2121n m =-=.【答案】C10.(数列)设{}n a 是等比数列,且123+1a a a +=,2342a a a ++=,则678+a a a +=A.12B.24C.30D.32【解析】设{}n a 的公比为q ,∵234123(+)2a a a q a a a ++=+=,∴2q =,∴55678123+(+)232a a a q a a a +=+==.【答案】D11.(解析几何)设1F ,2F 是双曲线22:13y C x -=的两个焦点,O 为坐标原点,点P 在C 上且|OP |=2,则∆12PF F 的面积为A.72B.3C.52D.2【解析】由题可知1,2a b c ===,12(2,0),(2,0)F F -,解法一:设(,)P m n ,∵||2OP =,故有224m n +=,又∵点P 在C 上,故有2213n m -=,联立方程2222413m n n m ⎧+=⎪⎨-=⎪⎩,解得3||2n =,故∆12PF F 的面积为12113||||43222n F F ⋅=⨯⨯=.解法二:∵||2OP =,故点P 在以F 1、F 2为直径的圆上,故PF 1⊥PF 2,则22212||||(2)16PF PF c +==,又∵12||||22PF PF a -==,即222121212||||||||2||||4PF PF PF PF PF PF -=+-=,∴12||||6PF PF =,∴∆12PF F 的面积为1211||||6322PF PF =⨯=.图A11【答案】B12.(立体几何)已知A ,B ,C 为球O 的球面上的三个点, 1O 为△ABC 的外接圆.若 1O 的面积为4π,1AB BC AC OO ===,则球O 的表面积为A .64πB .48πC .36πD .32π【解析】由题意可知, 1O 为的半径r =2,由正弦定理可知,2sin =ABr C,则12sin 2sin 6023==== OO AB r C r O 的半径2214R r OO =+=,∴球O 的表面积为24π64πR =.图A12【答案】A二、填空题:本题共4小题,每小题5分,共20分。

近五年全国卷数学考点分布全国新课标近五年全国卷数学考点分布全国新课标的文章应由本人根据自身实际情况书写,以下仅供参考,请大家根据自身实际情况撰写。
近五年全国卷数学考点分布全国新课标数学是一门基础学科,对于高考来说,数学也是必考科目之一。
在全国新课标卷中,数学的考点分布是比较稳定的,近五年的考点分布如下:一、代数代数是数学中的一个重要分支,也是高考数学中的必考内容。
在近五年的全国新课标卷中,代数的考点主要集中在以下几个方面:1、集合与逻辑用语。
主要考查集合的基本概念、集合的交并补运算以及充分必要条件的判断。
2、不等式。
主要考查不等式的性质、一元一次不等式(组)的解法以及含有绝对值的不等式的解法。
3、函数与方程。
主要考查函数的定义域、值域、解析式以及函数的性质,同时也考查了解方程的方法,例如换元法、待定系数法等。
4、数列。
主要考查数列的基本概念、通项公式以及前n项和公式的计算。
同时也考查了等差数列和等比数列的性质和计算方法。
二、几何几何是数学中的另一个重要分支,也是高考数学中的必考内容。
在近五年的全国新课标卷中,几何的考点主要集中在以下几个方面:1、平面几何。
主要考查三角形的面积、周长、内切圆半径等计算,四边形的基本性质和判定定理,圆的基本概念和性质,以及直线与圆、圆与圆的位置关系等。
2、立体几何。
主要考查空间几何体的基本概念、性质和计算方法,例如表面积、体积的计算,角度、距离的计算等。
3、解析几何。
主要考查直线、圆、椭圆、双曲线和抛物线的性质和计算方法,例如方程的求解、交点、切线、法线等。
三、概率与统计概率与统计是数学中的一个重要分支,也是高考数学中的必考内容。
在近五年的全国新课标卷中,概率与统计的考点主要集中在以下几个方面:1、概率。
主要考查古典概型和几何概型的概率计算方法,条件概率、相互独立事件概率的计算方法等。
2、统计。
主要考查数据的收集、整理、分析和描述方法,例如平均数、中位数、众数、方差等统计量的计算方法,直方图、折线图等统计图的绘制方法等。
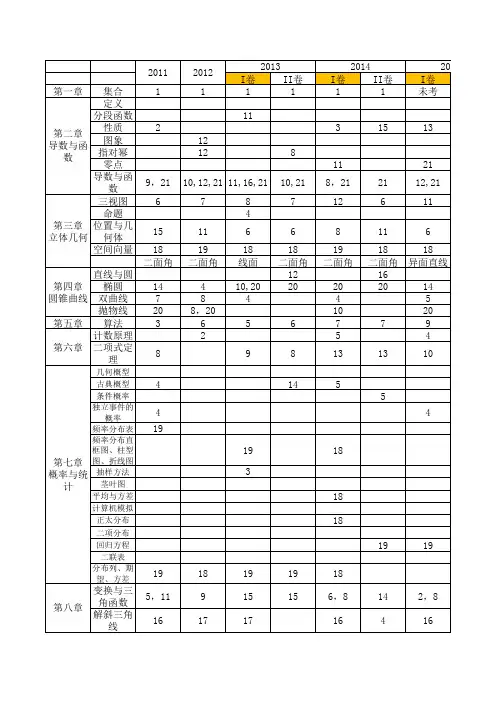
高考数学】近五年全国卷数学考点分布--全国新课标全国新课标2020数学考试涵盖了复数运算、集合交集、指数对数等基础知识,同时也考察了黄金分割、函数图象等高阶概念。
2019年考试同样涉及了这些基础知识,其中复数运算模、补集不等式、饼图信息、等差数列和、三次奇函数切线方程等内容也在考试范围内。
2018年考试重点考察了集合交集、复数运算模等内容。
2017年考试则着重考察了集合交集并集、几何概型、命题真假等知识点。
2016年考试则涉及了复数点象限参、集合并集、向量坐标垂直等基础知识,同时也考察了抛物线焦半径、线性回归方程等高阶概念。
在2020年的文科数学考试中,同样考察了复数运算、集合交集、指数对数等基础知识,同时也考察了黄金分割等高阶概念。
2019年考试同样涉及了集合交集、复数运算模等内容。
2018年考试则重点考察了集合交集,2017年考试则着重考察了集合交集并集、统计平均数中位数等知识点。
2016年考试则涉及了集合交集、复数相等求参等基础知识,同时也考察了饼图信息、椭圆离心率等高阶概念。
总体来说,这些年的数学考试都注重考察学生的基础知识,同时也会涉及到一些高阶概念。
学生在备考过程中需要注重基础知识的巩固,同时也需要了解高阶概念的应用。
XXX GraphsProgram FlowchartsCuboid Face DiagonalsAngle of XXXXXX DerivativesRangesPerpendicular VectorsXXX IdentitiesArea of Lines。
Circles。
and Planes7 XXX8 XXX9 Program Flowcharts10 XXX11 Properties of HyperbolasProgram FlowchartsEccentricity of HyperbolasSolving Trianglesds。
Extremums。
XXXXXX DerivativesCuboid Edge。
第二章 函数概念与基本初等函数函数与方程考点1 函数的零点与方程根的个数1. 【2020年高考天津卷9】已知函数3,0,(),0.x x f x x x ⎧=⎨-<⎩若函数2()()2()g x f x kx xk =--∈R 恰有4个零点,则k 的取值范围是( ) A .1,(22,)2⎛⎫-∞-+∞ ⎪⎝⎭ B .1,(0,22)2⎛⎫-∞- ⎪⎝⎭C .(,0)(0,22)-∞D .(,0)(22,)-∞+∞【答案】D【解析】注意到(0)0g =,所以要使()g x 恰有4个零点,只需方程()|2|||f x kx x -=恰有3个实根 即可,令()h x =()||f x x ,即|2|y kx =-与()()||f x h x x =的图象有3个不同交点.因为2,0()()1,0x x f x h x x x ⎧>==⎨<⎩, 当0k =时,此时2y =,如图1,2y =与()()||f x h x x =有2个不同交点,不满足题意; 当k 0<时,如图2,此时|2|y kx =-与()()||f x h x x =恒有3个不同交点,满足题意; 当0k >时,如图3,当2y kx =-与2yx 相切时,联立方程得220x kx -+=,令0∆=得280k -=,解得k =,所以k > 综上,k 的取值范围为(,0)(22,)-∞+∞,故选D .2. 【2019年高考浙江】已知,a b ∈R ,函数32,0()11(1),032x x f x x a x ax x <⎧⎪=⎨-++≥⎪⎩.若函数()y f x ax b =--恰有3个零点,则 A .a <–1,b <0 B .a <–1,b >0 C .a >–1,b <0 D .a >–1,b >0【答案】C【解析】当x <0时,y =f (x )﹣ax ﹣b =x ﹣ax ﹣b =(1﹣a )x ﹣b =0,得x =b1−a , 则y =f (x )﹣ax ﹣b 最多有一个零点;当x ≥0时,y =f (x )﹣ax ﹣b =13x 3−12(a +1)x 2+ax ﹣ax ﹣b =13x 3−12(a +1)x 2﹣b ,2(1)y x a x =+-',当a +1≤0,即a ≤﹣1时,y ′≥0,。
2020年数学新高考i卷考点分布第一部分:数与代数1. 整式与分式的运算1.1 整式的加减乘除运算规则1.2 分式的加减乘除运算规则1.3 合并同类项1.4 分式的化简与拆分2. 一元一次方程与不等式2.1 一元一次方程的解法2.2 一元一次不等式的解法2.3 一元一次方程与不等式的实际应用3. 二次函数与一元二次方程3.1 二次函数的性质及图像3.2 一元二次方程的解法3.3 二次函数与一元二次方程的实际应用4. 数列与数列的通项公式4.1 等差数列的概念及通项公式4.2 等比数列的概念及通项公式4.3 数列的求和公式5. 实数与复数5.1 实数的性质及表示方法5.2 复数的性质及表示方法5.3 实数与复数的运算规则第二部分:平面几何与空间几何6. 平面与空间中的直线与平面6.1 直线的性质及倾斜角计算6.2 平面的性质及法向量求解6.3 直线与平面的关系与交点计算7. 二维图形的性质与判定7.1 三角形的性质与判定7.2 四边形的性质与判定7.3 圆的性质与判定8. 空间中的向量运算8.1 向量的加法与减法8.2 向量的数量积与向量积8.3 向量的投影与模长计算9. 三维图形与空间向量9.1 立体图形的性质与计算9.2 空间中直线与面的位置关系9.3 空间向量的共线与垂直判定第三部分:概率与统计10. 概率的基本概念与计算10.1 随机事件的概念与性质10.2 概率的计算方法10.3 古典概型与几何概型的应用11. 统计与数据的分析11.1 数据的收集与整理11.2 数据的描述性统计11.3 数据的推断性统计12. 概率与统计的实际应用12.1 抽样调查与样本容量计算12.2 投资与风险的概率分析12.3 排列组合与概率计算的实际问题注:以上内容为2020年数学新高考i卷考点分布,考生需重点掌握各个考点的基本概念、性质及解题方法,灵活运用于各类数学问题中。
在考前复习中,建议根据自己的掌握情况有针对性地进行习题训练,加深对知识点的理解和应用能力的提升。
2016年高考全国课标Ⅰ卷数学试题分析诏安一中沈玉川自2004年以来,福建高考今年首次使用全国卷,2016年高考新课标Ⅰ卷数学试题,试卷结构、考点、题型与往年基本一致,延续了前几年的命题风格,保持了“总体稳定,稳中有变”的命题理念,理科数学难度总体适中,文科数学难度相对于福建卷略有提高,没有偏题怪题,大多是常见题型,但求解方法也是灵活多样;对于学生整体数学素质的要求相比去年有所提高,对于数学成绩不是很稳定的学生来说是个不小的挑战,可以说,今年的高考数学试卷经过前面几年的积累完成了质的飞跃。
一、对试卷整体评析2016年高考数学新课标全国Ⅰ卷遵循《课程标准》基本理念,严格贯彻《2016年全国统一高考考试大纲》基本要求,试卷的结构保持了新课程高考数学试卷的一贯风格,以能力立意,在多角度多层次地考查基础知识和基本技能的同时,关注数学的应用意识与创新意识,注重对考生数学思想和学科能力的考查。
整个试卷呈“由易到难,循序渐进”的趋势,难度合理,区分度较好,有利于高校选拔人才,依然体现了“以学生为本”,“在基础中考察能力”的要求。
1.注重基础性,覆盖全面重点突出2016年高考数学新课标Ⅰ卷对基础知识与基础技能的考察既注重全面,又突出重点,贴切教学实际,试卷所涉及的知识几乎覆盖了高中所学的全部重要内容,许多试题都是单一知识点或是最基础的知识交汇点上设置,例如理科第1题考查集合的关系与运算,第2题考查复数的概念与模,第3题、第15题考查等差数列与等比数列的基本运算,第4题考查几何概型,第13题考查平面向量的坐标运算,第14题考查二项展开式的系数,第17题考查正弦、余弦定理及三角形面积公式,这是和新课标数学“两年数列两年三角” 的命题规律完全吻合的,应该说是在预料当中;文科第3题考查考查古典概型,第4题考查余弦定理,第5题考查椭圆的几何性质,第6题考查三角函数图象的平移,第17题考查等差数列与等比数列的基本运算,这些都是课本中的问题,大部分属于常规题型,是学生在高三平时的训练中常见的类型,难度适中。