下载文档原格式
期中考试题一． 判断题。
（ R ）1、当x(t)为实信号时，其频谱与翻转频谱互为共轭。
（ R ）2、若信号x(t)的频谱为X(f)，则延迟信号x(t-5)的振幅谱将不发生变化。
（W ）3、若信号x(t)的频谱为X(f)，则X(t)的频谱为x(f)。
（ R ）4、若信号x(t)的频谱为X(f)，则x(t)cos(2πf0t)的频谱为(1/2)[X(f-f0)＋X(f ＋f0)]。
（ R ）5、若信号x(t)的频谱为X(f)，则x(－t)的频谱为X(－f)。
（ W ）6、信号x(n)=cos(n/7-π/3)为一周期信号。
二． 计算证明题。
1、 在[-2,2]上有一方波0,21,()2,11,0,1 2.t x t t t -≤<-⎧⎪=-≤≤⎨⎪<<⎩求它的傅氏级数。
（p11） 解：002212421000000,21,()2,11,0,1 2.4,1/411()20,1;2sin sin 220,;2lim 1,2sin sin 22.2i nti nf t n n n n n n t x t t t T f c x t e dt e dtT n c nnf n c nf n c nnf c nf n ππππππππππ-++---→-≤<-⎧⎪=-≤≤⎨⎪<<⎩======≠===∴==⎰⎰2、 求方波2,||4,()0,|| 4.t x t t <⎧=⎨>⎩的频谱。
（p14） 解：42242,||4,()0,|| 4.2sin 8()2.i ft i ftf t x t t f X x t e dt e dt f ππππ+∞+---∞-<⎧=⎨>⎩===⎰⎰3、 求信号sin ()tx t t ππ=的频谱。
（p20）解：1,||,sin 2()()0,||.sin 1/2,()()()1,||1/2,sin ()()0,||1/2.t f x t X f t f f X f f X t x f t t x t X f t t δπδδππδπππ<⎧=⇔=⎨>⎩∧==-⇔<⎧=⇔=⎨>⎩4、写出离散信号()2(3)3(3)(1)x n n n n δδδ=-+++-的数学表达式。
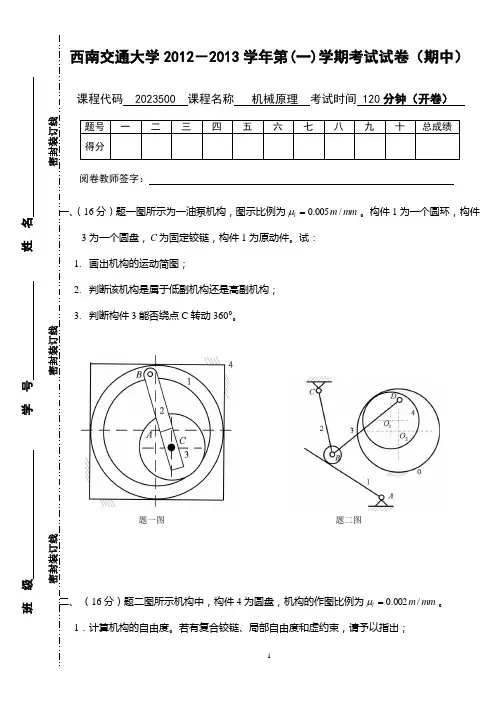
西南交通大学2012－2013学年第(一)学期考试试卷（期中）课程代码 2023500 课程名称 机械原理 考试时间 120分钟（开卷）阅卷教师签字：一、（16分）题一图所示为一油泵机构，图示比例为mm m l /005.0=μ。
构件1为一个圆环，构件3为一个圆盘，C 为固定铰链，构件1为原动件。
试： 1. 画出机构的运动简图；2. 判断该机构是属于低副机构还是高副机构；3. 判断构件3能否绕点C 转动360°。
二、 （16分）题二图所示机构中，构件4为圆盘，机构的作图比例为mm m l /002.0=μ。
1．计算机构的自由度。
若有复合铰链、局部自由度和虚约束，请予以指出； 2．确定机构在图示位置时，构件1与构件2之间的速度瞬心12P ； 3．画出机构的低副运动等效机构。
题一图 题二图班 级 学 号 姓 名密封装订线 密封装订线 密封装订线题三图题五图题四图三、（16分）题三图所示为一个连杆机构的示意图。
已知mm l mm l BC AB60 ,20==。
设计要求构件1为曲柄。
1.写出机构的邻接矩阵；2.试确定偏距e 的取值范围；3.在偏距e 的取值范围内任取一值，画出滑块3的极限位置；4.如果曲柄1为原动件，并且匀速转动，问当偏距e 取何值时，机构的行程速比系数达到最大？并给出行程速比系数的最大值max k四、 （16分）题四图所示机构。
已知机构中各个固定铰链点的坐标和各个构件的杆长，取构件1为原动件1、拆出机构中所包含的基本杆组，并判断机构的级别；2、现在要确定构件5的角运动，试按照求解顺序写出机构运动分析的位置方程，并简要说明如何求解其角速度和角加速度；3、利用构件2与机架0的速度瞬心02P ，画出当原动件1的转向如图中1ω所示时，铰链点E 在图示位置时的速度方向，进而标出构件4相对构件5的相对速度45v 的方向。
五、 （16分）题五图所示为一个摇块机构的示意图。
已知mm AC mm l AB40 ,10==。
数字信号处理试卷及答案1一、填空题（每空1分, 共10分）1．序列()sin(3/5)x n n π=的周期为 。
2．线性时不变系统的性质有 律、 律、 律。
3．对4()()x n R n =的Z 变换为 ，其收敛域为 。
4．抽样序列的Z 变换与离散傅里叶变换DFT 的关系为 。
5．序列x(n)=(1，-2，0，3；n=0，1，2，3), 圆周左移2位得到的序列为 。
6．设LTI 系统输入为x(n) ，系统单位序列响应为h(n)，则系统零状态输出y(n)= 。
7．因果序列x(n)，在Z →∞时，X(Z)= 。
二、单项选择题（每题2分, 共20分） 1．δ(n)的Z变换是（ ）A.1 B.δ(ω) C.2πδ(ω) D.2π 2．序列x 1（n ）的长度为4，序列x 2（n ）的长度为3，则它们线性卷积的长度是 （ ）A. 3 B. 4 C. 6 D. 73．LTI 系统，输入x （n ）时，输出y （n ）；输入为3x （n-2），输出为 （ ） A. y （n-2） B.3y （n-2） C.3y （n ） D.y （n ） 4．下面描述中最适合离散傅立叶变换DFT的是（ ）A.时域为离散序列，频域为连续信号B.时域为离散周期序列，频域也为离散周期序列C.时域为离散无限长序列，频域为连续周期信号D.时域为离散有限长序列，频域也为离散有限长序列5．若一模拟信号为带限，且对其抽样满足奈奎斯特条件，理想条件下将抽样信号通过 即可完全不失真恢复原信号（ ）A.理想低通滤波器 B.理想高通滤波器 C.理想带通滤波器 D.理想带阻滤波器 6．下列哪一个系统是因果系统（ ）A.y(n)=x (n+2) B. y(n)= cos(n+1)x (n) C. y(n)=x (2n) D.y(n)=x (- n)7．一个线性时不变离散系统稳定的充要条件是其系统函数的收敛域包括 （ ）A. 实轴B.原点C.单位圆D.虚轴8．已知序列Z变换的收敛域为｜z｜>2，则该序列为（）A.有限长序列 B.无限长序列 C.反因果序列 D.因果序列9．若序列的长度为M，要能够由频域抽样信号X(k)恢复原序列，而不发生时域混叠现象，则频域抽样点数N需满足的条件是( )A.N≥MB.N≤MC.N≤2MD.N≥2M10．设因果稳定的LTI系统的单位抽样响应h(n)，在n<0时，h(n)= ( )A.0B.∞C. -∞D.1三、判断题（每题1分, 共10分）1．序列的傅立叶变换是频率ω的周期函数，周期是2π。
数字信号处理试题及答案一、 填空题（30分，每空1分）1、对模拟信号（一维信号，是时间的函数）进行采样后，就是 离散时间 信号，再进行幅度量化后就是 数字 信号。
2、已知线性时不变系统的单位脉冲响应为)(n h ，则系统具有因果性要求)0(0)(<=n n h ，系统稳定要求∞<∑∞-∞=n n h )(。
3、若有限长序列x （n ）的长度为N ，h(n ）的长度为M ，则其卷积和的长度L为 N+M-1。
4、傅里叶变换的几种形式：连续时间、连续频率-傅里叶变换;连续时间离散频率—傅里叶级数；离散时间、连续频率—序列的傅里叶变换；散时间、离散频率—离散傅里叶变换5、 序列)(n x 的N 点DFT 是)(n x 的Z 变换在 单位圆上 的N 点等间隔采样。
6、若序列的Fourier 变换存在且连续，且是其z 变换在单位圆上的值，则序列x （n)一定绝对可和.7、 用来计算N ＝16点DFT ，直接计算需要__256___次复乘法,采用基2FFT 算法，需要__32__ 次复乘法 .8、线性相位FIR 数字滤波器的单位脉冲响应()h n 应满足条件()()1--±=n N h n h 。
9. IIR 数字滤波器的基本结构中， 直接 型运算累积误差较大； 级联型 运算累积误差较小； 并联型 运算误差最小且运算速度最高。
10. 数字滤波器按功能分包括 低通 、 高通 、 带通 、 带阻 滤波器.11. 若滤波器通带内 群延迟响应 = 常数，则为线性相位滤波器。
12. ()⎪⎭⎫ ⎝⎛=n A n x 73cos π的周期为 14 13. 求z 反变换通常有 围线积分法（留数法)、部分分式法、长除法等.14. 用模拟滤波器设计IIR 数字滤波器的方法包括：冲激响应不变法、阶跃响应不变法、双线性变换法。
15. 任一因果稳定系统都可以表示成全通系统和 最小相位系统 的级联。
二、选择题（20分，每空2分）1。
西南交通大学2012－2013学年第( 1 )学期期中考试试卷课程代码 3130100 课程名称 《数字信号处理A 》 考试时间 120分钟阅卷教师签字：一、选择题：（20分）本题共10个小题，每题回答正确得2分，否则得零分。
每小题所给答案中只有一个是正确的。
1.如题图所示的滤波器幅频特性曲线，可以确定该滤波器类型为( C )A.低通滤波器B.高通滤波器C.带通滤波器D.带阻滤波器2. 对5点有限长序列［1 3 0 5 2］进行向右1点圆周移位后得到序列( B ) A.［1 3 0 5 2］ B.［2 1 3 0 5］ C.［3 0 5 2 1］ D.［3 0 5 2 0］3.已知某序列Z 变换的收敛域为5>|z|>3，则该序列为（ D ）A.有限长序列B.右边序列C.左边序列D.双边序列 4.离散序列x(n)为实、偶序列，则其频域序列X(k)为：（ A ）。
A ．实、偶序列 B. 虚、偶序列 C ．实、奇序列 D. 虚、奇序列 5. 用窗函数法设计FIR 低通滤波器，当窗函数类型确定后，取窗的长度越长，滤波器的过渡带越 ( A )A. 窄B. 宽C. 不变D. 无法确定6. 当用循环卷积计算两个有限长序列的线性卷积时，若两个序列的长度分别是N 和M ，则循环卷积等于线性卷积的条件是：循环卷积长度（ A ）。
A.L≥N+M -1 B.L<N+M-1 C.L=N D.L=M7 序列3π()cos 5x n n ⎛⎫= ⎪⎝⎭的周期为( C )A. 3B. 5C. 10D. ∞8. 在基2 DIT —FFT 运算时，需要对输入序列进行倒序，若进行计算的序列点数N=16，倒序前信号点序号为8，则倒序后该信号点的序号为（ C ）。
班 级 学 号 姓 名密封装订线 密封装订线 密封装订线A. 8B. 16C. 1D. 49. 已知序列()()x n n δ=，其N 点的DFT 记为X(k)，则X(0)=（ B ）A ．N-1B ．1C . 0D . N 10. 关于双线性变换法设计IIR 滤波器正确的说法是（ D ） A ．双线性变换是一种线性变换 B ．不能用于设计高通和带阻滤波器C ．双线性变换法将线性相位的模拟滤波器映射为一个线性相位的数字滤波器D ．需要一个频率非线性预畸变 二、（10分）判断题（对以下各题的说法，认为对的在括号内填“〇”，认为错的在括号内填 “╳”；每小题2分，共10分）1．（〇）用基2时间抽取FFT 计算1024点DFT 的计算量不到直接计算量的二百分之一。
电子科技大学第一页（共4页）2011–2012学年第二学期期中考试试卷（参考答案）开课学院： 物理与电子信息学院 课程名称： 数字信号处理 考试形式：开卷，所需时间90分钟注意事项：1、教师出题时请勿超出边界虚线；2、学生答题前将密封线外的内容填写清楚，答题不得超出密封线；3、答题请用蓝、黑钢笔或圆珠笔。
一、填空（共20分，每空2分）1. 采样频率f s 对应于模拟角频率Ω= 2πf s ，对应于数字角频率ω= 2π 。
2. 如果8点序列x(n)的 16点DFT 为X 16(k)={X(0),X(1),X(2),……X(15)},则其8点DFT 为X 8(k)= {X(0), X(2), X(4), X(6), X(8), X(10), X(12), X(14)} 。
3. 对模拟信号进行数字信号处理，在A/D 转换器前信号要经过前置低通，该低通滤波器的作用是__防混叠滤波__;在D/A 转换器后信号要经过后置低通，该低通滤波器的作用是 防镜像滤波 。
4. 已知序列x (n )= a n u (n )的Z 变换收敛域为|Z|>|a |,序列y (n )= a n u (n -M)的Z 变换的收敛域为|Z|>|a |，则序列x(n)-y(n)的Z 变换的收敛域为 |Z|>0 。
5. 当单位脉冲响应分别为h 1(n )和h 2(n )的两个线性时不变离散时间系统级联（串联）时，其级联系统的单位脉冲响应为 h 1(n )*h 2(n ) ，系统函数为 H 1(z )H 2(z ) 。
6. 凡是因果系统，系统的极点只能在单位圆内。
（对或错）( 错 )7. 若某序列的傅立叶变换（DTFT ）存在，则其离散傅立叶变换（DFT ）也存在。
（对或错）( 对 )二、计算题（共20分，每题10分）1. 计算周期序列x[n]=cos(πn/M)的自相关序列R xx ，其中M 为正整数，并确定R xx 的周期。
西南交通大学2014－2015学年第( 1 )学期期中考试试卷课程代码 3130100 课程名称 《数字信号处理A 》 考试时间 120分钟题号 一 二 三 四 五 总成绩 得分阅卷教师签字：一、选择题：（30分）本题共10个小题，每题回答正确得3分，否则得零分。
每小题所给答案中只有一个是正确的。
1.如题图所示的滤波器幅频特性曲线，可以确定该滤波器类型为( C )A.低通滤波器B.高通滤波器C.带通滤波器D.带阻滤波器2. 对5点有限长序列［1 3 0 5 2］进行向右1点圆周移位后得到序列( B ) A.［1 3 0 5 2］ B.［2 1 3 0 5］ C.［3 0 5 2 1］ D.［3 0 5 2 0］3.已知某序列Z 变换的收敛域为5>|z|>3，则该序列为（ D ）A.有限长序列B.右边序列C.左边序列D.双边序列 4.离散序列x(n)为实、偶序列，则其频域序列X(k)为：（ A ）。
A ．实、偶序列 B. 虚、偶序列 C ．实、奇序列 D. 虚、奇序列 5. 用窗函数法设计FIR 低通滤波器，当窗函数类型确定后，取窗的长度越长，滤波器的过渡带越 ( A )A. 窄B. 宽C. 不变D. 无法确定6. 当用循环卷积计算两个有限长序列的线性卷积时，若两个序列的长度分别是N 和M ，则循环卷积等于线性卷积的条件是：循环卷积长度（ A ）。
A.L≥N+M -1 B.L<N+M-1 C.L=N D.L=M7 序列3π()cos 5x n n ⎛⎫= ⎪⎝⎭的周期为( C )A. 3B. 5C. 10D. ∞8. 在基2 DIT —FFT 运算时，需要对输入序列进行倒序，若进行计算的序列点数N=16，倒序前信号点序号为8，则倒序后该信号点的序号为（ C ）。
班 级 学 号 姓 名密封装订线 密封装订线 密封装订线A. 8B. 16C. 1D. 49. 已知序列()()x n n δ=，其N 点的DFT 记为X(k)，则X(0)=（ B ）A ．N-1B ．1C . 0D . N 10. 连续周期信号f （t ）的频谱)(ωj F 的特点是（ D ）。
数字信号处理试卷答案完整版一、填空题：每空1分,共18分1、 数字频率ω是模拟频率Ω对 的归一化,其值是 连续还是离散 ;2、 双边序列z 变换的收敛域形状为 ;3、 某序列的DFT 表达式为∑-==10)()(N n knMW n x k X ,由此可以看出,该序列时域的长度为 ,变换后数字频域上相邻两个频率样点之间的间隔是 ;4、 线性时不变系统离散时间因果系统的系统函数为252)1(8)(22++--=z z z z z H ,则系统的极点为 ；系统的稳定性为 ;系统单位冲激响应)(n h 的初值 ；终值)(∞h ;5、 如果序列)(n x 是一长度为64点的有限长序列)630(≤≤n ,序列)(n h 是一长度为128点的有限长序列)1270(≤≤n ,记)()()(n h n x n y *=线性卷积,则)(n y 为 点的序列,如果采用基FFT 2算法以快速卷积的方式实现线性卷积,则FFT 的点数至少为 _____点;6、 用冲激响应不变法将一模拟滤波器映射为数字滤波器时,模拟频率Ω与数字频率ω之间的映射变换关系为Tω=Ω;用双线性变换法将一模拟滤波器映射为数字滤波器时,模拟频率Ω与数字频率ω之间的映射变换关系为 或 ; 7、当线性相位FIR 数字滤波器满足偶对称条件时,其单位冲激响应)(n h 满足的条件为 ,此时对应系统的频率响应)()()(ωϕωωj j e H e H =,则其对应的相位函数为 ;8、请写出三种常用低通原型模拟滤波器 , , 二、判断题每题2分,共10分1、 模拟信号也可以与数字信号一样在计算机上进行数字信号处理,只要加一道采样的工序就可以了;2、 已知某离散时间系统为)35()]([)(+==n x n x T n y ,则该系统为线性时不变系统;3、 一个信号序列,如果能做序列的傅里叶变换DTFT ,也就能对其做DFT 变换;4、 用双线性变换法进行设计IIR 数字滤波器时,预畸并不能消除变换中产生的所有频率点的非线性畸变;5、 阻带最小衰耗取决于窗谱主瓣幅度峰值与第一旁瓣幅度峰值之比; 三、15分、已知某离散时间系统的差分方程为)1(2)()2(2)1(3)(-+=-+--n x n x n y n y n y系统初始状态为1)1(=-y ,2)2(=-y ,系统激励为)()3()(n u n x n =, 试求：1系统函数)(z H ,系统频率响应)(ωj e H ;2系统的零输入响应)(n y zi 、零状态响应)(n y zs 和全响应)(n y ;四、回答以下问题：（1） 画出按时域抽取4=N点基FFT 2的信号流图;（2） 利用流图计算4点序列)4,3,1,2()(=n x 3,2,1,0=n 的DFT ; （3） 试写出利用FFT 计算IFFT 的步骤;五、12分已知二阶巴特沃斯模拟低通原型滤波器的传递函数为1414.11)(2++=s s s H a试用双线性变换法设计一个数字低通滤波器,其3dB 截止频率为πω5.0=c rad,写出数字滤波器的系统函数,并用正准型结构实现之;要预畸,设1=T六、12分设有一FIR 数字滤波器,其单位冲激响应)(n h 如图1所示：图1试求：1该系统的频率响应)(ωj eH ；2如果记)()()(ωϕωωj j e H eH =,其中,)(ωH 为幅度函数可以取负值,)(ωϕ为相位函数,试求)(ωH 与)(ωϕ；3判断该线性相位FIR 系统是何种类型的数字滤波器 低通、高通、带通、带阻,说明你的判断依据;4画出该FIR 系统的线性相位型网络结构流图;答案 一1采样频率s f 连续连续 2圆环或空集 3 NMπ2 42,2121-=-=z z 不稳定 4)0(=h 不存在5 64+128-1＝191点 256 6)2tan(2ωT =Ω )2arctan(2T Ω=ω 7)1()(n N h n h --= ωωϕ21)(--=N8巴特沃什滤波器 、 切比雪夫滤波器 椭圆滤波器 二 XXXOX 三解：1系统函数为23223121)(22211+-+=+-+=---z z z z z z z z H系统频率响应232)()(22+-+===ωωωωωωj j j j e z j eee e z H eH j解一：2对差分方程两端同时作z 变换得)(2)(])2()1()([2])1()([3)(1221z X z z X z y z y z Y z z y z Y z z Y ---+=-+-++-+-即：)(231)21(231)2(2)1(2)1(3)(211211z X z z z z z y y z y z Y ------+-+++------=上式中,第一项为零输入响应的z 域表示式,第二项为零状态响应的z 域表示式,将初始状态及激励的z 变换3)(-=z zz X 代入,得零输入响应、零状态响应的z 域表示式分别为 23223121)(22211+-+-=+---=---z z z z z z z z Y zi3232323121)(22211-⋅+-+=-⋅+-+=---z zz z z z z z z z z z Y zs 将)(),(z Y z Y zs zi 展开成部分分式之和,得2413232)(2--+-=+-+-=z z z z z z z Y zi 32152812331232)(22-+--+-=-⋅+-+=z z z z z z z z z z Y zs 即 2413)(--+-=z z z z z Y zi 321528123)(-+--+-=z zz z z z z Y zs对上两式分别取z 反变换,得零输入响应、零状态响应分别为)(])2(43[)(k k y k zi ε-=)(])3(215)2(823[)(k k y k k zs ε+-=故系统全响应为)()()(k y k y k y zs zi +=)(])3(215)2(1229[k k k ε+-=解二、2系统特征方程为0232=+-λλ,特征根为：11=λ,22=λ； 故系统零输入响应形式为 k zi c c k y )2()(21+=将初始条件1)1(=-y ,2)2(=-y 带入上式得⎪⎪⎩⎪⎪⎨⎧=+=-=+=-2)41()2(1)21()1(2121c c y c c y zi zi 解之得 31=c ,42-=c , 故系统零输入响应为： k zi k y )2(43)(-= 0≥k 系统零状态响应为3232323121)()()(22211-⋅+-+=-⋅+-+==---z zz z z z z z z z z z X z H z Y zs 32152812331232)(22-+--+-=-⋅+-+=z z z z z z z z z z Y zs 即 321528123)(-+--+-=z zz z z z z Y zs对上式取z 反变换,得零状态响应为 )(])3(215)2(823[)(k k y k k zs ε+-=故系统全响应为)()()(k y k y k y zs zi +=)(])3(215)2(1229[k k k ε+-=四 解：1)0(x 1(x )2(x 3(x )0(X )1(X )2(X )3(Xkr001102W 02W 02W 12W k l001104W 04W 14W 2304W 04W 04W 24W 34W4点按时间抽取FFT 流图 加权系数2 ⎩⎨⎧-=-=-==+=+=112)2()0()1(532)2()0()0(00x x Q x x Q⎩⎨⎧-=-=-==+=+=341)3()1()1(541)3()1()0(11x x Q x x Q 1055)0()0()0(10=+=+=Q Q X 31)1()1()1(1140⋅+-=+=j Q W Q X 055)0()0()2(1240=-=+=Q W Q X j Q W Q X 31)1()1()3(1340--=+=即： 3,2,1,0),31,0,31,10()(=--+-=k j j k X 31对)(k X 取共轭,得)(k X *； 2对)(k X *做N 点FFT ； 3对2中结果取共轭并除以N; 五 解：1预畸2)25.0arctan(2)2arctan(2===ΩπωT T c c 2反归一划4828.241)2(414.1)2(1)()(22++=++==Ω=s s ss s H s H css a3 双线性变换得数字滤波器4112828.2)112(44828.24)()(1121121121111211++-⋅++-=++==----+-=-+--=--zz zz s s s H z H z z s zz T s2212211716.01)21(2929.0344.2656.13)21(4------+++=+++=z z z z z z4用正准型结构实现(n x )(n y六解：1)2,1,0,1,2()(--=n hωωωωωω4324)4()3()2()1()0()()(j j j j n nj j e h e h e h e h h en h eH ----=-++++==∑)()1(2223443ωωωωωωj j j j j j e e e e e e -------+-=--+=)]sin(2)2sin(4[)()(222222ωωωωωωωωωj j e e e e e e e j j j j j j j +=-+-=-----2)]sin(2)2sin(4[)]sin(2)2sin(4[)()22(22ωωωωωππωω+=+=--j jj j e eeeH)sin(2)2sin(4)(ωωω+=H , ωπωϕ22)(-=3)()sin(2)2sin(4)2sin(2)]2(2sin[4)2(ωωωωπωπωπH H -=--=-+-=- 故 当0=ω时,有)0()0()2(H H H =-=π,即)(ωH 关于0点奇对称,0)0(=H ；当πω=时,有))()(ππH H -=,即)(ωH 关于π点奇对称,0)(=πH 上述条件说明,该滤波器为一个线性相位带通滤波器; 4线性相位结构流图1-)(n x)(n y。
数字信号处理的技术考试试卷(附答案)数字信号处理的技术考试试卷（附答案）选择题（10分）1. 数字信号处理是指将连续时间信号转换为离散时间信号，并利用数字计算机进行处理。
这种描述表明数字信号处理主要涉及哪两个领域？- [ ] A. 数学和物理- [ ] B. 物理和电子工程- [x] C. 信号处理和计算机科学- [ ] D. 电子工程和计算机科学2. 数字滤波是数字信号处理的重要内容，其主要作用是：- [ ] A. 改变信号的频率- [x] B. 改变信号的幅度响应- [ ] C. 改变信号的采样率- [ ] D. 改变信号的量化级别3. 在离散时间信号处理中，离散傅里叶变换（Discrete Fourier Transform, DFT）和快速傅里叶变换（Fast Fourier Transform, FFT）有何区别？- [ ] A. DFT和FFT是完全相同的概念- [x] B. DFT是FFT的一种特殊实现- [ ] C. FFT是DFT的一种特殊实现- [ ] D. DFT和FFT无法比较4. 信号的采样率决定了信号的带宽，下面哪个说法是正确的？- [ ] A. 采样率越高，信号带宽越小- [ ] B. 采样率越低，信号带宽越小- [x] C. 采样率越高，信号带宽越大- [ ] D. 采样率与信号带宽无关5. 数字信号处理常用的滤波器包括：- [x] A. 低通滤波器- [x] B. 高通滤波器- [x] C. 带通滤波器- [x] D. 带阻滤波器简答题（20分）1. 简述离散傅里叶变换（DFT）的定义和计算公式。
2. 什么是信号的量化？请说明量化的过程。
3. 简述数字信号处理的应用领域。
4. 请解释什么是数字滤波器的频率响应。
5. 快速傅里叶变换（FFT）和傅里叶级数的关系是什么？编程题（70分）请使用Python语言完成以下程序编写题。
1. 编写一个函数`calculate_average`，输入一个由整数组成的列表作为参数，函数应返回列表中所有整数的平均值。
西南交通大学2012－2013学年第1学期期中考试试卷课程代码 2100505 课程名称 现代通信原理 考试时间 120分钟 一、判断题（正确填“T”，错误填“F”；每空2分，共10分）1. 信息与消息在概念上是一致的，即信息就是消息，消息就是信息。
2. 模拟调频抗噪声性能最好。
3. 作为数字基带信号其功率谱中一定含连续谱分量。
4. 在数字通信中，若无码间串扰，则误码率为0。
5. 对于调频信号，也可以用其上边带或下边带传输信息。
二、选择题（每题2分，共20分）（注意:答案写在下面表格内！）1. 数字通信系统的可靠性指标为( )A. 误码率B. 频带利用率C. 信号带宽D. 信息速率 2. 信号没有经过调制而直接送到信道中传输的通信方式，称之为( ) A.数字通信 B.模拟通信 C.基带传输 D.频带传输 3. 下列哪个描述不符合数字通信的特点( )A.抗干扰能力强B.差错不可控C.易加密D.占用频带宽班 级 学 号 姓 名密封装订线 密封装订线 密封装订线4.以下不能无限制地增大连续信道容量的方法是通过无限制地( )A.提高信噪比B.增大传输带宽C.提高信号功率D.减小噪声功率5.已知一个8进制信号的码元速率为4800波特，则其对应的信息速率是( )A. 14400bit/sB. 2400 bit/sC. 9600 bit/sD. 4800 bit/s6.设基带信号频谱如右图所示，以下模拟调制后的频谱中带载波的双边带调幅(常规AM)是A. B.C. D.7.属于非线性调制的是A) AM B) DSB C) VSB D) FM8.模拟调幅中DSB、SSB、VSB的已调信号所占用带宽大小关系为A．DSB＞SSB＞VSB Ｂ． SSB＞DSB＞VSB C．DSB＞VSB＞SSB Ｄ．VSB＞SSB＞DSB9.可以采用包络检波解调方式直接进行解调的数字调制方式是A．AM B．DSB C．SSB D．FM10.一个二进制数字信号码元时间长度为0.1μs，在传输过程中平均2.5秒产生一个错码，则其平均误码率近似为A) 5×10-6 B) 2×10-8 C) 2×10-7 D) 4×10-8 三、 填空题（每题2分，共30分）1. 加性高斯白噪声其中加性的含义是（噪声叠加在信号上），高斯的含义是（噪声的幅度服从高斯分布），白噪声的含义是（噪声的功率谱密度为常数）。
西南交通大学2012－2013学年第( 1 )学期期中考试试卷课程代码 课程名称 《数字信号处理A 》 考试时间 120分钟题号 一 二 三 四 五 六 七 八 九 十 总成绩 得分阅卷教师签字：一、选择题：（20分）本题共10个小题，每题回答正确得2分，否则得零分。
每小题所给答案中只有一个是正确的。
1.如题图所示的滤波器幅频特性曲线，可以确定该滤波器类型为( C )A.低通滤波器B.高通滤波器C.带通滤波器D.带阻滤波器2. 对5点有限长序列［1 3 0 5 2］进行向右1点圆周移位后得到序列( B ) A.［1 3 0 5 2］ B.［2 1 3 0 5］ C.［3 0 5 2 1］ D.［3 0 5 2 0］3.已知某序列Z 变换的收敛域为5>|z|>3，则该序列为（ D ）A.有限长序列B.右边序列C.左边序列D.双边序列 4.离散序列x(n)为实、偶序列，则其频域序列X(k)为：（ A ）。
A ．实、偶序列 B. 虚、偶序列 C ．实、奇序列 D. 虚、奇序列 5. 用窗函数法设计FIR 低通滤波器，当窗函数类型确定后，取窗的长度越长，滤波器的过渡带越 ( A )A. 窄B. 宽C. 不变D. 无法确定6. 当用循环卷积计算两个有限长序列的线性卷积时，若两个序列的长度分别是N 和M ，则循环卷积等于线性卷积的条件是：循环卷积长度（ A ）。
A.L≥N+M -1 B.L<N+M-1 C.L=N D.L=M7 序列3π()cos 5x n n ⎛⎫= ⎪⎝⎭的周期为( C )A. 3B. 5C. 10D. ∞8. 在基2 DIT —FFT 运算时，需要对输入序列进行倒序，若进行计算的序列点数N=16，倒序前信号点序号为8，则倒序后该信号点的序号为（ C ）。
班 级 学 号 姓 名密封装订线 密封装订线 密封装订线A. 8B. 16C. 1D. 49. 已知序列()()x n n δ=，其N 点的DFT 记为X(k)，则X(0)=（ B ）A ．N-1B ．1C . 0D . N 10. 关于双线性变换法设计IIR 滤波器正确的说法是（ D ） A ．双线性变换是一种线性变换 B ．不能用于设计高通和带阻滤波器C ．双线性变换法将线性相位的模拟滤波器映射为一个线性相位的数字滤波器D ．需要一个频率非线性预畸变 二、（10分）判断题（对以下各题的说法，认为对的在括号内填“〇”，认为错的在括号内填 “╳”；每小题2分，共10分）1．（〇）用基2时间抽取FFT 计算1024点DFT 的计算量不到直接计算量的二百分之一。
2．（〇）用DFT 进行频谱分析时，为保证能分辨由两个功率相同频率相近的单频信号合成的信号中这两个频率，在采样频率满足奈奎斯特定理的情况下需要足够多的采样点数。
3．（╳）对于线性移不变离散系统，当输入单一数字频率为ω0的正弦序列时，输出序列的频谱中一定包含ω0及ω0的谐波成分。
4．（〇）在利用原型模拟滤波器设计IIR 滤波器时，在相同的频率设计指标下，与切比雪夫原型低通滤波器相比，巴特沃兹原型低通滤波器通常需要更高的阶数。
5．（╳）调整FIR 或IIR 滤波器的频率响应都可通过调整其零点和极点位置来完成。
三、（15分）某因果系统的差分方程为y(n)–0.8 y(n －1) + a y(n －2) = x(n)，已知该系统的其中一个极点为0.3。
（1）（3分）求参数a 的值；（2）（3分）求系统所有的零、极点，并画出零、极点分布图； （3）（2分）判断该系统的稳定性；（4）（4分）画出由两个一阶系统级联的结构流图； （5）（3分）求该系统的冲激响应h(n)。
解：（1）根据系统差分方程，两边取Z 变换，可得系统函数为H(z)=z 2/(z 2-0.8z+a)因0.3为系统极点，故当z=0.3时，系统函数分母为0,即0.32-0.8x0.3+a=0,得a=0.15;(2) 根据系统函数H(z)=z 2/(z 2-0.8z+0.15),令分子为零，可得系统在z=0为二阶零点；令分母为零，在z=0.5获得另一个极点。
系统零机分布图如下：（3）由于系统是因果的，并且所有极点在单位圆内，故系统BIBO 稳定； （4）对系统函数分解成部分分式之积： H(z)=1/(1-0.3z -1)·1/(1-0.5z -1) 系统有的两个一阶网络的级联流图为)(n x )(n y 1-z 1-z 3.05.0（5）由于系统是因果的，其系统函数H(z)收敛域为以离原点最远的极点为半径的圆外区域，H(z)=z 2/(z 2-0.8z+0.15)= -0.15/(1-0.3z -1)+2.5/(1-0.5z -1)，|z|>0.5。
利用部分分式分解的方法，可知冲激响应为 h(n)=[-1.5(0.3)n +2.5(0.5)n ]u(n)四、（20分）若{}()3,2,1,2,1,2,05x n n =≤≤，1． 求序列()x n 的6点DFT ，即()X k 的值；2． 若)()]([)(26k X W n g DFT k G k ==，试确定6点序列()g n 的值； 3．求()()()l y n x n x n =*的值；4． 若()()()c y n x n x n =⑨ ，求()c y n 的值。
解：1.56023456666623266666()()32223222234cos 2cos 2(1)33[11,2,2,1,2,2]05,nkn k k k k k k k k k k kX k x n W W W W W W W W W W W k k k ππ=--==+++++=+++++=+++-=-≤≤∑2.72}212123{)2()()()]([)()2(652665026≤≤=-====--=-=∑∑n ，，，n x W k X W W k X k X W IDFT n g kn k k nk k k ，，3. 5()()*()()(){9,12,10,16,15,20,14,8,9,4,4}l m y n x n x n x m x n m ===-=∑4. 89990()()(())()(9)(){13,16,10,16,15,20,14,8,9}09c l m q y n x m x n m R n y n q R n n +∞==-∞⎡⎤=-=+⎢⎥⎣⎦=≤≤∑∑五、（15分）设FIR 滤波器的系统函数为)9.01.29.01(101)(4321----++++=z z z z z H 。
（1）求出该滤波器的单位取样响应)(n h 。
（2） 试判断该滤波器是否具有线性相位特点。
（3）求出其幅频响应函数和相频响应函数。
（4）如果具有线性相位特点，试画出其线性相位型结构，否则画出其直接型结构图。
解：1．∑∞-∞=-=nnznhzH)()(Θ4}1.009.021.009.01.0{)4(1.0)3(09.0)2(21.0)1(09.0)(1.0)(≤≤=-+-+-+-+=∴nnnnnnnhδδδδδ2．∴--=，nNhnh)1()(Θ该滤波器具有线性相位特点3．)9.01.29.01(101)()(432ωωωωωωjjjjezj eeeezHeH j----=++++==Θ)(2222)()21.0cos18.02cos2.0()21.0218.022.0(ωθωωωωωωωωωjjjjjjjeHeeeeee=++=++⨯++⨯=----幅频响应为21.0cos18.02cos2.0)(++=ωωωH相频响应为ωωθ2)(-=4．其线性相位型结构如右图所示。
4分六、（20分）设一个实际序列{}{}3,2,1,0]3[],2[],1[],0[][==xxxxnx，（1）请画出序列长度N=4时的基2按时间抽取FFT（DIT-FFT）计算流图，（输入序列为倒序，输出序列为自然顺序）。
（2）利用以上画出的计算流图求该有限长序列的DFT，即3,2,1,0],[=kkX。
（请按要求做，直接按DFT定义计算不得分）。
（3）若{}()(0),0,(1),0,(2),0,(3),0y n x x x x={}0,0,1,0,2,0,3,0=，使用最少的运算量求(),07Y k k ≤≤按DFT 定义直接计算不得分。
（提示：利用时域抽取法原理） 解（3）780332(21)8800332(21)8800340()()(2)(21)()(21)()()((21)0)0,1,...,7nkn rkr kr r rkr kr r rk r Y k y n W y r W y r W x r W y r W x r W X k y r k =+==+=====++=++==+==∑∑∑∑∑∑因当k=0,,1,2,3,Y(k)=X(k);当k=4,,5,6,7,利用DFT 的圆周性，Y(k)=Y(4+k ’)=X(4+k ’)=X(k ’),k ’=0,1,2,3;故 (){6,22,2,22,6,22,2,22}Y k j j j j =-+----+---[0]0x =[0]6X=[2]x =[1]x =[3]x =01N w =N[1]22j=-+[2]2X =-[3]22X j=--。
