测量不确定度评定记录_单次1

1.3测量不确定度的评定由于始终存在于测量过程中的随机误差影响和不可能完全消除或修正的系统误差影响，任何实际的测量都不可能获得被测量的真值，即测量结果总是不能准确确定的。

测量不确定度的评定就是要决定测量结果的不确定程度及其相应的置信概率，即给出一定置信概率的测量不确定度。

1.3.1 标准不确定度的A 类评定标准不确定度的A 类评定是对由重复性测量引起的不确定度分量进行评定。

对被测量X ，在重复性条件下进行n 次独立重复观测，观测值为i x （n ,,,i ⋅⋅⋅=21），算术平均值x 为∑==ni i x n x 11 （1.3.1） )x (s i 为单次测量的实验标准差，由贝塞尔公式计算得到112--=∑=n )x x ()x (s n i i i （1.3.2） )x (s 为平均值的实验标准差，其值为n )x (s )x (s i = （1.3.3）在某物理量的观测值中，若系统误差已消除或可以忽略不计，只存在随机误差，则观测值散布在其期望值附近。

当取若干组观测值，它们各自的平均值也散布在期望值附近，但比单个观测值更靠近期望值。

也就是说，多次测量的平均值比一次测量值更准确，随着测量次数的增多，平均值收敛于期望值。

因此，通常以样本的算术平均值作为被测量值的估计（即测量结果），以平均值的实验标准差)x (s 作为测量结果的标准不确定度，即A 类标准不确定度。

n /)x (s )x (u i = （1.3.4） 观测次数n 充分多，才能使A 类不确定度的评定可靠，一般认为n 应大于6。

但也要视实际情况而定，当该A 类不确定度分量对合成标准不确定度的贡献较大时，n 不宜太小，反之，当该A 类不确定度分量对合成标准不确定度的贡献较小时，n 小一些关系也不大。

1.3.2标准不确定度的B 类评定B 类不确定度主要来自于各种不同类型的仪器、不同的测量方法、方法的不同应用以及测量理论模型的不同近似等方面。

因此，B 类不确定度的评定主要从以上几个方面获得信息。

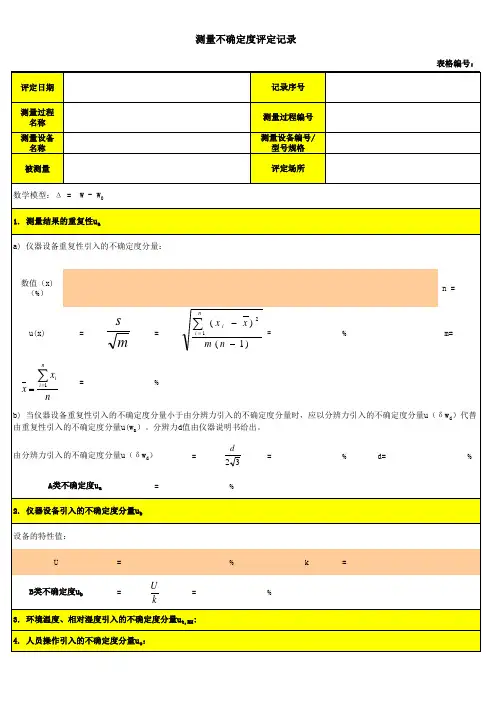
文件制修订记录对公司在体系中的测量设备的计量确认过程和测量过程控制的测量不确定度进行评定，使之符合预期的不确定度要求，确保测量结果的正确。

2.0适用范围本程序适用于在进行计量确认过程和测量过程策划或实施测量过程，及在使用测量结果时对测量不确定度进行分析。

有关人员在选用测量设备和测量方法时也可参照本程序。

3.0定义3.1测量不确定度：表征合理地赋予被测量之值的分散性。

3.2标准不确定度：以标准差表示的测量不确定度。

3.3 A类标准不确定度：用对观测列进行统计分析的方法来评定不确定度。

3.4 B类标准不确定度：用不同于对观测列进行统计分析的方法来评定标准不确定度。

4.0职责4.1各单位负责本单位实施的测量过程的测量不确定度评定；4.2质检部负责监督、考核各单位测量不确定度的评定工作。

5.0工作流程5.1测量不确定度评定过程5.1.1过程识别：测量不确定度评定过程的输入是国家法规、规范、统计数据、测量设备的证书(或报告)、测量方法、测量环境条件、测量人员素质等；输出是测量不确定度报告；其活动是对测量不确定度分量的分析、合成及扩展不确定度计算。

5.1.2测量管理体系覆盖的计量确认过程、关键测量过程的测量不确定度评定，在测量管理体系的运行过程中应不断完善。

5.1.3各部门应记录测量不确定度的评价。

确定测量不确定度的记录时，可对类似形式的测量设备给予一个通用的陈述，并同时对每个独立的测量过程所特有的变化给出说明。

5.1.4测量不确定度分析应在测量设备和测量过程的确认有效前完成。

5.1.5根据测量过程的重要程度的不同，测量不确定度的评定可以采用不同的方法进行评定。

对于使用要求较低的测量设备，其测量结果的不确定度可采用简化方法进行评定。

5.1.6测量不确定度评定的基本方法执行《测量不确定度评定与表示》的有效版本。

5.1.6.1确定不确定度的来源，一般从五个方面来分析：➢试验人员的因素；➢测量仪器的因素；➢环境条件的因素；➢试验方法的因素；➢被测量本身的因素。

仪器仪表测量不确定度评定方法作者：汪树青韦邦跃吴勇王亮来源：《电子技术与软件工程》2019年第10期摘要：针对计量校准中对实验数据后续处理的复杂性问题，主要是不确定度的评定方法进行研究，提出采用相对不确定度的评定方法。

在基于示值误差型计算模型下，进行测量不确定度评定方法分析，以数字多用表为例进行说明。

[关键词]计量学示值误差测量不确定度相对测量不确定度数据处理评定方法1引言测量不确定度指对测量结果的可信性、有效性的不能确定的程度，用来表征测量结果与真值的接近程度。

以计量校准中常用的示值误差型仪器仪表为例，结合其计量过程中使用的数学模型进行理论推导，得到其相对不确定度的计算模型。

以数字多用表代表同类型被检仪器仪表，以多功能校准仪为校准装置，进行计量校准试验、数据处理及不确定度评定。

2示值误差模型测量数学模型是用数学的函数形式描述测量的物理过程，是测量不确定度评定工作的基础。

计量校准工作中，示值误差型是常用的数据处理模型之一，其示值误差数学模型表达式如下：式中，y为被检仪表示值，yo为标准多功能源示值，△y为被检仪表示值误差。

上式中，y和yo互不相关时，由测量不确定度传递公式，有式中，u（△y）为合成标准不确定度，u（y）为被检仪器仪表A类标准不确定度，u（yo）为标准多功能源不确定度。

上式中，等号两边同除以y，得到注意到，计量校准中y和yo数值接近，即y=yo，则有上式中，分别表示被检仪表、标准多功能源的相对不确定度，为示值误差相对于被检仪表示值y的相对不确定度。

3输入量的相对不确定度评定3.1重复性测量引入的相对不确定度计算对于被校仪表而言，在相同条件下，重复测量n次，测量得到的结果的平均值为根据贝塞尔计算公式，单次测量值的实验标准偏差为重复性测量标准不确定度为重复性测量相对不确定度可表示为注意到重复测量n次后，y;与y近似相等，有y=y，则3.2标准源引入的相对不确定度计算多功能校准仪为校准装置，分辨率比被校仪表高一个甚至几个数量级，因此可以忽略此项不确定度。

多参数监护仪的计量检定注意事项及测量不确定度评定摘要：多参数监护仪是医疗卫生单位用于监测病人生命体征参数的一种计量器具，监测项目一般包括心电、无创血压、血氧、呼末二氧化碳等多种人体生理参数。

多参数监护仪为临床医生提供必需的病人生命体征参数，直接指导医生的治疗方案，其检定结果的可靠、客观与准确，直接影响临床疗效。

多参数监护仪属于强制检定计量器具，用于医疗卫生方面的多参数监护仪，应申请周期检定，从而保障医疗质量。

因此，加强对多参数监护仪的计量检定具有重要意义。

下面按多参数监护仪不同参数叙述计量检定注意事项及测量不确定度评定。

关键词：多参数监护仪；强制检定；心电；无创血压；血氧；呼末二氧化碳一、多参数监护仪的计量检定注意事项（一）心电参数计量检定注意事项电压测量误差、幅频特性检定一般在监护仪的Ⅱ导联进行测量，待波形满一屏并稳定后，冻结波形，选取屏幕水平中线位置的方波信号，用钢直尺测量其上升沿幅值长度，必要时可用读数放大器辅助读数，上下波形宽度只计入一次。

（二）无创血压参数计量检定注意事项用医用橡胶管和三通把监护仪、袖带及多参数监护仪检定装置连接起来组成检定系统。

将监护仪的袖带卷扎在一个圆柱体上，圆柱体直径为（70~102） mm，其松紧程度以能刚好插入一指为宜。

松紧程度不同会影响检定效果，过紧袖带容易崩开，过松则压力不稳定。

多参数监护仪无创血压平时工作模式为动态压力，进行静态压力和气密性检定时，需要将多参数监护仪设置调至静态压力测量模式。

大多数监护仪进入静态压力测量模式操作步骤为按下主菜单按钮，选择机器维护、厂家维护、输入密码、（密码可向监护仪生产厂家询问）进入维护模式。

选择 NIBP 校准选项，进入静态压力测量模式。

测量完静态压力后，点击停止校准，退出静态压力测量模式，则恢复为动态压力工作模式。

（三）血氧参数计量检定注意事项多参数监护仪的血氧夹应正确夹在多参数监护仪检定装置的信号接收器上，血氧夹发射红光应与信号接收器的接收面对应，这时检定装置屏幕显示有信号，反之没有信号，信号强弱可移动血氧夹进行微调，尽量让信号接近满格。

标准不确定度A类评定的实例【案例】对一等活塞压力计的活塞有效面积检定中,在各种压力下，测得10次活塞有效面积与标准活塞面积之比l （由l的测量结果乘标准活塞面积就得到被检活塞的有效面积)如下：0。

250670 0。

250673 0.250670 0。

250671 0.250675 0。

250671 0。

250675 0.250670 0。

250673 0。

250670问l 的测量结果及其A 类标准不确定度。

【案例分析】由于n =10, l 的测量结果为l ,计算如下∑===n i i .l n l 125067201 由贝塞尔公式求单次测量值的实验标准差()612100521-=⨯=--=∑.n l l )l (s n i i由于测量结果以10次测量值的平均值给出，由测量重复性导致的测量结果l 的A 类标准不确定度为610630-=⨯=.)l (u n )l (s A 【案例】对某一几何量进行连续4次测量,得到测量值:0。

250mm 0.236mm 0.213mm 0。

220mm ，求单次测量值的实验标准差。

【案例分析】由于测量次数较少,用极差法求实验标准差.)()(i i x u CR x s ==式中，R-—重复测量中最大值与最小值之差；极差系数c及自由度ν可查表3-2表3-2极差系数c及自由度ν查表得c n =2.06mm ../mm )..()x (u CR )x (s i i 018006221302500=-=== 2)测量过程的A 类标准不确定度评定对一个测量过程或计量标准，如果采用核查标准进行长期核查，使测量过程处于统计控制状态，则该测量过程的实验标准偏差为合并样本标准偏差S P 。

若每次核查时测量次数n 相同，每次核查时的样本标准偏差为Si ,共核查k 次，则合并样本标准偏差S P 为k s s ki ip ∑==12此时S P 的自由度ν=（n —1）k .则在此测量过程中，测量结果的A 类标准不确定度为 n S A P u '=式中的n '为本次获得测量结果时的测量次数。

测量不确定度的评估方法发布日期：2009-12-29 来源：原创北京医院卫生部临床检验中心周琦李小鹏徐建平谢伟李少男杨振华测量不确定度(uncertainty of measurement) 定义为表征合理地赋予被测量之值的分散性，与测量结果相联系的参数。

被测量之值的最佳估计值是测量结果，常用平均值表示。

参数可以是标准偏差、标准偏差的倍数或说明了置信水准区间的半宽度。

标准不确定度（standard uncertainty）是以标准偏差表示的测量不确定度，合成标准不确定度（combined standard uncertainty）是各标准不确定度分量的合成。

扩展不确定度(expanded uncertainty）是确定测量结果区间的量，合理赋予被测量之值分布的大部分可望含于此区间。

测量不确定度评价的步骤和算法如下：一、确定被测量注明被测量和被测量所依赖的输入量，如被测数量、常数和校准标准值等。

二、建立数学模型被测量Y和所有各影响量X i（i=1，2，•••，n）之间的具体函数关系，一般表达形式为Y=f（X1，X2，•••，X n）。

若被测量Y的估计值是y，输入量Xi的估计值是x i，则表达形式是y=f(x1，x2，•••，x n）。

三、求测量数据的最佳估计值最佳估计值的确定大体上可分为两类，一类是通过实验测量得到，另一类是通过信息来源等获得。

四、列出不确定度的来源在实践中，测量不确定度的典型来源有1. 取样；2. 存储条件；3. 仪器的影响；4. 试剂纯度；5. 假设的化学反应定量关系；6. 测量条件；7. 样品的影响；8. 计算影响；9. 空白修正；10. 操作人员的影响；11. 随机影响。

五、标准不确定度分量的确定被测量y的不确定度取决于各输入量最佳估计值xi的不确定度。

有A类评定（type A evaluation of uncertainty）和B类评定(type B evaluation of uncertainty)。

测量不确定度评定程序1目的对测量不确定度进行合理评定，确保检验检测报告结果的准确性，特制定本程序。

2范围对测量结果的不确定度评定过程管理。

3定义3.1测量不确定度：根据所用到的信息，表征赋予被测量值分散性的非负参数。

3.2标准不确定度：以标准偏差表示的测量不确定度。

3.3合成标准不确定度：由在一个测量模型中各输入量的标准测量不确定度获得的输出量的标准测量不确定度。

3.4扩展不确定度：合成标准不确定度与一个大于1的数字因子的乘积。

4职责4.1计量室提供本中心不确定度评定的相关信息。

4.2检测室负责对检验检测结果的不确定度评定。

4.3项目室负责本程序在本室的实施。

5 工作流程图本页此处无正文6程序要点6.1由测量所得的赋予被测量的值称为测量结果。

6.2测量结果仅仅是被测量的近似估计，完整的测量结果应当附有定量的不确定度说明。

6.3测量不确定度的来源在实践中，测量不确定度可能来源于以下10个方面：a.被测量的定义不完整；b.实现被测量的定义的复现不理想；c.取样的代表性不够，即被测量的样本不能代表所定义的被测量；d.对测量过程受环境影响的认识不足，或对环境条件的测不完善；e.模拟仪器的人员读数偏移；f.测量仪器的计量性能（如最大允许误差、灵敏度、鉴别力、分辨力、死区及稳定性等）的局限性即导致仪器的不确定度；G.测量标准或标准物质提供的标准值的不确定度；h.引用的常数或其他参数的不准确；i.测量方法和测量程序中的近似和假设；j.在相同的条件下，被测量重复观测值的变化。

6.4很多情况下，被测量Y不能直接测得，而是由N个其他量X1，X2，…，X N通过广义的函数关系f确定Y=f（X1，X2，…，X N）式（28-1）测量结果，即输出估计值y由输入估计值x1，x2，…，x n代入上式得到，即：y=f（x1，x2，…，x n）式（28-2）该表达式为广义的函数关系，其描述了一个测量过程，它应包含对测量过程有明显贡献的所有的量（包含环境、人员、设备、方法等多种因素）。

测量数据不确定度的评定在分析和确定测量结果不确定度时，应使测量数据序列中不包括异常数据。

即应先对测量数据进行异常判别，一旦发现有异常数据就应剔除。

因此，在不确定度的评定前均要首先剔除测量数据序列中的坏值。

1・A类标准不确定度的评定A类标准不确定度的评定通常可以采用下述统计与计算方法。

在同一条件下对被测参量X进行n次等精度测量,测量值为Xi(i=1,2,•…n)。

该样本数据的算术平均值为X=X的实验标准偏差(标准偏差的估计值)可用贝塞尔公式计算式中，冷(X)为实验标准偏差。

用疋作为被测量X测量结果的估计值，则A类标准不确定度uA为际站七佔(1)2•标准不确定度的B类评定方法当测量次数较少，不能用统计方法计算测量结果不确定度时，就需用B类方法评定。

对某一被测参量只测一次,甚至不测量（各种标准器）就可获得测量结果，则该被测参量所对应的不确定度属于B类标准不确定度，记为uB o B类标准不确定度评定方法的主要信息来源是以前测量的数据、生产厂的产品技术说明书、仪器的鉴定证书或校准证书等。

它通常不是利用直接测量获得数据，而是依据查证已有信息获得。

例如：①最近之前进行类似测试的大量测量数据与统计规律；②本检测仪器近期性能指标的测量和校准报告；③对新购检测设备可参考厂商的技术说明书中的指标；④查询与被测数值相近的标准器件对比测量时获得的数据和误差。

应说明的是，B类标准不确定度uB与A类标准不确定度uA同样可靠，特别是当测量自由度较小时，uA反而不如uB可靠。

B类标准不确定度是根据不同的信息来源，按照一定的换算关系进行评定的。

例如，根据检测仪器近期性能指标的测量和校准报告等，并按某置信概率P评估该检测仪器的扩展不确定度Up，求得Up的覆盖因子k则B类标准不确^（耳竺一逅业）（3）定度uB等于扩展不确定度Up除以覆盖因子k,即uB（X）=Up（X）/k（2）【例1】公称值为100g的标准砝码M,其检定证书上给出的实际值是100.0002.349，并说明这一值的置信概率为0.99的扩展不确定度是0.000120g，假定测量数据符合正态分布。

测量结果的评定和不确定度测量的目的是不但要测量待测物理量的近似值，而且要对近似真实值的可靠性做出评定（即指出误差范围），这就要求我们还必须掌握不确定度的有关概念。

下面将结合对测量结果的评定对不确定度的概念、分类、合成等问题进行讨论。

一、不确定度的含义在物理实验中，常常要对测量的结果做出综合的评定，采用不确定度的概念。

不确定度是“误差可能数值的测量程度”，表征所得测量结果代表被测量的程度。

也就是因测量误差存在而对被测量不能肯定的程度，因而是测量质量的表征，用不确定度对测量数据做出比较合理的评定。

对一个物理实验的具体数据来说，不确定度是指测量值（近真值）附近的一个范围，测量值与真值之差（误差）可能落于其中，不确定度小，测量结果可信赖程度高；不确定度大，测量结果可信赖程度低。

在实验和测量工作中，不确定度一词近似于不确知，不明确，不可靠，有质疑，是作为估计而言的；因为误差是未知的，不可能用指出误差的方法去说明可信赖程度，而只能用误差的某种可能的数值去说明可信赖程度，所以不确定度更能表示测量结果的性质和测量的质量。

用不确定度评定实验结果的误差，其中包含了各种来源不同的误差对结果的影响，而它们的计算又反映了这些误差所服从的分布规律，这是更准确地表述了测量结果的可靠程度，因而有必要采用不确定度的概念。

二、测量结果的表示和合成不确定度在做物理实验时，要求表示出测量的最终结果。

在这个结果中既要包含待测量的近似真实值x ，又要包含测量结果的不确定度σ，还要反映出物理量的单位。

因此，要写成物理含意深刻的标准表达形式，即 σ±=x x （单位）式中x 为待测量；x 是测量的近似真实值,σ是合成不确定度，一般保留一位有效数字。

这种表达形式反应了三个基本要素：测量值、合成不确定度和单位。

在物理实验中，直接测量时若不需要对被测量进行系统误差的修正，一般就取多次测量的算术平均值x 作为近似真实值；若在实验中有时只需测一次或只能测一次，该次测量值就为被测量的近似真实值。

测量结果不确定度评定步骤1．明确被测量，尽可能用方框图说明测量方法2．建立数学模型（或称测量模型）在实际测量中，被测量Y（输出量）不能直接得到。

而是由N个其他量（输入量）通过函数关系来确定，即在测量不确定度评定中，所有的测量值均应是测量结果的最佳估计值（即对所有测量结果中系统效应的影响均应进行修正），Y和X的最佳估计值为和，这时，由此，的不确定度是的不确定度来源。

关于数学模型的几点说明：①数学模型不是唯一的。

如果采用不同的测量方法和测量程序，就可能有不同的模型，如一个随温度t变化的电阻器两端的电压为V，在温度时的电阻为，电阻器的温度系数为，则电阻器的损耗功率（输出量）为超出此范围的均能出厂。

比较容易理解，被测量以均匀分布落在内。

②数字式仪表分辨力是此类仪表示值不确定度的组成之一。

输入仪器的信号在某个给定区间内变动时，示值不会发生变化。

如指示装置的分辨力为（一般称为步进量），产生某一指示值的激励源的值在∽区间内可以是任意的，且概率相等。

因此，可以考虑为一个宽的矩形分布，半宽度。

标准不确定度。

B类评定中的自由度a. B类不确定度分量的自由度与所估计的标准不确定度的相对标准不确定度有关。

其关系式为。

根据经验，按所依据的信息来源来判断可信度0 （100%）10% （90%） 5016% （84%） 2025% （75%） 842% （58%） 476% （24%） 2b. 在什么情况下可估计为校准证书上给出了校准结果的扩展不确定度或，该仪器稳定性很好或校准时间不长，保存条件较理想，其值不会有明显变化；按仪器最大允许误差或级别所评出的标准不确定度；按仪器等别的不确定度档次界限所作出的评定；按仪器的引用误差或其相应级别作出的评定。

在实际工作中，B类不确定度分量常根据区间的信息来评定，通常选择被测量落在区间以外的概率极小，这时可认为的自由度4．合成标准不确定度的评定此式称为不确定度传递率，式中，是输入量，是偏导数，称为灵敏系数，分别是输入量的标准不确定度，是的相关系数，设= ，= 是与的协方差。

精密压力表示值误差测量结果的不确定度评定1 概述1.1 测量依据JJG49-1999《弹簧管式精密压力表及真空表》。

1.2 环境条件温度(20±2)℃，相对湿度不大于80 %。

1.3 测量标准二等活塞压力计，准确度等级为0.05级。

1.4 被测对象准确度等级为0.25级的精密压力表。

1.5 测量过程通过升压和降压两个循环将被测压力表在各检定点与标准器比较，读取被检表示值。

此时被检表示值与标准器产生的标准压力值之差值即为被检压力表的示值误差。

1.6 评定结果的使用符合上述条件的测量结果，一般可直接使用本不确定度的评定结果。

2 数学模型2.1 数学模型δ= P X - P N式中: P X——被检精密压力表的示值；P N——加在标准器活塞承重盘上的标准压力值。

3 输入量的标准不确定度的评定3.1 被测精密压力表读数标准不确定度u（P X）引起的标准不确定度分量u1，主要由下列不确定度分量构成：（1）被测精密压力表重复测量引起的不确定度分量u X1（A 类） 为了获得重复性测量的不确定度，二等标准活塞压力计对精密压力表10MPa 点进行10次独立测量，测得数据如表1：表1平均值MPa x n x i i 0085.101==∑=单次测量标准差()MPa n xxS ni i0034.011=--=∑=实际测量时依据检定规程，取二次测量读数平均值MPa s u X 0024.020034.021===，其自由度νX1=9（2）被测精密压力表估读引起的不确定度分量u X2（B 类）实际测量时，精密压力表的估读误差为最小分度值的1/10，以0.25级，0～10MPa 精密压力表为例，其估读误差为0.005MPa ，误差分布服从均匀分布，包含因子k=3。

MPa u X 0029.03005.02==估计%1022=∆X X u u ,故自由度()50%102122=⨯=X v （3）环境温度引起的不确定度分量u X3（B 类）依据检定规程，精密压力表的检定温度为（20±2）℃，温度影响所产生的最大误差为k t （t-20）p ，这里温度系数k t ＝0.0004/℃，p ＝10MPa ，误差服从均匀分布，包含因子k=3。