系统工程学第讲系统动力学

系统动力学方法在工程系统优化中的应用研究引言：工程系统的优化是一个复杂而关键的问题。

传统的优化方法往往只能考虑系统的局部因素，难以全面地分析和解决问题。

而系统动力学方法则提供了一种全面、综合的视角，能够更好地理解和优化工程系统。

本文将探讨系统动力学方法在工程系统优化中的应用研究。

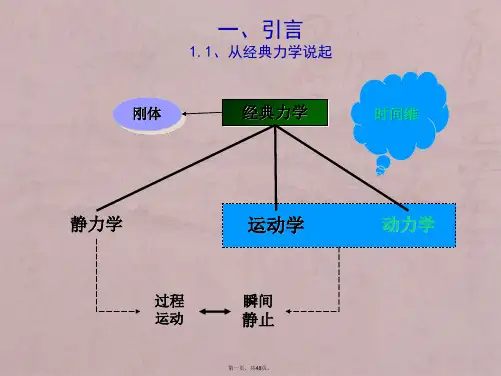
一、系统动力学方法的基本原理系统动力学方法是一种以时间为基础的建模和分析方法，旨在研究系统内部结构和行为之间的关系。

其核心思想是将系统视为一系列相互作用的变量和因果关系的集合，通过建立动态方程来描述系统的演化过程。

系统动力学方法强调整体性思维，注重系统内部的反馈机制和延迟效应。

二、系统动力学方法在工程系统优化中的应用案例1. 供应链管理优化供应链是一个典型的工程系统，涉及到多个环节和参与方。

传统的供应链管理方法往往只考虑到局部的因素，难以全面地分析和优化供应链的整体性能。

而系统动力学方法可以通过建立供应链各环节之间的动态方程，考虑到延迟效应和反馈机制，从而更好地优化供应链的整体性能。

2. 城市交通优化城市交通是一个复杂而庞大的工程系统，涉及到交通流量、道路容量、交通信号等多个因素。

传统的交通优化方法往往只能考虑到局部的交通状况，难以全面地分析和优化城市交通系统。

而系统动力学方法可以通过建立城市交通各要素之间的动态方程，考虑到交通流量的延迟效应和反馈机制，从而更好地优化城市交通系统的整体性能。

三、系统动力学方法的优势和挑战1. 优势系统动力学方法具有较强的整体性和综合性，能够更好地理解和分析工程系统的复杂性。

它能够考虑到系统内部的反馈机制和延迟效应，从而更准确地预测系统的行为和性能。

此外，系统动力学方法还能够帮助决策者更好地制定策略和决策，提高系统的鲁棒性和适应性。

2. 挑战系统动力学方法在应用过程中也存在一些挑战。

首先，系统动力学方法需要大量的数据支持，对数据的质量和可靠性要求较高。

其次，系统动力学方法需要对系统的结构和行为有较深入的理解，需要专业的领域知识和建模经验。

动力学系统动力学系统是一个非常重要的科学概念，是研究物理系统如何操作的一部分。

它涉及物体的方向性运动，是许多物理关系的基础。

本文将重点关注动力学系统的基本原理，例子和应用。

动力学是一门描述物体或物理系统在定义状态下的运动的学科。

这个定义状态包括：速度、加速度和位置。

动力学系统相对于其他物理系统而言，最大的特点在于它的运动是有序的，并且运动与定义状态之间有一一对应的关系。

在动力学中，物体的运动由受力而引起，并且运动受到重力影响。

动力学系统在物理学中被广泛应用，主要用于研究定义状态下物体的运动。

例如，在研究飞机飞行原理时，可以运用动力学系统来研究飞机的飞行轨迹。

动力学的原理也被用于研究城市规划，以及物体的旋转运动。

考虑粒子质量和物理环境，动力学系统可以描述物体的运动，用来模拟和研究物体的运动。

例如，研究一个物体在加速度下的运动，可以用此动力学系统来模拟，计算出一些定义状态下，物体在加速度下的运动轨迹。

动力学系统也可以用来分析和比较不同地区引起的摩擦和空气阻力。

例如，在研究风洞中的空气动力学时，可以使用动力学系统来分析和研究不同地区空气的摩擦和阻力。

在许多工程和科学领域，动力学系统是一种常见的模型，用于模拟各种现实系统。

例如，在自动控制工程中，我们可以使用动力学系统模型来模拟物体的控制规律，进而更好地操控机器的运动状态。

在建筑学中，动力学也被广泛应用，可以用来研究建筑物在不同情况下的运动特性。

例如，在研究桥梁受力情况时，可以利用动力学系统来模拟桥梁在不同状态下的受力情况，进而用来评估桥梁的稳定性。

以上就是动力学系统的基本概念，例子和应用。

动力学系统是一个重要的理论框架，用于描述物理系统在定义状态下的运动。

此外，动力学也被广泛应用于工程、科学和建筑学领域，为它们提供模型来研究物体的运动。

系统动力学模型系统动力学模型是指它是一种分析和模拟物理系统及其动力学过程的数学技术。

它可以用来研究运动学，控制系统，流体动力学，形式力学，电学，冲击学和弹性动力学等领域的数学模型，并可用于实际的工程问题的解决。

系统动力学模型基于物理系统的动力学处理和控制问题，用来研究物体的运动行为。

例如，系统动力学模型可以用来探讨汽车的运动性，即汽车在不同条件下的行驶特性，以确定汽车行驶性能的最佳状态。

此外，系统动力学模型还可以模拟任意静力学，力学，流体力学或热力学系统的运动模式。

系统动力学模型的建立要求具备完备的物理基础知识，形成一个系统模型的首要任务是了解物理系统的特性和行为，因此必须确定物理系统的运动方程和力学特征，物理量的表达式在构建模型时必须明确。

模式构建完成后，需要求解模型，并将模型运用到实际问题中，用以求解物理过程及其动力学运行状态。

为此，我们可以使用计算机模拟技术来求解模型，用以检验结果的正确性和准确性。

系统动力学模型在很多领域中都发挥着重要的作用，例如机械系统的设计，控制系统的调整，电子电气系统的设计，机器人的控制，航空航天技术，建筑工程设计等。

例如，在机器人技术中，系统动力学模型可以模拟机器人的运动特性，帮助机器人决定如何完成任务。

此外，系统动力学模型在工程设计中也有广泛应用，可用于分析和解决工程设计问题，以便改善工程性能。

例如，系统动力学模型可以帮助分析和解决结构物振动问题，提高结构物的稳定性和耐久性，以及改善系统的可靠性。

此外，系统动力学模型也可以帮助优化控制系统的性能，以提高系统的功率和可靠性。

综上所述，系统动力学模型是一个强大的工具，可以帮助我们研究和分析物理系统及其动力学过程，从而有效地改善工程性能。

它在机械，控制，电子，航空航天等各个领域都有广泛的应用，并被广泛用来分析和解决工程设计问题。

系统动力学建模步骤一、引言系统动力学是一种研究复杂系统行为的方法，它通过建立数学模型来描述系统的结构和运动规律。

这种方法在工程、经济、社会科学等领域得到了广泛应用。

本文将介绍系统动力学建模的步骤。

二、确定研究对象和目标在进行系统动力学建模之前，首先需要明确研究对象和目标。

研究对象可以是一个生态系统、一个产业链、一个城市交通网络等等，而目标则是要解决什么问题或达到什么效果。

例如，我们可能想要了解某个生态系统中物种数量的变化规律，或者预测某个城市交通拥堵情况的发展趋势。

三、建立概念模型接下来，需要建立概念模型。

概念模型是对研究对象进行抽象和简化的过程，它用图形和符号表示出各个元素之间的关系。

例如，在研究生态系统时，我们可以将各物种看作节点，并用箭头表示它们之间的食物链关系。

四、确定变量及其关系在概念模型确定后，需要明确变量及其关系。

变量可以分为状态变量和流量变量。

状态变量是指系统中的某一状态，如生态系统中各物种的数量，而流量变量则是指这些状态之间的转移。

例如，在生态系统中，食物链上的物种数量就是状态变量，而它们之间的捕食关系就是流量变量。

五、建立数学模型建立数学模型是系统动力学建模的核心步骤。

在这一步骤中，需要将概念模型转化为数学方程组。

这些方程通常采用微分方程或差分方程来描述系统中各个元素之间的关系。

例如，在研究生态系统时，我们可以使用Lotka-Volterra模型来描述各物种之间的捕食关系。

六、进行仿真和验证建立好数学模型后，需要进行仿真和验证。

仿真可以通过计算机程序来实现，它可以帮助我们预测系统在不同条件下的行为。

验证则是通过与实际观测数据进行比较来检验模型的准确性。

如果模型与实际情况相符，则说明该模型具有很好的预测能力。

七、应用和优化最后一步是应用和优化模型。

应用包括将模型用于实际问题求解，并针对特定问题进行优化。

例如，在研究城市交通拥堵问题时，我们可以通过模拟不同的交通管理措施来找到最佳的解决方案。

系统动力学基本要素系统动力学是一种研究不同组成部分相互作用和动态变化的学科，也是建立于系统思维和系统工程学基础之上的一个交叉学科，旨在描述和控制整个系统的产生和变化。

在系统动力学理论的研究过程中，一些基本要素被提出，并被广泛应用于系统动力学的建模与分析中。

下面，笔者将围绕系统动力学的基本要素，来谈一谈这一学科的基础。

1. 系统（System）：在系统动力学中，系统代表着我们要研究的现象或实体，可以是一个物理系统，也可以是一个社会经济系统或生态系统。

系统在既定的时间、空间范围内，与外界进行信息、物质和能量的交互作用，所以其被视为一个开放的整体。

2. 环境（Environment）：系统是和环境相互作用的整体，环境对系统的影响是一个直接的因素。

环境的特征因素包括天然资源的分配、大气和水的传输、土地和人类、环境污染的发生等等；所有这些都是制约和影响系统运行的非常重要的因素。

3. 反馈（Feedback）：系统中反馈的作用描述了系统自身的调节作用。

通过捕捉系统内不同组成部分之间的相互作用和调节联系，反馈可以被用于控制系统内的信息以及物质流动，促进系统自我调节和均衡的双向流动。

4. 资源（Resource）：资源是指系统内用来支持系统运转的物质或能量，例如自然资源、财富承载能力、人力和资本以及文化等。

在系统动力学建模中，通过对资源的描述和分析，可以对系统进行优化和调整。

5. 流（Flow）：系统内部各组成部分之间的相互作用和动态变化被称为流。

流是流量、速率、频率、单位等各种动态变化的表现。

在系统动力学中，流通常用于描述系统内不同组成部分之间的联系、物质和能量的动态变化过程以及时间演化的规律。

6. 股票（Stock）：股票在系统动力学中是指系统内能够积累的固定量，例如沉积的资本、植被的生长量、某种物质的库存、家庭的储蓄等。

股票是供给、需求以及资产评价的基础。

在系统动力学中，这些基本要素被用于对系统进行建模和分析，以发现系统内部的动态特性和稳定态之间的关系。

系统动力学9种模型引言系统动力学是一种研究动态系统行为的方法论，它通过构建系统模型来分析系统的各种因果关系和变化规律。

在系统动力学中，有9种基本模型被广泛应用于各种领域的问题分析和解决。

本文将对这9种模型进行全面、详细、完整且深入地探讨。

1. 积累模型积累模型是系统动力学中最基本的模型之一，它描述了一个变量或者一组变量的积累过程。

例如，当我们考虑人口增长的问题时，可以使用积累模型来描述人口数量随时间的变化。

积累模型通常使用微分方程表示。

1.1. 特点 - 变量之间存在流入和流出的关系； - 变量之间的积累是连续的； - 流入量和流出量可以是恒定的或者变化的。

1.2. 应用示例积累模型在生态学、经济学、工程管理等领域得到了广泛的应用。

例如，在生态学中，可以使用积累模型来研究物种数量的变化；在经济学中，可以使用积累模型来研究货币的流通和储蓄；在工程管理中，可以使用积累模型来研究项目进展和资源分配。

1.3. 示例方程dP/dt = b*P - d*P其中，P表示人口数量，t表示时间，b表示出生率，d表示死亡率。

2. 流动模型流动模型描述了一个变量或者一组变量之间的流动过程。

它通常用来研究物质、能量、信息等在系统中的传递和传播。

例如，在物流管理中，可以使用流动模型来研究物料的流动和分配。

2.1. 特点 - 变量之间存在流动的关系； - 流动可以是单向的或者双向的； -流动可以是连续的或者离散的。

2.2. 应用示例流动模型在供应链管理、信息传输、能量传递等领域具有广泛的应用。

例如，在供应链管理中，可以使用流动模型来优化物料的流动和库存的控制；在信息传输中，可以使用流动模型来研究信息的传播和处理；在能量传递中，可以使用流动模型来分析能量的转化和利用。

2.3. 示例方程dQ/dt = f - k*Q其中，Q表示物料的数量，t表示时间，f表示流入量，k表示流失率。

3. 动力平衡模型动力平衡模型描述了一个变量或者一组变量在达到平衡状态时的行为。

系统动力学（System Dynamics）是一门分析研究信息反馈系统的学科，也是一门认识系统问题和解决系统问题交叉的综合性学科。

它是系统科学和管理科学中的一个分支，它也是一门沟通自然科学和社会科学等领域的横向学科，是基于系统理论、控制理论、信息论和计算机仿真技术发展的新学科，是通过建立流位、流率系来研究信息反馈系统的一门学科。

其解决问题的独特性在于：系统动力学是基于因果关系和结构决定行为的观点，从系统内部的微观结构入手进行建模，以微分方程（组）为分析工具，借助于计算机仿真技术来分析研究系统结构功能与动态行为的内在关系，从而找出解决问题的对策。

系统动力学的出现始于1956年，创始人为美国麻省理工学院的福瑞斯特（Jay W.Forrester）教授。

1950年代后期，系统动力学逐步发展成为一门新的领域。

初期它主要应用于工业企业管理，处理诸如生产与雇员情况的波动，市场股票与市场增长的不稳定性问题。

1960年代福瑞斯特教授的《工业动力学》（Industrial Dynamics）成为系统动力学学科的经典著作，它阐述了系统动力学的基本原理与典型案例。

这本著作也是系统动力学发展过程中的重要里程碑。

系统动力学理论的基本点鲜明地表明了它的系统辩证的特征。

它强调系统、整体的观点和联系、发展、运动的观点。

系统动力学处理复杂系统问题的方法是定性与定量相结合的方法，这与国内著名专家钱学森提出的复杂系统分析方法——“综合研讨厅”（Metasynthesis）方法是相互适应的。

它强调系统综合推理的方法，按照系统动力学的理论与方法建立的模型，借助计算机模拟可以用于定性与定量地研究系统问题。

它可用于分析研究社会、经济、生态和生物等一类复杂大系统问题。

系统动力学模型可以作为实际系统，特别是社会、经济、生态复杂大系统的“实验室”。

模型的主要功用在于向人们提供一个进行学习（模型运行结果的比较、选择）与政策分析的工具，并使决策群体或到整个组织逐步成为一学习型组织。