2012高考数学分类汇编算法初步

2012高考数学新题分类汇编 算法初步与复数（高考真题+模拟新题）课标文数12.L1[2011·某某卷] 如图1－3所示，程序框图(算法流程图)的输出结果是________．图1－3课标文数12.L1[2011·某某卷] 【答案】 15 【解析】 第一次进入循环体有T ＝0＋0，第二次有：T ＝0＋1，第三次有T ＝0＋1＋2，…第k ＋1次有T ＝0＋1＋2＋…＋k ＝k k ＋12，若T ＝105，解得k ＝14，继续执行循环，这时k ＝15，T >105，所以输出的k 的值是15.课标理数11.L1[2011·某某卷] 如图1－3所示，程序框图(算法流程图)的输出结果是________．图1－3课标理数11.L1[2011·某某卷] 15 【解析】 第一次进入循环体有T ＝0＋0，第二次有：T ＝0＋1，第三次有T ＝0＋1＋2，…，第k ＋1次有T ＝0＋1＋2＋…＋k ＝k k ＋12，若T ＝105，解得k ＝14，继续执行循环，这时k ＝15，T >105，所以输出的k 的值是15.课标理数4.L1[2011·卷] D 【解析】 第(i ＝0)一步，i ＝0＋1＝1，s ＝2－12＋1＝13；第(i ＝1)二步，i ＝1＋1＝2，s ＝13－113＋1＝－12；第(i ＝2)三步，i ＝2＋1＝3，s ＝－12－1－12＋1＝－3；第(i ＝3)四步，i ＝3＋1＝4，s ＝－3－1－3＋1＝2；第(i ＝4)五步，i ＝4<4不成立，输出s ＝2，故选D.课标文数6.L1[2011·卷] 执行如图1－2所示的程序框图，若输入A 的值为2，则输出的P 值为( )图1－2A ．2B ．3C ．4D ．5课标文数6.L1[2011·卷] C 【解析】 第一步，P ＝1＋1＝2，S ＝1＋12＝32；第二步，P ＝2＋1＝3，S ＝32＋13＝116；第三步，P ＝3＋1＝4，S ＝116＋14＝2512>2，输出P ＝4，故选C.课标理数1.A1，L4[2011·某某卷] i 是虚数单位，若集合S ＝{－1,0,1}，则( )A ．i ∈SB ．i 2∈SC ．i 3∈S D.2i∈S课标理数1.A1、L4[2011·某某卷] B 【解析】 由i 2＝－1，而－1∈S ，故选B.课标文数5.L1[2011·某某卷] 阅读图1－1所示的程序框图，运行相应的程序，输出的结果是( )图1－1A ．3B ．11C ．38D ．123课标文数5.L1[2011·某某卷] B 【解析】 该程序框图是当型的循环结构，由程序框图可知，第一次循环，a ＝12＋2＝3；第二次循环，a ＝32＋2＝11； 当a ＝11时，a <10不成立，输出a ＝11，故选B.课标理数13.L1[2011·某某卷] 若执行如图1－3所示的框图，输入x 1＝1，x 2＝2，x 3＝3，x ＝2，则输出的数等于________．图1－3课标理数13.L1[2011·某某卷] 23【解析】 由累加的赋值符号S ＝S ＋(x i －x )2得到S ＝(1－2)2＋(2－2)2＋(3－2)2＝2，而最后输出的结果为S ＝1i S ＝13×2＝23.课标文数11.L1[2011·某某卷] 若执行如图1－2所示的框图，输入x 1＝1，x 2＝2，x 3＝4，x 4＝8，则输出的数等于________．图1－2课标文数11.L1[2011·某某卷] 154【解析】 由累加的赋值符号x ＝x ＋x i 得到x ＝x 1＋x 2＋x 3＋x 4＝1＋2＋4＋8＝15，而最后输出的结果为x ＝14x ＝14×15＝154.课标理数13.L1[2011·某某卷] 图1－6是某算法的程序框图，则程序运行后输出的结果是________．图1－6课标理数13.L1[2011·某某卷] 【答案】 10【解析】 第一次，s ＝0＋(－1)1＋1＝0，n ＝2，第二次，s ＝0＋(－1)2＋2＝3，n ＝3，第三次，s ＝3＋(－1)3＋3＝5，n ＝4，第四次，s ＝5＋(－1)4＋4＝10>9，终止循环，输出结果10.课标文数13.L1[2011·某某卷] 图1－6是某算法的程序框图，则程序运行后输出的结果是________．图1－6课标文数13.L1[2011·某某卷] 27 【解析】 第一次：s ＝(0＋1)×1＝1，n ＝1＋1＝2，第二次：s ＝(1＋2)×2＝6，n ＝3，第三次：s ＝(6＋3)×3＝27，n ＝4，而n ＝4>3，退出循环，输出s ＝27.故填27.课标理数3.L1[2011·课标全国卷] 执行如图1－1所示的程序框图，如果输入的N 是6，那么输出的p 是( )图1－1A．120 B．720C．1440 D．5040课标理数3.L1[2011·课标全国卷] B【解析】k＝1时，p＝1；k＝2时，p＝1×2＝2；k＝3时，p＝2×3＝6；k＝4时，p＝6×4＝24；k＝5时，p＝24×5＝120；k＝6时，p＝120×6＝720.课标文数9.L1[2011·某某卷] 执行下面的程序框图，如果输入的n是4，则输出的p 是( )图1－5A．8 B．5 C．3 D．2课标文数9.L1[2011·某某卷] C 【解析】由于n＝4，所以当k＝1时，p＝1，s＝1，t＝1；当k＝2时，p＝2，s＝1，t＝2；当k＝3时，p＝3，s＝2，t＝3，此时k＝4，输出p，此时p＝3，故选C.课标文数5.L1[2011·课标全国卷] 执行下面的程序框图，如果输入的N是6，那么输出的p是( )图1－1A．120 B．720C．1440 D．5040课标文数5.L1[2011·课标全国卷] B 【解析】k＝1时，p＝1；k＝2时，p＝1×2＝2；k＝3时，p＝2×3＝6；k＝4时，p＝6×4＝24；k＝5时，p＝24×5＝120；k＝6时，p＝120×6＝720.课标理数13.L1[2011·某某卷] 执行图1－3所示的程序框图，输入l＝2，m＝3，n＝5，则输出的y的值是________．图1－3课标理数13.L1[2011·某某卷] 68 【解析】把l＝2，m＝3，n＝5代入y＝70l＋21m ＋15n得y＝278，此时y＝278>105，第一次循环y＝278－105＝173，此时y＝173>105，再循环，y＝173－105＝68，输出68，结束循环．课标文数14.L1[2011·某某卷] 执行图1－4所示的程序框图，输入l＝2，m＝3，n＝5，则输出的y的值是________．图1－4课标文数14.L1[2011·某某卷] 68 【解析】把l＝2，m＝3，n＝5代入y＝70l＋21m ＋15n得y＝278，此时y＝278>105，第一次循环y＝278－105＝173，此时y＝173>105，再循环，y＝173－105＝68，输出68，结束循环．课标理数8.L1[2011·某某卷] 图1－3中，x1，x2，x3为某次考试三个评阅人对同一道题的独立评分，p为该题的最终得分．当x1＝6，x2＝9，p＝8.5时，x3等于( )图1－3A ．11B ．10C ．8D ．7课标理数8.L1[2011·某某卷] C 【解析】 由题目中所给的数据p ＝8.5，x 1＝6，x 2＝9，则若满足条件|x 3－x 1|s ＜|x 3－x 2|时，不成立，故应不满足条件|x 3－x 1|＜|x 3－x 2|，此时满足x 2＋x 32＝8.5，则x 3＝8，并且代入也符合题意，故选C.课标文数7.L1[2011·某某卷] 如下框图，当x 1＝6，x 2＝9，p ＝8.5时，x 3等于( )图1－4A ．7B ．8C ．10D ．11课标文数7.L1[2011·某某卷] B 【解析】 因为x 1＝6，x 2＝9，p ＝8.5，p ＝x 1＋x 22或p ＝x 2＋x 32，当x 1＝6，x 2＝9，p ＝x 1＋x 22＝7.5，不合题意，故p ＝x 2＋x 32＝8.5，x 2＝9，得x 3＝8，故答案为B.课标数学4.L1[2011·某某卷] 根据如图所示的伪代码，当输入a ，b 分别为2,3时，最后输出的m 的值为________．Read a ，b If a >b Then m ←a Else m ←b End If Print m课标数学4.L1[2011·某某卷] 3 【解析】 因为a ＝2<b ＝3，所以m ＝3.课标理数3.L1[2011·某某卷] 阅读程序框图1－1，运行相应的程序，则输出i的值为( )图1－1A．3 B．4 C．5 D．6课标理数3.L1[2011·某某卷] B 【解析】i＝1时，a＝1×1＋1＝2；i＝2时，a＝2×2＋1＝5；i＝3时，a＝3×5＋1＝16；i＝4时，a＝4×16＋1＝65>50，∴输出i＝4，故选B.图1－2课标文数3.L1[2011·某某卷] 阅读图1－2所示的程序框图，运行相应的程序，若输入x的值为－4，则输出y的值为( )A．0.5 B．1C．2 D．4课标文数3.L1[2011·某某卷] C 【解析】当x＝－4时，x＝|x－3|＝7；当x＝7时，x＝|x－3|＝4；当x＝4时，x＝|x－3|＝1<3，∴y＝2.课标理数12.L1[2011·某某卷] 若某程序框图如图1－4所示，则该程序运行后输出的k的值是________．图1－4课标理数12.L1[2011·某某卷] 5【解析】k＝3时，a＝43＝64，b＝34＝84，a<b；k＝4时，a＝44＝256，b＝44＝256，a＝b；k＝5时，a＝45＝256×4，b＝54＝625，a>b.图1－5课标文数14.L1[2011·某某卷] 某程序框图如图1－5所示，则该程序运行后输出的k 的值是________．课标文数14.L1[2011·某某卷] 5 【解析】k＝3时，a＝43＝64，b＝34＝84，a<b；k＝4时，a＝44＝256，b＝44＝256，a＝b；k＝5时，a＝45＝256×4，b＝54＝625，a>b.课标理数11.L2[2011·某某卷] 运行如图1－4所示的程序，输出的结果是________．a＝1b＝2a＝a＋bPRINT aEND图1－4课标理数11.L2[2011·某某卷] 【答案】 3【解析】由已知，输入a＝1，b＝2，把a＋b的值赋给a，输出a＝3.课标理数16.L3[2011·某某卷] 对于n ∈N *，将n 表示为n ＝a 0×2k ＋a 1×2k －1＋a 2×2k －2＋…＋a k －1×21＋a k ×20，当i ＝0时，a i ＝1，当1≤i ≤k 时，a i 为0或1.记I (n )为上述表示中a i 为0的个数(例如：1＝1×20,4＝1×22＋0×21＋0×20，故I (1)＝0，I (4)＝2)，则(1)I (12)＝________； (2)∑127n ＝12I(n)＝________.课标理数16.L3[2011·某某卷] (1)2 (2)1093【解析】 (1)本题实考二进制与十进制间的互化：因为I (12)＝1×23＋1×22＋0×21＋0×20，根据题目给出的定义可得到： I (12)＝2；(2)∑n ＝11272I (n )＝2I (1)＋2I (2)＋2I (3)＋…＋2I (127)利用二进制与十进制间的互化，列举得： I (1)＝1(2)共一个，则S 1＝2I (1)＝20＝1； I (2)＝10(2)，I (3)＝11(2)共2个，则S 2＝2I (2)＋2I (3)＝21＋20＝3；I (4)＝100(2)，I (5)＝101(2)，I (6)＝110(2)，I (7)＝111(2)共4个，则S 3＝2I (4)＋…＋2I (7)＝9；I (8)＝1000(2)，I (9)＝1001(2)，…，I (15)＝1111(2) 共8个，则S 4＝2I (8)＋…＋2I (15)＝27； ……I (64)＝100000(2)，…，I (127)＝1111111(2)共64个，则S 7＝2I (64)＋…＋2I (127)＝729；故∑n ＝11272I (n )＝2I (1)＋2I (2)＋2I (3)＋…＋2I (127)＝S 1＋S 2＋S 3＋S 4＋S 5＋S 6＋S 7＝1＋3＋9＋27＋81＋243＋729＝1093.课标文数1.L4[2011·某某卷] 设i 是虚数单位，复数1＋a i2－i为纯虚数，则实数a 为( )A ．2B ．－2C ．－12 D.12课标文数 1.L4[2011·某某卷] A 【解析】 法一：1＋a i 2－i ＝1＋a i ·2＋i2－i 2＋i＝2－a ＋2a ＋1i5为纯虚数，所以⎩⎪⎨⎪⎧2－a ＝0，2a ＋1≠0，解得a ＝2.法二：1＋a i 2－i ＝i a －i 2－i为纯虚数，所以a ＝2.答案为A.课标理数1.L4[2011·某某卷] 设i 是虚数单位，复数1＋a i2－i为纯虚数，则实数a 为( )A ．2B ．－2C ．－12 D.12课标理数 1.L4[2011·某某卷] A 【解析】 法一：1＋a i 2－i ＝1＋a i ·2＋i2－i 2＋i＝2－a ＋2a ＋1i5为纯虚数，所以⎩⎪⎨⎪⎧2－a ＝0，2a ＋1≠0， 解得a ＝2.法二：1＋a i 2－i ＝i ()a －i 2－i为纯虚数，所以a ＝2.答案为A.课标理数2.L4[2011·卷] 复数i －21＋2i＝( )A ．iB ．－iC ．－45－35iD ．－45＋35i课标理数2.L4[2011·卷] A 【解析】 i －21＋2i ＝i －21－2i 1＋2i1－2i ＝5i5＝i ，故选A.课标文数2.L4[2011·卷] 复数i －21＋2i＝( )A ．iB ．－iC ．－45－35iD ．－45＋35i课标文数2.L4[2011·卷] A 【解析】 i －21＋2i ＝i －21－2i 1＋2i1－2i ＝5i5＝i ，故选A.大纲理数1.L4[2011·全国卷] 复数z ＝1＋i ，z 为z 的共轭复数，则z z －z －1＝( )A ．－2iB ．－iC ．iD ．2i大纲理数1.L4[2011·全国卷] B 【解析】 ∵z ＝1－i ，∴z z －z －1＝(1＋i)(1－i)－(1＋i)－1＝－i ，故选B.课标文数2.L4[2011·某某卷] i 是虚数单位，1＋i 3等于( ) A ．i B ．－i C ．1＋i D ．1－i课标文数2.L4[2011·某某卷] D 【解析】 由1＋i 3＝1＋i 2·i＝1－i ，故选D.课标理数1.L4[2011·某某卷] 设复数z 满足(1＋i)z ＝2，其中i 为虚数单位，则z ＝( )A ．1＋iB ．1－iC ．2＋2iD ．2－2i课标理数1.L4[2011·某某卷] B 【解析】 z ＝21＋i ＝21－i 1＋i 1－i ＝21－i2＝1－i ，故选B.课标文数1.L4[2011·某某卷] 设复数z 满足i z ＝1，其中i 为虚数单位，则z ＝( ) A ．－i B ．i C ．－1 D ．1课标文数1.L4[2011·某某卷] A 【解析】 由i z ＝1得z ＝1i ＝ii2＝－i ，所以选A.课标理数1.L4[2011·某某卷] i 为虚数单位，则⎝ ⎛⎭⎪⎫1＋i 1－i 2011＝( )A ．－iB ．－1C ．iD ．1课标理数1.L4[2011·某某卷] A 【解析】 因为1＋i 1－i ＝()1＋i 2()1－i ()1＋i ＝i ，所以⎝ ⎛⎭⎪⎫1＋i 1－i 2011＝i 502×4＋3＝i 3＝－i.课标理数1.L4[2011·某某卷] 若a ，b ∈R ，i 为虚数单位，且(a ＋i)i ＝b ＋i ，则( ) A ．a ＝1，b ＝1 B ．a ＝－1，b ＝1 C ．a ＝－1，b ＝－1 D ．a ＝1，b ＝－1 课标理数1.L4[2011·某某卷] D 【解析】 由(a ＋i)i ＝b ＋i 得－1＋a i ＝b ＋i ，根据复数相等的充要条件，得a ＝1，b ＝－1，故选D.课标文数2.L4[2011·某某卷] 若a ，b ∈R ，i 为虚数单位，且(a ＋i)i ＝b ＋i ，则( ) A ．a ＝1，b ＝1 B ．a ＝－1，b ＝1 C ．a ＝1，b ＝－1 D ．a ＝－1，b ＝－1 课标文数2.L4[2011·某某卷] C 【解析】 由(a ＋i)i ＝b ＋i 得－1＋a i ＝b ＋i ，根据复数的相等，a ＝1，b ＝－1，故选C.课标理数1.L4[2011·某某卷] 若z ＝1＋2ii，则复数z ＝( )A ．－2－iB ．－2＋iC ．2－iD ．2＋i课标理数1.L4[2011·某某卷] D 【解析】 z ＝1＋2i i ＝i 1＋2ii 2＝－(i －2)＝2－i ，故z ＝2＋i.故选D.课标文数1.L4[2011·某某卷] 若(x －i)i ＝y ＋2i ，x ，y ∈R ，则复数x ＋y i ＝( ) A ．－2＋i B ．2＋iC ．1－2iD ．1＋2i课标文数1.L4[2011·某某卷] B 【解析】 由题设得x i ＋1＝y ＋2i ，∴x ＝2，y ＝1，即x ＋y i ＝2＋i.故选B.课标理数1.L4[2011·课标全国卷] 复数2＋i1－2i的共轭复数是( )A ．－35i B.35iC ．－iD ．i课标理数1.L4[2011·课标全国卷] C 【解析】 2＋i 1－2i ＝2＋i 1＋2i 1－2i 1＋2i ＝5i5＝i ，所以其共轭复数为－i.故选C.图1－1课标文数2.L4[2011·某某卷] i 为虚数单位，1i ＋1i 3＋1i 5＋1i7＝( )A ．0B ．2iC ．－2iD ．4i课标文数2.L4[2011·某某卷] A 【解析】 1i ＋1i 3＋1i 5＋1i 7＝－i ＋i －i ＋i ＝0，故选A.课标文数2.L4[2011·课标全国卷] 复数5i1－2i＝( )A ．2－iB ．1－2iC ．－2＋iD ．－1＋2i课标文数2.L4[2011·课标全国卷] C 【解析】 5i 1－2i ＝5i 1＋2i 1－2i 1＋2i ＝5i －105＝－2＋i.课标理数2.L4[2011·某某卷] 复数z ＝2－i2＋i(i 为虚数单位)在复平面内对应的点所在象限为( )A ．第一象限B ．第二象限C ．第三象限D ．第四象限课标理数2.L4[2011·某某卷] D 【解析】 z ＝2－i 2＋i ＝2－i 22＋i 2－i ＝3－4i 4＋1＝35－45i ，又点⎝ ⎛⎭⎪⎫35，－45在第四象限，所以该复数在复平面内对应的点也在第四象限．课标文数2.L4[2011·某某卷] 复数z ＝2－i2＋i(i 为虚数单位)在复平面内对应的点所在象限为( )A ．第一象限B ．第二象限C ．第三象限D ．第四象限课标文数2.L4[2011·某某卷] D 【解析】 z ＝2－i 2＋i ＝2－i 22＋i 2－i ＝3－4i 4＋1＝35－45i ，又点⎝ ⎛⎭⎪⎫35，－45在第四象限，所以该复数在复平面内对应的点也在第四象限．课标文数8.A1，L4[2011·某某卷] 设集合M ＝{y |y ＝|cos 2x －sin 2x |，x ∈R }，N ＝⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪⎪⎪⎪⎪⎪⎪x i ＜1，i 为虚数单位，x ∈R ，则M ∩N 为( )A ．(0,1)B ．(0,1]C ．[0,1)D ．[0,1]课标文数8.A1，L4[2011·某某卷] C 【解析】 对M ，由基本不等式得y ＝|cos 2x －sin 2x |＝|cos2x |，故0≤y ≤1.对N ，⎪⎪⎪⎪⎪⎪x i <1，即|－x i|<1，所以－1<x <1，故M ∩N ＝[0,1)，故答案为C.课标数学1.A1[2011·某某卷] 已知集合A ＝{－1,1,2,4}，B ＝{－1,0,2}, 则A ∩B ＝________.课标数学1.A1[2011·某某卷] {－1,2} 【解析】 因为集合A ，B 的公共元素为－1,2，故A ∩B ＝{－1,2}．课标数学3.L4[2011·某某卷] 设复数z 满足i(z ＋1)＝－3＋2i(i 为虚数单位)，则z 的实部是________．课标数学3.L4[2011·某某卷] 1 【解析】 因为z ＋1＝－3＋2i i ＝－3i ＋2i2i2＝2＋3i ，所以z ＝1＋3i ，故实部为1.大纲理数2.L4[2011·某某卷] 复数－i ＋1i＝( )A ．－2i B.12i C ．0 D ．2i大纲理数2.L4[2011·某某卷] A 【解析】 －i ＋1i＝－i －i ＝－2i ，所以选A.课标理数1.L4[2011·某某卷] i 是虚数单位，复数1－3i1－i＝( )A ．2＋iB ．2－iC ．－1＋2iD ．－1－2i课标理数1.L4[2011·某某卷] B 【解析】 1－3i 1－i ＝1－3i 1＋i 1－i 1＋i ＝4－2i2＝2－i.课标文数1.L4[2011·某某卷] i 是虚数单位，复数1－3i1－i＝( )A ．2－iB ．2＋iC ．－1－2iD ．－1＋2i课标文数1.L4[2011·某某卷] A 【解析】 1－3i 1－i ＝1－3i 1＋i 1－i 1＋i ＝4－2i2＝2－i.课标理数2.L4[2011·某某卷] 把复数z 的共轭复数记作z ，i 为虚数单位．若z ＝1＋i ，则(1＋z )·z ＝( )A ．3－iB ．3＋iC ．1＋3iD ．3课标理数2.L4[2011·某某卷] A 【解析】 ∵z ＝1＋i ，∴z ＝1－i ，∴(1＋z )·z ＝(2＋i)(1－i)＝3－i.课标文数2.L4[2011·某某卷] 若复数z ＝1＋i ，i 为虚数单位，则(1＋z )·z ＝( ) A ．1＋3i B ．3＋3i C ．3－i D ．3课标文数2.L4[2011·某某卷] A 【解析】 ∵z ＝1＋i ，∴(1＋z )·z ＝(2＋i)(1＋i)＝1＋3i.大纲理数1.L4[2011·某某卷] 复数i 2＋i 3＋i41－i＝( )A ．－12－12iB ．－12＋12iC.12－12iD.12＋12i 大纲理数 1.L4[2011·某某卷] C 【解析】 i 2＋i 3＋i 41－i ＝－1－i ＋11－i ＝－i1－i＝－i 1＋i 1－i 1＋i ＝－i －12＝12－12i.故选C.[2011·某某期末] 若框图(如图K48－2)所给的程序运行结果为S ＝20，那么判断框中应填入的关于k 的条件是( )[2011·某某期末] 已知(x ＋i)(1－i)＝y ，则实数x ，y 分别为( ) A ．x ＝－1，y ＝1 B ．x ＝－1，y ＝2 C ．x ＝1，y ＝1 D ．x ＝1，y ＝2[2011·高考样卷] 若a －ii＝b ＋2i ，其中a ，b ∈R ，i 是虚数单位，则a －b 的值为( )A ．－1B ．－3C ．3D ．1。

2012年高考真题理科数学解析汇编：算法初步一、选择题1 ．（2012年高考（天津理））阅读右边的程序框图,运行相应的程序,当输入x 的值为25-时,输出x 的值为（ ） A ．1-B ．1C ．3D ．92 ．（2012年高考（新课标理））如果执行右边的程序框图,输入正整数(2)N N ≥和实数12,,...,n a a a ,输出,A B ,则（ ）A ．AB +为12,,...,n a a a 的和 B ．2A B+为12,,...,n a a a 的算术平均数 C ．A 和B 分别是12,,...,n a a a 中最大的数和最小的数 D ．A 和B 分别是12,,...,n a a a 中最小的数和最大的数3 ．（2012年高考（陕西理））右图是用模拟方法估计圆周率π的程序框图,P 表示估计结果,则图中空白框内应填入 （ ）A ．1000NP =B ．41000NP =C ．1000MP =D ．41000MP =4 ．（2012年高考（山东理））执行下面的程序图,如果输入4a =,那么输出的n 的值为（ ）A ．2B ．3C ．4D ．55 ．（2012年高考（辽宁理））执行如图所示的程序框图,则输出的S 的值是（ ）A． 1B．23C．32D．46 ．（2012年高考（北京理））执行如图所示的程序框图,输出的S值为（）A．2B．4C．8D．16（第4题图）7 ．（2012年高考（安徽理））如图所示,程序框图(算法流程图)的输出结果是（）A．3B．4C．5D．8二、填空题8．（2012年高考（浙江理））若程序框图如图所示,则该程序运行后输出的值是______________.9 ．（2012年高考（江西理））下图为某算法的程序框图,则程序运行后输出的结果是______________.10．（2012年高考（江苏））下图是一个算法流程图,则输出的k 的值是____.11．（2012年高考（湖南理））如果执行如图3所示的程序框图,输入1x =-,n =3,S = ____.12．（2012年高考（湖北理））阅读如图所示的程序框图,运行相应的程序,输出的结果s =__________.13．（2012年高考（广东理））(算法)执行如图2所示的程序框图,若输入n 的值为8,则输出s 的值为______.14．（2012年高考（福建理））阅读右图所示的程序框图,运行相应地程序,输出的s 值等于_____________________.2012年高考真题理科数学解析汇编：算法初步参考答案一、选择题 1.【答案】C【命题意图】本试题主要考查了算法框图的读取,并能根据已给的算法程序进行运算. 【解析】根据图给的算法程序可知:第一次=4x ,第二次=1x ,则输出=21+1=3x ⨯. 2.【解析】选C3.解析:点(,)i i x y 落在单位圆内或圆上,随机产生1000个数,41000MP =,故选D. 第12题图4.【解析】当4=a 时,第一次1,3,140====n Q P ,第二次2,7,441====n Q P ,第三次3,15,1642====n Q P ,此时Q P <不满足,输出3=n ,选B.5.【答案】D【解析】根据程序框图可计算得24,1;1,2;,3;3s i s i s i ===-=== 3,4;4,5,2s i s i ====由此可知S 的值呈周期出现,其周期为4,输出时9i =因此输出的值与1i =时相同,故选D【点评】本题主要考查程序框图中的循环结构、数列的周期性以及运算求解能力, 属于中档题.此类题目需要通过计算确定出周期(如果数值较少也可直接算出结果),再根据周期确定最后的结果. 6.【答案】C【解析】0,11,12,23,8k s k s k s k s ==⇒==⇒==⇒==,循环结束,输出的S 为8,故选C【考点定位】 本小题主要考查程序框图,涉及到判断循环结束的时刻,以及简单整数指数幂的计算.二、填空题 8.【答案】1120【解析】T ,i 关系如下图:二、填空题9.3【解析】本题考查算法程序框图的应用以及运算求解的能力.由程序框图可知:第一次:T=0,k=1,sin 1sin 002π=>=成立,a=1,T=T+a=1,k=2,2<6,满足判断条件,继续循环;第二次:sin 0sin 12ππ=>=不成立,a=0,T=T+a=1,k=3, 3<6,满足判断条件,继续循环; 第三次:3sin 1sin 02ππ=->=不成立,a=0,T=T+a=1,k=4,4<6, 满足判断条件,继续循环;第四次: 3sin 20sin 12ππ=>=-成立,a=1,T=T+a=2,k=5, 满足判断条件,继续循环; 第五次: 5sin1sin 202ππ=>=成立,a=1,T=T+a=2,k=6,6<6不成立,不满足判断条件,跳出循环,故输出T 的值3.【点评】对于循环结构的算法框图问题,要观察什么时候刚好退出循环,,直到循环终止为止.体现考纲中要求理解输出语句,了解算法的含义与思想.来年需要注意判断条件的求解,程序的输出功能等.10.【答案】5.【考点】程序框图.【分析】根据流程图所示的顺序,程序的运行过程中变量值变化如下表:∴最终输出结果k=5. 11.【答案】4-【解析】输入1x =-,n =3,,执行过程如下:2:6233i S ==-++=-;1:3(1)115i S ==--++=;0:5(1)014i S ==-++=-,所以输出的是4-.【点评】本题考查算法流程图,要明白循环结构中的内容,一般解法是逐步执行,一步步将执行结果写出,特别是程序框图的执行次数不能出错. 12.考点分析:本题考查程序框图.解析:程序在运行过程中各变量的值如下表示:第一圈循环:当n=1时,得s=1,a=3. 第二圈循环: 当n=2时,得s=4,a=5 第三圈循环:当n=3时,得s=9,a=7,此时n=3,不再循环,所以解s=9 .13.解析:8.第一次循环,()11221s =⨯⨯=,4i =,2k =;第二次循环,()12442s =⨯⨯=,6i =,3k =;第三次循环,()14683s =⨯⨯=,8i =,4k =.此时退出循环,输出s 的值为8. 14.【答案】3-【解析】2111,2,22120,3,32033,4S k S k S k =⨯-===⨯-===⨯-=-=,输出3- 【考点定位】该题主要考查算法的基本思想、结构和功能,把握算法的基本思想是解好此类问题的根本.。

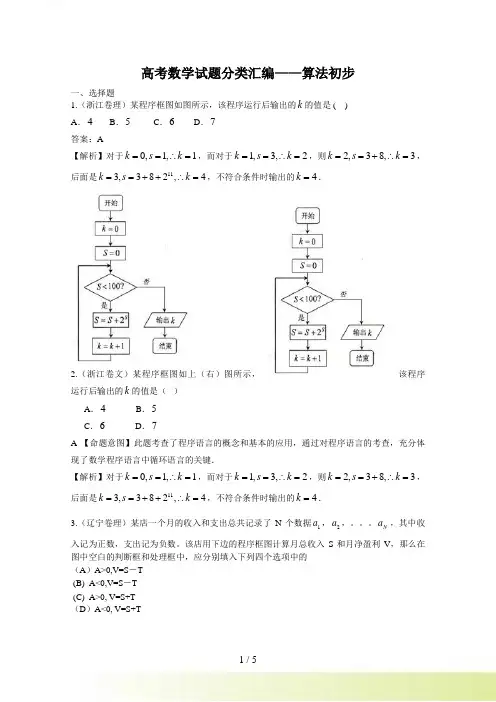
高考数学试题分类汇编——算法初步一、选择题1.（浙江卷理）某程序框图如图所示，该程序运行后输出的k 的值是 ( )A ．4B ．5C ．6D ．7答案：A【解析】对于0,1,1k s k ==∴=，而对于1,3,2k s k ==∴=，则2,38,3k s k ==+∴=，后面是113,382,4k s k ==++∴=，不符合条件时输出的4k =．2.（浙江卷文）某程序框图如上（右）图所示，该程序运行后输出的k 的值是（ ）A ．4B ．5C ．6D ．7A 【命题意图】此题考查了程序语言的概念和基本的应用，通过对程序语言的考查，充分体现了数学程序语言中循环语言的关键．【解析】对于0,1,1k s k ==∴=，而对于1,3,2k s k ==∴=，则2,38,3k s k ==+∴=，后面是113,382,4k s k ==++∴=，不符合条件时输出的4k =．3.（辽宁卷理）某店一个月的收入和支出总共记录了 N 个数据1a ，2a ，。

N a ，其中收入记为正数，支出记为负数。

该店用下边的程序框图计算月总收入S 和月净盈利V ，那么在图中空白的判断框和处理框中，应分别填入下列四个选项中的（A ）A>0,V=S －T(B) A<0,V=S －T (C) A>0, V=S+T（D ）A<0, V=S+T【解析】月总收入为S,因此A ＞0时归入S,判断框内填A ＞0支出T 为负数,因此月盈利V ＝S ＋T【答案】C 4.（宁夏海南卷理）如果执行上（右）边的程序框图，输入2,0.5x h =-=，那么输出的各个数的合等于（A ）3 （B ） 3.5 （C ） 4 （D ）4.5解析：选B.5.（辽宁卷文）某店一个月的收入和支出总共记录了 N 个数据1a ，2a ，。

N a ，其中收入记为正数，支出记为负数。

该店用右边的程序框图计算月总收入S 和月净盈利V ，那么在图中空白的判断框和处理框中，应分别填入下列四个选项中的（A ）A ＞0,V ＝S －T(B) A ＜0,V ＝S －T(C) A ＞0, V ＝S ＋T（D ）A ＜0, V ＝S ＋T【解析】月总收入为S,因此A ＞0时归入S,判断框内填A ＞0支出T 为负数,因此月盈利V ＝S ＋T【答案】C6.（天津卷理）阅读上（右）图的程序框图，则输出的S=A 26B 35C 40D 57【考点定位】本小考查框架图运算，基础题。

第一节算法初步程序框图的输出功能考向聚焦算法初步是新课标的新增内容,是高考的一个必考点,程序框图是考查的重点,特别是以循环结构为主的程序框图.程序框图常与分段函数求值、数据的大小关系、数列求和或求积、统计与概率等知识联系在一起,有的是输出计算次数、有的是输出计算结果,多以选择题、填空题的形式出现,一般为中等偏易题,所占分值4~5分备考指津复习考点应放在读懂框图上,尤其是循环结构,因为一个程序框图中只要有了循环结构,那么一定会涉及条件结构和顺序结构.对于循环结构,要注意当型与直到型的区别,搞清进入或退出的循环条件、循环次数,是做对题的关键1.(2012年某某卷,文7,5分)执行下面的程序框图,如果输入a=4,那么输出的n的值为( )(A)2 (B)3 (C)4 (D)5解析:本题考查程序框图的应用,由p=0≤Q=1∴P=0+40=1,Q=2×1+1=3,n=1;又P=1≤Q=3,∴P=1+4=5,Q=2×3+1=7,n=2;又P=5≤Q=7,∴P=5+42=21,Q=2×7+1=15,n=3,∵P=21>Q=15,∴输出n=3.答案:B.2.(2012年卷,文4,5分)执行如图所示的程序框图,输出的S值为( )(A)2 (B)4 (C)8 (D)16解析:第一步:k=0<3,S=1·20=1,k=0+1=1;第二步:k=1<3,S=1·21=2,k=1+1=2;第三步:k=2<3,S=2·22=8,k=2+1=3;第四步:k=3<3,执行否,输出S=8.故选C.答案:C.3.(2012年某某卷,文6,5分)阅读如图所示的程序框图,运行相应的程序,输出的s值等于( )(A)-3 (B)-10(C)0 (D)-2解析:当k=1时,s=2×1-1=1,当k=2时,s=2×1-2=0,当k=3时,s=2×0-3=-3,当k=4时,不满足判断框中的条件,输出s=-3,故选A.答案:A.4.(2012年新课标全国卷,文6,5分)如果执行如图的程序框图,输入正整数N(N≥2)和实数a1,a2,…,a N,输出A,B,则( )(A)A+B为a1,a2,…,a N的和(B)为a1,a2,…,a N的算术平均数(C)A和B分别是a1,a2,…,a N中最大的数和最小的数(D)A和B分别是a1,a2,…,a N中最小的数和最大的数解析:易知A、B分别为a1,a2,…,a N中最大的数和最小的数.故选C.答案:C.5.(2012年某某卷,文3,5分)阅读如图的程序框图,运行相应的程序,则输出S的值为( )(A)8 (B)18(C)26 (D)80解析:当n=1时,S=0+31-30=2,当n=2时,S=2+32-31=8,当n=3时,S=8+33-32=26,此时n=3+1=4.输出S为26,应选C.答案:C.6.(2012年某某卷,文6,5分)如图所示,程序框图(算法流程图)的输出结果是( )(A)3 (B)4(C)5 (D)8解析:程序运行:x=2,y=2;x≤4满足;x=4,y=3;x≤4满足;所以x=8,y=4;此时不满足x≤4,输出y=4.答案:B.7.(2012年某某卷,文9,5分)执行如图所示的程序框图,若输入n的值为6,则输出s的值为( )(A)105 (B)16(C)15 (D)1解析:本小题主要考查程序框图,由图知i=1时,S=1×1=1,i=3时,S=1×3=3,i=5时,S=3×5=15,i=7时,输出S.答案:C.8.(2012年某某卷,文10,5分)执行如图所示的程序框图,则输出的S值是( )(A)4 (B)(C)(D)-1解析:第一步:i=1<6,S==-1;第二步i=2<6,S==;第三步:i=3<6,S==;第四步:i=4<6,S==4;第五步:i=5<6,S==-1;第六步:i=6<6不成立,执行否,输出S=-1.答案:D.9.(2011年某某卷,文7)如框图,当x1=6,x2=9,p=8.5时,x3等于( )(A)7 (B)8 (C)10 (D)11解析:若执行“是”,则x1=6,x2=9,p===7.5,与p=8.5矛盾.∴应执行否.经验证合题.即p===8.5,x3=8.故选B.答案:B.10.(2011年某某卷,文5)阅读如图所示的程序框图,运行相应的程序,输出的结果是( )(A)3 (B)11 (C)38 (D)123解析:a的取值依次为a=1<10,∴a=12+2=3<10,∴a=32+2=11≥10,输出a的结果是11.答案:B.11.(2011年某某卷,文9)执行如图所示的程序框图,如果输入的n是4,则输出的p是( )(A)8 (B)5 (C)3 (D)2解析:∵输入n=4,k=1时,p=1,s=1,t=1;k=2时p=2,s=1,t=2;k=3时,p=3,s=2,t=3;k=4时输出p=3.答案:C.12.(2011年某某卷,文3)阅读如图的程序框图,运行相应的程序,若输入x的值为-4,则输出y的值为( )(A)0.5 (B)1 (C)2 (D)4解析:当x=-4时,∵|-4|>3,∴x=|-4-3|=7,又|7|>3,∴x=|7-3|=4,又|4|>3,∴x=|4-3|=1,又|1|<3,∴输出y=21=2.故选C.答案:C.13.(2011年卷,文6)执行如图所示的程序框图,若输入A的值为2,则输出的P值为( )(A)2 (B)3 (C)4 (D)5解析:∵A=2,P=1,S=1,∴S<A,∴P=2,S=1+=,又∵S<A,∴P=3,S=+=,∵S<A,∴P=4,S=+=>A,∴输出P=4,故选C.14.(2010年新课标全国卷,文8)如果执行如图所示的框图,输入N=5,则输出的数等于( )(A)(B)(C)(D)解析:法一:(逐项计算):k=1,S==,1<5进入循环;k=2,S=+,2<5进入循环;k=3,S=++,3<5进入循环;k=4,S=+++,4<5进入循环;k=5,S=++++=,5<5不成立.因此结束循环,S=,选择D.法二:(整体把握):由已知条件和程序框图可知,输出的S是数列{}的前5项和:S=++++=(-)+(-)+(-)+(-)+(-)=1-=,选择D. 答案:D.这是一道算法与数列的交汇问题,自然而巧妙,新颖而别致,解决此类问题的关键是:(1)搞清判断框内的循环控制条件是由计数变量,还是累加变量来表示;(2)要注意判断框内的不等式是否带有等号,这直接决定循环次数的多少;(3)要准确把握计数变量与累加变量的关系,利用程序框图的整体功能,减少运算次数,直接求解结果.15.(2012年某某卷,文15,5分)如图是某算法的程序框图,则程序运行后输出的结果是.解析:本题考查程序框图及递推数列等知识,考查枚举的数学思想方法及运算求解的数学能力.此框图依次执行如下循环:第一次:T=0,k=1,sin >sin 0成立,a=1,T=T+a=1,k=2,2<6,继续循环;第二次:sin π>sin 不成立,a=0,T=T+a=1,k=3,3<6,继续循环;第三次:sin >sin π不成立,a=0,T=T+a=1,k=4,4<6,继续循环;第四次:sin 2π>sin 成立,a=1,T=T+a=2,k=5,继续循环;第五次:sin >sin 2π成立,a=1,T=T+a=3,k=6,6<6不成立,跳出循环,输出T的值(T=3).答案:316.(2012年某某卷,文13,4分)若某程序框图如图所示,则该程序运行后输出的值是.解析:本题主要考查程序框图的认识和理解.根据程序框图,T=1,i=2,不满足条件;T=,i=3,不满足条件;T=,i=4,不满足条件;T=,i=5,不满足条件;T=,i=6,满足条件;输出T=.答案:T=17.(2012年某某卷,文16,5分)阅读如图所示的程序框图,运行相应的程序,输出的结果s=.解析:此框图依次执行如下循环:第一次:a=1,s=0,n=1,s=s+a=1,a=a+2=3,n=1<3成立,继续循环;第二次:n=n+1=2,s=s+a=1+3=4,a=a+2=5,n=2<3成立,继续循环;第三次:n=n+1=3,s=s+a=4+5=9,a=a+2=7,n=3<3不成立,跳出循环,输出s的值(s=9).答案:918.(2012年某某数学,4,5分)如图是一个算法流程图,则输出的k的值是.解析:本题考查程序框图中条件结构.因为k=1,k2-5k+4=0;k=2, k2-5k+4<0;k=3, k2-5k+4<0;k=4, k2-5k+4=0;k=5, k2-5k+4>0,所以输出的k的值为5.答案:519.(2012年某某卷,文14,5分)如果执行如图所示的程序框图,输入x=4.5,则输出的数i=.解析:程序运行如下x=4.5,i=1;x=3.5,i=2;x=2.5,i=3;x=1.5,i=4;x=0.5,此时x<1成立,输出i=4.答案:4算法按框图运行,写出各变量的值,注意循环条件.20.(2011年某某卷,文11)若执行如图所示的框图,输入x1=1,x2=2,x3=4,x4=8,则输出的数等于.解析:该框图的功能具有类加功能,当i=1时,x=x1;当i=2时,x=x1+x2;当i=3时,x=x1+x2+x3;当i=4时,x=x1+x2+x3+x4.执行否的结果,输出x=,∴x=,∴输出的数为.答案:21.(2011年某某卷,文14)执行如图所示的程序框图,输入l=2,m=3,n=5,则输出的y的值是.解析:由输入l=2,m=3,n=5,计算得出l2+m2+n2=38≠0,则执行否,y=278>105,执行是,y=173>105,执行是,y=68≤105,执行否,y=68.即输出68.答案:6822.(2011年某某卷,文14)某程序框图如图所示,则该程序运行后输出的k的值是.解析:k=2时,k=3,a=43,b=34,a<b.执行否;k=4,a=44,b=44,a=b,执行否;k=5,a=45,b=54,a>b,执行是,输出k=5.答案:523.(2011年某某卷,文12)如图所示,程序框图(算法流程图)的输出结果是.解析:由程序框图知T=,易知当k=14时T=105,当k=15时,T>105,故输出结果为15.答案:1524.(2010年某某卷,文13)如图所示,程序框图(算法流程图)的输出值x=.解析:据程序框图,x的取值依次是1,2,4,5,6,8,9,10,12,输出x的取值为12.答案:1225.(2010年某某卷,文11)某城市缺水问题比较突出,为了制定节水管理办法,对全市居民某年的月均用水量进行了抽样调查,其中4位居民的月均用水量分别为x1,…,x4(单位:吨).根据如图所示的程序框图,若x1,x2,x3,x4分别为1,1.5,1.5,2,则输出的结果s为.解析:由流程图知,第一次循环时s1=0+x1=1,第二次循环时s1=1+1.5,第三次循环时s1=1+1.5+1.5, 第四次循环时s1=1+1.5+1.5+2=6,s=s1==.答案:程序框图的填充考向聚焦此类程序框图的内容补全问题仍然会成为2013年高考命题的热点,以选择、填空题的形式出现,分值占5分左右.解决这类题的根本办法就是要搞清楚顺序结构、条件结构和循环结构这三种基本逻辑结构的功能和使用办法26.(2012年某某卷,文5,5分)如图是计算某年级500名学生期末考试(满分为100分)及格率q的程序框图,则图中空白框内应填入( )(A)q= (B)q= (C)q= (D)q=解析:因为执行判断框“是”计算的及格的总人数M,“否”统计的是不及格的人数,所以及格率q=.选D.答案:D.27.(2010年某某卷,文5)如图是求x1,x2,…,x10的乘积S的程序框图,图中空白框中应填入的内容为( )(A)S=S*(n+1)(B)S=S*x n+1(C)S=S*n(D)S=S*x n解析:由循环结构的特点知图中空白的处理框中表示前n个数的连乘积,故选D.答案:D.28.(2010年某某卷,文4)某程序框图如图所示,若输出的S=57,则判断框内为( )(A)k>4? (B)k>5? (C)k>6? (D)k>7?解析:由已知运行程序框图得:k=1,S=1;k=2,S=4;k=3,S=11;k=4,S=26;k=5,S=57,结合选项,从而判断框中应填k>4?.答案:A.29.(2010年卷,文9)已知函数y=图中表示的是给定x的值,求其对应的函数值y 的程序框图.①处应填写;②处应填写.解析:结合函数,分析程序框图.分段函数中x=2是分界线,当x<2时有y=2-x,否则y=log2x,故①处填写x<2,②处填写y=log2x.答案:x<2 y=log2x30.(2010年某某卷,文12)如图,是某某数x的绝对值的算法程序框图,则判断框①中可填.解析:由于|x|=或|x|=故根据所给的程序框图,易知可填x>0或x ≥0.答案:x>0或x≥031.(2010年某某卷,文11)2010年某某世博会园区每天9:00开园,20:00停止入园.在下边的框图中,S表示某某世博会官方在每个整点报道的入园总人数,a表示整点报道前1个小时内入园人数,则空白的执行框内填入.解析:由题意知此空为累加求和S←S+a.答案:S←S+a。

2012高考数学分类汇编算法初步2012高考数学分类汇编-算法1. （安徽3）如图所示，程序框图（算法流程图）的输出结果是（）()A3()B4()C5()D82.北京4．执行如图所示的程序框图，输出的S值为（）A. 2 B .4 C.8 D. 163.福建12.阅读右图所示的程序框图，运行相应地程序，输出的s值等于_____________________。

4.广东13. 执行如图2所示的程序框图，若输入n的值为8，则输出s的值为5.湖北12．阅读如图所示的程序框图，运行相应的程序，输出的结果s =.6.湖南14.如果执行如图3所示的程序框图，输入1x=-,n=3,则输出的数S=.第6题7.江苏4．（2012年江苏省5分）下图是一个算法流程图，则输出的k的值是▲ ．8江西14下图为某算法的程序框图，则程序运行后输出的结果是______________.9辽宁9. 执行如图所示的程序框图，则输出的S值是第513新课标（6）如果执行右边的程序框图，输入正整数(2)N N ≥和实数12,,...,n a a a ，输出,A B ，则（）()A A B +为12,,...,n a a a 的和 ()B 2A B+为12,,...,n a a a 的算术平均数 ()C A 和B 分别是12,,...,n a a a 中最大的数和最小的数 ()D A 和B 分别是12,,...,n a a a 中最小的数和最大的数开A=xB=xx否 输出是输入N ，结x <Bk ≥k =1,A =a 1k =kx 是 否否是14浙江12．若程序框图如图所示，则该程序运行后输出的值是______________．x1 2 4 8y12 3 4 22=⇒=k ，8=s ，循环结束，输出的s 为8，故选C 。

【答案】3.考点：算法初步。

难度：易。

分析：本题考查的知识点为算法中流程图的读法，直接根据箭头的指向运算即可。

解答： 1,1==s k ；2,1112==-⨯=k s ； 3,0212==-⨯=k s ； 4,3302=-=-⨯=k s ；结束4.【解析】输出s 的值为 8 S 1 2 4 8 i 2 4 6 8 k 1 2 3 45.考点分析：本题考查程序框图. 难易度：★★解析：程序在运行过程中各变量的值如下表示： 第一圈循环：当n=1时，得s=1，a=3. 第二圈循环: 当n=2时，得s=4，a=5 第三圈循环：当n=3时，得s=9，a=7 此时n=3，不再循环，所以解s=9 . 6.【答案】4-【解析】输入1x =-,n =3,，执行过程如下：2:6233i S ==-++=-；1:3(1)115i S ==--++=；0:5(1)014i S ==-++=-，所以输出的是4-.【点评】本题考查算法流程图，要明白循环结构中的内容，一般解法是逐步执行，一步步将执行结果写出，特别是程序框图的执行次数不能出错. 7.【答案】5。

算法初步考纲导算法的含义、程序框图（一）了解算法的含义，了解算法的思想。

（二）理解程序框图的三种基本逻辑结构：顺序结构、条件结构和循环结构。

知识高考导算法不仅是数学及其应用的重要组成部分，也是计算机科学的重要基础。

算法初步虽然是新课标增加的内容，但与前面的知识有着密切的联系，并且与实际问题的联系也非常密切。

因此，在高考中算法初步知识将与函数、数列、三角、概率、实际问题等知识点进行整合，是高考试题命制的新“靓”点。

这样试题就遵循了“在知识网络交汇处设计试题”的命制原则，既符合高考命题“能力立意”的宗旨，又突出了数学的学科特点。

这样做，可以从学科的整体高度和思维价值的高度考虑问题，可以揭示数学各知识之间得到的内在联系，可以使考查达到必要的深度。

考查形式与特点是：（1）选择题、填空题主要考查算法的含义、流程图、基本算法语句等内容，一般在每份试卷中有1～2题，多为中档题出现。

(2)在解答题中可通过让学生读程序框图去解决其它问题，此类试题往往是与数列题结合在一起，具有一定的综合性，可以考查学生的识图能力及对数列知识的掌握情况.第1课时算法的含义基础1．算法的概念:对一类问题的机械的、统一的求解方法称为算法。

2．算法的特性:（1）有限性 （2）确定性例1.给出求1+2+3+4+5的一个算法。

解：算法1第一步：计算1+2，得到3第二步：将第一步中的运算结果3与3相加，得到6 第三步：将第二步中的运算结果6与4相加，得到10 第四步：将第三步中的运算结果10与5相加，得到15 算法2 第一步：取n=5 第二步：计算第三步：输出运算结果 变式训练1.写出求111123100++++的一个算法． 解：第一步：使1S =，； 第二步：使2I =； 第三步：使1n I=； 第四步：使S S n =+； 第五步：使1I I =+；第六步：如果100I ≤，则返回第三步，否则输出S ．例2. 给出一个判断点P ),(00y x 是否在直线y=x-1上的一个算法。

6.枣核 1.掌握以具体事物作贯穿全文的线索,围绕事物设置悬念的写法。

2.体会海外华人依恋故土的感情。

3.诵读赏析明白如话的散文语言中饱含的游子深情。

●重点: 1.了解作者写枣核的真正目的。

2.体会文中蕴含的深厚复杂的感情。

1.下面是某同学在预习文章时做的笔记,请你帮助他补充完整。

萧乾,　蒙古　族人,著名作家、翻译家和　记者　。

晚年多次出访欧美及东南亚国家进行文化交流活动,写出了三百多万字的回忆录、散文、特写、随笔及译作。

主要著作、译作有《篱下集》《梦之谷》《人生百味》《一本褪色的相册》《　莎士比亚戏剧故事集　》《尤利西斯》等。

1998年10月出版的《萧乾文集》收集了他的主要著作、译作。

? 2.给下列加点字注音。

蹊跷(qī)(qiāo) 嫣红(yān) 掐指(qiā) 山坳(ào) 玛瑙(nǎo)感慨(kǎi)诞生(dàn)踏访(tà) 拓展:请根据语境,给加点字注音。

(1)父亲劈(pī)头就问:“你为何将这块木头劈(pǐ)成两半,它可是有用的一块材料啊!” (2)解放军叔叔们帮受灾群众灌溉(ài)了很多农田,老百姓被他们这种不怕困难的大无畏的英雄气概(ài)深深感染,每当回首往事时都感慨(kǎi)良深。

3.请根据括号内的解释,结合上下文语境,写出相应的词语。

(1)掐指一算,分手快有半个世纪了,现在都已是(比喻老年人所剩的日子不多了,随时会死去)。

　风烛残年　? (2)她把我安顿在二楼临湖的一个房间后,就领我去(实地察访)她的后花园。

踏访 ? (3)他一面(故意玩弄花招,使人高深莫测)地说:“等会儿你就明白啦。

”　故弄玄虚　? (4)追忆起当年在北海(坐船游玩)的日子。

泛舟 ? 4.朗读课文,根据下面图示填空。

问题一:阅读文章,整体感知。

1.文章紧扣“枣核”这个线索,先后写了哪些事件?你觉得“旧时同窗”的思乡之情重点表现在哪些事情上呢? 示例:先后写了索枣核——见枣核——话枣核,思乡之情重点体现在“旧时同窗”栽垂杨柳、建睡莲池、修建“北海”、月夜追忆往事等事件上。

L 算法初步与复数L1 算法与程序框图6．L1[2012·课标全国卷] 如果执行右边的程序框图，输入正整数N(N≥2)和实数a1，a2，…，a N，输出A，B，则( )A．A＋B为a1，a2，…，a N的和B.A＋B2为a1，a2，…，a N的算术平均数C．A和B分别是a1，a2，…，a N中最大的数和最小的数D．A和B分别是a1，a2，…，a N中最小的数和最大的数图1－16．C [解析] 根据程序框图可知x>A时，A＝x，x≤A且x<B时，B＝x，所以A是最大值，B是最小值，故选C.6．L1[2012·某某卷] 如图1－)的输出结果是( )A．3 B．4C．5 D．86．B [解析] 由程序框图可知，第一次循环后，得到x＝2，y＝2，满足判断条件；第二次循环后，得到x＝4，y＝3，满足判断条件；第三次循环后，得到x＝8，y＝4，不满足判断条件，故跳出循环，输出y＝4.4．L1[2012·卷] 执行如图1－2所示的程序框图，输出的S值为( )A．2 B．4C．8 D．164．C [解析] 本题考查了循环结构的流程图，简单的整数指数幂计算等基础知识．根据循环k＝0，S＝1；k＝1，S＝2；k＝2，S＝8，当k＝3，时，输出S＝8.6．L1[2012·某某卷] 阅读如图1－1所示的程序框图，运行相应的程序，输出的s值等于( )A．－3 B．－10 C．0 D．－26．A [解析] 第一次循环由于k＝1<4，所以s＝2－1＝1，k＝2；第二次循环k＝2<4，所以s＝2－2＝0，k＝3；第三次循环k＝3<4，所以s＝0－3＝－3，k＝4，结束循环，所以输出s＝－3.16．L1[2012·某某卷] 某地区规划道路建设，考虑道路铺设方案，方案设计图中，点表示城市，两点之间连线表示两城市间可铺设道路，连线上数据表示两城市间铺设道路的费用．要求从任一城市都能到达其余各城市，并且铺设道路的总费用最小，例如：在三个城市道路设计中，若城市间可铺设道路的线路图如图1－2①，则最优设计方案如图1－2②，此时铺设道路的最小总费用为10.2现给出该地区可铺设道路的线路图如图1－2③，则铺设道路的最小总费用为________．16．16 [解析] 根据题意先选择中间最优线路，中间有三条，分别是A→F→G→D、E→F→B、E→G→C，费用最低的是A→F→G→D为3＋1＋2＝6；再选择A→F→G→D线路到点E的最低费用线路是：A→E费用为2；再选择A→F→G→D到C、B的最低费用，则选择：G→C→B，费用最低为3＋5＝8，所以铺设道路的最小费用为：6＋2＋8＝16.9．L1[2012·某某卷] 执行如图1－2所示的程序框图，若输入n的值为6，则输出s 的值为( )图1－2A．105 B．16C．15 D．19．C [解析] 第一次循环结果是：s＝1，i＝3；第二次循环结果是：s＝3，i＝5；第三次循环结果是：s＝15，i＝7，此时i>n，结束循环，输出s＝15.所以选择C.16．L1[2012·某某卷] 阅读如图1－5所示的程序框图，运行相应的程序，输出的结果s＝________.16．[答案] 9[解析] 因为已知a＝1，s＝0，n＝1，所以第一次运行后：s＝s＋a＝1，a＝a＋2＝3，n＝1<3成立，满足判断条件；第二次运行后：n＝n＋1＝2，s＝s＋a＝1＋3＝4，a＝a＋2＝5，n＝2<3成立，满足判断条件；第三次运行后：n＝n＋1＝3，s＝s＋a＝4＋5＝9，a＝a＋2＝7，n＝3<3不成立，不满足判断条件，输出s的值(s＝9)．14．L1[2012·某某卷] 如果执行如图1－4所示的程序框图，输入x＝4.5，则输出的数i图1－414．4 [解析] 本题考查程序框图和循环结构，意在考查考生的逻辑推理能力和对循环结构的理解能力；具体的解题思路和过程：依次循环，达到条件退出．当i＝1时x＝3.5，当i＝2时x＝2.5，当i＝3时x＝1.5，当i＝4时x＝0.5，此时退出循环，故i＝4.[易错点] 本题易错一：循环条件弄错，多计一次，或者少计一次，得到错误结果． 4．L1[2012·某某卷] 图1－1是一个算法流程图，则输出的k 的值是________．图1－14．5 [解析] 本题为对循环结构的流程图的含义的考查．解题突破口为从循环终止条件入手，再一一代入即可．将k ＝1,2,3，…，分别代入可得k ＝5.15．L1[2012·某某卷] 图1－5是某算法的程序框图，则程序运行后输出的结果是________．图1－515．3 [解析] 当k ＝1时，此时sin π2＝1>sin0＝0成立，因此 a ＝1，T ＝0＋1＝1，k＝1＋1＝2，k <6成立，再次循环；因sinπ＝0>sin π2＝1不成立，因此a ＝0，T ＝1＋0＝1，k ＝2＋1＝3，此时k <6成立，再次循环；因sin 3π2＝－1> sinπ＝0不成立，因此a ＝0，T＝1＋0＝1，k ＝3＋1＝4，此时k <6成立，再次循环；因sin2π＝0>sin 3π2＝－1成立，因此a ＝1，T ＝1＋1＝2，k ＝4＋1＝5，此时k <6成立，再次循环；因sin 5π2＝1> sin2π＝0成立，因此a ＝1，T ＝2＋1＝3，k ＝5＋1＝6，此时k <6不成立，退出循环，此时T ＝3.10．L1[2012·某某卷] 执行如图1－2所示的程序框图，则输出的S 值是( )图1－1图1－2A ．4 B.32 C.23D ．－110．D [解析] 本小题主要考查程序框图的应用．解题的突破口为分析i 与6的关系．当i ＝1时，S ＝22－4＝－1；当i ＝2时，S ＝22－－1＝23；当i ＝3时，S ＝22－23＝32；当i ＝4时，S ＝22－32＝4；当i ＝5时，S ＝22－4＝－1；当i ＝6时程序终止，故而输出的结果为－1.7．L1[2012·某某卷] 执行如图1－1所示的程序框图，如果输入a ＝4，那么输出的n 的值为( )图1－1A ．2B ．3C ．4D ．57．B [解析] 本题考查算法与程序框图，考查数据处理能力，容易题．当n ＝0时，P ＝1，Q ＝3，P <Q 成立，执行循环；当n ＝1时，P ＝5，Q ＝7，P <Q 成立，执行循环；当n ＝2时，P ＝21，Q ＝15，P <Q 不成立，但是n ＝2＋1＝3后，再输出．5．L1[2012·某某卷] 图1－2是计算某年级500名学生期末考试(满分为100分)及格率q 的程序框图，则图中空白框内应填入( )A ．q ＝N MB ．q ＝M NC ．q ＝NM ＋ND ．q ＝MM ＋N图1－25．D [解析] 从框图中可以看出M代表及格的人数，N代表不及格的人数，M＋N代表总人数，故填入的应为及格率q＝MM＋N.3．L1[2012·某某卷] 阅读如图1－1所示的程序框图，运行相应的程序，则输出S的值为( )A．8 B．18C．26 D．80图1－13．C [解析] 当n＝1时，S＝2；当n＝2时，S＝2＋32－3＝8；当n＝3时，S＝8＋33－32＝26；当n＝4时输出S＝26.13．L1[2012·某某卷] 若某程序框图如图1－4所示，则该程序运行后输出的值是________．图1－413.1120 [解析] 当i ＝1时，T ＝11＝1，而i ＝1＋1＝2，不满足条件i >5；接下来，当i ＝2时，T ＝12，而i ＝2＋1＝3，不满足条件i >5；接下来，当i ＝3时，T ＝123＝16，而i ＝3＋1＝4，不满足条件i >5；接下来，当i ＝4时，T ＝164＝124，而i ＝4＋1＝5，不满足条件i >5；接下来，当i ＝5时，T ＝1245＝1120，而i ＝5＋1＝6，满足条件i >5；此时输出T ＝1120，故应填1120.L2 基本算法语句 L3 算法案例 L4 复数的基本概念与运算2．L4[2012·某某卷] 已知i 是虚数单位，则3＋i1－i＝( )A ．1－2iB ．2－iC ．2＋iD ．1＋2i2．D [解析] 本题主要考查复数的四则运算，检测学生对基础知识的掌握情况． 3＋i 1－i ＝3＋i 1＋i 1－i 1＋i ＝2＋4i2＝1＋2i ，故应选D. 1．L4[2012·某某卷] i 是虚数单位，复数5＋3i4－i＝( )A ．1－iB ．－1＋iC ．1＋iD ．－1－i1．C [解析] 5＋3i 4－i ＝5＋3i 4＋i 4－i 4＋i ＝5×4－3＋3×4＋5i42＋12＝1＋i. 15．L4[2012·某某卷] 若1＋2i 是关于x 的实系数方程x 2＋bx ＋c ＝0的一个复数根，则()A ．b ＝2，c ＝3B ．b ＝2，c ＝－1C ．b ＝－2，c ＝－1D ．b ＝－2，c ＝315．D [解析] 考查复数的概念和一元二次方程中根与系数的关系(即韦达定理)，可利用方程的两根是共轭复数解题．由韦达定理可知：－b ＝(1＋2i)＋(1－2i)＝2，∴b ＝－2， c ＝(1＋2i)(1－2i)＝1＋2＝3，∴c ＝3，所以选D.此题还可以直接把复数根1＋2i 代入方程中，利用复数相等求解．1．L4[2012·某某卷] 计算：3－i1＋i＝________(i 为虚数单位)1．1－2i [解析] 考查复数的除法运算，是基础题，复数的除法运算实质就是分母实数化运算．原式＝3－i 1－i1－i 2＝1－2i. 4．A2、L4[2012·某某卷] 设a ，b ∈R ，i 是虚数单位，则“ab ＝0”是“复数a ＋bi为纯虚数”的( )A ．充分不必要条件B ．必要不充分条件C ．充分必要条件D ．既不充分也不必要条件4．B [解析] 本小题主要考查充要条件的概念以及复数的相关知识，解题的突破口为弄清什么是纯虚数，然后根据充要条件的定义去判断．a ＋b i ＝a －b i ，若a ＋bi 为纯虚数，a＝0且b ≠0，所以ab ＝0不一定有a ＋b i 为纯虚数，但a ＋bi 为纯虚数，一定有ab ＝0，故“ab＝0”是“复数a ＋bi为纯虚数”的必要不充分条件，故选B.1．L4[2012·某某卷] 若复数z 满足z (2－i)＝11＋7i(i 为虚数单位)，则z 为( ) A ．3＋5i B ．3－5i C ．－3＋5i D ．－3－5i1．A [解析] 本题考查复数的概念及运算，考查运算能力，容易题．设z ＝a ＋b i(a ，b ∈R )，由题意得(a ＋b i)(2－i)＝(2a ＋b )＋(2b －a )i ＝11＋7i ，即⎩⎪⎨⎪⎧2a ＋b ＝11，2b －a ＝7， 解之得⎩⎪⎨⎪⎧a ＝3，b ＝5.3．L4[2012·某某卷] 复数11＋i＝( ) A.12－12i B.12＋12i C ．1－i D ．1＋i3．A [解析] 解题的突破口为分子分母同乘以分母的共轭复数．因为11＋i ＝1－i 1＋i 1－i ＝1－i 2＝12－i 2，所以答案选A.2．L4[2012·课标全国卷] 复数z ＝－3＋i2＋i的共轭复数是( )A ．2＋iB ．2－iC ．－1＋iD ．－1－i2．D [解析] 因为z ＝－3＋i 2＋i ＝－3＋i 2－i2＋i 2－i ＝－1＋i ，所以z ＝－1－i.故选D.1．L4[2012·某某卷] 若复数z ＝1＋i(i 为虚数单位)，z 是z 的共轭复数，则z 2＋z2的虚部为( )A ．0B ．－1C ．1D ．－21．A [解析] ∵z ＝1＋i ，∴z 2＝(1＋i)2＝2i ，z ＝1－i ，z 2＝(1－i)2＝－2i ，∴z 2＋z 2＝0，故选A.3．L4[2012·某某卷] 设a ，b ∈R ，a ＋b i ＝11－7i1－2i(i 为虚数单位)，则a ＋b 的值为________．3．8 [解析] 本题考查复数的四则运算．解题突破口为将所给等式右边的分子、分母同时乘以分母的共轭复数即可．因为11－7i 1－2i ＝11－7i 1＋2i 5＝5＋3i ，所以a ＝5，b ＝3.2．L4[2012·某某卷] 复数z ＝i(i ＋1)(i 为虚数单位)的共轭复数是( ) A ．－1－i B ．－1＋i C ．1－i D ．1＋i2．A [解析] 本题考查复数的乘法运算和复数的共轭复数，意在考查考生对复数的简单运算和共轭复数的掌握．复数z ＝i(i ＋1)＝i 2＋i ＝－1＋i ，其共轭复数为z ＝－1－i ，所以选A.[易错点] 本题易错一：把i 2等于1，导致错选C ；易错二：忘记共轭复数的定义．12．L4[2012·某某卷] 若3＋b i1－i＝a ＋b i(a ，b 为实数，i 为虚数单位)，则a ＋b ＝________.12．[答案] 3[解析] 由3＋b i1－i＝a ＋b i ，得3＋b i ＝(a ＋b i)(1－i)＝a ＋b ＋(b －a )i ，即a ＋b －3－a i＝0.所以⎩⎪⎨⎪⎧a ＋b －3＝0，－a ＝0， 解得⎩⎪⎨⎪⎧a ＝0，b ＝3，所以a ＋b ＝3.1．L4[2012·某某卷] 设i 为虚数单位，则复数3＋4ii＝( )A ．－4－3iB ．－4＋3iC ．4＋3iD ．4－3i1．D [解析] 因为3＋4i i ＝3＋4i i i·i ＝3i －4－1＝4－3i ，所以选择D.1．L4[2012·某某卷] 复数(2＋i)2等于( ) A ．3＋4i B ．5＋4i C ．3＋2i D ．5＋2i1．A [解析] 利用复数乘法运算求解，(2＋i)2＝4＋4i ＋i 2＝3＋4i ，所以选择A.2．L4[2012·卷] 在复平面内，复数10i3＋i对应的点的坐标为( )A ．(1,3)B ．(3,1)C ．(－1,3)D ．(3，－1)2．A [解析] 本题考查复数代数形式的除法运算和复数几何意义.10i3＋i＝10i 3－i3＋i 3－i ＝1＋3i ，所以它对应点的坐标为(1,3)．1．L4[2012·某某卷] 复数z 满足(z －i)i ＝2＋i ，则z ＝( ) A ．－1－i B ．1－i C ．－1＋3i D ．1－2i1．B [解析] 由()z －i i ＝2＋i ，得z －i ＝2＋ii＝1－2i ，所以z ＝1－i.L5 单元综合2012模拟题1．[2012·某某八校联考] 图K44－1为一个算法的程序框图，则其输出结果是( )图K44－1A ．0B ．2012C ．2011D ．11.A [解析] p ＝0，n ＝1，p ＝1，n ＝2，p ＝1，n ＝3，p ＝0，n ＝4，p ＝0，n ＝5，p ＝1，n ＝6，…，周期为4的循环变化，可知p ＝0，n ＝2012，是；p ＝0，n ＝2013；否，输出p ＝0.2．[2012·某某一中检测] 运行下面的程序，如果输入的n 是6，那么输出的p 是( )INPUT “n＝”；n k ＝1 p ＝1WHILE k<＝n p ＝p*k k ＝k ＋1WEND PRINT p ENDA ．120B ．720C ．1440D ．50402．B [解析] 如果输入的n 是6，k ＝1，p ＝1；k ＝2，p ＝2；k ＝3，p ＝6；k ＝4，p ＝24；k ＝5，p ＝120；k ＝6，p ＝720；输出720.3．[2012·某某质量评估] 执行下面的程序框图，若p ＝4，则输出的S 等于________．图K44－5图K44－63.1516 [解析] 因p ＝4，n ＝0，S ＝0；n ＝1，S ＝12；n ＝2，S ＝12＋122；n ＝3，S ＝12＋122＋123；n ＝4，S ＝12＋122＋123＋124＝1516；不满足n <p ，输出S ＝1516.4．[2012·某某师大附中月考] 设复数z 1＝1－3i ，z 2＝3－2i ，则z 1z 2在复平面内对应的点在( )A ．第一象限B ．第二象限C ．第三象限D ．第四象限4．D [解析] ∵z 1z 2＝1－3i 3－2i＝1－3i 3＋2i 3－2i 3＋2i ＝9－7i 13，∴z 1z 2在复平面内对应的点在第四象限． 5．[2012·某某师大附中月考] 已知x1＋i＝1－y i ，其中x 、y 是实数，i 是虚数单位，则x ＋y i 等于( )A ．1＋2iB ．1－2iC ．2＋iD ．2－i5．C [解析] x 1＋i ＝1－y i ⇒x ＝(1－y i)(1＋i)⇒x ＝(1＋y )＋(1－y )i ⇒⎩⎪⎨⎪⎧ 1－y ＝0，x ＝1＋y ⇒⎩⎪⎨⎪⎧x ＝2，y ＝1，故x ＋y i ＝2＋i.。