算法流程图

输出sum 用N-S图表示
N i<n?
Y t*=i;sum+=t;
iቤተ መጻሕፍቲ ባይዱ=2 输出sum
结束 用流程图表示
8.7 跟我上机
2. 将1到100之间 能用3或5整 除的数打印 出来。
开始
i赋初值为1
N i<=100?
Y N
i能被3或5整 除？ Y 打印i
i++
结束
用流程图表示
i赋初值为1
i<=100?
i能被3或5整 除？
N d>=0？
x2=x-sqrt(-d)/(2a) x1=x+ sqrt(-d)/(2a)
输出结果
8.7 跟我上机
开始 输入n的值
1. 求1！+3！+5！+……+N!的值。N
i赋值为1 t赋初值为1
由键盘输入，且为奇数。
sum赋初值为0
输入n的值 t赋初值为1； i赋值为1
sum赋初值为0 i<n? t*=I; s+=t; i+=2
求最大公约数通常用“辗转相除法”，
方法如下：
（1）比较两数，并使m大于n。 （2）将m作被除数，n作除数，相除 后余数为r。 （3）将m←n，n←r； （4）若r=0，则m为最大公约数，结 束循环。若r≠0，执行步骤步骤（2） 和（3）。
输入m,n
T
m<n?
F
交换m,n
r←m%n m←n，n←r
r ≠0 输出m
8.3.6 用计算机语言表示算法
计算机语言通常分为三类：即机器语言，汇编语 言和高级语言。
8.4 结构化程序设计方法
结构化程序设计的思想：自顶向下、逐步求 精；

算法、代码与流程图的关系理解下载温馨提示:该文档是我店铺精心编制而成，希望大家下载以后，能够帮助大家解决实际的问题。

文档下载后可定制随意修改，请根据实际需要进行相应的调整和使用，谢谢!并且，本店铺为大家提供各种各样类型的实用资料，如教育随笔、日记赏析、句子摘抄、古诗大全、经典美文、话题作文、工作总结、词语解析、文案摘录、其他资料等等，如想了解不同资料格式和写法，敬请关注!Download tips: This document is carefully compiled by theeditor. I hope that after you download them,they can help yousolve practical problems. The document can be customized andmodified after downloading,please adjust and use it according toactual needs, thank you!In addition, our shop provides you with various types ofpractical materials,such as educational essays, diaryappreciation,sentence excerpts,ancient poems,classic articles,topic composition,work summary,word parsing,copy excerpts,other materials and so on,want to know different data formats andwriting methods,please pay attention!1. 算法算法是解决问题的一系列明确步骤。

它描述了如何完成特定任务或解决特定问题的逻辑过程。

流 程 图
i) 顺序结构
三种基本算法结构
ii) 选择结构
Y A B A
p

N B
循环结构
算法2流程图:
算法2:
开始 T←1
S1
S2
T←1；
S←2；
S←2
T←T×S S←S+1 S>5 Y 输出T 结束 N
S3
S4 S5
T←T×S；
S←S+1； 如果S不大于5,返 回 S3,否则输出T。
开始
开始
i ← 0，Sum ← 0
2010辽宁文数如果执行下图左的程序框图输入那么输出的等于a720b360c240d12010aa1b2b1输出b结束缚目录点击添加标题点击添加标题点击添加标题点击添加标题添加文本点击添加文本点击添加文本点击添加文本点击添加文本点击添加文本点击添加文本添加文本点击添加文本点击添加文本点击添加文本点击添加文本添加文本点击添加文本点击添加文本点击添加文本添加文本点击添加文本点击添加文本点击添加文本点击添加文本点击添加文本点击添加文本添加文本点击添加文本点击添加文本点击添加文本点击添加文本点击添加文本添加文本点击添加文本点击添加文本点击添加文本添加文本点击添加文本点击添加文本点击添加文本点击添加文本点击添加文本点击添加文本点击添加文本01020304添加标添加文本点击添加文本点击添加文本点击添加文本点击添加文本会议基调年会视频
开始 Sum←0,i←1 Sum←Sum+1 i←i+1 否 i>100 是 输出Sum 结束
1.【2010· 浙江理数】 某程序框图如左图所 示，若输出的S=57， 则判断框内位（ ） A. k＞4? B.k＞5? C. k＞6? D.k＞7?
2.【2010· 辽宁文数】 如果执行下图（左）的 程序框图，输入 n 6 , m 4那么输出的 等于（ ） A.720 B.360 C.240 D.120

编程算法流程图，绘制软件和例⼦分享
算法流程图，专指以特定的图形符号加上说明表⽰算法的图。

⼀般有两种表⽰⽅法：传统流程图与结构流程图，其中传统流程图应该更⼴泛⼀些。

算法设计可以称之为程序设计的核⼼，⽽表⽰⼀个算法，有多种不同的⽅法，常⽤的有⾃然语⾔，流程图，伪代码，PAD图等。

算法流程图作⽤
程序⼀般可简单划分为两类：逻辑流程类程序、算法应⽤类程序，但复杂的应⽤多是⼆者的组合。

其中逻辑流程类更多强调的是时序、操作步骤等，⼀般都是⽤来简化⼈类的事务性劳动⽽设计，如打开12306⽹站，登录后查询并购买⽕车票，整个过程应涉及到⼀系列与⼈交互的逻辑动作，另有后台的数据查询匹配算法，属于典型的融合应⽤。

⼆者中，算法部分更复杂、抽象，需要⼀种图形化的⽅法来描述。

⽤图形表⽰算法，直观形象，易于理解，更⽅便开发交流及测试检验。

算法流程图不仅⽤来指导编写程序，⽽且在调试程序中可以⽤来检查程序的正确性。

如果框图是正确的⽽结果不对，则按照框图逐步检查程序是很容易发现其错误的。

核⼼算法流程图⼀般是软件开发中的重要⽂档，作为程序说明书的⼀部分进⾏存档，供合作伙伴、后加⼊同事参考，更好的帮助理解算法的思路和结构。

算法流程图绘制符号
下⾯为亿图图⽰中的流程图的基本构成元素：红框的和上述基本⼀致，箭头在下⾯也⼀样有。

顺序流程图：（数据是我胡乱写的，主要是看结构）
分⽀结构：（前是if 后是 switch）（数据是我胡乱写的，主要是看结构）
循环结构：（数据是我胡乱写的，主要是看结构）
算法流程图绘制要点
任何复杂的算法流程图都是由：顺序结构、分⽀结构和循环结构三种结构组合⽽成。

算法流程图绘制案例。

程序框图的发展趋势
可视化编程
随着可视化技术的发展，程序框 图成为一种直观的编程方式。通 过图形化的方式描述程序逻辑， 降低了编程难度，提高了开发效 率。
交互式编程
交互式编程让用户在编程过程中 能够实时查看程序运行结果，及 时调整代码。这种编程方式提高 了开发效率和程序质量。
智能生成与自动优
化
基于机器学习和人工智能技术， 程序框图可以自动生成和优化程 序代码。这大大减少了编程工作 量，提高了开发效率。
算法的复杂度分析
随着计算机科学的发展，算法的复杂度分析越来越受到重 视。人们不断探索更高效的算法，以提高计算效率和准确 性。
机器学习与人工智能算法
随着人工智能的兴起，机器学习与人工智能算法成为研究 热点。这些算法能够从大量数据中自动提取有用的信息， 为决策提供支持。
并行计算与分布式算法
为了处理大规模数据和复杂问题，并行计算和分布式算法 成为研究重点。这些算法能够充分利用多核处理器和分布 式系统的优势，提高计算性能。
算法的表示方法
01
自然语言描述
用简洁明了的文字描述算法的步骤。
流程图
用图形符号表示算法的步骤和流程。
03
02
伪代码
用类似于编程语言的简化和结构化 形式描述算法。
程序代码
用编程语言实现算法的具体代码。
04
算法的复杂度分析
时间复杂度
评估算法执行时间随输入规 模增长的情况，表示为 O(f(n))。
空间复杂度
选择结构是根据条件判断选择不同的执行路径的程序框图 结构。它使用判断框来表示条件判断，根据条件的结果选 择不同的执行路径。选择结构可以有效地处理具有多个分 支的情况，提高程序的灵活性和适应性。

第2章算法及算法的流程图表示
数据结构+算法=程序
2.1算法的概念及特性
2.1.1算法的概念
2.1.2算法的特性
2.2算法的流程图表示
2.2.1传统流程图
起止框
处理框
输入输出框
判断框
流程线
连接点
注释框
图2.1 常用的流程图符号
图2.2 求解例2.1的流程图
2(x 0)
2x 3y 0
(x 0)x 1
(x 0)
>⎧+⎪==⎨
⎪+<
⎩
图2.3 求解例2.2的流程图 图2.4 求解例2.3的流程图
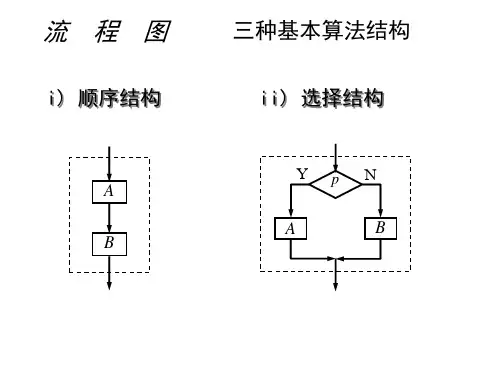
2.2.2 结构化程序的3种基本结构
图2.5 顺序结构图2.6 分支结构图2.7 当型循环结构图2.8 直到型循环结构2.2.3结构化流程图
A B
p
成立不成立
A B
当条件p成立
A
直到条件p成立
A
图2.9 顺序结构图2.10 分支结构图2.11 当型循环结构图2.12 直到型循环结构
输入x
x>0?
是否
y=2*x+3 是否
y=0 y=x*x+1
x==0?
输出y aver=0；count=0
输入x
aver=aver+x;count=count+1;
输入x
当x≠0时
aver=aver/count
输出aver
图2.13 例2.2的N-S图图2.14 例2.3的N-S图
习题2。

简介
计算机语言只是一种工具。光学习语言的规则还不够，最重要的是学会针对各种类型的问题，拟定出有效的 解决方法和步骤即算法。有了正确而有效的算法，可以利用任何一种计算机高级语言编写程序，使计算机进行工 作。因此，设计算法是程序设计的核心。为了表示一个算法，可以用不同的方法。常用的有自然语言，流程图， 伪代码，PAD图等。这其中以特定的图形符号加上说明，表示算法的图，称为算法流程图。
传统的流程图用流程线指出各框的执行顺序，对流程线的使用没有严格限制。因此，使用者可以毫不受限制 地使流程随意地转来转去，使流程图变得毫无规律，阅读者要花很大精力去追踪流程，使人难以理解算法的逻辑。 如果我们写出的算法能限制流程的无规律任意转向，而像一本书那样，由各章各节顺序组成，那样，阅读起来就 很方便，不会有任何困难，只需从头到尾顺序地看下去即可。
为了提高算法的质量，使算法的设计和阅读方便，必须限制箭头的滥用，即不允许无规律地使流程乱转向， 只能按顺序地进行下去。但是，算法上难免会包含一些分支和循环，而不可能全部由一个一个框顺序组成。如上 例不是由各框顺序进行的，包含一些流程的向前或向后的非顺序转移。为了解决这个问题，人们设想，如果规定 出几种基本结构，然后由这些基本结构按一定规律组成一个算法结构，整个算法的结构是由上而下地将各个基本 结构顺序排列起来的。1966年，Bohra和Jacoplni提出了以下三种基本结构，用这三种基本结构作为表示一个良 好算法的基本单元。
1、顺序结构：如图2所示的虚线框内，A和B两个框是顺序执行的。顺序结构是最简单的一种基本结构。
图2
2、选择结构：如图3所示的虚线框中包含一个判断框。
结构流程图
1973年美国学者提出了一种新的流程图形式。在这种流程图6中，完全去掉了带箭头的流程线。全部算法写 在一个矩形框内。在该框内还可以包含其它的从属于它的框，即可由一些基本的框组成一个大的框。这种适于结 构化程序设计的流程图称N-S结构化流程图，它用以下的流程图符号：

Pull 2
Jump from here to Pull Plan Subflow 2 (p. 5)
如果计划供应能完整的满足物料需求,计划就完 成了.(不必计划这个物料的子项了).
如果物料定义了时界,当分配库存时,就要考虑时 界..
4
Pull 2
Pull Plan Subflow 2
子 吗项 ? 需求满Ye足s
Push Plan Subflow 1
BOM 最 高 层 已 Yes 需求计划成功 (回到主流
经计划了吗?
程)
No
A Starting-point A
交叉Ye参s 照供应吗?
用交叉参照供应满 足需求
Jump from here to
A starting-point A on
this page
用BOM最低层次的子项开始向前推.
同页联结器.去到指明位置
流程的开始点.它是从前一页的继续 开始参考点,从同页连接器或离页连 接器 .
选择了所有BOM的制造 物料是停止时间界限吗?
是
拉子流程
"计划传递 B" (从完成日期拉且 忽视时间界限)
跳到拉子流程1 (4页) , 然后返回
如果需求上拉订单,就从 需求日期拉,而不是完成 日期.
不
No
物料的无限Y字es段选择了吗?
计划需求在当前日 期作为可用
No 是转移物料?
Yes
计划模式 =全局?
Yes
No
Pull 3
Jump from here to Pull Plan Subflow 3 (p. 6)
No
Pull 3-A
Jump from here to Pull Plan Subflow 3, starting-point A (p. 6)

. 算法的表示
可以用不同的方法表示算法，常用的有： 自然语言 传统流程图 结构化流程图 伪代码 PAD图
. 用流程图表示算法
美国国家标准化协会ANSI(American National Standard Institute)规定了一些常用的流程图 符号：
起止框
判断框
处理框
输入/输出框
总结：
两种流程图主要区别在于：N-S流程图完全
去掉了传统流程图的带箭头的流程线，比文 字描述直观、形象、 易于理解；比传统流程 图紧凑易画。而只能至上而下有序地运行， 避开了传统流程图运行的跳转。但是，两种 流程图都有确定性、有穷性、有效性。
Thank You !
Everyone !
N-S流程图用以下的流程图符号：
(1)顺序结构. (2)选择结构.
(3)循环结构.
用三种N-S流程图中的基本框，可以组成复杂 的N-S流程图。图中的A框或B框，可以是一个简 单的操作，也可以是三个基本结构之一。
A框可以是一个选择结构
B框可以是一个循环结构
例2.13 判定 闰年的算 法 将例2.3用 N-S图表 示
注释框
流向线
连接点
2.三种基本结构
Bohra和Jacopini提出了以下三种基本 结构：
顺序结构、选择结构、循环结构 用这三种基本结构作为表示一个良好算 法的基本单元。
三种基本结构的图示：
顺序结构
选择结构
循环结构的图示：
当型(While型)循环结构
直到型(Until型)循环
例2.8 将例 2.3判定闰年 的算法用流 程图表示
不正确的流程表示：
图中没有一条从入口到 出口的路径通过A框

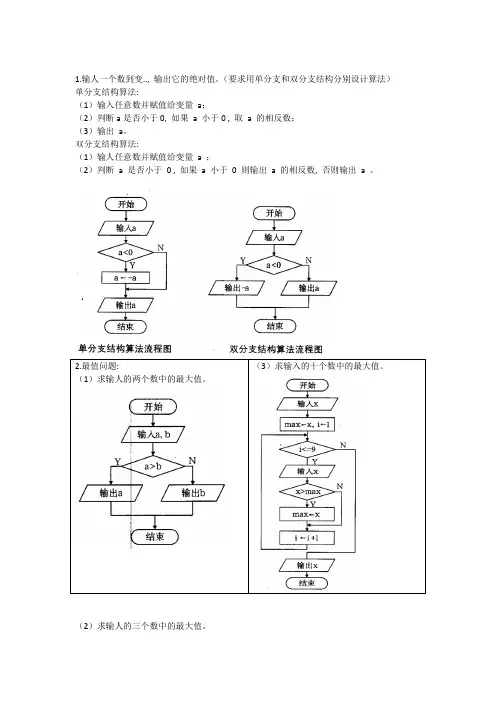
1.输人一个数到变.., 输出它的绝对值。

（要求用单分支和双分支结构分别设计算法）单分支结构算法:
（1）输入任意数并赋值给变量a；
（2）判断a是否小于0, 如果a 小于0 , 取a 的相反数；
（3）输出a。

双分支结构算法:
（1）输人任意数并赋值给变量 a ；
（2）判断a 是否小于0 , 如果a 小于0 则输出a 的相反数, 否则输出a 。

（3）求输入的十个数中的最大值。

2.最值问题:
（1）求输人的两个数中的最大值。

（2）求输人的三个数中的最大值。

3.循环求和（不同的控制循环方法）
1.求输.
2.个数的和。

(知道循环次数, 可以采用循环变量i 来控制循环次数)
计数法2.求输入的若干个学生成绩
的和, 输.-1表示结束。

（不能确定次数, 可以用输
入的数据的值来进行控制）
标志法
3.对输入的数据求和, 当所求
的和超.10.则停止输入并输出
求和结果（设此题中输人的数
皆为正数）。

（没有指出输人数据的具体个
数, 且不能依据对输入数据的
值来控制循环, 控制循环的关
键就在于对循环体中变量s
的判断）
（没有指出输人数据的具体个
数，且不能依据对输入数据的
值来控制循环，控制循环的关
键就在于对循环体中变量s
的判断）
输出如下图形:
**********
**********
**********
**********
**********
如下算法能输出哪种图形？（A）。

算法流程图(循环结 构)
目录
• 循环结构的概述 • 循环流程图的绘制 • 常见的循环结构算法 • 循环结构的应用场景 • 循环结构的注意事项 • 案例分析
01
循环结构的概述
循环结构的定义
循环结构是算法流程图中的一种基本结构，用于 01 重复执行一段代码，直到满足某个条件为止。
循环结构由三个基本部分组成：初始化、循环体 02 和终止条件。
详细描述
在for循环中，首先定义一个计数器变量和循环次数，然后在每次循 环中执行指定的操作，直到计数器达到设定的循环次数为止。
示例
以下是一个简单的for循环算法，用于计算1到10的累加和
for循环算法
```
sum = sum + i
for i = 1 to 10 do
for循环算法
end for ```
VS
详细描述
for循环通常用于已知循环次数的情况， 它包含三个基本部分：初始化、条件和后 续操作。在流程图中，for循环通常以矩 形表示，并在其中标明循环变量、初始值 、条件表达式和增量。例如，计算1到10 的累加和可以使用以下for循环实现
for循环的案例分析
```
for (int i = 1; i <= 10; i) {
控制条件的绘制
01 绘制一个菱形，标注为“条件”，表示循环的控
制条件。
02
在条件菱形内标注判断的具体内容，如“i<10” 。
循环次数的表示
使用一个数字标注在控制条件旁边，表示循环的 次数。
如果循环次数是动态变化的，可以使用变量代替 数字，如“n”。
03
常见的循环结构算法
for循环算法
总结词
for循环是一种预先设定循环次数的循环结构，通常用于已知循环次 数的情况。

1.该图是某算法的流程图，其输出值a是________ 312. 如图所示的流程图，若输入的x=- 9.5,则输出的结果为 ____________3. 某算法的程序框图如图，若输入a = 4, b= 2, c= 6,则输出的结果为.611*iJY（第1题）4. 一个算法的流程图如图所示，则输出的5•下面是一个算法的程序框图，当输入值S值为_______________ . 45x为8时，其输出的结果是_______________ . 2流程图一一三种基本算法逻辑结构顺序结构选择结构（第2题）（第4题）6. 运行如图所示的程序框图，则输出的结果 S = ___________ . 617. 如图所示的算法流程框图中， 若输入a = 4,b = 48,则最后输出的a 的值是 ________________ .96 8. 如图，程序执行后输出的结果为 _________ 6410.阅读下面的流程图，若输入______________a = 10, b = 6,则输出的结果是 211. _____________________________________________ 右图是一个算法的流程图，则输出 S 的值是 _________________________________________________ 7500开始/输出P/ 卩/9•按如图所示的流程图运算 ,则输出的S 二 _________20 （第6题）（第7题）I —12. ___________________________________________ 右图是一个算法的流•程图，最后输出的k= _________________ . 1113•阅读右边的流程图,则输出S= ________ . 3015、图中是一个算法流程图，则输出的n= ______ 1116. 右图是一个算法的流程图，最后输出的x= ________ .-1017.执行右边的程序框图，若p =15,则输出的n二fT-li S^-0（第16题）5/输入/n=l,S=0沪針严/5丽7ZE~~TM=n+1 ［结束］（第15题）（第17题））如图所示，其输出结果是127开始（第14 题）结束14•程序框图（即算法流程图（第12题）（第13题）c-2cr+'l/输出口/18. 根据如图所示的算法流程图，可知输出的结果i为______________ .719. 右图是一个算法的流程图，最后输出的n = ____________ .10020. 右图是一个算法的流程图，则输出a的值是_____________. log2321. 已知某算法的流程图如图所示，若将输出的数组（x, y）依次记为（X1, y1）, （X2, y2），…, （X n, y n）,…，则程序运行结束时输出的最后一个数组为22. _________________________________ 如图,该程序运行后输出的结果为______________________________ 1623•执行右边的程序框图，若p= 9，则输出的s= _（第19题）（第18题）（开始〕1 rm2托（第20题）(第22 题)—• (27,—6)2.5苏州市第六中学2014数学必修三（算法）。

01,,n1,,n1,,)n x及数值分析各算法流程图一、插值1、 拉格朗日插值流程图：( 相应程序：lagrintp(x,y,xx))2,,n ,,j n 1,2,,n 1,,)n 2、 牛顿插值流程图(1)产生差商表的算法流程图(相应程序：divdiff(x,y))注：1、另一程序divdiff1(x,y)，输出的矩阵包含了节点向量。

而divdiff(x,y)不含节点向量。

2、另一程序tableofdd(x,y,m)，输出的是表格形式，添加了表头。

1,,),,n m 及1,,m (2)非等距节点的牛顿插值流程图(相应程序：newtint11(x,y,xx,m)) 、注：1、虽然程序newtint11(x,y,xx,m)考虑了多种情形，看上去很复杂，但基本流程结构还是如上图所示。

2、程序中调用的子程序是divdiff 。

若调用的子程序是divdiff1的话，流程图中的第三，第四，第五步要相应的改一下数字。

2,3,,1m +1,,j1,2,,n=1,2,,)n m 及(3)求差分表的流程图(相应程序：difference(y,m))注：1、difference 输出的是矩阵D 。

而另一程序tableofd(y,m)，输出的是带有表头的差分表。

n x m1,,),,1,,m注：1、程序newtforward1(x,y,xx,m))的结构与上述流程图一致，xx可以是数组。

2、另一程序newtforward(x,y,xx,m))先求出插值多项式，再求插值多项式在插值点的函数值。

基本结构还是和上面的流程图一样。

n x m1,,),,-x x1,,m注：1、程序newtbackward1(x,y,xx,m))的结构与上述流程图一致，xx可以是数组。

2、另一程序newtbackward(x,y,xx,m))先求出插值多项式，再求插值多项式在插值点的函数值。

基本结构还是和上面的流程图一样。

1,2,,n1,2,,n ,2,,)n x及3、Hermite 插值流程图(1) 已知条件中一阶导数的个数与插值节点的个数相等时的Hermite 插值流程图。

一、算法的概念
算法（algorithm）这个词出现于12世纪，指的是用阿拉伯数字进行运算的过程。

在数学中，现代意义上的“算法”通常是指可以有计算机来解决的某一类问题的程序或步骤，这些程序或步骤必须是明确和有效的，而且能够在有限步之内完成。

例3、求1+2+3+···+100的和。

算法分析：
第一步：对称地取前后两数相加，即1+100，2+99，
3+98，···，50+51，得出两数之和都是101的规律。

第二步：这样的和式共有100/2个，即50个
第三步：总结出计算方法：101*100/2
第四步：计算上式得出结果5050。

方法二：直接累加求1+2+3+ ···+100的和，虽然也能求得结果，但是要做99次加法，这显然是十分烦琐的。

如何去设计算法呢？设计的算法又怎么表示呢？大家看到了，算法的设计分两个内容：一是寻找一种方法；二是描述一下实现这个方法的步骤。

刚才我们已经用语言的形式描述过算法了。

我们还可以用流程图的方法来描术算法。

流程图，又叫做程序框图，是一种较常用的算法表示方法。

流程图用一些几何图形符号表示各种类型的操作，并在框内以简明文字或符号表示具体操作。

实数根的算法（如下图）
用程序框图来表示算法，算法的基本逻辑结构展现得非常清楚，一共有三种不同的基本逻辑结构，分别称为顺序结构、条件结构和循环结构。

顺序结构：完全按照框图的排列顺序执行的结构。

如下图：
例4、用流程图描述求一元二次方程： )0(02
≠=++a c bx ax。

算法的流程图表示一、算法的概念要计算机解决某一个问题，必须编写相应的程序。

编写程序需要确定解决问题的方法和思路，并要正确地写出求解步骤，这就叫解决这个问题的算法（algorithm）。

计算机处理某一问题的过程与我们日常处理事情的过程十分相似，都要按一定的步骤和相应的方法来处理。

例如，邮寄一封信的过程可分为写信、写信封、贴邮票、投入信箱等四个步骤，这些步骤可以看作是写信的算法。

下面举三个计算机处理问题的算法的例子。

【例6-1-1】交换两个变量中的数据。

已知变量x和y中分别存放了数据，现在要交换其中的数据。

为了达到交换的目的，需要引进一个中间变量m，其算法如下：①将x中的数据送给变量m，即x→m；②将y中的数据送给变量x，即y→x；③将m中的数据送给变量y，即m→y。

【例6-1-2】输入三个不相同的数，求出其中的最小数。

先设置一个变量min，用于存放最小数。

当输入a、b、c三个不相同的数后，先将a与b进行比较，把小者送给变量min，再把c与min 进行比较，若c<min，则将c的数值送给min，最后min中就是三个数中的最小数，具体算法如下：①若a<b ，则a→min，否则b→min；②再将c与min进行比较，若c<min，则c→min。

这样，min 中存放的即是三个数中的最小数。

【例6-1-3】输入两个正整数a和b（a>b），求它们的最大公约数。

求两个正整数a、b(a>b)的最大公约数，可以归结为求一数列：a，b，r1，r2，……，r n-1，r n，r n+1，0此数列的首项与第二项是a和b，从第三项开始的各项，分别是前两项相除所得的余数，如果余数为0，它的前项r n+1即是a和b的最大公约数，这种方法叫做欧几里德辗转相除法，其算法如下：①输入a，b（a>b）；②求a/b的余数r；③如果r≠0，则将b→a，r→b，再次求a/b的余数r，转至③；④输出最大公约数b。