第四章运动学方程
- 格式:ppt
- 大小:966.50 KB
- 文档页数:44





第四章 经典质点动力学4-1.已知质量为2kg 的质点的运动学方程为22(61)(341)r t i t t j =-+++(国际制单位),求证质点所受合力为恒力.证 对运动学方程求时间导数()d 1264d r v t i t j t==++ 22d d 126d d v r a i j t t ===+ 2(126)=2412(N)F ma i j i j ==⨯++可见质点所受合力为恒力.4-2.已知质量为1kg 的质点,在合力128(N)F t i j =+作用下运动.已知1t =s 时,质点位于2x =m 、0y =处,并以速率3m s 沿y 轴正向运动.求质点运动学方程.解 由mr F =,知12x t =,8y =.可得d 12d x t t = ,d 8d y t =积分 01d 12d xt x t t =⎰⎰ ,31d 8d y ty t =⎰⎰ 求出 266x t =- ,85y t =-再根据 2d (66)d x t t =- ,d (85)d y t t =-再积分 221d (66)d xt x t t =-⎰⎰ ,01d (85)d y ty t t =-⎰⎰ 质点运动学方程为 3266x t t =-+ ,2451y t t =-+4-3.跳水运动员沿竖直方向入水,刚入水时速率为0v ,以入水点为O 点,y 轴竖直向下,运动员入水后浮力与重力抵消,受水的阻力与速度平方成正比,比例系数为k ,求入水后运动员速度随时间的变化规律.解 以运动员为质点,根据牛顿第二定律有 2d d yy v m kv t =- ,即2d d y y v k v t m =- 分离变量并积分 020d d y v t y v y v k t v m =-⎰⎰即可求出 011y k t v v m -= 也可以表示为 00y mv v m kv t=+4-4.跳水运动员由高处下落,设运动员入水后重力与浮力抵消,受水的阻力与速度平方成正比,比例系数0.4k m =(m 为运动员质量).求运动员速率减为入水速率的110时,其入水深度(均为国际制单位).解 以入水点为O 点,y 轴竖直向下,以运动员为质点,根据牛顿第二定律有2d 0.4d yy v m mv t =-做变量变换,得 2d d d 0.4d d d y y y y v v y v v y t y ==- 即 d 0.4d y y v v y=- 分离变量并积分 00100d 0.4d v y y v y v y v =-⎰⎰ 0010ln |0.4v y v v y =- 可知运动员速率减为入水速率的110时,其入水深度ln1004576(m)y ..==.4-5.质量为m 的小球系在一不可伸长的轻绳之一端,可在水平光滑桌面上滑动.绳的另一端穿过桌面上一小孔,握在一人手中使它以匀速率a 向下运动.设初始时绳是拉直的,小球与小孔的距离为R ,初速度在垂直于绳的方向上的分量为0v .试求小球运动和绳子的张力.解 小球m 视为质点,作为研究对象,受力分析如图.以桌面小孔为坐标原点O ,建立极坐标系如图,根据牛顿第二定律,有T N T ma F F mg F =++=在极坐标系中的投影方程为2()T m r r F θ-=- (1)(2)0m r r θθ+= (2)由题意可知 r a =- (3)由(3)式得0d d r tR r a t =-⎰⎰ 所以r R at =-,代入(2)式,得 ()20R at a θθ--= ,即 d ()2d R at a tθθ-= 初始时00R v θ=,即00v R θ=,把上式分离变量且积分 000d 2d d()2tt v R a t R at R at R at θθθ-==---⎰⎰⎰220ln 2ln ln ()R R at R v R R at θ-=-=- 所以 02d d ()v R t R at θθ==- 把上式分离变量且积分 0200d()d ()t v R R at a R at θθ-=--⎰⎰ 所以 0011()v R v t a R at R R atθ=-=-- 小球的运动学方程为r R at =-,0v t R atθ=-.由(1)式得 222220023()()[]()()T v R mv R F m r r mr m R at R at R at θθ=-==-=--4-6.已知质点所受合力为sin cos e tF t i t j k =++,求在0t =到2t π=时间内合力对质点的冲量.(国际制单位.)解 0t =到2t π=时间内合力对质点的冲量为 200d (sin cos e )d t t I F t t i t j k t π==++⎰⎰22000(sin d )(cos d )(d )t t t i t t j e t k πππ=++⎰⎰⎰ 222000(cos |)(sin |)(|)t t i t j e k πππ=-++2(e 1)i j k π=++-(国际制单位)4-7.用棒打击质量为0.5kg 、从西沿水平方向以速率20m 飞来的球,球落到棒的西面80m 处,球上升的最大高度为20m ,打击时间为0.05s ,打击时可略去重力,取210m s g =.求:(1)棒对球的冲量;(2)棒给予球的平均冲力.解 建立坐标系Oxy ,Ox 轴沿水平方向自东向西,Oy 轴竖直向上.先讨论球被棒打击后的运动,球仅受重力,可知2012y y v t gt =- ,0y y v v gt =- 当0y v =时球达到最大高度m 20m y =.根据0010y v t =-求出0010y t .v =,代入202050y v t .t =-得到 22200020010005005y y y .v .v .v =-=因00y v >,略去020y v =-,可求出020m s y v =.进而求出2s t =.由于球沿Ox 方向作匀速率运动,到4s t =时向西运动了80m ,所以020m x v =. 在碰撞中根据动量定理 21I mv mv =- 由于120v i =-,2002020x y v v i v j i j =+=+,所以棒对球的冲量2010(N s)I i j =+⋅平均冲力 2010400200 (N)0.05I i j F i j t +===+∆4-8.从高出枰盘 4.9m h =处,将每个质量m 均为0.02kg 的橡皮泥块,以每秒100n =个的速率注入枰盘,橡皮泥块落入枰盘后均黏附在盘上.以开始注入时为0t =,求10s t =时枰的读数.解 橡皮泥块在下落过程中只受重力,橡皮泥块落入枰盘的速率98(m v .=在橡皮泥块落入秤盘的过程中,对秤盘的平均冲力为(向上为正方向)21()100002[0(9.8)]196(N)F n mv mv ..=-=⨯⨯--=由于橡皮泥块由 4.9m h =处下落,由22119.8 4.922gt t =⨯⨯= 可知下落的时间1s t =.所以10s t =时枰盘内橡皮泥块受到的总重力g (10-1)1009002981764(N)F n mg ...==⨯⨯⨯=因此秤的读数为 g 1961764196(N)F F ..+=+=4-9.对例题4-4-2(见图),判断以下说法的正误:(1)质点对O 点角动量守恒;(2)质点对O '点角动量守恒;(3)质点对z 轴角动量守恒;(4)质点对x 轴角动量守恒.解 (1)摆锤所受合力指向O 点,摆锤所受合力对O 点力矩为零,所以质点对O 点角动量守恒.(2)合力对O'点力矩不为零,质点对O'点角动量不受恒.(3)质点所受合力的作用线过Oz 轴,对Oz 轴合力矩为零,所以质点对Oz 轴角动量守恒.(4)质点对O 点角动量守恒,所以质点对Ox 轴角动量守恒.4-10.在一直角坐标系Oxyz 中,一质点位于点(3m,4m,5m)处,并受一作用力7N 8N 9N F i i i =++,求:(1)力F 对O 点的力矩;(2)力F 对x 轴的力矩.解 345r i j k =++,所以(345)(789)484(N m)O M r F i j k i j k i j k =⨯=++⨯++=-+-⋅4N m x O M M i =⋅=-⋅4-11.在直角坐标系Oxyz 中,质点质量为2kg ,其速度1242(m s )v i j tk -=+-⋅,并已知0t =时位置矢量02(m)r i =.求:(1)质点对O 点的角动量;(2)质点对y 轴的角动量;(3)质点所受合力对O 点和y 轴的力矩.解 因为d d r v t=,d d r v t =,所以00d d r t r r v t =⎰⎰,即 00002(2d )(4d )(2d )t t tr r r i t i t j t t k -=-=+-⎰⎰⎰ 所以 2(22)4r t i tj t k =++- (1) 22[(22)4](242)O L r mv t i tj t k i j tk =⨯=⨯++-⨯+-22218(48)16(kg m s )t i t t j k -=-+++⋅⋅(2) 22148(kg m s )y O L L j t t -=⋅=+⋅⋅(3) d 16(88)(N m)d O O L M t i t j t==-++⋅ d 88(N m)d y y L M t t==+⋅4-12.设质点在Oxy 平面内运动,试判断以下论述是否正确:(1)若质点动量守恒,则对z 轴角动量守恒;(2)若质点对z 轴角动量守恒,则动量守恒;(3)若质点对z 轴角动量守恒,则动量的大小保持不变;(4)若质点对z 轴角动量守恒,则质点不可能作直线运动.解 (1)正确.质点动量守恒,则质点所受合力为零,质点所受合力对Oz 轴力矩为零,所以对Oz 轴角动量守恒.(2)不对.比如,质点在Oxy 平面内、绕O 点做匀速圆周运动,对Oz 轴角动量守恒,但是动量并不守恒.(3)不对.比如例题4-5-2,质点在Oxy 平面内做椭圆运动,它所受的合力是有心力,始终指向O 点,所以对Oz 轴的角动量守恒,但是动量的大小不断变化.(4)不对.在Oxy 平面内做匀速直线运动的质点对Oz 轴角动量守恒.4-13.质量为m 的质点在Oxy 平面内运动,其运动学方程为cos x a t ω=,sin y b t ω=,a 、b 、ω均为常量.求:(1)质点对z 轴的角动量;(2)质点所受对z 轴的合力矩.解 (1)对运动学方程cos sin r a ti b tj ωω=+求时间导数,可得 d sin cos d r v a ti b t j t ωωωω==-+ 所以 (cos sin )(sin cos )O L r mv a ti b tj m a ti b t j ωωωωωω=⨯=+⨯-+22(cos sin )m ab t ab t k mab k ωωωωω=+=z O L L k abm ω=⋅=(2)因z L 为常量,由对Oz 的角动量定理,可知质点所受对Oz 轴的合力矩d 0d z z L M t==4-14.如图,刚性转动系统放在盛有液体的容器内,长为l 的细杆一端固定一质量为m 的小球,另一端垂直地固定于转轴z .小球受液体阻力与小球质量及系统转动角速度的大小成正比,即F km ω=,k 为比例常量.z 轴及细杆的质量及所受阻力均忽略不计,问:经过多长时间系统的角速度的大小变为初始值0ω的1e .解 由题意知z M lkm ω=-,2z L ml ω=,根据d d z z L M t=,得 2d d ml lkm tωω=- 分离变量并积分 d d k t lωω=-⎰⎰ ln k t C lω=-+ 由0t =时0ωω=定出积分常数,0ln C ω=,则 0e kt l ωω-=所以,当0e ωω=时l t k=.4-15.如图所示,小球m 系于不可伸长的轻绳的一端,绳经O 点穿入竖直小管.开始时小球绕管在水平面内做半径为R 的圆周运动,每分钟转120转.由绳的A 端将绳拉入小管,拉绳后小球绕管在水平面内做半径为2R 的圆周运动.求:(1)拉绳以后小球每分钟之转数;(2)拉绳过程中小球对O 点角动量是否守恒?为什么?解 (1)在拉绳过程中,因为小球所受重力与OA 轴平行、绳拉力与OA 轴相交,对OA 轴力矩均为零,所以在拉绳过程中小球对OA 轴角动量守恒02R mvmv R = 拉绳前,每秒转两转,022R v π⋅=.设拉绳后,每秒转n 转,22R n v π⋅=.把04v R π=和v n R π=代入角动量守恒方程,得 42R mn R m R R ππ=⋅ 即可求出拉绳后小球每秒转8n =转,即每分钟480转.(2)因为小球所受合力对O 点力矩不为零,所以小球对O 点角动量不守恒.4-16.试判断以下说法是否正确:(1)静摩擦力一定不做功;(2)滑动摩擦力一定做负功;(3)摩擦力总是阻碍物体运动;(4)运动质点如受摩擦力作用,则能量一定减小.答 均不正确.4-17.试证明2(3sin e )(N)x F x x i =++是保守力.质点在F 作用下由0x =运动到1m x =,试用两种方法计算力F 对质点做的功.解 由于2(3sin e )(N)x F x x i =++在位移d r 中所做元功2d (3sin )(d d d )x F r x x e i xi yj zk ⋅=++⋅++2(3sin e )d x x x x =++3d(cos e )xx x =-+可以表示为只与位置有关的标量函数3()cos e x U x x x =-+的微分,所以此力为保守力.方法一:质点沿Ox 轴由0x =运动到1x =,F 对质点所做的功为 120d (3sin e )d x W F r x x x =⋅=++⎰⎰310(cos e )|x x x =-+ 1cos1e 11=-++-1cos1e =-+ 方法二:因F 为保守力,引入势能3p (cos e )x E U C x x C =-+=--++,则p2p1()W E E =--1cos1e 11=-++-1cos1e =-+4-18.如图,一劲度系数为k 的弹簧,一端固定于A 点,另一端与质量为m 的质点相连.弹簧处于自由伸张状态时,质点位于竖直面与半径为R 的半圆柱面的交界处B .质点在力F 的作用下,由B 点从静止开始运动到光滑半圆柱面的顶点C ,到达C 点时质点速率为C v .求力F 对质点所做的功.解 在质点由B 到C 点的过程中,所受重力和弹簧弹性力为保守力,以B 点为重力势能及弹性势能零点.质点受面的支撑力不做功,设力F 做功为F A .由质点的机械能定理k p k p ()()C C B B F E E E E A +-+=可得 22111[(R)](00)222F C A mv mgR k π=++-+ 2221128C mv mgR k R π=++4-19.接题4-18,质点到达C 点后,力F 被撤除,求质点运动到AB 之间的平衡位置时的速率.解 质点平衡时mg k l =∆,mg l k ∆=,即质点的平衡位置位于B 点下方mg k处. 在质点由C 到平衡位置的过程中,由于所受重力和弹簧弹性力为保守力,受面的支撑力不做功,所以机械能守恒.以B 点为重力势能及弹性势能零点,则()2222211112822C mv mgR k R mv mg l k l π++=-∆+∆ 22222122m g m g mv k k =-+222122m g mv k=- 即可求出质点运动到AB 之间的平衡位置时的速率2222121(2)4C k R mg v v gR m kπ=+++4-20.如题4-15图之装置.设小球质量0.5g m =,初态管外绳长12m l =,绳与竖直方向夹角130θ=,速度为1v .末态绳与竖直方向夹角260θ=,速度为2v .求:(1)1v 、2v ;(2)绳对小球所做的功.解 视小球为质点,受重力W 和绳的张力T F 如图.初态小球做水平圆周运动,合力T F W F =+指向圆轨道圆心,由牛顿第二定律2211111tg sin v v m m mg R l θθ== 所以 21111sin 1298238m s cos 23v l g ..θθ==⨯⨯= 设末态2l l =,小球做水平圆周运动,有22222tg sin v m mg l θθ= ,222222sin cos v l g θθ= 可知 22111212222122sin cos 1cos sin 33v l l v l l θθθθ== (1) 在由初态到末态的过程中,小球所受合力对竖直轴AB 的力矩为零,所以小球对轴AB 的角动量守恒111222sin sin mv l mv l θθ=所以 12222111sin 3sin v l l v l l θθ== (2) (1)(2)⨯得 313213v v = 可求出 13213343m s v v .==2(1)(2)得 313293l l = 13211()080m 93l l .== 由机械能定理,以O 点为势能零点,绳对小球所做的功为k p W E E =∆+∆2221121()(cos30cos60)2m v v mg l l =-+-000805J .=4-21.质量为0.2kg 的小球B 以弹性绳在光滑水平面上与固定点A 相连.弹性绳劲度系数为8N m ,其自由伸张长度为0.6m .小球初位置和速度0v 如图所示.当小球速率变为v 时,它与A 点距离最大且等于0.8m .求初态与末态之速率0v 和v .解 小球在水平面上仅受弹性绳弹性力,弹性力作用线过A ,所以小球在运动过程中对过A 的竖直轴角动量守恒;注意到小球与A 点距离最大时其速度与弹性绳垂直;则004sin3008.mv .mv =小球在水平面内仅受弹性绳弹性力,弹性力为保守力,因此小球在运动过程中机械能守恒,以弹性绳自由伸张时为弹性势能零点;则2220111(0806)222mv mv k ..=+- 所以 04v v = ,22016v v .-=联立求解上述二式即可求出0131m s v .=,033m s v .=.4-22.如图,在升降机内有一和升降机固定的光滑斜面,斜面相对水平方向的倾角为θ.当升降机以匀加速度a 沿竖直方向上升时,质量为m 的物体沿斜面下滑,试以升降机为参考系,求:(1)物体相对升降机的加速度;(2)物体对斜面的压力;(3)物体对地面的加速度.解 以升降机为非惯性参考系,建立与斜面固连的坐标系Oxy 如图.视物体为质点,受重力mg 、支承力N F 和惯性力I F ma =-,物体在非惯性系中的动力学方程为()sin m g a mx θ+=()N cos 0F m g a θ-+=所以,物体相对升降机的加速度()sin a x i g a i θ'==+物体对斜面的压力()NN cos F F m g a j θ'=-=-+ 物体对地面的加速度sin cos ()sin sin cos a a a a i a j g a i g i a j θθθθθ'=+=-+++=+地4-23.如图,一理想定滑轮固定于升降机上,一不可伸长之轻绳跨过滑轮后,两端各悬挂一物体,物体质量为1m 和2m ,12m m ≠.升降机以加速度a 沿竖直方向下降时,试以升降机为参考系,求:两个物体相对地面的加速度及绳内张力.解 以升降机为非惯性参考系,建立与升降机固连的坐标系Ox 如图.视二物体为质点,物体受重力、绳张力和惯性力I11F m a =-、I22F m a =-,在非惯性系中的动力学方程为1T1111m g F m a m x --=2T2222m g F m a m x --=绳不可伸长 12x x =-根据牛顿第三定律 T1T2T F F F ==所以 12211212()()m m g m m a x x m m -+-=-=+ 绳内张力 12T 122()m m F g a m m =-+ 两个物体相对地面的加速度为1221122111212()()()2m m g m m a m m g m a a a x i ai i i m m m m -+--+=+=+=++ 1221211121212()()()2m m g m m a m m g m a a a x i ai i i m m m m -+--+=+=-=++ 4-24.如图所示有一绕竖直z 轴以角速度k ωω=作匀角速度定轴转动的光滑水平大转台.在距z 轴R 的A 处立一竖直杆,杆端有一长度为l 的不可伸长的轻绳,绳末端挂一质量为m 的小球.当绳与竖直杆夹角θ保持不变时,以转台为参考系,求θ与ω的关系.解 以转台为非惯性参考系,视小球为质点,小球受重力mg ,绳的拉力T F ,惯性离心力It F ,2It (sin )F m R l ωθ=+.小球在非惯性系中受三个力平衡,水平方向的平衡方程为2(sin )tan m R l mg ωθθ+=所以 12tan ()sin g R l θωθ=+ 4-25.接题4-24,有人试图从O 点以初速0v 沿台面抛出一小球,而使小球沿转台上的直线OA 运动,此人的目的能否达到?试在转台参考系中加以说明.解 以转台为非惯性参考系,小球相对于转台具有速度,所以小球除受重力、支持力和惯性离心力以外,还受科里奥利力作用.由于科里奥利力与小球运动方向垂直,所以小球不可能沿转台上的直线OA 运动.(第四章题解结束)。

运动学方程及应用运动学是物理学中研究物体运动的学科,是研究物体位置、速度和加速度与时间之间关系的一门学科。
运动学方程是描述物体运动状态的方程,通过运动学方程可以计算物体的位移、速度和加速度等参数,进而揭示物体运动的规律和特点。
运动学方程及其应用在物理学、工程学等领域具有重要的意义。
一维运动学方程是研究物体沿着一条直线运动时的方程。
其中最基本的方程是位移-时间关系方程,即x = x0 + v0t + (1/2)at^2。
这里x0表示起始位置,v0表示起始速度,t表示时间,a表示加速度。
该方程表达了物体的位移与时间的关系,可以计算在给定初始条件下物体的具体位置。
在应用中,运动学方程可以用于解决诸如自由落体、匀速直线运动、匀加速直线运动等问题。
例如,可以利用x = x0 + v0t + (1/2)at^2来计算一个物体自由落体的高度。
如果物体自由落体时没有起始速度,即v0为0,方程简化为x = (1/2)gt^2,其中g为重力加速度。
通过该方程,可以计算物体在任意时间下的高度,从而揭示物体自由落体运动的规律。
另一方面,运动学方程也可用于解决匀速直线运动的问题。
在匀速直线运动中,物体的加速度为0,所以运动学方程可以写成x = x0 + v0t。
这里x0表示起始位置,v0表示起始速度,t表示时间。
通过该方程,可以计算物体在匀速直线运动中的位置。
运动学方程在匀加速直线运动中的应用也非常广泛。
在匀加速直线运动中,物体的加速度是恒定的,所以运动学方程可以写成x = x0 + v0t + (1/2)at^2。
这里x0表示起始位置,v0表示起始速度,t表示时间,a表示加速度。
通过该方程,可以计算物体在匀加速直线运动中的位置。
除了一维运动之外,运动学方程还可以推广到二维和三维运动中。
在二维和三维运动中,物体在平面或空间中的位置可以用矢量表示。
对于二维运动,可以用位矢r = xi + yj来表示物体的位置,其中i和j分别是x轴和y轴的单位矢量。

运动学方程
1运动学方程
运动学方程是物理学中重要的概念,它能描述物体在力学系统中的运动规律。
它不仅用于物理学,而且在航天、机械及其他科学和工程领域被广泛使用。
广义的运动学方程由物理学家Leonhard Euler提出,数学家Joseph Louis Lagrange也提出了一种更普遍的版本。
2概念介绍
运动学方程是一组常微分方程,用于描述物体在动力系统中的运动,包括速度、加速度等等。
它可以解释物体位置、速度及总能量的变化,以及力学系统的行为,还可以用于形成物理模型,并用数值计算的方法表示物体运动的轨迹。
3典型应用
运动学方程在航天工程和机械工程中有广泛应用。
它可以用来模拟物体的运动,为轨道系统的设计提供依据,以及应用于机械系统的建模与设计。
此外,它还被广泛应用于波动方程、布朗运动等各种动力系统中。
4小结
运动学方程是物理学和机械工程中重要的概念,它可以解释物体在力学系统中的运动规律,被广泛应用于航天工程、机械工程和动力系统的建模与设计中。

大一物理运动学方程知识点物理学是一门研究物质运动规律和物质相互关系的科学。
而运动学是物理学中的一个重要分支,它研究运动物体的运动方式、速度、加速度等参数的变化规律。
在大一的学习中,我们不可避免地要学习和掌握运动学方程,以便更好地理解和分析物体的运动。
在运动学中,最基本的方程就是运动学方程。
它是一组用来描述物体运动的数学表达式,包括位置-时间方程、速度-时间方程和加速度-时间方程。
理解这些方程的含义和应用,对于解决与物体运动相关的问题至关重要。
首先,我们来看一下位置-时间方程。
它描述了物体在运动过程中位置随时间变化的关系。
一般而言,位置-时间方程可以通过已知的初始位置、初始速度和加速度来求解。
比如,如果一个物体的初始位置为x0,初始速度为v0,加速度为a,那么它在时间t 时的位置x可以通过下面的方程得到:x = x0 + v0t + 0.5at^2在这个方程中,x表示物体的位置,t表示时间。
v0t项表示物体在时间t内的位移,0.5at^2表示物体在时间t内由于加速度的作用而产生的位移。
了解和应用这个方程,可以帮助我们计算物体在给定时间内的位置,进而分析与物体位置和时间有关的问题。
接下来,我们来看一下速度-时间方程。
它描述了物体在运动过程中速度随时间变化的关系。
一般而言,速度-时间方程可以通过已知初始速度和加速度来求解。
比如,如果一个物体的初始速度为v0,加速度为a,那么它在时间t时的速度v可以通过下面的方程得到:v = v0 + at在这个方程中,v表示物体的速度,t表示时间。
v0表示物体的初始速度,at表示物体在时间t内由于加速度的作用而产生的速度变化。
了解和应用这个方程,可以帮助我们计算物体在给定时间内的速度,进而分析与物体速度和时间有关的问题。
最后,我们来看一下加速度-时间方程。
它描述了物体在运动过程中加速度随时间变化的关系。
一般而言,加速度-时间方程可以通过已知初始速度和加速度来求解。
比如,如果一个物体的初始速度为v0,加速度为a,那么它在时间t时的加速度可以通过下面的方程得到:a = a在这个方程中,a表示物体的加速度,t表示时间。
力学运动与运动学方程力学运动是物体在受到力作用下的运动,而运动学方程则是描述物体运动的方程。
通过对力学运动和运动学方程的研究和应用,我们可以深入了解物体的运动规律,并利用这些规律解决实际问题。
一、力学运动力学运动是研究物体受到力作用下的运动规律的学科。
在力学运动中,主要考虑物体的速度、加速度以及运动的轨迹等因素。
力学运动可以分为匀速直线运动、变速直线运动、曲线运动等不同类型。
1. 匀速直线运动在匀速直线运动中,物体的速度保持恒定,而加速度为零。
这意味着物体在单位时间内所经过的路程相等。
匀速直线运动的运动学方程为:\[v = v_0\]\[s = v_0t\]其中,\(v\)表示物体的末速度,\(v_0\)表示物体的初速度,\(s\)表示物体的位移,\(t\)表示经过的时间。
2. 变速直线运动在变速直线运动中,物体的速度随时间而变化,加速度不为零。
变速直线运动的运动学方程为:\[v = v_0 + at\]\[s = v_0t + \frac{1}{2}at^2\]其中,\(a\)表示物体的加速度。
3. 曲线运动曲线运动是指物体运动的轨迹为曲线的运动。
在曲线运动中,物体的速度和加速度都是矢量,需要考虑其方向。
曲线运动常涉及到极坐标、曲线的参数方程等数学工具来描述。
二、运动学方程的应用运动学方程不仅是研究物体运动的基础,也是解决实际问题的重要工具。
以下是运动学方程的一些应用。
1. 路程-时间图运动学方程中的位移-时间方程可以用于绘制物体的路程-时间图。
通过分析路程-时间图,我们可以得到物体的运动方式,例如匀速运动、加速运动或者减速运动。
2. 速度-时间图在运动学方程中,速度-时间方程可以用于绘制物体的速度-时间图。
通过分析速度-时间图,我们可以了解物体的速度变化规律,例如加速度大小、正负号等。
3. 解决实际问题通过运动学方程,我们可以解决一系列与物体运动相关的实际问题。
例如,我们可以通过已知的位移和时间求解物体的平均速度、通过已知的加速度和时间求解物体的位移,或者求解加速度的大小等。
Z1 X1
Y1
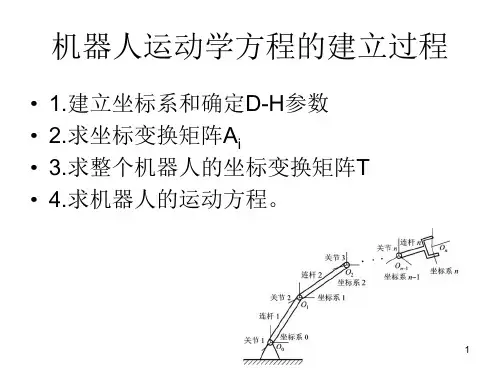
第一根杆长l1,第二根杆长l2,两杆之间夹角为θ。
在每个连杆都建立一个坐标系,x 轴为连杆方向,连杆可以绕Z 轴旋转,y 轴由x 轴和Z 轴决定。
第一个连杆的坐标系设为O1,第二个为o2.o2相对于o1的变化由四个变化完成。
1绕o1的x 轴旋转a 角。
使o1o2z 轴平行。
2沿x 轴移动L1。
4沿o1z 移动d ,使两坐标系完全重合。
可以得到矩阵T12=(图中(ai-1)为a ,ai-1为l1,)
上式中θ即为所求旋转角度。
若存在多个连杆,则将上述矩阵(T23,T34…)进行连乘。
最终得到终点坐标矩阵。
即T12*T23*T34…=P
求出θ1:求出T12的逆矩阵T21,并在等式两端进行左乘。
寻找合适的对应元素进行运算。
如计算。
左乘后左右两边第二列,第X2 Z2 Y2
三行相等。
可求出θ1=ARCtan(ox/oy)。
同理可求出θ2,θ3。