2位10进制计数器

同步和异步十进制加法计数器的设计全文共四篇示例，供读者参考第一篇示例：同步和异步是计算机系统中常用的两种通信机制，它们在十进制加法计数器设计中起到了至关重要的作用。

在这篇文章中，我们将深入探讨同步和异步十进制加法计数器的设计原理及应用。

让我们来了解一下十进制加法计数器的基本概念。

十进制加法计数器是一种用于执行十进制数字相加的数字电路。

它通常包含多个十进制加法器单元，每个单元用于对应一个十进制数位的运算。

在进行加法操作时，每个数位上的数字相加后，可能会产生进位，这就需要进位传递的机制来满足计数器的正确操作。

在同步十进制加法计数器中，每个十进制加法器单元都与一个时钟信号同步，所有的操作都按照时钟信号的节拍来进行。

具体来说，当一个数位的加法计算完成后，会将结果通过进位端口传递给下一个数位的加法器单元，这样就能确保每个数位的计算都是按照特定的顺序来进行的。

同步十进制加法计数器的设计较为简单，在时序控制方面有很好的可控性，但由于需要受限于时钟信号的频率，其速度受到了一定的限制。

在实际应用中，根据不同的需求可以选择同步或异步十进制加法计数器。

如果对计数器的速度要求较高，并且能够承受一定的设计复杂度，那么可以选择异步设计。

如果对计数器的稳定性和可控性要求较高，而速度不是首要考虑因素，那么同步设计可能更为适合。

无论是同步还是异步，十进制加法计数器的设计都需要考虑诸多因素，如延迟、数据传输、进位控制等。

通过合理的设计和优化，可以实现一个高性能和稳定的十进制加法计数器，在数字电路、计算机硬件等领域中有着广泛的应用。

同步和异步十进制加法计数器的设计都有其各自的优势和劣势，需要根据具体的需求来选择合适的设计方案。

通过不断的研究和实践，我们可以进一步完善十进制加法计数器的设计，为计算机系统的性能提升和应用拓展做出贡献。

希望这篇文章能够为大家提供一些启发和帮助，让我们共同探索数字电路设计的奥秘，开拓计算机科学的新境界。

第二篇示例：同步和异步计数器都是数字电路中常见的设计，用于实现特定的计数功能。

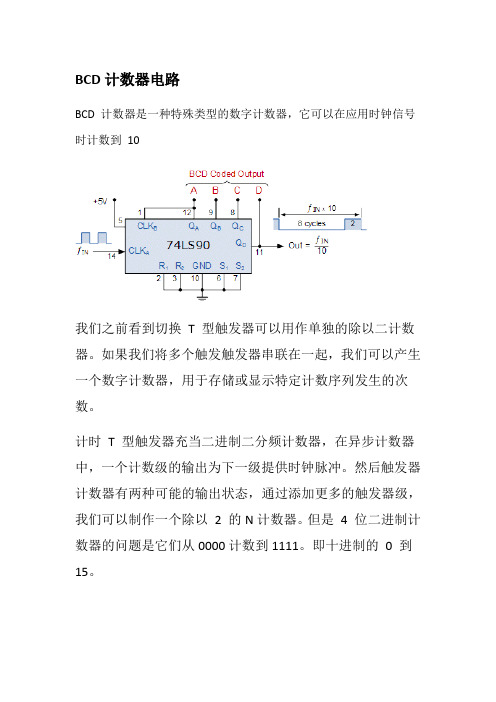
BCD计数器电路BCD 计数器是一种特殊类型的数字计数器，它可以在应用时钟信号时计数到10我们之前看到切换T 型触发器可以用作单独的除以二计数器。

如果我们将多个触发触发器串联在一起，我们可以产生一个数字计数器，用于存储或显示特定计数序列发生的次数。

计时T 型触发器充当二进制二分频计数器，在异步计数器中，一个计数级的输出为下一级提供时钟脉冲。

然后触发器计数器有两种可能的输出状态，通过添加更多的触发器级，我们可以制作一个除以 2 的N计数器。

但是 4 位二进制计数器的问题是它们从0000计数到1111。

即十进制的0 到15。

要制作一个从 1 到10 计数的数字计数器，我们需要让计数器只计算二进制数0000到1001。

那是十进制的0 到9，对我们来说幸运的是，计数电路很容易作为集成电路使用，其中一个这样的电路是异步74LS90 十进制计数器。

数字计数器在应用时钟信号时从零向上计数到某个预定计数值。

一旦达到计数值，重置它们会将计数器返回到零以重新开始。

十进制计数器按10 的顺序计数，然后在计数到9 后返回零。

显然，要计数到二进制值9，计数器必须在其链中至少有四个触发器来表示每个十进制数字，如图所示。

BCD 计数器状态图然后十进制计数器有四个触发器和16 个潜在状态，其中只使用了10 个，如果我们将一系列计数器连接在一起，我们可以计数到100 或1,000 或我们选择的任何最终计数数字。

计数器也可以计数的总数称为它的MODULUS。

在n 次计数后返回零的计数器称为模n 计数器，例如模8 (MOD-8) 或模16 (MOD-16) 计数器等，对于“n 位计数器” ”，计数的全范围是从0到2n-1。

但正如我们在异步计数器教程中看到的那样，一个计数器在十次计数后重置，从二进制0000（十进制“0”）到1001（十进制“9”）的除以10 计数序列被称为“二进制-coded-decimal counter”或简称BCD Counter和一个MOD-10 计数器可以使用最少四个触发触发器来构建。

10进制计数器课程设计一、课程目标知识目标：1. 学生能理解10进制计数器的基本概念，掌握10进制数的组成和计数规律。

2. 学生能运用10进制计数器进行数值的加减运算，并正确表达计算过程和结果。

3. 学生了解10进制计数器在日常生活和科学技术中的应用。

技能目标：1. 学生能够独立操作10进制计数器，进行简单的数值计算。

2. 学生通过实际操作，培养观察、分析、解决问题的能力。

3. 学生通过小组合作，提高沟通、协作和团队意识。

情感态度价值观目标：1. 学生对10进制计数器产生兴趣，激发学习数学的积极性。

2. 学生在探索过程中，培养耐心、细致、勇于尝试的精神。

3. 学生认识到数学知识在实际生活中的重要性，增强学以致用的意识。

课程性质：本课程属于数学学科，旨在帮助学生掌握10进制计数器的运用，提高数学运算能力和实际应用能力。

学生特点：四年级学生具有一定的数学基础，好奇心强，喜欢动手操作，但注意力集中时间较短。

教学要求：注重理论与实践相结合，以学生为主体，激发学生兴趣，培养动手操作能力和团队协作精神。

通过分解课程目标为具体的学习成果，使学生在愉快的氛围中掌握知识，提高能力。

二、教学内容1. 引入10进制计数器概念，介绍其在数学运算中的应用。

- 教材章节：第三章《数的认识》- 内容：10进制计数器的定义、计数规律、数位顺序表。

2. 学习10进制计数器的操作方法，进行数值的加减运算。

- 教材章节：第四章《简单的数学计算》- 内容：10进制计数器操作方法、数值加减运算、进位与退位。

3. 实践与应用，运用10进制计数器解决实际问题。

- 教材章节：第五章《生活中的数学》- 内容：运用10进制计数器进行购物找零、时间计算等实际问题的解决。

4. 小组合作，探讨10进制计数器在科学技术领域的应用。

- 教材章节：第六章《数学与科技》- 内容：10进制计数器在计算机、电子设备等领域的应用案例。

教学进度安排：第一课时：引入10进制计数器概念，学习计数规律和数位顺序表。

两片74ls192组成两位十进制减法计数器真值表两片74ls192组成两位十进制减法计数器,可以用于计算机编程和电子电路设计中。

74ls192是一款2x24位的动态存储器,可以在192位时钟周期内读写,具有高吞吐量和低延迟的特点。

在两位十进制减法计数器中,需要将输入的两位二进制数减去所需的减法值,并将结果存储在计数器的二进制位中。

为了实现这一功能,可以使用两片74ls192来实现一个简单的两位十进制减法计数器。

下面是两片74ls192组成的两位十进制减法计数器真值表的扩展:| 计数器 | 输入 | 减法值 | 真值表 || ---- | ---- | ---- | ---- || 1 | 10 | 0 | 00000000 || 2 | 11 | 1000 | 00000011 || 3 | 12 | 001000 | 00000010 || 4 | 13 | 101000 | 00000011 || 5 | 14 | 010010 | 00000010 || 6 | 15 | 001101 | 00000010 || 7 | 16 | 101100 | 00000011 || 8 | 17 | 011100 | 00000010 || 9 | 18 | 110101 | 00000011 || 10 | 19 | 101110 | 00000010 || 11 | 20 | 011011 | 00000010 || 12 | 21 | 101011 | 00000011 || 13 | 22 | 010010 | 00000010 || 14 | 23 | 001101 | 00000010 || 15 | 24 | 101101 | 00000011 || 16 | 25 | 011001 | 00000010 || 17 | 26 | 101100 | 00000011 || 18 | 27 | 011011 | 00000010 || 19 | 28 | 101111 | 00000011 || 20 | 29 | 011100 | 00000010 || 21 | 30 | 101011 | 00000011 || 22 | 31 | 011101 | 00000010 || 23 | 32 | 110101 | 00000011 || 24 | 33 | 011100 | 00000010 || 25 | 34 | 101100 | 00000011 || 26 | 35 | 011011 | 00000010 || 27 | 36 | 101101 | 00000011 || 28 | 37 | 011001 | 00000010 || 29 | 38 | 101100 | 00000011 || 30 | 39 | 011011 | 00000010 || 31 | 40 | 110101 | 00000011 |通过使用两片74ls192,我们可以实现一个复杂的两位十进制减法计数器,从而在计算机编程和电子电路设计中发挥重要的作用。

在数字系统中，常需要对时钟脉冲的个数进行计数，以实现测量、运算和控制等功能。

具有计数功能的电路，称为计数器。

计数器是一种非常典型、应用很广的时序电路，计数器不仅能统计输入时钟脉冲的个数，还能用于分频、定时、产生节拍脉冲等。

计数器的类型很多，按计数器时钟脉冲引入方式和触发器翻转时序的异同，可分为同步计数器和异步计数器；按计数体制的异同，可分为二进制计数器、二—十进制计数器和任意进制计数器；按计数器中的变化规律的异同，可分为加法计数器、减法计数器和可逆计数器。

二进制加法计数器运用起来比较简洁方便，结构图和原理图也比其它进制的简单明了，但二进制表示一个数时，位数一般比较长。

十进制是我们日常生活中经常用到的，不用转换，所以设计十进制加法计数器比设计二进制加法计数器应用广泛，加法器是以数据的累加过程，日常生活中，数据的累加普遍存在，有时候需要一种计数器对累加过程进行运算处理，所以设计十进制加法计数器应广大人们生活的需要，对我们的生活有一个积极地促进作用，解决了生活中许多问题，所以会设计十进制加法计数器使我们对数字电路的理论和实践知识的充分结合，也使我们对电子技术基础有了深刻的了解，而且增强了我们对电子技术基础产生了浓厚的兴趣，这次课程设计使我受益匪浅！一、设计题目 (3)二、设计目的 (3)三、设计依据 (3)四、设计内容 (3)五、设计思路 (4)六、设计方案 (7)七、改进意见 (10)八、设计总结 (11)九、参考文献 (12)一、设计题目十进制加法计数器二、设计目的1.学习电子电路设计任务。

2.通过课程设计培养学生自学能力和分析问题、解决问题的能力。

3.通过设计使学生具有一定的计算能力、制图能力以及查阅手册、使用国家技术标准的能力和一定的文字表达能力。

三、设计依据1.用JK触发器组成。

2.实现同步或异步加法计数。

四、设计内容1.复习课本，收集查阅资料，选定设计方案；2.绘制电气框图、电气原理图；3.对主要元器件进行计算选择，列写元器件的规格及明细表；4.设计总结及改进意见；5.参考资料；6.编写说明书。

verilog二位十进制计数下面是一个使用Verilog设计的二位十进制计数器的示例代码：```verilogmodule CNT10 (clk, rst, dout);//二位十进制计数器0~99input clk,rst;output reg [7:0] dout;reg q3;reg [3:0] q1;//低位reg [3:0] q2;//高位always @ (posedge clk or negedge rst) beginif (!rst) q1 <= 4'b0000; else if (q1<9) q1 <= q1+1; else q1 <= 4'b0000; endalways @ (posedge clk or negedge rst or posedge q1) beginif (!rst) q3 <= 1'b0; else if (q1<9) q3 <= 1'b0; else q3 <= 1'b1;endalways @ (posedge clk or negedge rst) beginif (!rst) q2 <= 4'b0000; else if (q2<9) begincase (q3)1'b1: q2 <= q2+1;default: q2 <= q2;endcaseelse beginif (q1<9) q2 <= q2; else q2 <= 4'b0000;endendalways @ (*) begindout <= {q2, q1};end```这个计数器可以对输入的时钟信号进行计数，并在输出端输出二位十进制的计数值。

它使用了三个寄存器来存储计数值的高位、低位和进位信号，并通过逻辑判断和计数器的级联实现了二位十进制的计数功能。

//设计一个2位10进制计数器，每秒加1，在LED上显示#include "reg51.h"#define THCO 0xee#define TLCO 0x0#define THC1 0xee#define TLC1 0x0unsigned char code Duan[]={0x3F, 0x06,0x5B,0x4F,0x66,0x6D,0x7D,0x07,0x7F,0x6F};unsigned char Data_Buffer[2]={0,0};unsigned int count=0;sbit P10=P1^0;sbit P11=P1^1;sbit P12=P1^2;sbit P13=P1^3;void main(){TMOD=0x11;TH0=THCO;TL0=TLCO;TR0=1;ET0=1;TH1=THC1;TL1=TLC1;TR1=1;ET1=1;EA=1;while(1);}void timer1() interrupt 3{static unsigned char Bit1;TH1=THC1;TL1=TLC1;count++;if(count>200){count=0;Bit1++;if(Bit1>99)Bit1 = 0;Data_Buffer[0]=Bit1/10;Data_Buffer[1]=Bit1%10; }}void timer0() interrupt 1{static unsigned char Bit=0;TH0=THCO;TL0=TLCO;Bit++;if(Bit>=2)Bit=0;P1|=0x0f;P0=Duan[Data_Buffer[Bit]]; switch(Bit){case 0: P10=0;break;case 1: P11=0;break;}}实验5思考题#include "reg51.h"#define THCO 0xee#define TLCO 0x00#define THC1 0xee#define TLC1 0x00unsigned char code Duan[]={0x3F, 0x06,0x5B,0x4F,0x66,0x6D,0x7D,0x07,0x7F,0x6F};unsigned char Data_number[4]={1,2,3,4};unsigned char Data_time[2]={0,0};sbit P10=P1^0;sbit P11=P1^1;sbit P12=P1^2;sbit P13=P1^3;sbit key=P3^2;int mode=0,Bit1=0,Bit=0;void main(){TMOD=0x11;TH0=THCO;TL0=TLCO;TR0=1;ET0=1;EX0=1;IT0=1;TH1=THC1;TL1=TLC1;TR1=0;ET1=1;EA=1;while(1);}void tans_mode() interrupt 0{int t;if(key==0){for(t=0;t<1000;t++);if(key==0){while(!key);mode++;if(mode==3)mode=0;Bit=0;if(mode==2){TR1=1;Bit1=0;}else{TR1=0;}}}}void timer1() interrupt 3{static unsigned int count=0;TH1=THC1;TL1=TLC1;count++;if(count>200){count=0;Bit1++;if(Bit1>99)Bit1=0;Data_time[0]=Bit1/10;Data_time[1]=Bit1%10; }}void timer0() interrupt 1{TH0=THCO;TL0=TLCO;P1=0x0f;if(mode==0){P0=Duan[0];}if(mode==1){Bit++;if(Bit>=4)Bit=0;P0=Duan[Data_number[Bit]]; }if(mode==2){Bit++;if(Bit>=2)Bit=0;P0=Duan[Data_time[Bit]];}switch(Bit){case 0: P10=0;break; case 1: P11=0;break; case 2: P12=0;break; case 3: P13=0;break; }}。