小学奥数韩信点兵典型例题和解题思路

第二十三讲：韩信巧点兵例1．一个数除以3余2，除以5余3，除以7余2，求满足条件的最小数。

例2．有一队少先队员，一至三报数余2人，一至五报数余3人，一至七报数余4人。

这队少先队员有多少人？例3．有一筐鸡蛋，每次取出5只，最后还剩3只；每次取出6只，最后还剩2只；每次取出其不7只，最后还剩1只。

这筐鸡蛋至少有多少只？例4．在1000以内，除以4余3，除以5余2，除以7余4，的最大数是几？例5．在1000以内，除以5余3，除以7余6，除以9余7的数有多少个？例6．一个三位数，除以7余1，除以8余2，除以9余3，求该数。

例7．我国古代算术中有一道“韩信点兵”的题：有卫兵若干，列成五行纵队，末行一人；列成六行纵队，末行五人；列成七行纵队，末行四人；列成十一行纵队，末行十人。

求至少有卫兵多少人？例8．一个数被2除余a, 被3除余b, 被5除余c, 被7除余d.这个数最少是多少？第二十三讲：韩信巧点兵练习姓名_____________ 2011.7.8 1．一个数被3除余2, 除以5余4，除以7余5，求适合条件的最小数。

2．有一箱橘子，每次取出3只，最后还剩1只；每次取出5只，最后还剩2只；每次取出7只，最后还剩3只。

这箱橘子至少有多少只？3．在2000~5000之间，除以3余1，除以5余3，除以7余4的数有多少个？4．有兵100多人，如排成三列不多也不少，如排成五列则少2人；如排成七列则少4人。

一共有多少人？5．七数剩一，八数剩二，九数剩四，问本数。

（杨辉《续古摘奇算法》）6．召开学生座谈会，每组五人则多1人，每组六人则多2人，每组七人则缺4人，至少有学生多少人？7．水果箱内有苹果若干只，每次取出3只，最后还剩1只；每次取出5只或八只，最后都剩4只；水果箱里至少有苹果多少只？8．把几十个苹果平均分成若干份，每份9个余8个，每份8个余7个，每份4个余3个。

这堆苹果共有多少个？9．有一堆棋子，三个三个地数，最后还剩二个；十三个十三个地数，最后还剩三个；十九个十九个地数，最后还剩五个。

韩信点兵解法韩信点兵是一个有趣的猜数游戏。

如果你随便拿一把蚕豆（数目约在100粒左右），先3粒3粒地数，直到不满3粒时，把余数记下来；第二次再5粒5粒地数，最后把余数记下来；第三次是7粒一数，把余数记下来。

然后根据每次的余数，就可以知道你原来拿了多少粒蚕豆了。

不信的话，你还可以试验一下。

例如，假如3粒一数余1粒，5粒一数余2粒，7粒一数余2粒，那么，原有蚕豆有多少粒呢？这类题目看起来是很难计算的，可是我国古时候却流传着一种算法，名称也很多，宋朝周密叫它“鬼谷算”，又名“隔墙算”；杨辉叫它“剪管术”；而比较通行的名称是“韩信点兵”。

最初记述这类算法的是一本名叫《孙子算经》的书，后来在宋朝经过数学家秦九韶的推广，又发现了一种算法，叫做“大衍求一术”。

这在数学史上是极有名的问题，外国人一般把它称为“中国剩余定理”。

至于它的算法，在《孙子算经》上就已经有了说明，而且后来还流传着这么一道歌诀：三人同行七十稀，五树梅花廿一枝，七子团圆正半月，除百零五便得知。

这就是韩信点兵的计算方法，它的意思是：凡是用3个一数剩下的余数，将它用70去乘（因为70是5与7的倍数，而又是以3去除余1的数）；5个一数剩下的余数，将它用21去乘（因为21是3与7的倍数，又是以5去除余1的数）；7个一数剩下的余数，将它用15去乘（因为15是3与5的倍数，又是以7去除余1的数），将这些数加起来，若超过105，就减掉105，如果剩下来的数目还是比105大，就再减去105，直到得数比105小为止。

这样，所得的数就是原来的数了。

根据这个道理，你可以很容易地把前面的五个题目列成算式：1×70＋2×21＋2×15－105 ＝142－105 ＝37 因此，你可以知道，原来这一堆蚕豆有37粒。

1900年，德国大数学家大卫·希尔伯特归纳了当时世界上尚未解决的最困难的23个难题。

后来，其中的第十问题在70年代被解决了，这是近代数学的五个重大成就。

二韩信点兵例1我们先考虑以下的问题：假设兵不满一万，每5人一列、9人一列、13人一列、17人一列都剩3人，则兵有多少？首先我们先求5、9、13、17之最小公倍数9945〔注：因为5、9、13、17为两两互质的整数，故其最小公倍数为这些数的积〕，然后再加3，得9948〔人〕。

例2有一个数，除以3余2，除以4余1，问这个数除以12余几？解：除以3余2的数有：2，5，8，11，14，17，20，23….它们除以12的余数是：2，5，8，11，2，5，8，11，….除以4余1的数有：1，5，9，13，17，21，25，29，….它们除以12的余数是：1，5，9，1，5，9，….一个数除以12的余数是唯一的.上面两行余数中，只有5是共同的，因此这个数除以12的余数是5.如果我们把问题改变一下：有一个数，除以3余2，除以4余1，问这个数是几？不求被12除的余数，而是求这个数是几？.很明显，这个数最小是5，满足条件的数是很多的，它们是5＋12×n (n=0，1，2，3…)，事实上，我们首先找出5后，注意到12是3，4的最小公倍数，再加上12的整数倍，就都是满足条件的数.这样就是把“除以3余2，除以4余1”两个条件合并成“除以12余5”一个条件.题目中提出的条件有三个，我们可以先把两个条件合并成一个.然后再与第三个条件合并，就可找到答案.例3秦朝末年，楚汉相争.韩信帅1500名将士与楚王大将李锋交战。

苦战一场，楚军不敌，败退回营，汉军也死伤四五百人，于是韩信整顿兵马也返回大本营。

当行至一山坡，忽有后军来报，说有楚军骑兵追来。

只见远方尘土飞扬，杀声震天。

汉军本来已十分疲惫，这时队伍大哗。

韩信急速点兵迎敌。

他命令士兵3人一排，结果多出2名；接着命令士兵5人一排，结果多出3名；他又命令士兵7人一排，结果又多出2名。

韩信马上向将士们宣布：我军有1073人，敌人不足五百，我们居高临下，以众击寡，一定能打败敌人。

韩信点兵例今有物不知其数，凡三三数之剩二，五五数之剩三，七七数之剩二，问物几何？意思为：一个数除以3余2，，除以5余3，除以7余2，求适合这个条件的最小数。

解答方法一：先分别求出能被5和7整除而被3除余1的数（70），能被3和7整除而被5除余1的数（21），能被3和5整除而被7除余1的数（15），然后用原题中被3、5、7除所得的余数2、3、2分别去乘70、21、15，再把所得的积相加。

70×2＋21×3＋15×2＝233例1一个数除以3余2，，除以5余2，除以7余4，求适合这个条件的最小数。

例2一个数除以5余3，，除以6余4，除以7余1，求适合这个条件的最小数。

解答方法二［6、7］=42 而42÷5余2 并且2×（4）=8 8÷5余3 所以取42×4=168［5、7］=35 而35÷6余5 并且5×（2）=10 10÷6余4 所以取35×2=70［5、6］=30 而30÷7余2 并且2×（4）=8 8÷7余1 所以取30×4=120168+70+120=358 而［5、6、7］=210 358—210=148 所以：适合条件的数为148。

例3 篮子里有鸡蛋若干只，每次取出3只，最后剩1只；每次取出5只，最后剩2只；每次取出7只，最后剩3只；问篮子里至少有多少只鸡蛋？例4 一个自然数被7、8、9除分别余1、2、3，并且三个商数的和使570，求这个自然数。

例5 有一个数，除以3余数是2，除以4余数是1，这个数除以12余数是几？例6 卫兵一队列成5行纵队，末行1人；列成6行纵队，末行5人；列成7行纵队，末行4人；列成11行纵队，末行10人；求兵数。

课后练习：1 一个数除以3余2，，除以5余3，除以7余4，求适合这个条件的最小数。

2 一筐苹果，三三数之余一，四四数之余三，五五数之不足一只，这筐苹果最少有几只?3 召开学生座谈会，每组5人则多1人，每组6人则多2人，每组7人则多3人，问至少有多少个学生？4 某班学生若4人一组多1人，5人一组正好分，6人一组少3人，这个班最少有几人？5 用一辆卡车运货，如果每次运9袋余1袋，如果每次运8袋余3袋，如果每次运7袋余2袋，问这批货物至少有多少袋？6 今有物不知其数，九九数之，八八数之，七七数之……三三数之，二二数之皆余一，问物至少几何？7 篮子里有鸡蛋若干只，每次取出3只，最后剩2只；每次取出5只，最后剩3只；每次取出7只，最后剩1只；问篮子里至少有多少只鸡蛋？8 有铅笔若干支，若按12支一扎多11支，按15支一扎多14支，原有铅笔多少支？9 箩筐里有一批橘子，三个三个一数余一个，五个五个一数余四个，七个七个一数余二个，箩筐里原有多少个橘子？10 一个数除以5余数是2，除以3余数是1，这个数除以15余数是几？11 一排吊灯，3个3个的数剩2个，4个4个的数剩3个，6个6个的数剩5个，这排吊灯至少有几个？12 某数被2、3、4、5、6除都余1，正好被7整除，求符合条件的最小数。

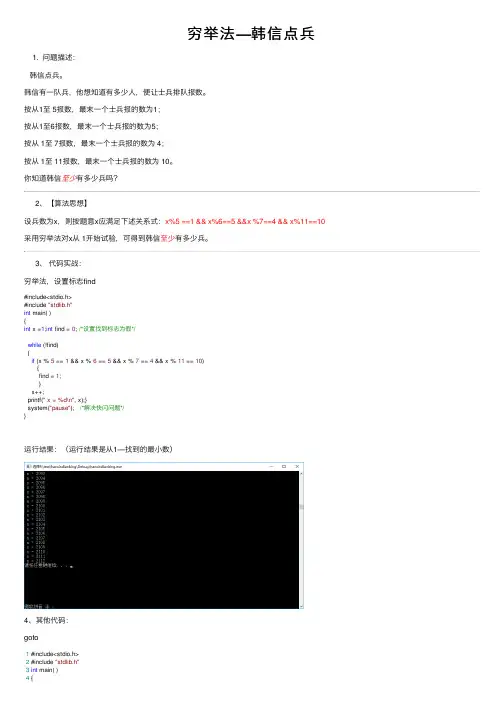
穷举法—韩信点兵1. 问题描述：韩信点兵。

韩信有⼀队兵，他想知道有多少⼈，便让⼠兵排队报数。

按从1⾄ 5报数，最末⼀个⼠兵报的数为1；按从1⾄6报数，最末⼀个⼠兵报的数为5；按从 1⾄ 7报数，最末⼀个⼠兵报的数为 4；按从 1⾄ 11报数，最末⼀个⼠兵报的数为 10。

你知道韩信⾄少有多少兵吗？2、【算法思想】设兵数为x，则按题意x应满⾜下述关系式：x%5 ==1 && x%6==5 &&x %7==4 && x%11==10采⽤穷举法对x从 1开始试验，可得到韩信⾄少有多少兵。

3、代码实战：穷举法，设置标志find#include<stdio.h>#include "stdlib.h"int main( ){int x =1;int find = 0; /*设置找到标志为假*/while (!find){if (x % 5 == 1 && x % 6 == 5 && x % 7 == 4 && x % 11 == 10){find = 1;}x++;printf(" x = %d\n", x);}system("pause"); /*解决快闪问题*/}运⾏结果：（运⾏结果是从1—找到的最⼩数）4、其他代码：goto1 #include<stdio.h>2 #include "stdlib.h"3int main( )4 {5int x ;6for(x=1; ;x++)7 {8if(x % 5 == 1 && x % 6 == 5 && x % 7 == 4 && x % 11 == 10 ) 9 { printf("最⼩值是x= %d\n ",x);10goto end;11 }12 }13 end:;14 system("pause");15 }break语句执⾏代码1 #include<stdio.h>2 #include "stdlib.h"3int main( )4 {5int x ;6for(x=1; ;x++)7 {8if(x % 5 == 1 && x % 6 == 5 && x % 7 == 4 && x % 11 == 10 ) 9 { printf("最⼩值是x= %d\n ",x);10break;11 }12 }1314 system("pause");15 }结果相同，不再赘述。

[阅读材料]世界名题与小升初之：韩信点兵问题在各类竞赛中，各类小升初考试中相关的世界名题出现的概率极高，这是由小升初与数学竞赛的特点决定，这特点便是：知识性，趣味性，思想性相结合。

例1：韩信点兵又称为中国剩余定理，相传汉高祖刘邦问大将军韩信统御兵士多少，韩信答说，每3人一列余1人、5人一列余2人、7人一列余4人、13人一列余6人……。

刘邦茫然而不知其数。

我们先考虑下列的问题：假设兵不满一万，每5人一列、9人一列、13人一列、17人一列都剩3人，则兵有多少？首先我们先求5、9、13、17之最小公倍数9945（注：因为5、9、13、17为两两互质的整数，故其最小公倍数为这些数的积），然後再加3，得9948（人）这个数就满足要求。

韩信点兵问题，是后人对物不知其数问题的一种故事化。

这个问题俗为［韩信点兵］，又叫做「秦王暗点兵」、「鬼谷算」、「隔墙算」、「剪管术」、「神奇妙算」、「大衍求一术」等等），它属于数论(Number theory) 中的「不定方程问题」(Indeterminate equations)。

例2：物不知其数问题出自一千六百年前我国古代数学名著《孙子算经》。

在《孙子算经》里（共三卷，据推测约成书于公元400年左右），下卷的第26题，就是鼎鼎有名的「孙子问题」原题为："今有物不知其数，三三数之二，五五数之三，七七数之二，问物几何？"这道题的意思是：有一批物品，不知道有几件。

如果三件三件地数，就会剩下两件；如果五件五件地数，就会剩下三件；如果七件七件地数，也会剩下两件。

问：这批物品共有多少件？变成一个纯粹的数学问题就是：有一个数，用3除余2，用5除余3，用7除余2。

求这个数。

这个问题很简单：用3除余2，用7除也余2，所以用3与7的最小公倍数21除也余2，而用21除余2的数我们首先就会想到23；23恰好被5除余3，所以23就是本题的一个答案。

这个问题之所以简单，是由于有被3除和被7除余数相同这个特殊性。

韩信点兵问题的初等解法
“韩信点兵”的由来
据说有一次韩信出兵千余人打仗，让军士清点人数，军士回报说：士兵们站3人一排，多出2人；站5人一排，多出4人；站7人一排，多出6人。

韩信稍加思索就得到了准确的士兵数量：1049人。

这个小故事就成为了“韩信点兵”问题的由来了。

事实上，早在《孙子算经》当中就曾经出现过类似的问题：
今有物不知其数，三三数之剩二，五五数之剩三，七七数之剩二，问物几何？
用“韩信点兵”的表达方式就是：每3个士兵站一排，那么就多出来2个人；每5个士兵站一排，就多出来3个人；每7个士兵站一排，就多出来2个人。

那么士兵总共有多少人？
大家可以发现这两道题的相似之处了吧，这就是“韩信点兵”问题通常的题目结构，在数学上属于初等数论当中的“解同余式”问题。

“韩信点兵”的解题思路
通常我们接触到的这类题目都会出现3个左右的同余式。

我们简单的解题技巧就是两两处理已知条件。

实际上对于这个问题是可以利用口诀进行解题的，即：
三人同行七十稀，五树梅花二十一。

七子团圆正半月，除百零五便得知。

这个口诀其实是针对《孙子算经》中那道题目的一个通用解题规则的，四句话意思是：
三人同行七十稀：将除以3的余数乘以70
五树梅花二十一：将除以5的余数乘以21
七子团圆正半月：将除以7的余数乘以15（正半月即15）
除百零五便得知：将以上三个数字相加，求得这个和除以105的余数。

这样就很容易知道《孙子算经》当中所要求的数为23了。

韩信点兵类型题解题思路题目：站队：如：每队3人多2人，每队5人多4人，每队7人多5人，最少有多少人？如果在1000——1200人之间，这个数是多少？分物体：如：2个2个地分多1个，5个5个地分多3个，9个9个地分多6个，最少多少个？如果在200——400个之间，这个数是多少？等类似题思路：总的数除以A，余几（A′）；除以B，余几（B′）；除以C，余几（C′）方法：1、首先找被A和B整除（也就是AB的最小公倍数），被C 除余1 的数是多少，以AB乘积翻倍去找，直到找到满足被C 除余1用这个数×C′=D2、再找被A和C整除（也就是AC的最小公倍数），被B除余1 的数是多少，以AC乘积翻倍去找，直到找到满足被B除余1用这个数×B′=E3、再找被B和C整除（也就是BC的最小公倍数），被A除余1 的数是多少，以BC乘积翻倍去找，直到找到满足被A除余1用这个数×A′=F4、找ABC最小公倍数是多少（G）5、（D+E+F）÷G=H……KK就是这题的答案（最少的这个数），如果指定在某一范围内，则用G（ABC的最小公倍数）乘以整数倍后加上K（保证得数在指定的范围内的数），就是答案。

例题：一堆苹果，每次拿3个最后剩余2，每次拿7个最后剩3个，每次拿8个最后剩5个，问这堆苹果最少是多少？如果个数在800到1000之间，这堆苹果是多少个？解答：1、首先找被3和7整除（21），被8 除余1 的数（21、42、63、84、105……）是105 105×5=5252、被3和8整除（24），被7除余1 的数是（24、48、72、96、120……）是120120×3=3603、被7和8整除（56），被3除余1 的数是（56、112……）是112112×2=2244、3和7和8两两互质的整数故其最小公倍数是168（525+360+224）÷168=6 (101)101就是最少的苹果数。

韩信点兵算法及其原理【问题】求最小非负整数N，使他在除以3,5,7以后所得余数分别是a,b,c。

【韩信点兵法的口诀】三人同行七十稀，五树梅花廿一枝，七子团圆整半月，除百零五便得知。

【韩信点兵法口诀的释义】前三句意思较为明确，假如说一个非负整数N，在除以3,5,7以后所得余数分别是a,b,c。

那么70a+21b+15c 一定是符合题意要求的数。

第四句“除”字作“减”字解。

因为符合要求的最小数N必满足0≤N＜105，但是70a+21b+15c 却有可能大于105，甚至大于210，所以还不一定是符合要求的最小数。

那么当他大于或等于105时，还必须减去105，可能还要再减去105，直到比105小为止，才可以得到符合题意要求的最小数。

【说明】这里105是3,5,7的最小公倍数，70a+21b+15c + 105k 也一定满足“除以3,5,7以后所得余数分别是a,b,c”。

【例如】a=b=c=2，70a+21b+15c=212，70a+21b+15c-105=107＞105。

而符合题意要求的最小数是 2，即 212-105-105=2.【再如】a=2,b=4,c=6，70a+21b+15c=314，314-105=209＞105。

而符合题意要求的最小数是 104，即 314-105-105=104.【韩信点兵法口诀的原理】①能被5,7除尽数是35k,其中k=2，即70除3正好余1，70a 除3正好余a。

②能被3,7除尽数是21k,其中k=1，即21除5正好余1，21b 除5正好余b。

③能被3,5除尽数是15k,其中k=1，即15除7正好余1，15c 除7正好余c。

这样——根据①可知 70a+21b+15c 除3正好余a。

根据②可知 70a+21b+15c 除5正好余b。

根据③可知 70a+21b+15c 除7正好余c。

【韩信点兵法口诀的局限性】只适宜于如题所示的一个极为特殊的问题，要推广到同类问题必须另行制作口诀（即公式）。