机器人学-第3章_机器人运动学
- 格式:ppt
- 大小:2.80 MB
- 文档页数:28

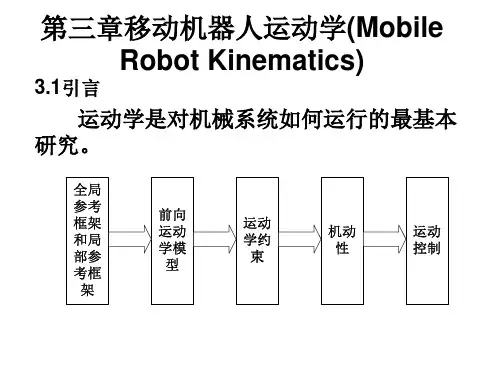
第三章机器人运动学机器人运动学是研究机器人如何在二维或三维空间中进行运动的学科。
它涉及到机器人的轨迹规划、运动控制和路径规划等重要内容。
本章将介绍机器人运动学的基本概念和常用模型,帮助读者全面了解机器人的运动规律和控制原理。
1. 机器人运动学的基本概念机器人运动学是研究机器人位置和姿态变化的学科,包括正运动学和逆运动学两个方面。
正运动学研究机器人的末端执行器的位置和姿态如何由关节变量确定;逆运动学则研究机器人如何通过末端执行器的位置和姿态来确定关节变量的值。
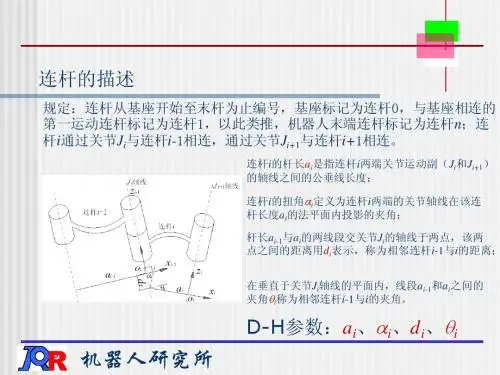
机器人的运动学建模一般采用DH(Denavit-Hartenberg)参数表示方法。
DH 参数是由Denavit和Hartenberg提出的一种机器人坐标系的选择和旋转轴的确定方法。
通过定义一系列关节坐标系,建立起机器人的坐标系链,并确定各个关节的旋转轴和约定的方向,可以方便地描述机器人的运动学特性。
2. 机器人正运动学机器人正运动学是研究机器人末端执行器位置和姿态如何由关节变量确定的问题。
在机器人的正运动学中,常用的方法有几何法和代数法。
2.1 几何法几何法是一种较为直观的方法,通过对机器人各个关节坐标系的位置和旋转进行推导,得到机器人末端执行器的位置和姿态。
几何法适用于无约束和无外力干扰的情况,可以简单快速地推导出机器人的正运动学方程。
2.2 代数法代数法是一种基于运动学链的代数运算的方法,通过DH参数建立起机器人的坐标系链,并通过矩阵运算推导出机器人的正运动学方程。
代数法在机器人正运动学的推导和计算过程中更具有普适性和灵活性。
3. 机器人逆运动学机器人逆运动学是研究机器人如何通过末端执行器的位置和姿态来确定关节变量的值的问题。
机器人逆运动学在机器人运动规划和路径控制中起到重要的作用。
机器人逆运动学的求解一般采用迭代方法,通过迭代计算来逼近解析解,实现对机器人关节变量的求解。
逆运动学的求解过程中可能会出现奇异点和多解的情况,需要通过约束条件和优化方法来处理。



机器人学第三章机器人运动学正解机器人学是研究机器人行为和控制的学科,其中机器人运动学是机器人学的一个重要分支。
机器人运动学正解是指通过分析和计算机器人的构型和外部参数,得出机器人在给定时间和空间条件下的运动状态和轨迹。
本文将介绍机器人运动学正解的基本概念、解析方法和应用。
一、机器人运动学正解的基本概念在机器人学中,机器人的运动学分为正解和逆解两种。
机器人运动学正解是解决机器人构型和外部参数已知时,推导机器人末端执行器的运动学特征。
而逆解则是解决机器人末端执行器的位置和姿态已知时,求解机器人的构型参数和外部参数。
机器人运动学正解中的基本概念包括机器人构型、外部参数、欧式空间和坐标转换等。
1. 机器人构型:机器人构型是指机器人在空间中的位置和姿态参数,用来描述机器人的状态。
常用的机器人构型参数包括关节角度、关节长度、关节位移等。
2. 外部参数:外部参数是指机器人相对于参考坐标系的位置和姿态参数。
外部参数可以通过传感器获得,也可以通过标定技术确定。
3. 欧式空间:欧式空间是指具有三个直角坐标轴的空间,通常用来描述机器人的位置和姿态。
欧式空间中的点可以表示为(x, y, z),其中x、y、z分别表示点在三个坐标轴上的位置。
4. 坐标转换:坐标转换是将点在一个坐标系下的表示方式转换到另一个坐标系下的过程。
在机器人运动学正解中,常用的坐标转换矩阵包括旋转矩阵和平移矩阵。
二、机器人运动学正解的解析方法机器人运动学正解可以通过解析方法和数值方法两种方式求解。
解析方法是通过建立数学模型和方程组,利用数学推导和计算得出机器人的运动学特征。
数值方法则是通过迭代计算和数值逼近的方式,得出机器人的运动学特征。
1. DH参数法:D-H参数法是一种常用的机器人运动学正解方法,通过建立机器人的坐标系和关节间的转动关系,推导出机器人的运动学正解方程。
D-H参数法可以推导出机器人的位姿变换矩阵,进而得到机器人末端执行器的位置和姿态。