- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
G dG = T
因 故 G T
p, n
G dT + p p,n
G = –S ; p
T,n
dp + ∑
G nB
T,p,nC≠B
dnB = B
T, n
G = V; ni
T,p,nC≠B
dG = – SdT + Vdp + ∑BdnB
§3. 2
化学势判据
化学势
在定温定压条件下,dG = ∑BdnB = Wr’ 故∑BdnB 是定温定压条件下一多组分均相系统 在发生状态变化时所能够做出的最大有效功。 ∑BdnB 0 过程为自发过程 ∑BdnB = 0 过程达平衡 故化学势是决定物质传递方向和限度的强度因素
2. 混合理想气体的化学势
2.混合理想气体的化学势
B = B + RT ln( pB / p )
pB——混合气体中气体B的分压
B——分压 pB = p 时气体B的化学势,称气体B的标
准态化学势,仅是温度的函数
对混合气体系统的总吉布斯函数,可用集合公式表示 G =∑nBB
3. 实际气体的化学势
例: P93/习题6 B (1) T (3)
p
化学势
(2) B p
T
= – SB
= VB
HB T
p
= Cp,B
(4) B = HB – T SB
T,p,nC≠B
证明: (1) B B T
p
G = nB T
=
G nB
T,p,nC≠B
=
p
G nB T
化学势
将dG = –SdT + Vdp + ∑B dnB代入上式 dA = –SdT – pdV + ∑B dnB A = f ( T,V,n1,n2,… ) A dA = T
V,n
A dT + V
T,V,nC≠B
T,n
dV +∑
A nB
T,V,nC≠B
dnB
A B = n B
对于实际气体,特别是压力比较高时,理想气体的化学势公式 不能应用,因此,引入一个逸度的概念。 (1)定义
实际气体的有效压力为逸度 f 。
f = p 其中逸度系数 = f / p ,标志该气体与理想气体偏差的程度, 数值不仅与气体的特性有关,还与气体所处的温度和压力 有关。 当压力趋于零时,实际气体的行为接近于理想气体的行为, 这时 趋于1 。
p
S = – nB
T,p,nC≠B
T,p,nC≠B
= – SB
§3. 2
证明: (2) B B p
化学势
=
T
G = nB =
= p V nB T
T,p,nC≠B
T
G nB
T,p,nC≠B
G nB p
T
T,p,nC≠B
T,p,nC≠B
= VB =
p
证明: (3)
HB T
p
= =
H nB
T,p,nC≠B
H nB T
p
Cp nB
T,p,nC≠B
T,p,nC≠B
= Cp,B
§3. 2
证明: (4) B
化学势
= HB – T SB
T,p,nC≠B
G = nB
=
T,p,nC≠B
(H–TS) nB
将这些公式对比纯物质的公式,可以推知: 在多组分体系中的热力学公式与纯物质的公式具有完全 相同的形式, 所不同的只是用偏摩尔量代替相应的摩尔量而已。
3. 实际气体的化学势
(2)实际气体的化学势
= + RT ln( f / p )
注意此式表示实际气体化学势时,校正的是实际 气体的压力,而没有改变 ,所以仍是理想气 体的标准态化学势。 即是该气体的压力等于标准压力p ,且符合理 想气体行为时的化学势,亦称为标准态化学势。
对于纯物质来说,不存在偏摩尔量,它的偏摩尔量就是 摩尔量。
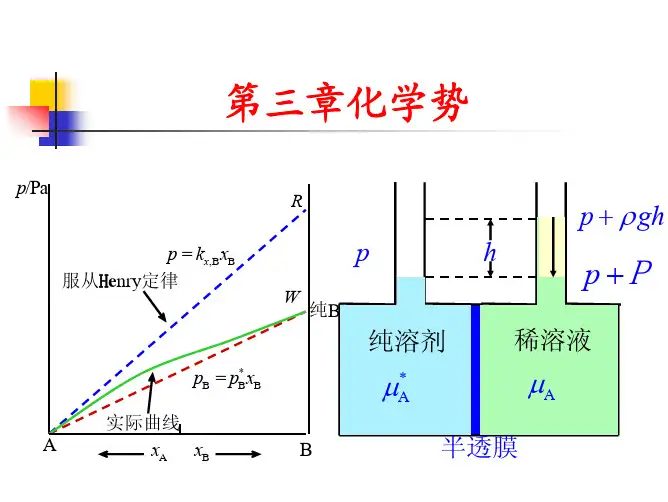
2. 化学势在多相平衡中的应用
在定温定压下及W’=0的条件下,如果系统已经达成平衡时: dG = ∑B dnB = 0 对于两相系统,如系统有α和β两个相时,在定温定压条件 下,如果有dnB的B物质从α相转移到β相,
则α、 β相的吉布斯自由能变化为: dG() = –B () dnB dG() = B () dnB dG = dG( ) + dG ( ) = [ B ( ) – B ( )] dnB 平衡时 dG = 0
§3. 1
1. 单组分系统
偏摩尔量
• 前两章讨论的热力学系统多数是纯物质,称为单组分系统。
• 描述单组分密闭系统的状态,只需要两个状态性质(T,P ,S,
V )就可以了,即双变量系统。 dU = TdS – pdV
dH = TdS + Vdp 热力学基本公式 dA = – SdT – pdV
dG = – SdT + Vdp
2. 偏摩尔量的物理意义
其物理意义:在定温定压条件下往无限大的系统中加 入1mol物质B 所引起系统中某个热力学量X的变化; 或者是在有限量的系统中加入dnB后,系统容量性质改 变了dX,dX与dnB 之比就是XB 。 实际上是一个微商的概念。 例 以系统的体积对物质B的物质的量nB作图 当浓度为 m 时,曲线的斜率即为浓度 m 时系统中物质B的偏摩尔体积。 V 斜率 = n B
T,p,nj
dn2 + · · ·
其中 nk—表示所有物质的量都固定; nj —表示除指定的物质外,其它物质的量固定。
1. 偏摩尔量的定义
在定温定压条件下,定义: X XB = nB T,p,nC≠B
则 注意:
dX = ∑XB dnB
XB称为物质B 偏摩尔量,X是系统中任意一个容量性质。 只有容量性质才有偏摩尔量,而偏摩尔量是强度性质; 只有在定温定压条件下才称偏摩尔量; 纯物质的偏摩尔量就是它的摩尔量; 任何偏摩尔量都是温度、压力及组成的函数。
§3. 1
偏摩尔量
不论什么系统中,质量总是具有加和性的,系统的 质量等于构成该系统的各个部分的质量总和。 但是除了质量以外,其它容量性质除非在纯物质中
或理想溶液中,一般都不具有加和性。
在讨论两种或两种以上物质所构成的均相体系时,必 须引入一个新的概念—— 偏摩尔量。
1. 偏摩尔量的定义
多组分系统的任一种容量性质X( X 可分别代表V, U, H, S, A, G等)可以看作是温度T,压力P,以及各物 质的量的n1,n2,…, nk的函数 X = f ( T,p,n1,n2,…,nk ) 当系统的状态发生任意无限小量的变化时,全微分 可用下式表示: X dX = T X dT + p p,nk X dp + n T,nk 1 X dn1 + n T,p,nj 2
偏摩尔量 V VB = nB U UB = nB H HB = nB S SB = nB A AB = nB G GB = nB
T,p,nC≠B T,p,nC≠B T,p,nC≠B
T,p,nC≠B
T,p,nC≠B T,p,nC≠B
3. 偏摩尔量的集合公式
吉布斯-杜亥姆(Gibbs-Duhem)公式 设 X = f ( T,p,nB,nC,… ) X X X dT + dX = T p T,n dp + ∑ nB p,n 在定温定压条件下: X dX = ∑ n B 表明 在定 温定 压下, 偏摩 尔量 之间 是具 有一 定的 联系。
§3. 1
2. 多组分系统
偏摩尔量
• 在研究化学问题的过程中,时常会遇到多种物质组成的系统,如 混合气体、溶液等,称为多组分系统。 • 对于多组分均相系统,仅规定温度和压力,系统的状态并不能确 定,还必须指明系统中每种物质的量(或浓度)。
nB 物质的量的分数x B n(总) nB 质量摩尔浓度 m B mA 物质的量浓度c nB B V (总) 质量分数w m B B m (总)
它仅是温度的函数。
3. 实际气体的化学势
实际气体的逸度求算
= + RT ln( f / p )
T,p,nC≠B
V
m
=VB
nb
这是偏摩尔量的求法之一。
3. 偏摩尔量的集合公式
假设一个系统由物质A和B组成, 在定温定压下,按一定的比例加入dnA和dnB的物质A和物 质B时,可得 dX = XAdnA + XBdnB 若连续不断地往此系统中加入dnA和dnB, 保持dnA:dnB = nA :nB,即保持系统的浓度不变, 此时,XA和XB应当为一常数。
ቤተ መጻሕፍቲ ባይዱ
B ( ) = B ( )
多组分系统多相平衡的条件:温度、压力相等,物质在 各相中的化学势相等。
3. 化学势在化学平衡中的应用
例:2SO3 = 2SO2 + O2 2dn 2dn dn 当反应在定温定压及W’=0的条件下进行时 dG = ∑BdnB = 2 (SO2)dn + (O2)dn – 2 (SO3)dn = [2 (SO2) + (O2) – 2 (SO3)]dn 平衡时 dG = 0 2 (SO2) + (O2) = 2 (SO3) 结论:对任意化学反应,有 ∑BB(产物) = ∑BB(反应物) 化学平衡条件 ∑BB(产物) < ∑BB(反应物) 正向反应自发进行 ∑BB(产物) >∑BB(反应物) 逆向反应自发进行
化学反应由物质的化学势较大的一边向化学势较小的一边进行
§3. 3 气体物质的化学势
1. 纯组分理想气体的化学势 在一定温度下,纯组分理想气体 GB = Gm