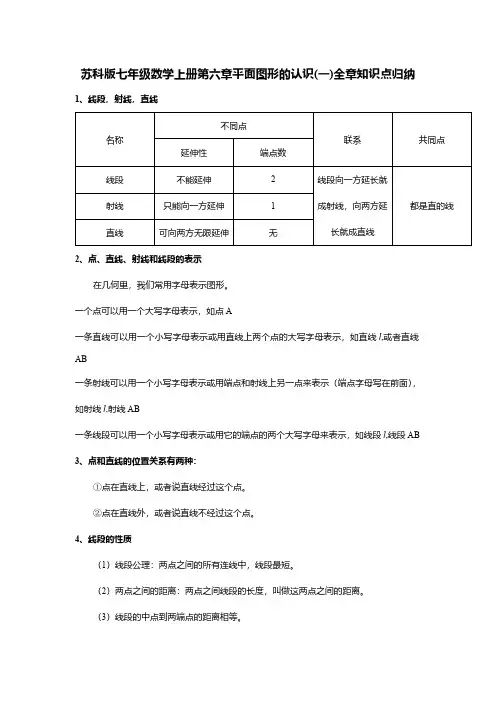
(完整版)第六章:平面图形的认识知识点总结
- 格式:doc
- 大小:139.14 KB
- 文档页数:6

七年级数学6章知识点七年级数学的第六章主要涉及到三个部分:平面图形的认识、定理与推论、空间图形的认识。
这些内容都是数学中非常基础的概念,是后续学习的重要基石。
本文将逐一介绍这些知识点,并尽可能用通俗易懂的语言来让学生掌握这些基础知识。
一、平面图形的认识平面图形是指在平面上展开的图形,包括三角形、四边形、多边形等。
其中三角形是最基本的平面图形,是由三条线段连接成的一个三角形;四边形则是由四条线段连接成的四边形。
多边形则是由多条线段连接成的多边形,如五边形、六边形等。
除了基础的三角形、四边形和多边形之外,还有一些特殊的平面图形,如圆形、椭圆形等。
其中圆形是指由一个圆心和圆周上所有点组成的图形,而椭圆则是由两个焦点和其距离之和为常数的所有点组成的图形。
二、定理与推论在平面图形中,有很多定理和推论,用来描述不同图形之间的关系。
其中一些比较重要的定理和推论包括:1.相等定理相等定理主要是用于判断两个图形是否相等。
包括:全等三角形的判定、等腰三角形的判定、等角三角形的判定等。
2.平行定理平行定理是用来判断两条直线是否平行。
其中包括平行线性质、平行四边形性质等。
3.垂直定理垂直定理主要是用来判断两条直线是否垂直。
包括垂线性质、垂直平分线等。
4.中线定理中线定理是用于描述三角形中线特点的。
其中包括中线定理、三角形中位线定理等。
三、空间图形的认识空间图形是指存在于三维空间中的图形,包括球体、长方体、正方体等。
其中球体是最基本的空间图形,是由一个球心和球面上的所有点组成的图形;长方体则是由长方体的六个面所组成的图形;而正方体则是从长方体中特殊的一种,所有的面都是正方形。
四、结语七年级数学的第六章知识点,主要涉及到了平面图形的认识、定理与推论、空间图形的认识等方面。
这些知识点是数学中非常基础的概念,但是也是非常重要的基础。
希望各位同学在学习的过程中认真掌握这些基础知识,以便更好地应对后续的学习和考试。

第六章 平面图形的认识(一)第1课时 6.1线段、射线、直线(1)认识并会用符号表示线段、射线、直线,掌握它们的表示法,理解它们的联系和区别,掌握线段有关性质。
【学习重点和难点】:1.重点:线段、射线和直线的概念的区别与联系;两点之间线段最短。
1.小兔子想从A 地到B 地.①图1中的三条路线哪一条相对近一些? ②有没有最短的路线? 请在图中画出来。
2.生活常识告诉我们:(1)两点之间的所有连线中,_______最短。
(2)________________叫做这两点之间的距离。
2.感悟新知1.线段表示:2.射线表示:3.直线表示:活动一:图中以A 为端点的线段有 条?以B 为端点的线段有 条?以C 为端点的线段有 条?以D 为端点的线段有 条?图中一共有 条线段?活动二: 如图,已知点A 、B .(1)过点A 任意画直线,可以画出多少条?(2)过两点A 、B 画直线呢?你可以得出 。
活动三:做一做:如图,已知点A 、B 、C .(1)画线段BC (连接BC ),画直线AB 、AC ;(2)在线段BC 上取一点D ,画射线AD .(3)规定同桌按要求画图。
【学习目标】: 2.难点:几何的图形语言、符号语言以及文字语言的相互转化。
【课前预习】1. 分别画一条线段、一条射线、一条直线,并举出一些日常生活中线段、射线、直线的实例。
【课堂导学】1.组内助学、小组展示:图A B DC【拓展延伸】1.如图,以点A 为端点的线段有多少条?以点B 为一个端点的线段有多少条?请分别表示这些线段。
2.下图中各有多少条线段?你发现了什么规律?(用含n 的代数式表示)……反思与心得:【课堂检测】1.下列说法中,错误的是( )A.经过一点的直线可以有无数条B.经过两点的直线只有一条C.一条直线只能用一个字母表示D.线段CD 和线段DC 是同一条线段2.下列说法中正确的是( )A.画一条3厘米长的射线B.画一条3厘米长的直线C.画一条5厘米长的线段D.在线段、射线、直线中直线最长3.一个钉子把一根细木条钉在木板上,木条能转动,这说明______________________.4.平面上三条直线两两相交,最少有__ __个交点,最多有__ __个交点。

平面图形总结知识点平面图形的基本组成元素是点和线。
点是几何中的最简单的图形元素,它没有大小和形状,只有位置。
线是由无穷多个点组成的,是一种没有宽度和厚度的平面图形。
根据点和线的组合方式,我们可以构造出不同的平面图形,比如线段、射线、角、多边形等。
线段是由两个端点和它们之间的所有点构成的一条有限长的线。
线段有长度,可以用两个端点的坐标表示。
射线是由一个端点和它的一侧的所有点构成的半条直线,没有固定的长度。
角是由两条相邻的射线构成的,用来衡量两条射线之间的夹角大小。
多边形是由若干条线段构成的封闭图形,它的边数和顶点数是相等的。
在学习平面图形时,我们需要掌握几何构图的方法。
几何构图是指用已知图形的一些性质或要求,通过不使用任何测量工具,只使用尺规和直尺等几何工具,画出所要求的图形。
常见的几何构图有画线段、作垂线、作平行线、作角平分线、作垂直平分线、作三角形等。
在证明平面几何问题时,我们需要运用一些几何定理和性质。
比如平行线的性质、垂直线的性质、相似三角形的性质、勾股定理、等边三角形的性质等。
这些性质和定理是我们进行平面几何证明的重要工具,通过合理运用它们可以快速解决问题。
在平面几何中,平行线是一个非常重要的概念。
平行线是指在一个平面内,其间没有任何交点的两条直线。
平行线的性质有很多,比如平行线与同一条直线的交点连线平行于平行线,平行线的性质可以用来解决许多几何问题,比如平行线截割线段、平行线截割三角形等问题。
相似三角形也是平面几何中的一个重要概念。
相似三角形是指三角形的对应角相等,对应边成比例。
相似三角形的性质有很多,比如相似三角形的高、中线、角平分线、中位线、垂心、外心等重要性质。
利用相似三角形的性质可以快速解决许多几何问题,比如求三角形的面积、判定两个三角形是否相似、求线段的长度等问题。
勾股定理是平面几何中的一个著名定理,它是用毕达哥拉斯学派的学生勾股所发现的。
勾股定理指出,在直角三角形中,直角边的平方和等于斜边的平方。


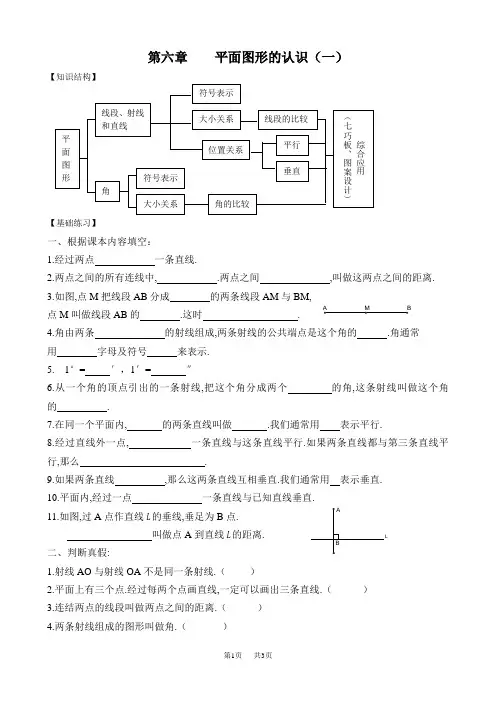
第六章 平面图形的认识(一)【知识结构】【基础练习】一、根据课本内容填空:1.经过两点 一条直线.2.两点之间的所有连线中, .两点之间 ,叫做这两点之间的距离.3.如图,点M 把线段AB 分成 的两条线段AM 与BM, 点M 叫做线段AB 的 .这时 .4.角由两条 的射线组成,两条射线的公共端点是这个角的 .角通常 用 字母及符号 来表示.5. 1°= ′,1′= ″6.从一个角的顶点引出的一条射线,把这个角分成两个 的角,这条射线叫做这个角的 .7.在同一个平面内, 的两条直线叫做 .我们通常用 表示平行.8.经过直线外一点, 一条直线与这条直线平行.如果两条直线都与第三条直线平行,那么 .9.如果两条直线 ,那么这两条直线互相垂直.我们通常用 表示垂直. 10.平面内,经过一点 一条直线与已知直线垂直. 11.如图,过A 点作直线L 的垂线,垂足为B 点.叫做点A 到直线L 的距离. 二、判断真假:1.射线AO 与射线OA 不是同一条射线.()2.平面上有三个点.经过每两个点画直线,一定可以画出三条直线.()3.连结两点的线段叫做两点之间的距离.( )4.两条射线组成的图形叫做角.()5.角的大小与角的两边的长短无关.( )6.不相交的两条直线叫做平行线.()7.平面内,有且只有一条直线与已知直线垂直.( )三、解下列各题:1.如右图,直线L 上四个点A 、B 、C 、D,则: AD = BD + = CD + BC = BD - = AC -2.已知线段AB=5cm,C 为AB 上一点,且AC=3cm, M 、N 分别为AC 、BC 的中点.求线段MN 的长.3. 右上图中,以O 为顶点的角有 个, 它们分别是 .4.计算:①1.5°= ′= ″;②450″= ′= °; ③90°- 54°48′6″= .5.如右图,OA ⊥OB,直线CD 过点O,且∠AOC=50°, 则∠DOB=°6.如图,两块三角尺拼在一起.试确定图中∠B 、∠E 、∠BAD 、∠DCE 的度数.7.在图中作出表示下列方向的射线:①北偏东30度;②南偏西45度.8.如图,在方格纸上有一条线段AB 和一点C. ①过点C 画出与AB 平行的直线; ②过点C 画出与AB 垂直的直线.9.如图,是用同学们熟悉的七巧板拼起来的,请你找出: (1)图中互相垂直的线段和互相平等的线段各一组,并表示出来; (2)图中的一个锐角、一个钝角、一个直角,并说出它们的角度。


平面图形手抄报知识点总结一、平面图形的基本概念1. 点、线、面的概念点是最基本的图形,没有长度和宽度,只有位置。
线是由无数个点连成的,没有宽度,有长度但没有面积。
面是由无数个点和线连成的,有长度和宽度,有面积。
2. 平面图形的分类平面图形可以根据不同的特征进行分类,主要包括几何图形和不规则图形。
几何图形是具有明确定义的形状和大小的图形,包括三角形、矩形、正方形、梯形、菱形、平行四边形等。
不规则图形是形状不规则且不能通过几何图形的特征区分的图形,例如圆、椭圆等。
二、平面图形的性质1. 三角形的性质三角形是最简单的多边形,具有以下性质:(1)三角形的内角和为180度。
(2)在任意一个三角形中,任意两边之和大于第三边。
(3)在任意一个三角形中,最长边对应的最大角最小。
(4)等腰三角形的底边中线、高、中位线、角平分线均相等。
(5)等边三角形的内角均为60度。
2. 矩形、正方形的性质矩形和正方形都是四边形,具有以下性质:(1)矩形的对角线相等,对角互补。
(2)矩形的相邻两边互相垂直。
(3)正方形是一种特殊的矩形,具有矩形的所有性质,同时具有四条边相等的性质。
3. 圆的性质圆是一个特殊的平面图形,具有以下性质:(1)圆的直径是圆上任意两点的连线,且通过圆心。
(2)圆的半径是由圆心到圆上的任意一点的长度。
(3)圆的面积公式为πr²,其中r为半径。
(4)圆的周长公式为2πr,其中r为半径。
三、平面图形的计算方法1. 平面图形的周长计算周长是指图形的所有边的长度之和,不同的平面图形的周长计算方法也不同。
其中,矩形、正方形、三角形、梯形、菱形等多边形的周长计算是将所有边长相加,而圆的周长计算方法是利用圆的周长公式2πr进行计算。
2. 平面图形的面积计算面积是指图形所覆盖的空间大小,不同的平面图形的面积计算方法也有所不同。
其中,矩形、正方形、三角形、梯形、菱形等多边形的面积计算是根据相应的面积公式进行计算,而圆的面积计算是利用圆的面积公式πr²进行计算。


第六章 平面图形的认识(一) 单元复习 知识填空 1.基本事实:两点之间, 最短。 确定一条直线。 2.若C是线段AB的中点,则:AC=BC= AB或AB= AC= BC。 3.若BD是∠ABC的平分线,则有:∠ =∠ = ∠ABC; ∠ABC=2∠ =2∠ 。 4.如果∠1和∠2互为余角,则有 ;如果∠1和∠2互为补角,则有 。 4.余角的性质: ;补角的性质: 。 5.如果∠1和∠2是对顶角,则有 。 6.过直线外一点 与这条直线平行。 7.过一点 与已知直线垂直。 8.直线外一点与直线上各点连接的所有线段中, 最短。 一、选择题(每题3分,共30分) 1.平面上有任意三点,过其中两点能画直线条数为 ( ) A.1 B.3 C.1或3 D.无数条 2.在直线l上顺次取A、B、C三点,使得AB=5㎝,BC=3㎝,如果O是线段AC的中点,那么线段OB的长度是 ( ) A.0.5㎝ B.1㎝ C.1.5㎝ D.2㎝
3.某测绘装置上一枚指针原来指向南偏西500(如图),把这枚指针按逆时针方向旋转41周,则结果指针的指向为 ( ) A.南偏东50º B.西偏北50º C.南偏东40º D.东南方向
第3题图 第4题图 C
BA第5题图 第7题图 4.如图,直线AB与CD相交于点O,EO⊥AB于O,∠1和∠2的关系是 ( ) A.∠1=∠2 B.∠1+∠2=180° C.∠1+∠2=90° D.∠1=2∠2 5.如图,把两块三角板按下图所示那样拼在一起,则∠ABC的大小为 ( ) A.90° B.100° C.1200 D.135° 6.已知∠AOB=80°,以O为顶点,OB为一边作∠BOC=20°,则∠AOC为 ( ) A.100° B.60° C.100°或60° D.80°或20° 7.如图,∠AOC=∠BOC=90°,ON是锐角∠COD的角平分线,OM是∠AOD的角平分线,那么∠MON为 ( )
1 MOa第六章:平面图形的认识 第一节:直线、射线、线段 知识点1:概念 线段:一段拉直的棉线可近似地看作线段,线段有两个端点。 线段的画法:(1)画线段时,要画出两个端点之间的部分,不要画出向任何一方延伸的情况.(2)以后我们说“连结 ”就是指画以A 、B 为端点的线段. 射线:将线段向一个方向无限延长,就形成了射线,射线有一个端点。如手电筒、探照灯射出的光线等。 射线的画法:画射线 一要画出射线端点 ;二要画出射线经过一点,并向一旁延伸的情况. 直线:将线段向两个方向无限延长就形成了直线,直线没有端点。如笔直的铁轨等。 直线的画法:用直尺画直线,但只能画出一部分,不能画端点。 知识点2:线段、直线、射线的表示方法:
(1) 点的记法:用一个大写英文字母 (2) 线段的记法:①用两个端点的字母来表示 ②用一个小写英文字母表示 如图:
记作线段AB或线段BA, 记作线段a, 与字母顺序无关 此时要在图中标出此小写字母 温馨提示:线段是直线(或射线)的一部分;2.线段不可向两方无限延伸,但可度量;3.延长线常化成虚线;4.延长线段AB是指按A到B的方向延长,延长线段BA是指按B到A的方向延长. (3) 射线的记法:用端点及射线上一点来表示,注意端点的字母写在前面 如图:
记作射线OM,但不能记作射线MO 温馨提示:1.射线是直线的一部分;2.射线是像一方无限延伸,有一个端点,不能度量,不能比较大小;3.射线可作反向延长线,不存在射线的延长线。 (4) 直线的记法:①用直线上两个点来表示 ②用一个小写字母来表示
如图:
记作直线AB或直线BA, 记作直线l 与字母顺序无关。 此时要在图中标出此小写字母
知识点3:线段、射线、直线的区别与联系: 联系:三者都是直的,线段向一个方向延长可得到射线,线段向两个方向延长可得到直线,故射线、线段都是直线的一部分,线段是射线的一部分。 区别:直线可以向两方延伸,射线可以向一方无限延伸,线段不能延伸,三者的区别见下表:
BABAl2
BAa
MOBA
kBA
名称 图形 表示方法 延伸、度量情况 端点 长度 共同点
线段 线段AB(或线段BA)(字母无序) 线段a 不能延伸,可度量 两个 有 都是直线,非曲线 射线 射线AB(字母有序) 只能向一方无限延伸,不可度量
一个 无
直线 直线AB(或直线BA)(字母无序) 直线l 可像两方无限延伸,不可度量 无 无 知识点4:直线的基本性质(重点) (1) 经过一点可以画无数条直线 (2) 经过两点只可以画一条直线 直线的基本性质:经过两点有且只有一条直线(也就是说:两点确定一条直线) 注:“确定”体现了“有”,又体现了“只有”。 如图:
经过点K可以画无数条直线 经过点A、B只可以画一条直线 温馨提示:两条射线(或线段)未必一定有交点 知识点5:两点的距离 连接两点的线段的长度,叫做这两点的距离。它是线段的长度,是数量,不是线段本身 知识点6:两点的距离 连接所有两点的线中,线段最短,简述为两点之间,线段最短。
l3
2)1(nnN
知识点7:线段的中点 如图,若点C将线段AB分为线段相等的两条线段AC和BC,则点C为线段AB的中点 A C B 温馨提示:1.一条线段的中点只有一个;2.某一点要成为线段的中点必须同时满足两个条件:点必须在这条线段上;它把这条线段分成相等的两条线段。 知识点8:线段的计数问题 阅读下表:
(1)根据表中规律可得到线段总数N与线段上点数n(包括线段的两个端点)存在着如下的关系
第二节:角——余角、补角 知识点1:角的定义 角是有两条具有公共顶点的射线组成的。两条射线的公共点叫做这个角的顶点。两条射线叫做角的两边。角也可以看成时一条射线绕它的顶点旋转而成的。 温馨提示: 1.因为射线是向一方无限延伸的,所以角的两边无所谓长短,即角的大小与它的边长无关。 2.角的大小可以度量,也可以比较。 3.根据角的度数,角可以分成锐角、直角、钝角、平角和周角。 锐角:大于0小于90;直角:等于90;钝角:大于90小于180; 平角:等于180(不能说成平角就是一条直线);周角:等于360(不能说成周角就是一条射线) 4.两条射线组成的图形叫做角或者角是由一条射线旋转而成的,这两种说法都是错误的 知识点2:角的表示 ●通常用三个大写字母表示,表示顶点的字母在中间。●在不引起混淆的情况下,也可以用表示顶点的大写字母表示角。●也可以用希腊字母(α,β,γ)或数字表示角。 4
2)1(nn知识点3:角的度量 概念:以度、分、秒为基本单位的角的度量制,叫做角度制。 1°=60′,1′=60″ ,1°=3600″,1周角=360,1平角=180. 温馨提示:1.角的度、分、秒是60进制的。2.在进行度分秒运算时,由低级单位向高级单位转换或者由高级单位向低级单位转换,要逐级转换,不能越级。
知识点4:角平分线(见课本) 知识点5:角的计数问题 数角与之前数线段是同一类问题,同样可从角的顶点出发引出n条射线,共有角的个数为:
知识点6:余角、补角 余角:如果两个角的和是一个直角,那么这两个角互为余角,其中一个角是另一个角的余角 补角:如果两个角的和是一个平角,那么这两个角互为补角,其中一个角是另一个角的补角 性质:●同角或等角的余角相等。●同角或等角的补角相等。 温馨提示:●钝角没有余角;●互为余角和补角是两个角之间的关系;如:
180321,不能说他们3个角互补。●互为余角、补角只与角的度数有关,与
角的位置无关,只要他们的度数等于90或者180,那一定互为余角或者补角。 知识点7:方向角 1.定义:一般是指以观测者的位置为中心,将正北或正南方向作为起始方向旋转到目标的方向线所成的角(一般指锐角),通常表达成北(南)偏东(西)××度。 2.度量:方向角系分由南北起算,角度值在零度及九十度之间。 3.表示方式:在角度值之前冠以南北字样,其后则书出东西字样。 正北:北偏东0度或者北偏西0度。 正南:南偏东0度或者南偏西0度。 正东:北偏东90度或者南偏东90度。 正西:北偏西90度或者南偏西90度。 东北:北偏东45度。 西北:北偏西45度。 东南:南偏东45度 西南:南偏西45度 知识点8:时针、分针的夹角 (1)普通钟表相当于圆,其时针或分针走一圈均相当于走过360°角;
(2)钟表上的每一个大格(时针的一小时或分针的5分钟)对应的角度是:3012360; (3)时针每走过1分钟对应的角度应为:5.06012360; 5
(4)分针每走过1分钟对应的角度应为:660360。 计算举例: 例1. 如图1所示,当时间为7:55时,计算时针与分针夹角的度数(不考虑大于180°的角)。 解析:依据常识,我们应该以时针、分针均在12点时为起始点进行计算。由于分针在时针前面,我们可以先算出分针走过的角度,再减去时针走过的角度,即可求出时针与分针夹角的度数。 分针走过的角度为:55×6°=330°
时针走过的角度为:5.2375.055307 则时针与分针夹角的度数为:5.925.2373306555.055307 例2. 如图2所示,当时间为7:15时,计算时针与分针夹角的度数(不考虑大于180°的角)。 解析:此题中分针在时针的后面,与上题有所不同,我们应该先算出时针走过的角度,再去减去分针走过的角度,即可求出时针与分针夹角的度数。
时针走过的角度为:5.2175.015307 分针走过的角度为:90615 则时针与分针夹角的度数为:5.127905.217 总结规律 从上述两例我们可以总结出规律如下:当分针在时针前面,可以先算出分针走过的角度,再减去时针走过的角度,即可求出时针与分针夹角的度数;当分针在时针后面,可以先算出时针走过的角度,再减去分针走过的角度,即可求出时针与分针夹角的度数。 用字母和公式表示:当时间为m点n分时,其时针与分针夹角的度数为:
(1)分针在时针前面:5.0306nmn (2)分针在时针后面:65.030nnm 依据此公式可以求出任意时刻时针与分针夹角的度数,计算起来非常便捷。如果题目中涉及到秒,我们可以先把秒换算为分,再套用上述规律和公式进行计算即可。
第三节:相交线与平行线
知识点1:直线的位置关系 在同一平面内直线与直线的位置关系只有两种:相交与平行。 知识点2:垂直 当两条直线相交所成的四个角中,有一个角是直角时,就说这两条直线互相垂直,其中一条直线叫做另一条直线的垂线,他们的交点叫做垂足。