矩阵图基本知识

矩阵知识点总结大学一、基本概念1.1 矩阵的定义矩阵是指一个按照矩形排列的数字元素集合。

一般地，矩阵用符号“A”、“B”、“C”等来表示，其中每个元素用小写字母加标记来表示其位置，如a_ij表示矩阵A的第i行第j列的元素。

矩阵A的元素一般用a_ij来表示，其中i表示元素所在的行数，j表示元素所在的列数。

如下所示：A = [a_11, a_12, ..., a_1n][a_21, a_22, ..., a_2n][..., ..., ..., ...][a_m1, a_m2, ..., a_mn]矩阵的大小一般用m×n来表示，其中m表示矩阵的行数，n表示矩阵的列数。

矩阵的元素一般用小写字母a、b、c、d等来表示。

1.2 特殊矩阵⑴方阵：行数和列数相等的矩阵称为方阵。

n阶方阵指的是行数和列数均为n的方阵。

⑵零矩阵：所有元素都为0的矩阵称为零矩阵，通常用0表示。

⑶单位矩阵：对角线上的元素全为1，其他元素均为0的方阵称为单位矩阵，通常用I表示。

⑷对角矩阵：除了对角线上的元素外，其他元素均为0的矩阵称为对角矩阵。

1.3 矩阵的运算规则矩阵的运算包括加法、乘法和数乘三种，具体规则如下：⑴矩阵的加法：若A、B是同型矩阵，则它们的和记为A+B，定义为A+B=[a_ij+b_ij]，其中a_ij和b_ij分别是A和B对应位置的元素。

⑵矩阵的数乘：若A是一个矩阵，k是一个数，则它们的数乘记为kA，定义为kA=[ka_ij]，其中a_ij是A的元素。

⑶矩阵的乘法：若A是一个m×n的矩阵，B是一个n×p的矩阵，则它们的乘积记为A·B，定义为A·B=C，其中C是一个m×p的矩阵，其中C的第i行第j列的元素c_ij等于A的第i行和B的第j列对应元素的乘积的和。

1.4 矩阵的转置若A是一个m×n的矩阵，其转置记作A^T，定义为A^T=[a_ji]，其中a_ji表示A的第i 行第j列的元素。

知识图谱的表现形式
知识图谱是一种以图形的形式表示知识的技术，它可以帮助人们更好地理解和掌握知识。

知识图谱是一种结构化的知识表示方法，它可以将复杂的知识结构化，以便更好地理解和
掌握。

知识图谱的表现形式主要有三种：网络图、树状图和矩阵图。

网络图是一种以节点和边的
形式表示知识的图形，它可以清晰地表示知识之间的关系，从而帮助人们更好地理解知识。

树状图是一种以树状结构表示知识的图形，它可以清晰地表示知识之间的层次关系，从而帮助人们更好地理解知识。

矩阵图是一种以矩阵的形式表示知识的图形，它可以清晰地表
示知识之间的相互关系，从而帮助人们更好地理解知识。

知识图谱的表现形式可以帮助人们更好地理解和掌握知识，它可以将复杂的知识结构化，
从而更好地理解和掌握知识。

知识图谱的表现形式也可以帮助人们更好地分析和推理知识，从而更好地理解和掌握知识。

总之，知识图谱的表现形式是一种有效的知识表示方法，它可以帮助人们更好地理解和掌握知识，从而更好地分析和推理知识。

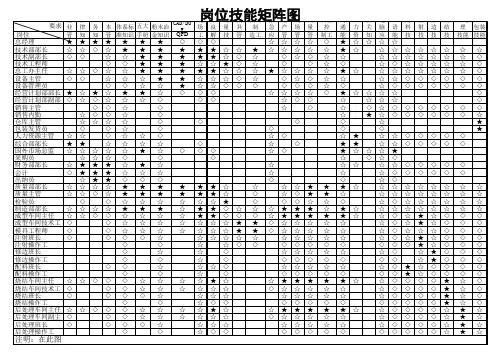
表1知识实现矩阵序号能力实现（课程/环节，包括必修课和选修课）1 基础科学知识高等数学、线性代数、概率与数理统计、大学语文、计算机文化基础、中国近代史纲要、思想道德修养与法律基础、毛泽东思想和中国特色社会主义理论体系、马克思主义基本原理、应用文写作、体育等2 专业基础知识管理学、微观经济学、宏观经济学、统计学、金融学、经济法、基础会计、财经法规与职业道德等3 专业核心知识中级财务会计、高级财务会计、成本与管理会计、财务管理、财务分析、审计学、税务会计、会计电算化等4 专业特色知识金融企业会计、公司战略与风险管理、会计理论专题、行业会计比较、政府与非盈利组织会计等表2能力实现矩阵序号能力实现（课程/环节，包括必修课和选修课）1 基本经济、管理问题分析能高等数学、线性代数、概率与数理统计、大学语文力中国近代史纲要、思想道德修养与法律基础、毛泽东思想和中国特色社会主义理论体系、马克思主义基本原理、军事理论、体育、管理学、微观经济学、宏观经济学、统计学、金融学、经济法等2 会计核算基本能力基础会计、中级财务会计、高级财务会计、成本会计、会计模拟实验、会计电算化等3 财务报表审计能力内部控制、审计原理、财务审计、财务分析、内部审计学、信息系统审计、EXCEL审计应用实训、会审对抗实训4 公司战略与风险管理能力微观经济学、管理学原理、财务管理、成本会计、财务分析、公司战略与风险管理等表3素质实现矩阵序号素质实现（课程/环节，包括必修课和选修课）1 身心素质思想品德与法律基础、大学英语、大学体育、大学语文、心理健康教育、马克思主义基本原理、毛泽东思想与中国特色社会主义理论体系概论、中国近代史纲要2 综合素质高等数学、概率论与数理统计、线性代数、计算机基础、计算机程序设计、应用文写作、经济学、职业生涯规划与创业教育、金融学、统计学3 道德素质经济法、税法、管理学、审计学专业导论4 专业素质基础会计、中级财务会计、成本会计、审计原理、财务审计、内部控制、财务分析、财务管理、EXCEL审计应用实训、ERP原理及沙盘模拟、会计电算化、会审对抗实训、信息系统审计等5 可持续发展素质公司战略与风险管理、财务分析、国际会计准则与惯例、ERP信息平台模拟实训、企业实习、资产评估等。

矩阵图知识点总结归纳一、矩阵图的概念矩阵图是一种以矩阵的形式展示数据的可视化方式。

矩阵的行和列分别代表数据的不同维度，而矩阵中的数值则表示不同维度之间的关系或相似度。

矩阵图通常使用颜色来标示不同数值的大小，一般采用颜色的深浅来表示数据的大小或者相关程度，从而使得人们可以直观地观察和理解数据的规律和特征。

二、矩阵图的原理矩阵图的原理主要是依靠颜色表达数据的大小或相关程度。

一般来说，我们将数据标准化到[0, 1]之间，然后通过一种颜色映射函数将数值映射到颜色上。

比如，我们可以使用从浅到深的色阶来表示数据的大小，越浅的颜色表示数值越小，越深的颜色代表数值越大。

这样就可以直观地观察和理解数据之间的关系。

三、矩阵图的应用矩阵图在生物信息学、金融分析、社交网络分析、医学图像分析等领域有着广泛的应用。

在生物信息学中，矩阵图常用于展示基因之间的相似性或者功能关联。

在金融分析中，矩阵图可以帮助人们发现不同金融产品之间的相关性或者关联度。

在社交网络分析中，矩阵图则可以用来展示不同用户之间的交互关系。

在医学图像分析中，矩阵图可以帮助人们理解不同医学影像之间的相似程度或者相关性。

四、矩阵图的制作方法矩阵图的制作方法较为简单，大致可以分为数据准备和矩阵图绘制两个步骤。

首先，我们需要准备好需要展示的数据，将数据标准化到[0, 1]之间。

然后，我们可以使用一些专业的可视化工具，比如Python中的Matplotlib、Seaborn库，或者R语言中的ggplot2包来绘制矩阵图。

在绘制矩阵图时，我们一般会根据数据的特点选择合适的颜色映射函数，并且添加一些标签或者注释以帮助观察者更好地理解数据。

总之，矩阵图是一种重要的数据可视化方式，它以矩阵的形式展示数据，通过颜色的深浅来表示不同数值的大小或相关程度，有助于人们更直观地理解数据之间的关系。

矩阵图在生物信息学、金融分析、社交网络分析、医学图像分析等领域有着广泛的应用，可以帮助人们发现数据的规律和特征。

矩阵知识点总结图解一、矩阵的定义1.1 矩阵的概念矩阵是一个由m行n列的数域中的数字组成的矩形数组。

例如，一个3行2列的矩阵可以表示为：\[ \begin{bmatrix}a_{11} & a_{12} \\a_{21} & a_{22} \\a_{31} & a_{32} \\\end{bmatrix}\]1.2 矩阵的基本术语- 行数：矩阵中的行数为m。

- 列数：矩阵中的列数为n。

- 元素：矩阵中的每个数字称为元素，如矩阵中的a11、a12等。

- 维数：一个m行n列的矩阵的维数为m×n。

1.3 矩阵的表示矩阵可以用方括号表示，矩阵中的元素用逗号隔开，例如：\[ A = \begin{bmatrix}1 &2 &3 \\4 &5 &6 \\\end{bmatrix}\]二、矩阵的基本运算2.1 矩阵的加法对于两个相同维数的矩阵A和B，它们的加法定义为矩阵中相应位置元素的和。

即：\[ A + B = \begin{bmatrix}a_{11}+b_{11} & a_{12}+b_{12} & a_{13}+b_{13} \\a_{21}+b_{21} & a_{22}+b_{22} & a_{23}+b_{23} \\\end{bmatrix}\]2.2 矩阵的数乘对于一个m行n列的矩阵A和一个数k，它们的数乘定义为矩阵中每个元素与k的乘积。

即：\[ kA = \begin{bmatrix}ka_{11} & ka_{12} & ka_{13} \\ka_{21} & ka_{22} & ka_{23} \\\end{bmatrix}\]2.3 矩阵的乘法对于一个m行n列的矩阵A和一个p行q列的矩阵B，若n=p，则它们的乘法定义为：\[ AB = C \]其中C是一个m行q列的矩阵，其中元素cij的计算方式为：\[ c_{ij} = a_{i1}b_{1j} + a_{i2}b_{2j} + \cdots + a_{in}b_{nj} \]2.4 矩阵的转置一个m行n列的矩阵A的转置是一个n行m列的矩阵，其中元素aij转置为aji。

矩阵及其性质知识点及题型归纳总结
1. 矩阵基本概念
- 矩阵是一个二维数组，由行和列组成。

- 矩阵的元素可以是实数、复数或其他数域中的元素。

2. 矩阵的性质和运算
- 矩阵的转置：交换矩阵的行和列, 记作A^T。

- 矩阵的加法：对应位置元素相加。

- 矩阵的数乘：将矩阵的每个元素乘以一个数。

- 矩阵的乘法：满足左乘法则和右乘法则。

- 矩阵的逆：对于可逆方阵，存在逆矩阵使得矩阵乘法满足乘法逆的要求。

3. 矩阵的特殊类型和性质
- 单位矩阵：一个方阵的主对角线上元素为1，其他元素为0。

- 零矩阵：所有元素都为0的矩阵。

- 对角矩阵：只有主对角线上元素非零，其他元素为0。

- 对称矩阵：矩阵的转置等于它本身。

- 上三角矩阵：主对角线及其以下的元素都不为0。

- 下三角矩阵：主对角线及其以上的元素都不为0。

4. 矩阵的题型归纳
- 矩阵的基本运算：加法、数乘、乘法和转置操作。

- 矩阵的性质判断：检查矩阵是否为对称矩阵、上三角矩阵、下三角矩阵等。

- 矩阵的逆和行列式：求逆矩阵、计算行列式的值等。

- 矩阵的方程求解：解线性方程组、求矩阵的特征值和特征向量等。

以上是矩阵及其性质的基本知识点及题型归纳总结。

通过掌握这些知识，你将能够更好地理解和应用矩阵在数学和工程等领域的相关问题。

矩阵知识知识点总结手写一、矩阵的基本概念1. 定义：矩阵是由m行n列的数按矩形排列所得到的数表。

一般用大写字母A、B、C...表示矩阵，元素用小写字母aij，bij，cij...表示。

2. 矩阵的阶：矩阵A中有m行n列，就称A是一个m×n（读作“m行n列”）的矩阵，m、n分别称为矩阵的行数和列数，记作A[m×n]。

3. 矩阵的元素：A[m×n]＝[aij]，其中i＝1,2,…,m，j＝1,2,…,n，称aij为矩阵A的第i行第j 列元素。

4. 矩阵的相等：两个矩阵A，B的阶都相同时，如果相应元素都相等，则称矩阵A，B相等，记作A＝B。

5. 矩阵的转置：将矩阵A的行、列互换得到的矩阵称为矩阵A的转置矩阵，记作AT。

6. 方阵：行数等于列数的矩阵称为方阵。

7. 零矩阵：所有元素均为零的矩阵称为零矩阵，记作O。

8. 单位矩阵：主对角线上元素全为1，其它元素均为0的矩阵称为单位矩阵，记作E或In。

二、矩阵的运算1. 矩阵的加法：设A[m×n]＝[aij]，B[m×n]＝[bij]，则矩阵C=A＋B的第i行第j列元素为：cij=aij+bij，即C[m×n]＝[aij+bij]。

2. 矩阵的数乘：数k与矩阵A[m×n]相乘的结果记作kA，即kA[m×n]＝[kaij]。

3. 矩阵的乘法：设A[m×n]，B[n×p]，那么它们的乘积C=A×B[m×p]的第i行第j列元素为：C[i][j]=a[i][1]×b[1][j]+a[i][2]×b[2][j]+…+a[i][n]×b[n][j]。

4. 矩阵的转置：若A[m×n]，则A的转置矩阵是AT[n×m]，其中a[i][j]=a[j][i]。

5. 矩阵的逆：若方阵A的行列式不为零，那么A存在逆矩阵A-1，使得A×A-1=A-1×A=I。

通用矩阵知识点总结一、矩阵的基本概念矩阵最初源于解线性方程组的需要。

它是一个数学对象，通常由若干个数排列成的矩形阵列。

矩阵通常用大写字母表示，如A、B、C等。

例如，一个矩阵可以表示为：A = \begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \end{bmatrix}在上面的例子中，矩阵A是一个2行3列的矩阵，它由6个数字组成，即1、2、3、4、5和6。

矩阵的元素通常用a_{ij}表示，其中i代表矩阵的行索引，j代表矩阵的列索引。

二、矩阵的运算法则1. 矩阵的加法和减法设A和B是同型矩阵，则它们的和A+B和差A-B分别是这两个矩阵的对应元素之和和差。

例如：A = \begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix},B = \begin{bmatrix} 5 & 6 \\ 7 & 8\end{bmatrix}则A+B = \begin{bmatrix} 1+5 & 2+6 \\ 3+7 & 4+8 \end{bmatrix} = \begin{bmatrix} 6 & 8\\ 10 & 12 \end{bmatrix}A-B = \begin{bmatrix} 1-5 & 2-6 \\ 3-7 & 4-8 \end{bmatrix} = \begin{bmatrix} -4 & -4 \\ -4 & -4 \end{bmatrix}2. 矩阵的数乘设k是一个实数或复数，A是一个矩阵，则kA是由A的每个元素乘以k所得的矩阵。

例如：A = \begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix}, k = 2则kA = 2 * A = \begin{bmatrix} 2*1 & 2*2 \\ 2*3 & 2*4 \end{bmatrix} = \begin{bmatrix} 2& 4 \\ 6 & 8 \end{bmatrix}3. 矩阵的乘法矩阵的乘法是一种复杂的运算，需要满足一定的条件。

矩阵图基本知识(一)矩阵图的概念所谓矩阵图是一种利用多维思考去逐步明确问题的方法。

其工具是矩阵图。

就是从问题的各种关系中找出成对要素L1，L2，…，L i，…，L n和R1，R2，…，R j，…，R n，用数学上矩阵的形式排成行和列，在其交点上标示出L和R各因素之间的相互关系，从中确定关键点的方法。

在分析质量问题的原因、整理顾客需求、分解质量目标时，将问题、顾客需求、质量目标(设为L)放在矩阵图的左边，将问题的原因、顾客需求转化来的质量目标或针对质量目标提出的质量措施(设为R)列在矩阵图的上方，用不同的符号表示它们之间关系的强弱，通常用◎表示关系密切，○表示有关系，△表示可能有关系，如图6.4-16所示。

通过在交点处给出行与列对应要素的关系及关系程度，可以从二元关系中探讨问题所在和问题的形态，并得到解决问题的设想。

在寻求问题的解决手段时，若目的(或结果)能够展开为一元性手段(或原因)，则可用树图法。

然而，若有两种以上的目的(或结果)，则其展开用矩阵图法较为合适。

(二)矩阵图的种类在矩阵图法中，按矩阵图的型式可将矩阵图分为L型、T型、X型和Y型四种。

如图6.4-17所示。

(1)L型矩阵图是一种最基本的矩阵图，如图6.4-17(a)所示，它是由A类因素和B类因素二元配置组成的矩阵图。

这种矩阵图适用于把若干个目的和为了实现这些目的的手段，或若干个结果及其原因之间的关联。

(2)T型矩阵图是由C类因素和B类因素组成的L型矩阵图和由C类因素和A类因素组成的L型矩阵图组合在一起的矩阵图，如图6.4-17(b)所示。

即表示C类因素分别与B类因素和A类因素相对应的矩阵图。

(3)Y型矩阵图是由A类因素和B类因素、B类因素和C类因素、C类因素和A类因素组成三个L型矩阵图，如图6.4-17(d)所示，即表示A和B、B和C、C和A三因素分别对应的矩阵图。

(4)X型矩阵图是由A类因素和C类因素、C类因素和B类因素、B类因素和D类因素、D类因素和A类因素的L型矩阵图组合在一起的矩阵图。

矩阵知识点总结大纲一、矩阵的基本概念1.1 矩阵的定义1.2 矩阵的元素1.3 矩阵的维数1.4 矩阵的转置1.5 矩阵的特殊矩阵二、矩阵运算2.1 矩阵的加法2.2 矩阵的数乘2.3 矩阵的乘法2.4 矩阵的转置2.5 矩阵的幂2.6 矩阵的逆2.7 矩阵的行列式2.8 矩阵的秩三、线性方程组与矩阵3.1 矩阵的行简化阶梯形式3.2 矩阵的列简化阶梯形式3.3 矩阵的增广矩阵3.4 矩阵的系数矩阵3.5 矩阵的齐次线性方程组3.6 矩阵的非齐次线性方程组四、矩阵的应用4.1 线性代数4.2 计算机图形学4.3 信号处理4.4 优化问题4.5 统计学4.6 量子力学五、矩阵分析5.1 矩阵的迹5.2 矩阵的本征值与本征向量5.3 矩阵的相似矩阵5.4 矩阵的对角化5.5 矩阵的奇异值分解5.6 矩阵的正交矩阵六、矩阵的特征6.1 矩阵的周期性6.2 矩阵的稀疏性6.3 矩阵的对称性6.4 矩阵的正定性6.5 矩阵的随机性七、矩阵的发展历程7.1 矩阵的起源7.2 矩阵的发展7.3 矩阵的应用八、矩阵的未来发展8.1 矩阵的应用领域拓展8.2 矩阵的理论深化8.3 矩阵的计算方法改进九、矩阵的教学与研究9.1 矩阵的教学模式9.2 矩阵的教学资源9.3 矩阵的研究方向十、矩阵的未来前景10.1 矩阵的应用前景10.2 矩阵的教学前景10.3 矩阵的研究前景十一、矩阵的总结与展望11.1 矩阵的总结11.2 矩阵的展望结语矩阵知识点总结一、矩阵的基本概念1.1 矩阵的定义矩阵是一个按照长方形排列的数表。

其中的元素可以是数字、符号或数学式。

矩阵是线性代数的基本概念，应用非常广泛，涉及几何学、概率论、微分方程以及物理学和工程学等各个学科。

1.2 矩阵的元素矩阵的元素是矩阵中的一个具体数值或符号。

1.3 矩阵的维数一个矩阵的维数是指矩阵的行数与列数。

如果一个矩阵有m行n列，则称其为m×n阶矩阵。

变速器分公司员工岗位技能矩阵图
标识注明：在此图
各岗位需要具备的知识和技能是为了满足履行岗位基本职能的需求，所需熟练、掌握和了解的知识和技能。

各岗位需要熟练、掌握和了解的知识和技能根据岗位的不同侧重点不同，如：综合计划管理员需要了解的成本管理知识，重点了解生产成本的构成和测算方法即可；生产管理知识，要根据各分公司的实际情况，要熟练掌握各分公司的生产组织模式、各种自制件产品投入产出周期、瓶颈工序和设备、各品种自制件的工艺流程和各工序生产能力等与生产有关的实际情况。

能根据市场变化及时有序的协调各分公司的产品转换和生产节拍，保障市场需求；法律知识，重点。

矩阵的总结知识点一、矩阵的基本概念1. 矩阵的定义矩阵是一个按照矩形排列的数学对象。

矩阵的概念最早出现在线性代数理论中，它是由m行n列的数字排成的矩形阵列。

通常表示为一个大写字母，比如A，而矩阵中的元素通常用小写字母表示，比如a_ij，表示在第i行第j列的元素。

2. 矩阵的类型根据矩阵的形状和性质不同，可以将矩阵分为多种类型，比如方阵、对称矩阵、对角矩阵、三角矩阵等。

方阵是指行数和列数相等的矩阵，对称矩阵是指矩阵关于主对角线对称，对角矩阵是指除了主对角线上的元素外，其他元素都为零，而三角矩阵是指上三角或下三角矩阵。

3. 矩阵的运算矩阵的运算包括矩阵的加法、减法、数乘、矩阵的乘法等。

其中，矩阵的加法和减法要求相加的矩阵具有相同的形状，即行数和列数相同；而矩阵的数乘是指矩阵中的每个元素都乘以一个标量；矩阵的乘法是指矩阵A的列数等于矩阵B的行数时，可以进行矩阵乘法运算。

4. 矩阵的转置和逆矩阵矩阵的转置是指将矩阵的行和列对调得到一个新的矩阵，记作A^T。

而逆矩阵是指如果一个矩阵A存在逆矩阵A^(-1)，使得A*A^(-1)=I，其中I是单位矩阵，则称矩阵A可逆，否则称矩阵A为奇异矩阵。

二、矩阵的应用1. 线性方程组的求解矩阵可以用来表示和求解线性方程组，线性方程组可以表示成AX=B的形式，其中A是系数矩阵，X是未知数矩阵，B是常数矩阵。

通过矩阵的基本变换和行列式的计算，可以求解线性方程组的解。

2. 数据处理和分析在数据处理和分析领域，矩阵可以用来表示和处理大规模的数据集。

比如，在机器学习算法中，可以通过矩阵的运算和矩阵分解来进行数据的降维和特征的提取。

3. 控制理论在控制理论中，矩阵可以用来描述线性系统的状态方程和控制方程，通过对状态矩阵和控制矩阵的计算和分析，可以得到系统的稳定性和控制性能。

4. 计算机图形学在计算机图形学中，矩阵可以用来描述和处理图形的旋转、平移、缩放等变换，通过矩阵的运算和矩阵乘法，可以实现图形的变换和动画效果。

矩阵知识点归纳(一)二阶矩阵与变换1．线性变换与二阶矩阵在平面直角坐标系xOy 中，由⎩⎪⎨⎪⎧x ′＝ax ＋by ，y ′＝cx ＋dy ，(其中a ，b ，c ，d 是常数)构成的变换称为线性变换．由四个数a ，b ，c ，d 排成的正方形数表⎣⎢⎡⎦⎥⎤a b c d 称为二阶矩阵，其中a ，b ，c ，d 称为矩阵的元素，矩阵通常用大写字母A ，B ，C ，…或(a ij )表示(其中i ，j 分别为元素a ij 所在的行和列)．2．矩阵的乘法行矩阵[a 11a 12]与列矩阵⎣⎢⎡⎦⎥⎤b 11b 21的乘法规则为[a 11a 12]⎣⎢⎡⎦⎥⎤b 11b 21＝[a 11b 11＋a 12b 21]，二阶矩阵⎣⎢⎡⎦⎥⎤a b c d 与列矩阵⎣⎢⎡⎦⎥⎤x y 的乘法规则为⎣⎢⎡⎦⎥⎤a b c d ⎣⎢⎡⎦⎥⎤x y ＝⎣⎢⎡⎦⎥⎤ax ＋by cx ＋dy .矩阵乘法满足结合律，不满足交换律和消去律．3．几种常见的线性变换(1)恒等变换矩阵M ＝⎣⎢⎡⎦⎥⎤1 00 1；(2)旋转变换R θ对应的矩阵是M ＝⎣⎢⎡⎦⎥⎤cos θ －sin θsin θ cos θ；(3)反射变换要看关于哪条直线对称．例如若关于x 轴对称，则变换对应矩阵为M 1＝⎣⎢⎡⎦⎥⎤1 00 －1；若关于y 轴对称，则变换对应矩阵为M 2＝⎣⎢⎡⎦⎥⎤－1 0 0 1；若关于坐标原点对称，则变换对应矩阵M 3＝⎣⎢⎡⎦⎥⎤－1 0 0 －1；(4)伸压变换对应的二阶矩阵M ＝⎣⎢⎡⎦⎥⎤k 1 00 k 2，表示将每个点的横坐标变为原来的k 1倍，纵坐标变为原来的k 2倍，k 1，k 2均为非零常数；(5)投影变换要看投影在什么直线上，例如关于x 轴的投影变换的矩阵为M ＝⎣⎢⎡⎦⎥⎤1 00 0； (6)切变变换要看沿什么方向平移，若沿x 轴平移|ky |个单位，则对应矩阵M ＝⎣⎢⎡⎦⎥⎤1 k 0 1，若沿y 轴平移|kx |个单位，则对应矩阵M ＝⎣⎢⎡⎦⎥⎤1 0k 1.(其中k 为非零常数)．4．线性变换的基本性质设向量α＝⎣⎢⎡⎦⎥⎤x y ，规定实数λ与向量α的乘积λα＝⎣⎢⎡⎦⎥⎤λx λy ；设向量α＝⎣⎢⎡⎦⎥⎤x 1y 1，β＝⎣⎢⎡⎦⎥⎤x 2y 2，规定向量α与β的和α＋β＝⎣⎢⎡⎦⎥⎤x 1＋x 2y 1＋y 2.(1)设M 是一个二阶矩阵，α、β是平面上的任意两个向量，λ是一个任意实数，则①M (λα)＝λMα，②M (α＋β)＝Mα＋Mβ.(2)二阶矩阵对应的变换(线性变换)把平面上的直线变成直线(或一点)．(二)矩阵的逆矩阵、特征值与特征向量1．矩阵的逆矩阵(1)一般地，设ρ是一个线性变换，如果存在线性变换σ，使得σρ＝ρσ＝I ，则称变换ρ可逆．并且称σ是ρ的逆变换．(2)设A 是一个二阶矩阵，如果存在二阶矩阵B ，使得BA ＝AB ＝E ，则称矩阵A 可逆，或称矩阵A 是可逆矩阵，并且称B 是A 的逆矩阵．(3)(性质1)设A 是一个二阶矩阵，如果A 是可逆的，则A 的逆矩阵是唯一的．A 的逆矩阵记为A －1．(4)(性质2)设A ，B 是二阶矩阵，如果A ，B 都可逆，则AB 也可逆，且(AB )－1＝B －1A －1. (5)已知A ，B ，C 为二阶矩阵，且AB ＝AC ，若矩阵A 存在逆矩阵，则B ＝C .(6)对于二阶可逆矩阵A ＝⎣⎢⎡⎦⎥⎤a b c d (ad －bc ≠0)，它的逆矩阵为A －1＝⎣⎢⎢⎡⎦⎥⎥⎤d ad －bc－b ad －bc －c ad －bcaad －bc. 2．二阶行列式与方程组的解对于关于x ，y 的二元一次方程组⎩⎪⎨⎪⎧ax ＋by ＝m ，cx ＋dy ＝n ，我们把⎪⎪⎪⎪⎪⎪a b c d 称为二阶行列式，它的运算结果是一个数值(或多项式)，记为det(A )＝⎪⎪⎪⎪⎪⎪a b c d ＝ad －bc .若将方程组中行列式⎪⎪⎪⎪⎪⎪a b c d 记为D ，⎪⎪⎪⎪⎪⎪m b n d 记为D x ，⎪⎪⎪⎪⎪⎪a m c n 记为D y ，则当D ≠0时，方程组的解为⎩⎨⎧x ＝D x D，y ＝D y D.3．二阶矩阵的特征值和特征向量 (1)特征值与特征向量的概念设A 是一个二阶矩阵，如果对于实数λ，存在一个非零向量α，使得Aα＝λα，那么λ称为A 的一个特征值，α称为A 的一个属于特征值λ的一个特征向量．(2)特征多项式设λ是二阶矩阵A ＝⎣⎢⎡⎦⎥⎤a b c d 的一个特征值，它的一个特征向量为α＝⎣⎢⎡⎦⎥⎤x y ，则A ⎣⎢⎡⎦⎥⎤x y ＝λ⎣⎢⎡⎦⎥⎤x y ，即⎩⎪⎨⎪⎧ ax ＋by ＝λx ，cx ＋dy ＝λy ，也即⎩⎪⎨⎪⎧(λ－a )x －by ＝0，－cx ＋(λ－d )y ＝0.(*) 定义：设A ＝⎣⎢⎡⎦⎥⎤a b c d 是一个二阶矩阵，λ∈R ，我们把行列式f (λ)＝⎪⎪⎪⎪⎪⎪λ－a －b －c λ－d ＝λ2－(a＋d )λ＋ad －bc 称为A 的特征多项式．(3)矩阵的特征值与特征向量的求法如果λ是二阶矩阵A 的特征值，则λ一定是二阶矩阵A 的特征多项式的一个根，即f (λ)＝0，此时，将λ代入二元一次方程组(*)，就可得到一组非零解⎣⎢⎡⎦⎥⎤x 0y 0，于是非零向量⎣⎢⎡⎦⎥⎤x 0y 0即为A 的属于λ的一个特征向量．所有变换矩阵单位矩阵：1001M ⎡⎤=⎢⎥⎣⎦，点的变换为(,)(,)x y x y → 伸压变换矩阵：001k M ⎡⎤=⎢⎥⎣⎦：1k >，将原来图形横坐标扩大为原来k 倍，纵坐标不变01k <<，将原来图形横坐标缩小为原来k 倍，纵坐标不变 点的变换为(,)(,)x y kx y →100M k ⎡⎤=⎢⎥⎣⎦： 1k >，将原来图形纵坐标扩大为原来k 倍，横坐标不变01k <<，将原来图形纵坐标缩小为原来k 倍，横坐标不变 点的变换为(,)(,)x y x ky →反射变换： 1001M ⎡⎤=⎢⎥-⎣⎦：点的变换为(,)(,)x y x y →- 变换前后关于x 轴对称 1001M -⎡⎤=⎢⎥⎣⎦：点的变换为(,)(,)x y x y →- 变换前后关于y 轴对称 1001M -⎡⎤=⎢⎥-⎣⎦：点的变换为(,)(,)x y x y →-- 变换前后关于原点对称 0110M ⎡⎤=⎢⎥⎣⎦：点的变换为(,)(,)x y y x → 变换前后关于直线y x =对称旋转变换：cos sin sin cos M θθθθ-⎡⎤=⎢⎥⎣⎦：逆时针090：0110M -⎡⎤=⎢⎥⎣⎦；顺时针090：0110M ⎡⎤=⎢⎥-⎣⎦旋转变化矩阵还可以设为：a b M b a -⎡⎤=⎢⎥⎣⎦投影变换：1000M ⎡⎤=⎢⎥⎣⎦：将坐标平面上的点垂直投影到x 轴上 点的变换为(,)(,0)x y x →0001M ⎡⎤=⎢⎥⎣⎦：将坐标平面上的点垂直投影到y 轴上 点的变换为(,)(0,)x y y →1010M ⎡⎤=⎢⎥⎣⎦：将坐标平面上的点垂直于x 轴方向投影到y x =上点的变换为(,)(,)x y x x →0101M ⎡⎤=⎢⎥⎣⎦：将坐标平面上的点平行于x 轴方向投影到y x =上点的变换为(,)(,)x y y y →11221122M ⎡⎤⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦：将坐标平面上的点垂直于y x =方向投影到y x =上 点的变换为(,)(,)22x y x yx y ++→ 切变变换：101k M ⎡⎤=⎢⎥⎣⎦：把平面上的点沿x 轴方向平移||ky 个单位 点的变换为(,)(,)x y x ky y →+101M k ⎡⎤=⎢⎥⎣⎦：把平面上的点沿y 轴方向平移||kx 个单位 点的变换为(,)(,)x y x kx y →+。