年金现值、资本回收系数等1%-50%的系数表
- 格式:doc
- 大小:406.00 KB
- 文档页数:18

2023年江苏省连云港市公务员省考行政职业能力测验测试卷(含答案) 学校:________ 班级:________ 姓名:________ 考号:________一、1.常识判断(10题)1.夏天,打开冰箱冷冻室的门,常常看到冷冻室中冒出一股白雾,这是()。
A.A.冰箱里的冰升华后,又凝结成小水滴B.冰箱里原有的水蒸气凝结成的小水滴C.冰箱里的水变为水蒸气D.冰箱外部空气中的水蒸气凝结成的小水滴2. 当前切实解决国有资产流失的关键是( )。
A.建立法人治理结构B.加强政府宏观调控C.改变国有资产经营管理方式D.明晰国有资产产权关系3. 根据我国公务员法的规定,公务员( )受法律保护。
A.行政行为B.依法履行职务的行为C.依法履行公务的行为D.职务行为4. 实践高于理论的原因是因为实践有( )。
A.普遍有用性B.主观能动性C.直接现实性D.客观现实性5. 中国共产党的最早组织是( )。
A.北京共产主义小组B.上海共产主义小组C.广州共产主义小组D.长沙共产主义小组6. 现行宪法规定,自治区的自治条例和单行条例的审批权属于( )。
A.全国人民代表大会B.全国人大常委会C.国务院D.本级人民代表大会7. 中国摄影协会所属的法人类别是( )。
A.机关单位法人B.事业单位法人C.社会团体法人D.企业法人8. 《诗经》中由文人创作,供宫廷宴享或朝会时所用的乐歌被称为( )。
A.风B.雅C.颂D.赋9. 中共十七届四中全会提出了深化干部人事制度改革,在培养和选拔干部的时候,必须坚持的用人标准是( )。
A.德才兼备、以才为先B.德才兼备、以德为先C.作风廉洁、与时俱进D.年轻化、知识化10. 下列对我国古代史书的表述不正确的一项是( )。
A.我国第一部国别体史书是《战国策》B.我国第一部叙事详细完整的历史著作是《左传》C.我国第一部纪传体通史是《史记》D.我国第一部断代史是《汉书》二、数量关系(10题)11.某海鲜档出售一批总共150斤(1斤=0.5千克)的鲜鱼,按原价每卖出一斤可赚5元。

90·罕少疾病杂志 2023年3月 第30卷 第 3 期 总第164期【第一作者】李林洁,女,主管技师,主要研究方向:新生儿疾病筛查。
Email:*****************【通讯作者】郑 琳,女,副主任医师,主要研究方向:出生缺陷防控。
Email:****************·论著·贵阳地区新生儿G-6-PD缺乏症筛查及基因突变分析*李林洁 杨 雪 刘兴宇 张晓怡 张禾璇 王侣金 郑 琳*贵阳市妇幼保健院优生遗传科 (贵州 贵阳 550003)【摘要】目的 分析贵阳地区出生人群葡萄糖-6-磷酸脱氢酶(G-6-PD)缺乏症筛查情况,了解本地区疾病的发生率以及基因突变情况,为指导新生儿疾病筛查工作提供策略依据。
方法 选取2020年9月-2021年12月期间送检贵阳市新生儿遗传代谢病筛查中心的干血斑样本,共计69537例(男37276例,女32261例),采用荧光定量法测定干血斑中的G-6-PD酶活性,筛查的可疑阳性新生儿召回使用基因突变分析及酶活性检测进行确诊。
结果 贵阳地区新生儿G-6-PD 缺乏症筛查总体阳性率为1.37%(954/69537),其中男、女阳性率分别为1.81%(674/37276)和0.87%(280/32261),两者阳性率比较,差异具有统计学意义(χ2=112.972,P <0.001);可疑阳性新生儿召回594例,召回率62.3%,确诊302例,推算贵阳地区新生儿G-6-PD缺乏症总体发生率为0.70%,345名新生儿中,检测出基因突变238例,共检出10种突变类型:90例(31.5%)c.1024C>T、64例(22.4%)c.1388G>A、52例(18.2%)c.95A>G、50例(17.5%)c.1376G>T、12例(4.2%)c.871G>A、8例(2.8%)c.487G>A、3例(1.0%)c.1004C>A、3例(1.0%)c.392G>T、2例(0.7%)c.592C>T、1例(0.3%)c.1360C>T和一种复合突变。


离骚全文注音《离lí骚sǎo》——屈qū原yuán帝dì高ɡāo阳yánɡ之zhī苗miáo裔yì兮xī,朕zhèn皇huánɡ考kǎo曰yuē伯bó庸yōnɡ。
摄shè提dǐ贞zhēn于yú孟mènɡ陬zōu兮xī,惟wéi庚ɡēnɡ寅y ín吾wú以yǐ降jiànɡ。
皇huánɡ览lǎn揆kuí余yú初chū度dù兮xī,肇zhào锡xī余yú以yǐ嘉jiā名mínɡ:名mínɡ余yú曰yuē正zhènɡ则zé兮xī,字zì余yú曰yuē灵línɡ均jūn。
纷fēn吾wú既jì有yǒu此cǐ内nèi美měi兮xī,又yòu重chón ɡ之zhī以yǐ修xiū能nénɡ。
扈hù江jiānɡ离lí与yǔ辟bì芷zhǐ兮xī,纫rèn秋qiū兰lán以yǐ为wéi佩pèi。
汨mì余yú若ruò将jiānɡ不bù及jí兮xī,恐kǒnɡ年nián岁suì之zhī不bù吾wú与yǔ。
朝cháo搴qiān阰pí之zhī木mù兰lán兮xī,夕xī揽lǎn洲zhōu之zhī宿sù莽mǎnɡ。
日rì月yuè忽hū其qí不bù淹yān兮xī,春chūn与yǔ秋qiū其q í代dài序xù。

弱D抗原鉴定标准操作规程
一、目的
为规范弱D抗原鉴定技术操作,保证血型鉴定结果无误,从而确保临床输血安全和有效。
二、适用范围
输血科负责鉴定RhD血型出现阴性反应时进行弱D抗原筛选鉴定的技术人员。
三、原理
采用3种不同来源的单克隆抗-D试剂(类型有IgM、IgG、及IgM /IgG混合型),用凝聚胺法检测红细胞表面的RhD。
四、步骤和方法
1,将用IgM型单克隆抗-D试剂初步鉴定为阴性的受检者血标本,配成3%—5%红细胞悬液备用。
2,盐水介质法复检:
2.1 用IgM、IgG、及IgM /IgG混合型3种单克隆抗-D试剂先以盐水介质法检测细胞表面的RhD抗原,若IgM和IgM /IgG混合型试剂与受检者红细胞出现“3+—4+”凝集反应,则受检者为RhD阳性;若三种试剂至少1管镜检有弱凝集时,则受检者为弱D型。
2.2 若三者都不与受检者红细胞凝集时,可继续采用凝聚胺法使IgG、IgM /IgG混合型2种试剂和红细胞反应,具体操作执行《凝聚胺法操作规程》:若IgG、IgM /IgG混合型单克隆抗-D试剂均与受检者红细胞成阴性反应,可确认为RhD阴性。
如果至少1种镜检可见凝集,则为弱D型。
五、质量控制
IgM、IgG、IgM /IgG混合型3种单克隆抗-D试剂有效期内使用。
六、注意事项
1,弱D型鉴定采用的试剂至少要有一种含有IgG型单克隆抗-D。
2,鉴定为弱D型的受检者如果是献血应视为阳性对待,若为受血者应视为阴性对待。
3,弱D型妇女与RhD阳性丈夫生育的新生儿有可能发生RhD新生儿溶血病。

中国人常见G6PD基因突变的快速检测肖奇志;李哲;周玉球;郑勤【摘要】目的葡萄糖-6-磷酸脱氢酶(glucose-6-phosphate dehydrogenase,G6PD)缺乏症是世界上最常见的遗传性红细胞酶缺陷病.本文探讨建立一种简便快速、准确可靠、经济实用的G6PD缺乏症分子诊断技术.方法采用DNA测序技术通过双盲法对所建立的单管多重PCR结合分子杂交技术进行方法学评价.结果所建立的新技术可成功地检出上述中国人常见的G6PD基因突变并能清楚区分男性杂合子、女性杂合子或纯合子或双重杂合子.盲法分析结果显示,该技术对经DNA直接测序确诊的G6PD标本的诊断准确度和重复性均达到100%.结论单管多重PCR结合分子杂交技术可准确、快速地检测中国人常见的G6PD基因突变且具有经济和实用的优点,非常适合于G6PD缺乏症的大人群分子筛查和临床样品的基因诊断.【期刊名称】《分子诊断与治疗杂志》【年(卷),期】2011(003)004【总页数】5页(P222-226)【关键词】葡萄糖-6-磷酸脱氢酶;基因突变;单管多重聚合酶链反应;反向点杂交【作者】肖奇志;李哲;周玉球;郑勤【作者单位】珠海市妇幼保健院检验科,珠海市医学遗传研究所,广东,珠海,519001;珠海市金湾区三灶医院检验科,广东,珠海,519040;珠海市妇幼保健院检验科,珠海市医学遗传研究所,广东,珠海,519001;珠海市妇幼保健院检验科,珠海市医学遗传研究所,广东,珠海,519001【正文语种】中文葡萄糖-6-磷酸脱氢酶(glucose-6-phosphate dehydrogenase, G6PD)广泛存在于各种生物体内,它是糖酵解磷酸戊糖旁路中的一个关键酶和限速酶,其主要的功能是产生NADPH。
而NADPH对于维持细胞的正常生理功能和形态具有极为重要的作用。
G6PD缺乏症是世界上最常见的一种遗传性红细胞酶缺陷病,全球约有4亿人受累,该病高发于热带和亚热带地区,中国南方也是该病的高发区[1]。
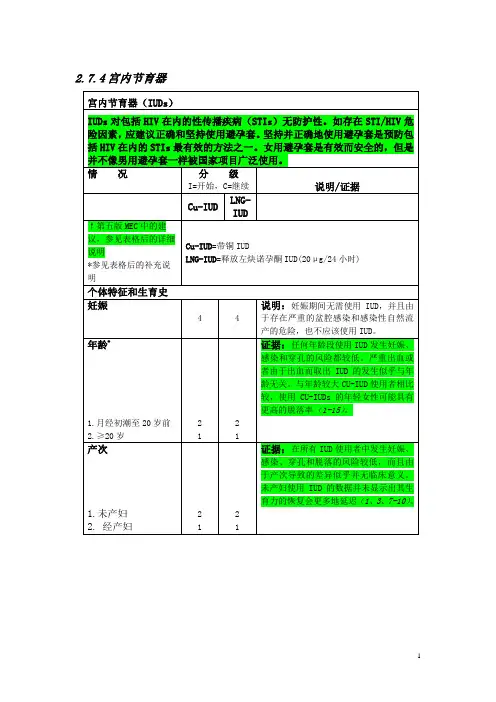
2.7.4宫内节育器(2)收缩压≥160或舒张压≥1001 2 4.血管病变 1 2 妊娠期间血压升高史(目前能够测量血压并且正常)1 1深静脉血栓形成(DVT)/肺栓塞(PE)*1.DVT/PE病史2.急性DVT/PE3. DVT/PE正在进行抗凝治疗4.DVT/PE家族史(一级亲属)5.经历大手术11112321证据:尽管有关使用POCs发生静脉血栓的风险的证据不一致,但其风险肯定低于使用COCs者(49-51)。
证据:尽管有关使用POCs发生静脉血栓的风险的证据不一致,但其风险肯定低于使用COCs者(49-51)。
有限的证据提示长期进行抗凝治疗的妇女放置LNG-IUD没有大的出血危险(52-54)。
(1)长期不能活动 1 2(2)无长期不能活动 1 1 6.小手术而无长期不能活动的问题1 1已知与凝血相关的突变(如:V因子雷登;凝血栓素突变;蛋白S、蛋白C和抗血栓素缺乏)1 2 说明:不宜做常规筛查,一方面发病罕见,另一方面筛查费用高。
表浅静脉异常1.静脉曲张2.表浅静脉血栓形成1111现患或曾患缺血性心脏病* 1I C2 3中风*(脑血管意外史)1 2不伴有其它已知的心血管风险因素的已知的血脂异常1 2 说明:不宜做常规筛查,一方面发病罕见,另一方面筛查费用高。
心脏瓣膜病1.无并发症2.有并发症(肺动脉高血压,房颤,亚急性细菌性心内膜炎病史)1212 说明:建议在放置IUD时预防性使用抗生素,以预防心内膜炎。
风湿性疾病系统性红斑狼疮(SLE)SLE患者缺血性心脏病、中风和静脉血栓栓塞的风险增加。
在《避孕方法选用的医学标准》中为此类情况所定的级别应当与存在这些情况的患有SLE的妇女的级别一致。
对于SLE的所有级别,分级是基于对不存在其他动脉心血管疾病的危险因素的假设;在存在这些危险因素的情况下,必须对这些分级进行调整(54-71)。
I C1.抗磷脂抗体阳性(或未知)2.严重的血小板减少症3.免疫抑制治疗4.无上述各项132112113222证据:抗磷脂抗体与较高的动脉和静脉血栓形成风险均有关联性(72、73)。

【压轴必刷】2023年中考数学压轴大题之经典模型培优案专题24函数与菱形存在性问题我们已经知道菱形是特殊的平行四边形,它的判定方法一共有五种,分别是①四边都相等的四边形是菱形;②两条对角线互相垂直的平行四边形是菱形;③邻边相等的平行四边形是菱形;④对角线互相垂直平分的四边形是菱形;⑤一条对角线平分一个顶角的平行四边形是菱形.在做几何证明题的时候我们常用的判定方法主要是前三种.二次函数和菱形存在性问题作为压轴题目,结合了“分类讨论思想”,“方程思想”“菱形的判定方法”,势必要比单纯的菱形判定思考难度要大的多,纵观历年中考真题,菱形存在性问题主要是以“两定两动”为设问方式,其中两定指的是四边形四个顶点其中有两个顶点的坐标是确定的或者是可求解的;两动指的是其中一个动点在一条直线或者抛物线上,另外一个动点是平面内任意一点或者该动点也在一条直线或者抛物线上.【例1】(2022春•锡山区校级期中)如图,在矩形ABCD中,BD是对角线,AB=6cm,BC=8cm,点E从点D出发,沿DA方向匀速运动,速度是2cm/s;点F从点B出发,沿BD方向匀速运动,速度是1cm/s,MN是过点F的直线,分别交AB、BC于点M、N,且在运动过程中始终保持MN⊥BD.连接EM、EN、EF,两点同时出发,设运动时间为t(s)(0<t<3.6),请回答下列问题:(1)求当t为何值时,△EFD∽△ABD?(2)求当t为何值时,△EFD为等腰三角形;(3)将△EMN沿直线MN进行翻折,形成的四边形能否是菱形?若存在,求出t的值;若不存在,请说明理由.【例2】(2022秋•南岸区校级期中)如图,点A、B分别在x轴和y轴的正半轴上,以线段AB为边在第一象限作等边△ABC,S△ABC=,且CA⊥x轴.(1)若点C在反比例函数y=(k≠0)的图象上,求该反比例函数的解析式;(2)在(1)中的反比例函数图象上是否存在点N,使四边形ABCN是菱形,若存在请求出点N坐标,若不存在,请说明理由;(3)在(2)的条件下,取OB的中点M,将线段OM沿着y轴上下移动,线段OM的对应线段是O1M1,直接写出四边形CM1O1N周长的最小值.【例3】(2022秋•龙华区期中)已知:在平面直角坐标系中,直线l1:y=﹣x+2与x轴,y轴分别交于A、B两点,直线l2经过点A,与y轴交于点C(0,﹣4).(1)求直线l2的解析式;(2)如图1,点P为直线l1一个动点,若△P AC的面积为10时,请求出点P的坐标.(3)如图2,将△ABC沿着x轴平移,平移过程中的△ABC记为△A1B1C1,请问在平面内是否存在点D,使得以A1、C1、C、D为顶点的四边形是菱形?若存在,直接写出点D的坐标.【例4】(2022秋•博罗县期中)如图,抛物线y=﹣x2+x+1与y轴交于点A,过点A的直线与抛物线交于另一点B,过点B作BC⊥x轴,垂足为点C(3,0).(1)求直线AB的函数解析式.(2)动点P在线段OC上,从原点O出发以每秒一个单位的速度向C移动,过点P作PN⊥x轴,交直线AB于点M,交抛物线于点N,设点P移动的时间为t秒,MN的长为s个单位,求s与t的函数解析式,并写出t的取值范围.(3)在(2)的条件下(不考虑点P与点O,C重合的情况),连接CM,BN,当t为何值时,四边形BCMN为平行四边形?对于所求的t的值,平行四边形BCMN是否为菱形?若存在,请直接写出四边形BCMN为菱形时t的值,若不能存在请说明理由.一.解答题1.(2022秋•思明区校级期中)如图,正方形OABC的边OA、OC分别在x轴和y轴上,顶点B在第一象限,AB=6,点E、F分别在边AB和射线OB上运动(E、F不与正方形的顶点重合),OF=2BE,设BE=t.(1)当t=2时,则AE=,BF=;(2)当点F在线段OB上运动时,若△BEF的面积为,求t的值;(3)在整个运动过程中,平面上是否存在一点P,使得以P、O、E、F为顶点,且以OF为边的四边形是菱形?若存在,求出t的值;若不存在,请说明理由.2.(2022•城西区开学)如图,在平面直角坐标系中,直线y=2x+4与x轴,y轴分别交于A,B两点,直线y=﹣x+1与x轴,y轴分别交于C,D两点,这两条直线相交于点P.(1)求点P的坐标;(2)求四边形AODP的面积;(3)在坐标平面内是否存在一点Q,使以A,P,D,Q为顶点的四边形是菱形?若存在,请求出点Q 的坐标,若不存在,请说明理由.3.(2022春•大足区期末)已知:在平面直角坐标系中,直线l1:y=﹣x+2与x轴,y轴分别交于A、B两点,直线l2经过点A,与y轴交于点C(0,﹣4).(1)求直线l2的解析式;(2)如图1,点P为直线l1一个动点,若△P AC的面积等于10时,请求出点P的坐标;(3)如图2,将△ABC沿着x轴平移,平移过程中的△ABC记为△A1B1C1,请问在平面内是否存在点D,使得以A1、C1、C、D为顶点的四边形是菱形?若存在,直接写出点D的坐标.4.(2022•崆峒区校级二模)如图,抛物线y=﹣x2+bx+c交y轴于点A(0,2),交x轴于点B(4,0)、C 两点,点D为线段OB上的一个动点(不与O、B重合),过点D作DM⊥x轴,交AB于点M,交抛物线于点N.(1)求抛物线的解析式;(2)连接AN和BN,当△ABN的面积最大时,求出点D的坐标及△ABN的最大面积;(3)在平面内是否存在一点P,使得以点A,M,N,P为顶点,以AM为边的四边形是菱形?若存在,请求出点P的坐标;若不存在,请说明理由.5.(2022•前进区三模)如图,在平面直角坐标系中,矩形ABCO的边OC与x轴重合,OA与y轴重合,BC=2,D是OC上一点,且OD,DC的长是一元二次方程x2﹣5x+4=0的两个根(OD>DC).(1)求线段OD,OC,AD的长;(2)在线段AB上有一动点P(不与A、B重合),点P从点A出发,以每秒1个单位长度的速度沿AB 方向匀速运动,到终点B停止,设运动的时间为t秒,过P点作PE∥BD交AD于E,PF∥AD交BD于F,求四边形DEPF的面积S与时间t的函数关系式;(3)在(2)的条件下,在点P运动的过程中,x轴上是否存在点Q,使以A、D、P、Q为顶点的四边形是菱形?若存在,请直接写出点Q的坐标,若不存在,请说明理由.6.(2021秋•莱西市期末)已知:如图,菱形ABCD中,AB=5cm,AC=6cm,动点P从点B出发,沿BA 方向匀速运动;同时,动点Q从点C出发,沿CB方向匀速运动,它们的运动速度均为1cm/s.过点P作PM∥BC,过点B作BM⊥PM,垂足为M,连接QP.设运动时间为t(s)(0<t<5).解答下列问题:(1)菱形ABCD的高为cm,cos∠ABC的值为;(2)在运动过程中,是否存在某一时刻t,使四边形MPQB为平行四边形?若存在,求出t的值;若不存在,请说明理由.(3)是否存在某一时刻t,使四边形MPQB的面积是菱形ABCD面积的?若存在,求出t的值;若不存在,请说明理由.(4)是否存在某一时刻t,使点M在∠PQB的角平分线上?若存在,求出t的值;若不存在,请说明理由.7.(2022•青岛一模)已知,在菱形ABCD中,对角线AC,BD相交于点O,AC=6cm,BD=8cm.延长BC至点E,使CE=BC,连接ED.点F从点E出发,沿ED方向向点D运动,速度为1cm/s,过点F 作FG⊥ED垂足为点F交CE于点G;点H从点A出发,沿AD方向向点D运动,速度为1cm/s,过点H作HP∥AB,交BD于点P,当F点停止运动时,点H也停止运动.设运动时间为t(0<t≤3),解答下列问题:(1)求证:∠BDE=90°;(2)是否存在某一时刻t,使G点在ED的垂直平分线上?若存在,求出t值;若不存在,请说明理由.(3)设六边形PCGFDH的面积为S(cm2),求S与t的函数关系式;(4)连接HG,是否存在某一时刻t,使HG∥AC?若存在,求出t值;若不存在,请说明理由.8.(2021秋•市南区期末)已知:如图,菱形ABCD中,对角线AC,BD相交于点O,且AC=6cm,BD=8cm.点P从点B出发,沿BA方向匀速运动,速度为1cm/s;同时,直线EF从点D出发,沿DB方向匀速运动,速度为1cm/s,EF⊥BD,且与AD,BD,CD分别交于点E,Q,F.当直线EF停止运动,点P也停止运动.连接PF,设运动时间为t(s).解答下列问题:(1)用含t的代数式表示线段EF:;(2)当t为何值时,四边形ADFP是平行四边形;(3)设四边形APFE的面积为y(cm2),求y与t之间的函数关系式;(4)是否存在某一时刻t,使得PF与EF的夹角为45°?若存在,求出t的值,若不存在,说明理由.9.(2022春•双峰县期末)问题情境:在综合实践课上,老师让同学们探究“平面直角坐标系中的旋转问题”,如图,在平面直角坐标系中,四边形AOBC是矩形,O(0,0),点A(5,0),点B(0,3).操作发现:以点A为中心,顺时针旋转矩形AOBC,得到矩形ADEF,点O,B,C的对应点分别为D,E,F.(1)如图1,当点D落在BC边上时,求点D的坐标;继续探究:(2)如图2,当点D落在线段BE上时,AD与BC交于点H,求证△ADB≌△AOB;拓展探究:如图3,点M是x轴上任意一点,点N是平面内任意一点,是否存在点N使以A、D、M、N 为顶点的四边形是菱形?若存在,请直接写出点N的坐标;若不存在,请说明理由.10.(2022春•营口期末)如图1,直线y=x+6与x,y轴分别交于A,B两点,∠ABO的角平分线与x轴相交于点C.(1)求点C的坐标;(2)在直线BC上有两点M,N,△AMN是等腰直角三角形,∠MAN=90°,求点M的坐标;(3)点P在y轴上,在平面上是否存在点Q,使以点A、B、P、Q为顶点的四边形为菱形?若存在,请直接写出点Q的坐标;若不存在,请说明理由.11.(2022春•曹妃甸区期末)如图,在矩形ABCD中,AB=3,∠CAB=30°,点P从点A出发,每秒个单位长度的速度沿AB方向运动,点Q从点C出发,以每秒2个单位长度的速度沿对角线CA方向运动.已知点P、Q两点同时出发.当点Q到达点A时,P、Q两点同时停止运动,连接PQ,设运动时间为t秒.(1)BC=,AC=;(2)当t为何值时,AP=AQ;(3)在运动过程中,是否存在一个时刻t,使所得△APQ沿它的一边翻折,翻折前后两个三角形组成的四边形为菱形?若存在,求出t的值;若不存在,请说明理由.(4)当点P关于点Q的对称点P′落在△ACD的内部(不包括边上)时,请直接写出t的取值范围.12.(2022春•巴东县期末)已知点E是平行四边形ABCD边CD上的一点(不与点C,D重合).(1)如图1,当点E运动到CD的中点时,连接AE、BE,若AE平分∠BAD,证明:CE=CB.(2)如图2,过点E作EF⊥DC交直线CB于点F,连接AF.若∠ABC=120°,BC=2.封AB=4.在线段CF上是否存在一点H.使得四边形AFHD为菱形?若存在,请求出ED,CH的长;若不存在,请简单地说明理由.13.(2022春•同江市期末)如图,平面直角坐标系中,把矩形OABC沿对角线OB所在的直线折叠,点A 落在点D处,OD与BC交于点E.OA,OC的长满足式子|OA﹣6|+=0.(1)求点A,C的坐标;(2)直接写出点E的坐标,并求出直线AE的函数解析式;(3)F是x轴上一点,在坐标平面内是否存在点P,使以O,B,P,F为顶点的四边形为菱形?若存在,请直接写出点P的坐标;若不存在,请说明理由.14.(2022春•抚远市期末)如图,平面直角坐标系中,把矩形OABC沿对角线OB所在的直线折叠,点A 落在点D处,OD与BC交于点E.OA,OC的长满足式子|OA﹣6|+=0.(1)求点A,C的坐标;(2)直接写出点E的坐标,并求出直线AE的函数解析式;(3)F是x轴上一点,在坐标平面内是否存在点P,使以O,B,P,F为顶点的四边形为菱形?若存在,请直接写出点P的坐标;若不存在,请说明理由.15.(2022春•东阳市期末)如图,在平面直角坐标系中,矩形OABC的顶点A、C分别在x轴、y轴上,且B(4,2),E为直线AC上一动点,连OE,过E作GF⊥OE,交直线BC、直线OA于点F、G,连OF.(1)求直线AC的解析式.(2)当E为AC中点时,求CF的长.(3)在点E的运动过程中,坐标平面内是否存在点P,使得以P、O、G、F为顶点的四边形为菱形,若存在,求出点P的横坐标,若不存在,请说明理由.16.(2022•大方县模拟)如图,抛物线与x轴交于A,B(4,0)两点,与y轴交于点C,直线经过点B,C,点P是抛物线上的动点,过点P作PQ⊥x轴,垂足为Q,交直线BC于点D.(1)求抛物线的解析式及点A的坐标;(2)当点P位于直线BC上方且△PBC面积最大时,求P的坐标;(3)若点E是平面直角坐标系内的任意一点,是否存在点E,使得以A,C,D,E为顶点的四边形是菱形?若存在,请直接写出所有符合条件的点E的坐标;若不存在,请说明理由.17.(2022•山西模拟)综合与探究如图,二次函数y=ax2+bx+4的图象与x轴分别交于点A(﹣2,0),B(4,0),点E是x轴正半轴上的一个动点,过点E作直线PE⊥x轴,交抛物线于点P,交直线BC于点F.(1)求二次函数的表达式.(2)当点E在线段OB上运动时(不与点O,B重合),恰有线段PF=EF,求此时点P的坐标.(3)试探究:若点Q是y轴上一点,在点E运动过程中,是否存在点Q,使得以点C,F,P,Q为顶点的四边形为菱形,若存在,直接写出点Q的坐标;若不存在,请说明理由.18.(2022•建华区二模)综合与实践如图,已知正方形OCDE中,顶点E(1,0),抛物线y=x2+bx+c经过点C、点D,与x轴交于A、B 两点(点B在点A的右侧),直线x=t(t>0)交x轴于点F.(1)求抛物线的解析式,且直接写出点A、点B的坐标;(2)若点G是抛物线的对称轴上一动点,且使AG+CG最小,则G点坐标为:;(3)在直线x=t(第一象限部分)上找一点P,使得以点P、点B、点F为顶点的三角形与△OBC全等,请你直接写出点P的坐标;(4)点M是射线AC上一点,点N为平面上一点,是否存在这样的点M,使得以点O、点A、点M、点N为顶点的四边形为菱形?若存在,请你直接写出点N的坐标;若不存在,请说明理由.19.(2022•红花岗区模拟)如图,在平面直角坐标系中,抛物线y=ax2+bx+4与x轴交于A(﹣1,0),B (4,0)两点,与y轴交于点C.(1)求抛物线的解析式;(2)点P在抛物线上,当∠PBA=∠ACO时,求点P的坐标;(3)将抛物线的对称轴沿x轴向右平移个单位得直线l,点M为直线l上一动点,在平面直角坐标系中是否存在点N,使以点B,C,M,N为顶点的四边形为菱形?若存在,请求出点N的坐标;若不存在,请说明理由.20.(2022•蒲城县一模)如图,已知直线与x轴、y轴分别交于B、C两点,抛物线y=ax2+3x+c 经过B、C两点,与x轴的另一个交点为A,点E的坐标为.(1)求抛物线的函数表达式;(2)点E,F关于抛物线的对称轴直线l对称,Q点是对称轴上一动点,在抛物线上是否存在点P,使得以E、F、P、Q为顶点的四边形是菱形?若存在,求出点P的坐标;若不存在,请说明理由.21.(2022春•兴宁区校级期末)如图,抛物线y=x2+bx+c与x轴交于A(﹣3,0),B(1,0)两点,与y 轴交于点C,连接AC,BC,点P是直线AC下方抛物线上的一个动点.(1)求抛物线的解析式;(2)连接AP,CP,设P点的横坐标为m,△ACP的面积为S,求S与m的函数关系式;(3)试探究:过点P作BC的平行线1,交线段AC于点D,在直线l上是否存在点E,使得以点D,C,B,E为顶点的四边形为菱形,若存在,请直接写出点E的坐标,若不存在,请说明理由.22.如图,已知抛物线y=ax2+bx﹣2的图象与x轴交于A,B两点,与y轴交于点C.﹣3和1是关于x的一元二次方程ax2+bx﹣2=0的两个根.(1)求该抛物线的解析式;(2)过点B作BD∥AC交抛物线于点D,BD与y轴交于点E,P为直线AC下方抛物线上的一个动点,连接PB交AC于点F,求S△PEF的最大值及此时点P的坐标;(3)在(2)的条件下,将该抛物线向右平移2个单位后得到新抛物线,新抛物线与原抛物线相交于点Q,点M为原抛物线对称轴上一点,在平面直角坐标系中是否存在点N,使得以点A,M,N,Q为顶点的四边形是菱形,若存在,请直接写出点N的坐标;如不存在,请说明理由.23.如图,已知抛物线y=ax2+bx﹣3与x轴交于A(﹣1,0),B两点,与y轴交于点C且tan∠ABC=1,连接AC、BC.(1)求抛物线的解析式;(2)若P点是直线BC下方一点,过P点作PE∥AC交BC于点E,PH∥y轴交BC于点H,求CE+BH 的最小值及此时P点的坐标.(3)在第(2)条件下,将该抛物线向右平移2个单位后得到新抛物线,新抛物线与原抛物线相交于点F,点M为原抛物线对称轴上一点,在平面直角坐标系中是否存在点,使得以点H,M,N,F为顶点的四边形是菱形,若存在,请直接写出点N的坐标;如不存在,请说明理由.24.(2022•渝北区自主招生)如图,在平面直角坐标系中,抛物线y=ax2+bx﹣与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,点B的坐标为(1,0),且tan∠OAC=.(1)求抛物线的解析式;(2)如图1,点M为直线AC下方抛物线上一点,过点M作MD∥y轴交AC于点D,求MD+DC的最大值及此时点M的坐标;(3)如图2,连接BC,将△BOC绕着点A逆时针旋转60°得到△B'O'C',将抛物线y=ax2+bx﹣沿着射线CB方向平移,使得平移后的新抛物线经过O',H是新抛物线对称轴上一点,在平面直角坐标系中是否存在点P,使以点B',C',H,P为顶点的四边形是以B'C'为边的菱形,若存在,请直接写出点P 的坐标;若不存在,请说明理由.。

流式检测CD%在肺结核患者外周血中的表达水平及其临床意义段艳辉"%2杨倩婷2周一平3王召钦2陈心春4【摘要】目的研究CD"6i在肺结核患者(P T B)外周血中的表达水平及其临床意义。
方法通过流式细胞仪检测103例潜伏性结核感染患者(L T B I)和154例P T B患者外周血CD3+CD i+6i、CD4+CD i+6i和CD:+CD i+6i T细胞的表达水平,比较其在L T B I与P T B间差异;分析外周血CD m+CD i F i、CD g+CD i+6i和CD:+CD i+6i T细胞的表达水平分别与白细胞总数、淋巴细胞(百分比和绝对值)、单核细胞(百分比和绝对值)的相关性。
结果P T B患者外周血CD3+CD i F i'CD g+CD i F i和CD:+CD i+6i T细胞的表达水平均显著低于L T B I患者(!<0.0001);P T B患者外周血CD3+CD"+6i和CD:+CD i+6i T细胞的表达水平和白细胞总数、单核细胞绝对值呈负相关(!<0. 05);P T B患者外周血CD g+CD i F i T细胞的表达水平和淋巴细胞绝对值呈负相关,而L T B I患者外周血CD g+C D F T细胞的表达水平和淋巴细胞绝对值呈正相关(!<0.05)。
结论本结果显示C D%能区分P T B和LTBI,可作为早期区分P T B和L T B I的分子标志。
【关键词】C D:;肺结核;流式细胞仪E xp re ssio n a n d clin ica l significance o f C D161in peripheral b l o o d o f patients w ith p u lm on a ry tuberculosis byflow cytom etric measurement DUAN Yan-hui,YAN GQian-ting,ZH O U Y i-ping,W ANGZhao-qin,CHEN Xin-chun Guangdong Medical University,Zhanjiang,Guangdong 524003,China【A b stra ct】O bjective To studytheexpression and clinical significance of CD%" in peripheral blood of patients with pulmonary tuberculosis. M ethods The expression levels of CD3+CD"8i,C D: C in 103 patients with latent tuberculosis infection ( LTBI) and 154 patients with pulmonary tuberculosis ( PTB) weredetected by flow^ cytometry,and the expression of LTBI and PTB were compared. Pearson correlation analysis wasused to analyze the correlation of the expression levels between CD?. CD181,C D/ CD181 and CD:+CD181T cells and thetotal number of white blood c ells ( W BC),lymphocytes ( percentages and absolute values) and mononuclear cells (percentages and absolute values) in peripheral blood. Results The expression levels of CD]. CD181,C D/ CD181 anddoi: 10. 3969/j'. issn. 1009 - 6663.2018. 02.010基金项目:广东省自然科学基金项目(No 2015A030313879 )、深圳市基础研究计划基础研究项目(No. JCYJ201504021450 15986、N o. JCYJ20150402111430656、N o. JCYJ201604271 53348709)作者单位:15240032. 5181123R5181124 518112通信作者:陈心春,[广东湛江广东医科大学广东深圳深圳市第三人民医院广东深圳深圳市福田(第四)人民医院 广东深圳深圳大学基础医学院mail : chenginchun@ 163. c o m[9]房秀清,尹丽欣,钞丽红,等.胸腔积液中癌胚抗原及C A125和C A153联合检测对肺癌的诊断意义[J] •新乡医学院学报,2012,29 (6):428 -429.[10] Skouras V S,Kalomenidis I. Pleural fliaid tests to diagnose tuberculous pleuritis-J]. Curr Opin Pulm Med,2016,22(4) :367 -377. [11 ]崔海燕,张青,粟波,等.结核性胸膜炎患者T h1/T h2及前炎症细胞因子的变化[J/C D].中华临床医师杂志(电子版),2012,6(14):4109 -4111.[12]张会强,张冬杰,文政芳.结核病性胸腔积液病人多项血清因子水平变化研究[J]•现代预防医学,2012,39(22):5944-5945,5950.[13] Cohen L A,Liligt RW. Tuberculous Pleural Effusion[ J]. Turk Tho-rac J,2015,16(1 ):1-9.[14]刘倩倩,张冰琰,郑建,等.结核性与肿瘤性胸腔积液中多种细胞因子的表达及其对鉴别诊断的作用[/].中华传染病杂志,2016,34(8):485 -489.[15]李明瑛,王和林,席秀娥,等.肿瘤坏死因子-/腺苷脱氨酶同工酶、干扰素-及白细胞介素-0对结核性胸腔积液的诊断意 义[J] •新乡医学院学报,2014,31 (2):107- 110.[16]郑建,欧勤芳,刘袁媛,等.结核性胸膜炎患者结核特异性T淋巴细胞的免疫应答及其迁徙作用[J] •中华传染病杂志,2013,31(12) :715 -718.[收稿日期 *2017 -05-16]CD8+CD i"8i T cells in perijDheral blood of PTB patients were significantly lower than those of LTBI patients ( !W 0. 0001 ) . The expression levels of CD m+ C D:" and CD:+CD i+6"T cells in peripheral blood of PTB patients were negatively correlated witli the total number of WBC and the absolute value of monocytes ( ! <0. 05). The expression level of CD4+ CD"6i T cells in peripheral blood of patients with PTB was negatively correlated with the absolute value of lymphocytes (! <0. 05),while the expression level of CD4+CD i6"T cells in peripheral blood of patients with LTBI was posi- tivvly correlated with the absolute value of lymphocytes (!< 0. 05 ).Conclusion Our results show that CD"6i can distinguish between PTBand LTBI,and it can be used as early molecular markers that distinguish PTBand LTBI.【K ey w o rd s】C D^; pulmonary tuberculosis; flowcytometry结核病仍旧是对全人类健康的一大威胁。

高考物理二轮复习 专项训练 带电粒子在磁场中的运动及解析一、带电粒子在磁场中的运动专项训练1.核聚变是能源的圣杯,但需要在极高温度下才能实现,最大难题是没有任何容器能够承受如此高温。
托卡马克采用磁约束的方式,把高温条件下高速运动的离子约束在小范围内巧妙实现核聚变。
相当于给反应物制作一个无形的容器。
2018年11月12日我国宣布“东方超环”(我国设计的全世界唯一一个全超导托卡马克)首次实现一亿度运行,令世界震惊,使我国成为可控核聚变研究的领军者。
(1)2018年11月16日,国际计量大会利用玻尔兹曼常量将热力学温度重新定义。
玻尔兹曼常量k 可以将微观粒子的平均动能与温度定量联系起来,其关系式为32k E kT =,其中k=1.380649×10-23J/K 。
请你估算温度为一亿度时微观粒子的平均动能(保留一位有效数字)。
(2)假设质量为m 、电量为q 的微观粒子,在温度为T 0时垂直进入磁感应强度为B 的匀强磁场,求粒子运动的轨道半径。
(3)东方超环的磁约束原理可简化如图。
在两个同心圆环之间有很强的匀强磁场,两圆半径分别为r 1、r 2,环状匀强磁场围成中空区域,中空区域内的带电粒子只要速度不是很大都不会穿出磁场的外边缘,而被约束在该区域内。
已知带电粒子质量为m 、电量为q 、速度为v ,速度方向如图所示。
要使粒子不从大圆中射出,求环中磁场的磁感应强度最小值。
【答案】(1)15210J k E -≈⨯ (2)03kmT(3)()222212 r mvq r r - 【解析】 【详解】(1)微观粒子的平均动能:1532102k E kT -=≈⨯J (2)2031kT mv 22= 解得: 03kT v m=由2v Bqv m R= 03kmT R =(3)磁场最小时粒子轨迹恰好与大圆相切,如图所示设粒子轨迹半径为r ,由几何关系得:()22221r r r r -=+解得22212:r 2r r r -=由牛顿第二定律 2qvB m v r=解得:()222212B r mvq r r =-2.如图所示,在两块长为3L 、间距为L 、水平固定的平行金属板之间,存在方向垂直纸面向外的匀强磁场.现将下板接地,让质量为m 、电荷量为q 的带正电粒子流从两板左端连线的中点O 以初速度v 0水平向右射入板间,粒子恰好打到下板的中点.若撤去平行板间的磁场,使上板的电势φ随时间t 的变化规律如图所示,则t=0时刻,从O 点射人的粒子P 经时间t 0(未知量)恰好从下板右边缘射出.设粒子打到板上均被板吸收,粒子的重力及粒子间的作用力均不计.(1)求两板间磁场的磁感应强度大小B .(2)若两板右侧存在一定宽度的、方向垂直纸面向里的匀强磁场,为了使t=0时刻射入的粒子P 经过右侧磁场偏转后在电场变化的第一个周期内能够回到O 点,求右侧磁场的宽度d 应满足的条件和电场周期T 的最小值T min . 【答案】(1)0mv B qL = (2)223cos d R a R L ≥+= ;min 0(632)3L T v π= 【解析】 【分析】 【详解】(1)如图,设粒子在两板间做匀速圆周运动的半径为R 1,则0102qv B m v R =由几何关系:222113(()2L LR R =+-解得0mv B qL=(2)粒子P 从O 003L v t =01122y L v t = 解得033y v v =设合速度为v ,与竖直方向的夹角为α,则:0tan 3yv v α== 则=3πα0023sin v v α== 粒子P 在两板的右侧匀强磁场中做匀速圆周运动,设做圆周运动的半径为R 2,则212sin L R α=, 解得23L R =右侧磁场沿初速度方向的宽度应该满足的条件为223cos 2d R R L α≥+=; 由于粒子P 从O 点运动到下极板右侧边缘的过程与从上板右边缘运动到O 点的过程,运动轨迹是关于两板间的中心线是上下对称的,这两个过程经历的时间相等,则:2min 0(22)2R T t vπα--=解得()min6323L T v π=【点睛】带电粒子在电场或磁场中的运动问题,关键是分析粒子的受力情况和运动特征,画出粒子的运动轨迹图,结合几何关系求解相关量,并搞清临界状态.3.正、负电子从静止开始分别经过同一回旋加速器加速后,从回旋加速器D型盒的边缘引出后注入到正负电子对撞机中.正、负电子对撞机置于真空中.在对撞机中正、负电子对撞后湮灭成为两个同频率的光子.回旋加速器D型盒中的匀强磁场的磁感应强度为B,回旋加速器的半径为R,加速电压为U;D型盒缝隙间的距离很小,带电粒子穿过的时间可以忽略不计.电子的质量为m、电量为e,重力不计.真空中的光速为c,普朗克常量为h.(1)求正、负电子进入对撞机时分别具有的能量E及正、负电子对撞湮灭后产生的光子频率v(2)求从开始经回旋加速器加速到获得最大能量的过程中,D型盒间的电场对电子做功的平均功率P(3)图甲为正负电子对撞机的最后部分的简化示意图.位于水平面的粗实线所示的圆环真空管道是正、负电子做圆周运动的“容器”,正、负电子沿管道向相反的方向运动,在管道内控制它们转变的是一系列圆形电磁铁.即图中的A1、A2、A4……A n共有n个,均匀分布在整个圆环上.每个电磁铁内的磁场都是匀强磁场,并且磁感应强度都相同,方向竖直向下.磁场区域的直径为d.改变电磁铁内电流大小,就可以改变磁场的磁感应强度,从而改变电子偏转的角度.经过精确调整,首先实现电子在环形管道中沿图甲中粗虚线所示的轨道运动,这时电子经过每个电磁铁时射入点和射出点都在电磁铁的同一直径的两端,如图乙所示.这就为进一步实现正、负电子的对撞做好了准备.求电磁铁内匀强磁场的磁感应强度B大小【答案】(1)22222e B R mcvmh h=+,2222e B REm=;(2)2e B Umπ;(3)02sinB Rndπ【解析】【详解】解:(1)正、负电子在回旋加速器中磁场里则有:2mvevBR=解得正、负电子离开回旋加速器时的速度为:0eB Rvm=正、负电子进入对撞机时分别具有的能量:22220122e B RE mvm==正、负电子对撞湮灭时动量守恒,能量守恒,则有:222E mc hv+=正、负电子对撞湮灭后产生的光子频率:22222e B R mcvmh h=+(2) 从开始经回旋加速器加速到获得最大能量的过程,设在电场中加速n 次,则有:2012neU mv =解得:2202eB Rn mU=正、负电子在磁场中运动的周期为:02mT eB π=正、负电子在磁场中运动的时间为:2022B R nt T Uπ==D 型盒间的电场对电子做功的平均功率:20e B UW E P t t mπ===(3)设电子在匀强磁场中做圆周运动的半径为r ,由几何关系可得sin2dr nπ=解得:2sind r nπ=根据洛伦磁力提供向心力可得:200mv ev B r=电磁铁内匀强磁场的磁感应强度B 大小:02sinB R n B dπ=4.如图甲所示,在直角坐标系0≤x ≤L 区域内有沿y 轴正方向的匀强电场,右侧有一个以点(3L ,0)为圆心、半径为L 的圆形区域,圆形区域与x 轴的交点分别为M 、N .现有一质量为m 、带电量为e 的电子,从y 轴上的A 点以速度v 0沿x 轴正方向射入电场,飞出电场后从M 点进入圆形区域,此时速度方向与x 轴正方向的夹角为30°.不考虑电子所受的重力.(1)求电子进入圆形区域时的速度大小和匀强电场场强E 的大小;(2)若在圆形区域内加一个垂直纸面向里的匀强磁场,使电子穿出圆形区域时速度方向垂直于x 轴.求所加磁场磁感应强度B 的大小和电子刚穿出圆形区域时的位置坐标; (3)若在电子刚进入圆形区域时,在圆形区域内加上图乙所示变化的磁场(以垂直于纸面向外为磁场正方向),最后电子从N 点处飞出,速度方向与进入磁场时的速度方向相同.请写出磁感应强度B 0的大小、磁场变化周期T 各应满足的关系表达式.【答案】(1)(2)(3)(n=1,2,3…)(n=1,2,3…)【解析】(1)电子在电场中作类平抛运动,射出电场时,速度分解图如图1中所示.由速度关系可得:解得:由速度关系得:v y=v0tanθ=v0在竖直方向:而水平方向:解得:(2)根据题意作图如图1所示,电子做匀速圆周运动的半径R=L根据牛顿第二定律:解得:根据几何关系得电子穿出圆形区域时位置坐标为(,-)(3)电子在在磁场中最简单的情景如图2所示.在磁场变化的前三分之一个周期内,电子的偏转角为60°,设电子运动的轨道半径为r,运动的T0,粒子在x轴方向上的位移恰好等于r1;在磁场变化的后三分之二个周期内,因磁感应强度减半,电子运动周期T′=2T0,故粒子的偏转角度仍为60°,电子运动的轨道半径变为2r,粒子在x轴方向上的位移恰好等于2r.综合上述分析,则电子能到达N点且速度符合要求的空间条件是:3rn=2L(n=1,2,3…)而:解得:(n=1,2,3…)应满足的时间条件为: (T0+T′)=T而:解得(n=1,2,3…)点睛:本题的靓点在于第三问,综合题目要求及带电粒子运动的半径和周期关系,则符合要求的粒子轨迹必定是粒子先在正B0中偏转60°,而后又在− B0中再次偏转60°,经过n次这样的循环后恰恰从N点穿出.先从半径关系求出磁感应强度的大小,再从周期关系求出交变磁场周期的大小.5.电子扩束装置由电子加速器、偏转电场和偏转磁场组成.偏转电场的极板由相距为d的两块水平平行放置的导体板组成,如图甲所示.大量电子由静止开始,经加速电场加速后,连续不断地沿平行板的方向从两板正中间OO’射入偏转电场.当两板不带电时,这些电子通过两板之间的时间为2t0;:当在两板间加最大值为U0、周期为2t0的电压(如图乙所示)时,所有电子均能从两板间通过,然后进入竖直宽度足够大的匀强酸场中,最后打在竖直放置的荧光屏上.已知磁场的水平宽度为L,电子的质量为m、电荷量为e,其重力不计.(1)求电子离开偏转电场时的位置到OO’的最远位置和最近位置之间的距离(2)要使所有电子都能垂直打在荧光屏上,①求匀强磁场的磁感应强度B②求垂直打在荧光屏上的电子束的宽度△y【答案】(1)2010U e y t dm ∆= (2)①00U t B dL =②2010U e y y t dm∆=∆= 【解析】 【详解】(1)由题意可知,从0、2t 0、4t 0、……等时刻进入偏转电场的电子离开偏转电场时的位置到OO ′的距离最大,在这种情况下,电子的最大距离为:2222000max 00000311222y U e U e U e y at v t t t t dm dm dm=+=+= 从t 0、3t 0、……等时刻进入偏转电场的电子离开偏转电场时的位置到OO ′的距离最小,在这种情况下,电子的最小距离为:220min 001122U e y at t dm== 最远位置和最近位置之间的距离:1max min y y y ∆=-,2010U e y t dm∆=(2)①设电子从偏转电场中射出时的偏向角为θ,由于电子要垂直打在荧光屏上,所以电子在磁场中运动半径应为:sin L R θ=设电子离开偏转电场时的速度为v 1,垂直偏转极板的速度为v y ,则电子离开偏转电场时的偏向角为θ,1sin y v v θ=,式中00y U ev t dm= 又:1mv R Be =解得:00U tB dL=②由于各个时刻从偏转电场中射出的电子的速度大小相等,方向相同,因此电子进入磁场后做圆周运动的半径也相同,都能垂直打在荧光屏上.由第(1)问知电子离开偏转电场时的位置到OO ′的最大距离和最小距离的差值为△y 1, 所以垂直打在荧光屏上的电子束的宽度为:2010U e y y t dm∆=∆=6.长为L 的平行板电容器沿水平方向放置,其极板间的距离为d ,电势差为U ,有方向垂直纸面向里的磁感应强度大小为B 的匀强磁场.荧光屏MN 与电场方向平行,且到匀强电、磁场右侧边界的距离为x ,电容器左侧中间有发射质量为m 带+q 的粒子源,如图甲所示.假设a 、b 、c 三个粒子以大小不等的初速度垂直于电、磁场水平射入场中,其中a 粒子沿直线运动到荧光屏上的O 点;b 粒子在电、磁场中向上偏转;c 粒子在电、磁场中向下偏转.现将磁场向右平移与电场恰好分开,如图乙所示.此时,a、b、c粒子在原来位置上以各自的原速度水平射入电场,结果a粒子仍恰好打在荧光屏上的O点;b、c中有一个粒子也能打到荧光屏,且距O点下方最远;还有一个粒子在场中运动时间最长,且打到电容器极板的中点.求:(1)a粒子在电、磁场分开后,再次打到荧光屏O点时的动能;(2)b,c粒子中打到荧光屏上的点与O点间的距离(用x、L、d表示);(3)b,c中打到电容器极板中点的那个粒子先、后在电场中,电场力做功之比.【答案】(1)242222222akL B dq m UEmB d= (2)1()2xy dL=+ (3)11224==5UqyW dUqW yd【解析】【详解】据题意分析可作出abc三个粒子运动的示意图,如图所示.(1) 从图中可见电、磁场分开后,a 粒子经三个阶段:第一,在电场中做类平抛运动;第二,在磁场中做匀速圆周运动;第三,出磁场后做匀速直线运动到达O 点,运动轨迹如图中Ⅰ所示.Uq Bqv d=, BdU v =, L LBd t v U==, 222122a Uq L B qdy t dm mU ==, 21()2a a k U U qy E m d Bd=- 242222222a k L B d q m U E mB d =(2) 从图中可见c 粒子经两个阶段打到荧光屏上.第一,在电场中做类平抛运动;第二,离开电场后做匀速直线运动打到荧光屏上,运动轨迹如图中Ⅱ所示.设c 粒子打到荧光屏上的点到O 点的距离为y ,根据平抛运动规律和特点及几何关系可得12=122dy L L x +, 1()2x y d L =+(3) 依题意可知粒子先后在电场中运动的时间比为t 1=2t 2如图中Ⅲ的粒子轨迹,设粒子先、后在电场中发生的侧移为y 1,y 22111·2Uq y t md =,11y Uq v t md =122221·2y Uq t m y t d v +=,22158qU y t md=, 124=5y y , 11224==5Uqy W d Uq W y d7.如图所示,在竖直平面内建立直角坐标系,y 轴沿竖直方向.在x = L 到x =2L 之间存在竖直向上的匀强电场和垂直坐标平面向里的匀强磁场,一个比荷(qm)为k 的带电微粒从坐标原点以一定初速度沿+x 方向抛出,进入电场和磁场后恰好在竖直平面内做匀速圆周运动,离开电场和磁场后,带电微粒恰好沿+x 方向通过x 轴上x =3L 的位置,已知匀强磁场的磁感应强度为B ,重力加速度为g .求:(1)电场强度的大小; (2)带电微粒的初速度;(3)带电微粒做圆周运动的圆心坐标.【答案】(1)g k (2)2gkB(3)2222232(,)28g k B L L k B g -【解析】 【分析】 【详解】(1)由于粒子在复合场中做匀速圆周运动,则:mg =qE ,又=qk m解得g E k=(2)由几何关系:2R cos θ=L ,粒子做圆周运动的向心力等于洛伦兹力:2v qvB m r= ;由cos y v vθ=在进入复合场之前做平抛运动:y gt =v0L v t =解得02g v kB=(3)由212h gt =其中2kBL t g = ,则带电微粒做圆周运动的圆心坐标:'32O x L =; 222'222sin 8O g k B L y h R k B g θ=-+=-8.如图所示,虚线MN 为匀强电场和匀强磁场的分界线,匀强电场场强大小为E 方向竖直向下且与边界MN 成θ=45°角,匀强磁场的磁感应强度为B ,方向垂直纸面向外,在电场中有一点P ,P 点到边界MN 的竖直距离为d 。

一、引言末端脱氧核苷酸转移酶(Terminal deoxynucleotidyl transferase,TdT)是一种重要的酶,它在DNA修复、免疫应答和DNA重组等生物学过程中起着至关重要的作用。
TdT在DNA修复和免疫应答中的作用尤为显著,因此其反应机理备受科学家们的关注和研究。
本文将从深度和广度的角度对TdT的反应机理进行全面评估,并据此撰写一篇有价值的文章。
二、TdT的基本介绍1. TdT的命名来源TdT是末端脱氧核苷酸转移酶的缩写,其中“T”代表“脱氧胸腺嘧啶核苷酸(deoxythymidine nucleotide)”,“d”代表“脱氧核苷酸(deoxynucleotide)”,“t”代表“转移酶(transferase)”。
2. TdT的生物学功能TdT是一种能够在DNA分子末端添加未配对的脱氧核苷酸的酶,常见于哺乳动物的淋巴细胞和胸腺细胞中。
其主要功能包括在DNA修复、免疫应答和DNA重组等生物学过程中发挥作用。
3. TdT的结构特点TdT是一种具有特殊功能的酶,其结构特点对于了解其反应机理至关重要。
其结构具有特定的活性中心和底物结合区域,这些结构特点直接影响了TdT的反应机理。
三、TdT的反应机理探讨1. TdT的底物特异性TdT在反应中对于底物的特异性至关重要。
其活性中心能够识别末端未配对的DNA分子,并对其进行催化反应。
这种底物特异性直接影响了TdT的反应机理。
2. TdT的催化反应TdT在催化DNA末端添加脱氧核苷酸的过程中,需要经历一系列特定的催化反应。
这些反应包括底物结合、底物转移和产物释放等步骤,深入了解这些反应对于理解TdT的反应机理至关重要。
3. TdT的活性调控TdT的活性受到多种因素的调控,包括底物浓度、反应条件和细胞内环境等因素。
这些因素对于TdT反应机理的理解和解释具有重要意义。
四、综合总结与个人观点通过对TdT的反应机理进行深入细致的探讨,我们可以更全面地理解这一重要酶的生物学功能。
江苏省无锡市华庄职业高级中学高二物理期末试题含解析一、选择题:本题共5小题,每小题3分,共计15分.每小题只有一个选项符合题意1. 如图所示的区域内有垂直于纸面的匀强磁场,磁感应强度为B.电阻为R、半径为L、圆心角为45°的扇形闭合导线框绕垂直于纸面的O轴以角速度ω匀速转动(O轴位于磁场边界)。
则线框内产生的感应电流的有效值为()A. B. C. D.参考答案:C【详解】半径切割磁感线产生的感应电动势:交流电流的有效值是根据电流的热效应得出的,线框转动周期为T,而线框转动一周只有的时间内有感应电流,则有:,解得:,故C正确,ABD错误。
2. (单选题)下列说法中正确的是( )A.电子和质子都是元电荷;B. 一个带电体的电荷量为205.5倍的元电荷;C. 元电荷是最小的带电单位;D. 元电荷有正、负之分.参考答案:C3. 下列属于磁感应强度的单位的是:A. B.T C. D.以上都不是参考答案:ABC4. (单选)为了让乘客乘车更为舒适,某搡究小组设计了一种新的交通工具,乘客的座椅能随着坡度的变化而自动调整,使座椅始终保持水平,如图所示,当此车减速上坡时(仅考虑乘客与水平面之间的作用),则关于乘客下列说法正确的是()A.不受摩擦力的作用B.受到水平向左的摩擦力作用C.处于超重状态D.所受合力竖直向上参考答案:解:A、B、对乘客进行受力分析,乘客受重力,支持力,由于乘客加速度沿斜面向下,而静摩擦力必沿水平方向,由于乘客有水平向左的分加速度,所以受到向后(水平向左)的摩擦力作用.故A错误,B正确.C、当此车减速上坡时,整体的加速度沿斜面向下,乘客具有向下的分加速度,所以根据牛顿运动定律可知乘客处于失重状态.故C错误;D、由于乘客加速度沿斜面向下,根据牛顿第二定律得所受力的合力沿斜面向下.故D错误.故选:B5. 真空中两个同性的点电荷q1、q2 ,它们相距较近,保持静止。
今释放q2 且q只在q1的库仑力作用下运动,则q2在运动过程中受到的库仑力()A.不断减小B.不断增加C.始终保持不变D.先增大后减小参考答案:A二、填空题:本题共8小题,每小题2分,共计16分6. 如图4所示,一个半径为R质量为M的半圆形光滑小碗,在它的边上1/4圆弧处让一质量为m的小滑块自由滑下,碗下是一台秤,当滑块在运动时,台秤的最大读数是_______。
根据测OD时光的波长,波长在紫外范围就能够测,如果不在,就不能测量。
非常感谢细履平沙.哪位能说的具体一点啊,我想测枯草芽孢杆菌的OD,我不太知道是在多少nm下测,我看过一些文献,上面说细菌大概600nm,还是我自己摸索吸收波长啊?另外是测吸光度还是透光率啊,空白用培养基做吗.请高人指点,谢谢了.一般测菌体密度的OD的波长范围是580nm-660nm我们哪会儿测的(枯草芽孢杆菌)用600nm,已经属于可见光区空白如用水做,需要离心洗涤菌体,空白如用不接种的培养基做就不需要洗涤,但是不接种的培养基要和接种的同时培养,以求条件一致最后注意如果OD大于2.0,一般要稀释后再测,因为OD太大了,分光光度计的灵敏度就会显著降低一般都测吸光值,而且最好是整个实验过程中,保持发酵液或菌体的稀释倍数一致,吸光值与稀释倍数不一定成正比,可保证整个实验点有可比性一般OD值在控制在0 .1-0.4最好,在这个区内的值就可靠,最好不要超过1.0取值的时候要连续读数,重复3次的数最好。
测菌体密度的OD的波长可以自己摸出来,看看用哪个波长有最大吸收就可以了。
有合适的现场用的分光光度计推荐吗?要求只用作菌浓的OD值测定,哪种最便宜的分光光度计可以选择?DNA合成常见问题及解答Q: 怎样对合成DNA制品进行定量?A: DNA的量与260 nm处的吸光度值(OD值)成正比,因此使用紫外分光光度计定量是最科学的。
1个OD值的合成DNA的重量约为33 mg。
Q: 怎样理解测定的OD值?A: 进行OD值测定时,分光光度计上显示的数值为每毫升溶液中的OD 值。
当测定200 ml溶液中的OD值为1.5时,溶液整体的OD量应该为多少?此时的OD值= 1.5 OD/ml × 0.2 l = 0.3 OD。
Q: 合成Oligo DNA应怎样保存?A: 保存合成的Oligo应该注意以下几点:1. 干燥制品很稳定,常温下数个月无问题。
但为保证万无一失,放置于-20℃保存为好。
安徽省巢湖市2024高三冲刺(高考物理)苏教版测试(押题卷)完整试卷一、单项选择题(本题包含8小题,每小题4分,共32分。
在每小题给出的四个选项中,只有一项是符合题目要求的)(共8题)第(1)题1720年,英国的斯蒂芬·格雷提出导体和绝缘体的概念,并发现了导体的静电感应现象——导体在静电场的作用下,自由电荷发生了再分布的现象。
如图所示,将一长为2L的光滑金属导体MN固定在绝缘水平面上,倾角为,P是固定于金属导体左上方的一带电荷量为+Q的点电荷,,且。
现将一质量为m、电荷量为+q的带绝缘壳的小球体(可视为点电荷)从金属导体的M端由静止释放,小球体开始沿金属导体向下滑动。
已知重力加速度为g,小球体的电荷量始终不变,则小球体从M运动到N的时间( )A.等于B.大于C.小于D.无法确定第(2)题在国际单位制中,属于基本量及基本单位的是()A.质量千克B.能量焦耳C.电阻欧姆D.电量库仑第(3)题如图,将洁净的锌板用导线连接在验电器上,用紫外线灯照射锌板时,观察到验电器指针发生偏转.此时A.光电子从锌板表面逸出,验电器带正电B.光电子从锌板表面逸出,验电器带负电C.正离子从锌板表面逸出,验电器带正电D.正离子从锌板表面逸出,验电器带负电第(4)题“V”形吊车在港口等地有重要的作用.如图所示,底座支点记为O点,OA为“V”形吊车的左臂,OA上端A处固定有定滑轮,OB为活杆且为“V”形吊车的右臂,一根钢索连接底座与B点,另一根钢索连接B点后跨过定滑轮吊着一质量为M的重物,重物静止.已知左臂OA与水平面的夹角为,左臂OA与钢索AB段的夹角为θ,且左臂OA与右臂OB相互垂直,左臂OA、右臂OB总质量为m,钢索质量忽略不计,不计一切摩擦,重力加速度为g。
则下列说法正确的是( )A.定滑轮对钢索的支持力为B.AB段钢索所受到的拉力为2MgC.右臂OB对钢索的支持力为D.底座对左臂OA、右臂OB、重物整体的支持力为第(5)题如图所示,一人在滑雪场滑雪。