下载文档原格式
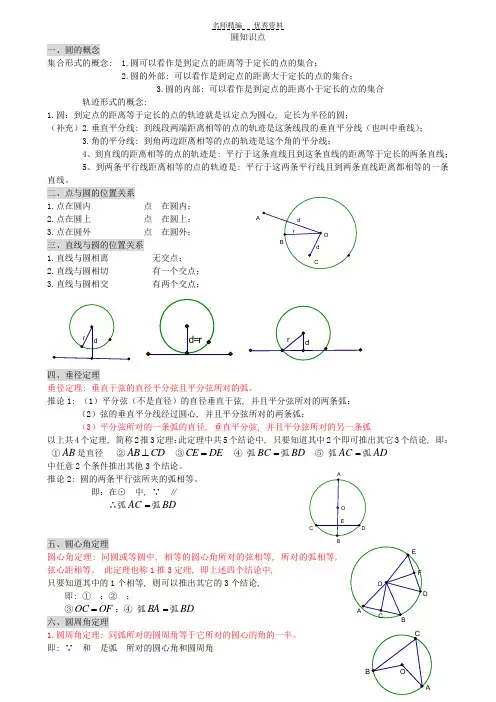
圆知识点一、圆的概念集合形式的概念: 1.圆可以看作是到定点的距离等于定长的点的集合；2.圆的外部: 可以看作是到定点的距离大于定长的点的集合；3.圆的内部: 可以看作是到定点的距离小于定长的点的集合轨迹形式的概念:1.圆：到定点的距离等于定长的点的轨迹就是以定点为圆心, 定长为半径的圆；（补充）2.垂直平分线: 到线段两端距离相等的点的轨迹是这条线段的垂直平分线（也叫中垂线）；3.角的平分线: 到角两边距离相等的点的轨迹是这个角的平分线；4、到直线的距离相等的点的轨迹是: 平行于这条直线且到这条直线的距离等于定长的两条直线；5、到两条平行线距离相等的点的轨迹是: 平行于这两条平行线且到两条直线距离都相等的一条直线。
二、点与圆的位置关系1.点在圆内点在圆内；2.点在圆上点在圆上；3.点在圆外点在圆外；三、直线与圆的位置关系1.直线与圆相离无交点；2.直线与圆相切有一个交点；3.直线与圆相交有两个交点；四、垂径定理垂径定理: 垂直于弦的直径平分弦且平分弦所对的弧。
推论1: （1）平分弦（不是直径）的直径垂直于弦, 并且平分弦所对的两条弧；（2）弦的垂直平分线经过圆心, 并且平分弦所对的两条弧；（3）平分弦所对的一条弧的直径, 垂直平分弦, 并且平分弦所对的另一条弧以上共4个定理, 简称2推3定理：此定理中共5个结论中, 只要知道其中2个即可推出其它3个结论, 即：①AB是直径②AB CD⊥③CE DE=④弧BC=弧BD⑤弧AC=弧AD中任意2个条件推出其他3个结论。
推论2: 圆的两条平行弦所夹的弧相等。
即：在⊙中, ∵∥∴弧AC=弧BD五、圆心角定理圆心角定理: 同圆或等圆中, 相等的圆心角所对的弦相等, 所对的弧相等,弦心距相等。
此定理也称1推3定理, 即上述四个结论中,只要知道其中的1个相等, 则可以推出其它的3个结论,即: ①；②；③OC OF=；④弧BA=弧BD六、圆周角定理1.圆周角定理: 同弧所对的圆周角等于它所对的圆心的角的一半。
初三圆的知识点和练习题一、圆的定义和基本概念圆是指平面上一组到定点的距离都相等的点的集合。
其中，定点称为圆心，到圆心的距离称为半径。
二、圆的性质1. 圆上任意两点的距离等于半径的长度。
2. 圆的半径相等。
3. 圆上的所有点到圆心的距离相等。
4. 圆上的点与圆心连线垂直。
三、圆的判定1. 判定两点是否在同一个圆上：计算两点之间的距离，若等于圆的半径，则两点在同一个圆上。
2. 判定一个点是否在圆上：计算该点到圆心的距离，若等于圆的半径，则该点在圆上。
四、圆的相关公式1. 圆的周长：C = 2πr，其中C表示周长，r表示半径，π约等于3.14。
2. 圆的面积：A = πr²，其中A表示面积。
五、练习题1. 已知圆A的半径为8cm，圆B的半径为5cm，计算两个圆的周长和面积。
解答：圆A的周长：C_A = 2πr_A = 2 × 3.14 × 8 = 50.24cm圆A的面积：A_A = πr_A² = 3.14 × 8² = 201.06cm²圆B的周长：C_B = 2πr_B = 2 × 3.14 × 5 = 31.4cm圆B的面积：A_B = πr_B² = 3.14 × 5² = 78.5cm²2. 已知圆C的周长为30.8cm，求其半径和面积。
解答：圆C的周长：C_C = 2πr_C = 30.8cm解方程：2πr_C = 30.8得到：r_C = 30.8 / (2π) ≈ 4.9cm圆C的面积：A_C = πr_C² = 3.14 × 4.9² ≈ 75.32cm²3. 在坐标平面上，圆D的圆心为(2, 3)，半径为4cm，判断点P(5, 3)是否在圆D上。
解答：计算点P到圆心的距离：d = √[(x_D - x_P)² + (y_D - y_P)²]= √[(2 - 5)² + (3 - 3)²]= √[9 + 0]= √9= 3圆D的半径为4cm，点P到圆心的距离为3cm，不等于半径的长度，因此点P不在圆D上。
圆相关知识点复习及练习题一、圆的定义1、以定点为圆心，定长为半径的点组成的图形。
2、在同一平面内，到一个定点的距离都相等的点组成的图形。
圆的有关概念：1、半径：圆上一点与圆心的连线段。
（1）、确定一个圆的要素是圆心和半径。
（2）连结圆上任意两点的线段叫做弦。
经过圆心的弦叫做直径。
（3）圆上任意两点间的部分叫做圆弧，简称弧。
小于半圆周的圆弧叫做劣弧。
大于半圆周的圆弧叫做优弧。
在同圆或等圆中，能够互相重合的弧叫做等弧。
（4）顶点在圆上，并且两边和圆相交的角叫圆周角。
（5）圆心角：以圆心为顶点，半径为角的边。
（6）经过三角形三个顶点可以画一个圆，并且只能画一个，经过三角形三个顶点的圆叫做三角形的外接圆，三角形外接圆的圆心叫做这个三角形的外心，这个三角形叫做这个圆的内接三角形，外心是三角形各边中垂线的交点；直角三角形外接圆半径等于斜边的一半。
（7）与三角形各边都相切的圆叫做三角形的内切圆，三角形的内切圆的圆心叫做三角形的内心，这个三角形叫做圆外切三角形，三角形的内心就是三角形三条内角平分线的交点。
直角三角形内切圆半径r满足：r=+。
+a2bc7、弦心距：圆心到弦的垂线段的长。
1、圆的有关性质1、圆的对称性。
（1）圆是轴对称图形，它的对称轴是直径所在的直线。
（2）圆是中心对称图形，它的对称中心是圆心。
（3）圆是旋转对称图形。
2、夹在平行线间的两条弧相等。
（1）定理在同圆或等圆中，如果圆心角相等，那么它所对的弧相等，所对的弦相等，所对的弦的弦心距相等。
推论在同圆或等圆中，如果两个圆心角、两条弧、两条弦或两条弦的弦心距中有一组量相等，那么它们所对的其余各组量都分别相等。
（2）垂径定理：垂直于弦的直径平分这条弦，并且平分弦所对的两条弧。
推论1（ⅰ）平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧。
（ⅱ）弦的垂直平分线经过圆心，并且平分弦所对的两条弧。
（ⅲ）平分弦所对的一条弧的直径，垂直平分弦，并且平分弦所对的另一条弧。
圆【知识点梳理】一、圆的概念集合形式的概念： 1、 圆可以看作是到定点的距离等于定长的点的集合； 2、圆的外部：可以看作是到定点的距离大于定长的点的集合； 3、圆的部：可以看作是到定点的距离小于定长的点的集合 轨迹形式的概念：1、圆：到定点的距离等于定长的点的轨迹就是以定点为圆心，定长为半径的圆；（补充）2、垂直平分线：到线段两端距离相等的点的轨迹是这条线段的垂直平分线（也叫中垂线）； 3、角的平分线：到角两边距离相等的点的轨迹是这个角的平分线；4、到直线的距离相等的点的轨迹是：平行于这条直线且到这条直线的距离等于定长的两条直线；5、到两条平行线距离相等的点的轨迹是：平行于这两条平行线且到两条直线距离都相等的一条直线。
二、点与圆的位置关系1、点在圆 ⇒ d r < ⇒ 点C 在圆；2、点在圆上 ⇒ d r = ⇒ 点B 在圆上；3、点在圆外 ⇒ d r > ⇒ 点A 在圆外； 三、直线与圆的位置关系1、直线与圆相离 ⇒ d r > ⇒ 无交点；2、直线与圆相切 ⇒ d r = ⇒ 有一个交点；3、直线与圆相交 ⇒ d r < ⇒ 有两个交点；四、圆与圆的位置关系外离（图1）⇒ 无交点 ⇒ d R r >+； 外切（图2）⇒ 有一个交点 ⇒ d R r =+； 相交（图3）⇒ 有两个交点 ⇒ R r d R r -<<+； 切（图4）⇒ 有一个交点 ⇒ d R r =-； 含（图5）⇒ 无交点 ⇒ d R r <-；A五、垂径定理垂径定理：垂直于弦的直径平分弦且平分弦所对的弧。
推论1：（1）平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧； （2）弦的垂直平分线经过圆心，并且平分弦所对的两条弧；（3）平分弦所对的一条弧的直径，垂直平分弦，并且平分弦所对的另一条弧以上共4个定理，简称2推3定理：此定理中共5个结论中，只要知道其中2个即可推出其它3个结论，即：①AB 是直径 ②AB CD ⊥ ③CE DE = ④ 弧BC =弧BD ⑤ 弧AC =弧AD 中任意2个条件推出其他3个结论。
初三数学圆基础练习题及答案练习题一：直径和半径的关系1. 若一个圆的半径为5cm，求其直径的长度是多少？答案：直径的长度是2倍的半径长度，因此直径的长度为10cm。
2. 若一个圆的直径为12cm，求其半径的长度是多少？答案：半径的长度是直径长度的一半，因此半径的长度为6cm。
练习题二：圆的周长和面积计算3. 已知一个圆的半径为3cm，求其周长和面积。
答案：圆的周长公式为C = 2πr，其中r为半径。
将半径代入公式，可得C = 2π × 3 = 6π ≈ 18.85cm。
圆的面积公式为A = πr²，将半径代入公式，可得A = π × 3² = 9π ≈ 28.27cm²。
4. 已知一个圆的周长为10π cm，求其半径和面积。
答案：圆的周长公式为C = 2πr，已知周长为10π，因此10π = 2πr，可得r = 5。
圆的面积公式为A = πr²，将半径代入公式，可得A = π × 5² = 25π ≈ 78.54cm²。
练习题三：相交圆的交点个数5. 如果两个圆相交于两个点，这两个圆的关系是什么？答案：两个相交的圆是相交圆。
6. 如果两个圆相交于一个点，这两个圆的关系是什么？答案：两个相交于一个点的圆是切圆。
7. 如果两个圆不相交，也不包含对方，这两个圆的关系是什么？答案：两个不相交也不包含对方的圆是相离圆。
练习题四：判断圆心在坐标系中的位置8. 圆心坐标为(2, 3)，半径为4的圆在坐标系中处于哪个位置？答案：根据圆心坐标和半径，我们可以在坐标系中画出这个圆。
圆心(2, 3)代表圆心在横坐标2，纵坐标3处，半径为4表示从圆心向外延伸4个单位的长度。
因此该圆处于横坐标为2，纵坐标为3的位置，并以该点为中心向外扩展4个单位的长度。
练习题五：圆的切线和切点9. 若一条直线与圆相切，这条直线与圆的关系是什么？答案：一条与圆相切的直线称为圆的切线。
九年级上册圆题型归纳一、圆的基本概念相关（5题）题1：已知圆的半径为5cm，求圆的周长和面积。
解析：圆的周长公式为C = 2π r，面积公式为S=π r^2，其中r = 5cm。
周长C=2π×5 = 10π cm≈ 10×3.14=31.4cm面积S=π×5^2=25π cm^2≈25× 3.14 = 78.5cm^2题2：在圆O中，弦AB的长为8，圆心O到弦AB的距离为3，求圆O的半径。
解析：设圆O的半径为r，圆心O到弦AB的距离为d = 3，弦长AB=8。
根据垂径定理，半弦长、圆心到弦的距离与圆的半径构成直角三角形。
半弦长为(AB)/(2)=(8)/(2) = 4由勾股定理r^2=d^2+<=ft((AB)/(2))^2r=√(3^2)+4^{2}=√(9 + 16)=√(25)=5题3：已知圆O的直径为10，点A在圆O上，求∠ AOB的度数（其中O为圆心，B为圆上另一点且AB为圆的弦）。
解析：因为圆O的直径为10，则半径r = 5。
当AB为直径时，∠ AOB=180^∘；当AB为非直径的弦时，0^∘<∠AOB<180^∘。
由于题目没有更多关于AB弦的信息，所以仅能得出∠ AOB的取值范围是0^∘<∠ AOB≤slant180^∘题4：圆O中，弧AB所对的圆心角为60^∘，半径为6，求弧AB的长。
解析：弧长公式l=(nπ r)/(180)（n为圆心角度数，r为半径）已知n = 60^∘，r=6弧AB的长l=(60π×6)/(180)= 2π题5：判断：相等的圆心角所对的弧相等。
（）解析：错误。
在同圆或等圆中，相等的圆心角所对的弧相等。
如果没有同圆或等圆这个前提条件，即使圆心角相等，所对的弧长也不一定相等。
二、与圆的切线相关（5题）题1：直线l与圆O相切于点A，圆O的半径为3，若OA与直线l的夹角为30^∘，求圆心O到直线l的距离。
圆【知识点梳理】一、圆的概念集合形式的概念： 1、 圆可以看作是到定点的距离等于定长的点的集合； 2、圆的外部：可以看作是到定点的距离大于定长的点的集合； 3、圆的内部：可以看作是到定点的距离小于定长的点的集合 轨迹形式的概念：1、圆：到定点的距离等于定长的点的轨迹就是以定点为圆心，定长为半径的圆；（补充）2、垂直平分线：到线段两端距离相等的点的轨迹是这条线段的垂直平分线（也叫中垂线）； 3、角的平分线：到角两边距离相等的点的轨迹是这个角的平分线；4、到直线的距离相等的点的轨迹是：平行于这条直线且到这条直线的距离等于定长的两条直线；5、到两条平行线距离相等的点的轨迹是：平行于这两条平行线且到两条直线距离都相等的一条直线。
二、点与圆的位置关系1、点在圆内 ⇒ d r < ⇒ 点C 在圆内；2、点在圆上 ⇒ d r = ⇒ 点B 在圆上；3、点在圆外 ⇒ d r > ⇒ 点A 在圆外； 三、直线与圆的位置关系1、直线与圆相离 ⇒ d r > ⇒ 无交点；2、直线与圆相切 ⇒ d r = ⇒ 有一个交点；3、直线与圆相交 ⇒ d r < ⇒ 有两个交点； 四、圆与圆的位置关系外离（图1）⇒ 无交点 ⇒ d R r >+； 外切（图2）⇒ 有一个交点 ⇒ d R r =+； 相交（图3）⇒ 有两个交点 ⇒ R r d R r -<<+； 内切（图4）⇒ 有一个交点 ⇒ d R r =-； 内含（图5）⇒ 无交点 ⇒ d R r <-； 五、垂径定理垂径定理：垂直于弦的直径平分弦且平分弦所对的弧。
推论1：（1）平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧； （2）弦的垂直平分线经过圆心，并且平分弦所对的两条弧；（3）平分弦所对的一条弧的直径，垂直平分弦，并且平分弦所对的另一条弧以上共4个定理，简称2推3定理：此定理中共5个结论中，只要知道其中2个即可推出其它3个结论，rd d CBAO即：①AB 是直径 ②AB CD ⊥ ③CE DE = ④ 弧BC =弧BD ⑤ 弧AC =弧AD 中任意2个条件推出其他3个结论。
《圆》章节知识点复习和练习附参考答案一、圆的概念集合形式的概念： 1、 圆可以看作是到定点的距离等于定长的点的集合； 2、圆的外部：可以看作是到定点的距离大于定长的点的集合； 3、圆的内部：可以看作是到定点的距离小于定长的点的集合 轨迹形式的概念：1、圆：到定点的距离等于定长的点的轨迹就是以定点为圆心，定长为半径的圆；（补充）2、垂直平分线：到线段两端距离相等的点的轨迹是这条线段的垂直平分线（也叫中垂线）； 3、角的平分线：到角两边距离相等的点的轨迹是这个角的平分线；4、到直线的距离相等的点的轨迹是：平行于这条直线且到这条直线的距离等于定长的两条直线；5、到两条平行线距离相等的点的轨迹是：平行于这两条平行线且到两条直线距离都相等的一条直线。
二、点与圆的位置关系1、点在圆内 ⇒ d r < ⇒ 点C 在圆内；2、点在圆上 ⇒ d r = ⇒ 点B 在圆上；3、点在圆外 ⇒ d r > ⇒ 点A 在圆外； 三、直线与圆的位置关系1、直线与圆相离 ⇒ d r > ⇒ 无交点；2、直线与圆相切 ⇒ d r = ⇒ 有一个交点；3、直线与圆相交 ⇒ d r < ⇒ 有两个交点；四、圆与圆的位置关系外离（图1）⇒ 无交点 ⇒ d R r >+； 外切（图2）⇒ 有一个交点 ⇒ d R r =+； 相交（图3）⇒ 有两个交点 ⇒ R r d R r -<<+； 内切（图4）⇒ 有一个交点 ⇒ d R r =-； 内含（图5）⇒ 无交点 ⇒ d R r <-；A五、垂径定理垂径定理：垂直于弦的直径平分弦且平分弦所对的弧。
推论1：（1）平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧； （2）弦的垂直平分线经过圆心，并且平分弦所对的两条弧；（3）平分弦所对的一条弧的直径，垂直平分弦，并且平分弦所对的另一条弧以上共4个定理，简称2推3定理：此定理中共5个结论中，只要知道其中2个即可推出其它3个结论，即：①AB 是直径 ②AB CD ⊥ ③CE DE = ④ 弧BC =弧BD ⑤ 弧AC =弧AD中任意2个条件推出其他3个结论。
圆复习教案知识点：一、圆的概念1、圆——到定点的距离等于定长的点的集合2、圆的内部——可以看作是圆心的距离小于半径的点的集合3、圆的外部——可以看作是圆心的距离大于半径的点的集合4、等圆——不相同，相等的圆；同心圆——相同，不等的圆。
5、弧——圆上任意两点间的部分叫做，简称。
按与半圆的大小关系可分为：和6、等弧——7、弦——，经过的弦叫做直径，直径是的弦。
8、弦心距——圆心到直线的距离9、弓形——弧与所对的弦所组成得图形。
10、圆的内部——到圆心的距离小于半径的点的集合叫做圆的内部11、圆的外部——到圆心的距离大于半径的点的集合叫做圆的外部12、圆心角：13、圆周角：。
14、弦切角、圆内角、圆外角及性质：顶点在圆上，一边和圆相交，另一边和圆相切的角叫做弦切角。
等于二、确定圆的条件1．过已知两点的圆的圆心组成的图形是__________________________，_____________________确定一个圆．2.三角形的三个顶点确定一个圆，这个圆叫做三角形的_____________，它的圆心叫做三角形的图4_______，它是三角形_______________________的交点；这个三角形叫做圆的__________________- 3．三角形外心的位置：锐角三角形的外心在_______________________;直角三角形的外心是_________________________; 钝角三角形的外心在_________________________．三、与圆有关的位置关系 (一) 点与圆的位置关系1、 点和圆的位置关系有三种：（1）_____________；（2）____________；（3）____________2、 点在圆内 ⇒ d r < ⇒ 点C ；点在圆上 ⇒ d r = ⇒ 点B ； 点在圆外 ⇒ d r > ⇒ 点A ；㈡直线和圆的位置关系1．直线和圆的位置关系有三种：（1）_____________；（2）____________；（3）____________ 2．当直线和圆 _____________公共点时，叫做直线和圆相交，此时圆心到直线的距离_______半径； 当直线和圆 _____________公共点时，叫做直线和圆相切，此时圆心到直线的距离_______半径； 当直线和圆 _____________公共点时，叫做直线和圆相离，此时圆心到直线的距离_______半径；（3）、圆与圆的位置关系外离（图1）⇒ 交点 ⇒ d R r >+； 外切（图2）⇒ 有 交点 ⇒ d R r =+； 相交（图3）⇒ 有 交点 ⇒ R r d R r -<<+内切（图4）⇒ 有 交点 ⇒ d R r =-； 内含（图5）⇒ 交点 ⇒ d Rr <-；A3．切线的性质：圆的切线___________________ 如图可表述为：_____________________________PA O ⎫⇒⎬⎭e 是的切线或：PA 切⊙O 于点A ⇒____________________________4．判定直线为圆的切线：经过_____________，并且垂直于_______________的直线是圆的切线。
圆知识点一、圆旳概念集合形式旳概念： 1、圆可以看作是到定点旳距离等于定长旳点旳集合；2、圆旳外部：可以看作是到定点旳距离不小于定长旳点旳集合；3、圆旳内部：可以看作是到定点旳距离不不小于定长旳点旳集合轨迹形式旳概念：1、圆：到定点旳距离等于定长旳点旳轨迹就是以定点为圆心，定长为半径旳圆；（补充）2、垂直平分线：到线段两端距离相等旳点旳轨迹是这条线段旳垂直平分线（也叫中垂线）；3、角旳平分线：到角两边距离相等旳点旳轨迹是这个角旳平分线；4、到直线旳距离相等旳点旳轨迹是：平行于这条直线且到这条直线旳距离等于定长旳两条直线；5、到两条平行线距离相等旳点旳轨迹是：平行于这两条平行线且到两条直线距离都相等旳一条直线。
二、点与圆旳位置关系1、点在圆内⇒d r<⇒点C在圆内；2、点在圆上⇒d r=⇒点B在圆上；3、点在圆外⇒d r>⇒点A在圆外；三、直线与圆旳位置关系1、直线与圆相离⇒d r>⇒无交点；2、直线与圆相切⇒d r=⇒有一种交点；3、直线与圆相交⇒d r<⇒有两个交点；四、垂径定理垂径定理：垂直于弦旳直径平分弦且平分弦所对旳弧。
推论1：（1）平分弦（不是直径）旳直径垂直于弦，并且平分弦所对旳两条弧；（2）弦旳垂直平分线通过圆心，并且平分弦所对旳两条弧；（3）平分弦所对旳一条弧旳直径，垂直平分弦，并且平分弦所对旳另一条弧A以上共4个定理，简称2推3定理：此定理中共5个结论中，只要懂得其中2个即可推出其他3个结论，即：①AB 是直径 ②AB CD ⊥ ③CE DE = ④ 弧BC =弧BD ⑤ 弧AC =弧AD 中任意2个条件推出其他3个结论。
推论2：圆旳两条平行弦所夹旳弧相等。
即：在⊙O 中，∵AB ∥CD ∴弧AC =弧BD五、圆心角定理圆心角定理：同圆或等圆中，相等旳圆心角所对旳弦相等，所对旳弧相等，弦心距相等。
此定理也称1推3定理，即上述四个结论中， 只要懂得其中旳1个相等，则可以推出其他旳3个结论， 即：①AOB DOE ∠=∠；②AB DE =；③OC OF =；④ 弧BA =弧BD 六、圆周角定理1、圆周角定理：同弧所对旳圆周角等于它所对旳圆心旳角旳二分之一。
