当前位置：文档之家 › 第六讲(像差理论)资料

第六讲(像差理论)资料

  • 格式：ppt
  • 大小：592.50 KB
  • 文档页数：13

下载文档原格式

  / 13

合集下载

ch6__光学系统的像差理论

ch6__光学系统的像差理论

谱线的选择原则： ①对接收器最灵敏的谱线校正单色像差； ②对接收器所接收波段范围两边附近的谱线校正色差； ③使接收器、光源、光学系统的材料的光谱特性一致。 不同的光学系统在计算和校正像差时，谱线的选择也各有 特点。
4
二、轴上点球差
1. 球差的定义与表示方法：
轴上发出的不同入射高度的光线经光学系统后，交于光轴的不 同位置，相对于近轴像点(理想像点）有不同程度的偏离，这
6
3. 球差的校正


单透镜自身不能校正球差。 正透镜产生负球差，负透镜产生正球差，所以，可以采用 正负透镜组合校正球差。 通常只能使边缘孔径的球差为零。
7

对于只含初级球差和二级球差的系统，当边缘带球差校正 为0时，在0.707带有最大剩余球差。

对于单个折射面，不存在球差的几个特殊点：
1）物点和像点都位于定点： L＝ L'＝0，β=1 2）物点和像点都位于球面的曲率中心：
第六章 像差理论
主讲人：仝卫国 华北电力大学 自动化系
1
主要内容
实际光学系统与理想光学系统之间存在差异，这种 差异被称作像差。
一、概述
二、轴上点球差 三、正弦差和慧差 四、像散和场曲 五、畸变
六、色差
2
一、概述
1. 基本概念
（1）像差：光学系统实际成像与理想像之间的差异。 （2）像差产生的原因： ①不同孔径的入射光线，成像位置不同； ②不同视场的入射光线，成像倍率不同； ③子午面和弧矢面光束成像的性质不尽相同； ④不同色光成像的大小和位置不同。
畸变的校正： 畸变校正困难，需同时满足正弦条件和正切条件； 对于β＝-1对称光学系统，畸变可自动校正； 校正边缘带畸变，此时0.775 ym处有最大畸变。
第六章像差理论

第六章像差理论

-ω f
照相系统视场角
1
第六章 像差理论
• §6-1 概述 • §6-2 轴上点的球差 • §6-3 彗差 • §6-4 细光束像散、场曲和畸变 • §6-5 色差 • §6-6 波像差
2
§6-1 概述
• 像差定义：实际像与理想像之间的差异。 • 几何像差的分类:
– 单色像差：光学系统对单色光成像时所产生的 像差。球差、彗差、像散、场曲、畸变
q yz yz y 100%
y y 20
一般畸变随视场增大呈单调变化，畸变为负时，实际像 高大于理想像高，放大率随视场增大而减小，得到桶形 畸变。 相反当畸变为正时，实际像高大于理想像高，放大率随 视场增大而增大，产生枕形畸变。 畸变是主光线的像差，不影响成像的清晰度，但会使像 产生变形。
为此作一B和球心C的辅助轴，则B点是辅助光轴上的一点，则三
条光线a、b、z对辅助轴相当于三条不同孔径角的轴上入射光线，
则它们在辅助光轴上存在球差且不相等。三条光线不能交于一点，
这样使得出射光线a′、b′不再关于主光轴z′对称。
10
则上下光线对的交点到主光线的垂直距离称为子午彗差。
如用个光线在像面上的交点值来表示，则子午彗差为：
11
彗差是轴外点以宽光束成像的一种失对称的垂轴像差，它随 视场的增大而增大，随孔径的增大而增大。彗差使像点变形 为一失对称的弥散斑。
主光线偏到弥散斑一边，在主光线与 像面交点处，积聚的能量最多，因此 最亮。在主光线以外能量逐渐散开， 慢慢变暗，因此弥散斑形成一个以主 光线与像面交点为顶点的锥形斑，其 形似彗星，因此称为彗差。
由于实际中的像散总是存在的，因此匹兹伐场曲总是附加在 子午场曲和弧矢场曲中。
场曲的存在使得实际像面是弯曲的，用垂轴像平面接收平面 物体的成像将无法获得整个视场的清晰，或是视场中心清晰 边缘模糊，或是边缘清晰中心模糊。
第六章像差理论

第六章像差理论


轴外点发出充满入瞳的一束光，这束光以通过入瞳中心的
主光线为对称中心，其中包含主光线和光轴的平面称为子
午面。过主光线且垂直于子午面的平面为弧矢面。显然子
午面是光束的对称面。
9
对子午面的情况：主光线Z和一对上下光线a、b，折射前， 上下光线与主光线对称，折射后，上下光线对不再对称于主 光线，它们的交点偏离了主光线。
14
弧矢 子午像点和弧矢像点 像面 都位于主光线上，通
子午 常可将子午像距和弧 像面 矢像距投影到光轴上，
像平 则像散表示为：
面
主光 线
xts lt ls
15
像散的存在使轴外物点的成像在子午方向和弧矢方向各 有不同的聚焦位置。子午方向的光线聚焦成垂直于子午 面的短焦线T′，而弧矢方向的光线聚焦成子午面内的短 焦线S′，两焦线之间是一系列由线到椭圆到圆再到椭圆 再到线的弥散斑变化。 因此，接收器在像方找不到同时能使各个方向的线条都 清晰的像面位置。
xt lt l

xs

ls

l
有像散必然有场曲，但如果没有像散存在，像面弯曲现
象也会因球面光学系统的本身特性而存在。
球面 物体
折射 球面
理想像 平面
17
根据物像同向移动的原则，B的像点进一步偏离理想像平面 P′，这种偏离随视场的大小而变化，使得垂直于光轴的平面 物体经球面成像后变得 弯曲，这种弯曲还没有考虑像散的 影响，把像散为0时的像面弯曲称为匹兹伐场曲。
Lm A1hm2 A2hm4 0 A1 A2hm2
L
h

2A1h 4A2h3
0
h 0.707hm
此时，在0.707孔径处的光线具有最大剩余球差。校正球
第六章像差理论

第六章像差理论


为：
W n Um LdU 2 20
波像差越小，系统的成像质量越好。瑞利判断认为：当光
学系统的最大波像差小于1/4波长时，其成像是完善的。
色差也可以用波色差来描述，对轴上点，λ1光λ2光在出瞳 处两波面之间的光程差称为波色差。对目视光学系统其计
算公式为：
n
WFC WF WC D d dn 1
球差的存在使轴上点成像不再清晰。 因此，球差的形成是折射球面系统成像的一种必然现象， 它是轴上物点以单色光成像时的唯一像差。
7
球差对于球面系统是不可避免的，一般正透镜产生负球差， 负透镜产生正球差，为校正球差常采用正负透镜的组合，但 也只能对个别孔径角校正球差。 在系统孔径角不太大的情况下，常对最大孔径角Um（或孔径 高度hm）校正球差，使:
因此以白光成像的物体即使在近轴区也不能获得白光的 清晰像。 一般正透镜产生负色差，负透镜产生正色差，因此校正 色差须用正负透镜组合。
25
600 nm
510 nm
正透镜的近轴 位置色差曲线
二、倍率色差
焦点位 置/mm
正负透镜胶 合后的位置 色差曲线
焦点位 置/mm
是指F光与C光的主光线的像点高度差，在参考像面 （常取D光）上度量。
27
§6-6 波像差
对高像质要求的光学系统，还需研究光波波面经光学系 统后的变形情况来评价系统的成像质量。
从物点发出的波面 经理想光学系统后， 其出射波面应该是 球面，但由于实际 光学系统存在像差， 实际波面与理想波 面在出瞳处相切时， 两波面间的光程差 就是波像差。
28
对轴上点，单色光的波像差由球差引起的，两者的关系
KT

1 2
Ya
几何光学-第六章-像差理论

几何光学-第六章-像差理论

2、通常情况下，不能以一定宽度的光束对一定大小的物体成完善像。
成像特点： 物点——弥散斑
计算：实际光线计算 追迹成像的位置、大小与理想像的偏离——像差
小结：几何像差
像差类型 轴 单色 球差 上 色球差 物 复色 位置（轴向）色差 点 轴 外 单色 场曲 物 畸变 点 复色 倍率色差 影响因素 孔径 孔径、波长 在高斯像面上 接收到的像 单色弥散圆斑 彩色弥散圆斑
1 1 1
2 2 2
1
2
例：远轴物点发出的同心细光束，经过有像散的光学系统， 同心性会受到破坏，垂直于主轴的光屏在沿轴不同位置时， 所接收到的成像光束截面形状会发生很大的变化。
像散差
子午 焦线
明晰 圆
弧矢 焦线
3、像散特征：一个物点有子午焦线和弧矢焦线同时出现。
物点离轴越远，像散差越显著。
5、像散的物理意义
波长 孔径、视场 视场
大物面 波长
彗差（正弦差） 细光束像散
形状复杂的 弥散斑
作业
1、简述球差的产生机制、表现形式和消除方法。 2、简述慧差的形成机理和影响。 3、简述像散的机制、特征和影响。 4、简述场曲的形成机制和影响。 5、简述畸变的形成机制和影响。 6、简述位置色差及倍率色差的形成机制和影响。
b1 c1
★ 波面的中心光线： b
F 2
2
F 2 F1
a1
b2
a2
a3 b3
c2
c3
F1
F1
F2
F 2
F1
——光束在相互垂直的两截面内， 各有不同的曲率中心。 ★ 焦线：光束曲率中心的轨迹 两条相互垂直的短线 F F F 和 F F F 。 ★ 像散差：沿中心光线上两焦线之间的距离 F F 。
6-像差

6-像差

-KT’ Bb’ Bz’
B0’
Ba’
-ya’
A p a z b B
-XT’
、彗差
• 总结： • 彗差是在轴外成像时产生的一种像差。 （如：从光轴外的某一点向镜头发出一束平行光线，经光 学系统后，在像平面上并不是成一个点的像，而是形成不 对称的弥散光斑，这种弥散光斑的形状象彗星，从中心到 边缘拖着一个由细到粗的尾巴，首端明亮、清晰，尾端宽 大、暗淡、模糊。这种轴外光束引起的像差就称为彗差。） • 彗差的大小既与孔径（光圈）有关，也与视场有关。适当 适当 采用较小的光圈来减少彗差对成像的影响。 采用较小的光圈来减少彗差对成像的影响。
h hm
h A1 ( )2 hm
1
0.85 0.707 0.5 0.3
A2 (
h 4 ) hm A1 ( h 2 ) hm
( h hm )2
1
0.5
-0.10
0
0.10
δL′
-0.10
0
δL′
10
轴上点球差
球差引起的模糊是与光圈的大小有关的。小光圈时， 球差引起的模糊是与光圈的大小有关的。小光圈时，由 于光阑挡去了远轴光线，弥散圆的直径就小， 于光阑挡去了远轴光线，弥散圆的直径就小，图像就会 清晰。大光圈时弥散圆直径就大，图像就会比较模糊。 清晰。大光圈时弥散圆直径就大，图像就会比较模糊。
′ ′ Lk = Lk −1 − d k −1 ′ ′ Uk = Uk −1 n′ = n′−1 k k
cos I′ − U ′ 2 sin U ′
6
sin I ′ ′ = r( 1 + L ) ′ sin U
sin U ′
校对公式： 校对公式： L ′ = EO cos( I ′ − U ′ ) = L sin U ⋅
工程光学讲稿(像差)

工程光学讲稿(像差)


§6－2 轴上点的球差 －
一、 球差定义及表示方法
1、轴向球差 由实际光线的光路计算公式知，当物距L为定值时，像距L 与入射高 由实际光线的光路计算公式知，当物距L为定值时，像距L’与入射高 及孔径角U有关，随着孔径角的不同，像距L 是变化的 即如图所示： 是变化的， 度h1及孔径角U有关，随着孔径角的不同，像距L‘是变化的，即如图所示： 轴上点A点发出的光束，对于光轴附近的光用近轴光路计算公式， 轴上点A点发出的光束，对于光轴附近的光用近轴光路计算公式，像点为 A0’（看作高斯像点），对于实际光线采用实际光计算公式，成像于A’1（实 ），对于实际光线采用实际光计算公式 （看作高斯像点），对于实际光线采用实际光计算公式，成像于A 际像）。 际像）。
球差是孔径的偶次方函数，因此 校正球差只能使某带的球差为零。 球差是孔径的偶次方函数，因此, 校正球差只能使某带的球差为零。如 果通过改变结构参数, 使初级球差系数A 和高级球差系数A 符号相反， 果通过改变结构参数 使初级球差系数 1和高级球差系数 2符号相反，并具 有一定比例，使某带的初级球差和高级球差大小相等，符号相反， 有一定比例，使某带的初级球差和高级球差大小相等，符号相反，则该带的 球差为零。在实际设计光学系统时，常通过使初级球差与高级球差相补偿， 球差为零。在实际设计光学系统时，常通过使初级球差与高级球差相补偿， 将边缘带的球差校正到零， 将边缘带的球差校正到零，即
4 δ L'0 .707 = − A 2 h m / 4
球差曲线图
从上分析知球差与孔径密切相关， 越大， 越大 越大， 从上分析知球差与孔径密切相关，U 越大，δL‘越大， 所以球差必须校 正。 对于光学系统而言，透镜是最为基本的元件： 对于光学系统而言，透镜是最为基本的元件： 正透镜――产生负球差； 产生负球差； 正透镜 产生负球差 负透镜――产生正球差。 产生正球差。 负透镜 产生正球差 这是由透镜本身结构特性决定的，所以，单个透镜不能校正球差。但若 这是由透镜本身结构特性决定的，所以，单个透镜不能校正球差。 是正负透镜组合，就可以实现球差的校正。 是正负透镜组合，就可以实现球差的校正。 所谓的消球差一般只是能使某一孔径带的球差为0， 所谓的消球差一般只是能使某一孔径带的球差为 ，而不能使各个孔径 带全部为0，一般对边缘光孔径校正球差，而此时一般在有最大的剩余球差 带全部为 ，一般对边缘光孔径校正球差， 0.707，且值为边缘带高级球差－1／4。 ，且值为边缘带高级球差－ ／ 。 3、单个折射球面得齐明点 、 对于单个折射球向面，有几个特殊的物点位置， 对于单个折射球向面，有几个特殊的物点位置，不管球面的曲率半径 如何，均不产生球差。 如何，均不产生球差。 (1) L＝0，此时亦有 ＝0，β＝1。即物点和像点均位于球面顶点时，不产 ＝ ，此时亦有L‘＝ ， ＝ 。即物点和像点均位于球面顶点时， 生球差。 生球差。
工程光学第6章 像差概论

工程光学第6章 像差概论


2、校正
选择透镜材料，正负透镜组合 选择透镜材料，
33
二、倍率色差
垂轴像差 目视光学系统： 目视光学系统：
′ ′ ′ YFC = YF YC
yC’ C D F A yD’ YF’ YD’ YC’ 34 yF’ YFC’
′ y ′ = y ′ yC FC F
大视场尤为严 重，必须校正
-y B
25
畸变
由于畸变的存在，物方的一条直线在像方就变成了一条曲 由于畸变的存在， 线，造成像的失真。 造成像的失真。 畸变可分为枕型畸变和桶型畸变两种。造成畸变的原因是 畸变可分为枕型畸变和桶型畸变两种。 镜头像场中央区的垂轴放大率与边缘区的垂轴放大率不一 镜头像场中央区的垂轴放大率与边缘区的垂轴放大率不一 致。如下图所示，如果边缘放大率大于中央放大率就产生 如下图所示， 枕型畸变，反之，则产生桶型畸变。 枕型畸变，反之，则产生桶型畸变。
共轴球面系统：单透镜不能校球差，需正 共轴球面系统：单透镜不能校球差， 负透镜组合。 负透镜组合。 齐明透镜 减小光阑直径
8
§6.2 彗差
子午面：光轴和主光线决定的面； 子午面：光轴和主光线决定的面； 弧矢面：过主光线且与子午面垂直。 弧矢面：过主光线且与子午面垂直。
9
一、光学现象及定量表示： 光学现象及定量表示： 1、光学现象
轴外物点在理想像面上形成的像点如同彗星状的光斑， 轴外物点在理想像面上形成的像点如同彗星状的光斑， 在理想像面上形成的像点如同彗星状的光斑 靠近主光线的细光束交于主光线形成一亮点， 靠近主光线的细光束交于主光线形成一亮点，而远离主光线 的不同孔径的光线束形成的像点是远离主光线的不同圆环。 的不同孔径的光线束形成的像点是远离主光线的不同圆环。
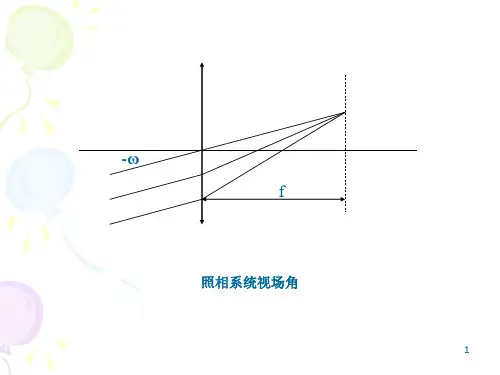
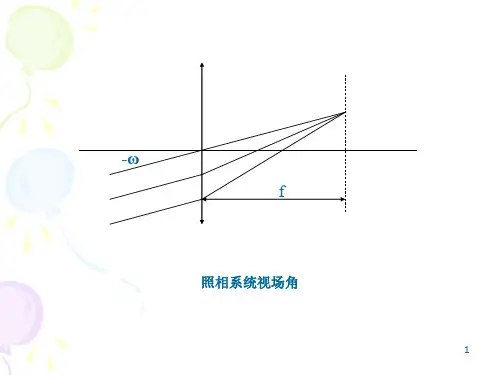
工程光学第六章像差理论解读

工程光学第六章像差理论解读


LF 0.707h LD 0.707h LC 0.707h LD 0.707h LFCD
20
二级 光谱
并称两种波长的球差之差称为 色球差，表示为：
LF LC LFC
lF LC lC LF lFC LFC
为此作一B和球心C的辅助轴，则B点是辅助光轴上的一点，则三 条光线a、b、z对辅助轴相当于三条不同孔径角的轴上入射光线， 则它们在辅助光轴上存在球差且不相等。三条光线不能交于一点， 这样使得出射光线a′、b′不再关于主光轴z′对称。 8
则上下光线对的交点到主光线的垂直距离称为子午彗差。 如用个光线在像面上的交点值来表示，则子午彗差为： 1 KT Ya Yb Yz 2 对弧矢面的情况：弧矢光束中的前后光线c、d入射前对称 于主光线，由于弧矢光线对称子午面，它们折射后仍然交 于子午面内的同一点。但它们的折射情况与主光线不同， 因此并没有交于主光线上。这样出射光线对不再关于主光 线对称，其交点到主光线的垂直距离称为弧矢彗差。
B点的 理想 像点
B点的 实际 像点
16
可见，轴外点B的实际像点偏离了理想像点，产生畸变； 而轴上点A的实际像点与理想像点重合，因此轴上点不存 在畸变。 畸变的度量有： ①绝对畸变：即主光线像点的高度与理想像点的高度之差。
y y z y
z
实际 像高
理想 像高
②相对畸变：即像对于像高的畸变，常用百分比表示。
xt lt l ls l xs
有像散必然有场曲，但如果没有像散存在，像面弯曲现 象也会因球面光学系统的本身特性而存在。
球面 物体
折射 球面
理想像 平面14源自根据物像同向移动的原则，B的像点进一步偏离理想像平面 P′，这种偏离随视场的大小而变化，使得垂直于光轴的平面 物体经球面成像后变得 弯曲，这种弯曲还没有考虑像散的 影响，把像散为0时的像面弯曲称为匹兹伐场曲。
几何光学 第六章 像差理论

几何光学 第六章 像差理论

不产生球差的共轭点位置。 ★ 物、像均位于球面顶点： L 0, 1 L0 ★ 物、像位于球面的曲率中心： sin I sin I 0
I I 0
★ 物、像位置： I U
L L r
L (n n)r / n L (n n)r / n
波长 孔径、视场 视场
大物面 波长
彗差（正弦差） 细光束像散
形状复杂的 弥散斑
作业
1、简述球差的产生机制、表现形式和消除方法。 2、简述慧差的形成机理和影响。 3、简述像散的机制、特征和影响。 4、简述场曲的形成机制和影响。 5、简述畸变的形成机制和影响。 6、简述位置色差及倍率色差的形成机制和影响。
4、消除球差的方法
（1）加光阑，选择近轴光束； （2）正、负透镜组合进行校正； （3）采用非球面透镜。
5、小结
轴上物点 1）像点位置的轴向偏离：球差
宽光束(不同孔径角) 2）高斯像面上的弥散圆斑：垂轴球差
**问题：
（1）轴外物点是否有类似球差的现象？ （2）轴外物点发出的宽光束，其对称轴是什么？
三、彗形像差（Coma，Comatic Aberration）
3、物理意义
★ 彗差：轴外像差（孔径、视场的函数）
——大视场（稍远轴物）宽光束成像的不对称。 ★ 正弦差：小视场（近轴物）宽光束成像的不对称。
4、影响：破坏轴外视场成像的清晰度。 **问题：
宽光束的原因造成了球差和彗差，如取无限细光束， 是否就可以避免像差？
四、像散（Astigmatism）
1、与主轴成较大倾斜角的同心光束： 即使是细光束，出射光束也难以保持仍为同心。 2、基本概念：非球面波与象散光束 垂直于波面元，彼此既不相平行也不交于一点的 非对称性光束，称为像散光束。
工程光学第六章像差理论重点讲解

工程光学第六章像差理论重点讲解


校对公式：
h lu lu nuy nuy J
最后可计算出像点位置和系统各基点位置。
焦点位置及焦距计算：l1 , u1 0
f ' h1 / u'k
2、轴外物点近轴光线光路计算（第二近轴光线）
仍用近轴光线光路计算公式和校对公式,所有量均注以下标z.
已知：物方物位、入瞳位置和物高，即 l, lz , uz 。 求解：像方物位、出瞳位置和像高，即 l, lz , uz 。
i
l
r
r
u（当l1
时， u1
0，i1
h1
/
r1）
i' n i
n'
u' u i i'
l' r(1 i' )
u'
l' n'lr
n'l n(l r)
第二节 光线的光路计算
对于有k个面的折射系统，需利用根据过渡公式：
过渡公式：
lk lk1 dk 1 uk uk 1 nk nk 1
对于小视场的光学系统，例如望远物镜和显微物镜等，只 要求校正与孔径有关的像差，所以只需计算上述第一种光线。 对大孔径、大视场的光学系统，如照相物镜等，要求校正所 有像差，所以需要计算上述三种光线。
第二节 光线的光路计算
由已知条件：
光学系统的结构参数（r,d,n）
物体的位置和大小 入瞳的位置和大小
解决问题：
第一节 概述
像差校正：
在实际光学系统中，各种像差是同时存在的，像差 影响光学系统成像的清晰度、相似性和色彩逼真度等 ，就降低了成像质量。故像差的大小反映了光学系统 质量的优劣。
除了平面镜成像以外，没有像差的光学系统是不 存在的。完全消除像、色差是不可能的，针对光学系 统的不同用途，只要把像、色差降低在某范围内，使 光接收器不能分辨，或者说这种差别只要能骗过光接 收器，就可以认为是理想的。

第六章_像差理论总结


二、球差（Spherical Aberration） 1、定义
A
高斯 像面
)U
m
Um
(
5 4
3 2 1
Lm
A0 T
L l
Lm
l
（轴向）球差：轴上物点发出的同心、宽光 束经光学系统后, 不再是同心光束。对于不 同孔径角（入射高度）的光线，将会聚在光 轴不同的位置，相对于理想像点有不同程度 的偏离。
F 1
F 1
——相互垂直的两截面内的 光束各有自己的曲率中心。 ★ 焦线：光束曲率中心的轨迹 F F F F F F 两条相互垂直的短线 和 。 ★ 像散差：两焦线之间的距离 F F 。
1 1 1
2 2 2
1 2
例：远轴物点发出的同心细光束，经过有象散的光学系统， 同心性会受到破坏，垂直于主轴的光屏在沿轴不同位置时， 所接收到的成像光束截面形状会发生很大的变化。
1、与主轴成较大倾斜角的同心光束： 即使是细光束，出射光束也难以保持仍 为同心。 2、基本概念：非球面波与象散光束 垂直于波面元，彼此既不相平行也不 交于一点的非对称性光束，称为象散光 束。
b2 F2 F1 ★ 波面中心 b2 的法线：
b1 c1
a1
b2
b3
c2
c3
F2
a2
a3
F2
F2
F1
相似性；
1、理想成像的条件
（4）像的各部分应保持具有与物同样的彩 色。 像不出现不正确的彩色，并发生像模 糊。
★ 像差（Aberrations）：实际像与理想像之 间的差异现象。
2、几何像差
（1）单色像差（Monochromatic Aberrations） a. 球面像差； 宽光束引起的 b. 彗形像差； c. 像散； d. 像场弯曲； e. 畸变

像差理论


70
-0.85
-0.68
在保证光焦度不变的情况下，可以通过增加透镜的 折射率来增大球面的曲率半径，因为选择高折射率 的材料有利于减小球差。
第一节 轴上点球差
1 2 在材料选定后，要保证透镜的光焦度， 2 也随之变 必须为定值。保持该定值，如果改变 1 ， 化，使得透镜的形状发生改变。或者说，同一光焦度 的透镜可以有不同的形状。这种保持焦距不变而改变 透镜形状的做法，称为透镜弯曲。 以物体在无穷远为例，图6-9给出了透镜不同形状下的 球差变化曲线。可以看出，无论是正透镜还是负透镜， 都存在一个最小球差的形状，称为透镜最优形式。
K S ' Ya 'YZ ' Yb 'YZ '
（6-8）
式中各符号的意义与式（6-7）类似。
第二节 慧差
慧差是轴外物点以宽光束成像的一种失对称的垂轴像差，除了 子午和弧矢两个截面外，其它截面也都有不同形式的失对称。 如果入瞳为一圆环，轴外点进入系统的光线就是以物点为顶点、 以主光线为对称中心的圆锥面光束，不同的孔径对应于不同大 小的光锥。此光束经系统后，由于存在慧差，不复为对称于主 光线的圆锥面光束，也不再会聚于一点，它与高斯像面相交成 一封闭的复杂曲线，曲线的形状对称于子午面。光锥角度越大， 失对称的程度也越大。整个入瞳可以看成由无数个大小不等的 圆环组成，由轴外物点发出的所有通过这些圆环的圆锥面光束， 经系统后在高斯像面上截得大小不等、形状不一、并在垂轴方 向上相互错开的封闭曲线，最终叠加成一个形状复杂、对称于 子午面的弥散斑。
第二节 慧差
再看弧矢面的情况，图6-13所示的是物点B以弧矢光线 成像的立体图，弧矢面内有一对前、后光线c、d，它 们对称于主光线，因此也对称于子午面，因此，成像 后的交点也必然在子午面内。这对光线在入射前虽然 对称于主光线，但是它们的折射情况与主光线不同。

应用光学第六章


0.707
0.707
0.707
L'
L'
L'
图6-3 球差曲线
图6-4球差校正不足和球差过校正
第一节 轴上点球差
由于共轴球面系统具有对称性，孔径角为U的整个圆 形光锥面上的光线都具有相同的球差而交于同一点， 延伸至理想像面上，将形成一个圆，其半径 T ' 称为 垂轴球差，如图6-2所示，垂轴球差与轴向球差之间关 系为 (6-2) T ' L' tgU'
C A,A' -U
图6-5 物点位于球心处
第一节 轴上点球差
2.物点位于球面顶点，即 L 0 。此时不论U角如 何，所有入射光线射向此点，经折射后也都将经此点 离开，即像点也位于顶点， ' 0 ，如图（6-6）所示 L n n' 3.物点位于 L n r 处。此时对于任意孔径角，有 I ' U 或 I U ' ，根据式（2-1）（2-4）计算得出， 像点将位于 L ' n n ' r 处，与孔径角无关。如图（6-7） n' 所示。 -I'
n U A O A'
) n'( >n
I A'
A
-U C n n' <n
( )
图6-6 物点位于顶点处
图6-7 物点位于齐明点处
第一节 轴上点球差
上述不产生球差的物点位置，称为齐明点，结合1和3 的两个齐明点位置可以构成无球差的齐明透镜。如图 6-8所示为正、负齐明透镜。
A'
A,C C2 1
C2
C1 A ,
图6-10 双胶合透镜合双分离透镜

像差理论

，并不会聚一点，相对于主光线而是呈彗星状 图形的一种失对称的像差
彗差通常用子午面上和弧矢面上对称于主光 线的各对光线，经系统后的交点相对于主光线 的偏离来度量，分别称为子午彗差和弧矢彗差
子午彗差指对子午光线度量的彗差
子午光线对交点离开主光线的垂直距离KT’用 来表示此光线对交点偏离主光线的程度
2020/7/4
如果将正负透镜组合起来，能否使球差得到校正？ 这种组合光组被称为消球差光组
2020/7/4
哈工大光电测控技术与装备研究所
8
光学系统中对某一给定孔径的光线
达到δL’ =0的系统称为消球差系统
单透镜的球差与焦距、相 对孔径、透镜的形状及折 射率有关。
对于给定孔径焦距和折射率 的透镜，通过改变其形状可 使球差达到最小。
-Umax A
-U
2020/7/4
hmax
h
A’
△y’
L’
δL’
哈工大光电测控技术与装备研l’ 究所
5
球差是轴上点唯一的单色像差
可在沿轴方向和垂轴方向来度量分别称为轴向球 差和垂轴球差。
轴向球差又称为纵向球差
它是沿光轴方向度量的球差，用符号δL’ 表示
垂轴球差是过近轴光线像点A’的垂轴平面内度
量的球差。用符号δT’ 表示
2020/7/4
哈工大光电测控技术与装备研究所
（2）弧矢场曲
用细光束弧矢场曲和宽光束弧矢场曲 来度量
2020/7/4
哈工大光电测控技术与装备研究所
32
弧矢细光束焦点相对于理想像面的偏离
称为细光束弧矢场曲，用符号xs’表示
xs' ls' l'
主光线 Z O1 O2
lt’

像差理论_精品文档

像差理论1、6像差理论1、6。

1非理想光学系统和像差所谓理想光学系统，就是能够对任意大的空间以任意宽的光束成完善像的光学系统。

一个物体发出的光经过理想光学系统后将产生一个清晰的、与物貌完全相似的像。

理想光学系统具有下述性质：①光学系统物方一个点（物点）对应像方一个点（像点），这两个点称为共轭点。

②物方每条直线对应像方的一条直线，称共轭线；物方每个平面对应像方的一个平面，称为共轭面。

③主光轴上任一点的共轭点仍在主光轴上。

任何垂直于主光轴的平面，其共轭面仍与主光轴垂直。

④对垂直于主光轴的共轭平面，横向放大率为常量。

实际中不存在真正的理想光学系统，平面反射镜是个例外，但其横向放大率恒为1。

虽然在近轴区域共轴球面系统可近似地满足理想光学系统的要求，但是实际光学系统成像都是需要一定大小的成像空间以及光束孔径的，同时还由于成像光束多是由不同颜色的光组成（同一种介质的折射率随波长而异）。

所以实际的光学系统成像都不是理想的，存在着一系列缺陷，这就是像差。

像差是指在光学系统中由透镜材料的特性或折射率（或反射）表面的集合形状引起实际像与理想像的偏差。

用高斯公式、牛顿公式或近轴光线追迹计算得到的像的位置和大小可以作为理想像的位置和大小，而实际光线追迹计算得到的像的位置和大小相对于理想像的偏差就可以作为像差的量度。

描述像差可以用几何像差和波像差（又叫光程差），本设计主要使用几何像差。

1、6。

2几何像差[2]几何像差主要有七种：其中单色像差有五种，即球差、彗差、像散、场曲和畸变；复色光成像像差有轴向色差和垂轴色差两种。

1、6。

2、1球差如图1-8表示的是轴上有限远同一物点发出的不同孔径的光线通过系统后不再交于一点，成像不理想。

为了表示这些对称光线在光轴方向上的离散程度，我''''A1、0、A0A0。

85表示，称为球差。

球们用不同孔径的光线对理想像点A0'的距离A0差是球面像差的简称，是由光学系统的口径而引起的，是光学系统口径的函数。

ch6__光学系统的像差理论解读


性质与校正：
细光束场曲是视场的函数，视场为0时场曲也为0；
校正场曲时，主要考虑细光束，对于大孔径大视场系统，有 时也要考虑宽光束； 对边缘视场校正场曲，0.707带剩余为-1/4。 注意：对于轴外宽光束，也可用轴外子午球差和轴外弧矢球 差来描述。
15
（2）像散
轴外光束的子午像点与弧矢像点不重和，两者分开的轴向距 离称为像散。
13
3. 像散和场曲：
对于轴外细光束，不存在由于光束的不对称性引起的慧差， 但细光束的场曲和像散依然存在。
（1）场曲 垂直于光轴的平面物体只有在近轴区域才近似成像为一个 平面，对较大物面，像面不是平面而是曲面，如下图所示：
14
不同视场，子午像面和弧矢像面对于理想像面的偏离用 x't和x's表示，分别称为子午场曲和弧矢场曲。
20

以数值表示，应首先确定对哪两种色光来考虑色差，对目 视光学系统是对红光（C光）和蓝光（F光）消色差。
对于近轴区： 位置色差仅与孔径有关，故其级数展开式为：
2 4 A0 Ah LFC A h 1 1 2 1
位置色差的校正： 不同孔径的光线有不同的色差值，一般对0.707带的光线校 正色差； 正透镜有负色差，负透镜有正色差，故单透镜不能校正色差。
6
3. 球差的校正


单透镜自身不能校正球差。 正透镜产生负球差，负透镜产生正球差，所以，可以采用 正负透镜组合校正球差。 通常只能使边缘孔径的球差为零。
7

对于只含初级球差和二级球差的系统，当边缘带球差校正 为0时，在0.707带有最大剩余球差。

对于单个折射面，不存在球差的几个特殊点：
1）物点和像点都位于定点： L＝ L'＝0，β=1 2）物点和像点都位于球面的曲率中心：
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

这种组合光组被称为消球差光组
2018/10/14
哈工大光电测控技术与装备研究所
8
光学系统中对某一给定孔径的光线 达到δ L’ =0的系统称为消球差系统
单透镜的球差与焦距、相 对孔径、透镜的形状及折 射率有关。
h/hmax
0.85 0.7 0.5 0.3 0.2
对于给定孔径焦距和折射率 的透镜，通过改变其形状可 使球差达到最小。
t
A
2018/10/14
2018/10/14
哈工大光电测控技术与装备研究所
2
像差的大小反映了光学系统质量的优劣
几何像差主要有七种：
单色光像差有五种： 复色光像差有两种：
球差 轴向像差(位置色差) 彗差(正弦差) 垂轴像差(倍率色差) 像散 场曲 畸变
2018/10/14
哈工大光电测控技术与装备研究所
3
在实际光学系统中，各种像 差是同时存在的。
13
2、彗差
了解成像光束光线的全貌： 子午平面和弧矢平面
由轴外物点和光轴所确定的平面称为子午平面 子午平面内的光束称子午光束 过主光线且与子午平面垂直的平面称为弧矢平面 弧矢平面内的光束称弧矢光束
2018/10/14
哈工大光电测控技术与装备研究所
14
彗差是轴外物点发出宽光束通过光学系统后 ，并不会聚一点，相对于主光线而是呈彗星状 图形的一种失对称的像差 彗差通常用子午面上和弧矢面上对称于主光 线的各对光线，经系统后的交点相对于主光线 的偏离来度量，分别称为子午彗差和弧矢彗差
这些像差影响光学系统成像的清晰 度、相似性和色彩逼真度等，降低 了成像质量。
1、球差：
球面像差的简称
2018/10/14
哈工大光电测控技术与装备研究所
4
对应孔径角Umax入射光线的高度hmax被称为全孔径（边 光球差） 对应孔径角U入射光线的高度h 若h/hmax=0.7，则称为0.7孔径或0.7带光（带光球差）
δT’= δL’ tanU’
2018/10/14
哈工大光电测控技术与装备研究所
6
对于单透镜来说，U越大则球差值越大
单透镜自身不能校正球差
入瞳 像面
a Z b
Ya’ YZ’
Yb’
2018/10/14
哈工大光电测控技术与装备研究所
7
单正透镜会产生负值球差，也被称为球差校正 不足或欠校正 单负透镜会产生正值球差，也被称为球差校正 过头或过校正 如果将正负透镜组合起来，能否使球差得到校正？
哈工大光电测控’失去了对称性
在折射前主光线是光束的轴线， 折射后主光线就不再是光束轴线
不同孔径的光线在像平面上形 成半径不同的相互错开的圆斑
C E A B
2018/10/14
By’ Ay’ F
O
D 哈工大光电测控技术与装备研究所
17
距离主光线向点越远，形成 的圆斑直径越大
第六讲 像差理论
2018/10/14
哈工大光电测控技术与装备研究所
1
§8-1 概
述
实际光学系统都有一定大小的相对孔径合 视场，远远超出近轴区所限定的范围。 与近轴区成像比较必然在成像位置和像 的大小方面存在一定的差异，被称为像差。
指在光学系统中由透镜材料的特性或折 射（或反射）表面的几何形状引起实际像与 理想像的偏差。
这些圆斑相互叠加的结果就形成 了带有彗星形状的光斑
光斑的头部（尖端）较亮，至 尾部亮度逐渐减弱，称为彗星 像差，简称彗差
C E A B
2018/10/14
By’ Ay’ F
O
D 哈工大光电测控技术与装备研究所
18
彗差的形状有两种：
彗星像斑的尖端指向视场中心的称为正彗差
彗星像斑的尖端指向视场边缘的称为负彗差 由于彗差没有对称轴只能垂直度量，所以它 是垂轴像差的一种 彗差对成像的影响： 像的清晰度，使成像的质量降低
-Umax A -U
hmax h
A’
△y’
L’
2018/10/14
δL’
5
l’ 哈工大光电测控技术与装备研究所
球差是轴上点唯一的单色像差
可在沿轴方向和垂轴方向来度量分别称为轴向球 差和垂轴球差。 轴向球差又称为纵向球差 它是沿光轴方向度量的球差，用符号δ L’ 表示 垂轴球差是过近轴光线像点A’的垂轴平面内度 量的球差。用符号δT’ 表示 它表示由轴向球差引起的弥散圆的半径
2018/10/14
哈工大光电测控技术与装备研究所
19
彗差对于大孔径系统和望远系统影响较大
彗差的大小与光束宽度、物体的大小、光阑位 置、光组内部结构（折射率、曲率、孔径）有关 对于某些小视场大孔径的系统（如显微镜）， 常用“正弦差”来描述小视场的彗差特性。
正弦差等于彗差与像高的比值，用符号SC’表示
SC' lim Ks' / y'
y
2018/10/14
哈工大光电测控技术与装备研究所
20
2018/10/14
哈工大光电测控技术与装备研究所
21
彗差
2018/10/14
哈工大光电测控技术与装备研究所
22
3、像散
轴外点细光束成像，将会产生像散和场曲 它们是互相关联的像差 轴外物点用光束成像时形成两条相互垂直且相 隔一定距离的短线像的一种非对称性像差被称 为像散
s
t
A
2018/10/14
哈工大光电测控技术与装备研究所
23
由子午光束所形成的像是一条垂直子午面的短线t 称为子午焦线 由弧矢光束所形成的像是一条垂直弧矢面的短线s 称为弧矢焦线
t
A
2018/10/14
s
哈工大光电测控技术与装备研究所
24
这两条短线不相交但相互垂直且隔一定距离 两条短线间沿光轴方向的距离即表示像散的大小 用符号Xts’表示 Xts’=Xt’-Xs’
δL’
9
2018/10/14
哈工大光电测控技术与装备研究所 0
大孔径产生的球差
2018/10/14
哈工大光电测控技术与装备研究所
10
加发散透镜消除球差
2018/10/14
哈工大光电测控技术与装备研究所
11
球差
2018/10/14
哈工大光电测控技术与装备研究所
12
球差
2018/10/14
哈工大光电测控技术与装备研究所
子午彗差指对子午光线度量的彗差 子午光线对交点离开主光线的垂直距离KT’用 来表示此光线对交点偏离主光线的程度
2018/10/14
哈工大光电测控技术与装备研究所
15
弧矢彗差指对弧矢光线度量的彗差
弧矢光线对交点离开主光线的垂直距离Ks’用来 表示此光线对交点偏离主光线的程度
入瞳 -KT’
像面
2018/10/14