波动 习题课

波动(习题课后作业)1. 传播速度为200m/s, 频率为50Hz 的平面简谐波, 在波线上相距为0.5m 的两点之间的相位差是( D )(A) π/3 (B) π/6 (C) π/2 (D) π/4 解: λ=u/λ=200/50=4(m) Δφ=(2π/λ)Δx =(2π/4)⨯0.5=π/42. 图为沿X 轴正向传播的平面余弦横波在某一时刻的波形图, 图中P 点距原点1m, 则波长为( C )(A) 2.75m (B) 2.5m (C) 3m (D) 2.75m Y(cm) 解: 设波表达式为)2 cos(ϕλπω+-=x t A y x =0处 3) cos(2=+=ϕωt yv =－2ωsin(ωt+φ)<0即23) cos(=+ϕωt ,sin(ωt+φ)>0 得6 πϕω=+t所以t 时刻的波形分布函数为)26cos(2x y λππ-=P 点t 时刻的位移 0)26cos(2=-=λππy P 点t 时刻的速度 0)26sin(2>--=λππωv32O P X得)26cos(=-λππ0)26sin(<-λππ226πλππ-=-∴ λ = 3m3. 一横波沿X 轴负方向传播, 若t 时刻波形曲线如图所示, 在t+T/4时刻原X 轴上的1、2、3三点的振动位移分别是( B ) (A) A 、0、-A (B) -A 、0、A (C) 0、A 、0 (D) 0、-A 、04. 两个相干波源S 1和S 2, 相距L=20m, 在相同时刻, 两波源的振动均通过其平衡位置, 但振动的速度方向相反, 设波速u=600m/s, 频率ν=100Hz, 试求在S 1和S 2间的连线上因干涉产生最弱点的所有位置(距S 1的距离).解: 已知φ1–φ2=π, 设S1为原点，在S 1和S 2连线间任取一点P ，其坐标为x∙∙xS 2∙S 1 L=20m L –xPxLx x L x r -=--=∆2)(r ∆--=∆λπϕϕϕ221)2(2L x --=λππ)(6100600m u===νλxx 32326)220(3ππππππ-++=-⨯+=x 3235ππ-=干涉减弱条件 πϕ)12(+=∆k πππ)12(3235+=-k x 即 得 ),2,1,0(31 ±±=-=k k x 因200≤≤x 即 20310≤-≤k 解得 31319≤≤-k 所以,1 ,2 ,3 ,4 ,5 ,6------=k )(1 , 4 , 7 , 10 , 13 , 16 , 19 m x =∴。

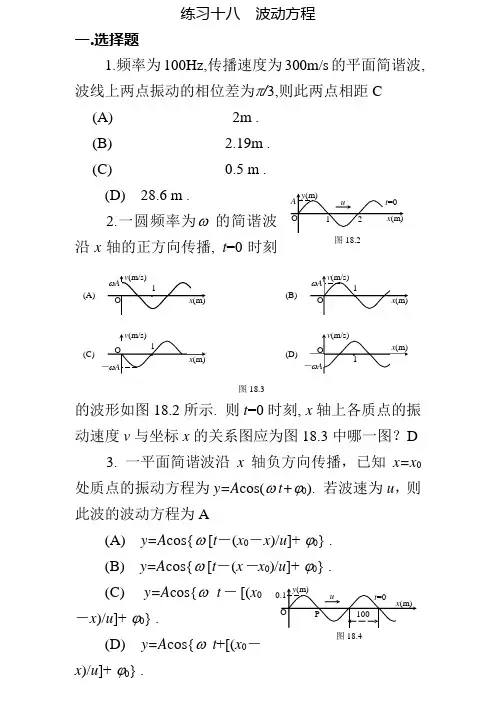
练习十八 波动方程一.选择题1.频率为100Hz,传播速度为300m/s 的平面简谐波,波线上两点振动的相位差为π/3,则此两点相距C (A) 2m . (B)2.19m . (C)0.5 m .(D) 28.6 m .2.一圆频率为ω 的简谐波沿x 轴的正方向传播, t =0时刻的波形如图18.2所示. 则t =0时刻, x 轴上各质点的振动速度v 与坐标x 的关系图应为图18.3中哪一图？D3. 一平面简谐波沿x 轴负方向传播，已知x=x 0处质点的振动方程为y=A cos(ω t+ϕ0). 若波速为u ，则此波的波动方程为A(A) y=A cos{ω [t －(x 0－x )/u ]+ ϕ0} . (B) y=A cos{ω [t －(x －x 0)/u ]+ ϕ0} . (C) y=A cos{ω t －[(x 0－x )/u ]+ ϕ0} .(D) y=A cos{ω t +[(x 0－图18.2(B)v (m/s)O 1 x (m)ωA(A)·(D)(C)图18.3图18.4x )/u ]+ ϕ0} .4. 如图18.4所示为一平面简谐波在t = 0时刻的波形图，该波的波速u =200m/s ，则P 处质点的振动曲线为图18.5中哪一图所画出的曲线？CC D A C 二.填空题1.一列余弦横波以速度u 沿x 轴正方向传播, t 时刻波形曲线如图18.6所示,试分别指出图中A 、B 、C 各质点在该时刻的运动方向:A ；B ; C 向下,向上; 向上 . 2.已知一平面简谐波沿x 轴正向传播,振动周期T =0.5s, 波长λ=10m,振幅A =0.1 m . 当t =0时波源振动的位移恰好为正的最大值. 若波源处为原点, 则沿波传播方向距离波源为λ/2处的振动方程为y = ; 当t=T /2时, x=λ/4处质点的振动速度为 0.1cos(4πt -π) (SI); -1.26m/s..(D)(C)(A)(B)图18.5图18.63.一简谐波的频率为5×104Hz, 波速为 1.5×103m/s,在传播路径上相距5×10－3m 的两点之间的振动相位差为 π/3 三.计算题1.图18.7所示一平面简谐波在t =0时刻的波形图,求(1) 该波的波动方程 ; (2) P 处质点的振动方程 .2.某质点作简谐振动,周期为2s, 振幅为0.06m, 开始计时(t =0)时, 质点恰好处在负向最大位移处, 求 (1)该质点的振动方程;(2)此振动以速度u =2m/s 沿x 轴正方向传播时,形成的一维简谐波的波动方程 ; (3)该波的波长.练习十九 波的能量 波的干涉一.选择题1．一平面简谐波，波速u =5m · s －1. t = 3 s 时波形曲线如图19.1. 则x =0处的振动方程为A (A) y =2×10－2cos(πt /2－π/2) ( S I ) . (B) y =2×10－2cos(πt ＋π ) ( S I ) . (C) y =2×10－2cos(πt /2+π/2) ( S I ) .(D) y =2×10－2cos(πt －3π/2) ( S I ) .－图18.7ux (m)y (10－2m)· · · · · ·· 0 51015 20 25 －2图19.12.一列机械横波在t 时刻的波形曲线如图19.2所示，则该时刻能量为最大值的媒质质元的位置是：B(A) o ′, b , d, f . (B) a , c , e , g . (C) o ′, d . (D) b , f .3.一平面简谐波在弹性媒质中传播，在某一瞬时，媒质中某质元正处于平衡位置，此时它的能量是C(A) 动能为零, 势能最大. (B) 动能为零, 势能为零. (C) 动能最大, 势能最大. (D) 动能最大, 势能为零. 4.如图19.3所示为一平面简谐机械波在t 时刻的波形曲线. 若此时A 点处媒质质元的振动动能在增大,则B(A) A 点处质元的弹性势能在减小. (B) 波沿x 轴负方向传播. (C) B 点处质元的振动动能在减小. (D) 各点的波的能量密度都不随时间变化. 5. 如图19.4所示，两相干波源s 1和s 2相距λ/4(λ为波长), s 1的位相比s 2的位相超前π/2 ,在s 1、s 2的连线上, s 1外侧各点(例如P 点)两波引起的两谐振动的位相差是:B(A) 0 .y x 波速u时刻t 的波形 ·· · · · · ··oo ′ a b c def g 图19.2图19.31 2图19.4(B) π . (C) π /2 . (D) 3π/2 .二.填空题1.一列平面简谐波沿x 轴正方向无衰减地传播, 波的振幅为2×10-3m, 周期为0.01s, 波速为400 m/s, 当t =0时x 轴原点处的质元正通过平衡位置向y 轴正方向运动,则该简谐波的表达式为 .2.一个点波源位于O 点, 以O 为圆心作两个同心球面,它们的半径分别为R 1和R 2. 在两个球面上分别取相等的面积∆S 1和∆S 2 ,则通过它们的平均能流之比21P P = .3.如图19.5所示,在平面波传播方向上有一障碍物AB,根据惠更斯原理,定性地绘出波绕过障碍物传播的情况. 三.计算题1.如图19.6所示,三个同频率,振动方向相同(垂直纸面)的简谐波,在传播过程中在O 点相遇,若三个简谐波各自单独在S 1、S 2和S 3的振动方程分别为图19.5y 1=A cos(ω t +π/2) y 2=A cos ω t y 3=2A cos(ωt －π/2) 且S 2O=4λ ,S 1O=S 3O=5λ(λ为波长)，求O 点的合成振动方程(设传播过程中各波振幅不变).2.如图19.7,两列相干波在P 点相遇,一列波在B 点引起的振动是y 10=3×10 –3cos2πt ( SI )另一列波在C 点引起在振动是y 20=3×10 –3cos(2πt +π/2) ( SI )BP =0.45m , CP =0.30m, 两波的传播速度 u=0.20m/s, 不考虑传播中振幅的减小,求P 点合振动的振动方程.练习二十 驻波 多普勒效应一.选择题1.在波长为λ的驻波中，两个相邻波腹之间的距离为B(A) λ/4 . (B) λ/2 . (C) 3λ/4 . (D) λ .2.某时刻驻波波形曲线如图20.1所示,则a 、b 两点的相位差是A(A) π.S3 图19.6图19.7(B) π/2.(C) 5π /4.(D) 0.3.沿相反方向传播的两列相干波，其波动方程为y1=A cos2π (νt－x/λ)y2=A cos2π (νt + x/λ)叠加后形成的驻波中,波节的位置坐标为D(A) x=±kλ.(B)x=±kλ/2 .(C)x=±(2k+1)λ/2 .(D) x=±(2k+1)λ/4 .其中k = 0 , 1 , 2 , 3…….4.如果在长为L、两端固定的弦线上形成驻波,则此驻波的基频波的波长为Da)L/2 .b)L .c)3L/2 .d)2L .5.一机车汽笛频率为750 Hz , 机车以时速90公里远离静止的观察者，观察者听到声音的频率是(设空气中声速为340m/s) A：a)810 Hz .b)699 Hz .c)805 Hz .d)695 Hz .二.填空题1.设平面简谐波沿x 轴传播时在x = 0 处发生反射,反射波的表达式为y 2=A cos[2π (νt －x /λ) +π /2] .已知反射点为一自由端,则由入射波和反射波形成驻波波节的位置坐标为 .2.设沿弦线传播的一入射波的表达式是y 1=A cos[2π (νt －x /λ) +ϕ]在x =L 处(B 点)发生反射,反射点为固定端(如图20.2), 设波在传播和反射过程中振幅不变,则弦线上形成的驻波表达式为y = .3.相对于空气为静止的声源振动频率为νs ,接收器R 以速率v R 远离声源,设声波在空气中传播速度为u , 那么接收器收到的声波频率νR = . 三.计算题1.在绳上传播的入射波方程为 y 1=A cos (ω t +2π x /λ).入射波在x =0处的绳端反射, 反射端为自由端,设反射波不衰减,求驻波方程.2.设入射波的方程式为 y 1=A cos2π (x /λ+t /T ) .在x =0处发生反射,反射点为一固定端,设反射时无能量损失,求:(1)反射波的方程式; (2)合成的驻波方程式; (3)波腹和波节的位置 .练习二十一 振动和波习题课图20.2一.选择题1.图21.1中三条曲线分别表示简谐振动中的位移x ,速度v,加速度a ,下面哪个说法是正确的？(A) 曲线3, 1, 2分别表示x , v , a 曲线.(B) 曲线2, 1, 3分别表示x , v , a 曲线.(C) 曲线1, 3, 2分别表示x , v , a 曲线. (D) 曲线2, 3, 1分别表示x , v , a 曲线. (E) 曲线1, 2, 3分别表示x , v , a 曲线.2.用余弦函数描述一简谐振子的振动,若其速度－时间(v －t )关系曲线如图21.2所示,则振动的初相位为(A) π / 6 . (B) π / 3. (C) π / 2. (D) 2π / 3. (A) 5π / 6 .3.一质点作简谐振动,周期为T , 质点由平衡位置向x 轴正方向运动时,由平衡位置到二分之一最大位移这段路程所需要的时间为(A) T / 4 . (B) T /12 . (C) T / 6 . (D) T / 8 .4.一平面简谐波在弹性媒质中传播,在媒质质元从最大位移处回到平衡位置的过程中图21.1－(A) 它的势能转换成动能. (B) 它的动能转换成势能.(C) 它从相邻的一段媒质质元获得能量,其能量逐渐增加.(D) 它把自己的能量传给相邻的一段媒质质元,其能量逐渐减小.5.在弦上有一简谐波,其表达式是y 1=2.0×10-2cos[2π ( t / 0.02－x / 20) +π / 3] ( SI ) 为了在此弦线上形成驻波, 并且在x =0处为一波节,此弦线上还应有一简谐波, 其表达式为:(A) y 2=2.0×10-2cos[2π ( t / 0.02 + x / 20) +π / 3] ( SI )(B) y 2=2.0×10-2cos[2π ( t / 0.02+x / 20) +2π / 3] ( SI )(C) y 2=2.0×10-2cos[2π ( t / 0.02+x / 20) +4π / 3] ( SI )(D) y 2=2.0×10-2cos[2π ( t / 0.02+x / 20)－π / 3] ( SI ) 二.填空题1.在静止的升降机中,长度为l 在单摆的振动周期为T 0 ,当升降机以加速度a =g /2竖直下降时,摆的振动周期T = .2. .如图21.3所示,一平面简谐波沿O x 轴负方向传播,波长为λ, 若P 处质点的振动方程是y P =A cos(2πνt +π /2) .图21.3则该波的波动方程是 .P 处质点 时刻的振动状态与O 处质点t 1时刻的振动状态相同.3一平面简谐波沿O x 轴传播,波动方程为y =A cos[2π (νt －x /λ) +ϕ]则: x 1=L 处介质质点振动初相位是 ;与x 1处质点振动状态相同的其它质点的位置是 ;与x 1处质点速度大小相同,但方向相反的其它各介质质点的位置是 .三.证明题1. 如图21.4所示,在竖直面内半径为R 的一段光滑圆弧形轨道上,放一小物体,使其静止于轨道的最低处,然后轻碰一下此物体,使其沿圆弧形轨道来回作小幅度运动,试证:(1) 此物体作简谐振动.(2) 此简谐振动的周期 T =2πg R. 图21.4。

振动波动一、例题（一）振动1。

证明单摆是简谐振动，给出振动周期及圆频率.2. 一质点沿x 轴作简谐运动，振幅为12cm,周期为2s 。

当t = 0时， 位移为6cm ，且向x 轴正方向运动。

求： （1） 振动表达式；(2) t = 0.5s 时，质点的位置、速度和加速度；(3)如果在某时刻质点位于x =—0.6cm ，且向x 轴负方向运动，求从该位置回到平衡位置所需要的时间。

3。

已知两同方向，同频率的简谐振动的方程分别为：x 1= 0.05cos （10 t + 0.75π) 20.06cos(100.25)(SI)x t π=+求：(1)合振动的初相及振幅.(2)若有另一同方向、同频率的简谐振动x 3 = 0。

07cos (10 t +ϕ 3 ）, 则当ϕ 3为多少时 x 1 + x 3 的振幅最大？又ϕ 3为多少时 x 2 + x 3的振幅最小？（二）波动1. 平面简谐波沿x 轴正方向传播，振幅为2 cm ，频率为 50 Hz ，波速为 200 m/s.在t = 0时，x = 0处的质点正在平衡位置向y 轴正方向运动，求:(1）波动方程(2)x = 4 m 处媒质质点振动的表达式及该点在t = 2 s 时的振动速度。

2. 一平面简谐波以速度m/s 8.0=u 沿x 轴负方向传播.已知原点的振动曲线如图所示.求:（1）原点的振动表达式；(2）波动表达式；（3）同一时刻相距m 1的两点之间的位相差.3. 两相干波源S 1和S 2的振动方程分别是1cos y A t ω=和2cos(/2)y A t ωπ=+.S 1距P 点3个波长，S 2距P 点21/4个波长。

求:两波在P 点引起的合振动振幅。

4。

沿X 轴传播的平面简谐波方程为：310cos[200(t )]200x y π-=- ，隔开两种媒质的反射界面A 与坐标原点O 相距2。

25m ，反射波振幅无变化，反射处为固定端，求反射波的方程.二、习题课（一)振动1. 一质点在x 轴上作简谐振动，振辐A = 4 cm,周期T = 2 s ，其平衡位置取作坐标原点.若t = 0时刻质点第一次通过x = -2 cm 处，且向x 轴负方向运动，则O 2.25m Ax t O A/2 -A x 1 x 2 质点第二次通过x = -2 cm 处的时刻为［ ］（A) 1 s (B) (2/3) s (C ） (4/3) s （D ） 2 s2.已知某简谐振动的振动曲线如图所示，则此简谐振动的振动方程为(A ） ⎪⎭⎫ ⎝⎛+=3232cos 2ππt x ;（B ） ⎪⎭⎫ ⎝⎛-=332cos 2ππt x ;（C) ⎪⎭⎫ ⎝⎛+=3234cos 2ππt x ；（D ） ⎪⎭⎫ ⎝⎛-=334cos 2ππt x 。

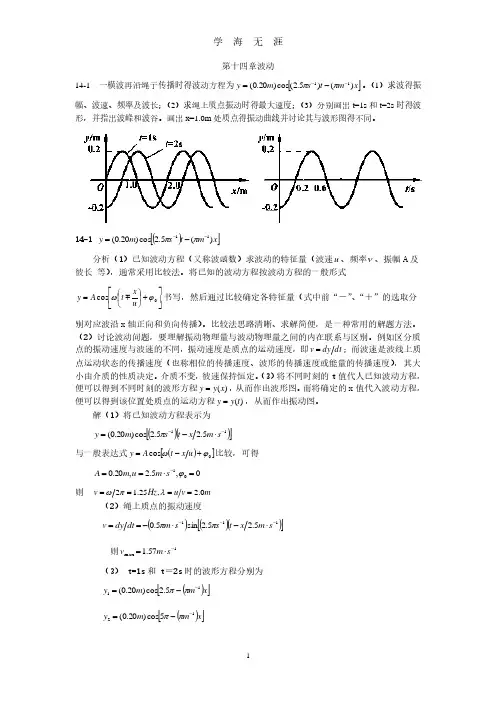
第十四章波动14-1 一横波再沿绳子传播时得波动方程为[]x m t s m y )()5.2(cos )20.0(11−−−=ππ。

（1）求波得振幅、波速、频率及波长；（2）求绳上质点振动时得最大速度；（3）分别画出t=1s 和t=2s 时得波形，并指出波峰和波谷。

画出x=1.0m 处质点得振动曲线并讨论其与波形图得不同。

14-1 ()[]x m t s m y )(5.2cos )20.0(11−−−=ππ分析（1）已知波动方程（又称波函数）求波动的特征量（波速u 、频率ν、振幅A 及彼长 等），通常采用比较法。

将已知的波动方程按波动方程的一般形式⎥⎦⎤⎢⎣⎡+⎪⎭⎫ ⎝⎛=0cos ϕωu x t A y 书写，然后通过比较确定各特征量（式中前“－”、“＋”的选取分别对应波沿x 轴正向和负向传播）。

比较法思路清晰、求解简便，是一种常用的解题方法。

（2）讨论波动问题，要理解振动物理量与波动物理量之间的内在联系与区别。

例如区分质点的振动速度与波速的不同，振动速度是质点的运动速度，即dt dy v =；而波速是波线上质点运动状态的传播速度（也称相位的传播速度、波形的传播速度或能量的传播速度），其大小由介质的性质决定。

介质不变，彼速保持恒定。

（3）将不同时刻的t 值代人已知波动方程，便可以得到不同时刻的波形方程)(x y y =，从而作出波形图。

而将确定的x 值代入波动方程，便可以得到该位置处质点的运动方程)(t y y =，从而作出振动图。

解（1）将已知波动方程表示为()()[]115.25.2cos )20.0(−−⋅−=s m x t s m y π 与一般表达式()[]0cos ϕω+−=u x t A y 比较，可得0,5.2,20.001=⋅==−ϕs m u m A则 m v u Hz v 0.2,25.12====λπω（2）绳上质点的振动速度()()()[]1115.25.2sin 5.0−−−⋅−⋅−==s m x t s s m dt dy v ππ 则1max 57.1−⋅=s m v（3） t=1s 和 t ＝2s 时的波形方程分别为()[]x m m y 115.2cos )20.0(−−=ππ()[]x m m y 125cos )20.0(−−=ππ波形图如图14－1（a ）所示。