实验五、优先队列式分支限界法解装载问题
- 格式:doc
- 大小:54.00 KB
- 文档页数:7


用分支限界算法解装载问题详解一、实验目的1、理解分支限界法的概念,掌握分支限界法的基本要素。
2、掌握设计分支限界法的一般步骤,针对具体问题,能应用分支限界法求解二、实验内容1、问题描述:有一批共个集装箱要装上2艘载重量分别为C1和C2的轮船,其中集装箱i的重量为Wi,且w1+…+wn<= C1+ C2; 装载问题要求确定是否有一个合理的装载方案可将这个集装箱装上这2艘轮船。
如果有,找出一种装载方案。
2、数据输入:文件输入或键盘输入。
3、要求:1)完成上述问题的队列式分支限界法解决问题,时间为1 次课。
2)独立完成实验及实验报告。
三、实验步骤1、理解方法思想和问题要求。
2、采用编程语言实现题目要求。
3、上机输入和调试自己所写的程序。
4、附程序主要代码:#include <bits/stdc++、h>using namespace std;class MaxHeapQNode{public: MaxHeapQNode*parent; int lchild; int weight; int lev;};structcmp{ bool operator()(MaxHeapQNode *&a, MaxHeapQNode *&b)const { return a->weight < b->weight; }};int n;int c;int bestw;int w[100];int bestx[100];voidInPut(){ scanf("%d %d", &n, &c); for(int i =1; i <= n;++i)scanf("%d", &w[i]);}voidAddAliveNode(priority_queue<MaxHeapQNode *,vector<MaxHeapQNode *>, cmp> &q, MaxHeapQNode *E, int wt, int i, int ch){ MaxHeapQNode *p = new MaxHeapQNode; p->parent = E; p->lchild = ch; p->weight = wt; p->lev = i +1; q、push(p);}voidMaxLoading(){ priority_queue<MaxHeapQNode *,vector<MaxHeapQNode *>, cmp > q; // 大顶堆 //定义剩余重量数组r int r[n +1]; r[n] = 0; for(int j = n-j)r[j] = r[j +1] + w[j +1]; int i =1; MaxHeapQNode *E; int Ew = 0; while(i != n +1){ if(Ew + w[i] <= c){ AddAliveNode(q, E, Ew + w[i] + r[i], i,1); } AddAliveNode(q, E, Ew + r[i], i, 0); //取下一节点 E = q、top(); q、pop(); i = E->lev; Ew = E->weight1]; } bestw = Ew; for(int j = n; j > 0;j){ bestx[j] = E->lchild; E = E->parent; }}void OutPut(){ printf("最优装载量为 %d\n", bestw); printf("装载的物品为 \n"); for(int i =1; i <= n; ++i)if(bestx[i] ==1)printf("%d ", i);}int main(){ InPut(); MaxLoading(); OutPut();}5、实验结果:4、装载问题实验分析:1、将wt<=c和Ew+r>=bestw作为限界判定。

五⼤算法设计思想(转载)⼀分治法1.1 概念: 将⼀个难以直接解决的⼤问题,分割成⼀些规模较⼩的相同问题,以便各个击破,分⽽治之。
1.2 思想策略: 对于⼀个规模为n的问题,若该问题可以容易地解决(⽐如说规模n较⼩)则直接解决,否则将其分解为k个规模较⼩的⼦问题,这些⼦问题互相独⽴且与原问题形式相同,递归地解这些⼦问题,然后将各⼦问题的解合并得到原问题的解。
1.3 特征:1) 该问题的规模缩⼩到⼀定的程度就可以容易地解决2) 该问题可以分解为若⼲个规模较⼩的相同问题,即该问题具有最优⼦结构性质。
3) 利⽤该问题分解出的⼦问题的解可以合并为该问题的解;4) 该问题所分解出的各个⼦问题是相互独⽴的,即⼦问题之间不包含公共的⼦⼦问题。
1.4 对特征的解析:第⼀条特征是绝⼤多数问题都可以满⾜的,因为问题的计算复杂性⼀般是随着问题规模的增加⽽增加;第⼆条特征是应⽤分治法的前提它也是⼤多数问题可以满⾜的,此特征反映了递归思想的应⽤;第三条特征是关键,能否利⽤分治法完全取决于问题是否具有第三条特征,如果具备了第⼀条和第⼆条特征,⽽不具备第三条特征,则可以考虑⽤贪⼼法或动态规划法。
第四条特征涉及到分治法的效率,如果各⼦问题是不独⽴的则分治法要做许多不必要的⼯作,重复地解公共的⼦问题,此时虽然可⽤分治法,但⼀般⽤动态规划法较好。
1.5 基本步骤:1 分解:将原问题分解为若⼲个规模较⼩,相互独⽴,与原问题形式相同的⼦问题;2 解决:若⼦问题规模较⼩⽽容易被解决则直接解,否则递归地解各个⼦问题3 合并:将各个⼦问题的解合并为原问题的解。
1.6 适⽤分治法求解的经典问题:1)⼆分搜索2)⼤整数乘法3)Strassen矩阵乘法4)棋盘覆盖5)合并排序6)快速排序7)线性时间选择8)最接近点对问题9)循环赛⽇程表10)汉诺塔⼆动态规划2.1 概念 每次决策依赖于当前状态,⼜随即引起状态的转移。
⼀个决策序列就是在变化的状态中产⽣出来的,所以,这种多阶段最优化决策解决问题的过程就称为动态规划。


摘要本文分析比较了tsp问题的动态规划算法,分支界限法,近似等算法。
分析了旅行商问题的时间度特点,针对启发式算法求解旅行商问题中存在的一些问题提出了改进算法。
此算法将群体分为若干小子集,并用启发式交叉算子,以较好利用父代个体的有效信息,达到快速收敛的效果,实验表明此算法能提高寻优速度,解得质量也有所提高。
关键词:旅行商问题TSPAbstractthis paper analyzed the time complexity of traveling salesman problem,then put forward some imprivement towards the genetic algorithm for solving this problen: divding the population into some small parent individual well.so it can quickly get into convergence, the experimental result indicates the impwoved algorithm can accelerate the apeed of finding solution and improve the precision.Keywords traveling salesman problem; genetic algorithm; subset; henristic crossover operator目录1、摘要--------------------------------------------------------------12、Abstract---------------------------------------------------------13、Tsp问题的提法------------------------------------------------24、回溯法求Tsp问题--------------------------------------------35、分支限界法求Tsp问题--------------------------------------76、近似算法求解Tsp问题-------------------------------------107、动态规划算法解Tsp问题----------------------------------12引言tsp问题刚提出时,不少人都认为很简单。

算法——分⽀限界法(装载问题)对⽐回溯法回溯法的求解⽬标是找出解空间中满⾜约束条件的所有解,想必之下,分⽀限界法的求解⽬标则是找出满⾜约束条件的⼀个解,或是满⾜约束条件的解中找出使某⼀⽬标函数值达到极⼤或极⼩的解,即在某种意义下的最优解。
另外还有⼀个⾮常⼤的不同点就是,回溯法以深度优先的⽅式搜索解空间,⽽分⽀界限法则以⼴度优先的⽅式或以最⼩耗费优先的⽅式搜索解空间。
分⽀限界法的搜索策略在当前节点(扩展节点)处,先⽣成其所有的⼉⼦节点(分⽀),然后再从当前的活节点(当前节点的⼦节点)表中选择下⼀个扩展节点。
为了有效地选择下⼀个扩展节点,加速搜索的进程,在每⼀个活节点处,计算⼀个函数值(限界),并根据函数值,从当前活节点表中选择⼀个最有利的节点作为扩展节点,使搜索朝着解空间上有最优解的分⽀推进,以便尽快地找出⼀个最优解。
分⽀限界法解决了⼤量离散最优化的问题。
选择⽅法1.队列式(FIFO)分⽀限界法队列式分⽀限界法将活节点表组织成⼀个队列,并将队列的先进先出原则选取下⼀个节点为当前扩展节点。
2.优先队列式分⽀限界法优先队列式分⽀限界法将活节点表组织成⼀个优先队列,并将优先队列中规定的节点优先级选取优先级最⾼的下⼀个节点成为当前扩展节点。
如果选择这种选择⽅式,往往将数据排成最⼤堆或者最⼩堆来实现。
例⼦:装载问题有⼀批共n个集装箱要装上2艘载重量分别为c1,c2的轮船,其中集装箱i的重量为wi,且要求确定是否有⼀个合理的装载⽅案可将这n个集装箱装上这2艘轮船。
可证明,采⽤如下策略可以得到⼀个最优装载⽅案:先尽可能的将第⼀艘船装满,其次将剩余的集装箱装到第⼆艘船上。
代码如下://分⽀限界法解装载问题//⼦函数,将当前活节点加⼊队列template<class Type>void EnQueue(Queue<Type> &Q, Type wt, Type &bestw, int i, int n){if(i == n) //可⾏叶结点{if(wt>bestw) bestw = wt ;}else Q.Add(wt) ; //⾮叶结点}//装载问题先尽量将第⼀艘船装满//队列式分⽀限界法,返回最优载重量template<class Type>Type MaxLoading(Type w[],Type c,int n){//初始化数据Queue<Type> Q; //保存活节点的队列Q.Add(-1); //-1的标志是标识分层int i=1; //i表⽰当前扩展节点所在的层数Type Ew=0; //Ew表⽰当前扩展节点的重量Type bestw=0; //bestw表⽰当前最优载重量//搜索⼦集空间树while(true){if(Ew+w[i]<=c) //检查左⼉⼦EnQueue(Q,Ew+w[i],bestw,i,n); //将左⼉⼦添加到队列//将右⼉⼦添加到队列即表⽰不将当前货物装载在第⼀艘船EnQueue(Q,Ew,bestw,i,n);Q.Delete(Ew); //取下⼀个节点为扩展节点并将重量保存在Ewif(Ew==-1) //检查是否到了同层结束{if(Q.IsEmpty()) return bestw; //遍历完毕,返回最优值Q.Add(-1); //添加分层标志Q.Delete(Ew); //删除分层标志,进⼊下⼀层i++;}}}算法MaxLoading的计算时间和空间复杂度为O(2^n).上述算法可以改进,设r为剩余集装箱的重量,当Ew+r<=bestw的时候,可以将右⼦树剪去。

第六章分支限界法1学习要点1.1学习要点明白得分支限界法的剪枝搜索策略。
把握分支限界法的算法框架(1)队列式(FIFO)分支限界法(2)优先队列式分支限界法通过应用范例学习分支限界法的设计谋略。
(1)单源最短途径问题(2)装载问题;(4)0-1背包问题;(8)批处置作业调度问题2分支限界法的大体思想2.1分支限界法描述采纳广度优先产生状态空间树的结点,并利用剪枝函数的方式称为分支限界法。
所谓“分支”是采纳广度优先的策略,依次生成扩展结点的所有分支(即:儿子结点)。
所谓“限界”是在结点扩展进程中,计算结点的上界(或下界),边搜索边减掉搜索树的某些分支,从而提高搜索效率。
原理依照广度优先的原那么,一个活扣点一旦成为扩展结点(E-结点)R后,算法将依次生成它的全数小孩结点,将那些致使不可行解或致使非最优解的儿子舍弃,其余儿子加入活扣点表中。
然后,从活扣点表中掏出一个结点作为当前扩展结点。
重复上述结点扩展进程,直至找到问题的解或判定无解为止。
2.2分支限界法与回溯法求解目标:回溯法的求解目标是找出解空间树中知足约束条件的所有解,而分支限界法的求解目标那么是找出知足约束条件的一个解,或是在知足约束条件的解中找出在某种意义下的最优解。
搜索方式的不同:回溯法以深度优先的方式搜索解空间树,而分支限界法那么以广度优先的方式搜索解空间树。
分支限界法常以广度优先或以最小花费(最大效益)优先的方式搜索问题的解空间树。
在分支限界法中,每一个活扣点只有一次机遇成为扩展结点。
活扣点一旦成为扩展结点,就一次性产生其所有儿子结点。
在这些儿子结点中,致使不可行解或致使非最优解的儿子结点被舍弃,其余儿子结点被加入活扣点表中。
尔后,从活扣点表中取下一结点成为当前扩展结点,并重复上述结点扩展进程。
那个进程一直持续到找到所需的解或活扣点表为空时为止。
2.3常见的两种分支限界法队列式(FIFO)分支限界法依照队列先进先出(FIFO)原那么选取下一个节点为扩展节点。

实验五箱子装载问题一、实验目的:1、理解和复习所学各种算法的概念;2、掌握和复习所学各种算法的基本要素;3、掌握各种算法的优点和区别;4、通过应用范例掌握选择最佳算法的设计技巧与策略;二、实验内容及要求:1、使用贪心算法、回溯法、分支限界法解决箱子装载问题。
(任选两种)2、通过上机实验进行算法实现。
3、保存和打印出程序的运行结果,并结合程序进行分析,上交实验报告。
三、实验原理:回溯法原理:从开始结点出发,以深度优先方式搜索整个解空间。
这个节点成为活结点,同时也成为当前的扩展节点。
在当前的扩展节点处,搜索向纵深方向一致一个新节点。
贪心算法原理:贪心算法通过一系列的选择来得到问题的解。
他所做的每一个选择都是当前状态下局部最好选择,即贪心选择。
四、程序代码:贪心算法:#include<iostream>#include<stdlib.h>#define N 100using namespace std;int main(){int t[N],w0[N],w[N],n,c,m,i,j;int max=0,weight=0;bool tx[N];cout<<"请输入轮船的载重量c:"<<endl;cin>>c;cout<<"请输入可以装入的集装箱的数目n:"<<endl;cin>>n;cout<<"请输入各集装箱的重量w[i](1<=i<=n):"<<endl; for(int i=0;i<n;i++){cin>>w0[i];w[i+1]=w0[i];tx[i+1]=false;}for(i=1;i<n;i++){for(j=i+1;j<=n;j++){if(w[i]>w[j]) {int tem;tem=w[j];w[j]=w[i];w[i]=tem;}}}for(i=1;i<=n;i++)printf("%d ",w[i]);printf("n");for(i=1;i<=n;i++){int min=weight+w[i];if(min<=c){weight+=w[i];tx[i]=true;}}m=i-1;cout<<"最优装载情况为:"<<endl;cout<<"装入轮船的集装箱为:";max=0;for(i=1;i<=m;i++){if(tx[i]){max+=w[i];cout<<w[i]<<"--";}}cout<<endl;cout<<"装入的集装箱的最大重量为:"<<max<<endl;system("pause");}回溯法:#include<iostream>using namespace std;class Loading{friend float MaxLoading(float[],float,int);public:void Backtrack(int i);int n;int *x,*bestx;float *w,c,cw,bestw,r;};float Maxloading(float w1[],float c1,float c2,int n1,int bestx1[]) {Loading k;int j;float MAXLoad;k.x= new int [n1+1];k.bestx=bestx1;k.w = w1;k.c = c1;k.n = n1;k.cw = 0;k.bestw = 0;k.r = 0;for(int i=1;i<=n1;i++)k.r+=w1[i];k.Backtrack(1);delete [] k.x;cout<<"船1最优装载:"<<k.bestw<<endl;MAXLoad=k.bestw;for( j=1;j<=n1;j++){if(k.bestx[j]==0){MAXLoad+=w1[j];c2-=w1[j];if(c2<0){cout<<"找不到合理装载方案!"<<endl;return -1;}}}cout<<"船1中的箱子:";for( j=1;j<=n1;j++)if(k.bestx[j]==1)cout<<j<<" ";cout<<endl;cout<<"船2中的箱子:";for( j=1;j<=n1;j++)if(k.bestx[j]==0)cout<<j<<" ";cout<<endl;return MAXLoad;}void Loading::Backtrack(int i) {if(i>n){if(cw>bestw){for(int j=1;j<=n;j++)bestx[j]=x[j];bestw = cw;}return;}r-=w[i];if(cw+w[i]<=c){x[i]=1;cw+=w[i];Backtrack(i+1);cw-=w[i];}if(cw+r>bestw){x[i] = 0;Backtrack(i+1);}r+=w[i];}int main(){float w[20];float c1,c2,k;int n,bestx[20];cout<<"输入箱子数:";cin>>n;cout<<"输入箱子重量:";for(int i=1;i<=n;i++)cin>>w[i];cout<<"输入容量船1,船2:";cin>>c1>>c2;k=Maxloading(w,c1,c2,n,bestx);if(k!=-1)cout<<"总体最优装载:"<<k<<endl;return 1;}五、结果运行与分析:贪心算法:回溯法:六、心得与体会:通过本次实验,自己再次的联系了贪心算法和回溯法的应用,本次实验自己测试了很多次才成功,收获蛮大的,自己的编程能力进一步的提高了。
实验5. 分支限界法Branch and Bound Method一、实验目的1.理解分支限界法的基本思想。
2.运用分支限界法解决实际问题。
二、实验环境与地点1.实验环境:Windows7,Eclipse2.实验地点:网络工程实验室三、实验内容与步骤编写程序完成下列题目,上机调试并运行成功。
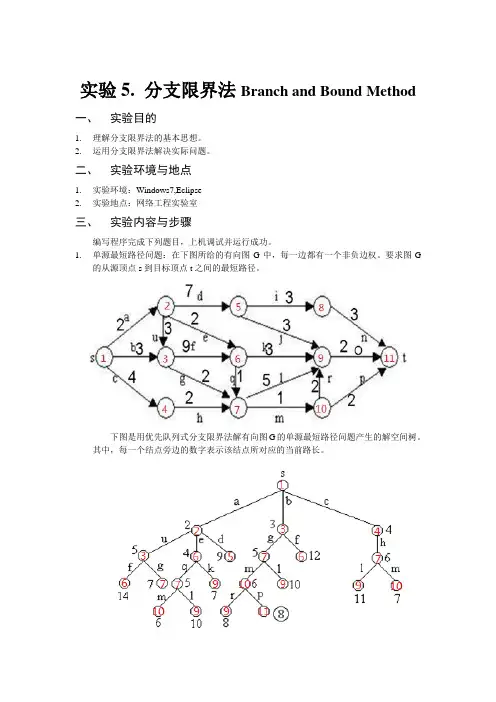
1.单源最短路径问题:在下图所给的有向图G中,每一边都有一个非负边权。
要求图G的从源顶点s到目标顶点t之间的最短路径。
下图是用优先队列式分支限界法解有向图G的单源最短路径问题产生的解空间树。
其中,每一个结点旁边的数字表示该结点所对应的当前路长。
算法思想:解单源最短路径问题的优先队列式分支限界法用一极小堆来存储活结点表。
其优先级是结点所对应的当前路长。
算法从图G的源顶点s和空优先队列开始。
结点s被扩展后,它的儿子结点被依次插入堆中。
此后,算法从堆中取出具有最小当前路长的结点作为当前扩展结点,并依次检查与当前扩展结点相邻的所有顶点。
如果从当前扩展结点i到顶点j有边可达,且从源出发,途经顶点i再到顶点j的所相应的路径的长度小于当前最优路径长度,则将该顶点作为活结点插入到活结点优先队列中。
这个结点的扩展过程一直继续到活结点优先队列为空时为止。
算法结束后,数组dist返回从源到各顶点的最短距离。
相应的最短路径容易从前驱顶点数组记录的信息构造出。
算法:public class BBShortest {static final float M=Float.MAX_VALUE;static class HeapNode implements Comparable {int i; // 顶点编号float length; // 当前路长HeapNode(int ii, float ll) {i = ii;length = ll;}public int compareTo(Object x) {float xl = ((HeapNode) x).length;if (length < xl)return -1;if (length == xl)return 0;return 1;}}// 1,2,3,4,5,6,7,8,9,10,11static float[][] a={{0,0,0,0,0,0,0,0,0,0,0,0,},{0,0,2,3,4,M,M,M,M,M,M,M,},//1{0,M,0,3,M,7,2,M,M,M,M,M,},//2{0,M,M,0,M,M,9,2,M,M,M,M,},//3{0,M,M,M,0,M,M,2,M,M,M,M,},//4{0,M,M,M,M,0,M,M,3,3,M,M,},//5{0,M,M,M,M,M,0,1,M,3,M,M,},//6{0,M,M,M,M,M,M,0,M,5,1,M,},//7{0,M,M,M,M,M,M,M,0,M,M,3,},//8{0,M,M,M,M,M,M,M,M,0,M,2,},//9{0,M,M,M,M,M,M,M,M,2,0,2,},//10{0,M,M,M,M,M,M,M,M,M,M,0,},//11}; // 图G的邻接矩阵static float[] dist=new float[a.length];static int[] p=new int[dist.length];public static void shortest(int v, float[] dist, int[] p) {int n = p.length - 1;MinHeap heap = new MinHeap();// 定义源为初始扩展结点HeapNode enode = new HeapNode(v, 0);for (int j = 1; j <= n; j++)dist[j] = Float.MAX_VALUE;dist[v] = 0;while (true) { // 搜索问题的解空间for (int j = 1; j <= n; j++)if (a[enode.i][j] < Float.MAX_VALUE && enode.length + a[enode.i][j] < dist[j]) {// 顶点i到顶点j可达,且满足控制约束dist[j] = enode.length + a[enode.i][j];p[j] = enode.i;HeapNode node = new HeapNode(j, dist[j]);heap.put(node); // 加入活结点优先队列}// 取下一扩展结点if (heap.isEmpty())break;elseenode = (HeapNode) heap.removeMin();}}}注意:实现算法时,MinHeap直接用PriorityQueue创建优先级队列。

分支限界法之装载问题分支限界法之装载问题做IT就要做精英,至少4000/月吧?JAVAV工程师权威认证[上海央邦]学一送一,超值!【安博亚威】CCIE考试通过率第一!定向委培RHCA,通过考试年薪10WWindows高级工程师的培训地中国IT实验室收集整理佚名 2009-9-25 保存本文推荐给好友收藏本页欢迎进入C/C++编程社区论坛,与200万技术人员互动交流>>进入装载问题(分支限界)Dlg.cpp#include "Queue.h"#ifdef _DEBUG#define new DEBUG_NEW#undef THIS_FILEstatic char THIS_FILE[] = __FILE__;#endif/////////////////////////////////////////////////////////////////// //////////// CAboutDlg dialog used for App Aboutclass CAboutDlg : public CDialog{public:CAboutDlg();// Dialog Data//{{AFX_DATA(CAboutDlg)enum { IDD = IDD_ABOUTBOX };//}}AFX_DATA// ClassWizard generated virtual function overrides//{{AFX_VIRTUAL(CAboutDlg)protected:virtual void DoDataExchange(CDataExchange* pDX); // DDX/DDV support//}}AFX_VIRTUAL// Implementationprotected://{{AFX_MSG(CAboutDlg)//}}AFX_MSGDECLARE_MESSAGE_MAP()};CAboutDlg::CAboutDlg() : CDialog(CAboutDlg::IDD){//{{AFX_DATA_INIT(CAboutDlg)//}}AFX_DATA_INIT}void CAboutDlg::DoDataExchange(CDataExchange* pDX){CDialog::DoDataExchange(pDX);//{{AFX_DATA_MAP(CAboutDlg)//}}AFX_DATA_MAP}BEGIN_MESSAGE_MAP(CAboutDlg, CDialog)//{{AFX_MSG_MAP(CAboutDlg)// No message handlers//}}AFX_MSG_MAPEND_MESSAGE_MAP()/////////////////////////////////////////////////////////////////// //////////// CNewDlg dialogCNewDlg::CNewDlg(CWnd* pParent /*=NULL*/): CDialog(CNewDlg::IDD, pParent){//{{AFX_DATA_INIT(CNewDlg)m_num = _T("");//}}AFX_DATA_INIT// Note that LoadIcon does not require a subsequent DestroyIcon in Win32m_hIcon = AfxGetApp()->LoadIcon(IDR_MAINFRAME);}void CNewDlg::DoDataExchange(CDataExchange* pDX){CDialog::DoDataExchange(pDX);//{{AFX_DATA_MAP(CNewDlg)DDX_Text(pDX, IDC_EDIT_NUM, m_num);//}}AFX_DATA_MAP}BEGIN_MESSAGE_MAP(CNewDlg, CDialog)//{{AFX_MSG_MAP(CNewDlg)ON_WM_SYSCOMMAND()ON_WM_PAINT()ON_WM_QUERYDRAGICON()ON_BN_CLICKED(IDC_BTN_LOAD, OnBtnLoad) ON_BN_CLICKED(IDC_BTN_CLEAR, OnBtnClear)//}}AFX_MSG_MAPEND_MESSAGE_MAP()/////////////////////////////////////////////////////////////////// //////////// CNewDlg message handlersBOOL CNewDlg::OnInitDialog(){CDialog::OnInitDialog();// Add "About..." menu item to system menu.// IDM_ABOUTBOX must be in the system command range.ASSERT((IDM_ABOUTBOX & 0xFFF0) == IDM_ABOUTBOX);ASSERT(IDM_ABOUTBOX < 0xF000);CMenu* pSysMenu = GetSystemMenu(FALSE);if (pSysMenu != NULL){CString strAboutMenu;strAboutMenu.LoadString(IDS_ABOUTBOX); if (!strAboutMenu.IsEmpty()){pSysMenu->AppendMenu(MF_SEPARATOR);pSysMenu->AppendMenu(MF_STRING, IDM_ABOUTBOX, strAboutMenu);}}// Set the icon for this dialog. The framework does this automatically// when the application's main window is not a dialogSetIcon(m_hIcon, TRUE); // Set big icon SetIcon(m_hIcon, FALSE); // Set small icon// TODO: Add extra initialization herenum=0;j=0;num_pri=0;boxmark_str="";m_num="";return TRUE; // return TRUE unless you set the focus to a control}void CNewDlg::OnSysCommand(UINT nID, LPARAM lParam) {if ((nID & 0xFFF0) == IDM_ABOUTBOX){CAboutDlg dlgAbout;dlgAbout.DoModal();}else{CDialog::OnSysCommand(nID, lParam);}}// If you add a minimize button to your dialog, you will need the code below // to draw the icon. For MFC applications using the document/view model, // this is automatically done for you by the framework.void CNewDlg::OnPaint(){if (IsIconic()){CPaintDC dc(this); // device context for paintingSendMessage(WM_ICONERASEBKGND, (WPARAM) dc.GetSafeHdc(), 0);// Center icon in client rectangleint cxIcon = GetSystemMetrics(SM_CXICON);int cyIcon = GetSystemMetrics(SM_CYICON);CRect rect;GetClientRect(&rect);int x = (rect.Width() - cxIcon + 1) / 2; int y = (rect.Height() - cyIcon + 1) / 2;// Draw the icondc.DrawIcon(x, y, m_hIcon);}else{CDialog::OnPaint();}}// The system calls this to obtain the cursor to display while the user drags// the minimized window.HCURSOR CNewDlg::OnQueryDragIcon(){return (HCURSOR) m_hIcon;}void CNewDlg::EnQueue(Queue *p_obj, int wt, int &bestw,int i,int n){if(i==n){if(wt>bestw)bestw=wt;}else p_obj-> add(wt);}int CNewDlg::MaxLoading(){p_obj=new Queue(1000);p_obj->add(-1);int i=0;//重大修改int i=1;int Ew=0;bestw=0;while(true){if(Ew+w[i]<=c)// Ew=w[i]<=cEnQueue(p_obj,Ew+w[i],bestw,i,n);EnQueue(p_obj,Ew,bestw,i,n);Ew=p_obj-> Delete();if(Ew==-1){if(p_obj-> Isempty())return bestw;p_obj-> add(-1);Ew=p_obj-> Delete();i++;}}}void CNewDlg::OnBtnLoad(){// TODO: Add your control notification handler code here GetDlgItemText(IDC_EDIT_AMOUNT,str);//箱子的数目n=atoi(str);// int *ptr=new int [n];w=new int[n];GetDlgItemText(IDC_EDIT_NUM,m_num);int m=m_num.GetLength();p=new char[m+1];// strcpy(p,s_num);for(int i=0;i<m;i++)p[i]=m_num.GetAt(i);for( i=0;i<m;i++)if(p[i]!=44) // num=atom(s.GetAt(i));{p[i]-=48;num=p[i];num_pri=num_pri*10+num;// num=0;}else{// num=num/10;if(j<n){w[j]=num_pri;j++;num_pri=0;}// ss=w[j];}GetDlgItemText(IDC_EDIT_MAXLOAD,s_maxload);c=atoi(s_maxload);MaxLoading();ss.Format("%d",bestw); SetDlgItemT ext(IDC_EDIT_OUTPUT,"轮船的最大载重量是:"+ss);}void CNewDlg::OnBtnClear(){// TODO: Add your control notification handler code herenum=0;j=0;num_pri=0;c=0;n=0;GetDlgItemText(IDC_EDIT_NUM,m_num);if(m_num!=""){delete[]w;delete[]p;delete[]p_obj;}else{AfxMessageBox("没有输入有效字符!");}// m_num="";SetDlgItemT ext(IDC_EDIT_OUTPUT,""); SetDlgItemT ext(IDC_EDIT_AMOUNT,""); SetDlgItemT ext(IDC_EDIT_MAXLOAD,""); SetDlgItemT ext(IDC_EDIT_NUM,"");}。

算法设计与分析实验指导书(计算机科学与技术系)编写兰州交通大学电子与信息工程学院2018年3月目录实验7 分支限界法-1 (3)一、实验目的 (3)二、实验仪器设备 (3)三、实验原理 (3)四、实验内容及注意事项 (3)五、实验步骤 (3)5.1 装载问题 (3)1)最基本的队列式分支限界法。
(3)2) 改进的队列式分支限界法 (4)3)队列式分支限界法,包含最优解 (5)4) 优先队列式分支限界法,包含最优解。
(8)六、实验数据整理与结果分析 (10)七、实验总结 (11)八、实验报告 (11)实验7 分支限界法-1一、实验目的(1)掌握分支限界法的各种不同的具体方法,包括队列式、改进的队列式以及优先队列式的区别。
(2)通过实验掌握分支限界法思想和方法;(3)培养学生的动手能力。
二、实验仪器设备(1)计算机;(2)C++编译调试环境。
三、实验原理掌握将算法转换为可运行程序的步骤。
四、实验内容及注意事项(1)装载问题。
五、实验步骤5.1 装载问题1)最基本的队列式分支限界法。
只计算最优值,没有计算最优解。
#include"stdafx.h"#include<cstdlib>#include<iostream>#include<queue>using namespace std;//子函数,将当前活节点加入队列template<class Type>void EnQueue(queue<Type> &Q, Type wt, Type &bestw, int i, int n){if (i == n) //可行叶结点{if (wt>bestw) bestw = wt;}else Q.push(wt); //非叶结点}//装载问题先尽量将第一艘船装满//队列式分支限界法,返回最优载重量template<class Type>Type MaxLoading(Type w[], Type c, int n){//初始化数据queue<Type> Q; //保存活节点的队列Q.push(-1); //-1的标志是标识分层int i = 1; //i表示当前扩展节点所在的层数Type Ew = 0; //Ew表示当前扩展节点的重量Type bestw = 0; //bestw表示当前最优载重量//搜索子集空间树while (true){if (Ew + w[i] <= c) //检查左儿子EnQueue(Q, Ew + w[i], bestw, i, n); //将左儿子添加到队列//将右儿子添加到队列即表示不将当前货物装载在第一艘船EnQueue(Q, Ew, bestw, i, n);Ew = Q.front(); Q.pop(); //取下一个节点为扩展节点并将重量保存在Ewif (Ew == -1) //检查是否到了同层结束{if (Q.empty()) return bestw; //遍历完毕,返回最优值Q.push(-1); //添加分层标志Ew = Q.front(); Q.pop(); //删除分层标志,进入下一层i++;}}return bestw;}int main(int argc, char* argv[]){int w[5] = { 0, 1, 2, 3 };int c = 5;int n = 3;int bestp = MaxLoading(w, c, n);cout << "best p=" << bestp << endl;return 0;}2) 改进的队列式分支限界法加入了进入右子树的上界函数。
第1篇一、实验目的1. 理解并掌握分枝限界法的基本原理和实现方法。
2. 通过实际编程,运用分枝限界法解决实际问题。
3. 比较分析分枝限界法与其他搜索算法(如回溯法)的优缺点。
4. 增强算法设计能力和编程实践能力。
二、实验内容本次实验主要涉及以下内容:1. 分支限界法的基本概念和原理。
2. 分支限界法在单源最短路径问题中的应用。
3. 分支限界法的实现步骤和代码编写。
4. 分支限界法与其他搜索算法的对比分析。
三、实验环境1. 操作系统:Windows 102. 编程语言:Python3.83. 开发环境:PyCharm四、实验步骤1. 算法描述:分支限界法是一种用于解决组合优化问题的算法,其基本思想是在问题的解空间树中,按照一定的搜索策略,优先选择有潜力的节点进行扩展,从而减少搜索空间,提高搜索效率。
2. 程序代码:下面是使用Python实现的分支限界法解决单源最短路径问题的代码示例:```pythonimport heapqclass Node:def __init__(self, vertex, distance, parent): self.vertex = vertexself.distance = distanceself.parent = parentdef __lt__(self, other):return self.distance < other.distancedef branch_and_bound(graph, source):初始化优先队列和已访问节点集合open_set = []closed_set = set()添加源节点到优先队列heapq.heappush(open_set, Node(source, 0, None))主循环,直到找到最短路径while open_set:弹出优先队列中最小距离的节点current_node = heapq.heappop(open_set)检查是否已访问过该节点if current_node.vertex in closed_set:continue标记节点为已访问closed_set.add(current_node.vertex)如果当前节点为目标节点,则找到最短路径if current_node.vertex == target:path = []while current_node:path.append(current_node.vertex)current_node = current_node.parentreturn path[::-1]遍历当前节点的邻居节点for neighbor, weight in graph[current_node.vertex].items():if neighbor not in closed_set:计算新节点的距离distance = current_node.distance + weight添加新节点到优先队列heapq.heappush(open_set, Node(neighbor, distance, current_node))没有找到最短路径return None图的表示graph = {0: {1: 2, 2: 3},1: {2: 1, 3: 2},2: {3: 2},3: {1: 3}}源节点和目标节点source = 0target = 3执行分支限界法path = branch_and_bound(graph, source)print("最短路径为:", path)```3. 调试与测试:在编写代码过程中,注意检查数据结构的使用和算法逻辑的正确性。
旅⾏售货员问题(分⽀限界法)⼀、实验内容运⽤分⽀限界法解决0-1背包问题(或者旅⾏售货员问题、或者装载问题、或者批处理作业调度)使⽤优先队列式分⽀限界法来求解旅⾏售货员问题⼆、所⽤算法基本思想及复杂度分析1.算法基本思想分⽀限界法常以⼴度优先或以最⼩耗费有限的⽅式搜索问题的解空间树。
问题的解空间树是表⽰问题解空间的⼀棵有序树,常见的有⼦集树和排列树。
在搜索问题的解空间树时,分⽀限界法和回溯法的主要区别在于它们对当前扩展节点所采⽤的扩展⽅式不同。
在分⽀限界法中,每⼀个活结点只有⼀次机会成为扩展节点。
活结点⼀旦成为扩展节点,就⼀次性产⽣其所有⼉⼦节点。
在这些⼉⼦节点中,导致不可⾏解或导致⾮最优解的⼉⼦节点被舍弃,其余⼉⼦节点被加⼊活结点表中。
此后,从活结点表中取下⼀节点为当前扩展节点。
并重复上述节点扩展过程。
这个过程移⾄持续到找到所需的解或活结点表为空为⽌。
从活结点表中选择下⼀扩展节点的不同⽅式导致不同的分⽀限界法。
最常见的有以下两种⽅式:(1)队列式分⽀限界法队列式分⽀限界法将活结点表组织成⼀个队列,并按队列的先进先出原则选取下⼀个节点为当前扩展节点。
(2)优先队列式分⽀限界法优先队列式的分⽀限界法将活结点表组织成⼀个优先队列,并按优先队列中规定的节点优先级选取优先级最⾼的下⼀个节点成为当前扩展节点。
2.问题分析及算法设计问题分析:(1)解旅⾏售货员问题的优先队列式分⽀限界法⽤优先队列存储活结点表。
(2)活结点m在优先队列中的优先级定义为:活结点m对应的⼦树费⽤下界lcost。
(3)lcost=cc+rcost,其中,cc为当前结点费⽤,rcost为当前顶点最⼩出边费⽤加上剩余所有顶点的最⼩出边费⽤和。
(4)优先队列中优先级最⼤的活结点成为下⼀个扩展结点。
(5)排列树中叶结点所相应的载重量与其优先级(下界值)相同,即:叶结点所相应的回路的费⽤(bestc)等于⼦树费⽤下界lcost的值。
算法设计:(1)要找最⼩费⽤旅⾏售货员回路,选⽤最⼩堆表⽰活结点优先队列。
算法分析与设计实验报告第 X次实验输出第1艘船的载重量输出第2艘船的载重量输出待装上轮船的集装箱的重量。
1代表对应集装箱装上轮船,0代表对应集装箱不装上轮船输出所有装上第1艘轮船的集装箱的重量。
输出是否可以将集装箱全部装上两艘轮船。
输出时间。
附录:完整代码#include "MaxHeap.h" #include <iostream>#include<cstdlib>#include<time.h>#include<iomanip>#include<stdlib.h> using namespace std; //定义集装箱的个数const int N = 4;class bbnode;/*============================================================================定义HeapNode类来存储最大堆中顶点的信息。
============================================================================*/ template<class Type>class HeapNode{template<class T>friend void AddLiveNode(MaxHeap<HeapNode<T>>& H,bbnode *E,T wt,bool ch,int lev);template<class Ty>friend Ty MaxLoading(Ty w[],Ty c,int n,int bestx[]);public:operator Type() const{return uweight;}private:bbnode *ptr; //指向活节点在子集树中相应节点的指针Type uweight; //活节点优先级(上界)int level; //活节点在子集树中所处的层序号};/*============================================================================定义bbnode类来定义子集空间树中的结点类型。
优先队列分支限界法的算法模拟1.引言1.1 概述优先队列分支限界法是一种常用的剪枝算法,用于解决许多实际问题的最优解或近似解。
该算法的核心思想是通过优先队列,按照一定的优先级对搜索空间进行探索,以找到最优解。
在解决一些组合优化问题时,通常需要遍历一棵决策树,枚举所有可能的解空间。
然而,遍历整个搜索空间是非常耗时的,因为搜索空间往往是巨大的。
为了降低搜索的复杂度,我们可以通过一些策略进行剪枝,从而减少搜索的冗余。
优先队列分支限界法就是其中一种常用的剪枝算法。
它利用了优先队列的数据结构,通过动态维护一个优先级队列来确定下一步搜索的位置。
每次选择队首的最优节点进行扩展,同时舍弃掉一些次优节点,以降低搜索的复杂度。
在算法模拟中,我们首先需要定义问题的解空间,然后确定问题的约束条件和目标函数。
接着,通过构建优先队列来存储待搜索的节点,并定义优先队列的排序规则。
在搜索过程中,不断从队首取出最优节点进行扩展,同时根据问题的约束条件进行剪枝。
通过优先队列分支限界法,我们可以在保证解的可行性的同时,尽可能地减少搜索的空间,从而更加高效地寻找最优解。
这种算法能应用于诸多实际问题,如旅行商问题、任务调度问题等。
在人工智能、运筹学等领域,优先队列分支限界法都有广泛的应用前景。
综上所述,本文将对优先队列分支限界法进行算法模拟,并探讨其应用前景。
进一步研究该算法在解决实际问题中的有效性和效率,有助于提高问题求解的效率和质量。
1.2 文章结构本篇长文将按照以下结构进行展开:1. 引言1.1 概述:简要介绍优先队列分支限界法的算法模拟背景和重要性。
1.2 文章结构:详细阐述本篇长文的结构和各个部分的内容安排。
1.3 目的:明确本篇长文的写作目的和对读者的具体要求。
2. 正文2.1 优先队列:首先解释优先队列的概念、特点和应用场景,并介绍常见的优先队列实现方式。
2.2 分支限界法:详细介绍分支限界法的基本思想、解题步骤和应用领域,以帮助读者全面理解该算法。
实验五优先队列式分支限界法解装载问题09电信实验班I09660118 徐振飞一、实验题目实现书本P201所描述的优先队列式分支限界法解装载问题二、实验目的(1)掌握并运用分支限界法基本思想(2)运用优先队列式分支限界法实现装载问题(3)比较队列式分支限界法和优先队列式分支限界法的优缺点三、实验内容和原理(1)实验内容有一批共n个集装箱要装上2艘载重量分别为c1和c2的轮船,其中集装箱i的重量为Wi,且∑=+≤niiccw121,要求确定是否有一个合理的装载方案可将这n个集装箱装上这2艘轮船。
如果有,请给出方案。
(2)实验原理解装载问题的优先队列式分支限界法用最大优先队列存储活结点表。
活结点x在优先队列中的优先级定义为从根结点到结点x的路径所相应的载重量再加上剩余集装箱的重量之和。
优先队列中优先级最大的活结点成为下一个扩展结点。
优先队列中活结点x的优先级为x.uweight。
以结点x为根的子树中所有结点相应的路径的载重量不超过x.uweight。
子集树中叶结点所相应的载重量与其优先级相同。
因此在优先队列式分支限界法中,一旦有一个叶结点成为当前扩展结点,则可以断言该叶结点所相应的解即为最优解,此时终止算法。
上述策略可以用两种不同方式来实现。
第一种方式在结点优先队列的每一个活结点中保存从解空间树的根结点到该活结点的路径,在算法确定了达到最优值的叶结点时,就在该叶结点处同时得到相应的最优解。
第二种方式在算法的搜索进程中保存当前已构造出的部分解空间树,在算法确定了达到最优值的叶结点时,就可以在解空间树中从该叶结点开始向根结点回溯,构造出相应的最优解。
在下面的算法中,采用第二种方式。
四、源程序import parator;import java.util.Iterator;import java.util.PriorityQueue;import java.util.Scanner;public class test5 {public void addLiveNode(PriorityQueue<HeapNode> H,bbnode E,int wt,boolean ch,int lev){bbnode b = new bbnode(E,ch);HeapNode N = new HeapNode(b, wt, lev);H.add(N);}public int maxLoading(int w[],int c,int n,boolean bestx[]){PriorityQueue<HeapNode> H = new PriorityQueue(1000,new comp());/*生成最大堆*/int[] r = new int[n+1];r[n] = 0;for(int j=n-1;j>0;j--){r[j] = r[j+1] + w[j+1];}int i = 1;bbnode E = new bbnode(null,false);int Ew = 0;while(i!=n+1){if(Ew+w[i]<=c){addLiveNode(H, E, Ew+w[i]+r[i], true, i+1);}addLiveNode(H, E, Ew+r[i], false, i+1);HeapNode N;N=H.poll();i = N.level;E = N.ptr;Ew = N.uweight - r[i-1];}//构造最优解for(int j=n;j>0;j--){bestx[j] = E.Lchild;E = E.parent;}return Ew;}public static void main(String[] args){System.out.println("请输入物品总数:");Scanner sc1 = new Scanner(System.in);int n = sc1.nextInt();int[] w = new int[n+1];System.out.println("请输入物品重量:");Scanner sc2 = new Scanner(System.in);for(int i=1;i<=n;i++){w[i] = sc2.nextInt();}System.out.println("请输入箱子重量:");Scanner sc3 = new Scanner(System.in);int c1 = sc3.nextInt();int c2 = sc3.nextInt();boolean[] bestx = new boolean[100];test5 t = new test5();//处理第一个箱子System.out.println("first:"+t.maxLoading(w, c1, n, bestx));System.out.print("可装重为:");int count = 0;for(int i=1;i<=n;i++){if(bestx[i]){count++;System.out.print(w[i]+" "); /*输出一个可行方案*/ }}System.out.println();/*处理第二个箱子*/int m = n - count;int[] ww = new int[m+1];int k = 1;for(int i=1;i<=n;i++){if(!bestx[i]){ww[k] = w[i];k++;bestx[i] = false;}}System.out.println();System.out.println("second:"+t.maxLoading(ww, c2, m, bestx));System.out.print("可装重为:");for(int i=1;i<=m;i++){if(bestx[i]){System.out.print(ww[i]+" "); /*输出一个可行方案*/ }}}}/*堆结点类*/class HeapNode{bbnode ptr;int uweight;int level;public HeapNode(){}public HeapNode(bbnode ptr,int uweight,int level){this.ptr = ptr;this.uweight = uweight;this.level = level;}public String toString(){return ""+this.uweight;}}class bbnode{bbnode parent;boolean Lchild;public bbnode(bbnode node,boolean ch){this.parent = node;this.Lchild = ch;}}//定义比较器类class comp implements Comparator<HeapNode>{@Overridepublic int compare(HeapNode o1, HeapNode o2) {int dif = o1.uweight-o2.uweight;if(dif>0){return -1;}else if(dif==0){return 0;}else{return 1;}}}五、实验结果和分析a.输入格式说明:(1)首先输入物品总数量(2)第二栏输入所有物品重量(3)第三栏输入2个箱子的重量b.输出格式说明:(1)首先输出first的字样,后面的数字表示第一个箱子所能装载的最大重量,紧接着的一行输出一种可以选择装载的方案(2)Second字样后面的数字表示第二个箱子所能装载的最大重量,紧接着的一行输出一种可行方案经过分析,上述结果正确。
六、实验心得和体会通过实验,了解了分支限界法的基本思想。
掌握了利用优先队列式分支限界法实现具体的装载问题。
由于本次实验利用java.util 包下的PriorityQueue代替算法中的最大堆,免去了编写实现最大堆的程序代码(但这并不表示我不会编写最大堆程序,在这次实验中,最大堆的实现并不是主要部分),所以本次实验实现的相对顺利。
存在的问题及分析:在此例中最合理的装载方法是第一个箱子装载重量为:10 50的物品,第二个箱子装载重量为20 20的物品。
分析:由于程序中先装载第一个箱子,然后再装载第二个箱子;而分支限界法一旦扩展结点到达叶子结点时,程序便终止退出。
所以在此例中当第一个箱子装满后(此时重量为10 20 30的物品已被装走),余下的物品重量只有50 20 两个,因此第二个箱子无法装满。
解决方法:可以对程序稍作改变,寻找所有可行的装载方案,然后利用装满率(装载量/箱子重量)来判断那种方案是最优的装载方案。
这样做必定会增加程序的时间和空间复杂度,当数据量很大时,不适合(此时可以改变输入数据的顺序去试探装载方案,然后人为确定一个相对最有的装载方案)。