四年级巧求面积

巧求面积教学目标：学会应用所学知识解决一些实际问题及较复杂的面积计算。

教学过程：一、知识要点我们已经学会了计算长方形、正方形的面积，运用这些知识可以解决许多有关面积的问题。

但是有些比较复杂的关于长方形、正方形的面积计算，生搬硬套公式往往不能奏效，这时，我们可以运用一些巧妙的解题技巧来解决问题。

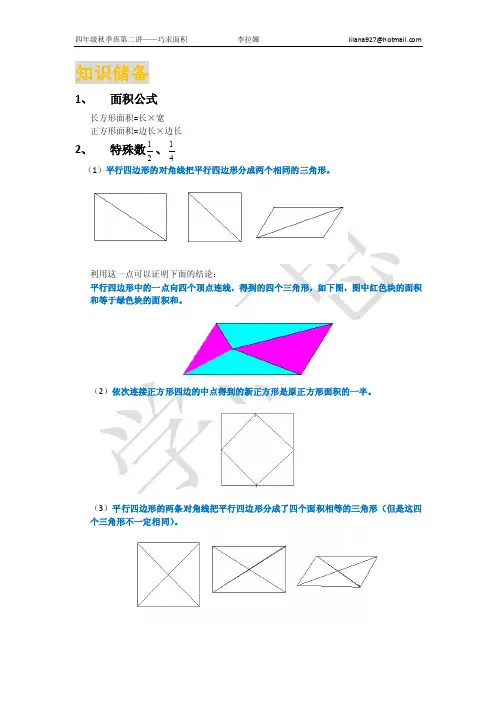
1、面积公式：长方形的面积=长×宽（S=a×b a表示长方形的长b表示长方形的宽）正方形的面积=边长×边长（S=a×a a表示正方形的边长）2、锦囊妙计。

（1）割补法：把图形分割或添补成可求面积的长方形或正方形，再用长方形或正方形的面积公式计算。

（2）平移法: 通过平移的方法把分散的面积集中到一个长方形或正方形中，再用长方形或正方形的面积公式计算。

二、典型例题1、割补法例1.张爷爷有一块如下图的菜地，你能帮他计算出菜地的面积吗？（单位:米）（1）学生先独立思考，说一说自己的想法。

（2）解析：通过观察可以看出，这个图形可以采用分割的方法，把图形分割成两个长方形，图形的面积=两个长方形面积的和；或者在图形的左上角补上一个正方形，把它变成一个大长方形，图形的面积=大长方形面积－正方形面积。

（课件动画演示）列式：30×20+（30+20）×40=2600（平方米）列式：30×40+（30+40）×20=2600（平方米）列式：（20+30）×（40+30）－30×30=2600（平方米）答：张爷爷的菜地面积是2600平方米。

例2：下图为一个长50米、宽25 米的标准游泳池。

它的四周铺设了宽2米的白瓷地砖(阴影部分)。

求游泳池面积和地砖面积。

长解析：从图中可以看出，游泳池是长方形，可直接运用长方形面积公式计算出来。

而瓷砖面积不规则，无法直接运用长方形面积公式计算。

如果把大长方形中间空白部分的小长方形割掉（课件动画演示），剩下的就是阴影部分的面积，所以阴影的面积=大长方形的面积－小长方形的面积，即可求出地砖面积。

第十三讲巧求面积知识点睛：长方形的面积＝长×宽，正方形的面积＝边长×边长。

但是，在平时的学习过程中，我们常常会遇到一些已知条件比较隐蔽、图形比较复杂、不能简单地用公式直接求出所求面积的题目，这就需要我们切实掌握有关概念，利用“割补”“平移”“旋转”等方法，使复杂的问题转化为普通的长方形、正方形面积的问题，从而正确解答。

例1:下图是一个养禽专业户用一段16米的篱笆围成的一个长方形养鸡场，求它的占地面积。

练习1：1、右图是某个养禽专业户用一段长13米的篱笆围成的一个长方形养鸡场，求养鸡场的占地面积。

2、用56米长的木栏围成长或宽是20米的长方形，其中一边利用围墙，怎样才能使围成的面积最大？例2:下图是一块水稻田，请计算它的面积（单位：米）练习2：1、求下图的面积。

（单位：分米）2、求下面图形的面积（单位：米）8471040302020151020155020例3：一个长方形，如果宽不变，长增加6米，那么它的面积增加54平方米；如果长不变，宽减少3米，那么它的面积减少36平方米。

这个长方形原来的面积是多少平方米？练习3：1、一个长方形，如果宽不变，长减少3米，那么它的面积减少24平方米；如果长不变，宽增加4米，那么它的面积增加60平方米。

这个长方形原来的面积是多少平方米？2、一个长方形，如果宽不变，长增加5米，那么它的面积增加30平方米；如果长不变，宽增加3米，那么它的面积增加48平方米。

这个长方形原来的面积是多少平方米？例4：如图所示，一块长方形草地。

长方形长16米，宽10米，中间有两条宽2米的道路，一条是长方形，另一条是平行四边形。

求有草部分（阴影部分）的周长。

练习4：1、求下图阴影部分的面积（单位：厘米）。

2、如图所示，公园里有一个长方形湖泊，湖上有一座景观桥（桥墩忽略不计）。

已知湖泊长30米，宽20米，桥面的宽度为2米，这座桥的面积是多少？210例5：街心花园有一个正方形花坛，四周有一条宽1米的通道（如图），如果通道的面积是12平方米，那么中间花坛的面积是多少平方米？练习5：1、有一个正方形水池，在它的周围修一条宽4米的路，这条路的面积是240平方米，这个水池的面积是多少？2、下图中阴影部分是边长为5厘米的正方形，四块完全一样的长方形的宽是8厘米，求这个图形的面积。

第二讲 巧求面积一、常用面积公式二、剪拼及构造思想很多题往往不能直接用公式算出来，这时应灵活思考，把原图尽量剪拼或构造成比较容易算的图形。

（该能力的培养及熟练掌握需要同学们大量练题） 1、割补：把不规则的剪拼为规则的、好算的。

2、容斥（重叠原理）：若在计算中出现重叠的情况，把多算的减出去即可。

例1 如图，一张长方形纸片，长7厘米，宽5厘米， 把它的右上角往下折叠，再把左下角往上折叠，未盖 住的阴影部分的面积是多少平方厘米？解析：本题的隐藏条件，右边及左下方均为正方形。

法一：阴影部分为长方形，尝试找它的长与宽长：7-5=2（CM） 宽：5-2=3（CM） 面积：3×2=6（CM 2）法二：阴影部分包含于大长方形中，可用大长方形的面积-两个正方形的面积大长方形面积：7×5=35（CM 2）两正方形面积：5×5+（7-5）×（7-5）=29（CM 2）阴影面积：35-29=6（CM 2）例2 一块长方形草坪（图中阴影部分）长是宽的2倍， 它的四周围是总面积为34平方米的1米宽的小路，求 草坪的面积是多少平方米？解析：面积已知的小路形状并不规则，我们可以先把它切割为规则的图形，如右图4个角都是边长为1米的正方形，其余是4个宽为1的长方形。

且A=2B34-4=30（M 2） ……减去4个角的面积30÷3=10（M 2）……2个B 合起来是1个A 的面积，一共就是3个A 的面积，所以÷3 草坪的长10÷1=10（M） 宽:10÷2=5（M）面积：10×5=50（M 2）S=abAA B B例3 一块长方形铁板，长15分米，宽12分米，如果长和宽各减少2分米，面积比原来减少多少平方分米？（图略）法一：将减少的部分切割为两个规则的长方形，求其面积和。

算式略法二：用大长方形面积减去小长方形面积就是所求面积大长方形：15×12=180（DM2）小长方形：（15-2）×（12-2）=130（DM2）减少的面积：180-130=50（DM2）例4 如图所示，外侧大正方形的边长是10cm，在里面画两条对角线、一个圆、两个正方形，阴影总面积为26cm2，最小的正方形的边长为多少厘米？解析：观察本图是一对称图形，阴影部分的面积不易一一求得，那就利用剪拼，将它们拼补在一块。

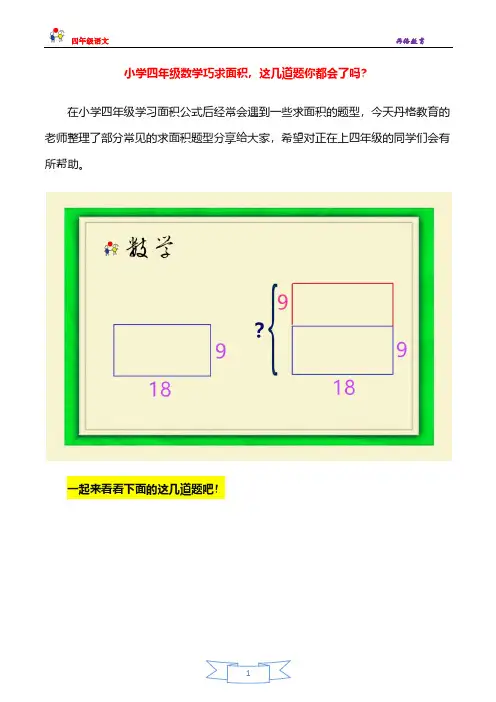
小学四年级数学巧求面积，这几道题你都会了吗？在小学四年级学习面积公式后经常会遇到一些求面积的题型，今天丹格教育的老师整理了部分常见的求面积题型分享给大家，希望对正在上四年级的同学们会有所帮助。

一起来看看下面的这几道题吧！例题1：把一个长18米，宽9米的长方形的宽增加9米，可以得到一个什么图形？它的面积是多少平方米？分析：在遇到这类题时，可以在练习本上画出图形，将已知条件标注到图形上去，在图形结合帮助我们分析和判断。

有时有同学觉得画图太麻烦，况且题目很简单，就是不画图分析也可以做出来。

但是画图图形可以直观地帮助我们建立模型，当模型建立起来后就可以不用再画图，直接在脑海里调用即可。

这道题已知宽为米9，将宽增加9米，得到的新的宽是：9+9＝18（米）。

宽和长相等，因此得到的新的图形是一个正方形。

再求正方形的面积，这道题就迎刃而解了。

解：宽：9+9＝18（米）面积：18×18＝324（平方米）综合列式：（9＋9）×18＝324（平方米）答：可以得到一个正方形，它的面积是324平方米。

例题2：一个长方形周长是40分米，且宽比长短2分米，求长方形的面积是多少？分析：长方形的周长公式为：周长＝（长＋宽）×2，容易知道：长＋宽＝周长÷2，在这道题目中，长加宽的和为：40÷2＝20。

这道题还告诉了“宽比长短2分米”，也就是知道长与宽的和，以及长与宽的差，是一个简单的和差问题。

宽（较小数）：（20－2）÷2＝9（分米），长（较大数）：20－9＝11（分米）。

解：宽：（20－2）÷2＝9（分米）长：20－9＝11（分米）面积：9×11＝99（平方分米）答：长方形的面积是99平方分米。

例题3：已知一个长方形的长为68厘米，宽为50厘米，在这个长方形中截取一个最大的正方形，求这个正方形的面积是多少？剩下部分是一个什么图形？它的面积是多少？分析：通过画图帮助我们分析判断，剪下的正方形的边长最大为50厘米，求正方形面积直接用正方形的面积公式即可得出答案。

我们曾经学过的三角形、长方形、正方形、平行四边形、梯形、菱形、圆和扇形等图形，一般称为基本图形或规则图形，我们的面积及周长都有相应的公式直接计算。

如下表：实际问题中，有些图形不是以基本图形的形状出现，而是由一些基本图形组合、拼凑成的，它们的面积及周长无法应用公式直接计算。

一般我们称这样的图形为不规则图形。

那么，不规则图形的面积及周长怎样去计算呢？我们可以针对这些图形通过实施割补、剪拼等方法将它们转化为基本图形的和、差关系，问题就能解决了。

例1：如右图，甲、乙两图形都是正方形，它们的边长分别是10厘米和12厘米求阴影部分的面积。

一句话：阴影部分的面积等于甲、乙两个正方形面积之和减去三个“空白”三角形（△ABG、△BDE、△EFG）的面积之和。

例2：如右图，正方形ABCD的边长为6厘米，△ABE、△ADF与四边形AECF的面积彼此相等，求三角形AEF的面积。

一句话：因为△ABE、△ADF与四边形AECF的面积彼此相等，都等于正方形ABCD 面积的三分之一，也就是12厘米.解：S△ABE=S△ADF=S四边形AECF=12在△ABE中，因为AB=6.所以BE=4，同理DF=4，因此CE=CF=2，∴△ECF的面积为2×2÷2=2。

所以S△AEF=S四边形AECF-S△ECF=12-2=10（平方厘米）。

例3：两块等腰直角三角形的三角板，直角边分别是10厘米和6厘米。

如右图那样重合.求重合部分（阴影部分）的面积。

一句话：阴影部分面积=S△ABG-S△BEF，S△ABG和S△BEF都是等腰三角形。

总结：对于不规则图形面积的计算问题一般将它转化为若干基本规则图形的组合，分析整体与部分的和、差关系，问题便得到解决。

常用的基本方法有1相加法这种方法是将不规则图形分解转化成几个基本规则图形，分别计算它们的面积，然后相加求出整个图形的面积。

例如：求下图整个图形的面积。

一句话：半圆的面积+正方形的面积=总面积2相减法这种方法是将所求的不规则图形的面积看成是若干个基本规则图形的面积之差。

四年级巧求面积练习题1、把一个长16米,宽9米的长方形的宽增加7米，可得到一个什么平面图形？面积是多少平方米？2、一个长方形的周长是40厘米，且宽比长短2厘米，求长方形的面积是多少？3、一个长62厘米，宽50厘米的长方形中截取一个最大的正方形，这个正方形的面积是多少？4、如果把一个边长是10厘米的正方形的边长增加3厘米，这个正方形的面积将增加多少平方厘米？5、有一个边长是20米的鱼塘,在它的四周有一条宽2米的道路，求道路的面积是多少平方米？6、求下面图形的面积是多少?（单位：厘米）7、大小两个正方形部分重合，边长分别是7厘米和5厘米，重合部分面积是10平方厘米，求两个正方形盖住的面积是多少？8、两个相同的长方形，长是14厘米，宽是6厘米,把它们按如图叠放在一起，这个图形的面积是多少？B组9、一个长方形的长是30厘米，宽是20厘米，如果长和宽各增加5厘米，求面积增加多少平方厘米？10、有两个一样的正方形,拼成一个长方形，周长比原来减少8厘米,求拼成的长方形的面积？11、四个同样大小的长方形和一正方形拼成了一个大正方形，大正方形的面积是100平方厘米，小正方形的面积是4平方厘米，求长方形的宽是多少？12、有一个长方形，如果它的长减少2米,或宽减少3米，它的面积就减少24平方米，求原来的长方形的面积是多少？13、一个打谷场,长是60米，宽是45米，扩建后长增加了15米,宽增加了8米，那么打谷场的面积增加了多少平方米？6、如图排列着两个正方形，左边一个大正方形的边长是6厘米，求阴影部分的面积？14、如图长方形ABCD的长是12厘米，宽是6厘米，M、N分别为AB、CD的中点,求阴影部分的面积？15、如果长方形的长是9厘米，宽是6厘米，三角形ADE和DCF的面积都是长方形面积的三分之一,求阴影部分的面积?。

师：今天的知识，都比较有挑战性。

消磨光你们的耐心了吗？生：没有。

师：看来大家意志都很坚定嘛。

那我们接着看一下更难理解的例题四吧。

给你们两分钟时间读题，然后跟同桌之间讨论讨论，思考一下如何解决这个问题。

师：想好了吗？生：想好了。

师：那哪组派个代表来说说自己的发现。

生1：长方形游泳池的面积是50乘以25等于1250平方米。

师：对吗？生：对。

师：没错，因为由题意我们可以知道游泳池的长和宽分别是50米和25米。

所以就很容易求出游泳池的面积。

师：那还有那个小组愿意说说自己的成果？生2：可以把白瓷砖的部分分成4个小长方形。

师：那可以怎么分呢？生：横着分也可以，竖着分也可以。

师：很好，那我们就先横着分。

【课件演示分割动画。

】师：这样的话，我们可以发现红色的这两个长方形面积怎么求？生2：50乘以2。

师：这样求出来的是几个小长方形的面积？生2：一个。

师：所以要再……生2：乘以2 。

师：没错，请坐。

这样我们就求出了红色的两个小长方形的面积，还剩两个小长方形呢。

怎么办？生：25加上4在乘以2。

师：为什么25要加上4？生：因为这两个长方形的两头都比游泳池的宽长2米，就是总共长4米了。

师：听懂了吗？生：听懂了。

师：没错，解释得非常到位。

【课件演示竖向的两个长方形的面积求解过程。

】师：刚刚我们是纵向的分割白瓷砖，先在我们还可以……生：横向的分割。

师：没错，现在请你们自己写在课堂练习本上吧。

【教师下台巡视。

然后讲解解题过程。

】师：我们刚刚了解两种分割方法，如果我们不分割的话，该怎么求？生：用大的减去小的。

师：大的指什么？小的指什么？生：大的指白瓷砖包括游泳池的面积。

师：这个大的长宽分别是多少？生：50加4和25加4。

师：没错，所以我们就可以求出大的长方形面积是1566平方米。

师：那刚刚说的小的面积是指什么？生：是指游泳池的面积。

【课件演示方法三的解题动画。

】师：没错，所以，我们只要把大的面积减去小的面积，就可以得到白色瓷砖的面积了。

我们曾经学过的三角形、长方形、正方形、平行四边形、梯形、菱形、圆和扇形等图形，一般称为基本图形或规则图形，我们的面积及周长都有相应的公式直接计算.如下表：实际问题中，有些图形不是以基本图形的形状出现，而是由一些基本图形组合、拼凑成的，它们的面积及周长无法应用公式直接计算.一般我们称这样的图形为不规则图形；；那么，不规则图形的面积及周长怎样去计算呢？我们可以针对这些图形通过实施割补、剪拼等方法将它们转化为基本图形的和、差关系，问题就能解决了.例1：如右图，甲、乙两图形都是正方形，它们的边长分别是10厘米和12厘米求阴影部分的面积.一句话：阴影部分的面积等于甲、乙两个正方形面积之和减去三个“空白”三角形（△ABG、△BDE、△EFG）的面积之和；；例2：如右图，正方形ABCD的边长为6厘米，△ABE、△ADF与四边形AECF的面积彼此相等，求三角形AEF的面积.一句话：因为△ABE、△ADF与四边形AECF的面积彼此相等，都等于正方形ABCD 面积的三分之一，也就是12厘米.；；解：S△ABE=S△ADF=S四边形AECF=12在△ABE中，因为AB=6.所以BE=4，同理DF=4，因此CE=CF=2，∴△ECF的面积为2×2÷2=2.所以S△AEF=S四边形AECF-S△ECF=12-2=10（平方厘米）.例3：两块等腰直角三角形的三角板，直角边分别是10厘米和6厘米.如右图那样重合.求重合部分（阴影部分）的面积；；一句话：阴影部分面积=S△ABG-S△BEF，S△ABG和S△BEF都是等腰三角形.总结：对于不规则图形面积的计算问题一般将它转化为若干基本规则图形的组合，分析整体与部分的和、差关系，问题便得到解决.常用的基本方法有1相加法这种方法是将不规则图形分解转化成几个基本规则图形，分别计算它们的面积，然后相加求出整个图形的面积.例如：求下图整个图形的面积；；；一句话：半圆的面积+正方形的面积=总面积2相减法这种方法是将所求的不规则图形的面积看成是若干个基本规则图形的面积之差.例如：下图，求阴影部分的面积.一句话：先求出正方形面积再减去里面圆的面积即可.3直接求法这种方法是根据已知条件，从整体出发直接求出不规则图形面积.例如：下图，求阴影部分的面积.一句话：通过分析发现阴影部分就是一个底是2、高是4的三角形.4重新组合法这种方法是将不规则图形拆开，根据具体情况和计算上的需要，重新组合成一个新的图形，设法求出这个新图形面积即可.例如：下图，求阴影部分的面积.一句话：拆开图形，使阴影部分分布在正方形的4个角处，如下图.5辅助线法这种方法是根据具体情况在图形中添一条或若干条辅助线，使不规则图形转化成若干个基本规则图形，然后再采用相加、相减法解决即可.例如：下图，求两个正方形中阴影部分的面积.一句话：此题虽然可以用相减法解决，但不如添加一条辅助线后用直接法作更简便（如下图）根据梯形两侧三角形面积相等原理（蝴蝶定理），可用三角形丁的面积替换丙的面积，组成一个大三角ABE，这样整个阴影部分面积恰是大正方形面积的一半.6割补法这种方法是把原图形的一部分切割下来补在图形中的另一部分使之成为基本规则图形，从而使问题得到解决.例如：下图，若求阴影部分的面积.一句话：把右边弓形切割下来补在左边，这样整个阴影部分面积恰是正方形面积的一半.7平移法这种方法是将图形中某一部分切割下来平行移动到一恰当位置，使之组合成一个新的基本规则图形，便于求出面积.例如：下图，求阴影部分的面积.一句话：可先沿中间切开把左边正方形内的阴影部分平行移到右边正方形内，这样整个阴影部分恰是一个正方形.8旋转法这种方法是将图形中某一部分切割下来之后，使之沿某一点或某一轴旋转一定角度贴补在另一图形的一侧，从而组合成一个新的基本规则的图形，便于求出面积.例如：下图（1），求阴影部分的面积.一句话：左半图形绕B点逆时针方向旋转180°，使A与C重合，从而构成右图（2）的样子，此时阴影部分的面积可以看成半圆面积减去中间等腰直角三角形的面积.9对称添补法这种方法是作出原图形的对称图形，从而得到一个新的基本规则图形.原来图形面积就是这个新图形面积的一半.例如：下图，求阴影部分的面积.一句话：沿AB在原图下方作关于AB为对称轴的对称扇形ABD.弓形CBD的面积的一半就是所求阴影部分的面积.10重叠法这种方法是将所求的图形看成是两个或两个以上图形的重叠部分.例如：下图，求阴影部分的面积.一句话：可先求两个扇形面积的和，减去正方形面积，因为阴影部分的面积恰好是两个扇形重叠的部分.。

我们曾经学过的三角形、长方形、正方形、平行四边形、梯形、菱形、圆和扇形等图形,一般称为基本图形或规则图形.我们的面积及周长都有相应的公式直接计算。

如下表：实际问题中,有些图形不是以基本图形的形状出现,而是由一些基本图形组合、拼凑成的,它们的面积及周长无法应用公式直接计算。

一般我们称这样的图形为不规则图形。

那么,不规则图形的面积及周长怎样去计算呢？我们可以针对这些图形通过实施割补、剪拼等方法将它们转化为基本图形的和、差关系,问题就能解决了。

先看三道例题感受一下↓↓↓例1：如右图,甲、乙两图形都是正方形,它们的边长分别是10厘米和12厘米求阴影部分的面积。

一句话：阴影部分的面积等于甲、乙两个正方形面积之和减去三个“空白”三角形（△ABG、△BDE、△EFG）的面积之和。

例2：如右图,正方形ABCD的边长为6厘米,△ABE、△ADF与四边形AECF的面积彼此相等,求三角形AEF的面积。

一句话：因为△ABE、△ADF与四边形AECF的面积彼此相等,都等于正方形ABCD面积的三分之一,也就是12厘米.解：S△ABE=S△ADF=S四边形AECF=12在△ABE中,因为AB=6.所以BE=4,同理DF=4,因此CE=CF=2,∴△ECF的面积为2×2÷2=2。

所以S△AEF=S四边形AECF-S△ECF=12-2=10（平方厘米）。

例3：两块等腰直角三角形的三角板,直角边分别是10厘米和6厘米。

如右图那样重合.求重合部分（阴影部分）的面积。

一句话：阴影部分面积=S△ABG-S△BEF,S△ABG和S△BEF都是等腰三角形总结：对于不规则图形面积的计算问题一般将它转化为若干基本规则图形的组合,分析整体与部分的和、差关系,问题便得到解决。

常用的基本方法有↓↓↓一、相加法这种方法是将不规则图形分解转化成几个基本规则图形,分别计算它们的面积,然后相加求出整个图形的面积。

例如：求下图整个图形的面积一句话：半圆的面积+正方形的面积=总面积二、相减法这种方法是将所求的不规则图形的面积看成是若干个基本规则图形的面积之差。

第十六章巧求面积知识导航同学们都知道，物体的表面或封闭图形的大小，叫作物体的面积。

我们已经学会运用公式求长方形和正方形的面积了。

但是，在平时的学习过程中，我们常常会遇到一些已知条件比较隐蔽、图形比较复杂、不能简单地用公式直接求出面积的题目。

这就需要我们切实掌握有关概念，利用“割补”“平移”“旋转”“分解”“合并”等转化方法，化难为易，化繁为简，从而正确解决问题。

图解思维训练题例1　一个长方形，如果宽不变，长增加6米，那么它的面积就增加54平方米；如果长不变，宽减少4米，那么它的面积就减少48平方米。

这个长方形的面积是多少平方米？图解思路如下图所示，这个长方形的宽用“增加的面积÷增加的长”可以求出，长用“减少的面积÷减少的宽”可以求出，然后用“长×宽”求出面积。

规范解答宽：54÷6＝9（米）长：48÷4＝12（米）面积：9×12＝108（平方米）答：这个长方形的面积是108平方米。

例2　下图中大正方形的边长比小正方形的边长多4厘米，大正方形的面积比小正方形的面积多96平方厘米。

大正方形和小正方形的面积各是多少平方厘米？图解思路如下图所示，把大正方形比小正方形多出的96平方厘米分成了三部分。

这三部分中一部分是带阴影的小正方形，另外两个部分是没有阴影的长方形。

可以先求出带阴影的小正方形的面积，再用多出的96平方厘米减去带阴影的小正方形的面积，得到两个长方形的面积，再除以2就是一个长方形的面积。

长方形的面积知道了，再除以宽就是长。

这个长等于小正方形的边长，边长求出来了，面积就迎刃而解了。

规范解答带阴影的小正方形的面积：4×4＝16（平方厘米）一个长方形的面积：（96-16）÷2＝40（平方厘米）长方形的长（也就是小正方形的边长）：40÷4＝10（厘米）小正方形的面积：10×10＝100（平方厘米）大正方形的面积：100＋96＝196（平方厘米）答：大正方形的面积是196平方厘米，小正方形的面积是100平方厘米。

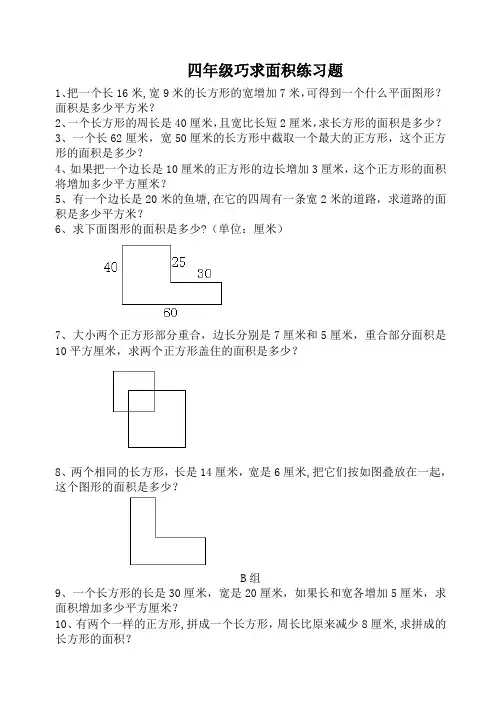
四年级巧求面积练习题 Document number：NOCG-YUNOO-BUYTT-UU986-四年级巧求面积练习题1、把一个长16米，宽9米的长方形的宽增加7米，可得到一个什么平面图形面积是多少平方米2、一个长方形的周长是40厘米，且宽比长短2厘米，求长方形的面积是多少3、一个长62厘米，宽50厘米的长方形中截取一个最大的正方形，这个正方形的面积是多少4、如果把一个边长是10厘米的正方形的边长增加3厘米，这个正方形的面积将增加多少平方厘米5、有一个边长是20米的鱼塘，在它的四周有一条宽2米的道路，求道路的面积是多少平方米6、求下面图形的面积是多少（单位：厘米）7、大小两个正方形部分重合，边长分别是7厘米和5厘米，重合部分面积是10平方厘米，求两个正方形盖住的面积是多少8、两个相同的长方形，长是14厘米，宽是6厘米，把它们按如图叠放在一起，这个图形的面积是多少B组9、一个长方形的长是30厘米，宽是20厘米，如果长和宽各增加5厘米，求面积增加多少平方厘米10、有两个一样的正方形，拼成一个长方形，周长比原来减少8厘米，求拼成的长方形的面积11、四个同样大小的长方形和一正方形拼成了一个大正方形，大正方形的面积是100平方厘米，小正方形的面积是4平方厘米，求长方形的宽是多少12、有一个长方形，如果它的长减少2米，或宽减少3米，它的面积就减少24平方米，求原来的长方形的面积是多少13、一个打谷场，长是60米，宽是45米，扩建后长增加了15米，宽增加了8米，那么打谷场的面积增加了多少平方米6、如图排列着两个正方形，左边一个大正方形的边长是6厘米，求阴影部分的面积14、如图长方形ABCD的长是12厘米，宽是6厘米，M、N分别为AB、CD的中点，求阴影部分的面积15、如果长方形的长是9厘米，宽是6厘米，三角形ADE和DCF的面积都是长方形面积的三分之一，求阴影部分的面积。

巧求面积教学目标：学会应用所学知识解决一些实际问题及较复杂的面积计算。

教学过程：一、知识要点我们已经学会了计算长方形、正方形的面积，运用这些知识可以解决许多有关面积的问题。

但是有些比较复杂的关于长方形、正方形的面积计算，生搬硬套公式往往不能奏效，这时，我们可以运用一些巧妙的解题技巧来解决问题。

1、面积公式：长方形的面积=长×宽（S=a×b a表示长方形的长b表示长方形的宽）正方形的面积=边长×边长（S=a×a a表示正方形的边长）2、锦囊妙计。

（1）割补法：把图形分割或添补成可求面积的长方形或正方形，再用长方形或正方形的面积公式计算。

（2）平移法: 通过平移的方法把分散的面积集中到一个长方形或正方形中，再用长方形或正方形的面积公式计算。

二、典型例题1、割补法例1.张爷爷有一块如下图的菜地，你能帮他计算出菜地的面积吗？（单位:米）（1）学生先独立思考，说一说自己的想法。

（2）解析：通过观察可以看出，这个图形可以采用分割的方法，把图形分割成两个长方形，图形的面积=两个长方形面积的和；或者在图形的左上角补上一个正方形，把它变成一个大长方形，图形的面积=大长方形面积－正方形面积。

（课件动画演示）列式：30×20+（30+20）×40=2600（平方米）列式：30×40+（30+40）×20=2600（平方米）列式：（20+30）×（40+30）－30×30=2600（平方米）答：张爷爷的菜地面积是2600平方米。

例2：下图为一个长50米、宽25 米的标准游泳池。

它的四周铺设了宽2米的白瓷地砖(阴影部分)。

求游泳池面积和地砖面积。

长解析：从图中可以看出，游泳池是长方形，可直接运用长方形面积公式计算出来。

而瓷砖面积不规则，无法直接运用长方形面积公式计算。

如果把大长方形中间空白部分的小长方形割掉（课件动画演示），剩下的就是阴影部分的面积，所以阴影的面积=大长方形的面积－小长方形的面积，即可求出地砖面积。

巧求面积教学目标：学会应用所学知识解决一些实际问题及较复杂的面积计算。

教学过程：一、知识要点我们已经学会了计算长方形、正方形的面积，运用这些知识可以解决许多有关面积的问题。

但是有些比较复杂的关于长方形、正方形的面积计算，生搬硬套公式往往不能奏效，这时，我们可以运用一些巧妙的解题技巧来解决问题。

1、面积公式：长方形的面积=长×宽（S=a×b a表示长方形的长b表示长方形的宽）正方形的面积=边长×边长（S=a×a a表示正方形的边长）2、锦囊妙计。

（1）割补法：把图形分割或添补成可求面积的长方形或正方形，再用长方形或正方形的面积公式计算。

（2）平移法: 通过平移的方法把分散的面积集中到一个长方形或正方形中，再用长方形或正方形的面积公式计算。

二、典型例题1、割补法例1.张爷爷有一块如下图的菜地，你能帮他计算出菜地的面积吗？（单位:米）（1）学生先独立思考，说一说自己的想法。

（2）解析：通过观察可以看出，这个图形可以采用分割的方法，把图形分割成两个长方形，图形的面积=两个长方形面积的和；或者在图形的左上角补上一个正方形，把它变成一个大长方形，图形的面积=大长方形面积－正方形面积。

（课件动画演示）列式：30×20+（30+20）×40=2600（平方米）列式：30×40+（30+40）×20=2600（平方米）列式：（20+30）×（40+30）－30×30=2600（平方米）答：张爷爷的菜地面积是2600平方米。

例2：下图为一个长50米、宽25 米的标准游泳池。

它的四周铺设了宽2米的白瓷地砖(阴影部分)。

求游泳池面积和地砖面积。

宽长解析：从图中可以看出，游泳池是长方形，可直接运用长方形面积公式计算出来。

而瓷砖面积不规则，无法直接运用长方形面积公式计算。

如果把大长方形中间空白部分的小长方形割掉（课件动画演示），剩下的就是阴影部分的面积，所以阴影的面积=大长方形的面积－小长方形的面积，即可求出地砖面积。

中间有条宽 4 米的道路，求草地（阴影部分）例 2 】求右图的面积。

（单位：厘米）第 13 讲 巧算面积 巧点晴——方法和技巧解答比较复杂的关于长方形、正方形的周长和面积的计算问题 时，不能生搬硬套公式，需要运用移位、合并、分解、转化等解题技 巧。

因此，敏锐的观察力和灵活的思维在解题中至关重要。

巧指导——例题精讲A 级 冲刺名校·基础点晴【例 1】下图①是一块长方形草地， 长方形长 255米，宽 105米， 中间有两条道路，一条是长方形的，一条是平行四边形的。

问有草部 分的面积是多少？分析与解 将上图①中的四块阴影部分平移， 拼在一起， 组成一 个长、宽各少 5 米的长方形（如上图②阴影部分） 。

（255－5）×（ 105－5）=25000（平方米） 答：有草部分的面积是 25000 平方米。

小结 将图形进行适当平移，问题就变得容易解答了。

做一做 1 如下图所示，一块长方形草地，长 100 米，宽 80 米，ABC D②5的面44分析与解 1 把原图分割成两个长方形（如上图①） ，图中两个 长方形的面积之和就是该图的面积。

6×（ 10＋4）＋ 10×4=124（平方厘米）分析与解 2 把原图分割成两个长方形（如上图②） ，图中两个 长方形的面积分别为：（10+6）×4=64（平方厘米），10×6=60（平方 厘米）。

因此，该图的总面积是： 64+60=124（平方厘米）。

分析与解 3 如果把原图补上一个连长是 10 厘米的正方形（如 上图），就成了一个长方形，它的面积是： （6+10）×（ 10+4） =224 （平方厘米③）。

用这个长方形的面积减去正方形的面积，就是该图 的面积。

224-10×10=124（平方厘米） 答：面积为 124 平方厘米。

小结 想一想，该题的图还能怎样分，怎样计算它的面积？ 做一做 2 计算下列图形的面积。