最小生成树-数学建模
- 格式：ppt
- 大小：384.50 KB
- 文档页数：39
下载文档原格式
合集下载
最小生成树MinimumSpanningTree
设邻接矩阵初值：不存在的边其权值为Infinity
8
1、Prim算法
算法求精－初始化
将根r涂红加入红点集U，TE＝φ。
对每个白点i (0≤i ≤n-1, i≠r ), i所关联的最短紫边（r,i）的 长度为G[r][i], 这n-1条最短紫边构成了初始的候选轻边集。
因为树边为空，故将T[0..n-2]全部用来存放候选轻边集。
❖设V(G)={0,1,…,n-1}
❖算法的每一步均是在连接红、白点集的紫 边中选一轻边扩充到T（贪心），T从任意 一点r开始（r为根），直至U＝V为止。 MST性质保证了贪心选择策略的正确性。
3
1、Prim算法
如何找轻边？
❖可能的紫边集
设红点集|U|=k, 白点集|V-U|=n-k，则可能的紫边 数为：k(n-k)。
//将(u,v)涂红加入树中，白点v加入红点集
ModifyCandidateSet(…);
//根据新红点v调整候选轻边集
}
}
算法终止时U＝V，T=(V,TE)
6
1、Prim算法
实例
6 1
5
35 4
05
1
3
27 2
4
5
6
60 5
1
1
3
∞2
∞
4
5
0
151
3
2
5
2 4
4
5
0
151
3
2
5
2 4
4
5
0
151 2
int i, minpos, min=Infinity; for (i=k; i<n-1; i++) //遍历候选集找轻边
8
1、Prim算法
算法求精－初始化
将根r涂红加入红点集U，TE＝φ。
对每个白点i (0≤i ≤n-1, i≠r ), i所关联的最短紫边（r,i）的 长度为G[r][i], 这n-1条最短紫边构成了初始的候选轻边集。
因为树边为空，故将T[0..n-2]全部用来存放候选轻边集。
❖设V(G)={0,1,…,n-1}
❖算法的每一步均是在连接红、白点集的紫 边中选一轻边扩充到T（贪心），T从任意 一点r开始（r为根），直至U＝V为止。 MST性质保证了贪心选择策略的正确性。
3
1、Prim算法
如何找轻边？
❖可能的紫边集
设红点集|U|=k, 白点集|V-U|=n-k，则可能的紫边 数为：k(n-k)。
//将(u,v)涂红加入树中，白点v加入红点集
ModifyCandidateSet(…);
//根据新红点v调整候选轻边集
}
}
算法终止时U＝V，T=(V,TE)
6
1、Prim算法
实例
6 1
5
35 4
05
1
3
27 2
4
5
6
60 5
1
1
3
∞2
∞
4
5
0
151
3
2
5
2 4
4
5
0
151
3
2
5
2 4
4
5
0
151 2
int i, minpos, min=Infinity; for (i=k; i<n-1; i++) //遍历候选集找轻边
数学建模最小生成树例题
数学建模最小生成树例题摘要：一、最小生成树的定义和应用1.定义：最小生成树是一种图论中的算法，用于找到一个加权连通图的最小生成树。
2.应用：在网络分析、运筹学、数据压缩等领域具有广泛应用。
二、最小生成树的数学模型1.问题描述：给定一个加权连通图，求解其最小生成树。
2.模型建立：使用贪心算法，每次选择权值最小的边，累计得到最小生成树。
三、最小生成树的求解方法1.Kruskal 算法：按照权值从小到大的顺序依次选取边，每次选取的边需满足两个条件：一是选取的边所在的两个顶点不属于同一连通分量；二是选取的边的权值最小。
2.Prim 算法：从任意一个顶点开始，每次选择距离当前生成树距离最近的顶点，连接当前顶点与选取顶点之间的边，累计得到最小生成树。
四、最小生成树例题解析1.题目描述：给定一个加权连通图，求解其最小生成树。
2.解题步骤：a) 读题理解，提取关键信息；b) 建立数学模型，明确问题求解目标；c) 选择合适的算法，求解最小生成树；d) 输出结果，验证答案的正确性。
正文：最小生成树是一种图论中的算法，用于找到一个加权连通图的最小生成树。
最小生成树在网络分析、运筹学、数据压缩等领域具有广泛应用。
本文将介绍最小生成树的定义、数学模型、求解方法及例题解析。
一、最小生成树的定义和应用最小生成树是一种图论中的算法，用于找到一个加权连通图的最小生成树。
生成树是指一个连通图的生成树是指保留图中所有的节点，但只保留足以保持这些节点连通的边的集合。
最小生成树是生成树中边权值之和最小的生成树。
二、最小生成树的数学模型最小生成树问题的数学模型可以描述为：给定一个加权连通图G=(V,E)，其中每条边e=(u,v) 都关联一个非负权值w(u,v)，求解加权连通图的最小生成树。
三、最小生成树的求解方法目前求解最小生成树问题有两种经典算法：Kruskal 算法和Prim 算法。
1.Kruskal 算法：按照权值从小到大的顺序依次选取边，每次选取的边需满足两个条件：一是选取的边所在的两个顶点不属于同一连通分量；二是选取的边的权值最小。
最小生成树例子
最小生成树例子
最小生成树是一个在图论中常见的问题，通常在计算机网络和电路设计中出现。
它是指一个连通无环图，它的一棵生成树，如果再添加任何一条边都会产生环。
以下是一个简单的最小生成树的例子：
假设我们有一个由五个节点（A、B、C、D、E）和七条边组成的网络，每条边的权重表示连接两个节点所需的成本或距离。
节点 A - B: 3
节点 A - C: 5
节点 A - D: 6
节点 B - C: 4
节点 B - D: 7
节点 C - D: 8
节点 C - E: 2
节点 D - E: 9
节点 E - A: 10
我们可以使用Kruskal算法或Prim算法找到这个图的最小生成树。
在这个例子中，最小生成树可能是：A - B - C - D - E，总权重为18。
这是所有可能的生成树中权重最小的。
需要注意的是，这个结果可能会因图的结构和使用的算法而变化。
在实际应用中，可能还需要考虑其他因素，如网络的拓扑结构、流量需求等。
最小生成树算法详解
问题描述
Kruskal算法应用案例
问题描述
最小生成树问题的求解算法除了Prim算法和Kruskal算法之外，还有基于动态规划的算法、基于回溯的算法、基于分治的算法等。
应用场景
例如，在计算几何中，可以通过基于动态规划的算法求解最小包围矩形、最小包围圆、最小包围球等问题；在数值计算中，可以通过基于回溯的算法求解一元高次方程的根等。
其他算法比较与择优
Kruskal算法
Prim算法
Boruvka算法
各算法优缺点比较
根据实际应用场景选择算法
03
Boruvka算法
时间复杂度为O(ElogE)，其中E为边数，空间复杂度为O(E)。
各算法时间复杂度与空间复杂度比较
01
Kruskal算法
时间复杂度为O(ElogE)，其中E为边数，空间复杂度为O(E)。
时间复杂度：Prim算法的时间复杂度为O(ElogE)，其中E为边的数量。
Prim算法
总结词：Kruskal算法是另一种常用的最小生成树算法，其核心思想是通过将所有的边按照权值大小从小到大排序，然后依次选择每条边，如果这条边连接的两个顶点在已经生成的树中不构成环路，则将这条边加入到树中。详细描述：Kruskal算法的基本步骤如下将所有的边按照权值大小从小到大排序。初始化一颗空树作为生成的树的初始状态。从第一条边开始，遍历每条边，如果这条边连接的两个顶点在已经生成的树中不构成环路，则将这条边加入到树中。重复步骤3，直到所有的边都被遍历过。生成的树即为最小生成树。时间复杂度：Kruskal算法的时间复杂度为O(ElogE)，其中E为边的数量。
详细描述：Prim算法的基本步骤如下
1. 从一个任意顶点开始，将该顶点加入到已经访问过的顶点集合中。
Kruskal算法应用案例
问题描述
最小生成树问题的求解算法除了Prim算法和Kruskal算法之外，还有基于动态规划的算法、基于回溯的算法、基于分治的算法等。
应用场景
例如，在计算几何中，可以通过基于动态规划的算法求解最小包围矩形、最小包围圆、最小包围球等问题；在数值计算中，可以通过基于回溯的算法求解一元高次方程的根等。
其他算法比较与择优
Kruskal算法
Prim算法
Boruvka算法
各算法优缺点比较
根据实际应用场景选择算法
03
Boruvka算法
时间复杂度为O(ElogE)，其中E为边数，空间复杂度为O(E)。
各算法时间复杂度与空间复杂度比较
01
Kruskal算法
时间复杂度为O(ElogE)，其中E为边数，空间复杂度为O(E)。
时间复杂度：Prim算法的时间复杂度为O(ElogE)，其中E为边的数量。
Prim算法
总结词：Kruskal算法是另一种常用的最小生成树算法，其核心思想是通过将所有的边按照权值大小从小到大排序，然后依次选择每条边，如果这条边连接的两个顶点在已经生成的树中不构成环路，则将这条边加入到树中。详细描述：Kruskal算法的基本步骤如下将所有的边按照权值大小从小到大排序。初始化一颗空树作为生成的树的初始状态。从第一条边开始，遍历每条边，如果这条边连接的两个顶点在已经生成的树中不构成环路，则将这条边加入到树中。重复步骤3，直到所有的边都被遍历过。生成的树即为最小生成树。时间复杂度：Kruskal算法的时间复杂度为O(ElogE)，其中E为边的数量。
详细描述：Prim算法的基本步骤如下
1. 从一个任意顶点开始，将该顶点加入到已经访问过的顶点集合中。
最小树与最小树形图(数学建模)讲解
最小树与最小树形图（数学建模）讲解一、最小树的定义及性质1. 定义：最小树，又称最小树，是指在给定的带权无向图中，包含图中所有顶点的一个树形结构，且树中所有边的权值之和最小。
2. 性质：（1）最小树中不存在回路；（2）对于最小树中的任意两个顶点，它们之间有且仅有一条路径；（3）最小树中边的数量等于顶点数量减一；（4）在最小树中添加任意一条边，都会形成一条回路；（5）最小树不唯一，但权值之和相同。
二、求解最小树的方法1. Prim算法Prim算法是一种贪心算法，其基本思想是从图中的一个顶点开始，逐步添加边和顶点，直到形成最小树。
具体步骤如下：（1）初始化：选择一个顶点作为最小树的起点，将其加入最小树集合；（2）迭代：在最小树集合和非最小树集合之间，寻找一条权值最小的边，将其加入最小树集合；（3）重复步骤2，直到所有顶点都加入最小树集合。
2. Kruskal算法Kruskal算法同样是一种贪心算法，其基本思想是将图中的所有边按权值从小到大排序，然后依次选择权值最小的边，判断是否形成回路，若不形成回路，则将其加入最小树集合。
具体步骤如下：（1）初始化：将所有顶点视为独立的树；（2）按权值从小到大排序所有边；（3）迭代：选择权值最小的边，判断其是否形成回路，若不形成回路，则将其加入最小树集合；（4）重复步骤3，直到所有顶点都在同一棵树中。
三、最小树形图的定义及求解方法1. 定义：最小树形图，又称最优树形图，是指在给定的有向图中，找到一个包含所有顶点的树形结构，使得树中所有边的权值之和最小。
2. 求解方法：朱刘算法（Edmonds' Algorithm）朱刘算法是一种用于求解最小树形图的算法，其基本思想是通过寻找图中的最小权值环，进行收缩和扩展操作，最终得到最小树形图。
具体步骤如下：（1）寻找最小权值环；（2）对最小权值环进行收缩操作，将环中的顶点合并为一个新顶点；（3）在新图中寻找最小树形图；（4）将新图中的最小树形图扩展回原图，得到原图的最小树形图。
图的常用算法——最小生成树
TE= {（V1，V4）5，（V4，V2）3 ，（V4，V6）7，
（V6，V3）2 ，（V3，V5）6 } LW= {（V4，V7）15
9
第六次 U={ V1，V4，V2 ，V6，V3 ，V5，V7 } TE= {（V1，V4）5，（V4，V2）3 ，（V4，V6）7， （V6，V3）2 ，（V3，V5）6}，（V4，V7）15 } LW= { }
3
5
7
20
所以最小生成树由GE数组中的1，2，3，5，7 边组成。 2012-1-10
2012-1-10
10
2012-1-10
11
（4）算法如下： Procedure Prim(GA,CT); begin for I:=1 to n-1 do { 给CT赋初值，对应第0次的LW值 } [ CT[I].from :=1 ; ct[I].end: =I+1 ; ct[I].w:=GA[1, i+1 ]; for k:=1 to n-1 do { 进行n-1次循环，求出最小生成树的第K条边 } ①[ min:=maxint ; m:=k ; for j:=k to n-1 do if ct[j].w < min then min:=ct[j].w ; m:=j; ] ② if m<> k then ct[k] 与ct[m] 的交换 { 将最短边调到第K单元 }
1. 从图“G”的选取一个顶点放到“G’” 中，因只有一个顶点，因此该图是连通 的； 2. 以后每加入一个顶点，都要加入以该点 为顶点与已连通的顶点之中的一个顶点 为端点的一条边，使其既连通而不产生 回路，进行n-1次后，就产生G’，在G’ 中有n个顶点，n-1条边且不产生回路。
二、图的最小生成树
最小生成树算法总结
最小生成树算法总结最小生成树是指在一个无向连通图中，找到一个子树，使得这棵子树中所有边的权值之和最小。
最小生成树可以用于最优化问题，例如道路铺设、网络布线等。
下面将介绍三种最小生成树算法：Prim算法、Kruskal算法、Boruvka算法。
1. Prim算法Prim算法是一种贪心算法，从一个点开始，每次添加连接到已有集合中的最小边，直到所有点都在同一个集合中。
可以用以下步骤描述Prim算法：(1) 选择一个起点，将该起点加入最小生成树的顶点集合，然后将该顶点相邻的边加入边集合中。
(2) 从边集合中找到权值最小的一条边，将该边对应的顶点加入最小生成树的顶点集合，同时将该顶点相邻的边加入边集合中。
(3) 重复上述步骤，直到所有顶点都在最小生成树的顶点集合中。
Prim算法的实现可以使用堆优化，时间复杂度为O(E + VlogV)，其中E为边数，V为顶点数。
2. Kruskal算法Kruskal算法也是一种贪心算法，与Prim算法不同的是，Kruskal算法是按照边的权值从小到大依次添加，直到所有顶点都在同一个集合中。
可以用以下步骤描述Kruskal算法：(1) 将所有边按照权值从小到大排序。
(2) 依次取出排好序的边，如果该边所连接的两个顶点不在同一个集合中，就将这条边加入最小生成树的边集合中，并将这两个顶点合并到同一个集合中。
(3) 重复步骤(2)，直到所有顶点都在同一个集合中。
Kruskal算法的实现可以使用并查集，时间复杂度为O(ElogE)，其中E为边数。
3. Boruvka算法Boruvka算法是一种基于集合的分治算法，与Prim算法和Kruskal算法不同，Boruvka算法的时间复杂度是线性的。
可以用以下步骤描述Boruvka算法：(1) 对每个顶点建立单元素集合。
(2) 对每个集合，选择与该集合相连的最小权值的边，将这些边添加到最小生成树的边集合中，并将这些集合合并到同一个集合中。
(3) 如果只剩下一个集合，算法结束。
第3讲最小生成树
介绍最小树的两种算法： 介绍最小树的两种算法： Kruskal算法和 算法和Prim破圈法 破圈法. 算法和 破圈法
T
A Kruskal算法（或避圈法） 算法（或避圈法） 算法 步骤如下： 步骤如下： 1) 选择边 1，使得 1)尽可能小； 选择边e 使得w(e 尽可能小 尽可能小； 2) 若已选定边 e1, e2 ,..., ei ，则从 E \ {e1, e2 ,..., ei } 使得: 中选取ei +1 ，使得 i) G[{e1, e2 ,..., ei +1}] 为无圈图， 为无圈图， ii) w(ei +1 ) 是满足 的尽可能小的权， 是满足i)的尽可能小的权 的尽可能小的权， 3) 当第 步不能继续执行时，则停止 当第2)步不能继续执行时 则停止. 步不能继续执行时， 定理 由Kruskal算法构作的任何生成树 算法构作的任何生成树 T * = G[{e1, e2 ,..., eν −1}] 都是最小树 都是最小树.
v1
v2
v3
v4
v5
平凡树
（2）找图中生成树的方法 ） 可分为两种： 可分为两种：避圈法和破圈法 A 避圈法 : 深探法和广探法 B 破圈法
A 避圈法 定理3的充分性的证明提供了一种构造图的生 定理 的充分性的证明提供了一种构造图的生 成树的方法. 成树的方法 这种方法就是在已给的图G中 这种方法就是在已给的图 中，每步选出一 条边使它与已选边不构成圈，直到选够n-1条边为 条边使它与已选边不构成圈，直到选够 条边为 这种方法可称为“避圈法” 加边法” 止. 这种方法可称为“避圈法”或“加边法” 在避圈法中，按照边的选法不同， 在避圈法中，按照边的选法不同，找图中生 成树的方法可分为两种：深探法和广探法. 成树的方法可分为两种：深探法和广探法
最小生成树(最小支撑树)
(a)
图11-12
(b)
(c)
§3 最小生成树问题
一、求解最小生成树的破圈算法 算法的步骤：
1、在给定的赋权的连通图上任找一个圈。
2、在所找的圈中去掉一个权数最大的边（如果有两条或两条 以上的边都是权数最大的边，则任意去掉其中一条）。
3、如果所余下的图已不包含圈，则计算结束，所余下的图即最小生成树问题
给了一个无向图G=(V,E)，我们保留G的所有点，而删掉部分G的边或 者说保留一部分G的边，所获得的图G，称之为G的生成子图。在图11-12中， (b)和(c)都是(a)的生成子图。 如果图G的一个生成子图还是一个树，则称这个生成子图为生成树， 在图11-12中，(c)就是(a)的生成树。 最小生成树问题就是指在一个赋权的连通的无向图G中找出一个生成 树，并使得这个生成树的所有边的权数之和为最小。
个网络能联通7个学院办公室，并使总的线路长度为最短。
v2 3 1 4 v7 3 v6 5 2 8 v5 v3
7
v4
图11-14
v1 10
3
4
解：此问题实际上是求图11-14的最小生成树，这在例4中已经求得， 也即按照图11-13的(f)设计，可使此网络的总的线路长度为最短，为19 百米。 “管理运筹学软件”有专门的子程序可以解决最小生成树问题。
§3 最小生成树问题
例4 用破圈算法求图（a）中的一个最小生成树
v2 3 3 1 v3 v2 3 3 v6 v2 v4 v1 3 3 v6 v2 1 v3 v4
v1
10
7 3 4 v7 2 4 5 v5 v3 8
v4
v1
7 3 4 v7 2
4 5 v5 v3 7 8
v6
v2 v1 3 3 v6 v2 v1 3 3 v6
最小生成树(Minimal Spanning Tree，MST)问题
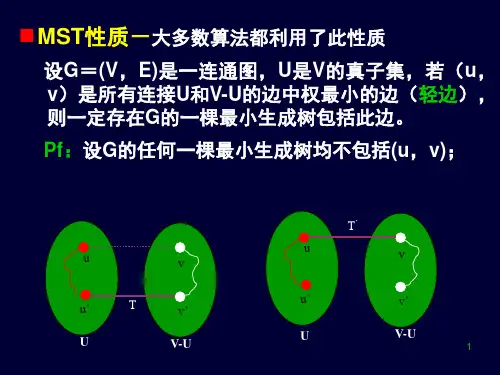
例7.6 最小生成树（Minimal Spanning Tree，MST）问题求解最小生成树的方法虽然很多，但是利用LINGO建立相应的整数规划模型是一种新的尝试。
这对于处理非标准的MST问题非常方便。
我们主要参考了文[7]。
在图论中，称无圈的连通图为树。
在一个连通图G中，称包含图G全部顶点的树为图G 的生成树。
生成树上各边的权之和称为该生成树的权。
连通图G的权最小的生成树称为图G 的最小生成树。
许多实际问题都可以归结为最小生成树。
例如,如何修筑一些公路把若干个城镇连接起来；如何架设通讯网络将若干个地区连接起来；如何修筑水渠将水源和若干块待灌溉的土地连接起来等等。
为了说明问题,以下面的问题作为范例。
范例：假设某电话公司计划在六个村庄架设电话线，各村庄之间的距离如图所示。
试求出使电话线总长度最小的架线方案。
为了便于计算机求解，特作如下规定：（1）节点V1表示树根；（2）当两个节点之间没有线路时，规定两个节点之间的距离为M（较大的值）。
MST的整数规划模型如下：Array运用WinSQB软件：Network Modeling1——3——4——2，，，，4——6——5 最短距离为8Solution for Minimal Spanning Tree Problem road07-25-2000 From Node Connect To Distance/Cost From Node Connect To Distance/Cost1 Node4 Node2 2 4 Node6 Node5 22 Node1 Node3 1 5 Node4 Node6 13 Node3 Node4 2Total Minimal Connected Distance or Cost = 8直接用人脑算：避圈法：把图中所以的点分为V 与_V 两个部分。
其步骤为：（1） 从图中任选一点i v 为树根， 让i v V ∈，图中其余的点均包含在_V 中。
最小生成树算法详解
最小生成树算法详解常见的最小生成树算法包括普里姆（Prim）算法和克鲁斯卡尔（Kruskal）算法。
下面将详细介绍这两种算法的原理和步骤。
普里姆算法的基本思想是从一个顶点出发，每次选择与当前生成树相连的权重最小的边，直到生成树包含所有的顶点。
具体步骤如下：1.初始化一个空的生成树和一个空的候选边集合。
2.随机选择一个起始顶点，将其加入生成树中，并将与该顶点相连的边加入候选边集合。
3.从候选边集合中选择权重最小的边，如果该边的另一个顶点不在生成树中，则将该顶点加入生成树，并将与该顶点相连的边加入候选边集合。
4.重复步骤3，直到生成树包含所有的顶点。
克鲁斯卡尔算法的基本思想是从所有边中选取权重最小的边，然后逐步扩展生成树，直到生成树包含所有的顶点。
具体步骤如下：1.初始化一个空的生成树和一个空的候选边集合。
2.将图中的所有边按权重从小到大排序，并加入候选边集合中。
3.从候选边集合中选择权重最小的边，如果该边的两个顶点不在同一个连通分量中，则将该边加入生成树，并将其两个顶点合并到同一个连通分量中。
4.重复步骤3，直到生成树包含所有的顶点。
普里姆算法和克鲁斯卡尔算法都能够求解最小生成树，它们的主要区别在于选择候选边的方式不同。
普里姆算法每次选择与当前生成树相连的权重最小的边，而克鲁斯卡尔算法每次选择整个图中权重最小的边。
因此，普里姆算法适用于稠密图，而克鲁斯卡尔算法适用于稀疏图。
总结起来，最小生成树算法是图论中的一种重要算法，用于求解连通图中的一棵权重最小的生成树。
普里姆算法和克鲁斯卡尔算法是常见的最小生成树算法，它们的主要区别在于选择候选边的方式不同。
这些算法的时间复杂度与图的边数有关，通常为O(ElogE)。
在实际应用中，可以根据具体问题选择适合的算法来求解最小生成树。
最小生成树-数学建模.ppt
用Kruskal算法可求出最小生成树，在前面 给出的Kruskal算法的MATLAB程序中，边权矩阵b 的值改为此处的边权矩阵，顶点数n改为9即可。
上一页 下一页 主 页
T= 7 8 15 12 39 46 47 45 13
c = 4.4300
机器的分组：{3， 9}，
{1，2，5}，
{4，6，7，8}。
返回
整理边权矩阵
初始化：j0, T, c0, k0； 对所有顶点i ,t(i)i .
B: 图的边权矩阵; T: 生成树的边集; C: 生成树的权; t: 顶点所属子树的编号
jj+1
t(B(1,j))t(B(2,j)) Y
N
TT(B(1,j),B(2,j)), cc+B(3,j),kk+1，i 0
i i+1
引例：计算机网络的线路设计
最小生成树
最大生成树 1) 一个完全图Kn有多少不同 的生成树？ 2) 如何求其最小生成树?
引例：计算机网络的线路设计
10个顶点的完全图，其不同的生成树就有 一亿棵。
一般地，n个顶点的完全图，其不同的生成 树个数为nn-2。
30 个 顶 点 的 完 全 图 就 有 3028 个 生 成 树 ， 求 最小生成树时用穷举法是无效的。
假设有13种零件，需在9台机器上 加工。在各台机器上加工的零件号在下 表中给出。
范例：制造系统的分组技术
机器 1 2 3 4 5 6 7 8 9
加工 2,3, 2,7, 1,6 3, 3,7, 5 4, 4, 6
的零 7,8, 8, 件 9, 11,1
12, 2
5, 8,9, 10 12,
13
10 10
3
上一页 下一页 主 页
T= 7 8 15 12 39 46 47 45 13
c = 4.4300
机器的分组：{3， 9}，
{1，2，5}，
{4，6，7，8}。
返回
整理边权矩阵
初始化：j0, T, c0, k0； 对所有顶点i ,t(i)i .
B: 图的边权矩阵; T: 生成树的边集; C: 生成树的权; t: 顶点所属子树的编号
jj+1
t(B(1,j))t(B(2,j)) Y
N
TT(B(1,j),B(2,j)), cc+B(3,j),kk+1，i 0
i i+1
引例：计算机网络的线路设计
最小生成树
最大生成树 1) 一个完全图Kn有多少不同 的生成树？ 2) 如何求其最小生成树?
引例：计算机网络的线路设计
10个顶点的完全图，其不同的生成树就有 一亿棵。
一般地，n个顶点的完全图，其不同的生成 树个数为nn-2。
30 个 顶 点 的 完 全 图 就 有 3028 个 生 成 树 ， 求 最小生成树时用穷举法是无效的。
假设有13种零件，需在9台机器上 加工。在各台机器上加工的零件号在下 表中给出。
范例：制造系统的分组技术
机器 1 2 3 4 5 6 7 8 9
加工 2,3, 2,7, 1,6 3, 3,7, 5 4, 4, 6
的零 7,8, 8, 件 9, 11,1
12, 2
5, 8,9, 10 12,
13
10 10
3
最小生成树-数学建模
城市电信局有许多业务如收费， 营业，112，114等，希望在全市范围 实现计算机联网服务，共享各种资源。 一个主要关心的问题是：用数据通讯 线把一组站点联结起来，而不允许通 讯线在非站点处相交，如何连接可使 通讯线的花费最小？
A
5
上一页 下一页 主 页
引例：计算机网络的线路设计
8
1
2
5
7
1
5
6
3
10
1
.5
.5 3
1
2
9
.14
5
80
.87
7
.75
.67 4
6
.5 3
.5
1
2
9
.14
5
80
7
.75
.67 4
6
模型结果
机器的分组： {3，9}，
.5 3 9
.5
1
2
.14
{1，2，5}，
5
{4，6，7，8}。
8
0 7
.75
.67 4
6
你能给出对应于该机器分组
的零件分类吗？
A
30
返上一回页 下一页 主 页
5 9 0 7 9 11 7 12 12 17
11]
9 15 7 0 3 17 10 7 15 15
12]
12 16 9 3 0 8 10 6 15 15
13]
14 8 11 17 8 0 9 14 8 16
14]
12 11 7 10 10 9 0 8 6 11
15]
16 18 12 7 6 14 8 0 11 11
2 边权矩阵：
6 b=[1 1 1 2 2 3 3 4; 2 4 5 3 5 4 5 5;
数学建模四大模型归纳
四类基本模型1 优化模型1.1 数学规划模型线性规划、整数线性规划、非线性规划、多目标规划、动态规划。
1.2 微分方程组模型阻滞增长模型、SARS 传播模型。
1.3 图论与网络优化问题最短路径问题、网络最大流问题、最小费用最大流问题、最小生成树问题(MST)、旅行商问题(TSP)、图的着色问题。
1.4 概率模型决策模型、随机存储模型、随机人口模型、报童问题、Markov 链模型。
1.5 组合优化经典问题● 多维背包问题(MKP)背包问题：n 个物品，对物品i ，体积为i w ，背包容量为W 。
如何将尽可能多的物品装入背包。
多维背包问题：n 个物品，对物品i ，价值为i p ，体积为i w ，背包容量为W 。
如何选取物品装入背包，是背包中物品的总价值最大。
多维背包问题在实际中的应用有：资源分配、货物装载和存储分配等问题。
该问题属于NP 难问题。
● 二维指派问题(QAP)工作指派问题：n 个工作可以由n 个工人分别完成。
工人i 完成工作j 的时间为ij d 。
如何安排使总工作时间最小。
二维指派问题（常以机器布局问题为例）：n 台机器要布置在n 个地方，机器i 与k 之间的物流量为ik f ，位置j 与l 之间的距离为jl d ，如何布置使费用最小。
二维指派问题在实际中的应用有：校园建筑物的布局、医院科室的安排、成组技术中加工中心的组成问题等。
●旅行商问题(TSP)旅行商问题：有n个城市，城市i与j之间的距离为d，找一条经过n个城ij市的巡回（每个城市经过且只经过一次，最后回到出发点），使得总路程最小。
●车辆路径问题(VRP)车辆路径问题（也称车辆计划）：已知n个客户的位置坐标和货物需求，在可供使用车辆数量及运载能力条件的约束下，每辆车都从起点出发，完成若干客户点的运送任务后再回到起点，要求以最少的车辆数、最小的车辆总行程完成货物的派送任务。
TSP问题是VRP问题的特例。
●车间作业调度问题(JSP)车间调度问题：存在j个工作和m台机器，每个工作由一系列操作组成，操作的执行次序遵循严格的串行顺序，在特定的时间每个操作需要一台特定的机器完成，每台机器在同一时刻不能同时完成不同的工作，同一时刻同一工作的各个操作不能并发执行。
数学建模最小生成树例题
数学建模最小生成树例题例题1：某城市计划建设一条高速公路，需要在若干个村庄之间选择一条最优路径。
已知各个村庄之间的距离，请使用最小生成树算法为高速公路选择最优路径。
参考答案：最小生成树算法可以用于解决此类问题。
常用的最小生成树算法有Kruskal算法和Prim算法。
1. Kruskal算法：按照边的权重从小到大排序，依次将边加入生成树，如果加入的边与已选择的边不构成环，则加入，否则不加入。
2. Prim算法：首先选择权重最小的边加入生成树，然后从剩余的边中选择一条与已选择的边相连且权重最小的边加入生成树，直到所有边都加入生成树。
例题2：一个通信网络由若干个节点和边组成，节点代表城市，边代表通信线路。
已知各个城市之间的距离和通信需求，请使用最小生成树算法为该通信网络设计一个最优的通信线路网。
参考答案：最小生成树算法可以用于解决此类问题。
通过最小生成树算法，我们可以找到一个包含所有节点且边的总权重最小的树形结构，以满足各个城市之间的通信需求。
常用的最小生成树算法有Kruskal算法和Prim算法。
1. Kruskal算法：按照边的权重从小到大排序，依次将边加入生成树，如果加入的边与已选择的边不构成环，则加入，否则不加入。
2. Prim算法：首先选择权重最小的边加入生成树，然后从剩余的边中选择一条与已选择的边相连且权重最小的边加入生成树，直到所有边都加入生成树。
例题3：一个城市的电力网由多个节点和边组成，节点代表发电厂或变电站，边代表输电线路。
已知各个节点之间的电抗和传输功率，请使用最小生成树算法为该城市电力网设计一个最优的输电线路。
参考答案：最小生成树算法可以用于解决此类问题。
通过最小生成树算法，我们可以找到一个包含所有节点且边的总电抗最小的树形结构，以满足各个节点之间的电力传输需求。
常用的最小生成树算法有Kruskal算法和Prim算法。
1. Kruskal算法：按照边的电抗从小到大排序，依次将边加入生成树，如果加入的边与已选择的边不构成环，则加入，否则不加入。
最小生成树-数学建模
1
.5
.5 3
1
2
9
.14
5
80
.87
7
.75
.67 4
6
.5 3
.5
1
2
9
.14
5
80
7
.75
.67 4
6
模型结果
机器的分组： {3，9}，
.5 3 9
.5
1
2
.14
{1，2，5}，
5
{4，6，7，8}。
8
0 7
.75
.67 4
6
你能给出对应于该机器分组
的零件分类吗？
返回
最小生成树问题的0-1规划模型
17]
22 22 17 15 15 16 11 11 10 0;
18] enddata
最小生成树问题的0-1规划模型
19]n=@size(cities); !The model size; 20]! Minimize total distance of the links; 21]min=@sum(link(i,j)|i #ne# j: distance(i,j)*x(i,j)); 22]!There must be an arc out of city 1; 23]@sum(cities(i)|i #gt# 1: x(1,i))>=1; 24]!For city i, except the base (city 1); 25]@for(cities(i) | i #gt# 1 : 26]! It must be entered; 27] @sum(cities(j)| j #ne# i: x(j,i))=1; 28]! level(j)=levle(i)+1, if we link j and i;
数据结构最小生成树
数据结构最小生成树数据结构最小生成树（Minimum Spanning Tree，简称MST）是一种常用的图算法，用来找到一个无向图中权重最小的连通子图，使得该子图包含图中的所有顶点，并且任意两个顶点之间的路径都是该子图中的边。
MST问题在许多实际应用中都有广泛的应用，例如电力传输网络、通信网络、交通网络等。
通过求解MST问题，可以找到一个连接所有节点且总权重最小的网络。
本文将介绍MST问题的定义、经典算法以及一些相关扩展。
MST问题的定义非常直观，即在一个加权无向图G=(V,E)中，找到一个子图T=(V,E')，其中V为图中所有节点的集合，E为图中所有边的集合，E'为E的子集，使得T满足以下条件：1.T是一个连通图，即任意两个节点之间都存在路径。
2.T中不包含回路，即不存在闭合的路径。
3.T的边权重之和最小。
典型的MST算法有Prim算法和Kruskal算法。
Prim算法是通过贪心策略逐步扩展子图T的边集合来构造最小生成树。
算法的基本思想是，从任意一个节点开始，选择一个权重最小的边，将其加入到T的边集合E'中。
然后，将新加入的边连接的节点加入到T的节点集合V中，并以它们为起点，选择与之相连的权重最小的边加入到E'中。
重复这个过程直到图中所有的节点都加入到V中。
Kruskal算法则是通过将图中的所有边按照权重排序，然后逐步将权重最小的边加入到T的边集合E'中，并保证E'中不存在回路，直到E'中的边数达到n-1（其中n为图中节点的个数）或者图中的所有边都加入完毕。
算法的关键在于判断新加入的边是否会形成回路，通常能够通过并查集等数据结构来帮助解决这个问题。
除了Prim和Kruskal算法之外，还存在其他一些改进或者特殊情况下的MST算法。
例如，如果图是稠密图，即边的数量非常多，可以使用优先队列等数据结构来快速找到权重最小的边，提高算法的效率。
如果图是带权的有向图，可以将其转化为无向图再求解MST。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
30 个 顶 点 的 完 全 图 就 有 3028 个 生 成 树 ， 求 最小生成树时用穷举法是无效的。
返回
最小生成树与算法
定义 设T = (V , E1)是赋权图G = (V , E)的一棵生 成树，称T中全部边上的权数之和为生成树的权，记为
w(T )，即w(T ) = w(e).
eE1
如果生成树T *的权 w(T *)是G 的所有生成树的权中最 小者，则称 T*是G 的最小生成树 ，简称为 最小树 ，即
确定应在哪些站点之间铺设通讯 线路，是否可看作是在相应的加 权图中构造最小费用的生成树的 问题？
引例：计算机网络的线路设计
最小生成树
最大生成树 1) 一个完全图Kn有多少不同 的生成树？ 2) 如何求其最小生成树?
引例：计算机网络的线路设计
10个顶点的完全图，其不同的生成树就有 一亿棵。
一般地，n个顶点的完全图，其不同的生成 树个数为nn-2。
引例：计算机网络的线路设计
8
1
2
5
7
1
5
6
3
10
4
3
9
最经济的网络不应该有任何封闭的
回路。
引例：计算机网络的线路设计
生成树或支撑树(spanning tree)：G的子
图且是树，其顶点集等于G的顶点集；
8 1
5
7
2
1
5
6 如何简便地得到
3
10
左图的生成树？
4
3
它应有几条边？
9
引例：计算机网络的线路设计
w(T*) = min{w(T )}，式中取遍G 的所有生成树 T.
T
返回
最小生成树算法及其MATLAB程序实 现
Kruskal算法 算法的MATLAB程序实 现 Prim算法
返回
Kruskal 算
法
基本思想:
最初把图的n个顶点看作n个分离的部分树，每个树具有 一个顶点，算法的每一步选择可连接两分离树的边中权最 小的边连接两个部分树，合二为一,部分树逐步减少，直到 只有一个部分树（n-1步之后）便得到最小生成树。
2 边权矩阵：
6 b=[1 1 1 2 2 3 3 4; 2 4 5 3 5 4 5 5;
4 9
3
8 1 5 6 7 9 10 3];
b=[1 1 1 2 2 3 3 4;2 4 5 3 5 4 5 5;8 1 5 6 7 9 10 3];
[B,i]=sortrows(b',3);B=B’; m=size(b,2);n=5;
赵根 赵亮
赵丽
赵虹 赵云 赵霞
赵松 赵梅
形象地表 示家族
树图——直观形象的表示工具
树： 没有圈的连通图 • 树中任意两点间有唯一路径。 • 树的边数恰好为顶点数减1。
引例：计算机网络的 线路设计
城市电信局有许多业务如收费， 营业，112，114等，希望在全市范围 实现计算机联网服务，共享各种资源。 一个主要关心的问题是：用数据通讯 线把一组站点联结起来，而不允许通 讯线在非站点处相交，如何连接可使 通讯线的花费最小？
t=1:n; k=0; T=[ ]; c=0;
for i=1:m
if t(B(1,i))~=t(B(2,i))
k=k+1; T(k,1:2)=B(1:2,i), c=c+B(3,i)
tmin=min(t(B(1,i)),t(B(2,i)));
tmax=max(t(B(1,i)),t(B(2,i)));
for j=1:n
if t(j)==tmax if k==n-1
t(j)=tmin;
break ;
end
end
end
end
end
T,c
Kruskal 算 法
程序运行结果：
T=
1
2
7
14
4
5
1
5
6
23
3
2
5
4
3
c=
17
返回
Prim算法
● 基本思想：任选一个顶点v0开始，连接 与v0最近的顶点v1,得子树T1，再连接与T1 最近的顶点v2得子树T2，如此继续下去， 直到所有顶点都用到为止。
1) 贪婪法可被用于各种各样问题的 处理。该法只是一种试探法，计 算上简便有效，可提供正确解的 一个近似。但一般情况下，不能 保证输出的解是正确的。其正确 性需要证明，这往往比较困难。
2) 已证明,求最小生成树的Kruskal算 法和Prim算法都是正确的
子树
3号 子树
返回
整理边权矩阵
初始化：j0, T, c0, k0； 对所有顶点i ,t(i)i .
B: 图的边权矩阵; T: 生成树的边集; C: 生成树的权; t: 顶点所属子树的编号
jj+1
t(B(1,j))t(B(2,j)) Y
N
TT(B(1,j),B(2,j)), cc+B(3,j),kk+1，i 0
8
1
2
ห้องสมุดไป่ตู้
5
7
时间复杂度: O(m)
1
5
6 其中m为图的边数
3
10
4
3
Kruskal 算 法
步骤
1) 选择边e1，使得w(e1)尽可能小；
2) 若已选定边 e1,e2,..e.i,，则从 E\{e1,e2,..ei.}, 中选取 ei 1，使得: i) G [e { 1,e2,.e .i .1} , 为]无圈图，
i i+1
N
k=n-1或j=m
Y
T, c
t(i)=max{t(B(1,j)), t(B(2,j))
Y
N
t(i) min{t(B(1,j)), t( B(2,j)),
终止
Y
i=n
N
Kruskal 算 法
例 : 用 Kruskal 算 法 求 引 例 中 的 加 权
图的最小生成树。
8 1
5
7
1
5
3
10
ii) w(ei1) 是满足i)的尽可能小的权，
3) 当第2)步不能继续执行时，则停止.
定理 由Kruskal算法构作的任何生成树
T *=G [e { 1 ,e2,.e . .1 } ,都]是最小生成树.
Kruskal 算 法
给每个子 树一个不 同的编号
1号 子树
8
1
2
5
7
1
5
3
6
10
4
3
9 2号
● 时间复杂度：O(n2) , n为图的顶点数
1) Kruskal算法和Prim算法都蕴涵了 贪婪法的思想，是贪婪法；
2) 贪婪法的基本思想：把解看成是 由若干个部件构成，每一步求出 解的一个部件（不是从整体或长 远的角度考虑，只是局部或当前 的最好选择）。求出的一个个部 件组合而作为最终的解。
最小生成树算法
参考书： 1.傅鹂 龚劬 刘琼荪 何中市 《数学实验》科学出版社 2.张绍民 李淑华 《数据结构教程C语言版》中国电力出版社
主要内容
一个例子 基本概念与结论 Kruskal算法 Prim算法 最小生成树问题的0-1规划模型
树图——直观形象的表示工具
类似于自 然界中的
树
赵明 赵雷 赵雨
返回
最小生成树与算法
定义 设T = (V , E1)是赋权图G = (V , E)的一棵生 成树，称T中全部边上的权数之和为生成树的权，记为
w(T )，即w(T ) = w(e).
eE1
如果生成树T *的权 w(T *)是G 的所有生成树的权中最 小者，则称 T*是G 的最小生成树 ，简称为 最小树 ，即
确定应在哪些站点之间铺设通讯 线路，是否可看作是在相应的加 权图中构造最小费用的生成树的 问题？
引例：计算机网络的线路设计
最小生成树
最大生成树 1) 一个完全图Kn有多少不同 的生成树？ 2) 如何求其最小生成树?
引例：计算机网络的线路设计
10个顶点的完全图，其不同的生成树就有 一亿棵。
一般地，n个顶点的完全图，其不同的生成 树个数为nn-2。
引例：计算机网络的线路设计
8
1
2
5
7
1
5
6
3
10
4
3
9
最经济的网络不应该有任何封闭的
回路。
引例：计算机网络的线路设计
生成树或支撑树(spanning tree)：G的子
图且是树，其顶点集等于G的顶点集；
8 1
5
7
2
1
5
6 如何简便地得到
3
10
左图的生成树？
4
3
它应有几条边？
9
引例：计算机网络的线路设计
w(T*) = min{w(T )}，式中取遍G 的所有生成树 T.
T
返回
最小生成树算法及其MATLAB程序实 现
Kruskal算法 算法的MATLAB程序实 现 Prim算法
返回
Kruskal 算
法
基本思想:
最初把图的n个顶点看作n个分离的部分树，每个树具有 一个顶点，算法的每一步选择可连接两分离树的边中权最 小的边连接两个部分树，合二为一,部分树逐步减少，直到 只有一个部分树（n-1步之后）便得到最小生成树。
2 边权矩阵：
6 b=[1 1 1 2 2 3 3 4; 2 4 5 3 5 4 5 5;
4 9
3
8 1 5 6 7 9 10 3];
b=[1 1 1 2 2 3 3 4;2 4 5 3 5 4 5 5;8 1 5 6 7 9 10 3];
[B,i]=sortrows(b',3);B=B’; m=size(b,2);n=5;
赵根 赵亮
赵丽
赵虹 赵云 赵霞
赵松 赵梅
形象地表 示家族
树图——直观形象的表示工具
树： 没有圈的连通图 • 树中任意两点间有唯一路径。 • 树的边数恰好为顶点数减1。
引例：计算机网络的 线路设计
城市电信局有许多业务如收费， 营业，112，114等，希望在全市范围 实现计算机联网服务，共享各种资源。 一个主要关心的问题是：用数据通讯 线把一组站点联结起来，而不允许通 讯线在非站点处相交，如何连接可使 通讯线的花费最小？
t=1:n; k=0; T=[ ]; c=0;
for i=1:m
if t(B(1,i))~=t(B(2,i))
k=k+1; T(k,1:2)=B(1:2,i), c=c+B(3,i)
tmin=min(t(B(1,i)),t(B(2,i)));
tmax=max(t(B(1,i)),t(B(2,i)));
for j=1:n
if t(j)==tmax if k==n-1
t(j)=tmin;
break ;
end
end
end
end
end
T,c
Kruskal 算 法
程序运行结果：
T=
1
2
7
14
4
5
1
5
6
23
3
2
5
4
3
c=
17
返回
Prim算法
● 基本思想：任选一个顶点v0开始，连接 与v0最近的顶点v1,得子树T1，再连接与T1 最近的顶点v2得子树T2，如此继续下去， 直到所有顶点都用到为止。
1) 贪婪法可被用于各种各样问题的 处理。该法只是一种试探法，计 算上简便有效，可提供正确解的 一个近似。但一般情况下，不能 保证输出的解是正确的。其正确 性需要证明，这往往比较困难。
2) 已证明,求最小生成树的Kruskal算 法和Prim算法都是正确的
子树
3号 子树
返回
整理边权矩阵
初始化：j0, T, c0, k0； 对所有顶点i ,t(i)i .
B: 图的边权矩阵; T: 生成树的边集; C: 生成树的权; t: 顶点所属子树的编号
jj+1
t(B(1,j))t(B(2,j)) Y
N
TT(B(1,j),B(2,j)), cc+B(3,j),kk+1，i 0
8
1
2
ห้องสมุดไป่ตู้
5
7
时间复杂度: O(m)
1
5
6 其中m为图的边数
3
10
4
3
Kruskal 算 法
步骤
1) 选择边e1，使得w(e1)尽可能小；
2) 若已选定边 e1,e2,..e.i,，则从 E\{e1,e2,..ei.}, 中选取 ei 1，使得: i) G [e { 1,e2,.e .i .1} , 为]无圈图，
i i+1
N
k=n-1或j=m
Y
T, c
t(i)=max{t(B(1,j)), t(B(2,j))
Y
N
t(i) min{t(B(1,j)), t( B(2,j)),
终止
Y
i=n
N
Kruskal 算 法
例 : 用 Kruskal 算 法 求 引 例 中 的 加 权
图的最小生成树。
8 1
5
7
1
5
3
10
ii) w(ei1) 是满足i)的尽可能小的权，
3) 当第2)步不能继续执行时，则停止.
定理 由Kruskal算法构作的任何生成树
T *=G [e { 1 ,e2,.e . .1 } ,都]是最小生成树.
Kruskal 算 法
给每个子 树一个不 同的编号
1号 子树
8
1
2
5
7
1
5
3
6
10
4
3
9 2号
● 时间复杂度：O(n2) , n为图的顶点数
1) Kruskal算法和Prim算法都蕴涵了 贪婪法的思想，是贪婪法；
2) 贪婪法的基本思想：把解看成是 由若干个部件构成，每一步求出 解的一个部件（不是从整体或长 远的角度考虑，只是局部或当前 的最好选择）。求出的一个个部 件组合而作为最终的解。
最小生成树算法
参考书： 1.傅鹂 龚劬 刘琼荪 何中市 《数学实验》科学出版社 2.张绍民 李淑华 《数据结构教程C语言版》中国电力出版社
主要内容
一个例子 基本概念与结论 Kruskal算法 Prim算法 最小生成树问题的0-1规划模型
树图——直观形象的表示工具
类似于自 然界中的
树
赵明 赵雷 赵雨