8.5++对称振子天线的辐射特性
- 格式：pdf
- 大小：1.22 MB
- 文档页数：11
下载文档原格式
合集下载
线天线
c 3 108 2.5(m) 6 f 120 10
所以
0.6 0.24 2.5
h
第8章 线天线
查图 8 - 4 得 RΣ=65(Ω)
由式(8 -1 -14)得对称振子的平均特性阻抗为
2h Z 0 120 (ln 1) 454 .5() a
由h/a=60查图 8 - 6 得 n1=1.04
I m sin (h | z |)
第8章 线天线
三、对称振子天线的方向特性 1、方向函数
方向函数与 无关，因此在H面内的方向图为圆。
在E面内的方向性与电长度（
cos( h cos ) cos h F ( , ) sin
2h
）有关。
半波振子：
2h 0.5 2h
式中 , R1 和 L1 分别是对称振子单位长度的电阻和电感。 导线半径a越大, L1越小, 相移常数和自由空间的波数k=2π/λ相
差就越大, 令n1=β/k, 由于一般情况下L1的计算非常复杂, 因此 n1通常由实验确定。
第8章 线天线
在不同的h/a值情况下 , n1=β/k与 h/λ的关系曲线如图 8 -6 所示。公式和图 8 -6都表明, 对称振子上的相移常数β大于自
由空间的波数k, 亦即对称振子上的波长短于自由空间波长, 这 是一种波长缩短现象, 故称n1为波长缩短系数。
n1 k a
式中, λ和λa分别为自由空间和对称振子上的波长。
造成上述波长缩短现象的主要原因有:
① 对称振子辐射引起振子电流衰减, 使振子电流相速减小,
相移常数β大于自由空间的波数k, 致使波长缩短;
因而相移常数为
半波对称阵子天线辐射特性
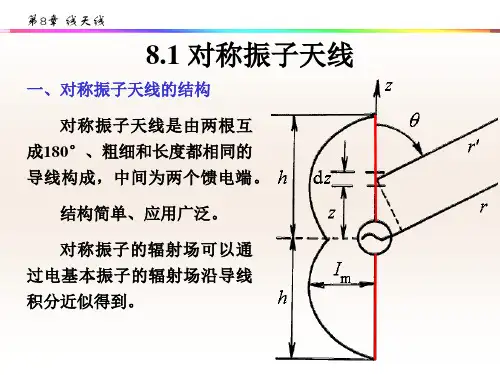
半波对称振子天线辐射特性对称振子是中间馈电，其两臂由两段等长导线构成的振子天线。
一臂的导线半径为a，长度为l。
两臂之间的间隙很小，理论上可以忽略不计，所以振子的总长度L=2l。
对称振子的长度与波长相比拟，本身已可以构成实用天线。
图1 对称振子对称结构及坐标在计算天线的辐射场时，经过实践证实天线上的电流可以近似认为是按正弦律分布。
取图1的坐标，并忽略振子损耗，则其电流分布可以表示为：式中，Im为天线上波腹点的电流；k=w/c为相移常数、根据正弦分布的特点，对称振子的末端为电流的波节点；电流分布关于振子的中心店对称；超过半波长就会出现反相电流。
在分析计算对称振子的辐射场时，可以把对称振子看成是由无数个电流I(z)、长度为dz的电流元件串联而成。
利用线性媒介中电磁场的叠加原理，对称振子的辐射场是这些电流元辐射场之矢量和。
电流元I(z)dz所产生的辐射场为图2 对称振子辐射场的计算如图2 所示，电流元I(z)所产生的辐射场为其中将上式沿振子全长作积分此式说明，对称振子的辐射场仍为球面波；其极化方式仍为线极化；辐射场的方向性不仅与有关，也和振子的电长度有关。
根据方向函数的定义，对称振子亿波腹电流归算的方向函数为上式实际上也就是对称振子E面的方向函数；在对称振子的H面上，方向函数与无关，其方向图为圆。
图3 对称振子E面方向图图4 对称振子的方向系数与辐射电阻随一臂电长度变化的图形1.2 对称振子的输入阻抗由于对称振子的实用性，因此必须知道它的输入阻抗，以便与传输线相连。
对称振子可看作是由长度为l的开路平行双导线构成的，它与传输线的区别及修正主要有以下两点：1.平行双导线的对应线元间距离不变，结构沿线均匀，因此特性阻抗沿线不变；二对称振子对应线元间的距离沿振子臂的中心到末端从小到大变化，故其特性阻抗沿臂长相应地不断变大。
对此的修正为用一平均特性阻抗来代替沿振子全长不断变化的特性阻抗。
2.传输线为非辐射结构，能量沿线传输，主要的损耗为导线的欧姆损耗；而对称振子为辐射电磁波的天线，恰好可忽略欧姆损耗。
天线理论与设计
2. 螺旋天线直径的电尺寸由小变大时，其方向图将发生 改变，因此螺旋天线一般分成三种模式，这三种模式分 别是 ， ， 。
3.轴向模螺旋天线上沿螺旋线行进的行波的相速度比在 自由空间时平面波的速度 （大或小），这种螺旋线 导行的波被称为 。 4.根据第六章宽带天线所学内容说出三种具有宽带特性的 天线型式： ， 和 。
10.天线辐射方向图,按不同辐射特性主要定义为 方向图,二者关系的数学表示是 。
概念原理复习
11.发射天线是垂直极化，接收天线为水平极化，则极化失配 因子等于 ；发射天线是圆极化，接收天线为水平极化， 则极化失配因子等于 。 12.均匀激励等间距线阵，当N较大时第一副瓣电平趋于 余弦渐削分布的旁瓣电平为 dB。 13.天线的远区场角分布与 无关,电场与磁场满随着振子长度的增加,方向性系数 方向图开裂,方向性系数急剧下降。 15．等幅同相二元阵间距大于
,但振子长度超过
方向图将出现多瓣。
概念原理复习
三、试叙述微带贴片天线的结构，辐射机理及其优缺点。 四、试叙述八木－宇田天线的结构及其工作原理。 五、试叙述对数周期振子阵的结构及辐射机理。
概念原理复习
相似原理（缩比原理）: 指天线的所有尺寸和工作频率（或波长）按相同的比例 变化，天线的性能将保持不变。（换言之，若天线的电 尺寸保持不变，天线的性能也将不变。）
方向性系数:最大辐射方向上的方向性值
概念原理复习
一、填空题
1.根据天线产生场的特性可以将离天线从近到远的空间 区域划分为 、 和 三个场区。一般天线方向图 是在 场区定义。
六、利用一在轨卫星上36 dB增益的天线，以点波束指向最远2000km外地 球上的用户，系统在频率3GHz时能发射的功率最大可达7W。如果用户的 2 dB增益天线指向卫星，为使其在最大距离处至少收到100dBm功率， 求卫星所需的发射功率，且系统发射功率是否满足所需功率要求？
3.轴向模螺旋天线上沿螺旋线行进的行波的相速度比在 自由空间时平面波的速度 （大或小），这种螺旋线 导行的波被称为 。 4.根据第六章宽带天线所学内容说出三种具有宽带特性的 天线型式： ， 和 。
10.天线辐射方向图,按不同辐射特性主要定义为 方向图,二者关系的数学表示是 。
概念原理复习
11.发射天线是垂直极化，接收天线为水平极化，则极化失配 因子等于 ；发射天线是圆极化，接收天线为水平极化， 则极化失配因子等于 。 12.均匀激励等间距线阵，当N较大时第一副瓣电平趋于 余弦渐削分布的旁瓣电平为 dB。 13.天线的远区场角分布与 无关,电场与磁场满随着振子长度的增加,方向性系数 方向图开裂,方向性系数急剧下降。 15．等幅同相二元阵间距大于
,但振子长度超过
方向图将出现多瓣。
概念原理复习
三、试叙述微带贴片天线的结构，辐射机理及其优缺点。 四、试叙述八木－宇田天线的结构及其工作原理。 五、试叙述对数周期振子阵的结构及辐射机理。
概念原理复习
相似原理（缩比原理）: 指天线的所有尺寸和工作频率（或波长）按相同的比例 变化，天线的性能将保持不变。（换言之，若天线的电 尺寸保持不变，天线的性能也将不变。）
方向性系数:最大辐射方向上的方向性值
概念原理复习
一、填空题
1.根据天线产生场的特性可以将离天线从近到远的空间 区域划分为 、 和 三个场区。一般天线方向图 是在 场区定义。
六、利用一在轨卫星上36 dB增益的天线，以点波束指向最远2000km外地 球上的用户，系统在频率3GHz时能发射的功率最大可达7W。如果用户的 2 dB增益天线指向卫星，为使其在最大距离处至少收到100dBm功率， 求卫星所需的发射功率，且系统发射功率是否满足所需功率要求？
对称振子天线
z
o sin
y
图8-2a 电流元E面方向图 z
z
y
sin 900 1
x
图8-2b电流元H面方向图
y
x 图8-2c 电流元立体 方向图
实际天线的方向图要比图8-2复杂。图8-3 为某 天线的方向图，它有很多波瓣，分别称为主瓣、副 瓣和后瓣。其中最大辐射方向的波瓣称为主瓣，其 他波瓣统称为副瓣，把位于主瓣正后方的波瓣称为 后瓣。
H 0
(8-22c)
再根据麦克斯韦方程 E 1 H，可得电流环产生
的电场为
j
E
j
I a 2k 2
4π
j
kr
1 (kr) 2
sin
e jkr
Er E 0
(8-23a) (8-23b)
对于电流环感兴趣的是其远区场，因 kr 1 ， 由式（8-22）和式（8-23）得
H
I a 2k 2 4πr
方向性天线所需的辐射功率Pr
与被研究天线的辐射
0
功率 Pr 之比，即
D Pr0 Pr Emax E0
（8-10）
对于被研究的天线，其辐射功率
Pr
S
Sav
dS
S
1 2
E( ,) 2 0
dS
1 2
2 0
0
Emax
2 F 2 ( ,) r 2 sin d d 0
Emax 2 r 2
20
2
0
0
F 2 ( ,) sin d d
称为零功率波瓣宽度，用 表示2。0由图8-2可见，
电流元的主瓣宽度
2，0.5零 9功0率波瓣宽
度 2 0 180。
副瓣最大辐射方向上的功率密度与主瓣最大辐 射方向上的功率密度之比的对数值，称为副瓣电平， 用dB表示。通常离主瓣近的副瓣电平要比远的高， 所以副瓣电平通常是指第一副瓣电平。一般要求副 瓣电平尽可能低。
天线辐射的方向特性
实验报告：天线辐射的方向特性一、实验题目：天线辐射的方向特性二、实验目的：1 理解天线辐射的相关原理知识，对天线的方向图及其相关参数有一定的认识。
2 测定右手螺旋天线的方向特性。
三、实验仪器:旋转天线盘、喇叭形天线、微波吸收器、右手螺旋天线、波导式天线、计算机及测试软件。
四、实验原理：任何实用天线的辐射都具有方向性，通常将天线远区辐射场的振幅与方向间的关系用曲线表示出来，这种曲线图被称之为天线的辐射方向图；而将离开天线一定距离R 处的天线远区的辐射场量与角度坐标间的关系式称为天线的方向图函数，记为|F(θ,φ)|。
电流元的远区辐射场量在相同距离R的球面上不同方向的各点，场强是不同的，它与|sinθ|成正比，因此，电流元的方向图函数，记为|F(θ, φ)| =| F(θ)| = |sinθ|。
为了画出电流元的辐射方向图，将电流元中心置于坐标原点，向各个方向作射线，并取其长度与场强的大小成正比，即得到一个立体图形，也就是得到电流元的立体方向图，它的形状像汽车轮胎。
如图1（a）所示。
天线的立体方向图一般较难画出，通常只画出相互垂直的两个平面内的方向图，即E面和H面方向图。
电流元E面的方向图处于子午面，即电场分量Eθ所处的平面内的方向图，故称为E面方向图，H面方向图处于赤道面内，即与磁场分量Hφ平行的平面内的方向图，故称为H面方向图。
(a) 立体方向图； (b) E面方向图； (c) H面方向图图1 电流元的方向图二维平面方向图可以在极坐标系中绘制，也可以在直角坐标系中绘制，但在极坐标系中绘制的方向图较为直观，因此较为常用。
在极坐标系中绘制的电流元的E面和H面方向图如图1(b)T和（c）所示。
显然，E面方向图关于电流元的轴线呈轴对称分布，在θ=90˚方向出现最大值“1”，其他方向上按矢径作出，而在轴线（θ=0˚和θ=90˚）上其值为零。
在H 面（θ=90˚）上，各方向场强均相同，故其方向图是一个单位圆，这样，将E面方向图绕电流元的轴线旋转一周，即可得到电流元的立体方向图。
电磁波的辐射与散射
天线的损耗电阻R1
2P R1 21 Im
用电阻表示的天线的效率
R 1 A R R1 1 R1 R
要提高天线效率，应尽可能提高R ，降低R1
极化特性 •极化特性是指天线在最大辐射方向上电场矢量的方向随时间变 化的规律。按天线所辐射的电场的极化形式，可将天线分为线 极化天线、圆极化天线和椭圆极化天线。线极化又可分为水平 极化和垂直极化；圆极化和椭圆极化都可分为左旋和右旋。 输入阻抗与频带宽度 天线的输入阻抗等于传输线的特性阻抗，才能使天线获得最 大功率。 当天线工作频率偏离设计频率时，天线与传输线的匹配变坏， 致使传输线上电压驻波比增大，天线效率降低。因此在实际 应用中，还引入电压驻波比参数，并且驻波比不能大于某一 规定值。 •天线的有关电参数不超出规定的范围时对应的频率，范围称 为频带宽度，简称为天线的带宽。
8.2.5 辐射功率和辐射电阻 辐射功率 Radiation Power
电流元所辐射的总功率可由其平均功率流密度在包围电流元的球 面上的面积分来得出。 其平均功率密度为
S
av
1 | E | 0 Il 1 * ˆ ˆ Re E H r r sin 2 0 2 2 r 2
b
天线增益G（Gain）与方向性GD
天线增益是在波阵面某一给定方向天线辐射强度的量度，它是 被研究天线在最大辐射方向的辐射强度与被研究天线具有同等 输入功率的各向同性天线在同一点所产生的最大辐射强度之比
单位立体角最大辐射功率 G 馈入天线总功率 4
天线方向性GD与天线增益但与天线增益定义略有不同
定量地描述主叶的宽窄程度 功率降为为主射方向上功率的1/2时，两个方向之间的夹角 以20.5表示,2 0.5 为两个零射方向之间的夹角称为零功率宽 度，以20表示。 电流元的半功率宽度:
对称阵子天线
第1章 天线基础知识
1.4.2 对称振子的辐射场
确定了对称振子的电流分布以后，就可以计算它 的辐射场。 欲计算对称振子的辐射场，可将对称振子分成无 限多电流元，对称振子的辐射场就是所有电流元辐射 场之和。在图1―4―3的坐标系中，由于对称振子的辐 射场与 φ 无关，而观察点 P(r,θ) 距对称振子足够远，因 而每个电流元到观察点的射线近似平行，因而各电流
I m sin k (l z ) z 0 I ( z ) I m sin k (l z ) I m sin k (l z ) z 0
（1―4―1）
第1章 天线基础知识
式中，Im为电流波腹点的复振幅； k=2π/λ=ω/c为相
移常数。根据正弦分布的特点，对称振子的末端为电
E r
r′
－l
~
O
z dz l
z
第1章 天线基础知识
图1―4―4绘出了对称振子E面归一化方向图。由图
可见，由于电基本振子在其轴向无辐射，因此对称振子 在其轴向也无辐射；对称振子的辐射与其电长度 l/λ密切 相关。当 l≤0.5λ 时，对称振子上各点电流同相，因此参 与辐射的电流元越多，它们在θ=90°方向上的辐射越强， 波瓣宽度越窄。当 l=0.5λ 时，对称振子上出现反相电流， 也就开始出现副瓣。当对称振子的电长度继续增大至 l=0.72λ 后，最大辐射方向将发生偏移，当 l=1λ 时，在 θ=90°的平面内就没有辐射了。
流的波节点；电流分布关于振子的中心点对称；超过 半波长就会出现反相电流。
图1―4―2绘出了理想正弦分布和依靠数值求解方
法（矩量法）计算出的细对称振子上的电流分布，后 者大体与前者相似，但二者也有明显差异，特别在振 子中心附近和波节点处差别更大。这种差别对辐射场 的影响不大，但对近场计算（例如输入阻抗）有重要 影响。
对称振子天线辐射
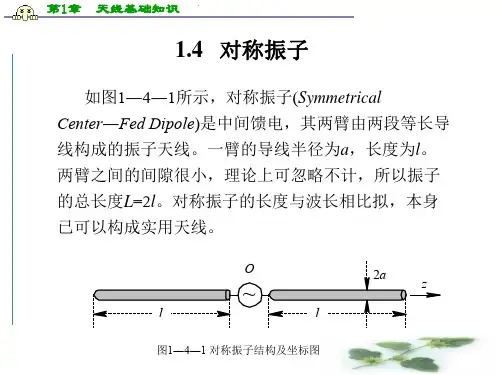
对称振子天线辐射JZOBEL一、对称振子天线的辐射场对称振子天线是一种经典的、迄今为止使用最广泛的天线,特别是半波对称振子天线. 单个半波对称振子可单独使用或作为抛物面天线的馈源,也可采用多个半波对称振子组成各种天线阵。
如图 1 所示，对称振子天线由两根长度均为的细导线构成。
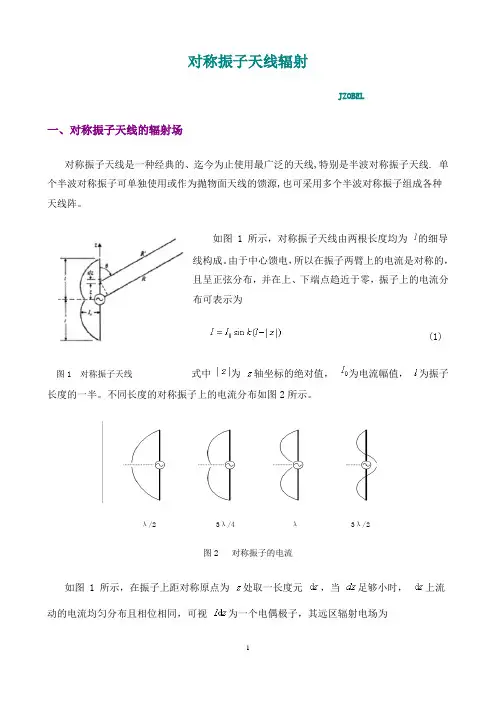
由于中心馈电，所以在振子两臂上的电流是对称的，且呈正弦分布，并在上、下端点趋近于零，振子上的电流分布可表示为(1)图1 对称振子天线式中为轴坐标的绝对值，为电流幅值，为振子长度的一半。
不同长度的对称振子上的电流分布如图2所示。
λ/2 3λ/4 λ 3λ/2图2 对称振子的电流如图 1 所示，在振子上距对称原点为处取一长度元，当足够小时，上流动的电流均匀分布且相位相同，可视为一个电偶极子，其远区辐射电场为'0'sin sin ()2jkR I dE jk l z e dz Rθθλ-=- (2) 为求得对称振子天线的辐射电场，可对式 (2) 进行积分运算，为保证积分能在简单的情况下进行，先对式 (2) 中变量进行分析。
式中的积分变量是 ，式中 也随 变化，是的函数，这样被积函数显得有点复杂，为此，可做些近似处理，在 的情况下，射线与在振子附近可视为平行的射线，因此(3)在远区，由于 和 的值差别极小，因此在式 (2) 的分母中，可用 代替 ，但在相位项中与的微小差距将会引起较大的相位差，因此必须考虑式 (3) 给出的近似关系。
故式 (2) 变为(4)对式 (4) 进行积分得到利用积分公式得到对称振子天线的辐射电场(5)同理，可获得对称振子天线的辐射磁场(6) 可见，对称振子天线的方向性函数为(7)(a) (b)(c) (d)图 3对称振子的方向图图 3 给出了四种不同长度的对称振子天线的方向图。
二、半波振子天线的辐射当对称振子长度等于半个波长时，即，称之为半波振子天线，其方向图如图3（a）所示。
将代入式 (5) 和式 (6) 中，可得半波振子天线的辐射场为(8)(9) 其方向性函数为(10) 其平均坡印廷矢量为(11)其总辐射功率为在包围半波振子天线的闭合球面上的面积分，即上式中对的积分可用数值法计算，结果为所以(12) 由此得出半波振子天线的辐射电阻为(13)在自由空间，则辐射电阻(14) 可计算出半波振子的方向性系数为(15) 其半功率波瓣宽度由下列方式计算该方程的两个解之间的夹角即为波瓣宽度，用数值法计算得(16)。
【最新精选】对称振子天线远区场分析
对称振子天线远区场分析一、实验目的了解振子天线远区辐射场结构及天线电参数二、实验步骤1、创建一个工程创建一个工程，设置求解类型为Driven Modal，设置模型单位为in，设置材料为真空。
2、创建模型创建对称振子模型,创建ring_1，在菜单栏中选择Draw\Cylinder，在坐标栏中输入圆柱中心点的坐标X:0,Y:0，Z:0,在坐标栏中输入圆柱半径，dX:0.31，dY:0，dZ：0，输入圆柱的高度5.0，将其名称改为ring_inner。
创建另一个圆柱，在坐标栏中输入圆柱中心点的坐标X:0,Y:0，Z:0,在坐标栏中输入圆柱半径，dX:0.37，dY:0，dZ：0，输入圆柱的高度5.0，将其名称改为ring_1。
将新建的两个圆柱进行相减，效果如下，创建对称振子模型创建ring_2，复制ring_1，将其半径改为0.435in。
创建Arm_1，新建一个Box，将其起始坐标设置为X:-0.1,Y:-0.31，Z:5.0，设置长方体三个方向的尺寸，dX:0.2，dY:-4.69，dZ：-0.065，并将其名称改为Arm_1，然后将创建好的模型组合到一起。
创建Center pin，在菜单栏中点击Draw\Cylinder，输入圆柱的中心坐标X:0,Y:0，Z:0，输入圆柱的半径dX:0.1，dY:0，dZ:0，并输入圆柱的高度dZ:5.1，并将名称修改为center_pin。
创建Arm_2，建一个Box，将其起始坐标设置为X:-0.1,Y:-0，Z:5.1，设置长方体三个方向的尺寸，dX:0.2，dY:-5.0，dZ：-0.065，并将其名称改为Arm_2。
创建Grounding pin，在菜单栏中点击Draw\Cylinder，输入圆柱的中心坐标X:0,Y:1.0，Z:0，输入圆柱的半径dX:0.0625，dY:0，dZ:0，并输入圆柱的高度dZ:5.1，并将名称修改为pin，然后将创建好的模型组合起来。
对称振子天线课程设计
对称振子天线课程设计一、课程目标知识目标：1. 学生能理解对称振子天线的概念、原理和应用；2. 学生能掌握对称振子天线的阻抗特性、辐射特性及影响参数；3. 学生能运用相关公式计算对称振子天线的长度及间距。
技能目标：1. 学生能运用所学知识，分析对称振子天线的性能，并进行优化设计；2. 学生能通过实际操作，制作并测试对称振子天线；3. 学生能运用相关软件（如CST、HFSS等）进行对称振子天线的仿真分析。
情感态度价值观目标：1. 学生培养对无线电通信及天线技术的兴趣，增强对物理学科的学习热情；2. 学生通过团队协作，培养沟通、合作能力，增强集体荣誉感；3. 学生在学习过程中，培养严谨、细致的科学态度，提高解决问题的能力。
课程性质：本课程为高二年级物理选修课程，旨在让学生了解对称振子天线的基本原理和实际应用，提高学生的实践能力和创新能力。
学生特点：高二学生对物理学科有一定的基础，具备一定的分析、计算能力，对实际操作和新技术具有浓厚兴趣。
教学要求：结合学生特点，注重理论与实践相结合，充分调动学生的积极性，提高学生的动手能力和创新能力。
在教学过程中，将目标分解为具体的学习成果，便于后续教学设计和评估。
二、教学内容1. 引入对称振子天线的基本概念，介绍其发展历程及应用领域；相关教材章节：第三章第1节“天线的基本概念与发展”2. 讲解对称振子天线的原理、结构特点及分类；相关教材章节：第三章第2节“对称振子天线的基本原理与结构”3. 详细阐述对称振子天线的阻抗特性、辐射特性及影响参数；相关教材章节：第三章第3节“对称振子天线的阻抗与辐射特性”4. 探讨对称振子天线的优化设计方法，包括长度、间距等参数的调整；相关教材章节：第三章第4节“对称振子天线的优化设计”5. 实践操作：指导学生制作对称振子天线，并进行测试；相关教材章节：第三章第5节“对称振子天线的制作与测试”6. 介绍相关软件（如CST、HFSS等）在对称振子天线仿真分析中的应用；相关教材章节：第三章第6节“对称振子天线的计算机仿真”7. 分析实际应用案例，让学生了解对称振子天线在现代通信系统中的作用；相关教材章节：第三章第7节“对称振子天线的应用实例”教学内容安排与进度：1. 第1课时：引入对称振子天线的基本概念、发展历程及应用领域；2. 第2课时：讲解对称振子天线的原理、结构特点及分类；3. 第3课时：详细阐述对称振子天线的阻抗特性、辐射特性及影响参数；4. 第4课时：探讨对称振子天线的优化设计方法；5. 第5课时：实践操作，制作对称振子天线并进行测试；6. 第6课时：介绍相关软件在对称振子天线仿真分析中的应用；7. 第7课时：分析实际应用案例，总结本章节内容。
第三讲 对称振子和接地短鞭天线
第三讲对称振子和接地短鞭天线一、概述1．手机通常使用的天线有四种类型：（1）PIFA天线：即平面倒F天线，这种天线的基本组成形式是互相平行的平面辐射单元和接地面，在辐射单元上彼此靠近的位置有一个接地的短路片和一个馈电片。
（2）单极子变形天线：即类似于外置天线的变形，它只有一个馈电的接触弹片，内部可以有多种几何结构形式。
（3）PCB板天线：这种天线也可以认为是单极子天线的变形，只是将天线辐射体做在PCB板上。
这种天线可以为外置，由PCB走线和过孔共同绕成螺旋状，也可以是内置形式，并允许多种几何结构。
（4）陶瓷介质天线：即将天线做在高介电常数的陶瓷材料上，从而达到减小尺寸的目的。
手机蓝牙天线多采用陶瓷介质天线的形式。
2．所有手机天线都可以认为是从对称振子和接地单极子天线的基础上发展而来，所以这一讲主要给出对称振子和接地单极子天线的理论分析。
二、对称振子（Dipole）天线1．对称振子的结构对称振子由两根同样粗细、同样长度的直导线构成，在中间的两个端点馈电。
每根导线的长度是，它又称为对称振子的臂长。
在谐振条件下，为四分之波长。
这种天线结构简单，适用于多个波段。
它可以作为独立的天线使用，也可以作为复杂天线（如天线阵）的单元或面天线的组成部分（如馈源）。
手机使用的所有天线都可以以这种天线为出发点作进一步的分析。
2．对称振子分析对称振子的分析可以采用集总等效电路法。
可以将它看做由终端开路的两根长导线的电流分布张开所形成。
无耗开路长线上的电流是正弦分布的，对称振子上的电流也近似按正弦分布，波型与臂长的电长度有关。
取对称振子中心为坐标原点，振子轴沿x轴，则对称振子的电流分布可以近似表示为：（1）其中是波腹电流，是对称振子的电流传输相移常数，（是振子上的波长），如果不考虑损耗，则，其中和分别是自由空间的相移常数和波长。
（1）式还可以写成：（2）全长的对称振子称为全波振子，全长为的对称振子称为半波振子。
实际使用的振子都是半波振子。
基于液态金属的频率可重构天线研究与设计
I
重庆邮电大学硕士论文
II
Abstract
Abstract
The liquid metal antenna which has unique characteristic of high flexibility and self- healing is widely recognized in recent years. Replacing the traditional solid metal with liquid metal, antenna prototype was wrapped in microfluidic channels etched by high elasticity polymer. Antenna which gets tensile deformation can be used in the design of reconfigurable antenna. There are some achievements abroad, but domestic research less. Thesis focuses on EGaIn antenna, and researches the frequency reconfigurable antenna using EGaIn. The research includes the innovation of design method, and the improvement of the liquid-reconfigurable antenna feed. Analyze the characteristic of self- healing, and present a new method of frequency reconfigurable antenna design using liquid metal. Use the self- healing simulate the break over state, add one insulation piece simulate the open circuit state, and get the reconfigurable frequency by adjusting the position of insulation piece. Compared with the traditional method of solid copper antenna using electronic switches, the method is more simple and easy to adjust parameters. Use dipole as antenna prototype, design and simulate a reconfigurable antenna which operates at frequency region from 1.6GHz to 3.0GHz. A curve-fitting frequency-estimation formula which is suitable for the antenna was given. The simulation results show that the antenna has good bandwidth, impedance matching, and keep a high gain. Radiation performance is good. There is bad contact or separation between the liquid metal and feed probe when antenna is stretched in order to achieve reconfigurable performance. A new aperture coupling feed was presented through comparative analysis in order to avoid above case. It is the combination of aperture coupling feed and close coupling feed. H-slot is on the ground plane, but the feed is below the ground. There is no aperture coupling layer between feed and ground. The feed line works through the way of close coupling. The antenna structure is simpler. Use the bow-tie microstrip antenna as prototype, and analyze the bow-tie antenna and H-slot. A liquid-frequency reconfigurable antenna using the new aperture coupling feed was designed. In the results analysis, not only analyzed the reconfigurable frequency, but also compared with traditional solid copper antenna. The simulation shows that the antenna keeps a higher gain, features good bandwidth. A new method of frequency reconfigurable antenna design using liquid metal was presented in thesis. Besides, a new aperture coupling was presented in order to avoid the
对称振子天线解析
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 h/
图 8-4 对称振子的辐射电阻与h/λ的关系曲线
第8章 线天线
1.
半波振子广泛地应用于短波和超短波波段, 它既可作为独 立天线使用, 也可作为天线阵的阵元。 在微波波段, 还可用作 抛物面天线的馈源（这将在第9章介绍）。
a 0
1I 2
2
(Z
)R1dz
对称振子的辐射功率为
p
1 2
I
2 m
R
因为PL就是PΣ, 即PL=PΣ, 故有
第8章 线天线
h 0
1 2
I
2
(
z
)
R1dz
1 2
I
2 m
RZ
对称振子的沿线电流分布为
I(Z)
Im
sin
2
(h
z)
将上式代入式（8 -1 -19）得
R1
1
2R
sin 4
4 h
h
h
第8章 线天线
RΣ=73.1 (Ω)
将F(θ)代入式（6 -3 -8）得半波振子的方向函数:
D=1.64
(8 -1 -11)
方向图的主瓣宽度等于方程:
cos( cos )
F( ) 2
1
0°＜θ＜180°的两个解之间的夹角
sin
2
由此可得其主瓣宽度为78°。 因而, 半波振子的方向性比 电基本振子的方向性（方向系数1.5, 主瓣宽度为90°）稍强 一些。
解: 对称振子的工作波长为
c f
3 108 120 10
6
2.5(m)
所以
h 0.6 0.24
2.5
图 8-4 对称振子的辐射电阻与h/λ的关系曲线
第8章 线天线
1.
半波振子广泛地应用于短波和超短波波段, 它既可作为独 立天线使用, 也可作为天线阵的阵元。 在微波波段, 还可用作 抛物面天线的馈源（这将在第9章介绍）。
a 0
1I 2
2
(Z
)R1dz
对称振子的辐射功率为
p
1 2
I
2 m
R
因为PL就是PΣ, 即PL=PΣ, 故有
第8章 线天线
h 0
1 2
I
2
(
z
)
R1dz
1 2
I
2 m
RZ
对称振子的沿线电流分布为
I(Z)
Im
sin
2
(h
z)
将上式代入式（8 -1 -19）得
R1
1
2R
sin 4
4 h
h
h
第8章 线天线
RΣ=73.1 (Ω)
将F(θ)代入式（6 -3 -8）得半波振子的方向函数:
D=1.64
(8 -1 -11)
方向图的主瓣宽度等于方程:
cos( cos )
F( ) 2
1
0°＜θ＜180°的两个解之间的夹角
sin
2
由此可得其主瓣宽度为78°。 因而, 半波振子的方向性比 电基本振子的方向性（方向系数1.5, 主瓣宽度为90°）稍强 一些。
解: 对称振子的工作波长为
c f
3 108 120 10
6
2.5(m)
所以
h 0.6 0.24
2.5
对称振子的辐射电阻、方向系数
《天线原理》对称振子程序该程序主要包括四部分：辐射电阻的求解、方向系数的求解、归一化方向图的求解及半功率波束宽度的计算。
其中各个参数的计算均采用课本最原始的公式。
半功率波束宽度的计算采用的是先寻找半功率点和最大值点，然后求差的形式，计算结果较为准确。
经程序运行可知，其结果与课本较为吻合， 以下为程序求解结果： （1）辐射电阻的计算结果00.511.52 2.5350100150200250300350400l/lambda辐射电阻R对称振子的辐射电阻随电长度的变化曲线（2）方向系数的计算结果（3）半波对称振子的E 面归一化方向图00.511.522.531.522.533.544.555.56l/lambda方向系数D对称振子的方向系数随电长度的变化曲线（4）全波对称振子的E 面归一化方向图（5）方向系数最大所对应的对称振子的归一化E 面方向图902701800半波对称振子的E 面的归一化方向图902701800全波对称振子的E 面的归一化方向图（6）半功率波束宽度的计算结果半波对称振子的半功率波束宽度为76.896000度 全波对称振子的半功率波束宽度为47.304000度最大方向系数所对应对称振子的半功率波束宽度为31.608000度902701800最大方向系数所对应对称振子的E 面的归一化方向图求解程序：clcclose allclear all%对称振子辐射电阻的计算llambda=0.1:0.01:3;%长度l与波长lamda的比值kl=2*pi*llambda;R=zeros(1,length(llambda));sum=0;%求辐射电阻for i=1:length(llambda)for j=0.05:0.05:pisum=sum+(cos(kl(i)*cos(j))-cos(kl(i)))^2/sin(j)*0.05;%积分endR(i)=60*sum;sum=0;endfigure(1)plot(llambda,R)xlabel('l/lambda')ylabel('辐射电阻R')title('对称振子的辐射电阻随电长度的变化曲线')%对称振子方向系数的计算llambda=0.01:0.01:3;%长度l与波长lamda的比值kl=2*pi*llambda;D=zeros(1,length(llambda));big=zeros(1,100);%用于确定方向函数的最大值sum=0;%求方向系数for i=1:length(llambda)for k=1:100j=k*pi/100;sum=sum+(cos(kl(i)*cos(j))-cos(kl(i)))^2/sin(j)*pi/100;%积分big(k)=(cos(kl(i)*cos(j))-cos(kl(i)))/sin(j);endD(i)=2*(max(abs(big)))^2/sum;sum=0;endfigure(2)plot(llambda,D)xlabel('l/lambda')ylabel('方向系数D')%axis([0,3,0,5.1])title('对称振子的方向系数随电长度的变化曲线')%求解最大方向系数所对应的电长度[u,v]=max(D) %u是最大方向系数的值，v是u所对应的电长度的标号%求解三个不同电长度时的归一化方向函数kll=[0.5*pi,pi,kl(v)];%3个不同电长度的对应取值F=zeros(length(kll),100);%归一化方向函数的值t=zeros(1,100);big=zeros(1,100);%用于确定方向函数的最大值maxx=zeros(1,3);for i=1:length(kll)for k=1:100t(k)=2*k*pi/100;big(k)=abs((cos(kll(i)*cos(t(k)))-cos(kll(i)))/sin(t(k)));endfor k=1:100F(i,k)=big(k)/max(big);maxx(i)=max(big);endendfor k=1:length(F(1,:))t(k)=2*k*pi/length(F(1,:));end%半波对称振子的方向图figure(3)polar(t,abs(F(1,:)))title('半波对称振子的E面的归一化方向图')%全波对称振子的方向图figure(4)polar(t,abs(F(2,:)))title('全波对称振子的E面的归一化方向图')figure(5)polar(t,abs(F(3,:)))title('最大方向系数所对应对称振子的E面的归一化方向图')%半功率波束宽度的计算a=zeros(1,3);%最大值处所对应的点b=zeros(1,3);%半功率点syms th1for n=1:3for i=1:5000%分成5000个点搜索if(abs((cos(kll(n)*cos(i*pi/5000))-cos(kll(n)))/sin(i*pi/5000)-maxx(n)*sqrt(2)/2)<0.001) b(n)=i*180/5000; %求解半功率点break;endendfor i=1:5000if(abs((cos(kll(n)*cos(i*pi/5000))-cos(kll(n)))/sin(i*pi/5000)-maxx(n))<0.0001)a(n)=i*180/5000;%求解最大值处所对应的点break;endendendfprintf('半波对称振子的半功率波束宽度为%f度\n',(a(1)-b(1))*2);fprintf('全波对称振子的半功率波束宽度为%f度\n',(a(2)-b(2))*2);fprintf('最大方向系数所对应对称振子的半功率波束宽度为%f度\n',(a(3)-b(3))*2);。
对称阵子天线
第1章 天线基础知识
1.4.2 对称振子的辐射场
确定了对称振子的电流分布以后，就可以计算它 的辐射场。 欲计算对称振子的辐射场，可将对称振子分成无 限多电流元，对称振子的辐射场就是所有电流元辐射 场之和。在图1―4―3的坐标系中，由于对称振子的辐 射场与 φ 无关，而观察点 P(r,θ) 距对称振子足够远，因 而每个电流元到观察点的射线近似平行，因而各电流
输入端的电流非常敏感，而对称振子的实际电流分布与
理想正弦分布在输入端和波节处又有一定的差别，因此 若仍然认为振子上的电流分布为正弦分布，对称振子输 入阻抗的计算会有较大的误差。为了较准确地计算对称 振子的输入阻抗，除了采用精确的数值求解方法之外， 工程上也常常采用“等值传输线法”。也就是说，考虑 到对称振子与传输线的区别，可将对称振子经过修正等 效成传输线后，再借助于传输线的阻抗公式来计算对称 振子的输入阻抗。此方法计算简便，有利于工程应用。
第1章 天线基础知识
6 00 0 5 00 0 4 00 0 Z0 A ＝1 00 0 3 00 0 2 00 0 1 00 0 Z0 A ＝1 00 0 5 60 4 60
平均特性阻抗来代替沿振子全长不断变化的特性阻抗。
z
dz
2a
l z
dz
~
O
D z z l z
~
O
图1―4―6
dz 2a
(a )
(b )
第1章 天线基础知识
（ 2 ）传输线为非辐射结构，能量沿线传输，主要 的损耗为导线的欧姆损耗；而对称振子为辐射电磁波 的天线，恰好可忽略欧姆损耗。对此的修正为将对称 振子的辐射功率看作是一种电阻损耗，均匀分布在等 效传输线上，并由此计算其衰减常数。经过这两点修 正以后，对称振子最终可以等效成具有一平均特性阻 抗的有耗传输线。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
8.5 对称振子天线的辐射
1.什么是对称振子？
2.对称振子的辐射特性
3.半波振子的辐射特性
1. 什么是对称振子？
两段长度为的直导线，从中间对称馈电，就构成对称振子。
l 如图所示:
对称振子上的电流分布为：
0sin (||)
I I k l z =-2/2l λ=23/4l λ=2l λ=23/2
l λ=
在振子上取一小段d z ，将其视为电偶极子，其辐射场为：
2. 对称振子的辐射场
j 0sin (||)e
d j sin d 2kR I k l z E z
R θηθλ'
--=⋅'
该对称振子的辐射场就是整个振子
长度上的积分:
d l
E E θθ
=⎰因为：R l
>>//R R
'||cos R R z θ'≈-R R
'≈在分母上
在指数上
j j ||cos 0j sin e sin[(||)]e d 2l kR k z l I k l z z
R
θηθλ--=-⎰辐射电场为：d l
E E θθ
=
⎰0j -j cos 0j cos 0
j sin e {sin[()]e d 2sin[()]e
d }
kR kz l l
kz I k l z z R
k l z z θ
θ
ηθλ--=++
-⎰⎰
j 0e cos(cos )cos()
j []
2πsin kR
I kl kl R θηθ
--=⋅
对称振子的辐射场：
j 0e cos(cos )cos()
ˆj []2πsin kR
I kl kl E a
R θθηθ
--=⋅j 0e cos(cos )cos()
ˆj []2sin kR
I kl kl H a
R ϕθπθ
--=⋅cos(cos )cos()()sin kl kl F θθθ
-=
对称振子的方向性函数：
不同长度振子的方向图：
lλ=2/1
2/1/2
lλ=
lλ=
2/3/2
lλ=2/2
3. 半波振子的辐射j 0π
cos(cos )e 2ˆj []2πsin kR
I E a R θθηθ
-=⋅已知：对称振子的辐射场：j 0e cos(cos )cos()
ˆj []2πsin kR
I kl kl E a
R θθηθ
--=⋅将代入上式
2/2l =λj 0e cos(cos )cos()
ˆj []2πsin kR
I kl kl H a
R ϕθθ
--=⋅j 0π
cos(cos )e 2ˆj []2πsin kR
I H a R ϕθθ
-=⋅可得半波振子的辐射场：（1）半波振子的辐射场
（2）半波振子的方向性函数：
π
cos(cos )
2()sin F θθθ
=
2/1/2
l λ=E 面方向图
x
z
θ
半波振子的方向图：
(4)半波振子的总辐射功率：
22
2ππrav rav 2002πcos (cos )2d d d 8πsin 1.2194π
o S o
I P S S I θηθϕ
θη=⋅==⎰⎰⎰(3) 半波振子的平均坡印廷矢量：
2
2
0rav 22πcos(cos )12ˆRe()28πsin R I E H R θηθ*⎛⎫ ⎪=⨯= ⎪ ⎪
⎝⎭
S a
π
cos(cos )
12()sin 2
F θθθ==
50.5
θ=(5) 辐射电阻：rav r 22 1.219
(Ω)2π
o P R I η==
(6) 方向性系数： 1.64D =(7)半功率波瓣宽度：0
0.5279θ=E 面方向图
x
z
θ
0.5
2θ000
0.59050.539.5
θ=-=
小结：
1.什么是对称振子？
2.对称振子的辐射特性
3.半波振子的辐射特性。