概率运算公式
- 格式:doc
- 大小:12.06 KB
- 文档页数:1

随机概率公式大全
1、事件的绝对概率公式
P(A) = n(A) / n(S),其中P(A)表示事件A发生的概率,n(A)表示事件A发生的次数,n(S)表示样本空间S中的元素个数。
2、事件的相对概率公式
P(A) = f(A) / f(S),其中P(A)表示事件A发生的概率,f(A)表示事件A发生的频率,f(S)表示样本空间S中的频率总和。
3、事件的条件概率公式
P(A|B) = P(A∩B) / P(B),其中P(A|B)表示在事件B发生的条件下事件A发生的概率,P(A∩B)表示事件A和事件B同时发生的概率,P(B)表示事件B发生的概率。
4、事件的加法法则
P(A∪B) = P(A) + P(B) - P(A∩B),其中P(A∪B)表示事件A或事件B 发生的概率,P(A)和P(B)分别表示事件A和事件B发生的概率,P(A ∩B)表示事件A和事件B同时发生的概率。
5、事件的乘法法则
P(A∩B) = P(A) * P(B|A),其中P(A∩B)表示事件A和事件B同时发生的概率,P(A)表示事件A发生的概率,P(B|A)表示在事件A发生的条件下事件B发生的概率。
6、事件的全概率公式
P(A) = ΣP(A|B) * P(B),其中P(A)表示事件A发生的概率,P(A|B)表示在事件B发生的条件下事件A发生的概率,P(B)表示事件B发生
的概率,Σ表示对所有可能的事件B求和。
7、事件的贝叶斯公式
P(B|A) = P(A|B) * P(B) / P(A),其中P(B|A)表示在事件A发生的条件下事件B发生的概率,P(A|B)表示在事件B发生的条件下事件A发生的概率,P(B)表示事件B发生的概率,P(A)表示事件A发生的概率。

第一章P(A+B)=P(A)+P(B)- P(AB) 特别地,当A 、B 互斥时,P(A+B)=P(A)+P(B) 条件概率公式概率的乘法公式全概率公式:从原因计算结果Bayes 公式:从结果找原因第二章)()()|(B P AB P B A P =)|()()(B A P B P AB P =)|()(A B P A P =∑==nk k k B A P B P A P 1)|()()(∑==nk kki i k B A P B P B A P B P A B P 1)|()()|()()|(∑≤==≤=xk k X P x X P x F )()()(1),(0≤≤y x F },{),(y Y x X P y x F ≤≤=二项分布(Bernoulli 分布)——X~B(n,p)泊松分布——X~P(λ)概率密度函数怎样计算概率均匀分布X~U(a,b)指数分布X~Exp (θ)),...,1,0()1()(n k p p C k X P k n k k n =-==-,,...)1,0(!)(===-k e k k X P k,λλ1)(=⎰+∞∞-dx x f )(b X a P ≤≤⎰=≤≤badx x f b X a P )()()0(1)(/≥=-x e x f x θ)(1)(b x a ab x f ≤≤-=分布函数 对离散型随机变量对连续型随机变量分布函数与密度函数的重要关系:二元随机变量及其边缘分布 分布规律的描述方法联合密度函数 联合分布函数联合密度与边缘密度⎰∞-=≤=xdt t f x X P x F )()()(⎰∞-=≤=xdt t f x X P x F )()()(),(y x f ),(y x F 0),(≥y x f 1),(=⎰⎰+∞∞-+∞∞-dxdy y x f ⎰+∞∞-=dy y x f x f X ),()()()('x f x F =离散型随机变量的独立性连续型随机变量的独立性第三章 数学期望离散型随机变量,数学期望定义连续型随机变量,数学期望定义● E(a)=a ,其中a 为常数● E(a+bX)=a+bE(X),其中a 、b 为常数 ● E(X+Y)=E(X)+E(Y),X 、Y 为任意随机变量随机变量g(X)的数学期望⎰+∞∞-=dx y x f y f Y ),()(}{}{},{j Y P i X P j Y i X P =====)()(),(y f x f y x f Y X =∑+∞-∞=⋅=k kkP xX E )(⎰+∞∞-⋅=dxx f x X E )()(∑=kkk p x g X g E )())((常用公式方差 定义式常用计算式∑∑=ijiji p x X E )(dxdy y x xf X E ⎰⎰=),()()()()(Y E X E Y X E +=+∑∑=ijijj i p y x XY E )(dxdy y x xyf XY E ⎰⎰=),()()()()(,Y E X E XY E Y X =独立时与当()⎰+∞∞-⋅-=dx x f X E x X D )()()(2[]22)()()(X E X E X D -=常用公式当X 、Y 相互独立时:方差的性质D(a)=0,其中a 为常数D(a+bX)=b2D(X),其中a 、b 为常数 当X 、Y 相互独立时,D(X+Y)=D(X)+D(Y) 协方差与相关系数协方差的性质))}())(({(2)()()(Y E Y X E X E Y D X D Y X D --++=+)()()(Y D X D Y X D +=+)()()(),(Y E X E XY E Y X Cov -=)()(),(Y D X D Y X Cov XY=ρ[][]{})()()()()(Y E X E XY E Y E Y X E X E -=--())()()(),(22X D X E X E X X Cov =-=),(),(Y X abCov bY aX Cov =独立与相关 独立必定不相关 相关必定不独立 不相关不一定独立 第四章 正态分布标准正态分布的概率计算 标准正态分布的概率计算公式)()()(a a Z P a Z P Φ=<=≤)(1)()(a a Z P a Z P Φ-=>=≥)()()(a b b Z a P Φ-Φ=≤≤1)(2)()()(-Φ=-Φ-Φ=≤≤-a a a a Z a P 一般正态分布的概率计算),(),(),(Z Y Cov Z X Cov Z Y X Cov +=+),(~2σμN X 222)(21)(σμσπ--=x e x f 2)(,)(σμ==X D X E )(1)(a a -Φ-=Φ)1,0(~),(~2N X Z N X σμσμ-=⇔一般正态分布的概率计算公式第五章卡方分布t 分布F 分布 )()()(σμ-Φ=<=≤a a X P a X P )(1)()(σμ-Φ-=>=≥a a X P a X P )()()(σμσμ-Φ--Φ=≤≤a b b X a P )(~)1,0(~212n X N X ni i χ∑=,则若())(~1),,(~21222n Y N Y ni iχμσσμ∑=-则若),(~//),(~),(~21212212n n F n V n U n V n U 则若χχ则若),(~),1,0(~2n Y N X χ)(~/n t nY X正态总体条件下 样本均值的分布:样本方差的分布:两个正态总体的方差之比第六章点估计:参数的估计值为一个常数 矩估计 最大似然估计似然函数均值的区间估计——大样本结果),(~2nN X σμ)1,0(~/N nX σμ-)1(~)1(222--n S n χσ)1(~/--n t ns X μ)1,1(~//2122212221--n n F S S σσ);(1θi ni x f L ∏==);(1θi ni x p L ∏==⎪⎫⎛z x σα/—正态总体方差的区间估计⎪⎪⎭⎫ ⎝⎛-±n p p z p )1(2/α正态分布的分位点—大样本要求样本容量—样本比例—2/)50(αz n np >已知准差小样本、正态总体、标σ⎪⎭⎫ ⎝⎛±n z x σα2/未知准差小样本、正态总体、标σ⎪⎭⎫ ⎝⎛-±n s n t x )1(2/α分布的分位点的自由度为—t n n t 1)1(2/--α()22)1()1(--Sn Sn 样本方差—22S两个正态总体均值差的置信区间大样本或正态小样本且方差已知两个正态总体方差比的置信区间第七章假设检验的步骤① 根据具体问题提出原假设H0和备择假设H1② 根据假设选择检验统计量,并计算检验统计值③ 看检验统计值是否落在拒绝域,若落在拒绝域则拒绝原假设,否则就不拒绝原假设。

概率论与数理统计计算公式概率论和数理统计是数学中的两个重要分支,广泛应用于自然科学、社会科学和工程技术等领域。
在实际中,我们经常需要计算各种概率和统计量,因此理解和掌握概率论和数理统计中的计算公式是十分重要的。
接下来,我将给出概率论和数理统计中一些常用的计算公式。
一、概率计算公式:1.加法原理:如果A和B是两个事件,那么它们的和事件(A∪B)的概率可以由如下公式计算:P(A∪B)=P(A)+P(B)-P(A∩B)2.条件概率:如果A和B是两个事件,且P(A)>0,那么事件B在已知事件A发生的条件下发生的概率可以由如下公式计算:P(B,A)=P(A∩B)/P(A)3.全概率公式:如果{B1,B2,...,Bn}是一个对样本空间Ω的一个划分,那么对于任意事件A,我们有:P(A)=ΣP(A,Bi)P(Bi),其中i取1到n。
4.贝叶斯公式:如果{B1,B2,...,Bn}是一个对样本空间Ω的一个划分,那么对于任意事件A和i取1到n,我们有:P(Bi,A)=P(A,Bi)P(Bi)/ΣP(A,Bj)P(Bj),其中j取1到n。
5.乘法定理:如果A和B是两个事件,那么它们的交事件的概率可以由如下公式计算:P(A∩B)=P(A)P(B,A)=P(B)P(A,B)二、统计量计算公式:1.样本均值:对于由n个观测值组成的样本,样本的均值可以由如下公式计算:\(\bar{X} = \frac{1}{n} \sum\limits_{i=1}^n x_i\)2.样本方差:对于由n个观测值组成的样本,样本的方差可以由如下公式计算:\(S^2 = \frac{1}{n-1} \sum\limits_{i=1}^n (x_i - \bar{X})^2\) 3.标准差:样本的标准差是样本方差的平方根\(S = \sqrt{S^2}\)4.相关系数:对于两个随机变量X和Y,它们的相关系数可以由如下公式计算:\(\rho_{XY} = \frac{Cov(X,Y)}{\sigma_X \sigma_Y}\)5.协方差:样本的协方差可以由如下公式计算:\(Cov(X,Y) = \frac{1}{n-1} \sum\limits_{i=1}^n (X_i-\bar{X})(Y_i-\bar{Y})\)以上只是概率论和数理统计中的一些常用计算公式,实际应用中还有很多其他的公式和方法。

概率的基本公式(一)
概率的基本公式
1. 概率的定义
•概率是描述随机事件发生可能性的数值,通常在0和1之间取值,表示最小可能性为0,最大可能性为1。
2. 事件与样本空间
•样本空间:所有可能事件发生的集合,通常用S表示。
•事件:样本空间中的一个子集,通常用A、B、C等表示。
3. 概率公式
•A事件的概率:P(A)
•互斥事件的概率求和公式:P(A∪B) = P(A) + P(B)
•独立事件的概率乘积公式:P(A∩B) = P(A) * P(B) 4. 互斥事件
•互斥事件:两个事件不可能同时发生。
•举例:抛一枚硬币,正面朝上为事件A,反面朝上为事件B。
因为硬币不可能既正面朝上又反面朝上,所以事件A与
事件B是互斥事件。
5. 独立事件
•独立事件:一个事件的发生不会影响另一个事件的发生。
•举例:从一副扑克牌中摸一张红桃牌为事件A,从同一副牌中再摸一张黑桃牌为事件B。
因为第一次摸牌的结果不会影响第二次摸牌的结果,所以事件A与事件B是独立事件。
6. 补事件
•补事件:某个事件不发生的情况。
•补事件的概率公式:P(A’) = 1 - P(A)
•举例:在一次投掷骰子的实验中,事件A为投出奇数点数,事件A’为投出偶数点数。
因为骰子的点数要么是奇数要么是偶数,两个事件互为补事件。
以上是概率的基本公式及相关解释,希望对您有所帮助。

高中数学概率公式大全概率是数学中一个重要的概念,它可以用来衡量某件事情发生的可能性。
概率学的研究对于现代社会非常重要,因为它可以帮助我们分析和预测事物的发展方向,从而为我们提供决策和指导。
尤其是在经济、金融、保险等领域,概率学尤为重要。
在高中数学中,学习概率也是重要的一环,学生需要掌握多种概率计算公式,以便能够根据给定的条件来计算出概率。
在本文中,我们将综述常见的概率计算公式,以便高中学生能够更好地掌握概率相关知识。
一、概率的基本定义概率是客观概念,它是指某个事件发生的可能性,也可以说是某个事件发生的机会大小。
其计算公式如下:概率=假设情况下A事件发生的次数/总共事件发生的次数这里,A事件发生次数是指给定实验条件下,A事件在多次实验中发生的次数;总共事件发生次数则指多次实验中,出现的所有事件的次数总和。
二、独立重复试验中的概率独立重复试验是概率学中一个基本概念,它指的是每次实验中,每一种可能结果发生的概率都是一样的,且每一次实验都是独立的,不会相互影响。
其计算公式如下:独立重复试验概率=A发生概率*B发生概率*…*N发生概率这里,A、B、…、N分别表示多次实验中,出现的一系列事件,而每一个事件发生的概率分别用P(A)、P(B),…,P(N)表示。
三、二项式定理的应用高中数学中的二项式定理是概率计算的重要公式,其计算公式如下:二项式定理=nCr*P^r*(1-P)^(n-r)这里,n表示实验次数,r是某个事件发生的次数,P是该事件发生的概率,nCr表示从n个中选择r个的组合数,即n!/[r!*(n-r)!]。
四、条件概率条件概率是概率学中一个重要概念,它是用来衡量在某个事件发生的情况下,另一个事件发生的可能性。
条件概率的计算公式如下:条件概率=P(B|A) = P(AB)/P(A)这里,P(B|A)表示在A事件发生的情况下,B事件发生的概率,P(AB)表示A与B事件同时发生的概率,P(A)表示A事件单独发生的概率。

概率分布计算公式概率分布是概率论中重要的概念之一,它描述了随机变量在各个取值上的取值概率。
在实际问题中,我们常常需要计算概率分布以解决相关的概率统计问题。
本文将介绍几种常见的概率分布以及它们的计算公式。
一、二项分布(Binomial Distribution)二项分布是概率论中常用的离散型概率分布,它描述了在一定次数的独立重复试验中,成功事件发生的次数的概率分布。
其计算公式为:P(X=k) = C(n, k) * p^k * (1-p)^(n-k)其中,P(X=k)表示成功事件发生k次的概率,n表示试验次数,p表示每次试验成功的概率,C(n, k)表示组合数,可以使用n个数任取k个的方式计算。
二项分布的期望为E(X)=np,方差为Var(X)=np(1-p)。
二、泊松分布(Poisson Distribution)泊松分布是一种离散型概率分布,适用于描述单位时间(或单位空间)内随机事件发生的次数。
其计算公式为:P(X=k) = (λ^k * e^(-λ))/k!其中,P(X=k)表示事件发生k次的概率,λ表示单位时间(或单位空间)内事件发生的平均次数,e为自然对数的底。
泊松分布的期望为E(X)=λ,方差为Var(X)=λ。
三、正态分布(Normal Distribution)正态分布是概率论中最重要的连续型概率分布,也称为高斯分布。
它的形状呈钟型曲线,对称于均值。
正态分布在实际问题中得到广泛应用。
其概率密度函数的计算公式为:f(x) = (1 / (σ * √(2π))) * e^((-1/2)*((x-μ)/σ)^2)其中,f(x)表示随机变量X的概率密度函数,μ为均值,σ为标准差,π为数学常数3.14159。
正态分布的期望为E(X)=μ,方差为Var(X)=σ^2。
四、指数分布(Exponential Distribution)指数分布是一种连续型概率分布,其概率密度函数具有常数倍衰减的特点。

条件概率相关公式
条件概率是指在已知事件B发生的前提下,事件A发生的概率,用P(A|B)表示。
条件概率有以下公式:
1. 乘法公式:
当事件A和B都是独立事件时,P(A∩B) = P(A) * P(B)
当事件A和B不是独立事件时,P(A∩B) = P(A|B) * P(B)
2. 加法公式:
当事件A和B互不相交时,P(A∪B) = P(A) + P(B)
当事件A和B不互不相交时,P(A∪B) = P(A) + P(B) - P(A∩B)
3. 全概率公式:
设事件B1、B2、…、Bn为样本空间S的一个划分,即B1∪B2∪…∪Bn = S,且P(Bi) > 0,则对任意事件A,有:
P(A) = ∑(i=1)^nP(A|Bi)*P(Bi)
其中,P(A|Bi)代表在Bi发生的条件下,A发生的概率。
4. 贝叶斯公式:
设事件B1、B2、…、Bn为样本空间S的一个划分,即B1∪B2∪…∪Bn = S,且P(Bi) > 0,则对任意事件A,有:
P(Bi|A) = P(A|Bi)*P(Bi)/∑(j=1)^nP(A|Bj)*P(Bj)
其中,P(Bi|A)代表在A发生的条件下,Bi发生的概率。



概率计算公式加法法则
PA∪B=PA+PB-PAB
条件概率
当PA>0;PB|A=PAB/PA
乘法公式
PAB=PA×PB|A=PB×PA|B
计算方法
“排列组合”的方法计算
记法
PA=A
加法法则
定理:设A、B是互不相容事件AB=φ;PAB=0.则
PA∪B=PA+PB-PAB=pA+PB
推论1:设A1、 A2、…、 An互不相容;则:PA1+A2+...+ An= PA1 +PA2 +…+ PAn 推论2:设A1、 A2、…、 An构成完备事件组;则:PA1+A2+...+An=1
推论3: PA=1-PA'
推论4:若B包含A;则PB-A= PB-PA
推论5广义加法公式:
对任意两个事件A与B;有PA∪B=PA+PB-PAB
条件概率
条件概率:已知事件B出现的条件下A出现的概率;称为条件概率;记作:PA|B
条件概率计算公式:
当PA>0;PB|A=PAB/PA
当PB>0;PA|B=PAB/PB
乘法公式
PAB=PA×PB|A=PB×PA|B
推广:PABC=PAPB|APC|AB
全概率公式
设:若事件A1;A2;…;An互不相容;且A1+A2+…+An=Ω;则称A1;A2;…;An构成一个完备事件组..
的形式如下:
以上公式就被称为全概率公式..。
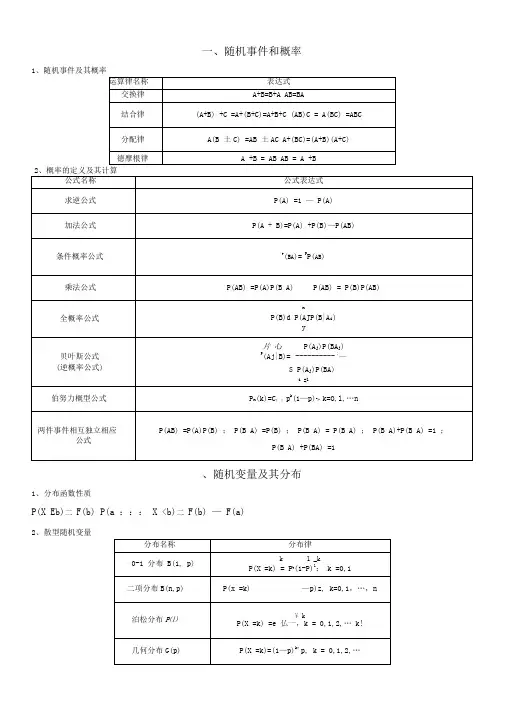
一、随机事件和概率1、随机事件及其概率、随机变量及其分布1、分布函数性质P(X Eb)二F(b) P(a ::: X <b)二F(b) — F(a)2、散型随机变量3三、多维随机变量及其分布1、 离散型二维随机变量边缘分布 P i.=P(X=X j )=' P(X=X i ,Y=y j )=' pjP j=P(丫 = yj)=' P(X=X j ,Y=yj)=' pjjji i2、 离散型二维随机变量条件分布x y3、 连续型二维随机变量(X ,Y )的分布函数F (x, y)=匕打二f (u,v)dvdu4、 连续型二维随机变量边缘分布函数与边缘密度函数x ■: : ■::分布函数: Fx (x) f (u,v)dvdu y -beF Y (y) f (u,v)dudv5、二维随机变量的条件分布 s(yx)—XY (xy)fyp —四、随机变量的数字特征1、 数学期望■bo 鈕离散型随机变量: E(X) X k P k连续型随机变量: E(X ) = xf (x)dxk=1一北2、 数学期望的性质(1) E(C) =C,C 为常数 E[E(X)] =E(X) E(CX) =CE(X)pi j= P(X=xi 丫= yj)史二二上,i”P(Y =y j)P j.pj i= P(Y = yjX =x i)7 丫知P(X =X i )P i .密度函数:fx (x)二 f(x,v)dv_f?0■ho fY(y)二 f(u, y)du⑵ E(X _Y) =E(X) -E(Y) E(aX —b)二aE(X) _b EGX1 C n X n) ^汨*) C n E(X n)⑶若XY相互独立则:E(XY) =E(X)E(Y) (4)[E(XY)]2空 E2(X)E2(Y)3、方差:D(X) =E(X2) —E2(X)4、方差的性质2 2(1)D(C) =0 D[D(X)] =0 D(aX _b) =a2D(X) D(X) ::: E(X _C)2(2)D(X _Y) =D(X) D(Y) _2Cov(X,Y) 若 XY 相互独立则: D(X 二丫)= D(X) D(Y)5、协方差:Cov(X,Y) =E(X,Y) -E(X)E(Y) 若 XY 相互独立则: Cov(X,Y)=06、相关系数:P XY = P(X,丫) = Cov(X,Y)若XY相互独立则:P XY =0即XY不相关W(X)jD(Y)7、协方差和相关系数的性质(1) Cov(X,X) =D(X) Co VX,Y) =Co VY,X) ⑵ Cov(X i X2,Y) =Cov(X i,Y) C OV(X2,Y) Cov(aX c,bY d) =abCo%,Y) 8、常见数学分布的期望和方差五、大数定律和中心极限定理1、切比雪夫不等式若 E(X) ==D(X) =;「2,对于任意0 有 P{X -E(X) 一 } 一卫孚或 P{X -E(X) :: } 一1-卫冷91n1nXT X n相互独立且n T旳时,丄瓦Xi ― 丄瓦E(X i) n y nid2、大数定律:若⑸样本k 阶中心距:n1 _— k B k 二M k (X i -X)k,k =2,3…⑹次序统计量:设样本 (人必2…X n )的观察值 区也…冷),将“X ?…冷按照由小到大的次序重新排列,得到X (1)岂乂⑵乞…岂Xg ,记取值为X(Q 的样本分量为X(Q ,则称X (1)岂X (2) <<X (n)为样本以皿 X .)的次序统计 量。
概率的运算和事件的运算概率是数学中的一个分支,它研究随机事件发生的可能性。
在概率论中,事件是指一个或多个结果的集合,它们可能会发生或不发生。
事件的运算是对事件的组合进行操作,从而得到新的事件。
本文将着重介绍概率的运算和事件的运算。
一、概率的运算1. 加法原理加法原理是指,如果事件A和事件B是不相交的,那么它们的联合事件(即事件A或事件B发生)的概率等于事件A的概率与事件B 的概率之和。
例如,如果A表示抛掷一枚骰子时得到1或2的事件,B表示抛掷一枚骰子时得到3或4的事件,那么P(A或B)=P(A)+P(B)=2/6+2/6=4/6。
2. 乘法原理乘法原理是指,如果事件A和事件B是独立的,那么它们的交集事件(即事件A和事件B都发生)的概率等于事件A的概率与事件B 的概率之积。
例如,如果A表示从一副扑克牌中抽取一张红色牌的事件,B表示从一副扑克牌中抽取一张大牌(即A、K、Q、J、10中的一张)的事件,那么P(A且B)=P(A)×P(B)=26/52×20/52=5/26。
3. 条件概率条件概率是指,在已知事件B发生的情况下,事件A发生的概率。
条件概率的计算公式为P(A|B)=P(A且B)/P(B),其中P(A且B)表示事件A和事件B都发生的概率,P(B)表示事件B发生的概率。
例如,如果A表示某人患有某种疾病的事件,B表示某人的年龄在40岁以上的事件,那么P(A|B)表示在已知某人年龄在40岁以上的情况下,他患有某种疾病的概率。
二、事件的运算1. 并集并集是指由两个或多个事件的所有结果组成的集合。
例如,如果A 表示抛掷一枚骰子时得到1或2的事件,B表示抛掷一枚骰子时得到2或3的事件,那么A和B的并集表示抛掷一枚骰子时得到1、2或3的事件。
2. 交集交集是指由两个或多个事件的公共结果组成的集合。
例如,如果A 表示从一副扑克牌中抽取一张红色牌的事件,B表示从一副扑克牌中抽取一张大牌的事件,那么A和B的交集表示从一副扑克牌中抽取一张既是红色牌又是大牌的事件。
概率论与数理统计必背公式在概率论与数理统计中,掌握好一些重要的公式是非常重要的,这些公式可以帮助我们解决问题、推导证明以及计算概率和统计量。
下面将介绍一些必须掌握的概率论与数理统计的重要公式。
一、概率论公式:1.加法定理:如果事件A和B是互不相容的(即A和B不会同时发生),则它们的和事件的概率为P(A∪B)=P(A)+P(B)。
2.条件概率公式:对于两个事件A和B,A在给定B发生的条件下发生的概率定义为P(A,B)=P(A∩B)/P(B)。
3.乘法定理:对于两个事件A和B,其交事件的概率可以通过条件概率公式来计算,即P(A∩B)=P(A,B)*P(B)。
4.全概率公式:如果事件B1,B2,...,Bn是一组互不相容的且其并集为样本空间(即事件B1∪B2∪...∪Bn=S),则对于事件A,它的概率可以通过条件概率公式和全概率公式来计算,即P(A)=P(A,B1)*P(B1)+P(A,B2)*P(B2)+...+P(A,Bn)*P(Bn)。
5.贝叶斯公式:贝叶斯公式是条件概率公式的推广,对于事件A和B,其交事件的概率可以通过贝叶斯公式来计算,即P(A,B)=P(B,A)*P(A)/P(B)。
二、数理统计公式:1.期望:对于一组随机变量X,其期望(也称为均值)定义为E(X)=ΣX*P(X),即随机变量X乘以其概率的和。
2. 方差:对于一组随机变量X,其方差定义为Var(X) = E((X - μ)^2),其中μ为X的期望。
3. 协方差:对于两组随机变量X和Y,其协方差定义为Cov(X,Y) = E((X - μx)(Y - μy)),其中μx和μy分别为X和Y的期望。
4. 标准差:对于一组随机变量X,其标准差定义为σ = √Var(X),即方差的平方根。
5. 协方差矩阵:对于多组随机变量X1,X2,...,Xn,其协方差矩阵定义为Cov(X) = [Cov(Xi,Xj)],其中i和j分别表示第i组和第j组随机变量。
运算公式 第一章事件的运算性质( “ ”=“+”,“ ”=“*”): 1、交换律:A B B A =,BA AB =2、结合律:)()(C B A C B A =,)()(BC A C AB =3、分配律:BC AC C B A =)(,)()()(C B C A C B A =4、对偶律(得摩根公式):事件并的对立等于对立的交:B A B A = 事件交的对立等于对立的并:B A B A = 概率的性质 有限可加性:∑===ni in i iA P A P 11)()(若A B ⊂,则)()()(B P A P B A P -=-对任意事件A ,B ,有)()()(AB P A P B A P -=-(若A ,B 独立,则0)(=AB P ) 加法公式:)()()()(AB P A P A P B A P -+= (若A ,B 独立,则0)(=AB P ) 半可加性:)()()(A P A P B A P +≤条件概率:)()()|(B P AB P B A p =乘法公式:(1)0)(>B P ,则)|()()(B A P B P AB P =;(2)0)(1-21>n A A A P ,则)|()|()|()()(1121312121-=n n n A A A P A A A P A A P A P A A A P全概率公式:n 21B B B ,,, 互不相容,且 ni iB1=Ω=,则)|()()(1i ni i B A P B P A P ∑==贝叶斯公式:n 21B B B ,,, 互不相容,且 ni iB1=Ω=,如果0)(>A P ,0)(>i B P 则)|()()|()()|(1jnj ji i i B A P B P B A P B P A B P ∑==第二章切比雪夫不等式:2)())((εεX Var X E X P ≤≥-或者2)(1))((εεX Var X E X P -≥<-连续随机变量函数的分布()(X g Y =):)(x g 严格单调设X 是连续型随机变量,其密度函数为)(x P X 。
利用Venn图巧记概率的运算公式
概率是数学中的一个重要概念,它描述了某个事件发生的可能性。
在概率的运算中,Venn图是一种非常有用的工具,可以帮助我们理解和记忆概率的运算公式。
Venn图是一种由欧拉发展起来的图形,它由一条包围线和多个圆组成。
我们可以将概率的运算公式与Venn图对应起来,从而更加直观地理解这些公式。
下面,我们将介绍几个常见的概率运算公式,并结合Venn图给出记忆技巧。
1. 加法公式:P(A∪B) = P(A) + P(B) - P(A∩B)
加法公式描述的是两个事件的并集的概率。
在Venn图中,我们可以将A和B分别用两个圆表示,它们的交集部分就是A∩B。
我们可以用两个圆的面积和减去交集的面积,得到并集的面积,从而计算出并集的概率。
3. 条件概率公式:P(A|B) = P(A∩B) / P(B)
条件概率公式描述的是在事件B已经发生的条件下,事件A发生的概率。
在Venn 图中,事件A∩B表示的是事件A和事件B的交集,它同时属于A和B。
我们可以通过计算事件A∩B的概率除以事件B的概率,得到在事件B已经发生的条件下,事件A发生的概率。
通过利用Venn图巧记概率的运算公式,我们可以更加直观地理解和记忆这些公式。
在解题时,我们可以先根据题目中的信息画出Venn图,然后利用公式计算出相应的概率。
这样不仅可以提高解题的速度和准确性,还能够加深对概率概念的理解。
希望这些记忆技巧可以对你在学习概率时有所帮助!。
概率运算公式
概率运算公式是计算事件发生概率的重要工具,包括以下几个公式:
1. 加法公式:P(A ∪ B) = P(A) + P(B) P(A ∩ B),其中A、B为两个事件,∪表示并集,∩表示交集。
2. 乘法公式:P(A ∩ B) = P(A) × P(B|A),其中A、B为两个事件,|表示在A发生的条件下B发生的概率。
3. 条件概率公式:P(A|B) = P(A ∩ B) / P(B),其中A、B为两个事件,|表示在B发生的条件下A发生的概率。
4. 全概率公式:P(A) = ∑ P(A ∩ Bi),其中B1、B2、B3…Bn 为互不相交的事件,并且每个Bi都有非零概率。
5. 贝叶斯公式:P(Bi|A) = P(A|Bi) × P(Bi) / ∑ P(A|Bj) ×P(Bj),其中Bi为一系列互不相交的事件,A为某个事件。
掌握这些概率运算公式可以帮助我们更好地理解和计算概率,应用于统计学、数据分析、机器学习等领域。
- 1 -。