2008年高三数学第二轮专题复习测试之极限、导数

高三数学第2、3章《极限》《导数》测试及答案一、选择题:本题共12小题，每小题5分，共60分，在每小题给出的四个选项中只有一个选项正确 1．（理）若复数z 满足方程022=+z ，则=3z（ ）A ．22±B ． 22-C ．i 22-D ． i 22±(文)曲线y=4x －x 3在点(－1,－3)处的切线方程是（ ）A ． y=7x+4B ． y=7x+2C ． y=x －4D ． y=x －22．函数y=x 2(－21≤x ≤21)图像上一点P,以点P 为切点的切线为直线l,则直线l 的倾斜角的范围是（ ）A ．［0,4π］∪［43π,π］B ．［0,π］C ．［4π,43π］D ．［0,4π］∪(2π,43π) 3．（理）若2lim →x 434222=--+x ax x ,则a 的值为（ ）A ．0B ．1C ．－1D ．21（文）在曲线y=x 2+1的图像上取一点（1,2）及邻近一点（1+Δx ,2+Δy ）,则yx∆∆为（ ） A ．Δx+x∆1+2 B ．Δx －x ∆1－2 C ．Δx+2D ．2+Δx －x ∆14．曲线y=51x 5+3x 2+4x 在x =－1处的切线的倾斜角是（ ）A ．－4πB ．4πC ．43πD ．45π5．函数f(x)=x 3－ax 2－bx+a 2在x=1时,有极值10,则a 、b 的值为（ ）A ．⎩⎨⎧=-=⎩⎨⎧-==1143,3b a b a 或 B ．⎩⎨⎧==⎩⎨⎧=-=1141,4b -a b a 或 C ．⎩⎨⎧=-=51b aD ．以上皆错6．（理）已知()23,12,1x x f x x +≠⎧=⎨=⎩，下面结论正确的是（ ）A ．()f x 在1x =处连续B ．()5f x =C ．()1lim 2x f x -→= D ．()1lim 5x f x +→=（文）设f （x ）=a x 3+3x 2+2,若f ′（－1）=4,则a 的值等于A ．319B ．316 C ．313 D ．3107．函数f(x )=x 3－3x +1,x ∈［－3,0］的最大值、最小值分别是（ ）A ．1,－1B ．1,－17C ．3, －17D ．9,－198．（理）数列{a n }中，a 1=1,S n 是前n 项和.当n ≥2时，a n =3S n ,则∞→n lim311-++n n S S 的值是（ ）A ．－31B ．－2C ．1D ．－54（文）曲线y=x 3－3x 2+1在点（1，－1）处的切线方程为（ ）A ．y=3x －4B ．y=－3x+2C ．y=－4x+3D ．y=4x －5 9．（理）2+23i 的平方根是（ ）A ．3+iB ．3±iC ．±3+iD ．±(3+i)（文）已知f （x ）=2x 3－6x 2+m （m 为常数）在［－2，2］上有最大值3，那么此函数在［－2，2］上的最小值是（ ）A ．－37B ．－29C ．－5D ．以上都不对10．已知函数)(x f x y '=的图像如右图所示（其中 )(x f '是函数)(x f 的导函数），下面四个图像中)(x f y =的图像大致是11．设f(x)、g(x)分别是定义在R 上的奇函数和偶函数,当x ＜0时,)()()()(x g x f x g x f '-' ＞0.且g(3)=0.则不等式f(x)g(x)＜0的解集是（ ）A ．（－3,0)∪(3,+∞)B ．(－3,0)∪(0, 3)C ．(－∞,- 3)∪(3,+∞)D ．(－∞,－ 3)∪(0, 3)12．已知两点O （0,0），Q （a ,b ）,点P 1是线段OQ 的中点，点P 2是线段QP 1的中点，P 3是线段P 1P 2的中点，┅，2+n P 是线段n P 1+n P 的中点，则点n P 的极限位置应是（ ） A ．（2a ,2b） B ．(3,3b a ) C ．(32,32b a ) D ． (43,43ba )二、填空题(本大题共4小题，每小题4分，共16分.把答案填在题中横线上)13．垂直于直线2x －6y+1=0且与曲线y=x 3+3x 2－1相切的直线方程的一般式是__________.14．(理) （2006年安徽卷）设常数0a >，42ax ⎛ ⎝展开式中3x 的系数为32，则2lim()n n a a a →∞++⋅⋅⋅+=_____.(文)(2006福建高考)已知直线10x y --=与抛物线2y ax =相切，则______.a = 15．函数f(x)=2x 3+3x 2－12x －5,则函数f(x)的单调增区间是______. 16．（理）用数学归纳法证)"(212111211214131211"*N n nn n n n ∈+++++=--++-+- 的过程中，当n=k 到n=k+1时，左边所增加的项为_______________.（文）若函数f （x ）=x 3+x 2+mx+1是R 上的单调递增函数，则m 的取值范围是______________．三、解答题(本大题共6小题，共74分.解答应写出文字说明、证明过程或演算步骤) 17．（本小题满分12分）（理）设函数⎪⎪⎩⎪⎪⎨⎧≥-<≤-+-<≤<=)3(4)31(24)10()0(0)(2x xx x x x x x x f（1）画出函数的图像；（2）在x=0，x=3处函数)(x f 是否连续； （3）求函数)(x f 的连续区间. （文）已知函数ax ax x f 313)(23-+-=. （1）讨论函数)(x f 的单调性；（2）若曲线)(x f y =上两点A 、B 处的切线都与y 轴垂直，且线段AB 与x 轴有公共点，求实数a 的取值范围.18．（本题满分12分）（理）已知复数z 1=cosθ－i ，z 2=sinθ+i ，求| z 1·z 2|的最大值和最小值.（文）(2006福建高考)已知()f x 是二次函数，不等式()0f x <的解集是(0,5),且()f x 在区间[]1,4-上的最大值是12。

全国名校高考专题训练12导数与极限一、选择题1、（江苏省启东中学2008年高三综合测试一）函数y=2x3-3x2-12x+5在区间［0,3］上最大值与最小值分别是（）A. 5,-15B. 5,-4C. -4,-15D. 5,-16答案：A2、（安徽省皖南八校2008届高三第•次联考）若存在，则/（x）不可能为5 x +X（）A.兀2； B . Ixl； C . x ； D . — X ；答案：B3、（江曲省五校2008届高三幵学联考）设函数/'（X）= sin（®r + -）-l（ty > 0）的导数广（X）的最大值为3,则/（x）的图象的■条对■称轴的方程是7171A. x ——B. X ——967171C. x ——D. X ——32答案：A力-3/•（*）4、（江西省五校2008届高三开学联考）已知f（3）= 2,f,（3）= -2,则毁* -' x 3A. -4B. 8C. 0D.不存在答案：B5、（安徽省蚌埠二中2008届高三8月月考）函数/（X）在x = x0处连续是/（X）在X = 处有极限的（A）充分不必要条件（B）必要不充分条件（C）充要条件（D）既不充分也不必要条件答案：A6、（安徽省蚌埠二中2008届高三8月月考）已知/（X）是关于x的三次函数，且= —2, = 5,则lim^4 的值是x_2 X — 2X—3 兀―3 4 4X—A3 3答案：Any -I- p )x -L 17、 (安徽省蚌埠二中2008届高三8月月考)已知H m= 3 ,则b 的值为XT1 X — 1 (A) 4(B) -5(C) -4(D) 5答案：B8、 (安徽省蚌埠二中2008届高三8月月考)已知数列｛a”｝是由正数组成的数列，= 3 ,且 2"J -a满足lga” = lga”_]+lgc ,其中n>l,c>2且为整数，则]im —□ ------------------------------ 等于2"T + a n1 1 (A) -1 (B)1(C)2(D)-C答案：A9 、(安徽省蚌埠二中2008届 高 三 8 月月考〕 1设a” = 1 + q + q - + q" + ... + q" 1, A n = c't/j + c~cij + + ... + c ：a”，且一3 < g < 1,贝!]Alim*的值为答案：B10、(四川省成都市一诊)黒『n的值为，2+?+丄答案：A lim 2/r +3/? + 1=lim —=2.选 A n —>oo n 2-L 9n —>oo _ Z"十 Z 1 + —n~11、(四川省乐山市2008届第一次调研考试)函数f(X )= \x 2-l X-1(A)10 T(B) (C) 3(D) 不存在1(A)- q(B)1 i_q(C) q (D) 1-qA 、2B 、0C 、B l ；C_3；D.-连续，则实数加=( 12、(四川省成都市新都一中高2008级12月月考)设a>0, ^x)=ax 1+bx+c,曲线y=/W 在点P(x 0, f(x 0))处切线的倾斜角的取值范围为［0,勺，则点P 到曲线y =/«对称轴距离的 取值范围为()A 、［0, |］ B. ［0,占C 、［0, |守|］D 、［0,本题考查函数的切线、斜率、导数及距离等基础知识及其综合运用. 解析 依题设知点P 的横坐标xo 必须且只须满足JI0<f'(x 0)<tan-^^l因为 广(x) = 2ax+b所以 Os2axo+b£lb因为抛物线y=/W 的对称轴为直线/： x=—石 所以点P 到直线/的距离为宀|勺+守| 因为a>0所以 d=£j|2axo+b|g且d20,即得d 的取值范围为［0,痔］ 答案:B13、(安徽省淮南市2008届高三第一次模拟考试)若函数f(x)=e x cosx,则此函数图象在点(1/ ⑴)处的切线的倾斜角为( )A. 0B.锐角C. —D.钝角2答案：D14、(安徽省巢湖市2008届高三第二次教学质量检测)函数y = g 的图象经过原 点，且它的导函数y = /'W 的图象是如图所示的一条直线，则y = /(x)的图象不经 过 ()A.第一象限B.第二象限C.第三象限答案：B15、(湖北省鄂州市2008年高考模拟)若/'(Q 是定义在R 上的连续函数，且lim^^ = 2, i X-1D.第四象限广(x) = 0 有( )A、分别位于区间(1, 2)、(2,B、四个根兀(心1,2,3,4)C、分别位于区间(0, 1)、(1,D、分别位于区间(0, 1)、(1,3)、(3, 4)内的三个根2)、(2, 3)、(3, 4)内的四个根2)、(2, 3)内的三个根A. 2B. 1C. 0D. -1答案：C lim/(A-) = lim[^^ • (A- -1)] = 2 X 0 = 0 = / (l),故选 C.x->l x->l X — 1【总结点评】本题考查函数连续性的定义以及求函数极限的方法，以及思维的灵活性. 【误区警示】本题属于基础题，每步细心计算是求解本题的关键，否则将会遭遇“千里之堤, 溃于蚁穴”之尴尬.16、(北京市海淀区2008年高三统一练习一)定义在R上的函数/(x)满足f(4) = l. /'(x)为/(x)的导函数，已知函数丁 = /'(X)的图象如右图所示.若两正数满足b + 2f(2a + b)<l,则——的取值范围是()Q + 2(A)答案：C(B) (―8,*)U(3,+8)(C) (D) (-CO, -3)17、(北京市西城区2008年4月高三抽样测试)设« eR ,函数f (x) = e v +a-e"v的导函数3 是广(x),且/'(X)是奇函数.若曲线y = /(.r)的一条切线的斜率是寸，则切点的横坐标为()In 2 ’ c In 2 ,A. ----------B. — In 2C. -----D. In 22 2答案：D18、(北京市宣武区2008年高三综合练习二)对于R上可导的任意函数f(x),若满足(%—1)厂(%)>0,则必有( )A f(o)+f ⑵ <2和) B f(o)+f ⑵〉2凡1)C f(0)+ f(2)>2f(l)D f(0)+ f(2)<2/(1)答案:C19、(山东省博兴二中高三第三次月考)设函数/(x) = (x —l)(x —2)(x —3)(x —4),则*3 -a 2x20、(东北三校2008年高三第一次联考)已知函数f(x) = { x -a2则实数a 的值是()A. -1B. 1答案:C21、陈北三校2008年高三第一次联考)函数/(x)在定义域R 内可导，若/(.r) = /(2-X ),且当 x e (-00,1)时，(x —1)广(x)< 0,设 a = f (0), b = f (j), c = f (3).贝^ ()A. a<b <cB. c <a<bC. c <b <aD. b <c <a答案:B+ 2x - 3 --- x > 122、 (福建省泉州「中高2008届第•次模拟检测)已知函数f(X )= \x-1 ，_在点 ax +1, x < 1x = l 处连续，则a 的值是()A. 2B. 3C. -2D. -4答案：B23、 (福建省厦门市2008学年高三质量检查)一质点沿直线运动，如果由始点起经过t 称后的1 3位移为5 = -z 3--r+2/,那么速度为零的时刻是()3 2 A. 0秒B. 1秒末C. 2秒末D. 1秒末和2秒末答案：D24、 (福建省厦门市2008学年高三质量检查)我们把使得f(x) = 0的实数x 叫做函数y=f(x)的零点.对于区间［a,b ］上的连续函数y=f(x),若f(a)f(b)V0,那么那么函数y=f(x)在区间(a,b) 内有零点。

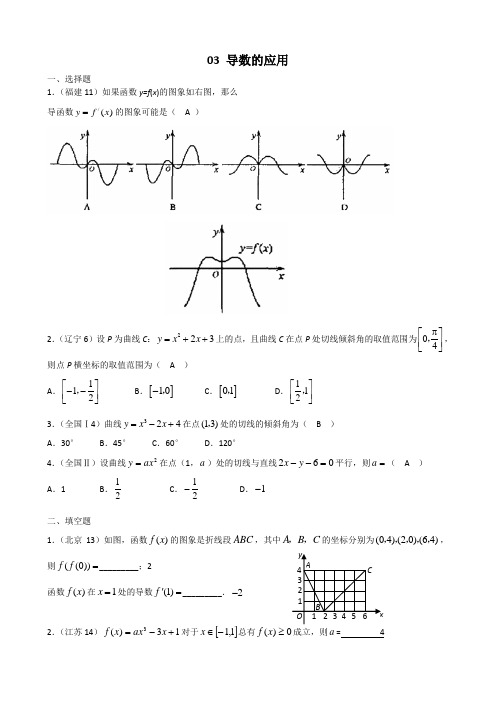
03 导数的应用一、选择题 1．（福建11）如果函数y=f (x )的图象如右图，那么 导函数/()y f x =的图象可能是（ A ）2．（辽宁6）设P 为曲线C ：223y x x =++上的点，且曲线C 在点P 处切线倾斜角的取值范围为04π⎡⎤⎢⎥⎣⎦，，则点P 横坐标的取值范围为（ A ）A ．112⎡⎤--⎢⎥⎣⎦，B ．[]10-，C ．[]01，D ．112⎡⎤⎢⎥⎣⎦，3．（全国Ⅰ4）曲线324y x x =-+在点(13)，处的切线的倾斜角为（ B ） A ．30°B ．45°C ．60°D ．120°4．（全国Ⅱ）设曲线2ax y =在点（1，a ）处的切线与直线062=--y x 平行，则=a （ A ）A ．1B ．12C ．12-D ．1-二、填空题1．（北京13）如图，函数()f x 的图象是折线段ABC ，其中A B C ，，的坐标分别为(04)(20)(64)，，，，，，则((0))f f =_________；2函数()f x 在1x =处的导数(1)f '=_________．2-2．（江苏14）13)(3+-=x ax x f 对于[]1,1-∈x 总有0)(≥x f 成立，则a = 42 BCAyx1 O 3 4 5 612 3 4三、解答题 1．（安徽20）（本小题满分12分） 设函数323()(1)1,32a f x x x a x a =-+++其中为实数。

（Ⅰ）已知函数()f x 在1x =处取得极值，求a 的值；（Ⅱ）已知不等式'2()1f x x x a >--+对任意(0,)a ∈+∞都成立，求实数x 的取值范围。

解: (1) '2()3(1)f x ax x a =-++，由于函数()f x 在1x =时取得极值，所以 '(1)0f =即 310,1a a a -++==∴ (2) 方法一由题设知：223(1)1ax x a x x a -++>--+对任意(0,)a ∈+∞都成立 即22(2)20a x x x +-->对任意(0,)a ∈+∞都成立设 22()(2)2()g a a x x x a R =+--∈, 则对任意x R ∈，()g a 为单调递增函数()a R ∈ 所以对任意(0,)a ∈+∞，()0g a >恒成立的充分必要条件是(0)0g ≥ 即 220x x --≥，20x -≤≤∴ 于是x 的取值范围是}{|20x x -≤≤方法二由题设知：223(1)1ax x a x x a -++>--+对任意(0,)a ∈+∞都成立 即22(2)20a x x x +-->对任意(0,)a ∈+∞都成立于是2222x x a x +>+对任意(0,)a ∈+∞都成立，即22202x xx +≤+ 20x -≤≤∴于是x 的取值范围是}{|20x x -≤≤2．（北京17）（本小题共13分）已知函数32()3(0)f x x ax bx c b =+++≠，且()()2g x f x =-是奇函数． （Ⅰ）求a ，c 的值；（Ⅱ）求函数()f x 的单调区间．解：（Ⅰ）因为函数()()2g x f x =-为奇函数，所以，对任意的x ∈R ，()()g x g x -=-，即()2()2f x f x --=-+． 又32()3f x x ax bx c =+++所以32323232x ax bx c x ax bx c -+-+-=----+． 所以22a a c c =-⎧⎨-=-+⎩，．解得02a c ==，．（Ⅱ）由（Ⅰ）得3()32f x x bx =++． 所以2()33(0)f x x b b '=+≠．当0b <时，由()0f x '=得x b =±-．x 变化时，()f x '的变化情况如下表：x()b -∞--，b --()b b ---，b - b -+∞（，）()f x '+-+所以，当0b <时，函数()f x 在()b -∞--，上单调递增，在()b b ---，上单调递减，在()b -+∞，上单调递增．当0b >时，()0f x '>，所以函数()f x 在()-∞+∞，上单调递增． 3．(福建21)（本小题满分12分）已知函数32()2f x x mx nx =++-的图象过点（-1，-6），且函数()()6g x f x x '=+的图象关于y 轴对称. (Ⅰ)求m 、n 的值及函数y =f (x )的单调区间；(Ⅱ)若a ＞0，求函数y =f (x )在区间（a -1,a +1）内的极值. 解：（1）由函数f (x )图象过点（－1，－6），得m -n =-3, ……① 由f (x )=x 3+mx 2+nx -2，得f ′（x ）=3x 2+2mx +n , 则g (x )=f ′(x )+6x =3x 2+(2m +6)x +n ; 而g (x )图象关于y 轴对称，所以－3262⨯+m ＝0，所以m =-3, 代入①得n =0.于是f ′(x )＝3x 2-6x =3x (x -2). 由f ′(x )>得x>2或x <0,故f (x )的单调递增区间是（－∞，0），（2，＋∞）； 由f ′(x )<0得0<x <2,故f (x )的单调递减区间是（0，2）.(Ⅱ)由（Ⅰ）得f ′(x )＝3x (x -2), 令f ′(x )＝0得x =0或x=2.当x 变化时，f ′(x )、f (x )的变化情况如下表： X (-∞.0) 0 (0,2) 2 (2,+ ∞) f ′(x ) + 0 － 0 ＋ f (x )极大值极小值由此可得：当0<a <1时，f (x )在（a -1,a +1）内有极大值f (O )=-2,无极小值； 当a =1时，f (x )在（a -1,a +1）内无极值；当1<a <3时，f (x )在（a -1,a +1）内有极小值f (2)＝－6，无极大值； 当a ≥3时，f (x )在（a -1,a +1）内无极值.综上得：当0<a <1时，f (x )有极大值－2，无极小值，当1<a <3时，f (x )有极小值－6，无极大值；当a=1或a ≥3时，f (x )无极值. 4．（宁夏）（本小题满分12分） 设函数()bf x ax x=-， ()y f x =在点(2(2))f ，处的切线方程为74120x y --=． （Ⅰ）求()f x 的解析式；（Ⅱ）证明：曲线()y f x =上任一点处的切线与直线0x =和直线y x =所围成的三角形面积为定值，并求此定值． ．解：（Ⅰ）方程74120x y --=可化为734y x =-． 当2x =时，12y =． ················································································································· 2分 又2()b f x a x '=+， 于是1222744b a b a ⎧-=⎪⎪⎨⎪+=⎪⎩，，解得13.a b =⎧⎨=⎩，故3()f x x x=-． ······················································································································· 6分 （Ⅱ）设00()P x y ，为曲线上任一点，由231y x'=+知曲线在点00()P x y ，处的切线方程为002031()y y x x x ⎛⎫-=+- ⎪⎝⎭，即00200331()y x x x x x ⎛⎫⎛⎫--=+- ⎪ ⎪⎝⎭⎝⎭．令0x =得06y x =-，从而得切线与直线0x =的交点坐标为060x ⎛⎫- ⎪⎝⎭，．令y x =得02y x x ==，从而得切线与直线y x =的交点坐标为00(22)x x ，． ················ 10分所以点00()P x y ，处的切线与直线0x =，y x =所围成的三角形面积为016262x x-=． 故曲线()y f x =上任一点处的切线与直线0x =，y x =所围成的三角形的面积为定值，此定值为6． ····················································································································································· 12分 5．（江西21）已知函数4322411()(0)43f x x ax a x a a =+-+> （1）求函数()y f x =的单调区间；（2）若函数()y f x =的图像与直线1y =恰有两个交点，求a 的取值范围． 解：（1）因为322()2(2)()f x x ax a x x x a x a '=+-=+- 令()0f x '=得1232,0,x a x x a =-== 由0a >时，()f x '在()0f x '=根的左右的符如下表所示x(,2)a -∞-2a -(2,0)a - 0(0,)a a (,)a +∞ ()f x ' -+-+()f x极小值极大值极小值所以()f x 的递增区间为(2,0)(,)a a -+∞与()f x 的递减区间为(2)(0)a a -∞-，与， （2）由（1）得到45()(2)3f x f a a =-=-极小值，47()()12f x f a a ==极小值 4()(0)f x f a ==极大值要使()f x 的图像与直线1y =恰有两个交点，只要44571312a a -<<或41a <， 即4127a >或01a ≤<.6．（湖南21）已知函数43219()42f x x x x cx =+-+有三个极值点。

2008届全国百套高考数学模拟试题分类汇编11导数与极限三、解答题(第二部分)51> 已知函数f (尤)=e x -ln(x + l)-l(x>0),(1)求函数f(x)的最小值；(2)若0 <yvx,求证：e x~y -1 > ln(x + l)-ln(j + l).解:(1) f\x)=e x, .................................................. 2分x + 1当x>0 时，>1,—<1,所以当x>0 时，f\x) > 0 ,x + 1则函数/(X)在[0, + 8)上单调递增，所以函数f(x)的最小值/(0) = 0 ；......................................... 5分(2)由(1)知，当尤〉0时，/(x) > 0,x > y ,f(x-y) = e x~y -ln(x-y+ 1)-1 >0, e x~y - l>ln(x-y + l) ① ........................................ 7分ln(.x - v +1) - [ln(x +1) - ln( v + 1)] =ln 火*-')""' >。

，-X + l/. ln(x- y+ 1) > ln(x + l) -ln(y + 1) ②................................. 10 分由①②得e'-v -1 > ln(x +1) — ln(y + 1) .......................................... 12 分52、(河南省许昌市2008年上期末质量评估)已知函数r(x)=-|x2 + 2ax, g(x) =3a2lnx+b,其中a〉0.设两曲线y = r (x),y=g(x)有公共点，且在公共点处的切线相同.(I )用a表示b；(II)求证：f (x) ^g(x), (x>0).20. 解：(I )设y=f(x)与尸g(，)(x>0)在公共点(s’。

2008高考试卷分类汇编02----函数与导数2三、解答题80.（安徽理20）（本小题满分12分） 设函数1()(01)ln f x x x x x=>≠且（Ⅰ）求函数()f x 的单调区间；（Ⅱ）已知12ax x >对任意(0,1)x ∈成立，求实数a 的取值范围。

解 （Ⅰ） '22ln 1(),ln x f x x x+=-若 '()0,f x = 则 1x e=列表如下（Ⅱ） 在 12ax x > 两边取对数, 得1ln 2ln a x x>,由于01,x <<所以1ln 2ln a x x>(*)由(1)的结果可知,当(0,1)x ∈时, 1()()f x f e e≤=-,为使(*)式对所有(0,1)x ∈成立,当且仅当ln 2a e >-,即ln 2a e >-设函数323()(1)1,32a f x x x a x a =-+++其中为实数。

（Ⅰ）已知函数()f x 在1x =处取得极值，求a 的值；（Ⅱ）已知不等式'2()1f x x x a >--+对任意(0,)a ∈+∞都成立，求实数x 的取值范围。

解: (1)'2()3(1)f x ax x a =-++，由于函数()f x 在1x =时取得极值，所以 '(1)0f = 即 310,1a a a -++==∴ (2) 方法一由题设知：223(1)1ax x a x x a -++>--+对任意(0,)a ∈+∞都成立 即22(2)20a x x x +-->对任意(0,)a ∈+∞都成立设 22()(2)2()g a a x x x a R =+--∈, 则对任意x R ∈，()g a 为单调递增函数()a R ∈ 所以对任意(0,)a ∈+∞，()0g a >恒成立的充分必要条件是(0)0g ≥ 即 220x x --≥，20x -≤≤∴， 于是x 的取值范围是}{|20x x -≤≤ 方法二由题设知：223(1)1ax x a x x a -++>--+对任意(0,)a ∈+∞都成立 即22(2)20a x x x +-->对任意(0,)a ∈+∞都成立 于是2222x x a x +>+对任意(0,)a ∈+∞都成立，即22202x x x +≤+20x -≤≤∴， 于是x 的取值范围是}{|20x x -≤≤已知函数22()(1)x b f x x -=-，求导函数()f x '，并确定()f x 的单调区间．解：242(1)(2)2(1)()(1)x x b x f x x ----'=- 3222(1)x b x -+-=-32[(1)](1)x b x --=--．令()0f x '=，得1x b =-．当11b -<，即2b <时，()f x '的变化情况如下表：当11b ->，即2b >时，()f x '的变化情况如下表：所以，当2b <时，函数()f x 在(1)b -∞-，上单调递减，在(11)b -，上单调递增，在(1)+∞，上单调递减． 当2b >时，函数()f x 在(1)-∞，上单调递减，在(11)b -，上单调递增，在(1)b -+∞，上单调递减． 当2b =时，2()1f x x =-，所以函数()f x 在(1)-∞，上单调递减，在(1)+∞，上单调递减．已知函数32()3(0)f x x ax bx c b =+++≠，且()()2g x f x =-是奇函数． （Ⅰ）求a ，c 的值；（Ⅱ）求函数()f x 的单调区间．解：（Ⅰ）因为函数()()2g x f x =-为奇函数，所以，对任意的x ∈R ，()()g x g x -=-，即()2()2f x f x --=-+．又32()3f x x ax bx c =+++所以32323232x ax bx c x ax bx c -+-+-=----+． 所以22a a c c =-⎧⎨-=-+⎩，．解得02a c ==，．（Ⅱ）由（Ⅰ）得3()32f x x bx =++．所以2()33(0)f x x b b '=+≠． 当0b <时，由()0f x '=得x =x 变化时，()f x '的变化情况如下表：所以，当0b <时，函数()f x 在(-∞-，上单调递增，在(上单调递减，在)+∞上单调递增．当0b >时，()0f x '>，所以函数()f x 在()-∞+∞，上单调递增．已知函数321()23f x x x =+-.（Ⅰ）设}{n a 是正数组成的数列，前n 项和为n S ，其中13a =.若点211(,2)n n n a a a ++-(n ∈N*)在函数'()y f x =的图象上，求证：点(,)n n S 也在'()y f x =的图象上； （Ⅱ）求函数()f x 在区间(1,)a a -内的极值.解：(Ⅰ)证明： 因为321()2,3f x x x =+-所以'2()2f x x x =+，由点211(,2)(N )n n n a a a n +++-∈在函数'()y f x =的图象上,221122n n n n a a a a ++-=+ 所以12n n a a +-=，}{n a 是13,2a d ==的等差数列 所以2(1)32=22n n n S n n n -=+⨯+,又因为'2()2f n n n =+,所以()n S f n '=,故点(,)n n S 也在函数'()y f x =的图象上.(Ⅱ)解:2()2(2)f x x x x x '=+=+,令()0,f x '=得02x x ==-或. 当x 变化时,()f x '﹑()f x 的变化情况如下表:注意到(1)12a a --=<,从而①当212,21,()(2)3a a a f x f -<-<-<<--=-即时的极大值为,此时()f x 无极小值；②当10,01,()a a a f x -<<<<即时的极小值为(0)2f =-,此时()f x 无极大值； ③当2101,()a a a f x ≤--≤≤≥或或时既无极大值又无极小值.已知函数()ln(1)f x x x =+- （Ⅰ）求()f x 的单调区间；（Ⅱ）记()f x 在区间[]0,n （n ∈N*）上的最小值为n b 令ln(1)n n a n b =+- ①如果对一切nc <c 的取值范围；②求证：1313211224242 1.n na a a a a a a a a a a a -+++<解：（I ）因为()ln(1)f x x x =+-，所以函数定义域为(1,)-+∞，且'1()111x f x xx-=-=++。

2008年全国名校高考专题训练12导数与极限二、填空题1、(安徽省蚌埠二中2008届高三8月月考)若lim n →∞1，则常数a 的值=_________ 答案：22、(安徽省蚌埠二中2008届高三8月月考)设函数⎪⎩⎪⎨⎧≥+<--=)0()0(11)(2x x a x xxx f ，要使)(x f 在（-∞，+∞）内连续，则a =_______。

答案：123、(四川省巴蜀联盟2008届高三年级第二次联考)已知函数f （x ）=21(1)1(1)x x x x a x ⎧->⎪-⎨⎪+≤⎩在x=1处连续，则实数a 的值为 ； 答案：14、(四川省乐山市2008届第一次调研考试)曲线C ：2(02)xy x =≤≤两端分别为M 、N ，且NA x ⊥轴于点A 。

把线段OA 分成n 等份，以每一段为边作矩形，使与x 轴平行的边一个端点在C 上，另一端点在C 的下方（如右图），设这n 个矩形的面积之和为n S ，则())lim 231n n n S →∞⎡⎤-=⎣⎦＿＿＿＿＿答案：245、(四川省成都市新都一中高2008级12月月考)已知函数322()3f x x mx nx m =+++在x ＝－1时有极值0，则m ＝_________；n ＝_____________； 本题主要考查函数、导数、极值等基本概念和性质 解析：f '(x )＝3x 2＋6mx ＋n由题意，f '(－1)＝3－6m ＋n ＝0f (－1)＝－1＋3m －n ＋m 2＝0解得⎩⎨⎧m ＝1n ＝3或⎩⎨⎧m ＝2n ＝9但m ＝1，n ＝3时，f '(x )＝3x 2＋6x ＋3＝3(x ＋1)2≥0恒成立即x ＝－1时不是f(x)的极值点，应舍去 答案：m ＝2，n ＝9.6、(北京市东城区2008年高三综合练习一）=--+-→)131(lim 21x x x x x . 答案：27、(北京市海淀区2008年高三统一练习一)已知点P ()2,2在曲线3y ax bx =+上，如果该曲线在点P 处切线的斜率为9，那么ab =____________；函数()3f x ax bx =+，3[,3]2x ∈-的值域为____________.答案：－3；[－2,18]8、(北京市十一学校2008届高三数学练习题)如图为函数32()f x ax bx cx d =+++的图象，'()f x 为函数()f x 的导函数，则不等式'()0x f x ⋅<的解集为______ ______．答案：(,-∞⋃9、(北京市宣武区2008年高三综合练习二)22lim232--→x xx x =答案：410、(东北区三省四市2008年第一次联合考试)已知函数()x f 的导函数为()x f '，且满足()()2'232xf x x f +=，则()=5'f 。

2008年高考数学导数汇编答案2008年高考数学导数汇编答案1、解 (1)'22ln 1(),ln x f x x x +=-若 '()0,f x = 则 1x e= 列表如下x 1(0,)e1e 1(,1)e(1,)+∞'()f x+0 --()f x单调增极大值1()f e单调减单调减(2)在 12a xx > 两边取对数, 得 1ln 2ln a x x >,由于01,x <<所以1ln 2ln a x x>(1)由(1)的结果可知,当(0,1)x ∈时, 1()()f x f e e ≤=-, 为使(1)式对所有(0,1)x ∈成立,当且仅当ln 2ae >-,即ln 2a e >-2、解：（Ⅰ）22(2cos )cos sin (sin )2cos 1()(2cos )(2cos )x x x x x f x x x +--+'==++．当2π2π2π2π33k x k -<<+（k ∈Z ）时，1cos 2x >-，即()0f x '>； 当2π4π2π2π33k x k +<<+（k ∈Z ）时，1cos 2x <-，即()0f x '<． 因此()f x 在每一个区间2π2π2π2π33k k ⎛⎫-+ ⎪⎝⎭，（k ∈Z ）是增函数，()f x 在每一个区间2π4π2π2π33k k ⎛⎫++ ⎪⎝⎭，（k ∈Z ）是减函数．（Ⅱ）令()()g x ax f x =-，则22cos 1()(2cos )x g x a x +'=-+2232cos (2cos )a x x =-+++211132cos 33a x ⎛⎫=-+- ⎪+⎝⎭．故当13a ≥时，()0g x '≥．又(0)0g =，所以当0x ≥时，()(0)0g x g =≥，即()f x ax ≤．当103a <<时，令()sin 3h x x ax =-，则()cos 3h x x a '=-．故当[)0arccos3x a ∈，时，()0h x '>．因此()h x 在[)0arccos3a ，上单调增加．故当(0arccos3)x a ∈，时，()(0)0h x h >=，即sin 3x ax >．于是，当(0arccos3)x a ∈，时，sin sin ()2cos 3x xf x ax x =>>+．当0a ≤时，有π1π0222f a ⎛⎫=>• ⎪⎝⎭≥．因此，a 的取值范围是13⎡⎫+∞⎪⎢⎣⎭，．3、解：(Ⅰ)因为2(),()2.f x ax bx c f x ax b '=++=+所以又因为曲线()y f x =通过点（0，2a +3）,故(0)23,(0),2 3.f a f c c a =+==+而从而又曲线()y f x =在（-1，f (-1)）处的切线垂直于y 轴，故(1)0,f '-=即-2a +b =0,因此b=2a .(Ⅱ)由(Ⅰ)得2392(23)4(),44bc a a a =+=+-故当34a =-时，bc 取得最小值-94.此时有33,.22b c =-=从而233333(),(),42222f x x x f x x '=--+=--2333()()(),422x x g x f x c x x e --=-=+-所以23()(()()(4).4x x g x f x f x e x e --''=-=--令()0g x '=，解得122, 2.x x =-=当(,2),()0,()(,2)x g x g x x '∈-∞-<∈-∞-时故在上为减函数； 当(2,2)()0,()(2,).x g x g x x '∈->∈+∞时，故在上为减函数 当(2,)()0()(2,)x g x g x x '∈+∞<∈+∞时，，故在上为减函数.由此可见，函数()g x 的单调递减区间为（-∞，-2）和（2，+∞）；单调递增区间为（-2，2）.4、解：242(1)(2)2(1)()(1)x x b x f x x ----'=-3222(1)x b x -+-=-32[(1)](1)x b x --=--．令()0f x '=，得1x b =-． 当11b -<，即2b <时，()f x '的变化情况如下表：当11b ->，即2b >时，()f x '的变化情况如下表：所以，当2b <时，函数()f x 在(1)b -∞-，上单调递减，在(11)b -，上单调递增，在(1)+∞，上单调递减．当2b >时，函数()f x 在(1)-∞，上单调递减，在(11)b -，上单调递增，在(1)b -+∞，上单调递减． 当11b -=，即2b =时，2()1f x x =-，所以函数()f x 在(1)-∞，上单调递减，在(1)+∞，上单调递减．5、(Ⅰ)证明：因为321()2,3f x x x =+-所以f ′(x )=x 2+2x ,由点211(,2)(N )n n n a a a n +++-∈在函数y =f ′(x )的图象上,得221122n n n n a a a a ++-=+，即11()(2)0,n n n n a a a a -+---=又0(N ),n a n +>∈所以12n n a a +-=，又因为13a =，所以2(1)32=22n n n S n n n -=+⨯+,又因为f ′(n )=n 2+2n ,所以()n S f n '=,故点(,)n n S 也在函数y=f ′(x )的图象上.(Ⅱ)解:2()2(2)f x x x x x '=+=+,由()0,f x '=得02x x ==-或. 当x 变化时,()f x '﹑()f x 的变化情况如下表:注意到(1)12a a --=<,从而①当212,21,()(2)3a a a f x f -<-<-<<--=-即时的极大值为,此时()f x 无极小值；②当10,01,()a a a f x -<<<<即时的极小值为(0)2f =-,此时()f x 无极大值；③当2101,()a a a f x ≤--≤≤≥或或时既无极大值又无极小值.6、解1,1,1()(),1,kx x xF x f x kx kx x ⎧-<⎪-=-=⎨⎪≥⎩，21,1,(1)'(),1,k x x F x k x ⎧-<⎪-⎪=⎨⎪≥⎪⎩对于1()(1)1F x kx x x=-<-，当0k ≤时，函数()F x 在(,1)-∞上是增函数；当0k >时，函数()F x在(,1-∞上是减函数，在(1上是增函数；对于()(1)F x k x =-≥，当0k ≥时，函数()F x 在[)1,+∞上是减函数；当0k <时，函数()F x 在211,14k ⎡⎫+⎪⎢⎣⎭上是减函数，在211,4k ⎡⎫++∞⎪⎢⎣⎭上是增函数。

2008年高考数学试题分类汇编函数与导数一． 选择题：1.(全国一1)函数y =D ）A ．{|1}x x ≤B ．{|0}x x ≥C ．{|10}x x x ≥或≤ D ．{|01}x x ≤≤2.（全国一2）汽车经过启动、加速行驶、匀速行驶、减速行驶之后停车，若把这一过程中汽车的行驶路程s 看作时间t 的函数，其图像可能是（ A ）3.（全国一4）曲线324y x x =-+在点(13)，处的切线的倾斜角为（ B ） A ．30°B ．45°C ．60°D ．120°4.（全国一8）若函数()y f x =的图象与函数l 1y =的图象关于直线y x =对称，则()f x =（ A ） A ．22ex -B ．2exC ．21ex +D ．2+2ex5.（全国二4）函数1()f x x x=-的图像关于（ C ） A ．y 轴对称 B ． 直线x y -=对称 C ． 坐标原点对称 D ． 直线x y =对称6.（全国二5）若13(1)ln 2ln ln x e a x b x c x -∈===，，，，，则（ C ）A ．a <b <cB ．c <a <bC ． b <a <cD ． b <c <a 7.（全国二7）设曲线2ax y =在点（1，a ）处的切线与直线062=--y x 平行，则=a （ A ）A ．1B ．12C ．12- D ．1-8.（安徽卷6）函数2()(1)1(0)f x x x =-+≤的反函数为( C ) A．1()11)f x x -=≥B ．1()11)f x x -=≥C．1()12)f x x -=≥D ．1()12)f x x -=≥9.（安徽卷9）．设函数1()21(0),f x x x x=+-< 则()f x （ A ）A ．有最大值B ．有最小值C ．是增函数D ．是减函数 10.（北京卷2）若372log πlog 6log 0.8a b c ===，，，则（ A ） A ．ab c >> B ．b a c >>C ．c a b >>D ．b c a >>11.（北京卷5）函数2()(1)1(1)f x x x =-+<的反函数为（ B ）A．1()11)f x x -=> B．1()11)f x x -=> C．1()11)f x x -=≥D．1()11)f x x -=≥12.（福建卷11）如果函数y=f (x )的图象如右图，那么导函数y=f (x )的图象可能是( A )13.(广东卷8)命题“若函数()log (0,1)a f x x a a =>≠在其定义域内是减函数，则log 20a <”的逆否命题是（ A ）A 、若l o g20a≥，则函数()log (0,1)a f x x a a =>≠A ．B ．C ．D ．在其定义域内不是减函数 B 、若l o g20a<，则函数()log (0,1)a f x x a a =>≠在其定义域内不是减函数 C 、若l o g20a≥，则函数()log (0,1)a f x x a a =>≠在其定义域内是减函数 D 、若l o g20a<，则函数()log (0,1)a f x x a a =>≠在其定义域内是减函数14.（广东卷9）设a R ∈，若函数x y e ax =+，x R ∈，有大于零的极值点，则（ A ）A 、1a <- B 、1a >- C 、1a e <-D 、1a e>- 15.（海南卷4）设()ln f x x x =，若0'()2f x =，则0x =（ B ）A. 2eB. eC.ln 22D. ln 2 16.（湖北卷6）已知()f x 在R上是奇函数，且2(4)(),(0,2)()2,(7)f x f x x f x x f +=∈==当时，则( A )A.-2B.2C.-98D.98 17.（湖北卷8）函数1()1f x n x=域为（ D ）A.(,4][2,)-∞-+∞B. (4,0)(0,1)-⋃C.[4,0)(0,1]-D.[4,0)(0,1]-⋃ 18.（福建卷4）函数f (x )=x 3+sin x +1(x ∈R)，若f (a )=2,则f (-a )的值为( B )A.3B.0C.-1D.-2 19.（湖南卷4）函数)0()(2≤=x x x f 的反函数是( B ))0()(.1≥=-x x x f A )0()(.1≥-=-x x x f B )0()(.1≤--=-x x x f C )0()(.21≤-=-x x x f D20.（湖南卷6）下面不等式成立的是( A )A ．322log 2log 3log 5<<B ．3log 5log 2log 223<<C ．5log 2log 3log 232<<D ．2log 5log 3log 322<< 21.（江西卷3）若函数()y f x =的定义域是[0,2]，则函数(2)()1f xg x x =-的定义域是（ B ）A ．[0,1]B ．[0,1)C ．[0,1)(1,4] D ．(0,1) 22.（江西卷4）若01x y <<<，则( C )A ．33y x< B ．log 3log 3x y <C ．44log log x y <D ．11()()44x y <23.（江西卷12）已知函数2()2(4)4f x x m x m =+-+-，()g x mx =，若对于任一实数x ，()f x 与()g x 的值至少有一个为正数，则实数m 的取值范围是( C )A ． [4,4]-B ．(4,4)-C ． (,4)-∞D ．(,4)-∞- 24.（辽宁卷2）若函数(1)()y x x a =+-为偶函数，则a =（ C ）A ．2-B ．1-C ．1D ．225.（辽宁卷6）设P 为曲线C ：223y x x =++上的点，且曲线C 在点P 处切线倾斜角的取值范围为04π⎡⎤⎢⎥⎣⎦，，则点P 横坐标的取值范围为（ A ）A ．112⎡⎤--⎢⎥⎣⎦， B ．[]10-， C ．[]01， D ．112⎡⎤⎢⎥⎣⎦， 27.（辽宁卷8）将函数21x y =+的图象按向量a 平移得到函数12x y +=的图象，则（ A ）A ．(11)=--，aB ．(11)=-，aC ．(11)=，aD ．(11)=-，a28.（山东卷3）函数ππln cos 22y x x ⎛⎫=-<< ⎪⎝⎭的图象是（ A ）29.（山东卷4）给出命题：若函数()y f x =是幂函数，则函数()y f x =的图象不过第四象限．在它的逆命题、否命题、逆否命题三个命题中，真命题的个数是（ C ） A ．3B ．2C ．1D ．030.（山东卷5）设函数2211()21x x f x x x x ⎧-⎪=⎨+->⎪⎩，，，，≤则1(2)f f ⎛⎫⎪⎝⎭的值为（ A ）A ．1516B ．2716- C ．89D ．18 31.（山东卷12）已知函数()l o g (21x af x b a a =+->≠，的图象如图所示，则a b ，满足的关系是（ AA ．101ab -<<<B ．101b a -<<<C ．101b a -<<<-D ．1101a b --<<<32.（陕西卷7）已知函数3()2x f x +=，1()f x -是()f x 的反函数，若16mn =（m n ∈+R ，），则11()()f m f n --+的值为（ D ）A ．10B ．4C ．1D ．2-33.（陕西卷11）定义在R 上的函数()f x 满足()()()2f x y f x f y x y +=++（x y ∈R ，），(1)2f =，则(2)f -等于（ A ）A ．2B ．3C ．6D ．934.（四川卷２）函数()1ln 212y x x ⎛⎫=+>- ⎪⎝⎭的反函数是( C ) （Ａ）()112x ye x R =-∈ （Ｂ）()21x y e x R =-∈ （Ｃ）()()112xy e x R =-∈ （Ｄ）()21xy e x R =-∈35.（四川卷9）函数()f x 满足()()213f x f x ⋅+=，若()12f =，则()99f =( C )（Ａ）13 （Ｂ）2 （Ｃ）132（Ｄ）21336.（天津卷3）函数14)y x =≤≤的反函数是（ A ） A ．2(1)(13)y x x =-≤≤ B ．2(1)(04)y x x =-≤≤C ．21(13)y xx =-≤≤ D ．21(04)y x x =-≤≤37.（天津卷10）设1a>，若对于任意的[]2x a a ∈，，都有2y a a ⎡⎤∈⎣⎦，满足方程log log 3a a x y +=，这时a 的取值的集合为（ B ）A ．{}12a a <≤B ．{}2a a ≥C ．{}23a a ≤≤D ．{}23，38.（重庆卷6)函数1210-=xy(0＜x ≤1)反函数是（ D ）(A)1)10y x =＞ (B)y =x ＞110)(C) y =110＜x ≤)1(D) y 110＜x ≤)139.（重庆卷7)函数f (x B ） (A)25(B)12(D)140.（重庆卷12）函数f (x ≤x ≤2π)的值域是（ C ） (A)[-11,44] (B)[-11,33] (C)[-11,22] (D)[-22,33] 二． 填空题：1.（安徽卷13）函数2()f x =的定义域A ．B ．C ．D ．x为 ．[3,)+∞ 2.（北京卷13）如图，函数()f x 的图象是折线段ABC ，其中A B C，，的坐标分别为(04)(20)(64)，，，，，，则((0))f f = ；函数()f x 在1x =处的导数(1)f '= ．3.（北京卷14）已知函数2()cos f x x x =-，对于ππ22⎡⎤-⎢⎥⎣⎦，上的任意12x x ，，有如下条件：①12x x >；②2212x x >； ③12x x >．其中能使12()()f x f x >恒成立的条件序号是 ．②4.（湖北卷13）方程223x x -+=的实数解的个数为 . 2 5.（湖南卷15）设[]x 表示不超x 的最大整数，（如[]145,22=⎥⎦⎤⎢⎣⎡=）。