钢结构基本原理讲稿压弯构件

第5章 整体结构中的压杆和压弯构件前面讲过对于结构和构件丧失稳定属于整体性问题。

需要通过整体分析来确定它们的临界条件。

实际计算中所计算的受压构件(或压弯构件)从整体结构中分离出来,计算时考虑结构其他部分对它的约束,通过计算长度来体现这种约束。

5.1 桁架中压杆的计算长度5.1.1 弦杆和单系腹杆的计算长度通常我们认为桁架节点看作理想铰接，杆件发生转动不会对其他杆件产生影响，实际上衍架不论是有节点板的双角钢桁架还是没有节点板的方钢或圆钢桁架,节点都接近刚性连接。

上弦杆屈曲时将带动其他杆件一起变形。

（170页图）杆件约束作用大小：1.杆件的轴力性质：拉力使杆件拉直，约束作用大；压力使杆件弯曲，约束作用小。

2.杆件线刚度：线刚度大，约束作用大；线刚度小，约束作用小。

桁架平面内计算长度：弦杆、支座斜杆及支座竖杆的计算长度取l l ox =l ：杆件的节间长度 x ：代表杆件截面垂直于桁架平面的轴 支座斜杆、支座竖杆两端所连拉杆甚少,而受压弦杆不仅两端所连拉杆较少且自身线刚度大,腹杆难于约束它的变形。

计算长度取l 。

中间腹杆l l ox 8.0=因在上弦节点处所连拉杆少,视铰接。

在下弦节点所连拉杆较多且线刚度大，嵌固作用比较大。

桁架平面外：计算长度用oy l 代表。

腹杆：l l oy =（其中l 为节点中心间距离）节点板对于腹杆发生屋架平面外的变形 (即垂直屋架平面的变形)来说抗弯刚度很小,相当于板铰，。

腹杆端部在平面外的计算中属于不动铰,是以弦杆在屋架平面外不发生移动为前提的。

受压弦杆在节点处有刚性屋面板或者连于支撑的檩条,可做到出平面无移动。

受拉弦杆依靠本身的抗弯刚度,因此受拉弦杆在屋架平面外的刚度应该大些,系杆间距不应过大。

单角钢腹杆及双角钢十字形放置的腹杆,因为绕最小主轴弯曲时杆轴处于斜平面内,其端部所受嵌固作用介于屋架平面内外的两种情况之间,取计算长度为0.9l 。

上弦的1l 在有檩时取水平支撑节间长度，当檩条在支撑斜杆交叉处连接时取该长度之半。

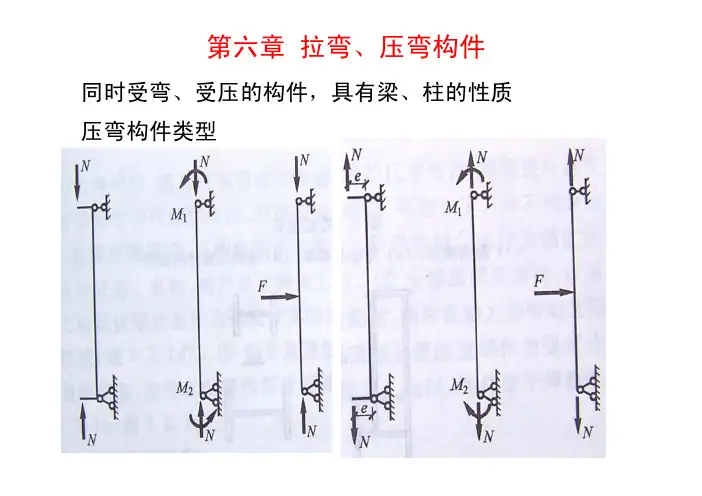
第六章拉弯、压弯构件同时受弯、受压的构件，具有梁、柱的性质压弯构件类型）实腹式压弯构件失稳形式1、弯矩作用平面内失稳－－弯曲屈曲、N~v曲线实腹式压弯构件失稳形式M作用在弱轴平面（yz),产生绕强轴（x)的弯曲。

只有y轴位移v1、弯矩作用平面内失稳－－弯曲屈曲2、弯矩作用平面外失稳－－弯扭屈曲Y轴位移：vX轴位移：u转角：θ（2）横向荷载和端弯矩β=1.0 （同向曲率）；mxβ =0.85（异向曲率） mx（3）有横向荷载，无端弯矩β=1.0mx出现塑性破坏，补充验算较小翼缘：无翼缘端毛截面模量2X-----实腹式构件弯矩作用平面外稳定计算•边缘屈服准则：要验算疲劳、格构式、受压翼缘超限•全截面屈服准则•部分塑性准则：静力荷载、间接动载格构式压弯构件高大的厂房柱，由于截面宽度大， 常用缀条式（刚度大）1、弯矩绕虚轴（x轴）作用，有Mxx 的边缘纤维达到屈服为临界状态，由于空心，外边缘的距离或轴线距离） y0弯矩绕虚轴作用2)单肢稳定性按轴心压杆验算单肢绕其两个主轴的稳定性 12x N a N y M ⋅=⋅+ 12()/x N N y M a =⋅+12N N N −=a)缀材只在缀材平面内对两个分肢起联系作用，b)缀材在其平面外刚度小，不起作用。

缀条平面内（绕x1轴失稳）计算长度＝节间长度 111/x x l i λ=缀条平面外（绕y 轴失稳）计算长度=侧向支撑距离 /y y y l i λ= y 2y 1x yx 1弯矩绕实轴作用受力性能与实腹式完全相同，用实腹式公式，只是平面外稳定系数要用虚轴的换算长细比查表。

结束谢谢!。