化工原理例题物料衡算

化工原理物料衡算公式好嘞，以下是为您生成的关于“化工原理物料衡算公式”的文章：咱先来说说化工原理里的物料衡算公式，这玩意儿可重要啦！就像咱们过日子得算计着柴米油盐一样，化工厂里也得把各种物料的进出算得明明白白。

物料衡算公式简单来说，就是“进去的等于出来的”。

这听起来好像挺简单，可实际操作起来，那可得费一番心思。

我还记得有一次去一家化工厂参观，那是个生产化肥的厂子。

我看到工人们在控制台前忙碌着，各种仪表数据不停地跳动。

当时我就好奇，这生产过程中到底怎么保证原料不浪费，产品质量又有保障呢？后来和厂里的技术员交流才知道，物料衡算公式在这里面发挥了大作用。

比如说，他们要生产一定量的化肥，就得先根据物料衡算公式，算出需要投入多少原料。

而且，这个过程可不只是简单的加减乘除。

就拿氮元素来说吧，从原材料里含有的氮，到反应过程中氮的转化，再到最终产品里氮的含量，都得精确计算。

要是哪一步算错了，要么原料浪费了，增加成本；要么产品不合格，影响销售。

在化工生产中，物料衡算公式就像是一个严格的管家。

它能告诉我们每个环节物料的流向和变化，帮助我们优化生产工艺，提高生产效率，降低成本。

比如说，在一个连续的反应装置中，如果我们知道了进料的流量和组成，通过物料衡算公式，就能算出出料的流量和组成。

这就好比我们知道了家里每个月进了多少米、面、油，就能大概算出能做出多少顿饭一样。

而且，物料衡算公式还能帮助我们发现生产中的问题。

如果实际的出料和通过公式计算出来的结果不一样，那就说明可能哪里出了故障，比如有物料泄漏啦，或者反应不完全啦。

再举个例子，假设一个化工厂要生产一种塑料，需要用到两种原材料 A 和 B 。

根据化学反应式和物料衡算公式，我们知道每生产一定量的塑料，需要消耗一定比例的 A 和 B 。

如果在实际生产中，发现 A 消耗得比预期多，而 B 还有剩余，那就要找找原因了，是不是反应条件没控制好，还是某个设备出了问题？总之啊，化工原理中的物料衡算公式虽然看起来只是一些数字和符号的组合，但它背后可是有着大学问。

化工原理物料衡算和热量衡算引言化工工程涉及许多物料的处理和转化过程，同时也需要考虑热量的平衡。

物料衡算和热量衡算是化工原理的重要内容，对于工程实践和过程优化具有重要的意义。

本文将介绍化工原理中的物料衡算和热量衡算的基本原理和计算方法。

物料衡算物料衡算是指对于化工工程中物料流动和转化过程的计算和分析。

在化工工程中，物料的流动和转化是实现各种反应和分离操作的基础，因此正确的物料衡算是保证工程设计和操作的关键。

在物料衡算中，我们通常需要考虑以下几个方面： 1. 物料的质量衡算：即对物料的质量输入和输出进行计算和分析。

对于物料的质量衡算，我们需要注意物料流动的平衡原则，即质量的输入必须等于输出。

2. 物料的能量衡算：即对物料的能量输入和输出进行计算和分析。

能量的输入和输出会影响物料的温度和相变过程，因此在能量衡算中需要考虑物料的热力学性质。

3. 物料的流动速度衡算：即对物料流动速度进行计算和分析。

物料的流动速度决定了反应和分离操作的效率，因此在物料衡算中需要合理地确定流量和速度的关系。

4. 物料的浓度衡算：即对物料中组分浓度的计算和分析。

物料的浓度会影响其反应和分离的速率和效果，因此在物料衡算中需要考虑不同组分浓度的变化规律。

物料衡算通常使用质量守恒和能量守恒等基本原理进行计算。

同时，还可以利用化学反应平衡的原理和质量流动的平衡原则进行衡算过程中的参数确定。

热量衡算热量衡算是化工工程中热力学过程的计算和分析。

在化工工程中，热量的平衡是保证反应和分离操作能够正常进行的基础。

热量衡算需要考虑以下几个方面： 1. 热量的输入和输出：即对于热量的输入和输出进行计算和分析。

在化工工程中，我们通常需要对热量的输入和输出进行平衡，以保证工程操作的稳定性。

2. 热量的传递和转化：即对于热量的传递和转化过程进行计算和分析。

热量的传递可以通过传导、对流和辐射等方式进行，因此在热量衡算中需要考虑传热方式的影响。

3. 热平衡的计算：即对于反应和分离过程中热量平衡的计算和分析。

三 计算题1 （15分）在如图所示的输水系统中，已知 管路总长度（包括所有当量长度，下同）为 100m ，其中压力表之后的管路长度为80m ，管路摩擦系数为0.03，管路内径为0.05m ， 水的密度为1000Kg/m 3，泵的效率为0.85， 输水量为15m 3/h 。

求：（1）整个管路的阻力损失，J/Kg ； （2）泵轴功率，Kw ； （3）压力表的读数，Pa 。

解：（1）整个管路的阻力损失，J/kg ； 由题意知，s m A V u s /12.2)405.03600(152=⨯⨯==π 则kg J u d l h f /1.135212.205.010003.0222=⨯⨯=⋅⋅=∑λ （2）泵轴功率，kw ；在贮槽液面0-0´与高位槽液面1-1´间列柏努利方程，以贮槽液面为基准水平面，有：∑-+++=+++10,121020022f e h p u gH W p u gH ρρ 其中， ∑=kg J h f /1.135, u 0= u 1=0， p 1= p 0=0（表压）, H 0=0， H=20m 代入方程得： kg J h gH W f e /3.3311.1352081.9=+⨯=+=∑又 s kg V W s s /17.41000360015=⨯==ρ 故 w W W N e s e 5.1381=⨯=， η=80%， kw w N N e 727.11727===η2 （15分）如图所示，用泵将水从贮槽送至敞口高位槽，两槽液面均恒定不变，输送管路尺寸为φ83×3.5mm ，泵的进出口管道上分别安装有真空表和压力表，真空表安装位置离贮槽的水面高度H 1为4.8m ，压力表安装位置离贮槽的水面高度H 2为5m 。

当输水量为36m 3/h 时，进水管道全部阻力损失为 1.96J/kg ，出水管道全部阻力损失为 4.9J/kg ，压力表读数为 2.452×H=20m H 1=2m105Pa ，泵的效率为70%，水的密度ρ为1000kg/m 3，试求： （1）两槽液面的高度差H 为多少？ （2）泵所需的实际功率为多少kW ？ （3）真空表的读数为多少kgf/cm 2？解：（1）两槽液面的高度差H在压力表所在截面2-2´与高位槽液面3-3´间列柏努利方程，以贮槽液面为基准水平面，得：∑-+++=++32,323222222f h p u gH p u gH ρρ 其中， ∑=-kg J h f /9.432,, u 3=0, p 3=0,p 2=2.452×105Pa, H 2=5m, u 2=Vs/A=2.205m/s代入上式得： m H 74.2981.99.481.9100010452.281.92205.2552=-⨯⨯+⨯+= （2）泵所需的实际功率在贮槽液面0-0´与高位槽液面3-3´间列柏努利方程，以贮槽液面为基准水平面，有：∑-+++=+++30,323020022f e h p u gH W p u gH ρρ 其中， ∑=-kg J h f /9.864.630,, u 2= u 3=0, p 2= p 3=0, H 0=0， H=29.4m代入方程求得： W e =298.64J/kg ， s kg V W s s /101000360036=⨯==ρ 故 w W W N e s e 4.2986=⨯=， η=70%， kw N N e 27.4==η（3）真空表的读数在贮槽液面0-0´与真空表截面1-1´间列柏努利方程，有：∑-+++=+++10,1211020022f h p u gH p u gH ρρ 其中，∑=-kg J hf /96.110,, H 0=0， u 0=0, p 0=0, H 1=4.8m,u1=2.205m/s代入上式得，24 21/525.01015.5)96.12205.28.481.9( 1000cm kgf Pap -=⨯-=++⨯-=3 用离心泵把20℃的水从储槽送至水洗塔顶部，槽内水位维持恒定。

化工原理(上册)课后习题1、某湿物料原含水量为10%，在干燥器内干燥至含水量为%。

试求每吨湿物料除去的水量。

解：方法一：设G1 =1t=1000Kg 。

已知w1=10%、w2=%物料衡算：?1G1?W?(G1?W)?% 解：W=90Kg方法二：G1(1??)?(G1?W)(1??2)1 解：W=90Kg2、采用两个连续操作的串联蒸发器以浓缩NaOH水溶液，每小时有10吨12%的NaOH水溶液送入第一个蒸发器，经浓缩后的NaOH水溶液再送入第二个蒸发器进一步浓缩至50%的碱液排出。

若每个蒸发器蒸发水量相等，试求送入第二个蒸发器的溶液量及其组成。

W F0=104kg/h ω0=12% F1=F0-W ω1 W F2=F0-2W ω2=50%解：不变组份衡算式第一蒸发器第二蒸发器F0?0?F2?2?104??(104?2W)??W?3800kg/hF1F0W1000038006200kg/h以第一蒸发器为衡算范围：F0?0?F1?1?104??6200?1??1?%3、一间壁式换热器用冷却水将间壁另一侧1500kg/h、800C的某有机液体冷却到400C，冷却水的初温为300C，出口温度为350C，已知该有机液体的平均定压比热容为/。

试求冷却水用量。

解：C??(kg?C)水0?C 1500p液(t?o?to)?W?C?水(t?1?t1)W3956Kg/h第一章1、试求氨在和160C下的密度。

已知当地大气压强为100kPa。

解：3??10?100?2650kPa P绝P ??绝MRTH2 40 ?2650?17?289N2 20 CO 32 CO2 7 CH4 1 2、某气柜内压强为Mpa(表压)，温度为400C，混合气体中各组分的体积百分数为： v i% 试求混合气的密度。

当地大气压强为100kPa。

解： P3??10?100?175kPa 绝M?40?2?20?28?32?28?7?44?1?16?100PM17531387kPa地区，仍要求塔顶绝压维持在相同数值下操作，问此时真空表读数应为多少kPa?3、在大气压强为100kPa地区，某真空蒸馏塔塔顶的真空表读数为90kPa。

三 计算题1 （15分）在如图所示的输水系统中，已知管路总长度（包括所有当量长度，下同）为 100m ，其中压力表之后的管路长度为80m ， 管路摩擦系数为0.03，管路径为0.05m ， 水的密度为1000Kg/m 3，泵的效率为0.85， 输水量为15m 3/h 。

求：（1）整个管路的阻力损失，J/Kg ； （2）泵轴功率，Kw ； （3）压力表的读数，Pa 。

解：（1）整个管路的阻力损失，J/kg ； 由题意知，s m A Vu s /12.2)405.03600(152=⨯⨯==π 则kg J u d l h f /1.135212.205.010003.0222=⨯⨯=⋅⋅=∑λ （2）泵轴功率，kw ；在贮槽液面0-0´与高位槽液面1-1´间列柏努利方程，以贮槽液面为基准水平面，有：∑-+++=+++10,121020022f e h p u gH W p u gH ρρ 其中， ∑=kg J h f /1.135, u 0= u 1=0， p 1= p 0=0（表压）, H 0=0， H=20m 代入方程得： kg J h gH W f e /3.3311.1352081.9=+⨯=+=∑又 s kg V W s s /17.41000360015=⨯==ρ 故 w W W N e s e 5.1381=⨯=， η=80%， kw w N N e 727.11727===η2 （15分）如图所示，用泵将水从贮槽送至敞口高位槽，两槽液面均恒定不变，输送管路尺寸为φ83×3.5mm ，泵的进出口管道上分别安装有真空表和压力表，真空表安装位置离贮槽的水面高度H 1为4.8m ，压力表安装位置离贮槽的水面高度H 2为5m 。

当输水量为36m 3/h 时，进水管道全部阻力损失为1.96J/kg ，出水管道全部阻力损失为4.9J/kg ，压力表读数为2.452×105Pa ，泵的效率为70%，水的密度ρ为1000kg/m 3，试求： （1）两槽液面的高度差H 为多少？ （2）泵所需的实际功率为多少kW ？ （3）真空表的读数为多少kgf/cm 2？解：（1）两槽液面的高度差H在压力表所在截面2-2´与高位槽液面3-3´间列柏努利方程，以贮槽液面为基准水平面，得：∑-+++=++32,323222222f h p u gH p u gH ρρ 其中， ∑=-kg J h f /9.432,, u 3=0, p 3=0,p 2=2.452×105Pa, H 2=5m, u 2=Vs/A=2.205m/s代入上式得： m H 74.2981.99.481.9100010452.281.92205.2552=-⨯⨯+⨯+= （2）泵所需的实际功率在贮槽液面0-0´与高位槽液面3-3´间列柏努利方程，以贮槽液面为基准水平面，有：∑-+++=+++30,323020022f e h p u gH W p u gH ρρ 其中， ∑=-kg J h f /9.864.630,, u 2= u 3=0, p 2= p 3=0, H 0=0， H=29.4m代入方程求得： W e =298.64J/kg ， s kg V W s s /101000360036=⨯==ρ 故 w W W N e s e 4.2986=⨯=， η=70%， kw N N e 27.4==η（3）真空表的读数在贮槽液面0-0´与真空表截面1-1´间列柏努利方程，有：∑-+++=+++10,1211020022f h p u gH p u gH ρρ 其中，∑=-kg J hf /96.110,, H 0=0， u 0=0, p 0=0, H 1=4.8m,u 1=2.205m/s代入上式得， 2421/525.01015.5)96.12205.28.481.9(1000cm kgf Pap -=⨯-=++⨯-= 3 用离心泵把20℃的水从储槽送至水洗塔顶部，槽水位维持恒定。

化工原理Unit Operations of Chemical Engineering绪论化工过程计算基本关系1. 物料衡算（material balance ） ∑G i =∑G 0+∑G a∑G i —输入物料的总和；∑G 0—输出物料的总和；∑G a —累计的物料量 物料衡算的理论依据：质量守恒定律 2. 能量衡算（energy balance ） （1）∑Q i =∑Q 0+∑Q L∑Q i —随物料进入系统的总热量；∑Q 0—随物料离开系统的总热量； ∑Q L —向系统周围散失的热量 （2）∑（wH ）i =∑(wH)0+∑Q LW —物料的质量；H —物料的焓。

热量（能量）衡算的理论依据：能量守恒定律3.按照化工单元操作所遵循的基本规律的不同，可以将单元操作分为动量传递、热量传递、质量传递。

第一章 流体流动一．流体静力学基本方程1.流体的密度 （1）定义：单位体积流体所具有的流体质量称为密度，用ρ表示。

（2）V m=ρ。

对于一定的流体，其密度是压力和温度的函数，即ρ=f(p,T)。

液体通常视为不可压缩流体，认为其密度仅随温度变化（极高压力除外）； n wn B wB A wA m x x x ρρρρ+++=.......1 n B A ρρρ......,—液体混合物中各纯组分的密度； wn wB wA x x x ......,—液体混合物中各组分的质量分数。

对于气体，当压力不太高、温度不太低时，可按理想气体状态方程计算。

RT pM =ρ或004.22Tp p MT =ρ n n m y M y M y M M +++=......2211（m M 是平均摩尔质量） 理想气体：n n x x x ρρρρ+++=......2211（体积分率=摩尔分率）2.静止流体的压力（流体静压强）（1）定义：垂直作用于流体单位面积上的表面力称为流体的静压强，简称压强，俗称压力，以p 表示，单位是Pa 。

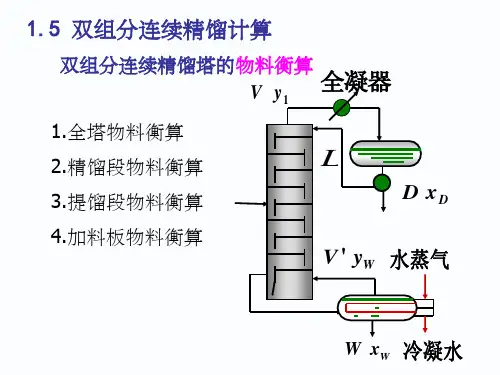
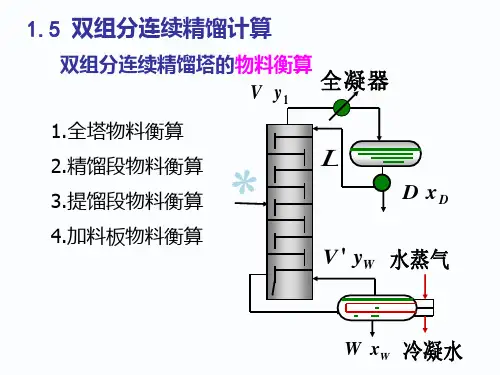
全塔物料衡算公式好的，以下是为您生成的文章：在化工生产的奇妙世界里，全塔物料衡算公式就像是一把神奇的钥匙，能帮我们解开很多复杂的谜题。

先来说说啥是全塔物料衡算公式。

其实呀，它就是用来描述进入塔设备的物料总量和离开塔设备的物料总量之间关系的一个数学表达式。

简单点儿说，就好比你去超市买东西，买进去的和卖出去的得对得上账，全塔物料衡算公式就是帮咱们把这个“账”算清楚的工具。

我给您举个例子吧。

有一次，我在一家化工厂实习，当时厂里正在优化一个精馏塔的操作。

这个精馏塔是用来分离两种混合物的，大家都知道，如果分离效果不好，那产品质量可就没保障啦。

我们一群人围着这个塔，又是查数据，又是做检测。

这时候，全塔物料衡算公式就派上用场了。

我们把各种进料的流量、组成，还有塔顶和塔底产品的流量、组成都测了出来，然后代入公式里一算。

嘿，发现实际情况和理论计算有偏差！这可把大家急坏了。

经过一番仔细排查，原来是有个进料管道出现了轻微的泄漏，导致进料量不准确。

找到问题后，工人们赶紧抢修，修好之后再次进行物料衡算，这次终于对上啦！产品质量也稳定了下来。

从这个小小的例子就能看出来，全塔物料衡算公式可不是纸上谈兵的东西，它在实际生产中真的太重要了。

那这个公式具体长啥样呢？一般来说，对于一个连续稳定操作的塔设备，全塔物料衡算公式可以表示为：进料量等于出料量。

这里的进料量包括各种进入塔的物料，而出料量则包括塔顶和塔底的产品。

比如说，如果我们要分离一种混合物 A 和 B，进料中 A 的含量是a%，进料流量是 F，塔顶产品中 A 的含量是 b%，流量是 D，塔底产品中A 的含量是c%，流量是W，那么全塔物料衡算公式就可以写成：F×a% = D×b% + W×c% 。

在实际应用中，全塔物料衡算公式可以帮助我们确定很多重要的参数。

比如说，通过已知的进料组成和流量，以及期望得到的产品组成，我们可以计算出塔顶和塔底产品的流量。

化工原理物料衡算嘿，朋友们！今天咱来聊聊化工原理里超级重要的物料衡算呀！这玩意儿就像是化工世界的一把钥匙，能打开好多神奇的大门呢！你想想看，化工生产就好比是一场盛大的魔术表演，各种原料进去，经过一系列奇妙的变化，最后变成我们想要的产品出来。

那物料衡算呢，就是搞清楚这场魔术里到底发生了什么，东西怎么变来变去的。

比如说，我们把一堆材料放进一个大罐子，经过搅拌啊、加热啊之类的操作，那最后得到的产品和剩下的原料之间得有个平衡关系吧。

要是算不清楚，那不就乱套啦！就好像你做饭，放了多少米和水，最后得知道能煮出多少饭来呀，不然不是要么煮多了浪费，要么煮少了不够吃嘛！物料衡算可不仅仅是简单的加减乘除哦！它需要我们细心、耐心，还得有点小机智呢！我们得把每一个环节都考虑到，不能有遗漏。

这就像是拼图游戏，每一块都得放对地方，才能拼出完整的画面。

咱再打个比方，物料衡算就像是给化工过程拍照片，要把每一个瞬间都清晰地记录下来。

而且这照片还得是高清无码的，不能模糊不清呀！只有这样，我们才能准确地知道每个步骤都发生了什么，有没有浪费原料，有没有达到我们想要的效果。

有时候啊，这物料衡算也会遇到一些难题呢！就像走路遇到了小水坑，得小心地跨过去。

比如说，有些反应可能不完全，或者会有副产物生成，这时候就得好好琢磨琢磨怎么算才准确啦。

那怎么做好物料衡算呢？首先得对整个化工过程非常熟悉，就像熟悉自己的手掌纹路一样。

然后要认真收集数据，一个小数点都不能马虎。

这可不是开玩笑的，万一弄错了，那可就麻烦大啦！大家想想，如果物料衡算没做好，那生产出来的东西质量能有保证吗？成本能控制好吗？那肯定不行呀！所以说呀，物料衡算可真是化工的命根子呀！总之呢，物料衡算在化工原理里那可是至关重要的。

它就像一个默默守护化工世界的卫士，保障着一切都能顺顺利利地进行。

咱可得好好重视它，把它玩转了，这样才能在化工的海洋里畅游无阻呀！大家说是不是这个理儿呢？。