伺服系统Matlab仿真教学
- 格式:ppt
- 大小:472.50 KB
- 文档页数:38

基于Matlab的数控交流伺服系统的仿真研究赵涛1,2,朱晓春1,2,陈桂1,2(11南京工程学院自动化学院,江苏南京211167)(21南京工程学院先进数控技术江苏省高校重点建设实验室,江苏南京210013)摘要:为实现高性能的伺服控制,针对基于矢量控制的PMSM伺服系统的速度调节和控制进行了分析。
利用Matlab平台构建了PMSM矢量控制仿真模型,根据数控伺服系统的性能要求,对不同插补方式下的速度控制进行了仿真研究,结果证明了该系统模型的有效性。
关键词:伺服;永磁同步电动机;矢量控制;插补;仿真中图分类号:TP273文献标识码:A文章编号:1672-1616(2007)19-0034-04伺服系统是数控机床的重要组成部分之一,主要功用是接受来自数控系统CNC的指令信息,控制执行部件的运动方向、进给速度与位移量,以便加工出符合要求的零件。
伺服系统的动态响应和伺服精度是影响数控机床加工精度、表面质量和生产率的主要因素,因此数控机床的速度和精度等技术指标在很大程度上由伺服系统的性能所决定。
伺服系统性能主要体现在稳态跟踪误差、动态响应的精确性和快速性及对系统参数变化和随机干扰的鲁棒性等几个方面。
伺服系统要获得高性能和高精度,主要是通过提高执行机构、测量装置的精度和性能,或者是选择先进的控制策略来达到的[1,2]。
目前在小型和经济型数控机床上还使用步进电机,中高档数控机床大多采用直流伺服电机和交流伺服电机,而高精度数控机床已采用交流数字伺服系统,伺服电机的位置、速度等都已实现了数字化,并采用了新的控制理论,实现了不受机械负荷变动影响的高速响应伺服系统[2]。
如FANU C公司在其16i/18i/21i系列产品中采用高响应矢量控制(High Response Vector,简称HRV),实现了数控机床的高速、高精度和高效率。
交流伺服系统按驱动电机的类型,主要可分为永磁同步和感应异步两种交流伺服系统,其中由于基于正弦波的永磁同步电动机(PMSM)具有功率密度大、效率高、转子损耗小等优点,具备了十分优良的低速特性和很宽的调速范围,符合高性能伺服驱动的要求,在运动控制领域得到了广泛的应用。

MATLAB仿真教程一、MATLAB的基本操作1.启动MATLAB:在桌面上双击MATLAB图标,即可启动MATLAB软件。
3.基本运算:在命令窗口中输入基本运算表达式,如加减乘除,然后按下回车键即可得到结果。
4.变量的定义和操作:在MATLAB中,可以定义变量,并对其进行各种运算操作。
例如,定义一个变量a,并对其进行加法运算,如a=2+35.矩阵操作:MATLAB中的矩阵操作非常方便。
可以使用矩阵运算符进行矩阵的相加、相乘等操作。
6. 绘图功能:MATLAB提供了丰富的绘图功能,可以绘制曲线、散点图、三维图等。
通过plot函数可以绘制曲线,scatter函数绘制散点图,surf函数绘制三维图。
二、MATLAB的仿真研究1.数值计算:MATLAB可以进行各种数值计算,如解线性方程组、求解微分方程、进行最优化等。
通过编写相应的代码,调用MATLAB提供的函数库,可以实现这些仿真研究。
2.信号处理:MATLAB提供了丰富的信号处理工具箱,可以进行信号的滤波、谱分析、频谱绘制等操作。
通过调用相应的函数库,可以实现这些功能。
3.控制系统仿真:MATLAB提供了强大的控制系统工具箱,可以进行控制系统的建模、仿真和优化。
可以使用MATLAB的控制系统工具箱进行系统的响应、稳定性分析和控制器设计。
4.图像处理与计算机视觉:MATLAB可以进行基本的图像处理操作,如图像的灰度化、二值化、滤波、边缘检测等。
通过调用MATLAB的计算机视觉工具箱,还可以进行目标检测、图像识别等高级图像处理操作。
5.多体动力学仿真:MATLAB提供了多体动力学仿真工具箱,可以进行机械系统的建模、动力学仿真和分析。
可以通过编写相应的代码,定义机械系统的运动方程和控制方程,实现仿真研究。
总结:MATLAB是一种强大的数值计算和编程软件,广泛应用于科学、工程、金融等领域。
本教程介绍了MATLAB的基本操作以及如何进行仿真研究。
通过学习MATLAB,可以提高数值计算和仿真研究的效率,为科研工作提供有力的支持。


文章编号:1009-671X(2005)01-0001-03基于M AT LAB 的数控进给伺服系统设计与仿真董玉红,张立勋(哈尔滨工程大学机电工程学院,黑龙江哈尔滨150001)摘 要:利用M AT L AB 控制系统工具箱中的SISO 设计器设计了数控进给伺服系统.在建立了直流电机和进给系统的数学模型后,根据数控伺服系统的性能要求,使用SISO 设计器设计了进给伺服系统的校正补偿器,得到了反映系统性能的特性曲线和Simulink 仿真模型,并根据仿真模型验证了系统设计的正确性.该项研究对伺服系统的性能分析及用根轨迹法设计控制系统具有一定的参考价值.关 键 词:M AT L AB;伺服系统;SISO 设计器;仿真中图分类号:T P272 文献标识码:A收稿日期:2004-06-08.作者简介:董玉红(1965-),女,副教授,主要研究方向:机械电子工程.Design and simulation of NC feed servo system by MATLABDONG Yu -hong,ZHANG L-i xun(School of M echanical and Electrical Engineering,Harbin Eng ineering U niversity,Harbin 150001,China)Abstract:NC feed servo system w as designed by applying SISO designer in MAT LAB control system too-l box.After m athematic models of DC motor and feed system w ere built up,a kind of com pensator was de -vised according to performance requirements of NC servo system.Characteristic curves of the system re -sponses and Simulink simulation model w ere obtained and the design w as verified by the model.This study prov ides a reference for analy zing performances of servo system and applying root locus method to design control system.Key words:M ATLAB;servo system;SISO designer;simulation 数控伺服系统是以机床移动部件的位移和速度为控制对象的自动控制系统,它的作用是接受数控系统发出的进给速度和位置指令信号,经转换放大后,由伺服驱动装置和机械传动机构驱动机床的工作台实现进给运动.伺服系统是数控机床的重要组成部分,包括主运动伺服系统和进给伺服系统,进给伺服系统的性能在很大程度上决定了数控机床的加工精度与质量.本文使用M ATLAB 中的SISO 设计器设计了进给伺服系统,在SISO 设计器中可以根据系统的根轨迹和开环伯德图方便地添加零极点,改变系统零极点的位置,从而使伺服系统的稳态和动态性能满足设计要求.1 数控进给伺服系统的模型数控进给伺服系统如图1所示.对于永磁直流电动机,其微分方程式为[1]图1 数控进给伺服系统第32卷第1期 应 用 科 技 Vol.32, .12005年1月 Applied Science and Technology Jan.2005L a=d i a(t)d t+R a i a(t)=u a(t)-e b(t),e b(t)=K b M(t),T M=K T i a(t),(1) Jd M(t)d t+B M(t)=T M.式中:L a为电枢回路的电感,R a为电枢回路的总电阻,i a(t)为电枢回路的电流,u a(t)为电枢回路的控制电压,e b(t)为电机的反电动势,K b为电机反电动势常数, M为电机输出转速,T M为电机输出力矩,K T为电机转矩常数,J为折算到电机轴上的总转动惯量,B为折算到电机轴上的总粘性阻尼系数.若设功率放大器的增益为K a,电机的输出转角为 o1,将式(1)进行拉氏变换,整理可得直流电机的传递函数为G m= o1(s)X i(s)=K a K Ts(L a s+R a)(Js+B)+K T K b s .(2)若考虑直流电机电感很小,可忽略不计时,则式(2)变为G M(s)=K a K ts(Js+B)+K T K b s.(3)减速齿轮、丝杠螺母进给系统的传递函数为[1]G J(s)=X o(s) o1(s)=z1 z2 L22ns2+2 n s+ 2n.(4)式中:z1,z2,L为齿轮1,2的齿数和丝杠导程, n=kJ为进给系统的无阻尼固有频率, = B2Jk为进给系统的阻尼比.当直流电机及进给系统的各参数取值为: L a=0 0018,R a=1 36,K a=5,K T=K b= 0 025,J=1 07 10-4,B=4 3 10-4,z1/z2= 1/2,L=4mm, =0 5, n=100,时,直流进给伺服系统的传递函数为G(s)=G M(s)G J(s)=37500s(s3+162.5s2+16250s+625000).(5)2 数控进给伺服系统设计SISO设计器是MATLAB控制系统工具箱所提供的一个非常强大的单输入单输出线性系统设计器,它为用户设计单输入单输出线性控制系统提供了非常友好的图形界面.在SISO设计器中,设计者可以同时使用根轨迹图与开环伯德图,通过添加或改变系统补偿器的零极点以及增益等参数实现对单输入单输出控制系统的设计[2].首先在MATLAB命令窗口中键入: siso-tool启动SISO设计器.在默认情况下,SISO设计器同时启动系统根轨迹编辑器与开环伯德图编辑器.然后在MATLAB命令窗口中键入被控对象(plant)为: G=tf(37500,[1162.5162506250000])输入系统数据.接着在SISO设计器的file下输入系统的数据,并选择控制系统结构,则在SISO设计器中就绘出了被控对象的根轨迹和开环伯德图,如图2所示.图2 被控对象的根轨迹和开环伯德图在图2中,可以通过添加或拖动补偿器的零极点,或拖动根轨迹中的方块改变系统增益等办法,来改变进给系统的特性.根据被控对象的传递函数中含有积分环节,且由图2中的开环伯德图可知,被控对象稳定性及准确性较好,但其快速性要求不能得到满足.在此设计超前校正补偿器来改善系统的动态性能,提高系统的快速性.添加补偿器零点在其极点的右侧,并调整增益,得到补偿器C(s)传递函数和设计后系统的根轨迹、伯德图,如图3所示.从图3中的开环伯德图可知,系统仍然具有较好的稳定性.系统设计完成以后,可以使用M ATLAB中的线性时不变浏览器LTI View er绘制系统的阶2应 用 科 技 第32卷图3 设计补偿器后系统的根轨迹和开环伯德图跃响应、脉冲响应、开环伯德图等特性曲线,如图4所示.根据被设计系统的这些特性曲线可知,系统具有很好的准确性、稳定性和快速性.图4 用LT I 浏览器绘制的系统特性曲线3 数控进给伺服系统仿真SISO 设计器还提供了与Simulink 集成的方法,可以直接生成被设计系统的Simulink 仿真模型.在模型生成之前,必须保存线性系统的被控对象、补偿器以及传感器等LT I 对象至MAT -LAB 工作空间中.生成数控进给伺服系统的Simulink 模型如图5所示,由此便可以对设计好的系统的系统进行仿真,验证系统设计的正确性.图6是仿真模型加上阶跃输入信号的响应曲线,比较图6与图4中的阶跃响应曲线,就可以验证系统设计的正确性.图5 系统的Simulink模型图6 系统Simulink 模型的阶跃特性曲线4 结 论本文利用MATLAB 控制系统工具箱中的SISO 设计器设计了数控进给伺服系统,使系统满足准确性、稳定性和快速性的要求.在设计的过程中,不仅得到了补偿器的传递函数,而且还得到了反映系统性能的特性曲线以及系统的Simulink 仿真模型,并通过仿真模型验证了系统设计的正确性.本文的研究对伺服系统的性能分析及用根轨迹法设计控制系统具有一定的参考价值.参考文献:[1]董玉红,杨清梅.机械控制工程基础[M ].哈尔滨:哈尔滨工业大学出版社,2003.[2]姚 俊,马松辉.Simulink 建模与仿真[M ].西安:西安电子科技大学出版社,2002.[责任编辑:李雪莲]3 第1期 董玉红,等:基于M ATLAB 的数控进给伺服系统设计与仿真。

文章编号:1001-2265(2006)08-0067-03收稿日期:2006-02-27 3基金项目:广东省自然科学基金资助项目(32364);广东省高教厅基金资助项目(Z02067)作者简介:王小东(1981—),男,内蒙古赤峰人,五邑大学机电工程系硕士研究生,研究方向为数控系统及其仿真,(E -mail )wangxiaodong1816@ 。
基于Matlab /Si m ulink 数控伺服系统的建模仿真3王小东,王大承(五邑大学机电工程系,广东 江门 529020)摘要:利用M atlab /Si m ulink 软件,通过对永磁同步电机(P M S M )本体、d /q 坐标系向a /b /c 坐标系转换、三相电流源逆变器等功能模块建立与组合,构建了永磁同步电机控制系统的速度和电流双闭环仿真模型。
根据数控伺服系统的性能要求,进行参数选择及仿真。
仿真结果证明了该系统模型的有效性,为数控伺服控制系统的设计和调试提供了理论基础。
关键词:M atlab /Si m ulink;数控伺服系统;永磁同步电机;仿真中图分类号:TP273 文献标识码:AS i m ul a ti on and M odeli n g of P M S M Ba sed on M a tl abWANG Xiao 2dong,WANG Da 2cheng(Depart m ent of Mechanical and Electrical Engineering,W uyi University,J iang men Guangdong 529020,China )Abstract:I n Matlab /Si m ulink,the bl ocks,such as P MS M bl ock,coordinate transfor mati on f or med q /d t o a /b /c bl ock,three phase current s ource inveter contr oller bl ock,etc .have been modeled .By the organic combi 2nati on of these bl ocks,t w o contr ol l oop s are used .The para meters are chosed by the perf or mance of servo sys 2te m.The reas onability and validity have been testified by si m ulate result and this novel method offers a ne w thought for designing and debugging actual mot or .Key words:Matlab /Si m ulink,NC servo syste m;P MS M ,si m ulati on0 引言数控机床的伺服系统一般由电流环和速度环组成[1]。

M A T L A B电液位置伺服控制系统设计及仿真数控机床工作台电液位置伺服控制系统设计及仿真姓名:雷小舟专业:机械电子工程子方向:机电一体化武汉工程大学机电液一体化实验室位置伺服系统是一种自动控制系统。
因此,在分析和设计这样的控制系统时,需要用自动控制原理作为其理论基础,来研究整个系统的动态性能,进而研究如何把各种元件组成稳定的和满足稳定性能指标的控制系统。
若原系统不稳定可通过调整比例参数和采用滞后校正使系统达到稳定,并选取合适的参数使系统满足设计要求。
1 位置伺服系统组成元件及工作原理数控机床工作台位置伺服系统有不同的形式,一般均可以由给定环节、比较环节、校正环节、执行机构、被控对象或调节对象和检测装置或传感器等基本元件组成[1]。
根据主机的要求知系统的控制功率比较小、工作台行程比较大,所以采用阀控液压马达系统。
系统物理模型如图1所示。
图1 数控机床工作台位置伺服系统物理模型系统方框图如图2所示。
图2 数控机床工作台位置伺服系统方框图数控机床工作台位置伺服系统是指以数控机床工作台移动位移为控制对象的自动控制系统。
位置伺服系统作为数控机床的执行机构,集电力电子器件、控制、驱动及保护为一体。
数控机床的工作台位置伺服系统输出位移能自动地、快速而准确地复现输入位移的变化,是因为工作台输出端有位移检测装置(位移传感器)将位移信号转化为电信号反馈到输入端构成负反馈闭环控制系统。
反馈信号与输入信号比较得到差压信号,然后把差压信号通过伺服放大器转化为电流信号,送入电液伺服阀(电液转换、功率放大元件)转换为大功率的液压信号(流量与压力)输出,从而使液压马达的四通滑阀有开口量就有压力油输出到液压马达,驱动液压马达带动减速齿轮转动,从而带动滚珠丝杠运动。
因滚珠丝杠与工作台相连所以当滚珠丝杠 运动时,工作台也发生相应的位移。
2数控工作台的数学模型 2.1 工作台负载分析工作台负载主要由切削力c F ,摩擦力f F 和惯性力a F 三部分组成,则总负载力为:a f c L F F F F ++=2.2液压执行机构数学模型工作台由液压马达经减速器和滚珠丝杠驱动。

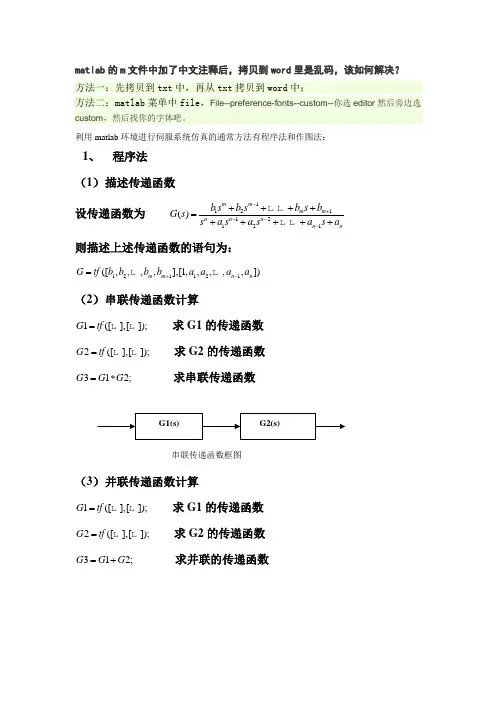
matlab 的m 文件中加了中文注释后,拷贝到word 里是乱码,该如何解决? 方法一:先拷贝到txt 中,再从txt 拷贝到word 中;方法二:matlab 菜单中file ,File--preference-fonts--custom--你选editor 然后旁边选custom ,然后找你的字体吧。
利用matlab 环境进行伺服系统仿真的通常方法有程序法和作图法:1、 程序法 (1) 描述传递函数设传递函数为 112112121()m m m m n n n n nb s b s b s b G s s a s a s a s a -+---++++=+++++ 则描述上述传递函数的语句为:121121([,,,,],[1,,,,,])m m n n G tf b b b b a a a a +-=(2) 串联传递函数计算1([],[]);G tf = 求G1的传递函数 2([],[]);G tf = 求G2的传递函数 312;G G G =* 求串联传递函数(3) 并联传递函数计算1([],[]);G tf = 求G1的传递函数 2([],[]);G tf = 求G2的传递函数 312;G G G =+ 求并联的传递函数串联传递函数框图(4) 求闭环传递函数1([],[]);G tf = 求G1的传递函数 2([],[]);G tf = 求G2的传递函数(1,2);GB feedback G G =闭环系数只与G1,G2相关(5) 求阶跃响应1([],[]);G tf = 求G1的传递函数step(G1) 求G1的单位阶跃响应 (6) 求频率特性1([],[]);G tf = 求G1的传递函数bode(G1); 求G1的幅频特性和相频特性 (7) 求稳定裕度闭环传递函数框图并联传递函数框图1([],[]);G tf = 求G1的传递函数margin(G1); 求G1的幅值裕度和相位裕度 例题一:闭环传递函数与G1无关G1=tf([0.06],[0.0000024,1]); G2=tf([0.0044,1],[0.0002,0]); G3=tf([28],[0.0001,1]); G4=tf([0.6],[0.005,1]); G5=tf([0.06],[0.0000024,1]); GK=G1*G2*G3*G4; figure; bode(GK); grid ontitle('开环特性曲线');GB=feedback(G2*G3*G4,G5); figure bode(GB); grid ontitle('闭环特性曲线'); figure step(GB); grid ontitle('阶跃响应');G1G2G3G4例题2:G1=tf([0.15,1],[0.051,0]);G2=tf([70],[0.0067,1]);G3=tf([0.21],[0.15,1]);G4=tf([0.1],[0.01,1]);GB1=feedback(G1*G2*G3,G4);G5=tf([0.17,1],[0.085,0]);G6=tf([1],[0.01,1]);G7=tf([0.0044],[0.01,1]);G8=tf([130],[1,0]);GK=G5*G6*GB1*G7*G8; %求开环传递函数figurebode(GK); %求开环频率特性grid on %打坐标title('开环频率特性曲线');figure;margin(GK); %求幅值裕度与相位裕度GB=feedback(G5*G6*GB1*G8,G7); %求闭环传递函数bode(GB); %求闭环频率特性grid ontitle('闭环频率特性曲线');figure;margin(GB);step(GB);grid ontitle('阶跃响应特性曲线');2、作图法利用Matlab提供的SIMULINK动态系统仿真环境进行仿真。

MATLAB驱动模型与仿真技巧分享概述:MATLAB是一种广泛应用于工程和科学领域的数学软件。
它不仅提供了丰富的数学函数库,还具有强大的数据可视化和模型仿真功能。
本文将分享一些关于MATLAB驱动模型和仿真技巧的经验。
一、MATLAB的模型驱动能力MATLAB具有出色的数学建模能力,可以利用其各个工具箱进行系统的建模与仿真。
通过MATLAB,我们可以将数学模型应用于实际问题,并对其进行模拟分析。
例如,利用Simulink工具箱,我们可以建立各种各样的动态系统模型,并进行精确仿真。
此外,MATLAB还提供了其他相关工具箱,如Control System Toolbox、Signal Processing Toolbox等等,使得模型驱动变得更加便捷。
二、如何进行MATLAB模型驱动1. 建立模型在进行MATLAB模型驱动之前,首先需要清楚我们要建立的模型是什么。
这包括确定系统的输入和输出,反映系统行为的数学方程等。
一旦我们了解了系统的特性和行为,我们可以使用MATLAB提供的建模工具,如Simulink等,开始建立模型。
2. 设置模型参数在建立模型之后,需要设置模型的参数,这可以通过直接给定数值或使用符号变量来实现。
符号变量提供了对参数的更灵活的控制,使得我们可以轻松地改变参数的值,从而分析不同情况下的系统行为。
3. 添加边界条件在建模过程中,我们还需要考虑系统的边界条件。
这些条件可能包括系统的初始状态、外部输入等。
通过设置适当的边界条件,我们可以更准确地模拟系统的实际行为。
4. 运行模型在设置完模型参数和边界条件之后,我们可以利用MATLAB提供的仿真工具运行模型。
通过运行模型,我们可以获得关于系统行为的详细信息,包括系统的响应、稳定性等。
三、MATLAB仿真技巧分享1. 选择适当的仿真时间步长在进行模型仿真时,我们需要选择适当的仿真时间步长。
时间步长的选择会直接影响仿真结果的准确性与计算效率。


伺服电机怎么控制角度大小matlab代码(最新版)目录1.伺服电机简介2.控制伺服电机角度的方法3.使用 Matlab 控制伺服电机角度的实现4.总结正文一、伺服电机简介伺服电机是一种将电脉冲转换为角位移的电机,它能够准确地控制旋转角度和转速。
伺服电机主要由电机本体、控制器和编码器组成。
编码器通常采用霍尔传感器,能够检测电机的旋转角度,并将检测结果以脉冲信号的形式反馈给控制器。
二、控制伺服电机角度的方法1.设定工作模式:伺服电机的工作模式分为速度控制模式和位置控制模式。
在位置控制模式下,伺服电机的角度可以通过设定目标位置和当前位置的差值来实现。
2.设定脉冲当量:脉冲当量是指一个脉冲信号对应的电机旋转角度。
通过设定脉冲当量,可以控制伺服电机旋转的角度。
3.设定电子齿轮比:电子齿轮比是指电机旋转一圈所需的脉冲数与编码器检测到的脉冲数之间的比值。
通过调整电子齿轮比,可以控制伺服电机旋转的角度。
三、使用 Matlab 控制伺服电机角度的实现1.搭建控制系统:首先,需要搭建一个基于 Matlab 的控制系统,用于控制伺服电机的角度。
可以通过编写 Matlab 程序,实现对伺服电机的控制。
2.编写控制程序:在 Matlab 中,可以使用 PID 控制算法实现对伺服电机角度的控制。
根据实际需求,可以调整 PID 参数,以达到最佳的控制效果。
3.读取编码器信号:通过编写程序,读取编码器发出的脉冲信号,并计算出伺服电机的旋转角度。
4.控制伺服电机旋转:根据目标角度和当前角度的差值,计算出需要发送给伺服电机的脉冲数。
将这些脉冲数发送给伺服电机,使其旋转到目标角度。
四、总结通过使用 Matlab 编写控制程序,可以实现对伺服电机角度的精确控制。
基于matlab永磁同步电机控制系统建模仿真方法1. 建立永磁同步电机模型
我们可以通过matlab中的Simulink工具箱建立永磁同步电机的模型,模型中包括电机本身和电机驱动系统。
该模型可以包括各种控制系统,比如位置控制、速度控制、电流控制等。
2. 设计控制系统
根据永磁同步电机的特性和实际控制需求,选定相应的控制策略。
常见的控制策略有FOC(磁场定向控制)、DTC(直接扭矩控制)等。
设计控制系统包括建立系统数学模型、设计控制算法、仿真验证等步骤。
3. 仿真实现
在matlab中进行仿真实现,根据设计的控制系统和模型参数,运行仿真程序,验证设计的控制系统的性能和功能是否符合实际控制要求,以此优化和完善控制系统。
4. 实验验证
在实验室或者实际应用场景中,进行实验验证,对控制系统进行调试和优化。
实
验验证可以通过实际硬件搭建或者仿真器件模拟等方式实现。
根据验证结果,并结合实际应用需求,对控制系统进行进一步优化和改进。