高二数学直线的交点坐标与距离公式

直线与方程复习题 一、知识梳理：1距离公式(1)在平面直角坐标系中，两点A (x 1，y 1)，B (x 2，y 2)之间的距离公式为：|AB |＝__________．（2）线段的中点坐标公式：若点P 1，P 2的坐标分别为(x 1，y 1)，(x 2，y 2)，线段P 1P 2的中点M 的坐标为(x ，y )，则x=_______________; y=_______________;(3)点到直线的距离公式：点P 0(x 0，y 0)到直线l ：Ax ＋By ＋C ＝0的距离d ＝ ．(4)两条平行直线间的距离公式：两条平行直线l 1：Ax ＋By ＋C 1＝0与l 2：Ax ＋By ＋C 2＝0(C 1≠C 2)间的距离d ＝____________________．2．直线的斜率(1)直线的倾斜角与斜率：___________(2)经过两点P 1(x 1，y 1)，P 2(x 2，y 2)(x 1≠x 2)的直线的斜率公式为k ＝ ．(3)直线的一般式为0Ax By C ++=,则该直线的斜率k =____________3．直线的方程(1)截距：直线l 与x 轴交点(a ，0)的____________叫做直线l 在x 轴上的截距，直线l 与y 轴交点(0，b )的____________叫做直线l 在y 轴上的截距．(2)直线方程的主要形式：①点斜式： 斜截式：①一般式： 截距式：4．两条直线的位置关系(1)平行：对于两条不重合的直线l 1，l 2，其斜率分别为k 1，k 2，有l 1①l 2①____________，特别地，当直线l 1，l 2的斜率都不存在时，l 1与l 2的关系为____________．(2)垂直：如果两条直线l 1，l 2的斜率都存在，且分别为k 1，k 2，则有l 1①l 2①____________，特别地，若直线l 1：x ＝a ，直线l 2：y ＝b ，则l 1与l 2的关系为____________．5．两条直线的交点坐标：两条直线的交点坐标即方程组⎩⎪⎨⎪⎧A 1x ＋B 1y ＋C 1＝0，A 2x ＋B 2y ＋C 2＝0.的解。

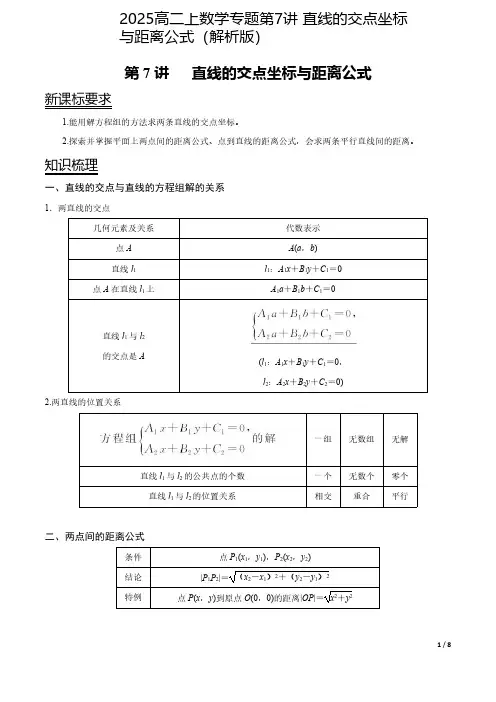
第7讲直线的交点坐标与距离公式新课标要求1.能用解方程组的方法求两条直线的交点坐标。

2.探索并掌握平面上两点间的距离公式、点到直线的距离公式，会求两条平行直线间的距离。

知识梳理一、直线的交点与直线的方程组解的关系1．两直线的交点几何元素及关系代数表示点A A (a ，b )直线l 1l 1：A 1x ＋B 1y ＋C 1＝0点A 在直线l 1上A 1a ＋B 1b ＋C 1＝0直线l 1与l 2的交点是A(l 1：A 1x ＋B 1y ＋C 1＝0，l 2：A 2x ＋B 2y ＋C 2＝0)2.两直线的位置关系一组无数组无解直线l 1与l 2的公共点的个数一个无数个零个直线l 1与l 2的位置关系相交重合平行二、两点间的距离公式条件点P 1(x 1，y 1)，P 2(x 2，y 2)结论|P 1P 2|＝（x 2－x 1）2＋（y 2－y 1）2特例点P (x ，y )到原点O (0，0)的距离|OP |＝x 2＋y 22025高二上数学专题第7讲 直线的交点坐标与距离公式（解析版）三、点到直线的距离1．概念：过一点向直线作垂线，则该点与垂足之间的距离，就是该点到直线的距离．2．公式：点P (x 0，y 0)到直线l ：Ax ＋By ＋C ＝0的距离d ＝|Ax 0＋By 0＋C |A 2＋B 2．四、两平行直线间的距离1．概念：夹在两条平行直线间的公垂线段的长度就是两条平行直线间的距离．2．公式：两条平行直线l 1：Ax ＋By ＋C 1＝0与l 2：Ax ＋By ＋C 2＝0之间的距离d ＝|C 1－C 2|A 2＋B 2．名师导学知识点1两直线的交点问题【例1-1】（宜昌期末）已知两直线1:3420l x y +-=，2:220l x y ++=，则1l 与2l 的交点坐标为．【例1-2】（雅安期末）过直线1:240l x y -+=与直线2:10l x y ++=的交点，且过原点的直线方程为()A ．20x y -=B ．20x y +=C ．20x y -=D ．20x y +=【例1-3】（芜湖期末）若三条直线2380x y ++=，10x y --=和0x ky +=交于一点，则k 的值为()A ．2-B ．12-C ．2D ．12【变式训练1-1】（阎良区期末）直线5y x =-+与直线1y x =+的交点坐标是()A ．(1,2)B ．(2,3)C ．(3,2)D ．(2,1)【变式训练1-2】（（安庆期末）直线210x y ++=与直线20x y -+=的交点在()A ．第一象限B ．第二象限C ．第三象限D ．第四象限【变式训练1-3】（（庐江县期中）直线230x y k +-=和直线120x ky -+=的交点在x 轴上，则k 的值为()A ．24-B ．24C ．6D ．6±知识点2直线过定点问题【例2-1】（宿迁期末）设直线2(3)260x k y k +--+=过定点P ，则点P 的坐标为()A ．(3,0)B ．(0,2)C ．(0,3)D ．(2,0)【例2-2】（江阴市期中）直线:1(2)l y k x -=+必过定点()A ．(2,1)-B ．(0,0)C ．(1,2)-D ．(2,1)--【变式训练2-1】（黄浦区期末）已知a R ∈，若不论a 为何值时，直线:(12)(32)0l a x a y a -++-=总经过一个定点，则这个定点的坐标是()A ．(2,1)-B ．(1,0)-C ．21(,)77-D ．12(,)77-【变式训练2-2】（慈溪市期末）直线1(y kx k k =++为常数）经过定点()A ．(1,1)B ．(1,1)-C ．(1,1)-D ．(1,1)--知识点3两点间距离公式的应用【例3-1】（南充期末）已知点(1A ，0，2)与点B (1，3-，1)，则||(AB =)A ．2B C ．3D【例3-2】（临川区校级一模）已知ABC ∆的三个顶点的坐标分别为(3,4)A ，(5,2)B ，(1,4)C --，则这个三角形是()A ．锐角三角形B ．直角三角形C ．钝角三角形D ．等腰直角三角形【变式训练3-1】（琼山区校级期末）已知ABC ∆的顶点坐标为(7,8)A ，(10,4)B ，(2,4)C -，则BC 边上的中线AM 的长为()A ．8B ．13C ．D 【变式训练3-2】（雁江区校级月考）如图，已知等腰梯形ABCD ，用坐标法证明：AC BD =．知识点4点到直线的距离【例4-1】（金凤区校级期末）已知点(2,1)P -．（1）若一条直线经过点P ，且原点到直线的距离为2，求该直线的一般式方程；（2）求过点P 且与原点距离最大的直线的一般式方程，并求出最大距离是多少？【例4-2】（韶关期末）已知点(1,3)A 和点(5,2)B 到直线l 的距离相等，且l 过点(3,1)-，则直线l 的方程为()A ．410x y ++=或3x =B ．410x y +-=或3x =C ．410x y ++=D ．410x y +-=【变式训练4-1】（保山期末）若直线l 过点，倾斜角为120︒，则点(1,到直线l 的距离为()A ．32B C ．332D ．532【变式训练4-2】（新课标Ⅲ）点(0,1)-到直线(1)y k x =+距离的最大值为()A ．1BC D ．2知识点5两平行线间距离公式及其应用【例5-1】（张家界期末）直线3430x y +-=与直线690x my ++=平行，则它们的距离为()A ．65B ．32C ．125D ．2【例5-2】（广州期末）若两平行直线20(0)x y m m ++=>与30x ny --=之间的距离是，则(m n +=)A ．0B ．1C ．1-D ．2-【变式训练5-1】（靖远县期末）已知直线240x y +-=与直线230x my m +++=平行，则它们之间的距离为()A B C ．352D ．3102【变式训练5-2】（连云港期末）两条平行直线6450x y -+=与32y x =的距离是()A ．13B ．26C ．13D ．26【变式训练5-3】（广东期末）已知直线1:(1)2l x m y m ++=-与2:24160l mx y ++=，若12//l l ，则实数m 的值为()A ．2或1-B ．1C ．1或2-D ．2-【变式训练5-4】（崇左期末）已知直线1:20l x y n ++=，2:440l x my +-=互相平行，且1l ，2l 之间的距离(m n +=)A ．3-或3B ．2-或4C ．1-或5D ．2-或2知识点6运用距离公式解决最值问题【例6-1】（北碚区校级期末）已知ABC ∆的三个顶点(1,2)A ，(2,1)B ，(3,3)C ，若ABC ∆夹在两条斜率为1的平行直线之间，则这两条平行直线的距离的最小值是()A ．355B C ．322D 【例6-2】（鼓楼区校级期中）已知直线1:4270l x y +-=和2:210l x y +-=，直线m 分别与1l ，2l 交于A ，B 两点，则线段AB 长度的最小值为．【变式训练6-1】（闵行区校级模拟）过点(1,2)-且与原点的距离最大的直线方程是．【变式训练6-2】（和平区校级期末）已知点(2,5)A 和点(4,7)B ，点P 在y 轴上，若||||PA PB +的值最小，则点P 的坐标为．名师导练A 组-[应知应会]1．（辽源期末）点(3,1)到直线3420x y -+=的距离是()A ．45B ．75C ．425D ．2542．（宁波期末）直线6820x y +-=与6830x y +-=间的距离为()A ．1B ．3C ．110D ．253．（内江期末）已知点(1,3)M 到直线:10l mx y +-=的距离等于1，则实数m 等于()A ．34B ．43C ．43-D ．34-4．（兴庆区校级期末）设有直线(3)1y k x =-+，当k 变动时，所有直线都经过定点()A ．(0,0)B ．(0,1)C ．(3,1)D ．(2,1)5．（沙坪坝区校级期中）已知直线1:10l x ay +-=与2:210l x y -+=平行，则1l 与2l 的距离为()A ．15B ．55C ．35D ．3556．（包头期末）点(,)P x y 在直线20x y +-=上，O 是坐标原点，则||OP 的最小值是()A ．1B C ．2D ．7．（河池期末）点2(2,)P m m 到直线70x y ++=的距离的最小值为()A ．4B ．C ．D ．8．（江阴市期中）直线l 过(1,2)P ，且(2,3)A ，(4,5)B -到l 的距离相等，则直线l 的方程是()A ．460x y +-=B ．460x y +-=C ．2370x y +-=或460x y +-=D ．3270x y +-=或460x y +-=9．（平顶山期末）已知(1,2)P -，(2,4)Q ，直线:3l y kx =+．若P 点到直线l 的距离等于Q 点到直线l 的距离，则(k =)A ．2.3或6B ．23C ．.0D ．.0或2310．（昆山市期中）已知(2,3)M -，(6,2)N ，点P 在x 轴上，且使得PM PN +取最小值，则点P 的坐标为()A ．(2,0)-B ．12(5，0)C ．14(5，0)D ．(6,0)11．（宝安区校级模拟）已知0x <<，0y <<M =则M 的最小值为()A ．B ．C ．2D ．12．（多选）（江阴市期中）若两条平行直线1:20l x y m -+=与2:260l x ny +-=之间的距离是则m n +的可能值为()A ．3B ．17-C ．3-D ．1713．（多选）（山东模拟）若三条直线1:10l ax y ++=，2:10l x ay ++=，3:0l x y a ++=不能围成三角形，则a 的取值为()A ．1a =B ．1a =-C ．2a =-D ．2a =14．（田家庵区校级期末）原点(0,0)到直线:20l x y -+=的距离是．15．（尖山区校级期末）两条平行直线110l y -+=与2:230l ax y +-=之间的距离为．16．（嘉兴期末）直线1:0l x y m --=与直线2:30l mx y -+=平行，则m =；1l 与2l 之间的距离为．17．（金华期末）已知直线:(1)2l x m y m ++=-，则当0m =时，直线l 的倾斜角为；当m 变化时，直线l 过定点．18．（镇江期末）已知直线1:0l x y a ++=与直线2:0l x y +=a 的值为．19．（珠海期末）已知平面直角坐标系xOy 中，点(4,1)A ，点(0,4)B ，直线:31l y x =-，则直线AB 与直线l 的交点坐标为．20．（苏州期末）已知A ，B 两点分别在两条互相垂直的直线20x y -=和5x ay +=上，且线段AB 的中点为(0,5)P ，则||AB =．21．（昆山市期中）在平面直角坐标xOy 中，已知(4,3)A ，(5,2)B ，(1,0)C ，平面内的点P 满足PA PB PC ==，则点P 的坐标为．22．（新余期末）已知直线:2(2)l y ax a =+-过一、三、四象限，其中a Z ∈，则点(1,3)A -到直线l 的距离为．23．（乐山期末）已知两条直线1:420l mx y +-=和2:10l x my ++=．（1）当12//l l 时，求m 的值；（2）在（1）的条件下，求1l 、2l 间的距离．24．（宁德期末）已知直线:260l x y --=与x 轴的交点为A ，且点A 在直线m 上．（1）若m l ⊥，求直线m 的方程；（2）若点(1,1)B 到直线m 的距离等于2，求直线m 的方程．25．（新都区期末）已知ABC ∆的三个顶点坐标为(3,1)A -，(3,3)B -，(1,7)C ．（1）求BC 边的中线所在直线方程的一般式方程；（2）求ABC ∆的面积．26．（沭阳县期中）已知直线:(12)(1)720l m x m y m ++-++=．（1）求证：不论m 为何实数，直线l 恒过一定点M ；（2）过定点M 作一条直线1l ，使夹在两坐标轴之间的线段被M 点平分，求直线1l 的方程．27．（宁城县期末）已知点ABC ∆三顶点坐标分别是(1,0)A -，(1,0)B ，(0,2)C ，（1）求A 到BC 边的距离d ；（2）求证AB 边上任意一点P 到直线AC ，BC 的距离之和等于d ．B 组-[素养提升]1．（尖山区校级期末）已知在ABC ∆中，顶点(4,2)A ，点B 在直线:20l x y -+=上，点C 在x 轴上，则ABC ∆的周长的最小值．2．（兰州期末）已知点(2,1)P -．（1）求过P 点与原点距离最大的直线l 的方程，最大距离是多少？（2）是否存在过P 点与原点距离为6的直线？若存在，求出方程；若不存在，请说明理由．第7讲直线的交点坐标与距离公式新课标要求1.能用解方程组的方法求两条直线的交点坐标。

第11讲 交点坐标与距离公式两条直线的交点坐标1. 一般地，将两条直线的方程联立，得到二元一次方程组1112220A x B y C A x B y C ++=⎧⎨++=⎩.若方程组有惟一解，则两条直线相交，此解就是交点的坐标； 若方程组无解，则两条直线无公共点，此时两条直线平行；若方程组有无数解，则两条直线有无数个公共点，此时两条直线重合.2. 方程111222()()0A x B y C A x B y C λ+++++=为直线系，所有的直线恒过一个定点，其定点就是1110A x B y C ++=与2220A x B y C ++=的交点.两点间的距离1. 平面内两点111(,)P x y ，222(,)P x y ，则两点间的距离为：22121212||()()PP x x y y -+-.特别地，当12,P P 所在直线与x 轴平行时，1212||||PP x x =-；当12,P P 所在直线与y 轴平行时，1212||||PP y y =-；点到直线的距离及两平行线距离1. 点00(,)P x y 到直线:0l Ax By C ++=的距离公式为0022d A B =+2. 利用点到直线的距离公式，可以推导出两条平行直线11:0l Ax By C ++=，22:0l Ax By C ++=之间的距离公式1222d A B =+，推导过程为：在直线2l 上任取一点00(,)P x y ，则0020Ax By C ++=，即002Ax By C +=-. 这时点00(,)P x y 到直线11:0l Ax By C ++=的距离为001122222d A BA B==++1.判断两直线是否相交，求交点坐标，点到直线的距离公式；2.两直线相交与二元一次方程的关系，点到直线距离公式的理解与应用。

1．两条直线A1x+B1y+C1=0与A2x+B2y+C2=0的交点坐标就是方程组的实数解，以下四个命题:(1)若方程组无解，则两直线平行 (2)若方程组只有一解，则两直线相交(3)若方程组有两个解，则两直线重合 (4)若方程组有无数多解，则两直线重合。

(4)特殊平行线与过定点(x0，y0)的直线系方程：当斜率k一定而m变动时，y＝kx＋m表示斜率为k的平行直线系，y－y0＝k(x－x0)表示过定点(x0，y0)的直线系(不含直线x＝x0)．
在求直线方程时，可利用上述直线系设出方程，再利用已知条件求出待定系数，从而求出方程．
例题精讲
【题型1、两直线的交点问题】
【例1】判断下列各对直线的位置关系，若相交，求出交点坐标：
(1)l1：2x＋y＋3＝0，l2：x－2y－1＝0；
(2)l1：x＋y＋2＝0，l2：2x＋2y＋3＝0；
(3)l1：x－y＋1＝0，l2：2x－2y＋2＝0.
【方法总结】1.方程组的解的组数与两条直线的位置关系
2．两条直线相交的判定方法：
(1)两直线方程组成的方程组只有一组解，则两直线相交；
(2)在两直线斜率都存在的情况下，若斜率不相等，则两直线相交．
特别提醒：若两直线的斜率一个不存在，另一个存在，则两直线一定相交．
11。

2024年新高二数学提升精品讲义直线的交点坐标与距离公式（原卷版）模块一思维导图串知识模块二基础知识全梳理（吃透教材）模块三核心考点举一反三模块四小试牛刀过关测1．会用解方程组的方法求两条相交直线的交点坐标；2．会根据方程解的个数判定两条直线的位置关系；3．会求两点间的距离、点到直线的距离、两条平行直线间的距离.知识点1两条直线的交点坐标1、点与坐标的一一对应关系几何元素及关系代数表示点P (,)P a b 直线l:0l Ax By C ++=点P 在直线l 上Aa Bb C ++=直线1l 与2l 的交点是P方程组11122200A xB yC A x B y C ++=⎧⎨++=⎩的解是x ay b =⎧⎨=⎩2、直线的交点与方程的解求两直线1111110(0)++=≠A x B y C A B C 与2222220(0)++=≠A x B y C A B C 的交点坐标，只需求两直线方程联立所得方程组1112220++=⎧⎨++=⎩A x B y C A x B y C 的解即可．若有111222==A B C A B C ，则方程组有无穷多个解，此时两直线重合；若有111222=≠A B C A B C ，则方程组无解，此时两直线平行；若有1122≠A B A B ，则方程组由唯一解，此时两直线相交，此解即两直线的交点坐标．3、判断两直线的位置关系关键是看两直线的方程组成的方程组的解的情况．（1）解方程组的重要思想就是消元，先消去一个变量，代入另外一个方程能解出另一个变量的值．（2）解题过程中注意对其中参数进行分类讨论．（3）最后把方程组解的情况还原为直线的位置关系．4、过两条直线交点的直线系方程一般地，具有某种共同属性的一类直线的集合称为直线系，它的方程叫做直线系方程，直线系方程中除含有,x y 以外，还有根据具体条件取不同值的变量，称为参变量，简称参数．由于参数取法不同，从而得到不同的直线系．经过两直线1111:0++=l A x B y C ，2222:0++=l A x B y C 交点的直线方程为111222()0+++++=A x B y C A x B y C λ，其中λ是待定系数．在这个方程中，无论λ取什么实数，都得不到2220++=A x B y C ，因此它不能表示直线2l ．知识点2两点间的距离1、距离公式：平面内两点()111,P x y ，()222,P x y 间的距离公式为：12=PP 【注意】公式中1P 和2P位置没有先后之分，也可以表示为：12=PP 2、三种特殊距离：（1）原点O 到任意一点(),P x y 的距离为=OP ；（2）当12PP 平行于x 轴时，1221=-PPx x ；（3）当12PP 平行于y 轴时，1221=-PP y y ．3、坐标法解题的基本步骤（1）建立适当的坐标系，用坐标表示有关的量；（2）进行有关代数运算；（3）把代数运算的结果“翻译”成几何关系．知识点3点到直线的距离1、定义：过一点向直线作垂线，则该点与垂足之间的距离，就是该点到直线的距离，即垂线段的长度．2、距离公式：点()00,P x y 到直线:0++=l Ax By C 的距离=d ．【注意】（1）直线方程应用一般式，若给出其他形式，应先化成一般式再用公式．（2）点到直线的距离是直线上的点与直线外一点的最短距离．（3）点到直线的距离公式适用任何情况，当点P 在直线l 上时，它到直线的距离为0．3、点到几种特殊直线的距离（1）点()00,P x y 到x 轴的距离0d y =；（2）点()00,P x y 到y 轴的距离0d x =；（3）点()00,P x y 到直线y a =的距离0d y a =-；（4）点()00,P x y 到直线x b =的距离0d x b =-．知识点4两条平行线间的距离1、定义：两条平行线间的距离是指夹在这两条平行线间的公垂线段的长．2、距离公式：两条平行直线11:0++=l Ax By C ，()2212:0++=≠l Ax By C C C ，它们之间的距离为：=d 【注意】在使用公式时，两直线方程为一般式，且x 和y 的系数对应相等．3、两平行线间的距离另外一种解法：转化为点到直线的距离，在任一条直线上任取一点（一般取直线上的特殊点），此点到另一条直线的距离即为两直线之间的距离．考点一：两条直线的交点问题例1．（23-24高二上·内蒙古呼伦贝尔·月考）直线1:3450l x y -+=与21:4303l x y --=的交点坐标为（）A ．(2,3)B ．7,33⎛⎫ ⎪⎝⎭C ．73,3⎛⎫ ⎪⎝⎭D ．3,37⎛⎫ ⎪⎝⎭【变式1-1】（23-24高二上·重庆长寿·期末）直线260x y -+=与直线3x y +=的交点坐标是（）A ．(30)，B ．(1,4)-C ．(3,6)-D ．(4,)1-【变式1-2】（23-24高二上·江苏·单元测试）已知直线250x y ++=与直线20kx y +=互相垂直，则它们的交点坐标为（）A ．()1,3--B ．()2,1--C ．1,12⎛⎫-- ⎪⎝⎭D ．()1,2--【变式1-3】（2023高二上·江苏·专题练习）分别判断下列直线l 1与l 2的位置关系，若相交，求出它们的交点坐标.(1)12:230,:210l x y l x y ++=--=；(2)12:310,:2620l x y l x y +-=+-=；(3)12:6230,:320l x y l x y -+=-+=.考点二：根据两直线交点求参数例2.（23-24高二上·北京·期中）已知直线420mx y +-=与250x y n -+=互相垂直，垂足为()1,P p ，则m n p -+的值是（）A ．24B ．0C ．20D ．4-【变式2-1】（23-24高二上·福建莆田·月考）若直线1:40l ax y +-=与直线22:0x y l --=的交点位于第一象限，则实数a 的取值范围是（）A ．()1,2-B ．()1,-+∞C ．(),2-∞D ．()(),12,-∞-+∞ 【变式2-2】（2023·海南海口·二模）若直线24y x =-+与直线y kx =的交点在直线2y x =+上，则实数k =（）A ．4B ．2C ．12D ．14【变式2-3】（23-24高二上·全国·课后作业）直线210x my ++=与直线1y x =+相交，则m 的取值范围为．考点三：三条直线的相交问题例3.（23-24高二上·安徽·月考）已知三条直线240,30,20x y kx y x y +-=-+=--=交于一点，则实数k =（）A ．1-B ．1C ．32-D ．14【变式3-1】（22-23高二上·山东聊城·月考）若三条直线370x y ++=，10x y --=，20x ny n ++=能围成一个三角形，则n 的值可能是（）A ．32B ．1C ．13-D ．12-【变式3-2】（23-24高二下·上海·期中）直线123:7210,:0,:10l x y l mx y l x my ++=+=+-=，若三条直线无法构成三角形，则实数m ）A ．3B ．4C ．5D ．6【变式3-3】（23-24高二上·湖南·期末）若三条不同的直线1:20l ax y ++=，2:10l x y +-=，3:30l x y -+=不能围成一个三角形，则a 的取值集合为（）A ．{1,1}-B ．{4,1}C ．1,12⎧⎫-⎨⎬⎩⎭D ．{4,1,1}-考点四：过两直线交点的直线方程例4.（23-24高二上·湖北武汉·月考）过两直线2023202210x y --=和2022202310x y ++=的交点且过原点的直线方程为．【变式4-1】（23-24高二上·全国·课后作业）经过点(1,0)P 和两直线1:220l x y +-=；2:3220l x y -+=交点的直线方程为.【变式4-2】（23-24高二上·安徽马鞍山·期中）平面直角坐标系xOy 中，过直线1:7310l x y -+=与2:430l x y +-=的交点，且在y 轴上截距为1的直线l 的方程为．（写成一般式）【变式4-3】（23-24高二·全国·假期作业）求过直线220x y -+=和10x y ++=的交点，且斜率为3的直线方程．考点五：两点间的距离公式例5.（23-24高二上·内蒙古呼伦贝尔·月考）已知()()3,6,2,4A B ，则A ，B 两点间的距离为（）A ．5B C ．3D【变式5-1】（23-24高二上·江苏徐州·期中）已知过(,2),(,1)A m B m m --两点的直线的倾斜角是45 ，则,A B 两点间的距离为（）A ．2B C ．D ．【变式5-2】（23-24高二上·天津·期末）三角形的三个顶点为()()()3,2,3,4,5,4A B C --，D 为AC 中点，则BD 的长为（）A ．3B ．5C ．9D ．25【变式5-3】（23-24高二上·海南·期中）在平面直角坐标系xOy 中，原点O 到直线1l ：240x y -+=与2l ：390x y +-=的交点的距离为（A B ．C D考点六：点到直线的距离公式例6.（23-24高二下·浙江·开学考试）已知点()0,3A 及直线:10l x y +-=上一点B ，则AB 的值不可能是（）A ．1B ．2C ．3D ．4【变式6-1】（23-24高二上·安徽马鞍山·月考）已知()3,4A --，()6,3B 两点到直线:10l ax y ++=的距离相等，求a 的值（）A ．13B ．97-C ．13-或79-D ．13或79-【变式6-2】（22-23高二上·云南临沧·月考）若点()3,1P 到直线:340(0)l x y a a ++=>的距离为4，则=a （）A ．2B ．3C ．5D ．7【变式6-3】（23-24高二上·广西南宁·月考）已知(4,0)A 到直线430x y a -+=的距离等于3，则a 的值为.考点七：平行线间的距离公式例7.（23-24高二上·河北石家庄·月考）两平行直线1:10l x y +-=和2:30l x y +-=之间的距离为（）A ．2B ．2C ．22D ．3【变式7-1】（23-24高二上·湖北孝感·期末）两条平行直线3420x y --=与6810x y -+=间的距离为（）A ．35B ．1C ．310D ．12【变式7-2】（23-24高二上·贵州铜仁·月考）（多选）已知两条平行直线m ，n ，直线:3420m x y ++=，直线:680n x y a ++=，直线m ，n 之间的距离为1，则a 的值可以是（）A ．8-B ．6-C ．12D ．14【变式7-3】（23-24高二上·广东茂名·期末）（多选）已知两条平行直线,m n ，直线:10m x y +-=，直线:220n x y a ++=，直线,m n 之间的距离为2，则a 的值可以是（）A ．-8B ．-6C ．2D ．4考点八：点与直线的对称问题例8.（22-23高二·全国·课堂例题）已知不同的两点(),P a b -与()1,1Q b a +-关于点()3,4对称，则ab =（）A ．5-B ．14C ．14-D ．5【变式8-1】（23-24高二上·安徽怀宁·月考）直线2360x y +-=关于点(1,1)对称的直线方程为（）A ．3220x y -+=B ．2370x y ++=C ．32120x y --=D ．2340x y +-=【变式8-2】（23-24高二下·四川雅安·开学考试）点()3,0关于直线30x y -+=对称的点的坐标为（）A ．()3,6B ．()6,3-C ．()6,3-D ．()3,6-【变式8-3】（23-24高二上·河北石家庄·月考）直线1y x =+关于直线2y x =对称的直线方程为（）A ．310x y --=B ．420x y --=C ．530x y --=D ．750x y --=一、单选题1．（23-24高二上·新疆喀什·期中）已知(6,0),(2,0)A B -，则||AB =（）A ．3B ．4C ．6D ．82．（23-24高二上·安徽马鞍山·月考）原点到直线912100x y +-=间的距离是（）A ．23B ．13C ．1D ．253．（23-24高二上·福建三明·期末）两条平行线1:220l x y +-=，2:690l ax y +-=间的距离等于（）ABCD4．（23-24高二上·浙江杭州·期中）已知1212//,:240,:620l l l x y l x ay ++=++=,则它们的距离为（）A．15BCD．35．（23-24高二上·四川绵阳·期末）已知()2,0A -，()4,B m 两点到直线l ：10x y -+=的距离相等，则m =（）A ．2-B ．6C ．2-或4D ．4或66．（23-24高二上·湖南·期中）已知()111,P x y ，()222,P x y 是直线2023y kx =+（k 为常数）上两个不同的点，则关于x 和y 的方程组112211x x y y x x y y +=⎧⎨+=⎩的解的情况，下列说法正确的是（）A ．无论k ，1P ，2P 如何，总是无解B ．无论k ，1P ，2P 如何，总有唯一解C ．存在k ，1P ，2P ，使12x y =⎧⎨=⎩是方程组的一组解D ．存在k ，1P ，2P ，使之有无穷多解二、多选题7．（22-23高二上·全国·期中）若直线1:32l y kx k =+-与直线2:30l x y +-=的交点在第四象限，则实数k 的取值可以是（）A ．0B ．13C ．12-D ．1-8．（23-24高二上·河南商丘·月考）（多选）平面上有三条直线250,10,0x y x y x ky -+=++=-=，将平面划分为六个部分，则实数k 的所有可能取值为（）A ．12B ．1-C ．2-D ．1三、填空题9．（22-23高二上·云南昆明·期中）在△ABC 中，点(1,1)A ，(4,2)B ，(4,1)C -，则ABC 的面积为．10．（2023高二上·全国·专题练习）直线230x y -=与321x y -=上任意两点最小距离为.11．（23-24高二下·上海黄浦·期中）已知直线1:40l x y +=，2:1l mx y +=，3:234l x my -=，若它们不能围成三角形，则实数m 的取值所构成的集合为．四、解答题12．（23-24高二上·山西大同·月考）已知直线:2310l x y -+=，点()1,2--A ．求：(1)点A 关于直线l 的对称点A '的坐标；(2)直线:3260m x y --=关于直线l 的对称直线m '的方程；(3)直线l 关于点()1,2--A 对称的直线l '的方程．13．（22-23高二上·云南临沧·月考）已知直线12:340,:3220l x y l x y --=-+=，设直线12,l l 的交点为P .(1)求点P 的坐标；(2)若直线l 过点P 且在两坐标轴上的截距相等，求直线l 的方程.。

高二数学《考点•题型 •技巧》精讲与精练高分突破系列(人教A 版选择性必修第一册)第二章 直线和圆的方程 2.3 直线的交点坐标与距离公式【考点梳理】考点一：两条直线的交点坐标1．两直线的交点已知直线l 1：A 1x ＋B 1y ＋C 1＝0；l 2：A 2x ＋B 2y ＋C 2＝0.点A (a ，b )． (1)若点A 在直线l 1：A 1x ＋B 1y ＋C 1＝0上，则有A 1a ＋B 1b ＋C 1＝0 .(2)若点A 是直线l 1与l 2的交点，则有⎩⎪⎨⎪⎧A 1a ＋B 1b ＋C 1＝0，A 2a ＋B 2b ＋C 2＝0.2．两直线的位置关系方程组⎩⎪⎨⎪⎧A 1x ＋B 1y ＋C 1＝0，A 2x ＋B 2y ＋C 2＝0的解一组 无数组 无解 直线l 1与l 2的公共点的个数 一个 无数个 零个 直线l 1与l 2的位置关系相交重合平行考点二： 两点间的距离公式（1）点P1(x 1，y 1)，P2(x 2，y 2)间的距离公式|P 1P 2|＝(x 2－x 1)2＋(y 2－y 1)2 (2) 原点O (0,0)与任一点P (x ，y )的距离|OP |＝x 2＋y 2.考点三：两条平行直线间的距离点到直线的距离 两条平行直线间的距离 定义点到直线的垂线段的长度夹在两条平行直线间公垂线段的长图示公式(或求法)点P (x 0，y 0)到直线l ：Ax ＋By ＋C ＝0的距离d ＝|Ax 0＋By 0＋C |A 2＋B 2两条平行直线l 1：Ax ＋By ＋C 1＝0与l 2：Ax ＋By ＋C 2＝0之间的距离d ＝|C 1－C 2|A 2＋B 2【题型归纳】题型一：直线的交点坐标1．直线460x y -+=和8180x y +-=与两坐标轴围成的四边形的面积为（ ） A ．2716B ．154C ．3316D ．3382．三条直线2x =，10x y --=，0x ky +=相交于一点，则k 的值为（ ） A ．2-B ．12-C ．2D ．123．直线l 经过直线240x y -+=和直线20x y +-=的交点，且与直线350x y ++=垂直，则直线l 的方程为（ ） A ．320x y -+= B ．320x y ++= C ．320x y -+=D ．320x y ++=题型二：由直线交点个数求参数4．已知直线1:10mx y l m -+-=与射线2:20(0)l x y x --=≥恒有公共点，则m 的取值范围是（ ） A ．(,1](1,)-∞-⋃+∞ B ．(,1][1,)-∞-+∞ C ．[1,1)-D ．[1,1]- 5．已知线段AB 两端点的坐标分别为()2,3A -和()4,2B ，若直线:10l x my m ++-=与线段AB 有交点，则实数m 的取值范围是（ ） A ．()3,1,4⎛⎫-∞-+∞ ⎪⎝⎭B ．31,4⎛⎫- ⎪⎝⎭C ．31,4⎡⎤-⎢⎥⎣⎦D ．(]3,1,4⎡⎫-∞-+∞⎪⎢⎣⎭6．设点()2,3A -,()3,2B ,若直线20ax y -++=与线段AB 没有交点,则a 的取值范围是( ) A ．45,32⎛⎫- ⎪⎝⎭B ．54,,23⎛⎤⎡⎫-∞-⋃+∞ ⎪⎥⎢⎝⎦⎣⎭C ．54,23⎛⎫- ⎪⎝⎭D ．45,,32⎛⎤⎡⎫-∞-+∞ ⎪⎥⎢⎝⎦⎣⎭题型三：两点间的距离公式应用7．直线0l ：440x y --=与1l ：220x y --=及2l ：43120x y +-=所得两交点间的距离为（ ） A ．3172B ．3172C ．91714D ．3178．已知ABC 三顶点为()1,4A --、()5,2B 、()3,4C ，则ABC 是（ ） A ．锐角三角形B ．直角三角形C ．钝角三角形D ．等腰三角形9．已知点(),1M m -，()5,N m ，且25MN =，则实数m 等于（ ） A ．1B ．3C ．1或3D ．1-或3题型四：点到直线的距离问题10．已知点()1,1P ，直线:1l y kx =+，则点P 到直线l 的距离的取值范围是（ ） A ．[]0,1B ．(]0,1C ．[)0,1D ．11[0,)(,1)22⋃11．已知在ABC 中，其中(1,4)B ，(6,3)C ，BAC ∠的平分线所在的直线方程为10x y -+=，则ABC 的面积为（ ） A ．52B ．102C ．8D ．21012．已知点()1,2P ，则当点P 到直线240ax y +-=的距离最大时，a =（ ） A ．1B ．14-C ．14D ．5题型五：点、直线的对称问题13．点()1,2关于直线20x y +-=的对称点是（ ） A ．()1,0B ．()0,1C ．()0,1-D ．()2,114．已知点()4,2M 与()2,4N 关于直线l 对称，则直线l 的方程为（ ） A ．60x y ++=B ．60x y +-=C ．0x y +=D ．0x y -=15．已知()20A ，，()60B ，，()04C ，，一条光线从点A 发出，经直线BC 反射后，恰好过原点O ，则入射光线所在直线的斜率为（ ） A ．83B ．125C ．269D ．3611题型六：两条平行直线间的距离16．已知直线1l ：()()()324220x y λλλ++++-+=（R λ∈），2l ：20x y +-=，若12//l l ，则1l 与2l 间的距离为（ ） A ．22B ．2C ．2D ．2217．已知直线1:32l y x =-，直线221:60l x y -+=，则1 l 与2 l 之间的距离为（ ） A ．52B ．54C ．102D ．10418．已知直线l 与直线1303l x y -+=：和2103l x y --=：的距离相等，则l 的方程是（ ） A ．320x y -+= B ．320x y --= C ．330x y --=D ．310x y -+=【双基达标】一、单选题19．已知直线420mx y +-=与直线250x y n -+=互相垂直，垂足为()1,p .则m n p +-等于（ ） A ．24B ．20C ．4D ．020．若直线:3l y kx =-与直线30x y +-=的交点位于第二象限，则直线l 的倾斜角的取值范围是（ ）A ．3,24ππ⎛⎤ ⎥⎝⎦B ．3,24ππ⎡⎫⎪⎢⎣⎭C ．3,34ππ⎛⎫ ⎪⎝⎭D ．3,24ππ⎛⎫ ⎪⎝⎭21．已知平面上两点(,2)A x x -，2(2B ，0)，则||AB 的最小值为（ ） A ．3B ．13C ．2D ．1222．已知m ，n 满足1m n +=，则点(1,1)到直线20mx y n -+=的距离的最大值为（ ） A ．0B ．1C ．2D ．2223．和直线20x y -+=关于x 轴对称的直线方程为（ ） A ．20x y -+-= B ．20x y -+-= C ．20x y ++=D ．20x y +-=24．已知()()0120A B ABC ，，，，的面积为5，则点C 的轨迹方程为（ ） A ．2120x y ++=或280x y ++= B ．2120x y +-=或280x y +-= C ．2120x y ++=或280x y +-=D ．2120x y +-=或280x y ++=25．若两条平行直线1:20(0)l x y m m -+=>与2:30l x ny +-=之间的距离是5，则m n +=（ ） A ．0B ．1C ．2-D ．1-26．在平面直角坐标系中，某菱形的一组对边所在的直线方程分别为210x y ++=和230x y ++=，另一组对边所在的直线方程分别为1340x y c -+=和2340x y c -+=，则12c c -=（ ） A ．23B ．25C ．2D ．427．过定点A 的直线0()x my m R -=∈与过定点B 的直线30()mx y m m R +-+=∈交于点(,)P x y ，则22||||PA PB +的值为（ ） A ．10B ．10C ．25D ．2028．已知直线:10(00)l Ax By C A B ++-=>>，恒过定点()0m ，，若点()22，到直线l 的最大距离为2，则112A C+的最小值为（ ） A ．14B ．34C ．4D ．92【高分突破】一：单选题29．已知ABC 的顶点为A （2，1），B (-2，3)，C (0，-1)，则AC 边上的中线长为（ ） A ．3B ．32C ．4D ．4230．一入射光线经过点(2,6)M ，被直线l ：30x y -+=反射，反射光线经过点(3,4)N -，则反射光线所在直线方程为（ ） A ．2130x y -+= B ．6220x y -+= C ．3150x y -+=D ．6270x y -+=31．已知直线1l 与2:230l x y --=平行，且1l 与2l 间的距离为5，则直线1l 的方程为（ ） A ．230x y +-=或290x y +-= B ．260x y --=或2120x y --= C ．220x y -+=或280x y --=D ．3.250x y -+=或3270x y --=32．已知直线1l ：30ax y -+=与直线2l 关于直线l ：10x y +-=对称，直线2l 与直线3l ：310x y +-=垂直，则a 的值为（ ）A ．13-B ．13C ．3D ．3-33．已知点()1,2A ，()2,3B -，直线:l y x =，在直线l 上找一点P 使得PA PB +最小，则这个最小值为（ ） A ．34B ．25C ．10D ．234．瑞士数学家欧拉（LeonhardEuler ）1765年在其所著的《三角形的几何学》一书中提出：任意三角形的外心、重心、垂心在同一条直线上，后人称这条直线为欧拉线.已知ABC ∆的顶点(4,0),(0,4),(2,0)A B C -，则该三角形的欧拉线方程是（ ） A ．20x y +-= B ．210x y -+= C ．20x y -+=D ．220x y -+=35．已知直线1:240l kx y k +--=恒过点M ，直线2:1l y x =-上有一动点P ，点N 的坐标为(4,6)，当||||PM PN +取得最小值时，点P 的坐标为（ ） A ．27,55⎛⎫-- ⎪⎝⎭B ．1712,55⎛⎫ ⎪⎝⎭C ．23,55⎛⎫- ⎪⎝⎭D ．127,55⎛⎫ ⎪⎝⎭36．若动点,A B 分别在直线1:60l x y +-=和2:20l x y +-=上，则AB 的中点M 到坐标原点的距离的最小值为（ ） A ．2 B ．22 C ．32 D ．42二、多选题37．下列说法正确的是（ ）A ．直线20x y --=与两坐标轴围成的三角形的面积是2B ．点(0,2)关于直线1y x =+的对称点为(1,1)C ．过11(,)x y ，22(,)x y 两点的直线方程为112121y y x x y y x x --=-- D ．经过点(1,2)且在x 轴和y 轴上截距都相等的直线方程为30x y +-=或10x y -+=38．已知(4,3)A -，(2,1)B -和直线l ：4320x y +-=，若在坐标平面内存在一点P ，使||||PA PB =，且点P 到直线l 的距离为2，则P 点坐标为（ ）A ．21(,)33-B ．(1,4)-C ．6(1,)5D ．278(,)77- 39．已知直线1:2310l x y +-=和2:4690l x y +-=，若直线l 到直线1l 的距离与到直线2l 的距离之比为1:2，则直线的方程为（ ） A ．2380x y +-= B ．4650x y ++= C ．69100x y +-=D ．1218130x y +-=40．（多选）已知直线l 经过点(3,4)，且点(2,2),(4,2)A B --到直线l 的距离相等，则直线l 的方程可能为（ ） A ．23180x y +-= B ．220x y --= C ．220x y ++=D ．2360x y -+=41．已知点P 是直线3450x y -+=上的动点，定点()1,1Q ，则下列说法正确的是（ ） A ．线段PQ 的长度的最小值为45B ．当PQ 最短时，直线PQ 的方程是3470x y +-=C ．当PQ 最短时P 的坐标为1341,2525⎛⎫⎪⎝⎭D ．线段PQ 的长度可能是2342．下列结论错误的是（ ）A ．过点()1,3A ，()3,1B -的直线的倾斜角为30B ．若直线2360x y -+=与直线20ax y ++=垂直，则32a =-C ．直线240x y +-=与直线2410x y ++=之间的距离是52D ．已知()2,3A ，()1,1B -，点P 在x 轴上，则PA PB +的最小值是5 三、填空题43．已知直线1:1l x ay +=，2:1l ax y +=，若12//l l ，则1l 与2l 的距离为______．44．设10x y -+=，求222261034430229d x y x y x y x y =++-+++--+的最小值是___________. 45．已知直线:(1)(1)(3)0l m x m y m ++-+-=，则原点到直线l 的距离的最大值等于___________.46．已知()1,12A ，()3,4B ， 过点()1,0-C 且斜率为k 的直线1l 与线段AB 相交，点()0,1D 到直线2:340l x y k ++=的距离为d ，则实数d 的取值范围是________________________.47．直线l 经过点()1,23P ，且分别与直线1:310l x y -+=和2:330l x y --=相交于A ，B 两点，若AB 4=，则直线l 的方程为________． 四、解答题48．已知直线l 经过点()2,3P --．（1）若原点到直线l 的距离为2，求直线l 的方程；（2）若直线l 被两条相交直线220x y --=和10x y +-=所截得的线段恰被点P 平分，求直线l 的方程．49．已知ABC 的三个顶点分别为()20A -，，()20B ，，()02C ，． （1）若过()12P ，的直线y ax b =+将ABC 分割为面积相等的两部分，求b 的值； （2）一束光线从()10E ，点出发射到BC 上的D 点，经BC 反射后，再经AC 反射到x 轴上的F 点，最后再经x 轴反射，反射光线所在直线为l ，证明直线l 经过一定点，并求出此定点的坐标．50．已知两定点()3,8A --，()10,4B 及两平行直线1:34100l x y ++=，2:34150l x y +-=，（1）求点()3,8A --关于点()10,4B 的对称点1A 的坐标；（2）求点()3,8A --关于直线1:34100l x y ++=的对称点2A 的坐标；（3）若点P ，Q 分别在直线1l ，2l 上，且1PQ l ⊥，求折线段APQB 的长度最短时直线PQ 的一般式方程． 51．已知()3,4P 为正方形ABCD 的中心(A ，B ，C ，D 逆时针排列)，AB 边所在直线方程为380x y +-=． （1）求对角线AC ，BD 所在直线的方程；（2）已知()6,4Q 是一个定点，(),0M t 是x 轴上一个动点，过点M 作直线MN ，满足MN 与MQ 斜率之和为零，且直线MN 与正方形ABCD 有公共点．①求出直线MN 分别过正方形各顶点时，M 点的坐标；②写出实数t 的最大值与最小值(不需要过程，直接写出答案即可)．【答案详解】1．B 【详解】直线8180x y +-=与x 轴的交点为904M ⎛⎫ ⎪⎝⎭，，直线460x y -+=与y 轴的交点为302N ⎛⎫⎪⎝⎭，，则MN ==如图所示：则由两点式可得直线MN 的方程为323924y x -=-，即4690x y +-=， 由4608180x y x y -+=⎧⎨+-=⎩解得22x y =⎧⎨=⎩，此为两直线的交点()22P ，， 根据点到直线的距离公式可得P 点到直线MN 的距离为d ===故OMNPMNOMPN S S S=+四边形19311524224=⨯⨯+=． 故选：B 2．A解：设三条直线交于一点P ，则直线2x =，10x y --=，交于点P ，联立210x x y =⎧⎨--=⎩，解得21x y =⎧⎨=⎩，即(2,1)P ，∴直线0x ky +=过点P ，即20k +=，2k ∴=-故选:A ． 3．A 【详解】联立24020x y x y -+=⎧⎨+-=⎩，解得(0,2)P ，直线l 与直线350x y ++=垂直，则直线直线l 的斜率为3l k =，所以直线l 的方程为()230y x -=-， 整理可得320x y -+=. 故选：A. 4．C 【详解】联立1020mx y m x y -+-=⎧⎨--=⎩，得11m x m --=-，∵直线1:10mx y l m -+-=与射线2:20(0)l x y x --=≥恒有公共点， ∴101m x m --=≥-， 解得11m -≤<.∴m 的取值范围是[)1,1-. 5．C 【详解】直线:10l x my m ++-=恒过的定点()1,1P -，4,13AP BP k k =-=.当0m =时，直线l 方程为1x =，与线段AB 有交点，符合题意. 当0m ≠时，直线l 的斜率为1m-，则[)14,1,3m ⎛⎤-∈-∞-⋃+∞ ⎥⎝⎦，解得10m -≤<或304m <≤，综上，31,4m ⎡⎤∈-⎢⎥⎣⎦.故选：C 6．C 【详解】直线20ax y -++=与线段AB 没有交点即直线2y ax =-与线段AB 没有交点对于直线2y ax =-, 令0x =,则2y =-,则直线恒过点()0,2C - 根据题意,作出如下图像: (0,2)C -,()2,3A -∴ 根据两点求斜率公式可得:直线AC 的斜率为32522AC k +==-- (0,2)C -,()3,2B∴ 根据两点求斜率公式可得:直线BC 的斜率为224303BC k +==- 直线20ax y -++=的斜率为a若直线20ax y -++=与线段AB 没有交点 则5423a -<<故选:C. 7．C 【详解】由440220x y x y --=⎧⎨--=⎩，得6747x y ⎧=⎪⎪⎨⎪=-⎪⎩，即直线0l 与1l 的交点坐标64,77A ⎛⎫- ⎪⎝⎭，由44043120x y x y --=⎧⎨+-=⎩，得322x y ⎧=⎪⎨⎪=⎩，即直线0l 与2l 的交点坐标3,22B ⎛⎫⎪⎝⎭，所以||AB ==. 故选：C 8．B 【详解】由已知，(6,6)AB =，(2,2)BC =-， ∴6(2)620AB BC ⋅=⨯-+⨯=，即AB BC ⊥， ∴ABC 是直角三角形. 故选：B. 9．C 【详解】因为||MN=2430m m -+=，解得1m =或3m =， 故选：C 10．C 【详解】点()1,1P 到直线:10l kx y -+=的距离d =当0k =时，0d =，当0k ≠时，d =，恒有2111k +>，于是得01d <<，综合得01d ≤<， 所以点P 到直线l 的距离的取值范围是[0,1). 故选：C11．C 【详解】直线BC 的方程为()1415y x -=--，即5210x y +-=. 由521010x y x y +-=⎧⎨-+=⎩解得811,33D ⎛⎫ ⎪⎝⎭.设()8,1,3A a a a +≠，直线,AB AC 的方程分别为()()3241,3616a a y x y x a a ---=--=--- ，即()()3131a x a y a ---+-，()()26360a x a y a -----=.根据角平分线的性质可知，D 到直线,AB AC 的距离相等，所以==83a ≠，所以上式可化为2得2803a a -=，解得0a =（83a ≠），所以()0,1A .所以()0,1A 到直线BC=，而BC =182ABC S ∆==. 故选：C 12．B 【详解】因为直线恒过定点4)0,A（， 则当PA 与直线垂直时﹐点P 到直线的距离达到最大值， 此时过P A 、的直线的斜率为2,-所以直线240ax y +-=的斜率为12，即122a -=，所以14a =-.故选：B ． 13．B 【详解】解：设点()1,2A 关于直线20x y +-=的对称点是(),B a b ， 则有211122022b a a b -⎧=⎪⎪-⎨++⎪+-=⎪⎩，解得0a =，1b =，故点()1,2关于直线20x y +-=的对称点是()0,1. 故选：B. 14．D 【详解】()4,2M ,()2,4N∴MN 的中点为(3,3)，42124MN k -==--，()4,2M 与()2,4N 关于直线l 对称，∴l 过点(3,3)，且斜率为1， ∴直线l 的方程为33y x -=-，即0x y -=， 故选：D 15．D 【详解】()60B ，，()04，C ，∴直线BC 的方程是164x y+=，即23120x y +-=， 光线经直线BC 反射后，恰好经过原点O ，∴原点O 关于直线BC 的对称点在入射光线上，设原点O 关于直线BC 的对称点是()00x y ，，则0000322312022y x x y ⎧=⎪⎪⎨⎪⨯+⨯-=⎪⎩，解得04813x =，07213y =，入射光线经过点()20A ，， ∴入射光线所在的直线的斜率为7236134811213k ==-，故选：D 16．B 【详解】 由12//l l 得32422112λλλ++-+=≠-，解得1λ=， 所以直线1l ：550x y +=，即0x y +=，所以1l 与2l 间的距离为d ==故选B ． 17．D 【详解】直线1l 的方程可化为6240x y --=，则1l 与2l 之间的距离d =． 故选：D 18．D设所求直线l 方程为：30x y c -+=，因为直线l 与1:330l x y -+=；2:310l x y --==1c =，所以所求直线方程为：310x y -+=， 故选：D. 19．D 【详解】由两直线垂直得24(5)0m ⋅+⨯-=， 解得10m =，所以原直线一可写为10420x y +-=， 又因为垂足为()1,p 同时满足两直线方程，所以代入得1014202150p p n ⨯+-=⎧⎨⨯-+=⎩，解得212p n =-⎧⎨=-⎩，所以-10-1220m n p +=+=， 故选:D 20．D联立方程组30y kx x y ⎧=⎪⎨+-=⎪⎩，解得x y =00>，解得1k <-， 设直线l 的倾斜角为θ，其中[0,)θπ∈，即tan 1θ<-，解得324ππθ<<，即直线l 的倾斜角的取值范围是3(,)24ππ.故选：D. 21．D 【详解】根据题意，平面上两点()A x x ，(2B ，0)，则222211||()2(44AB x x x =+=+，则有1||2AB ， 则||AB 的最小值为12， 故选：D. 22．C 【详解】将1n m =-代入直线方程，得(2)20x m y --+=，所以直线20mx y n -+=必过定点(2,2)，故点(1,1)到直线20mx y n -+=故选:C 23．C 【详解】直线20x y -+=交x 轴于点()2,0-，且直线20x y -+=的斜率为1， 故所求直线的方程为()2y x =-+，即20x y ++=. 故选：C. 24．D 【详解】()()0120A B ，，，，则AB ==设C 到AB 边所在直线的距离为d ，由ABC 的面积为5，得152d =，即d =∴顶点C 的轨迹是与AB 所在直线平行且与直线AB 距离为直线AB 的方程为121x y+=即220x y +-=，设点C 所在直线方程为20x y c ++=，=解得12c =-或8c =，∴点C 的轨迹方程为2120x y +-=或280x y ++=；故选：D 25．A由题意两直线平行，则112n=-，2n =-，又d =0m >，所以2m =． 所以0m n +=． 故选：A ． 26．B 【详解】设直线210x y ++=与直线2340x y c -+=的交点为A ，则2210340x y x y c ++=⎧⎨-+=⎩，解得2225310c x c y +⎧=-⎪⎪⎨-⎪=⎪⎩，故2223,510c c A +-⎛⎫- ⎪⎝⎭， 同理设直线210x y ++=与直线1340x y c -+=的交点为B ，则1123,510c c B +-⎛⎫- ⎪⎝⎭， 设直线230x y ++=与直线1340x y c -+=的交点为C ，则1169,510c c C +-⎛⎫- ⎪⎝⎭， 设直线230x y ++=与直线2340x y c -+=的交点为D ，则2269,510c c D +-⎛⎫- ⎪⎝⎭， 由菱形的性质可知BD AC ⊥,且,BD AC 的斜率均存在，所以1BD AC k k ⋅=-，则22222112393910101010126265555c c c c c c c c ------⋅=-++++-+--+-，即()()221221361416c c c c --=-⎡⎤--⎣⎦，解得12c c -=故选：B. 27．B 【详解】解：动直线0x my -=过定点()0,0A ，动直线30mx y m +-+=化为()130m x y -++=，令1030x y -=⎧⎨+=⎩，解得1x =，3y =-，故定点()1,3B -. 当0m =时，直线方程为0x =，30y +=，此时两直线垂直； 当0m ≠时，由两直线的斜率之积为()1211k k m m=⨯-=-可知两直线垂直， ∴PA PB ⊥，222||||10PA PB AB ∴+==， 故答案选：B. 28．C由题可知2=2m =，所以21A C +=．()11112·224222C A A C A C A C A C⎛⎫+=++=++≥ ⎪⎝⎭， 当且仅当2C A =，即14A =，12C =时，取等号．故选：C ． 29．B 【详解】设AC 的中点为D ，因为A （2，1），C (0，-1)，所以()1,0D ,所以AC 边上的中线长BD ==故选：B 30．D解：因为点(2,6)M 关于l ：30x y -+=的对称点为(3,5)M '， 所以反射光线M N '的方程为6270x y -+=. 故选：D. 31．C 【详解】解：设1:20l x y c -+=，1l 与2ld ∴==即|3|5c +=，得35c +=或35c +=-， 即2c =或8c =-，即线1l 的方程为220x y -+=或280x y --=， 故选：C ． 32．B 【详解】解：直线2l 与直线3l ：310x y +-=垂直，则231l l k k ⨯=-，即23l k =， ∵直线1l ：30ax y -+=与直线2l 关于直线l ：10x y +-=对称，∵由3010ax y x y -+=⎧⎨+-=⎩得2131x a a y a ⎧=-⎪⎪+⎨+⎪=⎪+⎩得交点坐标43,11a a a -⎛⎫- ⎪++⎝⎭， 在直线1l 上取点()0,3，设该点关于l 对称的点为()P m n ,，则()31022311m n n m+⎧+-=⎪⎪⎨-⎪⨯-=-⎪⎩，得2,1m n =-=，故23113221l a a k a +-+==-++，解得13a =，故选：B. 33．B 【详解】解：设A 关于直线y x =的对称点的坐标为,A a b '（），则212112122b a a b b a -⎧=-⎪=⎧⎪-⇒⎨⎨=++⎩⎪=⎪⎩， ∴PA PB +最小BA '= 故选：B 34．C 【详解】解：因为ABC 的顶点(4,0),(0,4),(2,0)A B C -，所以三角形的重心坐标为24,33⎛⎫- ⎪⎝⎭，AC 的中垂线方程为1x =-，1AB k =，AB 的中点坐标为()2,2-，所以AB 的中垂线方程为()212y x -=-+，即y x =-，所以三角形的外心为直线1x =-与y x =-的交点()1,1-，所以三角形的欧拉线方程为()()41311213y x --=+---，整理得20x y -+= 故选：C 35．B 【详解】直线1l ：240kx y k +--=，即()1240k x y -+-=， 令10x -=，求得1x =，2y =，可得该直线恒过点()1,2M . 直线2l ：1y x =-上有一动点P ，点N 的坐标为()4,6，故M 、N 都在直线2l ：1y x =-的上方．点()1,2M 关于直线2l ：1y x =-的对称点为()'3,0M ， 则'M N 直线方程为036043y x --=--，即618y x =-. 把'M N 直线方程和直线2l ：1y x =-联立方程组，求得175125x y ⎧=⎪⎪⎨⎪=⎪⎩，可得当PM PN +取得最小值时，点P 的坐标为1712,55⎛⎫⎪⎝⎭．故选：B 36．B 【详解】根据题意，可得M 的集合为与直线1l 和2l 距离都相等的直线， 则M 到原点的距离的最小值为原点到该直线的距离， 设点M 所在直线的方程为:0l x y m ++=，=|6||2|m m +=+，解得4m =-，可得:40l x y +-=， 所以M=故选：B. 37．AB 【详解】解：对于A ，当0x =时，2y =-，当0y =时，2x =，所以直线20x y --=与两坐标轴围成的三角形的面积为12222⨯⨯=，所以A 正确， 对于B ，设点(0,2)关于直线1y x =+的对称点为(,)m n ，则2122210n mn m +⎧=+⎪⎪⎨-⎪=-⎪-⎩，解得11m n =⎧⎨=⎩，所以点(0,2)关于直线1y x =+的对称点为(1,1)，所以B 正确，对于C ，当12x x =或12y y =时，不能利用两点式求直线方程，所以C 错误，对于D ，当直线的截距为零时，设直线方程为y kx =，则2k =，所以直线方程为20x y -=，当当直线的截距不为零时，设直线方程为1x ya a +=，则121a a+=，解得3a =，所以直线方程为30x y +-=，所以经过点(1,2)且在x 轴和y轴上截距都相等的直线方程为30x y +-=或20x y -=，所以D 错误， 故选：AB 38．BD【详解】设点P 的坐标为(,)a b ，线段AB 的中点M 的坐标为(3,2)-，31142AB k -+==--， ∴AB 的垂直平分线方程为23y x +=-，即50x y --=， ∵点(,)P a b 在直线50x y --=上，∴50a b --=， 又点(,)P a b 到直线l ：4320x y +-=的距离为2，2=，即43210a b +-=±， 联立可得1a =-、4b =-或277a =、87b =-，∴所求点P 的坐标为(1,4)-或278(,)77-， 故选：BD. 39．BD 【详解】 设直线:460l xy m ，2m ≠-且9m ，直线l 到直线1l 和2l 的距离分别为12,d d ， 由题知：121636m d ，291636m d ，因为1212d d =2916361636m m ， 即229m m ，解得5m =或133m =-， 即直线l 为4650x y ++=或1218130x y +-=。

高二春季数学“直线的交点坐标与距离公式”学生姓名授课日期教师姓名授课时长1. 掌握解方程组的方法，求两条相交直线的交点坐标.2. .掌握两点间距离公式，点到直线距离公式，会求两条平行直线间的距离.1直线的交点：求两直线与的交点坐标，只需求两直线方程联立所得方程组的解即可.若有，则方程组有无穷多个解，此时两直线重合；若有，则方程组无解，此时两直线平行；若有，则方程组有唯一解，此时两直线相交，此解即两直线交点的坐标.2两点间的距离公式两点间的距离公式为.3点到直线的距离公式点到直线的距离为.两平行线间的距离本类问题常见的有两种解法：①转化为点到直线的距离问题，在任一条直线上任取一点，此点到另一条直线的距离即为两直线之间的距离；②距离公式：直线与直线的距离为.注意：1)两条平行线间的距离，可以看作在其中一条直线上任取一点，这个点到另一条直线的距离，此点一般可以取直线上的特殊点，也可以看作是两条直线上各取一点，这两点间的最短距离；(2)利用两条平行直线间的距离公式时，一定先将两直线方程化为一般形式，且两条直线中x ，y 的系数要保持一致.【试题来源】【题目】求过直线l 1：x －2y ＋3＝0与直线l 2：2x ＋3y －8＝0的交点，且到点P (0,4)的距离为2的直线方程．【难度系数】3【试题来源】【题目】已知直线l ：3x －y ＋3＝0，求：(1)点P (4,5)关于l 的对称点；(2)直线x －y －2＝0关于直线l 对称的直线方程．【难度系数】3【试题来源】【题目】已知直线l 经过直线2x ＋y －5＝0与x －2y ＝0的交点，(1)点A (5,0)到l 的距离为3，求l 的方程；(2)求点A (5,0)到l 的距离的最大值．【难度系数】3【试题来源】【题目】两条平行线l 1：3x ＋4y ＋c 1＝0，l 2：6x ＋8y ＋c 2＝0之间的距离是 () A ．d ＝|c 1－c 2|5 B ．d ＝|2c 1－c 2|10C ．d ＝|2c 1－c 2|5 D ．以上皆非【难度系数】3【试题来源】【题目】当0＜k ＜12时，直线l 1：kx －y ＝k －1与直线l 2：ky －x ＝2k 的交点在() A ．第一象限 B ．第二象限C ．第三象限D ．第四象限【难度系数】3【试题来源】2009·哈尔滨模拟【题目】若k ，－1，b 三个数成等差数列，则直线y ＝kx ＋b 必经过定点( )A ．(1，－2)B ．(1,2)C ．(－1,2)D ．(－1，－2)【难度系数】3【试题来源】【题目】直线y ＝2x ＋10，y ＝x ＋1，y ＝ax －2交于一点，则a 的值为 ( )A.13B.43C.23D.53【难度系数】3【试题来源】【题目】点P (m －n ，－m )到直线x m ＋y n＝1的距离等于 ( )A.m 2＋n 2B.m 2－n 2C.－m 2＋n 2D.m 2±n 2【难度系数】3【试题来源】2009·海淀模拟【题目】若直线l 1：y ＝k (x －4)与直线l 2关于点(2,1)对称，则直线l 2恒过定点 ( )A ．(0,4)B ．(0,2)C ．(－2,4)D ．(4，－2)【难度系数】3【试题来源】【题目】若两平行直线3x －2y －1＝0,6x ＋ay ＋c ＝0之间的距离为21313，则c ＋2a的值为______． 【适用场合】课后练习题【难度系数】3【试题来源】【题目】直线3x －4y －27＝0上到点P (2,1)距离最近的点的坐标是________．【难度系数】3【试题来源】【题目】与直线x －y －2＝0平行，且它们的距离为22的直线方程是________________．【难度系数】3。