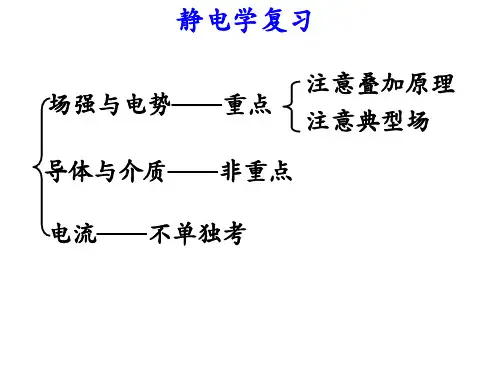
大学物理——静电场公式
- 格式:ppt
- 大小:714.00 KB
- 文档页数:6

大学物理复习第四章知识点总结大学物理复习第四章知识点总结一.静电场:1.真空中的静电场库仑定律→电场强度→电场线→电通量→真空中的高斯定理qq⑴库仑定律公式:Fk122err适用范围:真空中静止的两个点电荷F⑵电场强度定义式:Eqo⑶电场线:是引入描述电场强度分布的曲线。
曲线上任一点的切线方向表示该点的场强方向,曲线疏密表示场强的大小。
静电场电场线性质:电场线起于正电荷或无穷远,止于负电荷或无穷远,不闭合,在没有电荷的地方不中断,任意两条电场线不相交。
⑷电通量:通过任一闭合曲面S的电通量为eSdS方向为外法线方向1EdS⑸真空中的高斯定理:eSoEdSqi1int只能适用于高度对称性的问题:球对称、轴对称、面对称应用举例:球对称:0均匀带电的球面EQ4r20(rR)(rR)均匀带电的球体Qr40R3EQ240r(rR)(rR)轴对称:无限长均匀带电线E2or0(rR)无限长均匀带电圆柱面E(rR)20r面对称:无限大均匀带电平面EE⑹安培环路定理:dl0l2o★重点:电场强度、电势的计算电场强度的计算方法:①点电荷场强公式+场强叠加原理②高斯定理电势的计算方法:①电势的定义式②点电荷电势公式+电势叠加原理电势的定义式:UAAPEdl(UP0)B电势差的定义式:UABUAUBA电势能:WpqoPP0EdlEdl(WP00)2.有导体存在时的静电场导体静电平衡条件→导体静电平衡时电荷分布→空腔导体静电平衡时电荷分布⑴导体静电平衡条件:Ⅰ.导体内部处处场强为零,即为等势体。
Ⅱ.导体表面紧邻处的电场强度垂直于导体表面,即导体表面是等势面⑵导体静电平衡时电荷分布:在导体的表面⑶空腔导体静电平衡时电荷分布:Ⅰ.空腔无电荷时的分布:只分布在导体外表面上。
Ⅱ.空腔有电荷时的分布(空腔本身不带电,内部放一个带电量为q的点电荷):静电平衡时,空腔内表面带-q电荷,空腔外表面带+q。
3.有电介质存在时的静电场⑴电场中放入相对介电常量为r电介质,电介质中的场强为:E⑵有电介质存在时的高斯定理:SDdSq0,intE0r各项同性的均匀介质D0rE⑶电容器内充满相对介电常量为r的电介质后,电容为CrC0★重点:静电场的能量计算①电容:②孤立导体的电容C4R电容器的电容公式C0QQUUU举例:平行板电容器C圆柱形电容器C4oR1R2os球形电容器CR2R1d2oLR2ln()R1Q211QUC(U)2③电容器储能公式We2C22④静电场的能量公式WewedVE2dVVV12二.静磁场:1.真空中的静磁场磁感应强度→磁感应线→磁通量→磁场的高斯定理⑴磁感应强度:大小BF方向:小磁针的N极指向的方向qvsin⑵磁感应线:是引入描述磁感应强度分布的曲线。

第四章 电 场一、常见带电体的场强、电势分布2)均匀带电球面(球面半径 )的电场:3)无限长均匀带电直线(电荷线密度为): E = ,方向:垂直于带电直线。
2r( rR ) 4)无限长均匀带电圆柱面(电荷线密度为):E =2r (rR )5)无限大均匀带电平面(电荷面密度为)的电场: E =/20 ,方向:垂直于平面。
二、静电场定理 1、高斯定理:e = ÑE v dS v = q 静电场是有源场。
Sq 指高斯面内所包含电量的代数和;E 指高斯面上各处的电场强度,由高斯面内外的全 部电荷产生; Ñ E vdS v 指通过高斯面的电通量,由高斯面内的电荷决定。
2、环路定理: Ñ E v dl v =0 静电场是保守场、电场力是保守力,可引入电势能三、求场强两种方法1、利用场强势叠加原理求场强 分离电荷系统: E v = E v i ;连续电荷系统: E v = dE v i =12、利用高斯定理求场强 四、求电势的两种方法n1、利用电势叠加原理求电势 分离电荷系统:U =U i ;连续电荷系统: U = dU i =1电势零点v v 2、利用电势的定义求电势 U =电势零点Edl五、应用vv b点电荷受力: F = qE电势差: U ab =U a -U b = b EdraE =1 qU =q4r 24r1)点电荷:E =0 (rR ) q2 (rR ) 4r 2U =q (r R ) 4r q (r R ) 4Ra 点电势能:W a = qU a由 a 到 b 电场力做功等于电势能增量的负值 A ab = -W = -(W b -W a )六、导体周围的电场1、静电平衡的充要条件: 1)、导体内的合场强为 0,导体是一个等势体。
2)、导体表面的场强处处垂直于导体表面。
E v ⊥表面。
导体表面是等势面。
2、静电平衡时导体上电荷分布: 1)实心导体: 净电荷都分布在导体外表面上。


大学物理电磁学知识点总结篇一:大学物理电磁学知识点总结大学物理电磁学总结一、三大定律库仑定律:在真空中,两个静止的点电荷q1和q2之间的静电相互作用力与这两个点电荷所带电荷量的乘积成正比,与它们之间距离的平方成反比,作用力的方向沿着两个点电荷的连线,同号电荷相斥,异号电荷相吸。
uuurqqurF21=k122errurur高斯定理:a)静电场:Φe=EdS=∫s∑qiiε0(真空中)b)稳恒磁场:Φm=uurrBdS=0∫s环路定理:a)静电场的环路定理:b)安培环路定理:二、对比总结电与磁∫LurrLEdl=0∫urrBdl=0∑Ii(真空中)L电磁学静电场稳恒磁场稳恒磁场电场强度:E磁感应强度:B定义:B=ururF定义:E=(N/C)q0基本计算方法:1、点电荷电场强度:E=urrurdF(dF=Idl×B)(T)Idlsinθ方向:沿该点处静止小磁针的N极指向。
基本计算方法:urqurer4πε0r21ruruIdl×er0r1、毕奥-萨伐尔定律:dB=24πr2、连续分布的电流元的磁场强度:2、电场强度叠加原理:urnur1E=∑Ei=4πε0i=1rqiuueri∑r2i=1inrururur0Idl×erB=∫dB=∫4πr23、安培环路定理(后面介绍)4、通过磁通量解得(后面介绍) 3、连续分布电荷的电场强度:urρdVurE=∫ev4πεr2r0urdSururλdlurE=∫er,E=∫es4πεr2l4πεr2r004、高斯定理(后面介绍)5、通过电势解得(后面介绍)几种常见的带电体的电场强度公式:几种常见的磁感应强度公式:1、无限长直载流导线外:B=2、圆电流圆心处:电流轴线上:B=ur1、点电荷:E=qurer4πε0r210I2R0I2πr2、均匀带电圆环轴线上一点:urE=B=3、圆rqxi22324πε0(R+x)R2IN2(x2+R2)3210α23、均匀带电无限大平面:E=2ε0(N为线圈匝数)4、无限大均匀载流平面:B=4、均匀带电球壳:E=0(r<R)(α是流过单位宽度的电流)urE=qurer(r>R)4πε0r25、无限长密绕直螺线管内部:B=0nI(n是单位长度上的线圈匝数)6、一段载流圆弧线在圆心处:B=(是弧度角,以弧度为单位)7、圆盘圆心处:B=rurqr(rR)20I4πR0ωR2(是圆盘电荷面密度,ω圆盘转动的角速度)6、无限长直导线:E=λ2πε0xλ0(r>R)2πε0r7、无限长直圆柱体:E=E=λr(r<R)4πε0R2电场强度通量:N·m2·c-1)(磁通量:wb)(sΦe=∫dΦe=∫EcosθdS=∫ssururEdS通量uurrΦm=∫dΦm=∫BdS=∫BcosθdSsss若为闭合曲面:Φe=∫sururEdS若为闭合曲面:uurrΦm=BdS=BcosθdS∫∫ss均匀电场通过闭合曲面的通量为零。

物理电场公式大全电场是物理学中的一个重要概念,它描述了电荷之间相互作用的力场。
在现代科学和工程中,电场理论被广泛应用于各种领域,包括电子学、电力系统、通讯工程等。
本文将为您详细介绍物理电场的相关公式,帮助您更好地理解和应用电场理论。
1. 电场强度公式。
电场强度描述了单位正电荷在电场中所受到的力。
在真空中,电场强度E与电荷Q之间的关系可以用以下公式表示:E = k Q / r^2。
其中,E为电场强度,k为电场常数(8.9910^9 N·m^2/C^2),Q为电荷量,r 为距离。
2. 电场能量密度公式。
电场能量密度表示单位体积内的电场能量。
在电场强度为E的情况下,电场能量密度u可以用以下公式表示:u = 0.5 ε E^2。
其中,ε为介质的介电常数。
3. 静电势能公式。
静电势能表示电荷在电场中由于位置而具有的能量。
当电荷Q在电场中移动时,它的静电势能U可以用以下公式表示:U = k (Q1 Q2) / r。
其中,U为静电势能,Q1和Q2分别为两个电荷的大小,r为它们之间的距离。
4. 电场中的电势公式。
电势描述了单位正电荷在电场中所具有的势能。
在电场强度为E的情况下,电势V可以用以下公式表示:V = k Q / r。
其中,V为电势,其他符号的含义同上。
5. 电场中的电势能公式。
电场中的电势能可以用电势和电荷量来表示。
在电势为V的情况下,电场中的电势能可以用以下公式表示:U = Q V。
以上是物理电场中常见的几个重要公式,它们描述了电场强度、能量密度、势能、电势等重要物理量之间的关系。
通过这些公式,我们可以更好地理解电场的特性,并在实际应用中进行计算和分析。
在工程技术领域,电场理论被广泛应用于电力系统的设计与分析、电子电路的研究与开发、电磁场的模拟与优化等方面。
掌握电场公式,对于工程技术人员来说是非常重要的,它可以帮助他们更好地理解和应用电场理论,提高工作效率和解决问题的能力。
总之,物理电场公式是电场理论的重要组成部分,它们描述了电荷之间相互作用的规律,是现代科学和工程技术中不可或缺的重要知识。


第七章、静 电 场一、大体概念 1、电场 (1)、电荷在周围空间激发电场,电荷之间的彼此作用是通过电场传递的。
电场对身处其中的电荷有力的作用(2)库伦定律 沿连线方向,同号相斥,异号相吸2、电场强度⑴、 实验电荷在电场中不同点所受电场力的大小、方向都可能不同;而在 同一点,电场力的大小与实验电荷电量成正比,若实验电荷异号,则所受电场力的方向相反。
咱们就用qF来表示电场中某点的电场强度,用E 表示,即qF E =⑵、点电荷的电场强度以点电荷Q 所在处为原点O,任取一点P(场点),点O 到点P 的位矢为r,把试验电荷q 放在P 点,有库仑定律可知,所受电场力为:r Qq F E 2041επ==⑶常见电场公式无穷大均匀带电板周围电场:εσ02=E3、电势⑴、电场中给定的电势能的大小除与电场本身的性质有关外,还与查验电荷有关,而比值qE pa 0则与电荷的大小和正负无关,它反映了静电场中某给定点的性质。
为此咱们用一个物理量-电势来反映那个性质。
即qE p V 0=⑶常见电势公式 点电荷电势散布:rq V επ04=半径为R 的均匀带点球面电势散布:Rq V επ04=()R r ≤≤0rq V επ04=()R r ≥221r qq k F =二、定理1、场强叠加定理点电荷系所激发的电场中某点处的电场强度等于各个点电荷单独存在时对 该点的电场强度的矢量和。
即E E E n E +++= (21)2、电势叠加定理V 1 、V 2 ...V n 别离为各点电荷单独存在时在P 点的电势点电荷系的电场中,某点的电势等于各点电荷单独 存在时在该点电势的代数和。
3、高斯定理在真空中的静电场内,通过任意封锁曲面的电通量等于该闭合曲面包围的所有电荷的代数和除以ε说明:①高斯定理是反映静电场性质的一条大体定理。
②通过任意闭合曲面的电通量只取决于它所包围的电荷的代数和。
③高斯定理中所说的闭合曲面,通常称为高斯面。
三、静电平衡1、静电平衡当一带电体系中的电荷静止不动,从而电场散布不随时刻转变时,带电 体系即达到了静电平衡。

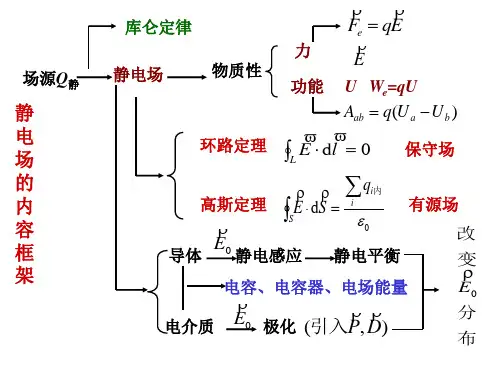
大学物理电磁学总结电磁学部分总结静电场部分第一部分:静电场的基本性质和规律电场是物质的一种存在形态,它同实物一样也具有能量、动量、质量等属性。
静电场的物质特性的外在表现是:(1)电场对位于其中的任何带电体都有电场力的作用(2)带电体在电场中运动, 电场力要作功——电场具有能量1、描述静电场性质的基本物理量是场强和电势,掌握定义及二者间的关系。
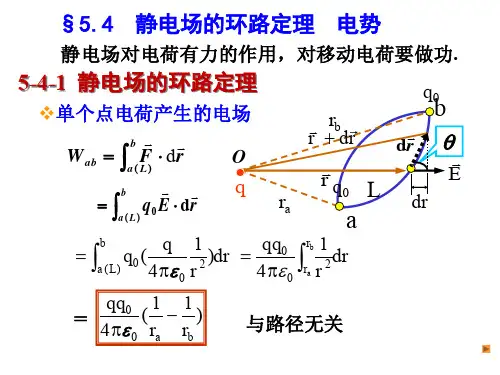
电场强度 E =q 0∞ W a 电势 U a ==E ⋅d rq 0a2、反映静电场基本性质的两条定理是高斯定理和环路定理Φe =E ⋅d S =ε0∑qL E ⋅d r =0要掌握各个定理的内容,所揭示的静电场的性质,明确定理中各个物理量的含义及影响各个量的因素。
重点是高斯定理的理解和应用。
3、应用(1)、电场强度的计算1q E =r 02a) 、由点电荷场强公式 4πεr 及场强叠加原理 E = ∑ E 计i 0算场强一、离散分布的点电荷系的场强1q i E =∑E i =∑r 2i 0i i 4πεr 0i二、连续分布带电体的场强 d q E =⎰d E =⎰r 204πε0r其中,重点掌握电荷呈线分布的带电体问题b) 、由静电场中的高斯定理计算场源分布具有高度对称性的带电体的场强分布一般诸如球对称分布、轴对称分布和面对称分布,步骤及例题详见课堂笔记。
还有可能结合电势的计算一起进行。
c) 、由场强和电势梯度之间的关系来计算场强(适用于电势容易计算或电势分布已知的情形),掌握作业及课堂练习的类型即可。
(2)、电通量的计算a) 、均匀电场中S 与电场强度方向垂直b) 、均匀电场,S 法线方向与电场强度方向成θ角E =-gradU =-∇U∂U ∂U ∂U =-(i +j +k )∂x ∂y ∂zc) 、由高斯定理求某些电通量(3)、电势的计算a) 、场强积分法(定义法)——计算U P =⎰E ⋅d rb) 、电势叠加法——q i ⎰电势叠加原理计算⎰∑U i =∑4πεr⎰0iU =⎰dq ⎰dU =⎰⎰⎰4πε0r ⎰第二部分:静电场中的导体和电介质一、导体的静电平衡状态和条件导体内部和表面都没有电荷作宏观定向运动的状态称为静电平衡状态。
大学物理(电磁学)参考公式第一章:一段带电直棒中垂线上一点的场强: 21220)4(4L x x LE +=πελ均匀带电细圆环轴线上任一点场强: 23220)(4x R qxE +=πε 电偶极子在匀强电场中所受的力矩:E P M ϖϖρ⨯= 高斯定理:∑⎰=⋅=Φint1qS d E e εϖρ第三章:静电场的环路定理:0d =⋅⎰Lr E ϖϖ; 电势的定义: ⎰⋅=0d P Pr E ϖϖϕ 均匀带电圆环轴线上一点的电势: 2/1220)(4x R q+=πεϕ 静电场的能量: ⎰⎰==VVeV E V w W d 2d 2ε移动电荷时电场力做功: 212112)(W W q A -=-=ϕϕ第五章:各向同性电介质中的电极化强度与电场强度的关系:()E P r ρρ10-=εε 电介质表面的面束缚电荷密度:n e P P ρρ⋅=='θσcos电介质中封闭面内的体束缚电荷:intq P ds '=-⋅⎰v v Ñ 电位移矢量:0D E P ε=+v v v电位移矢量D ρ的高斯定理:∑⎰=⋅int 0q s d D s ρρ 平行板电容器的电容:dSC r εε0=圆柱形电容器的电容:()120ln 2R R L C r επε=球形电容器的电容:122104R R R R C r -=επε电容器并联:∑=i C C 电容器串联:∑=iC C 11 电容器的能量:QU CU C Q W 21212122=== 静电场的总能量:dV E dV W e ⎰⎰==22εω 第七章: 一个运动电荷在另外的运动电荷周围所受的力 B v q E q F ϖϖϖϖ⨯+=霍尔电压 nqbIBU H =载流导线L 在磁场中受的力 ⎰⨯=L B l Id F ϖϖϖ载流线圈在均匀磁场中受的力矩 B e SI B m M n ϖϖϖωϖ⨯=⨯=线圈磁矩在磁场中的势能 B m W m ϖϖ⋅-=第八章:电流元产生的磁场(毕-萨定律)024r Idl e dB rμπ⨯=v vv磁通连续定理 ⎰=⋅S S d B 0ϖϖ 直线电流的磁场 ()210cos cos 4θθπμ-rIB =圆电流轴线上的磁场 ()2322202x R IR B +=μ载流直螺线管轴线上的磁场 ()120cos cos 2θθμ-=nIB运动电荷产生的磁场 204r e v q B rϖϖϖ⨯=πμ 安培环路定理⎰∑=⋅LI r d B int 0μϖϖ推广的安培环路定理 ⎰⎰⎰⋅⎪⎪⎭⎫ ⎝⎛∂∂+=⎪⎭⎫ ⎝⎛⋅+=⋅S c L s c S d t E J S d E dt d I r d B ϖϖϖϖϖϖϖ0000εμεμ 第九章:磁化强度 r 01M rB μμμ-r r= 磁化电流密度n j M e '=⨯r v r磁场强度 00BrB H M μμμ-v vr v == H 的环路定理0int LH dr I ⋅=∑⎰v vÑ第十章: 法拉第电磁感应定律: 动生电动势:感生电场:互感系数:211212M i i ψψ==互感电动势: 两个载流线圈的总磁能:自感系数:L Iψ=自感电动势:L d dI L dt dt εψ=-=- 自感磁能: 磁场能量密度: (非铁磁质) 磁场总磁能: (非铁磁质)d dtεΦ=-()bb ab ne aaE dl v B dlε=⋅=⨯⋅⎰⎰r r r r rd d d d LSd E l B s dt t εΦ=⋅=-==-⋅⎰⎰r r r rÑ感感1221212d dIM dt dtεψ=-=-2112121d dI M dt dtεψ=-=-212m WLI =221122121122m W L I L I M I I =++2122m B BH ωμ==12m m VVW dV BHdVω==⎰⎰。
第四章 电 场一、常见带电体的场强、电势分布 1)点电荷:2014q E r πε=04q U rπε=2)均匀带电球面(球面半径R )的电场:200()()4r R E qr R r πε≤⎧⎪=⎨>⎪⎩00()4()4qr R r U q r R R πεπε⎧>⎪⎪=⎨⎪≤⎪⎩3)无限长均匀带电直线(电荷线密度为λ):02E rλπε=,方向:垂直于带电直线。
4)无限长均匀带电圆柱面(电荷线密度为λ): 00()()2r R E r R rλπε≤⎧⎪=⎨>⎪⎩5)无限大均匀带电平面(电荷面密度为σ)的电场:0/2E σε=,方向:垂直于平面。
二、静电场定理 1、高斯定理:0e Sq E dS φε=⋅=∑⎰静电场是有源场。
q ∑指高斯面内所包含电量的代数和;E指高斯面上各处的电场强度,由高斯面内外的全部电荷产生;SE dS ⋅⎰指通过高斯面的电通量,由高斯面内的电荷决定。
2、环路定理:0lE dl⋅=⎰ 静电场是保守场、电场力是保守力,可引入电势能三、求场强两种方法1、利用场强势叠加原理求场强 分离电荷系统:1ni i E E ==∑;连续电荷系统:E dE =⎰2、利用高斯定理求场强 四、求电势的两种方法1、利用电势叠加原理求电势 分离电荷系统:1nii U U==∑;连续电荷系统: U dU =⎰2、利用电势的定义求电势 rU E dl =⋅⎰电势零点五、应用点电荷受力:F qE = 电势差: bab a b aU U U E dr =-=⋅⎰a由a 到b六、导体周围的电场1、静电平衡的充要条件: 1)、导体内的合场强为0,导体是一个等势体。
2)、导体表面的场强处处垂直于导体表面。
E ⊥表表面。
导体表面是等势面。
2、静电平衡时导体上电荷分布: 1)实心导体: 净电荷都分布在导体外表面上。
2)导体腔内无电荷: 电荷都分布在导体外表面,空腔内表面无电荷。
3)导体腔内有电荷+q ,导体电量为Q :静电平衡时,腔内表面有感应电荷-q ,外表面有电荷Q +q 。
普通物理学教程——大学物理电磁学公式总结(各种归纳差不多都一样)➢第一章(静止电荷的电场)1.电荷的基本性质:两种电荷,量子性,电荷守恒,相对论不变性。
2.库仑定律:两个静止的点电荷之间的作用力F ==3.电力叠加原理:F=ΣF i4.电场强度:E=,为静止电荷5.场强叠加原理:E=ΣE i用叠加法求电荷系的静电场:E=(离散型)E=(连续型)6.电通量:Φe=7.高斯定律:=Σq int8.典型静电场:1)均匀带电球面:E=0 (球面内)E=(球面外)2)均匀带电球体:E==(球体内)E=(球体外)3)均匀带电无限长直线:E=,方向垂直于带电直线4)均匀带电无限大平面:E=,方向垂直于带电平面9.电偶极子在电场中受到的力矩:M=p×E➢第三章(电势)1.静电场是保守场:=02.电势差:φ1–φ2=电势:φp=(P0是电势零点)电势叠加原理:φ=Σφi3.点电荷的电势:φ=电荷连续分布的带电体的电势:φ=4.电场强度E与电势φ的关系的微分形式:E=-gradφ=-▽φ=-(i+j+k)电场线处处与等势面垂直,并指向电势降低的方向;电场线密处等势面间距小。
5.电荷在外电场中的电势能:W=qφ移动电荷时电场力做的功:A12=q(φ1–φ2)=W1-W2电偶极子在外电场中的电势能:W=-p•E➢第四章(静电场中的导体)1.导体的静电平衡条件:E int=0,表面外紧邻处Es⊥表面或导体是个等势体。
2.静电平衡的导体上电荷的分布:Q int=0,σ=ε0E3.计算有导体存在时的静电场分布问题的基本依据:高斯定律,电势概念,电荷守恒,导体经典平衡条件。
4.静电屏蔽:金属空壳的外表面上及壳外的电荷在壳内的合场强总为零,因而对壳内无影响。
➢第五章(静电场中的电介质)1.电介质分子的电距:极性分子有固有电距,非极性分子在外电场中产生感生电距。
2.电介质的极化:在外电场中固有电距的取向或感生电距的产生使电介质的表面(或内部)出现束缚电荷。