一次函数难题练习【含解析】

最新初中数学一次函数难题汇编及答案解析一、选择题1．关于一次函数y=3x+m ﹣2的图象与性质，下列说法中不正确的是（ ） A ．y 随x 的增大而增大B ．当m≠2时，该图象与函数y=3x 的图象是两条平行线C ．若图象不经过第四象限，则m ＞2D ．不论m 取何值，图象都经过第一、三象限【答案】C【解析】【分析】根据一次函数的增减性判断A ；根据两条直线平行时，k 值相同而b 值不相同判断B ；根据一次函数图象与系数的关系判断C 、D ．【详解】A 、一次函数y=3x+m ﹣2中，∵k=3＞0，∴y 随x 的增大而增大，故本选项正确；B 、当m≠2时，m ﹣2≠0，一次函数y=3x+m ﹣2与y=3x 的图象是两条平行线，故本选项正确；C 、若图象不经过第四象限，则经过第一、三象限或第一、二、三象限，所以m ﹣2≥0，即m≥2，故本选项错误；D 、一次函数y=3x+m ﹣2中，∵k=3＞0，∴不论m 取何值，图象都经过第一、三象限，故本选项正确．故选：C ．【点睛】本题考查了两条直线的平行问题：若直线y 1=k 1x+b 1与直线y 2=k 2x+b 2平行，那么k 1=k 2，b 1≠b 2．也考查了一次函数的增减性以及一次函数图象与系数的关系．2．一次函数y x 1=-+的图象不经过的象限是( )A ．第一象限B ．第二象限C ．第三象限D ．第四象限【答案】C【解析】【分析】先根据一次函数y x 1=-+中k 1=-，b 1=判断出函数图象经过的象限，进而可得出结论．【详解】解：Q 一次函数y x 1=-+中k 10=-<，b 10=>， ∴此函数的图象经过一、二、四象限，不经过第三象限．故答案选：C ．【点睛】本题考查的是一次函数的性质，即一次函数()y kx b k 0=+≠中，当k 0<，b 0>时，函数图象经过一、二、四象限．3．如图，一次函数y ＝﹣x +4的图象与两坐标轴分别交于A 、B 两点，点C 是线段AB 上一动点（不与点A 、B 重合），过点C 分别作CD 、CE 垂直于x 轴、y 轴于点D 、E ，当点C 从点A 出发向点B 运动时，矩形CDOE 的周长（ ）A ．逐渐变大B ．不变C ．逐渐变小D ．先变小后变大【答案】B【解析】【分析】 根据一次函数图象上点的坐标特征可设出点C 的坐标为(m ，-m+4)(0<m<4)，根据矩形的周长公式即可得出C 矩形CDOE =8，此题得解．【详解】解：设点C 的坐标为(m ，-m+4)(0＜m ＜4)，则CE=m ，CD=-m+4，∴C 矩形CDOE =2(CE+CD)=8．故选B ．【点睛】本题考查了一次函数图象上点的坐标特征以及矩形的性质，根据一次函数图象上点的坐标特征设出点C 的坐标是解题的关键．4．如图，四边形ABCD 的顶点坐标分别为()()()()4,0,2,1,3,0,0,3A B C D ---，当过点B 的直线l 将四边形ABCD 分成面积相等的两部分时，直线l 所表示的函数表达式为（ ）A ．116105y x =+B ．2133y x =+C ．1y x =+D ．5342y x =+ 【答案】D【解析】【分析】由已知点可求四边形ABCD 分成面积()113741422B AC y =⨯⨯+=⨯⨯=；求出CD 的直线解析式为y=-x+3，设过B 的直线l 为y=kx+b ，并求出两条直线的交点，直线l 与x 轴的交点坐标，根据面积有1125173121k k k k --⎛⎫⎛⎫=⨯-⨯+ ⎪ ⎪+⎝⎭⎝⎭，即可求k 。

一次函数难题汇编及答案解析一、选择题1．一次函数y mx n =-+结果是( )A ．mB ．m -C ．2m n -D ．2m n -【答案】D【解析】【分析】根据题意可得﹣m ＜0，n ＜0，再进行化简即可．【详解】∵一次函数y ＝﹣mx +n 的图象经过第二、三、四象限，∴﹣m ＜0，n ＜0，即m ＞0，n ＜0，＝|m ﹣n |+|n |＝m ﹣n ﹣n＝m ﹣2n ，故选D ．【点睛】本题考查了二次根式的性质与化简以及一次函数的图象与系数的关系，熟练掌握一次函数的图象与性质是解题的关键.2．给出下列函数：①y ＝﹣3x +2：②y ＝3x ；③y ＝﹣5x：④y ＝3x ，上述函数中符合条件“当x ＞1时，函数值y 随自变量x 增大而增大”的是（ ） A ．①③B ．③④C ．②④D ．②③ 【答案】B【解析】【分析】分别利用一次函数、正比例函数、反比例函数的增减性分析得出答案．【详解】解：①y ＝﹣3x +2，当x ＞1时，函数值y 随自变量x 增大而减小，故此选项不符合题意； ②y ＝3x，当x ＞1时，函数值y 随自变量x 增大而减小，故此选项不符合题意； ③y ＝﹣5x，当x ＞1时，函数值y 随自变量x 增大而增大，故此选项符合题意； ④y ＝3x ，当x ＞1时，函数值y 随自变量x 增大而增大，故此选项符合题意； 故选：B ．【点睛】此题考查一次函数、正比例函数、反比例函数，正确把握相关性质是解题关键．3．一次函数y=ax+b与反比例函数a byx-=，其中ab＜0，a、b为常数，它们在同一坐标系中的图象可以是（）A．B．C．D．【答案】C【解析】【分析】根据一次函数的位置确定a、b的大小，看是否符合ab<0，计算a-b确定符号，确定双曲线的位置．【详解】A. 由一次函数图象过一、三象限，得a>0，交y轴负半轴，则b<0，满足ab<0，∴a−b>0，∴反比例函数y=a bx-的图象过一、三象限，所以此选项不正确；B. 由一次函数图象过二、四象限，得a<0，交y轴正半轴，则b>0，满足ab<0，∴a−b<0，∴反比例函数y=a bx-的图象过二、四象限，所以此选项不正确；C. 由一次函数图象过一、三象限，得a>0，交y 轴负半轴，则b<0，满足ab<0，∴a −b>0，∴反比例函数y=a b x-的图象过一、三象限， 所以此选项正确； D. 由一次函数图象过二、四象限，得a<0，交y 轴负半轴，则b<0，满足ab>0，与已知相矛盾所以此选项不正确；故选C.【点睛】 此题考查反比例函数的图象，一次函数的图象，解题关键在于确定a 、b 的大小4．如图，已知一次函数22y x =-+的图象与坐标轴分别交于A 、B 两点，⊙O 的半径为1，P 是线段AB 上的一个点，过点P 作⊙O 的切线PM ，切点为M ，则PM 的最小值为（ ）A ．2B 2C 5D 3【答案】D【解析】【分析】【详解】 解：连结OM 、OP ，作OH ⊥AB 于H ，如图，先利用坐标轴上点的坐标特征：当x=0时，y=﹣22，则A （0，2），当y=0时，﹣2=0，解得2，则B （2，0），所以△OAB 为等腰直角三角形，则2OA=4，OH=12AB=2， 根据切线的性质由PM 为切线，得到OM ⊥PM ，利用勾股定理得到22OP OM -21OP -当OP 的长最小时，PM 的长最小，而OP=OH=2时，OP 的长最小，所以PM 的最小值为2213-=【点睛】本题考查切线的性质；一次函数图象上点的坐标特征．5．在平面直角坐标系中，一次函数y=kx+b的图象如图所示，则k和b的取值范围是（）A．k＞0，b＞0 B．k＞0，b＜0 C．k＜0，b＞0 D．k＜0，b＜0【答案】C【解析】【分析】根据一次函数的图象与系数的关系进行解答即可．【详解】∵一次函数y=kx+b的图象经过一、二、四象限，∴k＜0，b＞0，故选C．【点睛】本题考查的是一次函数的图象与系数的关系，即一次函数y=kx+b（k≠0）中，当k ＜0，b＞0时图象在一、二、四象限．6．一次函数y=kx+b(k<0，b>0)的图象可能是（）A． B． C．D．【解析】【分析】根据k 、b 的符号来求确定一次函数y=kx+b 的图象所经过的象限．【详解】∵k<0，∴一次函数y=kx+b 的图象经过第二、四象限．又∵b ＞0时，∴一次函数y=kx+b 的图象与y 轴交与正半轴．综上所述，该一次函数图象经过第一象限．故答案为：C.【点睛】考查一次函数图象在坐标平面内的位置与k 、b 的关系．解答本题注意理解：直线y=kx+b 所在的位置与k 、b 的符号有直接的关系．k ＞0时，直线必经过一、三象限．k ＜0时，直线必经过二、四象限．b ＞0时，直线与y 轴正半轴相交．b=0时，直线过原点；b ＜0时，直线与y 轴负半轴相交．7．若点()11,x y ，()22,x y ，()33,x y 都是一次函数1y x =--图象上的点，并且123y y y <<，则下列各式中正确的是（ ）A ．123x x x <<B ．132x x x <<C ．213x x x <<D ．321x x x <<【答案】D【解析】【分析】根据一次函数的性质即可得答案．【详解】∵一次函数1y x =--中10k =-<，∴y 随x 的增大而减小，∵123y y y <<，∴123x x x >>．故选：D ．【点睛】本题考查一次函数的性质，对于一次函数y=kx+b(k≠0)，当k ＞0时，图象经过一、三、象限，y 随x 的增大而增大；当k ＜0时，图象经过二、四、象限，y 随x 的增大而减小；熟练掌握一次函数的性质是解题关键．8．某一次函数的图象经过点()1,2，且y 随x 的增大而减小，则这个函数的表达式可能是（ ）A ．24y x =+B ．24y x =-+C ．31y xD ．31y x -=-【答案】B【解析】【分析】 设一次函数关系式为y kx b =+，把（1，2）代入可得k+b=2，根据y 随x 的增大而减小可得k ＜0，对各选项逐一判断即可得答案．【详解】设一次函数关系式为y kx b =+，∵图象经过点()1,2，2k b ∴+=；∵y 随x 增大而减小，∴k 0<，A.2＞0，故该选项不符合题意，B.-2＜0，-2+4=2，故该选项符合题意，C.3＞0，故该选项不符合题意，D.∵31y x -=-，∴y=-3x+1，-3+1=-2，故该选项不符合题意，故选：B ．【点睛】本题考查一次函数的性质及一次函数图象上的点的坐标特征，对于一次函数y=kx+b(k≠0)，当k ＞0时，图象经过一、三、象限，y 随x 的增大而增大；当k ＜0时，图象经过二、四、象限，y 随x 的增大而减小；熟练掌握一次函数的性质是解题关键．9．如图，在矩形AOBC 中，A （–2，0），B （0，1）．若正比例函数y=kx 的图象经过点C ，则k 的值为（ ）A ．–12B ．12C ．–2D ．2【答案】A【解析】【分析】根据已知可得点C 的坐标为（-2，1），把点C 坐标代入正比例函数解析式即可求得k.【详解】∵A(－2，0)，B(0，1)，∴OA=2，OB=1，∵四边形OACB 是矩形，∴BC=OA=2，AC=OB=1，∵点C 在第二象限，∴C 点坐标为（-2，1），∵正比例函数y ＝kx 的图像经过点C ，∴-2k=1，∴k=－12， 故选A. 【点睛】本题考查了矩形的性质，待定系数法求正比例函数解析式，根据已知求得点C 的坐标是解题的关键.10．如图，在平面直角坐标系中，OABC 的顶点A 在x 轴上，定点B 的坐标为(6,4)，若直线经过定点(1,0)，且将平行四边形OABC 分割成面积相等的两部分，则直线的表达式（ ）A ．+1y x =B ．4455y x =-C ．1y x =-D ．33y x =-【答案】C【解析】【分析】 根据过平行四边形的中心的直线把平行四边形分成面积相等的两部分，先求出平行四边形中心的坐标，再利用待定系数法求一次函数解析式解答即可．【详解】∵点B 的坐标为(6,4)，∴平行四边形的中心坐标为(3,2)，设直线l 的函数解析式为y kx b =+，则320k b k b +=⎧⎨+=⎩，解得11k b =⎧⎨=-⎩，所以直线l 的解析式为1y x =-． 故选：C ．【点睛】本题考查了待定系数法求一次函数解析式，平行四边形的性质，熟练掌握过平行四边形的中心的直线把平行四边形分成面积相等的两部分是解题的关键．11．若一次函数y=kx+b 的图象经过一、二、四象限，则一次函数y=-bx+k 的图象不经过（ ）A ．第一象限B ．第二象限C ．第三象限D ．第四象限【答案】A【解析】【分析】根据一次函数y=kx+b 图象在坐标平面内的位置关系先确定k ，b 的取值范围，再根据k ，b 的取值范围确定一次函数y=-bx+k 图象在坐标平面内的位置关系，从而求解．【详解】解：一次函数y=kx+b 过一、二、四象限，则函数值y 随x 的增大而减小，因而k ＜0；图象与y 轴的正半轴相交则b ＞0，因而一次函数y=-bx+k 的一次项系数-b ＜0，y 随x 的增大而减小，经过二四象限，常数项k ＜0，则函数与y 轴负半轴相交，因而一定经过二三四象限，因而函数不经过第一象限．故选：A ．【点睛】本题考查了一次函数的图象与系数的关系．函数值y 随x 的增大而减小⇔k ＜0；函数值y 随x 的增大而增大⇔k ＞0；一次函数y=kx+b 图象与y 轴的正半轴相交⇔b ＞0，一次函数y=kx+b 图象与y 轴的负半轴相交⇔b ＜0，一次函数y=kx+b 图象过原点⇔b=0．12．若一次函数(2)1y k x =-+的函数值y 随x 的增大而增大，则（ ）A ．2k <B ．2k >C ．0k >D ．k 0<【答案】B【解析】【分析】根据一次函数图象的增减性来确定（k-2）的符号，从而求得k 的取值范围．【详解】∵在一次函数y=（k-2）x+1中，y 随x 的增大而增大，∴k-2＞0，∴k ＞2，故选B.【点睛】本题考查了一次函数图象与系数的关系．在直线y=kx+b （k≠0）中，当k ＞0时，y 随x 的增大而增大；当k ＜0时，y 随x 的增大而减小．13．一次函数 y = mx +1m -的图像过点（0,2），且 y 随 x 的增大而增大，则 m 的值为（ ）A ．-1B ．3C ．1D ．- 1 或 3【答案】B【解析】【分析】 先根据函数的增减性判断出m 的符号，再把点（0，2）代入求出m 的值即可．【详解】∵一次函数y=mx+|m-1|中y 随x 的增大而增大，∴m ＞0．∵一次函数y=mx+|m-1|的图象过点（0，2），∴当x=0时，|m-1|=2，解得m 1=3，m 2=-1＜0（舍去）．故选B ．【点睛】本题考查的是一次函数图象上点的坐标特点及一次函数的性质，熟知一次函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键．14．如图，过点1(1,0)A 作x 轴的垂线，交直线2y x =于点1B ；点2A 与点O 关于直线11A B 对称；过点2(2,0)A 作x 轴的垂线，交直线2y x =于点2B ；点3A 与点O 关于直线22A B 对称；过点3A 作x 轴的垂线，交直线2y x =于点3B ；按3B 此规律作下去，则点n B 的坐标为( )A ．(2n ，2n-1)B ．(12n -，2n )C ．(2n+1，2n )D ．（2n ，12n +）【答案】B【解析】【分析】 先根据题意求出点A 2的坐标，再根据点A 2的坐标求出B 2的坐标，以此类推总结规律便可求出点n B 的坐标．【详解】∵1(1,0)A∴11OA =∵过点1(1,0)A 作x 轴的垂线，交直线2y x =于点1B∴()11,2B∵2(2,0)A∴22OA =∵过点2(2,0)A 作x 轴的垂线，交直线2y x =于点2B∴()12,4B∵点3A 与点O 关于直线22A B 对称∴()()334,0,4,8A B以此类推便可求得点A n 的坐标为()12,0n -，点B n 的坐标为()12,2n n - 故答案为：B ．【点睛】本题考查了坐标点的规律题，掌握坐标点的规律、轴对称的性质是解题的关键．15．生物活动小组的同学们观察某植物生长，得到该植物高度y (单位：cm )与观察时间x (单位：天)的关系，并画出如图所示的图象(//CD x 轴)，该植物最高的高度是( )A ．50cmB ．20cmC ．16cmD ．12cm【答案】C【解析】【分析】 设直线AC 的解析式为()0y kx b k =+≠，然后利用待定系数法求出直线AC 的解析式，再把50x =代入进行计算即可得解．【详解】解：设直线AC 的解析式为()0y kx b k =+≠∵()0,6A ，()30,12B∴61230b k b =⎧⎨=+⎩∴156k b ⎧=⎪⎨⎪=⎩ ∴165y x =+ ∴当50x =时，16y =∴该植物最高的高度是16cm ．故选：C 【点睛】本题考查了一次函数的应用，主要利用了待定系数法求一次函数解析式，已知自变量求函数值，仔细观察图象，准确获取信息是解题的关键．16．如图1，在Rt △ABC 中，∠ACB=90°，点P 以每秒1cm 的速度从点A 出发，沿折线AC －CB 运动，到点B 停止．过点P 作PD ⊥AB ，垂足为D ，PD 的长y （cm ）与点P 的运动时间x （秒）的函数图象如图2所示．当点P 运动5秒时，PD 的长是（ ）A ．1.5cmB ．1.2cmC ．1.8cmD ．2cm【答案】B【解析】【分析】【详解】 由图2知，点P 在AC 、CB 上的运动时间时间分别是3秒和4秒，∵点P 的运动速度是每秒1cm ，∴AC=3，BC=4．∵在Rt △ABC 中，∠ACB=90°，∴根据勾股定理得：AB=5．如图，过点C 作CH ⊥AB 于点H ，则易得△ABC ∽△ACH ．∴CH AC BC AB =，即AC BC 3412CH CH AB 55⋅⨯=⇒==． ∴如图，点E （3，125），F （7，0）． 设直线EF 的解析式为y kx b =+，则 123k b {507k b=+=+， 解得：3k 5{21b 5=-=． ∴直线EF 的解析式为321y x 55=-+． ∴当x 5=时，()3216PD y 5 1.2cm 555==-⨯+==． 故选B ．17．函数()312y m x =+-中，y 随x 的增大而增大，则直线()12y m x =---经过( ) A ．第一、三、四象限B ．第二、三、四象限C ．第一、二、四象限D ．第一、二、三象限 【答案】B【解析】【分析】根据一次函数的增减性，可得310m +>；从而可得10m --<，据此判断直线()12y m x =---经过的象限．【详解】 解：函数()312y m x =+-中，y 随x 的增大而增大，310m ∴+>，则13m >- 10m ∴--<，∴直线()12y m x =---经过第二、三、四象限．故选：B ．【点睛】本题考查了一次函数的性质，正确掌握一次函数图象与系数的关系是解题的关键．即一次函数y=kx+b （k≠0）中，当k ＞0时，y 随x 的增大而增大，图象经过一、三象限；当k ＜0时，y 随x 的增大而减小，图象经过二、四象限；当b ＞0时，此函数图象交y 轴于正半轴；当b ＜0时，此函数图象交y 轴于负半轴．18．函数12y x =-与23y ax =+的图像相交于点(),2A m ，则( )A ．1a =B ．2a =C ．1a =-D ．2a =-【答案】A【解析】【分析】将点(),2A m 代入12y x =-，求出m ，得到A 点坐标，再把A 点坐标代入23y ax =+，即可求出a 的值．【详解】 解：函数12y x =-过点(),2A m ， 22m ∴-=，解得：1m =-，()1,2A ∴-，函数23y ax =+的图象过点A ，32a ∴-+=，解得：1a =．故选：A ．【点睛】本题考查了两条直线的交点问题：两条直线的交点坐标，就是由这两条直线相对应的一次函数表达式所组成的二元一次方程组的解．也考查了一次函数图象上点的坐标特征．19．已知一次函数21,y x =-+当0x ≤时， y 的取值范围为（ ）A ．1y ≤B ．0y ≥C ．0y ≤D ．1y ≥【答案】D【解析】【分析】根据不等式的性质进行计算可以求得y 的取值范围.【详解】解：∵0x ≤∴2x -0≥ 21x -+1≥故选：D.【点睛】此题主要考查一次函数的图象与性质，既可以根据函数的图象与性质，也可以根据不等式的性质求解，灵活选择简便方法是解题关键.20．在同一平面直角坐标系中的图像如图所示，则关于21k x k x b <+的不等式的解为（ ）．A ．1x >-B ．2x <-C ．1x <-D ．无法确定【答案】C【解析】【分析】 求关于x 的不等式12k x b k x +>的解集就是求：能使函数1y k x b =+的图象在函数2y k x =的上边的自变量的取值范围．【详解】解：能使函数1y k x b =+的图象在函数2y k x =的上边时的自变量的取值范围是1x <-． 故关于x 的不等式12k x b k x +>的解集为：1x <-．故选：C ．【点睛】本题考查了一次函数与一元一次不等式的关系，从函数的角度看，就是寻求使一次函数y ax b =+的值大于（或小于）0的自变量x 的取值范围；从函数图象的角度看，就是确定直线y kx b =+在x 轴上（或下）方部分所有的点的横坐标所构成的集合．利用数形结合是解题的关键．。

一次函数难题经典例题及答案知识点一、定义与定义式：自变量x和因变量y有如下关系：y=kx+b则此时称y是x的一次函数。

特别地，当b=0时，y是x的正比例函数。

即：y=kx （k为常数，k≠0）二、一次函数的性质：1.y的变化值与对应的x的变化值成正比例，比值为k 即：y=kx+b （k为任意不为零的实数b取任何实数）2.当x=0时，b为函数在y轴上的截距。

三、一次函数的图像及性质：1．作法与图形：通过如下3个步骤（1）列表；（2）描点；（3）连线，可以作出一次函数的图像——一条直线。

因此，作一次函数的图像只需知道2点，并连成直线即可。

（通常找函数图像与x轴和y轴的交点）2．性质：（1）在一次函数上的任意一点P（x，y），都满足等式：y=kx+b。

（2）一次函数与y轴交点的坐标总是（0，b)，与x轴总是交于（-b/k，0）正比例函数的图像总是过原点。

3．k，b与函数图像所在象限：当k＞0时，直线必通过一、三象限，y随x的增大而增大；当k＜0时，直线必通过二、四象限，y随x的增大而减小。

当b＞0时，直线必通过一、二象限；当b=0时，直线通过原点当b＜0时，直线必通过三、四象限。

特别地，当b=O时，直线通过原点O（0，0）表示的是正比例函数的图像。

这时，当k＞0时，直线只通过一、三象限；当k＜0时，直线只通过二、四象限。

四、确定一次函数的表达式：已知点A（x1，y1）；B（x2，y2），请确定过点A、B的一次函数的表达式。

（1）设一次函数的表达式（也叫解析式）为y=kx+b。

（2）因为在一次函数上的任意一点P（x，y），都满足等式y=kx+b。

所以可以列出2个方程：y1=kx1+b ……①和y2=kx2+b ……②（3）解这个二元一次方程，得到k，b的值。

（4）最后得到一次函数的表达式。

五、一次函数在生活中的应用：1.当时间t一定，距离s是速度v的一次函数。

s=vt。

2.当水池抽水速度f一定，水池中水量g是抽水时间t的一次函数。

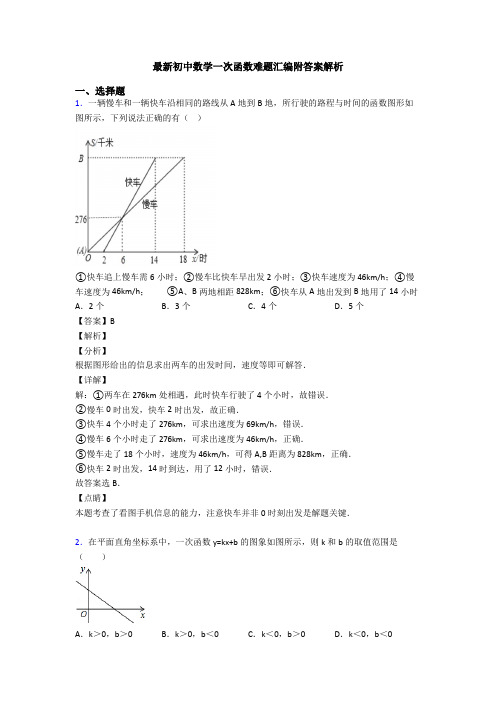
最新初中数学一次函数难题汇编附答案解析一、选择题1．一辆慢车和一辆快车沿相同的路线从A地到B地，所行驶的路程与时间的函数图形如图所示，下列说法正确的有（）①快车追上慢车需6小时；②慢车比快车早出发2小时；③快车速度为46km/h；④慢车速度为46km/h；⑤A、B两地相距828km；⑥快车从A地出发到B地用了14小时A．2个B．3个C．4个D．5个【答案】B【解析】【分析】根据图形给出的信息求出两车的出发时间，速度等即可解答．【详解】解：①两车在276km处相遇，此时快车行驶了4个小时，故错误．②慢车0时出发，快车2时出发，故正确．③快车4个小时走了276km，可求出速度为69km/h，错误．④慢车6个小时走了276km，可求出速度为46km/h，正确．⑤慢车走了18个小时，速度为46km/h，可得A,B距离为828km，正确．⑥快车2时出发，14时到达，用了12小时，错误．故答案选B．【点睛】本题考查了看图手机信息的能力，注意快车并非0时刻出发是解题关键．2．在平面直角坐标系中，一次函数y=kx+b的图象如图所示，则k和b的取值范围是（）A．k＞0，b＞0 B．k＞0，b＜0 C．k＜0，b＞0 D．k＜0，b＜0【答案】C 【解析】【分析】根据一次函数的图象与系数的关系进行解答即可． 【详解】∵一次函数y=kx+b 的图象经过一、二、四象限， ∴k ＜0，b ＞0， 故选C ．【点睛】本题考查的是一次函数的图象与系数的关系，即一次函数y=kx+b （k≠0）中，当k ＜0，b ＞0时图象在一、二、四象限．3．已知点M （1，a ）和点N （3，b ）是一次函数y ＝﹣2x+1图象上的两点，则a 与b 的大小关系是（ ） A ．a ＞b B ．a ＝bC ．a ＜bD ．无法确定【答案】A 【解析】 【分析】根据一次函数的图像和性质，k ＜0，y 随x 的增大而减小解答． 【详解】 解：∵k ＝﹣2＜0， ∴y 随x 的增大而减小， ∵1＜3， ∴a ＞b ． 故选A ． 【点睛】考查了一次函数图象上点的坐标特征，利用一次函数的增减性求解更简便．4．下列函数中，y 随x 的增大而增大的函数是（ ） A ．2y x =- B ．21y x =-+C ．2y x =-D ．2y x =--【答案】C 【解析】 【分析】根据一次函数的性质对各选项进行逐一分析即可． 【详解】∵y=-2x 中k=-2＜0，∴y 随x 的增大而减小，故A 选项错误； ∵y=-2x+1中k=-2＜0，∴y 随x 的增大而减小，故B 选项错误； ∵y=x-2中k=1＞0，∴y 随x 的增大而增大，故C 选项正确； ∵y=-x-2中k=-1＜0，∴y 随x 的增大而减小，故D 选项错误． 故选C ． 【点睛】本题考查的是一次函数的性质，一次函数y=kx+b （k≠0）中，当k ＞0时y 随x 的增大而增大；k<0时y 随x 的增大而减小；熟练掌握一次函数的性质是解答此题的关键．5．如图，直线y=-x+m 与直线y=nx+5n （n≠0）的交点的横坐标为-2，则关于x 的不等式-x+m ＞nx+5n ＞0的整数解为（ ）A ．-5，-4，-3B ．-4，-3C ．-4，-3，-2D ．-3，-2【答案】B 【解析】 【分析】根据一次函数图像与不等式的性质即可求解. 【详解】直线y=nx+5n 中，令y=0，得x=-5 ∵两函数的交点横坐标为-2，∴关于x 的不等式-x+m ＞nx+5n ＞0的解集为-5＜x ＜-2 故整数解为-4，-3，故选B. 【点睛】此题主要考查一次函数与不等式的关系，解题的关键是熟知一次函数的图像与性质.6．已知直线4y x ＝－＋与2y x ＝＋的图象如图，则方程组y x 4y x 2=-+⎧⎨=+⎩的解为（ ）A ．31x y ==，B ．13x y ==，C ．04x y ==，D ．40x y ==，【答案】B 【解析】 【分析】二元一次方程组的解就是组成二元一次方程组的两个方程的公共解，即两条直线的交点坐标． 【详解】解：根据题意知，二元一次方程组y x 4y x 2=-+⎧⎨=+⎩的解就是直线y ＝−x ＋4与y ＝x ＋2的交点坐标，又∵交点坐标为（1，3），∴原方程组的解是：13x y ==，． 故选：B ． 【点睛】本题考查了一次函数与二元一次方程组．二元一次方程组的解就是组成该方程组的两条直线的图象的交点．7．如图，矩形ABOC 的顶点坐标为()4,5-，D 是OB 的中点，E 为OC 上的一点，当ADE ∆的周长最小时，点E 的坐标是（ ）A ．40,3⎛⎫ ⎪⎝⎭B ．50,3⎛⎫ ⎪⎝⎭C ．()0,2D ．100,3⎛⎫ ⎪⎝⎭【答案】B 【解析】 【分析】作点A 关于y 轴的对称点A'，连接A'D ，此时△ADE 的周长最小值为AD+DA'的长；E 点坐标即为直线A'D 与y 轴的交点． 【详解】解：作点A 关于y 轴的对称点A'，连接A'D ，此时△ADE 的周长最小值为AD+DA'的长； ∵A 的坐标为（-4，5），D 是OB 的中点， ∴D （-2，0），由对称可知A'（4，5）， 设A'D 的直线解析式为y=kx+b ，5402k b k b =+⎧∴⎨=-+⎩5653k b⎧=⎪⎪∴⎨⎪=⎪⎩5563y x ∴=+ 当x=0时，y=5350,3E ⎛⎫∴ ⎪⎝⎭故选：B 【点睛】本题考查矩形的性质，线段的最短距离；能够利用轴对称求线段的最短距离，将AE+DE 的最短距离转化为线段A'D 的长是解题的关键．8．如图，在平面直角坐标系中，OABC 的顶点A 在x 轴上，定点B 的坐标为(6,4)，若直线经过定点(1,0)，且将平行四边形OABC 分割成面积相等的两部分，则直线的表达式（ ）A ．+1y x =B ．4455y x =- C ．1y x =- D ．33y x =-【答案】C 【解析】 【分析】根据过平行四边形的中心的直线把平行四边形分成面积相等的两部分，先求出平行四边形中心的坐标，再利用待定系数法求一次函数解析式解答即可． 【详解】∵点B 的坐标为(6,4)，∴平行四边形的中心坐标为(3,2)， 设直线l 的函数解析式为y kx b =+， 则320k b k b +=⎧⎨+=⎩，解得11k b =⎧⎨=-⎩，所以直线l 的解析式为1y x =-．故选：C ． 【点睛】本题考查了待定系数法求一次函数解析式，平行四边形的性质，熟练掌握过平行四边形的中心的直线把平行四边形分成面积相等的两部分是解题的关键．9．给出下列函数：①y ＝﹣3x +2：②y ＝3x ；③y ＝﹣5x：④y ＝3x ，上述函数中符合条件“当x ＞1时，函数值y 随自变量x 增大而增大”的是（ ） A ．①③ B ．③④ C ．②④ D ．②③ 【答案】B 【解析】 【分析】分别利用一次函数、正比例函数、反比例函数的增减性分析得出答案． 【详解】解：①y ＝﹣3x +2，当x ＞1时，函数值y 随自变量x 增大而减小，故此选项不符合题意； ②y ＝3x，当x ＞1时，函数值y 随自变量x 增大而减小，故此选项不符合题意； ③y ＝﹣5x，当x ＞1时，函数值y 随自变量x 增大而增大，故此选项符合题意； ④y ＝3x ，当x ＞1时，函数值y 随自变量x 增大而增大，故此选项符合题意； 故选：B ． 【点睛】此题考查一次函数、正比例函数、反比例函数，正确把握相关性质是解题关键．10．一次函数y ＝3x ＋b 和y ＝ax －3的图象如图所示，其交点为P(－2，－5)，则不等式3x ＋b ＞ax －3的解集在数轴上表示正确的是( )A．B．C．D．【答案】A【解析】【分析】直接根据两函数图象的交点求出不等式的解集，再在数轴上表示出来即可．【详解】解：∵由函数图象可知，当x＞-2时，一次函数y=3x+b的图象在函数y=ax-3的图象的上方，∴不等式3x+b＞ax-3的解集为：x＞-2，在数轴上表示为：故选：A.【点睛】本题考查的是一次函数与一元一次不等式，能利用函数图象求出不等式的解集是解答此题的关键．11．若一次函数y=kx+b的图象经过一、二、四象限，则一次函数y=-bx+k的图象不经过（）A．第一象限B．第二象限C．第三象限D．第四象限【答案】A【解析】【分析】根据一次函数y=kx+b图象在坐标平面内的位置关系先确定k，b的取值范围，再根据k，b 的取值范围确定一次函数y=-bx+k图象在坐标平面内的位置关系，从而求解．【详解】解：一次函数y=kx+b过一、二、四象限，则函数值y 随x 的增大而减小，因而k ＜0； 图象与y 轴的正半轴相交则b ＞0， 因而一次函数y=-bx+k 的一次项系数-b ＜0， y 随x 的增大而减小，经过二四象限， 常数项k ＜0，则函数与y 轴负半轴相交， 因而一定经过二三四象限， 因而函数不经过第一象限． 故选：A ． 【点睛】本题考查了一次函数的图象与系数的关系．函数值y 随x 的增大而减小⇔k ＜0；函数值y 随x 的增大而增大⇔k ＞0；一次函数y=kx+b 图象与y 轴的正半轴相交⇔b ＞0，一次函数y=kx+b 图象与y 轴的负半轴相交⇔b ＜0，一次函数y=kx+b 图象过原点⇔b=0．12．如图所示，已知()121,,2,2A y B y ⎛⎫ ⎪⎝⎭为反比例函数1y x=图象上的两点，动点(),0P x 在x 轴正半轴上运动，当AP BP -的值最大时，连结OA ，AOP ∆的面积是 （ ）A ．12B ．1C ．32D ．52【答案】D 【解析】 【分析】先根据反比例函数解析式求出A ，B 的坐标，然后连接AB 并延长AB 交x 轴于点P '，当P 在P '位置时，PA PB AB -=,即此时AP BP -的值最大，利用待定系数法求出直线AB 的解析式，从而求出P '的坐标，进而利用面积公式求面积即可． 【详解】 当12x =时，2y = ，当2x =时，12y = ，∴11(,2),(2,)22A B ．连接AB 并延长AB 交x 轴于点P '，当P 在P '位置时，PA PB AB -=,即此时AP BP -的值最大．设直线AB 的解析式为y kx b =+ ， 将11(,2),(2,)22A B 代入解析式中得122122k b k b ⎧+=⎪⎪⎨⎪+=⎪⎩解得152k b =-⎧⎪⎨=⎪⎩ ， ∴直线AB 解析式为52y x =-+． 当0y =时，52x = ，即5(,0)2P '，115522222AOP A S OP y '∴=⋅=⨯⨯=V ． 故选：D ． 【点睛】本题主要考查一次函数与几何综合，掌握待定系数法以及找到AP BP -何时取最大值是解题的关键．13．函数12y x =-与23y ax =+的图像相交于点(),2A m ，则( ) A ．1a = B ．2a =C ．1a =-D ．2a =-【答案】A 【解析】 【分析】将点(),2A m 代入12y x =-，求出m ，得到A 点坐标，再把A 点坐标代入23y ax =+，即可求出a 的值． 【详解】解：Q 函数12y x =-过点(),2A m ，22m ∴-=，解得：1m =-，()1,2A ∴-，Q 函数23y ax =+的图象过点A ，32a ∴-+=， 解得：1a =． 故选：A ． 【点睛】本题考查了两条直线的交点问题：两条直线的交点坐标，就是由这两条直线相对应的一次函数表达式所组成的二元一次方程组的解．也考查了一次函数图象上点的坐标特征．14．已知一次函数21,y x =-+当0x ≤时， y 的取值范围为（ ） A ．1y ≤ B ．0y ≥C ．0y ≤D ．1y ≥【答案】D 【解析】 【分析】根据不等式的性质进行计算可以求得y 的取值范围. 【详解】 解：∵0x ≤ ∴2x -0≥21x -+1≥ 故选：D. 【点睛】此题主要考查一次函数的图象与性质，既可以根据函数的图象与性质，也可以根据不等式的性质求解，灵活选择简便方法是解题关键.15．如图，已知一次函数3y x b =+与3y ax =-交于点P （－2，－5），则关于x 的不等式33x b ax +>-的解集在数轴上表示正确的是（ ）A ．B ．C ．D ．【答案】C【解析】【分析】直接根据两函数图象的交点求出不等式的解集，再在数轴上表示出来即可．【详解】解：∵由函数图象可知，当x＞−2时，一次函数y＝3x＋b的图象在函数y＝ax−3的图象的上方，∴不等式3x＋b＞ax−3的解集为x＞−2，在数轴上表示为：．故选：C．【点睛】本题考查的是一次函数与一元一次不等式，能利用函数图象求出不等式的解集是解答此题的关键．16．已知一次函数y＝kx+k，其在直角坐标系中的图象大体是（）A．B．C．D．【答案】A【解析】【分析】函数的解析式可化为y=k（x+1），易得其图象与x轴的交点为（﹣1，0），观察图形即可得出答案．【详解】函数的解析式可化为y=k（x+1），即函数图象与x轴的交点为（﹣1，0），观察四个选项可得：A符合．故选A．【点睛】本题考查了一次函数的图象，要求学生掌握通过解析判断其图象与坐标轴的交点位置、坐标．17．下列函数：①y x =；②4z y =；③4y x =，④21y x =+其中一次函数的个数是（ ）A ．1B ．2C ．3D ．4【答案】C【解析】【分析】 根据一次函数的定义条件进行逐一分析即可．【详解】①y=x 是一次函数，故①符合题意； ②4z y =是一次函数，故②符合题意； ③4y x=自变量次数不为1，故不是一次函数，故③不符合题意； ④y=2x+1是一次函数，故④符合题意．综上所述，是一次函数的个数有3个，故选：C ．【点睛】此题考查了一次函数的定义，解题关键在于掌握一次函数y=kx+b 的定义条件是：k 、b 为常数，k≠0，自变量次数为1．18．下列命题中哪一个是假命题（ ）A ．8的立方根是2B ．在函数y ＝3x 的图象中，y 随x 增大而增大C ．菱形的对角线相等且平分D ．在同圆中，相等的圆心角所对的弧相等【答案】C【解析】【分析】利用立方根的定义、一次函数的性质、菱形的性质及圆周角定理分别判断后即可确定正确的选项．【详解】A 、8的立方根是2，正确，是真命题；B 、在函数3y x =的图象中，y 随x 增大而增大，正确，是真命题；C 、菱形的对角线垂直且平分，故错误，是假命题；D 、在同圆中，相等的圆心角所对的弧相等，正确，是真命题，故选C ．【点睛】考查了命题与定理的知识，能够了解立方根的定义、一次函数的性质、菱形的性质及圆周角定理等知识是解题关键．19．在平面直角坐标系中，函数2(0)y kx k =≠的图象如图所示，则函数232y kx k =-+的图象大致是（）A ．B ．C ．D ．【答案】C【解析】【分析】根据函数图象易知k 0<，可得32k 0-+<，所以函数图象沿y 轴向下平移可得．【详解】解：根据函数图象易知k 0<，∴32k 0-+<，故选：C ．【点睛】此题主要考查一次函数的性质与图象，正确理解一次函数的性质与图象是解题关键．20．将直线23y x =-向右平移2个单位，再向上平移3个单位后，所得的直线的表达式为（ ）A ．24y x =-B ．24y x =+C ．22y x =+D ．22y x =-【答案】A【解析】【分析】直接根据“上加下减”、“左加右减”的原则进行解答即可．【详解】由“左加右减”的原则可知，将直线y=2x-3向右平移2个单位后所得函数解析式为y=2(x-2)-3=2x-7，由“上加下减”原则可知，将直线y=2x-7向上平移3个单位后所得函数解析式为y=2x-7+3=2x-4，故选A.【点睛】本题考查了一次函数的平移，熟知函数图象平移的法则是解答此题的关键．。

范文范例精心整理求一次函数解析式专项练习1．A〔2，﹣1〕，B〔3，﹣2〕，C〔a，a〕三点在同一条直线上．1〕求a的值；2〕求直线AB与坐标轴围成的三角形的面积．2．如图，直线l与x轴交于点A〔﹣，0〕，与y轴交于点B〔0，3〕1〕求直线l的解析式；2〕过点B作直线BP与x轴交于点P，且使OP=2OA，求△ABP的面积．3．一次函数的图象经过〔 1，2〕和〔﹣2，﹣1〕，求这个一次函数解析式及该函数图象与x轴交点的坐标．4．如下列图，直线l是一次函数y=kx+b的图象．1〕求k、b的值；2〕当x=2时，求y的值；3〕当y=4时，求x的值．5．一次函数y=kx+b的图象与x轴交于点A〔﹣6，0〕，与y轴交于点B．假设△AOB的面积为12，求一次函数的表达式．6．一次函数y=kx+b，当x=﹣4时，y的值为9；当x=6时，y的值为3，求该一次函数的关系式．word完美格式范文范例精心整理7．y与x+2成正比例，且x=0时，y=2，求：1〕y与x的函数关系式；2〕其图象与坐标轴的交点坐标．8．如果y+3与x+2成正比例，且x=3时，y=7．〔1〕写出y与x之间的函数关系式；〔2〕画出该函数图象；并观察当x取什么值时，y＜0？9．直线y=kx+b是由直线y=﹣x平移得到的，此直线经过点A〔﹣2，6〕，且与x轴交于点B．〔1〕求这条直线的解析式；〔2〕直线y=mx+n经过点B，且y随x的增大而减小．求关于x的不等式mx+n＜0的解集．10．y与x+2成正比例，且x=1时，y=﹣6．1〕求y与x之间的函数关系式，并建立平面直角坐标系，画出函数图象；2〕结合图象求，当﹣1＜y≤0时x的取值范围．11．y﹣2与2x+1成正比例，且当x=﹣2时，y=﹣7，求y与x的函数解析式．12．y与x﹣1成正比例，且当x=﹣5时，y=2，求y与之间的函数关系式．13．一次函数的图象经过点A〔，m〕和B〔，﹣1〕，其中常量m≠﹣1，求一次函数的解析式，并指出图象特征．（14．一次函数y=〔k﹣1〕x+5的图象经过点〔1，3〕．（1〕求出k的值；（2〕求当y=1时，x的值．word完美格式范文范例精心整理15．一次函数y=k1x﹣4与正比例函数y=k2x的图象经过点〔2，﹣1〕．1〕分别求出这两个函数的表达式；2〕求这两个函数的图象与x轴围成的三角形的面积．16．y﹣3与4x﹣2成正比例，且x=1时，y=﹣1．1〕求y与x的函数关系式．2〕如果y的取值范围为3≤y≤5时，求x的取值范围．17．假设一次函数y=3x+b的图象与两坐标轴围成的三角形面积为24，试求这个一次函数的解析式．18．如果一次函数y=kx+b的变量x的取值范围是﹣2≤x≤6，相应函数值是﹣11≤y≤9，求此函数解析式．19．某一次函数图象的自变量的取值范围是﹣3≤x≤6，相应的函数值的变化范围是﹣5≤y≤﹣2，求这个函数的解析式．20．，直线AB经过A〔﹣3，1〕，B〔0，﹣2〕，将该直线沿y轴向下平移3个单位得到直线MN．1〕求直线AB和直线MN的函数解析式；2〕求直线MN与两坐标轴围成的三角形面积．21．一次函数的图象经过点A〔0，﹣2〕，且与两条坐标轴截得的直角三角形的面积为3，求这个一次函数的解析式．22．如果y+2与x+1成正比例，当x=1时，y=﹣5．〔1〕求出y与x的函数关系式．〔2〕自变量x取何值时，函数值为4？23．y﹣3与4x﹣2成正比例，且当x=1时，y=5，〔1〕求y与x的函数关系式；word完美格式范文范例精心整理2〕求当x=﹣2时的函数值：3〕如果y的取值范围是0≤y≤5，求x的取值范围；4〕假设函数图象与x轴交于A点，与y轴交于B点，求S△AOB．24．y﹣3与x成正比例，且x=2时，y=7．〔1〕求y与x的函数关系式；〔2〕当时，求y的值；〔3〕将所得函数图象平移，使它过点〔2，﹣1〕．求平移后直线的解析式．25．：一次函数y=kx+b的图象与y轴的交点到原点的距离为3，且过A〔2，1〕点，求它的解析式．26．一次函数y=〔3﹣k〕x+2k+1．〔1〕如果图象经过〔﹣1，2〕，求k；〔2〕假设图象经过一、二、四象限，求k的取值范围．27．正比例函数与一次函数y=﹣x+b的图象交于点〔2，a〕，求一次函数的解析式．28．y+5与3x+4成正比例，且当x=1时，y=2．1〕求出y与x的函数关系式；2〕设点P〔a，﹣2〕在这条直线上，求P点的坐标．29．一次函数y=kx+b〔k≠0〕在x=1时，y=5，且它的图象与x轴交点的横坐标是6，求这个一次函数的解析式．word完美格式范文范例精心整理30．：关于x的一次函数y=〔2m﹣1〕x+m﹣2假设这个函数的图象与y轴负半轴相交，且不经过第二象限，且m为正整数．〔1〕求这个函数的解析式．〔2〕求直线y=﹣x和〔1〕中函数的图象与x轴围成的三角形面积．word完美格式范文范例精心整理一次函数的解析式30题参考答案：1．〔1〕设直线AB解析式为y=kx+b，4．〔1〕由图象可知，直线l过点〔1，0〕和〔0，〕，依题意，得，解得那么，解得：，∴直线AB解析式为y=﹣x+1∵点C〔a，a〕在直线AB上，∴a=﹣a+1，解得a=；即k=，b=；〔2〕直线AB与x轴、y轴的交点分别为〔1，0〕，〔0，〔2〕由〔1〕知，直线l的解析式为y=x+，1〕∴直线AB与坐标轴围成的三角形的面积为当x=2时，有y=×2+=；2．〔1〕设直线l的解析式为y=kx+b，〔3〕当y=4时，代入y=x+得：4=x+，∵直线l与x轴交于点A〔﹣，0〕，与y轴交于点B〔0，3〕，解得x=﹣5．5．∵图象经过点A〔﹣6，0〕，∴代入得：，∴0=﹣6k+b，解得：k=2，b=3，即b=6k①，∴直线l的解析式为y=2x+3；∵图象与y轴的交点是B〔0，b〕，∴?OB=12，即：，∴|b|=4，∴b1=4，b2=﹣4，〔2〕代入①式，得，，解：分为两种情况：①当P在x轴的负半轴上时，∵A〔﹣，0〕，B〔0，3〕，一次函数的表达式是或∴OP=2OA=3，0B=3，∴AP=3﹣，6．根据题意，得，∴△ABP的面积是×AP×OB=××；②当P在x轴的正半轴上时，解得．∵A〔﹣，0〕，B〔0，3〕，∴OP=2OA=3，0B=3，∴，故该一次函数的关系式是y=﹣x+．∴△ABP的面积是×AP×OB=××．7．〔1〕根据题意，得y=k〔x+2〕〔k≠0〕；3．设一次函数的解析式为y=kx+b〔k≠0〕，由x=0时，y=2得2=k〔0+2〕，解得k=1，所以y与x的函数关系式是y=x+2；由得：，〔2〕由，得；解得：，由，得，∴一次函数的解析式为y=x+1，当y=0时，x+1=0，所以图象与x轴的交点坐标是：〔﹣2，0〕；与y轴的交∴x=﹣1，点坐标为：〔0，2〕．∴该函数图象与x轴交点的坐标是〔﹣1，0〕8．〔1〕∵y+3与x+2成正比例，word完美格式范文范例精心整理∴设y+3=k〔x+2〕〔k≠0〕，∵当x=3时，y=7，7+3=k〔3+2〕，解得，k=2．那么y+3=2〔x+2〕，即y=2x+1；〔2〕从图上可以知道，当﹣1＜y≤0时x的取值范围﹣〔2〕由〔1〕知，y=2x+1．2≤x＜﹣．令x=0，那么y=1，．令y=0，那么x=﹣，11．∵y﹣2与2x+1成正比例，∴设y﹣2=k〔2x+1〕〔k≠0〕，所以，该直线经过点〔0，1〕和〔﹣，0〕，其图象如∵当x=﹣2时，y=﹣7，∴﹣7﹣2=k〔﹣4+1〕，图所示：∴k=3，∴y=6x+5．12．设y=k〔x﹣1〕，把x=﹣5，y=2代入，得2=〔﹣5﹣1〕k，解得．所以y与x之间的函数关系式是由图示知，当x＜﹣时，y＜013．设过点A，B的一次函数的解析式为y=kx+b，9．〔1〕一次函数y=kx+b的图象经过点〔﹣2，6〕，且那么m=k+b，﹣1=k+b，与y=﹣x的图象平行，那么y=kx+b中k=﹣1，两式相减，得m+1=k+k，即m+1=〔m+1〕，当x=﹣2时，y=6，将其代入y=﹣x+b，解得：b=4．∵m≠﹣1，那么k=2，那么直线的解析式为：y=﹣x+4；∴b=m﹣1，那么函数的解析式为y=2x+m﹣1〔m≠﹣1〕，其图象是平面〔2〕如下列图：内平行于直线y=2x〔但不包括直线y=2x﹣2〕的一切直∵直线的解析式与x轴交于点B，线∴y=0，0=﹣x+4，14．〔1〕∵一次函数y=〔k﹣1〕x+5的图象经过点〔1，∴x=4，3〕，∴B点坐标为：〔4，0〕，∴3=〔k﹣1〕×1+5．∵直线y=mx+n经过点B，且y随x的增大而减小，∴k=﹣1．∴m＜0，此图象与y=﹣x+4增减性相同，〔2〕∵y=﹣2x+5中，当y=1时，1=﹣2x+5∴关于x的不等式mx+n＜0的解集为：x＞4∴x=2．15．〔1〕把点〔2，﹣1〕代入y=k1x﹣4得：2k1﹣4=﹣1，解得：k1=，10．〔1〕设y=k〔x+2〕，所以解析式为：y=x﹣4；∵x=1时，y=﹣6．把点〔2，﹣1〕代入y=k2x∴﹣6=k〔1+2〕得：2k2=﹣1，k=﹣2．解得：k2=﹣，∴y=﹣2〔x+2〕=﹣2x﹣4．图象过〔0，﹣4〕和〔﹣2，0〕点所以解析式为：y=﹣x；word完美格式范文范例精心整理〔2〕因为函数y=x﹣4与x轴的交点是〔，0〕，且∴函数解析式为y=﹣x+4．两图象都经过点〔2，﹣1〕，因此，函数解析式为y=x﹣6或y=﹣x+4所以这两个函数的图象与x轴围成的三角形的面积是：S=××1=．19．设一次函数解析式为y=kx+b，根据题意①当k＞0时，x=﹣3时，y=﹣5，x=6时，y=﹣2，∴解得，16．〔1〕设y﹣3=k〔4x﹣2〕，〔2分〕当x=1时，y=﹣1，∴﹣1﹣3=k〔4×1﹣2〕，∴k=﹣2〔4分〕，∴y﹣3=﹣2〔4x﹣2〕，∴函数解析式为y=﹣8x+7．〔5分〕〔2〕当y=3时，﹣8x+7=3，解得：x=，当y=5时，﹣8x+7=5，解得：x=，∴x的取值范围是≤x≤．17．当x=0时，y=b，当y=0时，x=﹣，∴一次函数与两坐标轴的交点为〔0，b〕〔﹣，0〕，∴三角形面积为：×|b|×|﹣|=24，2即b=144，解得b=±12，∴这个一次函数的解析式为y=3x+12或y=3x﹣1218．根据题意，①当k＞0时，y随x增大而增大，∴当x=﹣2时，y=﹣11，x=6时，y=9∴解得，∴函数解析式为y=x﹣6；②当k＜0时，函数值随x增大而减小，∴当x=﹣2时，y=9，x=6时，y=﹣11，∴解得，∴函数的解析式为：y= x﹣4；②当k＜0时，x=﹣3时，y=﹣2，x=6时，y=﹣5，∴解得，∴函数解析式为y=﹣x﹣3；因此这个函数的解析式为y= x﹣4或y=﹣x﹣3．20．设直线AB的解析式为y=kx+b，∵A〔﹣3，1〕，B〔0，﹣2〕，∴，k=﹣1，∴直线AB的解析式为：y=﹣x﹣2，∵将该直线沿y轴向下平移3个单位得到直线MN，∴直线MN的函数解析式为：y=﹣x﹣5；2〕∵直线MN与x轴的交点为〔﹣5，0〕，与y轴的交点坐标为〔0，﹣5〕，∴直线MN与两坐标轴围成的三角形面积为×|﹣5|×||﹣．21．设与x轴的交点为B，那么与两坐标轴围成的直角三角形的面积=AO?BO，AO=2，∴BO=3，∴点B纵坐标的绝对值是3，∴点B横坐标是±3；设一次函数的解析式为：y=kx+b，当点B纵坐标是3时，B 〔3，0〕，把A〔0，﹣2〕，B〔3，0〕代入y=kx+b，得：k=，b=﹣2，所以：y=x﹣2，当点B纵坐标=﹣3时，B〔﹣3，0〕，把A〔0，﹣2〕，B〔﹣3，0〕代入y=kx+b，word完美格式范文范例精心整理y=kx﹣3，得k=﹣，b=﹣2，过A〔2，1〕，1=2k﹣3，所以：y=﹣x﹣2．k=2．22．〔1〕依题意，设y+2=k〔x+1〕，故解析式为：y=2x﹣3．将x=1，y=﹣5代入，得26．〔1〕∵一次函数y=〔3﹣k〕x+2k+1的图象经过〔﹣k〔1+1〕=﹣5+2，1，2〕，解得k=﹣，∴2=〔3﹣k〕×〔﹣1〕+2k+1，即2=3k﹣2，∴y+2=﹣〔x+1〕，解得k=；即y=﹣﹣；〔2〕把y=4代入y=﹣﹣中，得〔2〕〕∵一次函数y=〔3﹣k〕x+2k+1的图象经过一、﹣﹣3.5=4，二、四象限，解得x=﹣5，即当x=﹣5时，函数值为4∴，23．〔1〕设y﹣3=k〔4x﹣2〕，∵x=1时，y=5，解得，k＞3．∴5﹣3=k〔4﹣2〕，故k的取值范围是k＞3．解得k=1，27．根据题意，得∴y与x的函数关系式y=4x+1；，解得，，〔2〕将x=﹣2代入y=4x+1，得y=﹣7；所以一次函数的解析式是y=﹣x+3．〔3〕∵y的取值范围是0≤y≤5，28．〔1〕∵y+5与3x+4成正比例，∴0≤4x+1≤5，∴设y+5=k〔3x+4〕，即y=3kx+4k﹣5〔k是常数，且k≠0〕．∵当x=1时，y=2，解得﹣≤x≤1；∴2+5=〔3×1〕k，解得，k=1，〔4〕令x=0，那么y=1；令y=0，那么x=﹣，故y与x的函数关系式是：y=3x﹣1；〔2〕∵点P〔a，﹣2〕在这条直线上，∴A〔0，1〕，B〔﹣，0〕，∴﹣2=3a﹣1，∴S AOB=××1=．解得，a=﹣，△24．〔1〕∵y﹣3与x成正比例，∴P点的坐标是〔﹣，﹣2〕∴y﹣3=kx〔k≠0〕成正比例，把x=2时，y=7代入，得7﹣3=2k，k=2；29．把〔1，5〕、〔6，0〕代入y=kx+b中，得∴y与x的函数关系式为：y=2x+3，，解得，〔2〕把x=﹣代入得：y=2×〔﹣〕+3=2；∴一次函数的解析式是y=﹣x+6．〔3〕设平移后直线的解析式为y=2x+3+b，把点〔2，﹣1〕代入得：﹣1=2×2+3+b，30．〔1〕由题意得：，解得：b=﹣8，故平移后直线的解析式为：y=2x﹣5解得：＜m＜2，25．根据题意得：当b=3时，又∵m为正整数，y=kx+3，过A〔2，1〕．∴m=1，函数解析式为：y=x﹣1．1=2k+3〔2〕由〔1〕得，函数图象与x轴交点为〔1，0〕与yk=﹣1．轴交点为〔0，﹣1〕，∴解析式为：y=﹣x+3．∴所围三角形的面积为：×1×1=当b=﹣3时，word完美格式。

《1．等腰三角形底角与顶角之间的函数关系A ．正比例函数 B ．一次函数【答案】B【分析】根据一次函数的定义，可得答案【解析】设等腰三角形的底角为y ，顶角为所以，y=﹣12x+90°，即等腰三角形底角与【点睛】本题考查了实际问题与一次函数2．已知y 关于x 成正比例，且当x 时A ．3 B ．3-【答案】B【分析】先利用待定系数法求出y =【详解】设y kx =，Q 当2x =时，3y x ∴=-，∴当1x =时，3y =-【点睛】本题考查了待定系数法求正比例函点的坐标代入求出k 即可．3. 已知函数y =kx +b 的部分函数值如表所示A ．x =2 B ．x =3 C 【答案】A【解析】∵当x =0时，y =1，当x =1，y 当y =–3时，–2x +1=–3，解得：x =2，4．如图，直线y=kx+3经过点（2，0，A ．x ＞2B ．x ＜2 《一次函数》专项练习数关系是（ ） C ．反比例函数D ．二次函数答案．顶角为x ，由题意，得x+2y=180， 底角与顶角之间的函数关系是一次函数关系，故选函数，根据题意正确列出函数关系式是解题的关键2=时，6y =-，则当1x =时，y 的值为 C ．12D ．12-3x -，然后计算1x =对应的函数值． 6y =-，26k ∴=-，解得3k =-，13⨯=-．故选B ．比例函数的解析式：设正比例函数解析式为y kx k =表所示，则关于x 的方程kx +b +3=0的解是x … –2 –1 01… y…531 –1…．x =–2 D ．x =–3 =–1，∴，解得：，∴y =–，故关于x 的方程kx +b +3=0的解是x =2，故选A ），则关于x 的不等式kx+3＞0的解集是（ ）C ．x≥2 D ．x≤211b k b =+=-⎧⎨⎩21k b =-=⎧⎨⎩故选B ． 关键. ()0≠，然后把一个已知2x +1，．【答案】B【分析】直接利用函数图象判断不等式【解析】由一次函数图象可知：关于x的不【点睛】本题考查了一次函数的图象与性质等式之间的内在联系.5．如图，在平面直角坐标系中，直线l与直线l1在第一象限交于点C．若∠BOCAB【答案】B【分析】过C作CD⊥OA于D，利用直线3．依据CD∥BO，可得OD13=AOk的值．【解析】如图，过C作CD⊥OA于D．即A（，0），B（0，1），∴Rt△∵∠BOC＝∠BCO，∴CB＝BO＝1，∵CD∥BO，∴OD13=AO=，得：23=，即k =B式kx+3>0的解集在x轴上方,进而得出结果.的不等式kx+3>0的解集是x<2；故选B.与性质和一元一次不等式及其解法，解题的关键是掌1：y=x+1与x轴，y轴分别交于点A和点BOC=∠BCO，则k的值为（ ）C D．直线l1：y=+1，即可得到A（，0），B（0=CD23=BO23=，进而得到C23，），．直线l1：y=+1中，令x＝0，则y＝1，令AOB中，AB==3．AC＝2．CD23=BO23=，即C23，），把C23，．键是掌握一次函数与一元一次不B，直线l2：y=kx（k≠0），1），AB==，代入直线l2：y＝kx，可得令y＝0，则x＝，）代入直线l2：y＝kx，可【点睛】本题考查了两直线相交或平行问题组成的二元一次方程组的解．6．已知点A (-5,a ),B (4,b )在直线y =-3x 【答案】＞【分析】先根据一次函数的解析式判断出函【解析】∵直线y=-3x+2中，k=-3＜0，∵-5＜4，∴a ＞b ，故答案为＞.【点睛】本题考查了一次函数的性质，根据如果k>0，直线就从左往右上升，y 随7．如图，四边形ABCD 的顶点坐标分别ABCD 分成面积相等的两部分时，直线A ．116105y x =+ B ．23y =【答案】D【分析】由已知点可求四边形ABCD 分成y=-x+3，设过B 的直线l 为y=kx+b ，并求1125173121k k k k --⎛⎫⎛⎫=⨯-⨯+ ⎪⎪+⎝⎭⎝⎭，即可【解析】解：由()()4,0,2,1,A B ---∴四边形ABCD 分成面积(12AC =⨯设过B 的直线l 为y kx b =+，将点B 代入∴直线CD 与该直线的交点为45,k k -⎛+⎝∴1125173121k k k k --⎛⎫⎛=⨯-⨯+ ⎪ +⎝⎭⎝，∴直线解析式为5342y x =+；故选：【点睛】本题考查一次函数的解析式求法式的方法是解题的关键．行问题，两条直线的交点坐标，就是由这两条直线相+2上，则a ________b .（填“＞”“＜”或“=”号 断出函数的增减性，再比较出-5与4的大小即可解答，∴此函数是减函数， 根据题意判断出一次函数的增减性是解答此题的关x 的增大而增大，如果k<0，直线就从左往右下降分别()()()()4,0,2,1,3,0,0,3A B C D ---，当过点直线l 所表示的函数表达式为（ ） 13x + C ．1y x =+ D ．54y x =+分成面积()113741422B AC y =⨯⨯+=⨯⨯=；并求出两条直线的交点，直线l 与x 轴的交点坐标即可求k 。

求一次函数解析式专项练习1．已知A（2，﹣1），B（3，﹣2），C（a，a）三点在同一条直线上．（1）求a的值；（2）求直线AB与坐标轴围成的三角形的面积．2．如图，直线l与x轴交于点A（﹣1.5，0），与y轴交于点B（0，3）（1）求直线l的解析式；（2）过点B作直线BP与x轴交于点P，且使OP=2OA，求△ABP的面积．3．已知一次函数的图象经过（1，2）和（﹣2，﹣1），求这个一次函数解析式及该函数图象与x 轴交点的坐标．4．如图所示，直线l是一次函数y=kx+b的图象．（1）求k、b的值；（2）当x=2时，求y的值；（3）当y=4时，求x的值．5．已知一次函数y=kx+b的图象与x轴交于点A（﹣6，0），与y轴交于点B．若△AOB的面积为12，求一次函数的表达式．6．已知一次函数y=kx+b，当x=﹣4时，y的值为9；当x=6时，y的值为3，求该一次函数的关系式．1---求一次函数的解析式7．已知y与x+2成正比例，且x=0时，y=2，求：（1）y与x的函数关系式；（2）其图象与坐标轴的交点坐标．8．如果y+3与x+2成正比例，且x=3时，y=7．（1）写出y与x之间的函数关系式；（2）画出该函数图象；并观察当x取什么值时，y＜0？9．直线y=kx+b是由直线y=﹣x平移得到的，此直线经过点A（﹣2，6），且与x轴交于点B．（1）求这条直线的解析式；（2）直线y=mx+n经过点B，且y随x的增大而减小．求关于x的不等式mx+n＜0的解集．10．已知y与x+2成正比例，且x=1时，y=﹣6．（1）求y与x之间的函数关系式，并建立平面直角坐标系，画出函数图象；（2）结合图象求，当﹣1＜y≤0时x的取值范围．11．已知y﹣2与2x+1成正比例，且当x=﹣2时，y=﹣7，求y与x的函数解析式．12．已知y与x﹣1成正比例，且当x=﹣5时，y=2，求y与之间的函数关系式．（，﹣1），其中常量m≠（，m）和B﹣1．已知一次函数的图象经过点13A，求一次函数的解析式，并指出图象特征．14．已知一次函数y=（k﹣1）x+5的图象经过点（1，3）．（1）求出k的值；（2）求当y=1时，x的值．2 ---求一次函数解析式15．一次函数y=kx﹣4与正比例函数y=kx的图象经过点（2，﹣1）．21（1）分别求出这两个函数的表达式；（2）求这两个函数的图象与x轴围成的三角形的面积．16．已知y﹣3与4x﹣2成正比例，且x=1时，y=﹣1．（1）求y与x的函数关系式．（2）如果y的取值范围为3≤y≤5时，求x的取值范围．17．若一次函数y=3x+b的图象与两坐标轴围成的三角形面积为24，试求这个一次函数的解析式．18．如果一次函数y=kx+b的变量x的取值范围是﹣2≤x≤6，相应函数值是﹣11≤y≤9，求此函数解析式．19．某一次函数图象的自变量的取值范围是﹣3≤x≤6，相应的函数值的变化范围是﹣5≤y≤﹣2，求这个函数的解析式．20．已知，直线AB经过A（﹣3，1），B（0，﹣2），将该直线沿y轴向下平移3个单位得到直线MN．（1）求直线AB和直线MN的函数解析式；（2）求直线MN与两坐标轴围成的三角形面积．21．一次函数的图象经过点A（0，﹣2），且与两条坐标轴截得的直角三角形的面积为3，求这个一次函数的解析式．22．如果y+2与x+1成正比例，当x=1时，y=﹣5．（1）求出y与x的函数关系式．（2）自变量x取何值时，函数值为4？23．已知y﹣3与4x﹣2成正比例，且当x=1时，y=5，（1）求y与x的函数关系式；（2）求当x=﹣2时的函数值：3 ---求一次函数解析式（3）如果y的取值范围是0≤y≤5，求x的取值范围；．S点，求y轴交于B4）若函数图象与x轴交于A点，与（AOB△24．已知y﹣3与x成正比例，且x=2时，y=7．（1）求y与x的函数关系式；）当时，求y的值；（2（3）将所得函数图象平移，使它过点（2，﹣1）．求平移后直线的解析式．25．已知：一次函数y=kx+b的图象与y轴的交点到原点的距离为3，且过A（2，1）点，求它的解析式．26．已知一次函数y=（3﹣k）x+2k+1．（1）如果图象经过（﹣1，2），求k；（2）若图象经过一、二、四象限，求k的取值范围．．正比例函数与一次函数y=﹣x+b的图象交于点（2，a）27，求一次函数的解析式．28．已知y+5与3x+4成正比例，且当x=1时，y=2．（1）求出y与x的函数关系式；（2）设点P（a，﹣2）在这条直线上，求P点的坐标．29．已知一次函数y=kx+b（k≠0）在x=1时，y=5，且它的图象与x轴交点的横坐标是6，求这个一次函数的解析式．4 ---求一次函数解析式30．已知：关于x的一次函数y=（2m﹣1）x+m﹣2若这个函数的图象与y轴负半轴相交，且不经过第二象限，且m为正整数．（1）求这个函数的解析式．（2）求直线y=﹣x和（1）中函数的图象与x轴围成的三角形面积．5 ---求一次函数解析式一次函数的解析式30题参考答案：，解析式为y=kx+b（1）设直线AB1．，），0）和（0 ．（1）由图象可知，直线l过点（1，4依题意，得，解得，，解得：则∴直线AB解析式为y=﹣x+1∵点C（a，a）在直线AB上，a+1，解得；a=∴a=﹣b=；k=，即，0（2）直线AB与x轴、y轴的交点分别为（1，0），（y=l1）知，直线的解析式为x+，（2）由（1）AB与坐标轴围成的三角形的面积为∴直线=；2+当x=2时，有y=×l的解析式为y=kx+b，．2（1）设直线x+（3）当y=4时，代入，y=4= x+得：B，与y轴交于点（﹣x轴交于点A1.5，0）∵直线l与解得x=﹣5．3（0，），5．∵图象经过点A（﹣6，0），代入得：∴，∴0=﹣6k+b，即b=6k ①，，解得：k=2，b=3∵图象与y轴的交点是B（0，b）∴直线l的解析式为y=2x+3；，，?OB=12∴即：，∴|b|=4，b∴=4，b=﹣4，21）（2，，式，得代入①解：分为两种情况：①当P轴的负半轴上时，在x ），3B（0，∵A（﹣1.5，0），或一次函数的表达式是，∴OP=2OA=3，0B=3∴AP=3﹣1.5=1.5，，．根据题意，得6；AP×OB=×1.5×∴△ABP3=2.25的面积是×x轴的正半轴上时，②当P在解得．，（A∵（﹣1.5，0），B0，3）OP=2OA=3∴，0B=3，∴AP=3+1.5=4.5，x+．故该一次函数的关系式是y= ﹣ABP的面积是×APOB=×4.5××3=6.25．∴△7．（1）根据题意，得y=k（x+2）（k≠0）；由x=0时，y=2得2=k（0+2），解得）（．设一次函数的解析式为3y=kx+bk≠0，k=1，所以y与x的函数关系式是y=x+2；，由已知得：，得；）由（2，解得：，得由，∴一次函数的解析式为y=x+1，当y=0时，x+1=0，所以图象与x轴的交点坐标是：（﹣2，0）；与y轴的交x=∴﹣1，点坐标为：（0，2）．轴交点的坐标是（﹣该函数图象与∴x1），0 成正比例，x+2与y+3∵）1（．86 ---求一次函数解析式∴设y+3=k（x+2）（k≠0），，时，y=7∵当x=3 ，3+2）∴7+3=k（．解得，k=2 ；，即y=2x+1y+3=2（x+2）则（2）从图上可以知道，当﹣1＜y≤0时x的取值范围﹣2≤x．）由（1）知，y=2x+1（2＜﹣．，．令x=0，则y=111．∵y﹣2与2x+1成正比例，﹣x=，令y=0，则∴设y﹣2=k（2x+1）（k≠0），∵当x=﹣2时，y=﹣7，，其图象如））和（﹣，01所以，该直线经过点（0，∴﹣7﹣2=k（﹣4+1），∴k=3，图所示：∴y=6x+5．12．设y=k（x﹣1），把x=﹣5，y=2代入，得2=（﹣5﹣1）k，解得．之间的函数关系式是x 所以y与0y时，x由图示知，当＜＜﹣13．设过点A，B的一次函数的解析式为y=kx+b，，且2，）6y=kx+b．9（1）一次函数的图象经过点（﹣1=k+b，﹣k+b，则m= 的图象平行，xy=与﹣，﹣1k=则y=kx+b中m+1=（m+1）m+1=，k+k，即两式相减，得，﹣x+by=y=62当x=﹣时，，将其代入∵m≠﹣1，则k=2，解得：b=4．∴b=m﹣1，则直线的解析式为：y=﹣x+4；则函数的解析式为y=2x+m﹣1（m ≠﹣1），其图象是平面内平行于直线y=2x（但不包括直线y=2x ﹣2）的一切）如图所示：（2x直线的解析式与轴交于点，B∵直线y=0∴，，x+40=﹣14．（1）∵一次函数y=（k﹣1）x+5的图象经过点（1，，x=4∴3），∴3=（），（B∴点坐标为：40，k﹣1）×1+5．∴k=﹣1．的增大而减小，随，且经过点直线∵y=mx+nByxx+4增减性相同，﹣，此图象与＜m∴0y=（2）∵y=﹣2x+5中，当y=1时，1=﹣2x+5∴x的解集为：0＜＞x=2．4mx+nx∴关于的不等式15．（1）把点（2，﹣1）代入y=kx﹣4 1得：2k﹣4=﹣1，1=，解得：k 1y=x﹣4；所以解析式为：，）（y=k）设（．101x+2 6y=时，x=1∵﹣．把点（2，﹣1）代入y=kx 2﹣∴）（6=k1+2得：2k=﹣1，2．2﹣k=﹣，k解得：=2﹣y=∴=）x+2（2﹣4﹣2x．）和（﹣4，﹣0图象过（，20）点﹣x；y=所以解析式为：7 ---求一次函数解析式﹣x+4．∴函数解析式为y=，且x﹣4与x）轴的交点是（，0（2）因为函数y=，1）两图象都经过点（2，﹣﹣x+4 或y=y=x﹣因此，函数解析式为6轴围成的三角形的面积是：x所以这两个函数的图象与19．设一次函数解析式为y=kx+b，根据题意．S=1=××①当k＞0时，x=﹣3时，y=﹣5，x=6时，y=﹣2，解得，∴y=x﹣4∴函数的解析式为：；②当k＜0时，x=﹣3时，y=﹣2，x=6时，y=﹣5，解得，∴（16．1）设y﹣3=k（4x分）（2﹣2），1，x=1时，y=﹣当﹣2），1∴﹣1﹣3=k（4×﹣x﹣y=3；∴函数解析式为分）﹣∴k=2（4，∴），22（4x﹣y﹣3=﹣﹣x﹣y=3．因此这个函数的解析式为y=x﹣4或．（5分）8x+7∴函数解析式为y=﹣20．设直线AB，y=3时，﹣8x+7=3 的解析式为y=kx+b，）当（2∵A（﹣3，1），B（0，﹣2），，解得：x=∴，，时，﹣8x+7=5y=5当x=解得：，∴k=﹣1，∴直线AB的解析式为：y=﹣x﹣2，．x≤∴x的取值范围是≤∵将该直线沿y轴向下平移3个单位得到直线MN，∴直线MN的函数解析式为：y=﹣x﹣5；，y=bx=017．当时，（2）∵直线MN与x轴的交点为（﹣5，0），与y轴的﹣，x=y=0当时，交点坐标为（0，﹣5），与两坐标轴围成的三角形面积为×|，0），一次函数与两坐标轴的交点为（∴0b（﹣，）﹣MN5|×||∴直线﹣5=12.5．﹣|=24，||b|∴三角形面积为：××21．设与x轴的交点为B，则与两坐标轴围成的直角三2即b=144，=AO?角形的面积BO，12，±解得b=∵这个一次函数的解析式为AO=2，∴12 y=3xy=3x+12或﹣BO=3，∴∴点B纵坐标的绝对值是3，增大而增大，随时，0＞当．根据题意，18①kyx∴点B横坐标是y=9 x=6，11y=2x=当∴﹣时，﹣时，±3；设一次函数的解析式为：y=kx+b，∴解得，当点B纵坐标是3时，B（3，0），把A（0，﹣2），B（3，0）代入y=kx+b，∴；6﹣y=函数解析式为xk=，b=﹣2，得：增大而减小，x时，函数值随0k当②＜y=x﹣2，所以：﹣x=x=6，y=9时，211﹣时，y=，当∴当点B纵坐标=﹣3时，B（﹣3，0），∴解得，把A（0，﹣2），B（﹣3，0）代入y=kx+b，8 ---求一次函数解析式y=kx﹣3，，b=﹣2得k=，﹣过A（2，1），1=2k﹣3，所以：y=．﹣x﹣2k=2．故解析式为：y=2x﹣，3．22．（1）依题意，设y+2=k（x+1）26．（1）∵一次函数y=（3﹣y=将x=1，﹣5代入，得k）x+2k+1的图象经过（﹣1，2）（1+1）=﹣5+2，，k∴2=（3﹣k）×（﹣1）+2k+1，即2=3k﹣2， 1.5，﹣解得k= ，（y+2=﹣1.5x+1）∴k=；解得1.5x即y=﹣﹣3.5；（（2）把2））∵一次函数y=（﹣3.5中，得3﹣k）x+2k+1的图象经过一、y=4代入y=﹣1.5x二、四象限， 3.5=4﹣1.5x﹣，5，x=解得﹣∴，4 ﹣5时，函数值为即当x= y）设﹣3=k（4x﹣2），．23（1 y=5，时，∵x=1解得，k＞3．∴5﹣3=k（4﹣2，）故k的取值范围是k＞3．27．根据题意，得k=1解得，；y∴与x的函数关系式y=4x+1，解得，，7；，得﹣2）将x=2代入y=4x+1y=﹣（所以一次函数的解析式是y= ﹣x+3．28≤的取值范围是3（）∵y0≤y5，．（1）∵y+5与3x+4成正比例，∴设y+5=k（3x+4），即y=3kx+4k﹣5（k是常数，且k≠，≤∴0≤4x+15 0）．，时，y=2∵当x=1；≤解得﹣≤x1 ，）k（3×1∴2+5=，解得，k=1 ﹣x=，，则；令，则（4）令x=0y=1y=0 1；x的函数关系式是：y=3x﹣y故与2）在这条直线上，P（a，﹣（2）∵点∴A，，0）B）（0，1，（﹣1，﹣2=3a﹣∴S∴1=．×=×﹣解得，a=，AOB△1．24（）与3x成正比例，﹣∵y ）点的坐标是（﹣，﹣∴P2 ∴y≠k0）成正比例，（﹣3=kx 中，得）代入；，﹣代入，得y=7时，把x=273=2kk=2 y=kx+b、）（6，029．把（1，5，的函数关系式为：与∴yxy=2x+3，，解得y=2代入得：﹣；+3=2×（﹣）x=）把（2 x+6．y=∴一次函数的解析式是﹣3（）设平移后直线的解析式为y=2x+3+b，）由题意得：．（1，30 ，2+3+b1=21，﹣2把点（）代入得：﹣×﹣8，b=解得：5 ﹣y=2x故平移后直线的解析式为：，m＜＜2解得：25．根据题意得：时，当b=3为正整数，又∵m ．﹣1∴m=1，函数解析式为：y=x ．）12（A，过y=kx+3，y）与1，0轴交点为（）由（（211=2k+3 ）得，函数图象与x ），，﹣．﹣k=1轴交点为（01 ．x+3﹣y=解析式为：∴××∴所围三角形的面积为：11= 时，3﹣b=当9 ---求一次函数解析式。

初中数学一次函数难题汇编含答案一、选择题1．如图，矩形ABOC 的顶点坐标为()4,5-，D 是OB 的中点，E 为OC 上的一点，当ADE ∆的周长最小时，点E 的坐标是（ ）A ．40,3⎛⎫ ⎪⎝⎭B ．50,3⎛⎫ ⎪⎝⎭C ．()0,2D ．100,3⎛⎫ ⎪⎝⎭【答案】B【解析】【分析】 作点A 关于y 轴的对称点A'，连接A'D ，此时△ADE 的周长最小值为AD+DA'的长；E 点坐标即为直线A'D 与y 轴的交点．【详解】解：作点A 关于y 轴的对称点A'，连接A'D ，此时△ADE 的周长最小值为AD+DA'的长；∵A 的坐标为（-4，5），D 是OB 的中点，∴D （-2，0），由对称可知A'（4，5），设A'D 的直线解析式为y=kx+b ，5402k b k b =+⎧∴⎨=-+⎩5653k b ⎧=⎪⎪∴⎨⎪=⎪⎩5563y x ∴=+ 当x=0时，y=5350,3E ⎛⎫∴ ⎪⎝⎭故选：B【点睛】本题考查矩形的性质，线段的最短距离；能够利用轴对称求线段的最短距离，将AE+DE 的最短距离转化为线段A'D 的长是解题的关键．2．如图，函数4y x =-和y kx b =+的图象相交于点()8A m-,，则关于x 的不等式()40k x b ++>的解集为（ ）A ．2x >B ．02x <<C ．8x >-D ．2x <【答案】A【解析】【分析】 直接利用函数图象上点的坐标特征得出m 的值，再利用函数图象得出答案即可．【详解】解：∵函数y ＝−4x 和y ＝kx ＋b 的图象相交于点A （m ，−8），∴−8＝−4m ，解得：m ＝2，故A 点坐标为（2，−8），∵kx ＋b ＞−4x 时，（k ＋4）x ＋b ＞0，则关于x 的不等式（k ＋4）x ＋b ＞0的解集为：x ＞2．故选：A ．【点睛】此题主要考查了一次函数与一元一次不等式，正确利用函数图象分析是解题关键．3．如图，已知一次函数22y x =-+的图象与坐标轴分别交于A 、B 两点，⊙O 的半径为1，P 是线段AB 上的一个点，过点P 作⊙O 的切线PM ，切点为M ，则PM 的最小值为（ ）A ．22B ．2C ．5D ．3【答案】D【解析】【分析】【详解】 解：连结OM 、OP ，作OH ⊥AB 于H ，如图，先利用坐标轴上点的坐标特征：当x=0时，y=﹣x+22=22，则A （0，22），当y=0时，﹣x+22=0，解得x=22，则B （22，0），所以△OAB 为等腰直角三角形，则AB=2OA=4，OH=12AB=2， 根据切线的性质由PM 为切线，得到OM ⊥PM ，利用勾股定理得到PM=22OP OM -=21OP -，当OP 的长最小时，PM 的长最小，而OP=OH=2时，OP 的长最小，所以PM 的最小值为2213-=．故选D ．【点睛】本题考查切线的性质；一次函数图象上点的坐标特征．4．在平面直角坐标系中，一次函数y=kx+b 的图象如图所示，则k 和b 的取值范围是（ ）A ．k ＞0，b ＞0B ．k ＞0，b ＜0C ．k ＜0，b ＞0D ．k ＜0，b ＜0【答案】C【解析】 【分析】根据一次函数的图象与系数的关系进行解答即可．【详解】∵一次函数y=kx+b 的图象经过一、二、四象限，∴k ＜0，b ＞0，故选C ．【点睛】本题考查的是一次函数的图象与系数的关系，即一次函数y=kx+b （k≠0）中，当k ＜0，b ＞0时图象在一、二、四象限．5．已知点M （1，a ）和点N （3，b ）是一次函数y ＝﹣2x+1图象上的两点，则a 与b 的大小关系是（ ）A ．a ＞bB ．a ＝bC ．a ＜bD ．无法确定【答案】A【解析】【分析】根据一次函数的图像和性质，k ＜0，y 随x 的增大而减小解答．【详解】解：∵k ＝﹣2＜0，∴y 随x 的增大而减小，∵1＜3，∴a ＞b ．故选A ．【点睛】考查了一次函数图象上点的坐标特征，利用一次函数的增减性求解更简便．6．若一次函数32y x =-+的图象与x 轴交于点A ，与y 轴交于点,B 则AOB （O 为坐标原点）的面积为（ ）A ．32B ．2C ．23D ．3【答案】C【解析】【分析】根据直线解析式求出OA 、OB 的长度，根据面积公式计算即可.【详解】当32y x =-+中y=0时，解得x=23，当x=0时，解得y=2， ∴A(23，0)，B(0，2)， ∴OA=23，OB=2， ∴1122223AOB S OA OB =⋅=⨯⨯=23, 故选：C.【点睛】此题考查一次函数图象与坐标轴的交点坐标，正确理解交点坐标的计算方法是解题的关键.7．下列函数中，y 随x 的增大而增大的函数是（ ）A ．2y x =-B ．21y x =-+C ．2y x =-D ．2y x =-- 【答案】C【解析】【分析】根据一次函数的性质对各选项进行逐一分析即可．【详解】∵y=-2x 中k=-2＜0，∴y 随x 的增大而减小，故A 选项错误；∵y=-2x+1中k=-2＜0，∴y 随x 的增大而减小，故B 选项错误；∵y=x-2中k=1＞0，∴y 随x 的增大而增大，故C 选项正确；∵y=-x-2中k=-1＜0，∴y 随x 的增大而减小，故D 选项错误．故选C ．【点睛】本题考查的是一次函数的性质，一次函数y=kx+b （k≠0）中，当k ＞0时y 随x 的增大而增大；k<0时y 随x 的增大而减小；熟练掌握一次函数的性质是解答此题的关键．8．下列函数（1）y =x （2）y =2x ﹣1 （3）y =1x（4）y =2﹣3x （5）y =x 2﹣1中，是一次函数的有（ ）A ．4个B ．3个C ．2个D ．1个 【答案】B【解析】【分析】分别利用一次函数、二次函数和反比例函数的定义分析得出即可．【详解】解：（1）y =x 是一次函数，符合题意；（2）y =2x ﹣1是一次函数，符合题意；（3）y =1x是反比例函数，不符合题意； （4）y =2﹣3x 是一次函数，符合题意；（5）y =x 2﹣1是二次函数，不符合题意；故是一次函数的有3个．故选：B ．【点睛】 此题考查一次函数、二次函数和反比例函数的定义，正确把握相关定义是解题关键．9．一次函数y kx b =+是（,k b 是常数，0k ≠）的图像如图所示，则不等式0kx b +<的解集是（ ）A ．0x >B ．0x <C ．2x >D ．2x <【答案】C【解析】【分析】 根据一次函数的图象看出：一次函数y=kx+b （k ，b 是常数，k≠0）的图象与x 轴的交点是（2，0），得到当x ＞2时，y<0，即可得到答案．【详解】解：一次函数y=kx+b （k ，b 是常数，k≠0）的图象与x 轴的交点是（2，0）， 当x ＞2时，y<0．故答案为：x ＞2．故选：C.【点睛】本题主要考查对一次函数的图象，一次函数与一元一次不等式等知识点的理解和掌握，能观察图象得到正确结论是解此题的关键．10．如图，直线y=-x+m 与直线y=nx+5n （n≠0）的交点的横坐标为-2，则关于x 的不等式-x+m ＞nx+5n ＞0的整数解为（ ）A ．-5，-4，-3B ．-4，-3C ．-4，-3，-2D ．-3，-2【答案】B【解析】【分析】 根据一次函数图像与不等式的性质即可求解.【详解】直线y=nx+5n 中，令y=0，得x=-5∵两函数的交点横坐标为-2，∴关于x 的不等式-x+m ＞nx+5n ＞0的解集为-5＜x ＜-2故整数解为-4，-3，故选B.【点睛】此题主要考查一次函数与不等式的关系，解题的关键是熟知一次函数的图像与性质.11．如图在平面直角坐标系中，等边三角形OAB 的边长为4，点A 在第二象限内，将OAB ∆沿射线AO 平移，平移后点A '的横坐标为43，则点B '的坐标为（ ）A ．(3,2)-B ．(63,3)-C ．(6,2)-D ．(63,2)-【答案】D【解析】【分析】 先根据已知条件求出点A 、B 的坐标，再求出直线OA 的解析式，继而得出点A '的纵坐标，找出点A 平移至点A '的规律，即可求出点B '的坐标．【详解】解：∵三角形OAB 是等边三角形，且边长为4∴(23,2),(0,4)A B -设直线OA 的解析式为y kx =，将点A 坐标代入，解得：33k =- 即直线OA 的解析式为：33y x =- 将点A '的横坐标为43代入解析式可得：4y =-即点A '的坐标为(43,4)-∵点A 向右平移63个单位，向下平移6个单位得到点A '∴B '的坐标为(063,46)(63,2)+-=-．故选：D ．【点睛】本题考查的知识点是坐标与图形变化-平移，熟练掌握坐标平面图形平移的规律是解决本题的关键．12．如图，在平面直角坐标系中，函数y ＝2x 和y ＝﹣x 的图象分别为直线l 1，l 2，过点（1，0）作x 轴的垂线交l 1于点A 1，过点A 1作y 轴的垂线交l 2于点A 2，过点A 2作x 轴的垂线交l 1于点A 3，过点A 3作y 轴的垂线交l 2于点A 4，…，依次进行下去，则点A 2019的坐标为（ ）A ．（21009，21010）B ．（﹣21009，21010）C ．（21009，﹣21010）D ．（﹣21009，﹣21010）【答案】D【解析】【分析】 写出一部分点的坐标，探索得到规律A 2n +1[（﹣2）n ，2×（﹣2）n ]（n 是自然数），即可求解；【详解】A 1（1，2），A 2（﹣2，2），A 3（﹣2，﹣4），A 4（4，﹣4），A 5（4，8），… 由此发现规律：A 2n +1[（﹣2）n ，2×（﹣2）n ]（n 是自然数），2019＝2×1009+1，∴A 2019[（﹣2）1009，2×（﹣2）1009]，∴A 2019（﹣21009，﹣21010），故选D．【点睛】本题考查一次函数图象上点的特点；能够根据作图特点，发现坐标的规律是解题的关键．13．函数y=2x﹣5的图象经过（）A．第一、三、四象限B．第一、二、四象限C．第二、三、四象限D．第一、二、三象限【答案】A【解析】【分析】先根据一次函数的性质判断出此函数图象所经过的象限，再进行解答即可．【详解】∵一次函数y=2x-5中，k=2＞0，∴此函数图象经过一、三象限，∵b= -5＜0，∴此函数图象与y轴负半轴相交，∴此一次函数的图象经过一、三、四象限，不经过第二象限．故选A．【点睛】本题考查的是一次函数的性质，即一次函数y=kx+b（k≠0）中，当k＞0时，函数图象经过一、三象限，当b＜0时，（0，b）在y轴的负半轴，直线与y轴交于负半轴．14．已知直线y1=kx+1（k＜0）与直线y2=mx（m＞0）的交点坐标为（12，12m），则不等式组mx﹣2＜kx+1＜mx的解集为（）A．x>12B．12<x<32C．x<32D．0<x<32【答案】B 【解析】【分析】由mx﹣2＜（m﹣2）x+1，即可得到x＜32；由（m﹣2）x+1＜mx，即可得到x＞12，进而得出不等式组mx﹣2＜kx+1＜mx的解集为12＜x＜32．【详解】把（12，12m）代入y1=kx+1，可得1 2m=12k+1，解得k=m ﹣2，∴y 1=（m ﹣2）x+1，令y 3=mx ﹣2，则当y 3＜y 1时，mx ﹣2＜（m ﹣2）x+1，解得x ＜32； 当kx+1＜mx 时，（m ﹣2）x+1＜mx ，解得x ＞12， ∴不等式组mx ﹣2＜kx+1＜mx 的解集为12＜x ＜32， 故选B ．【点睛】本题考查了一次函数与一元一次不等式的关系：从函数的角度看，就是寻求使一次函数y=kx+b 的值大于（或小于）0的自变量x 的取值范围；从函数图象的角度看，就是确定直线y=kx+b 在x 轴上（或下）方部分所有的点的横坐标所构成的集合．15．生物活动小组的同学们观察某植物生长，得到该植物高度y (单位：cm )与观察时间x (单位：天)的关系，并画出如图所示的图象(//CD x 轴)，该植物最高的高度是( )A ．50cmB ．20cmC ．16cmD ．12cm【答案】C【解析】【分析】 设直线AC 的解析式为()0y kx b k =+≠，然后利用待定系数法求出直线AC 的解析式，再把50x =代入进行计算即可得解．【详解】解：设直线AC 的解析式为()0y kx b k =+≠∵()0,6A ，()30,12B∴61230b k b =⎧⎨=+⎩∴156k b ⎧=⎪⎨⎪=⎩ ∴165y x =+ ∴当50x =时，16y =∴该植物最高的高度是16cm ．故选：C【点睛】本题考查了一次函数的应用，主要利用了待定系数法求一次函数解析式，已知自变量求函数值，仔细观察图象，准确获取信息是解题的关键．16．函数()312y m x =+-中，y 随x 的增大而增大，则直线()12y m x =---经过( ) A ．第一、三、四象限B ．第二、三、四象限C ．第一、二、四象限D ．第一、二、三象限 【答案】B【解析】【分析】根据一次函数的增减性，可得310m +>；从而可得10m --<，据此判断直线()12y m x =---经过的象限．【详解】 解：函数()312y m x =+-中，y 随x 的增大而增大，310m ∴+>，则13m >- 10m ∴--<，∴直线()12y m x =---经过第二、三、四象限．故选：B ．【点睛】本题考查了一次函数的性质，正确掌握一次函数图象与系数的关系是解题的关键．即一次函数y=kx+b （k≠0）中，当k ＞0时，y 随x 的增大而增大，图象经过一、三象限；当k ＜0时，y 随x 的增大而减小，图象经过二、四象限；当b ＞0时，此函数图象交y 轴于正半轴；当b ＜0时，此函数图象交y 轴于负半轴．17．对于一次函数24y x =-+，下列结论正确的是（ ）A ．函数值随自变量的增大而增大B ．函数的图象不经过第一象限C ．函数的图象向下平移4个单位长度得2y x =-的图象0,4D．函数的图象与x轴的交点坐标是()【答案】C【解析】【分析】根据一次函数的系数结合一次函数的性质，即可得知A、B选项不正确，代入y=0求出与之对应的x值，即可得出D不正确，根据平移的规律求得平移后的解析式，即可判断C正确，此题得解．【详解】解：A、∵k=-2＜0，∴一次函数中y随x的增大而减小，故 A不正确；B、∵k=-2＜0，b=4＞0，∴一次函数的图象经过第一、二、四象限，故B不正确；C、根据平移的规律，函数的图象向下平移4个单位长度得到的函数解析式为y=-2x+4-4，即y=-2x，故C正确；D、令y=-2x+4中y=0，则x=2，∴一次函数的图象与x轴的交点坐标是（2，0）故D不正确．故选：C．【点睛】此题考查一次函数的图象以及一次函数的性质，解题的关键是逐条分析四个选项．本题属于基础题，难度不大，解决该题时，熟悉一次函数的性质、一次函数图象上点的坐标特征以及一次函数图象与系数的关系是解题的关键．18．已知一次函数y＝kx+k，其在直角坐标系中的图象大体是（）A．B．C．D．【答案】A【解析】【分析】函数的解析式可化为y=k（x+1），易得其图象与x轴的交点为（﹣1，0），观察图形即可得出答案．【详解】函数的解析式可化为y=k（x+1），即函数图象与x轴的交点为（﹣1，0），观察四个选项可得：A符合．故选A．【点睛】本题考查了一次函数的图象，要求学生掌握通过解析判断其图象与坐标轴的交点位置、坐标．19．如图，经过点B（﹣2，0）的直线y＝kx+b与直线y＝4x+2相交于点A（﹣1，﹣2），4x+2＜kx+b＜0的解集为（）A．x＜﹣2 B．﹣2＜x＜﹣1 C．x＜﹣1 D．x＞﹣1【答案】B【解析】【分析】由图象得到直线y=kx+b与直线y=4x+2的交点A的坐标（-1，-2）及直线y=kx+b与x轴的交点坐标，观察直线y=4x+2落在直线y=kx+b的下方且直线y=kx+b落在x轴下方的部分对应的x的取值即为所求．【详解】∵经过点B（﹣2，0）的直线y＝kx+b与直线y＝4x+2相交于点A（﹣1，﹣2），∴直线y＝kx+b与直线y＝4x+2的交点A的坐标为（﹣1，﹣2），直线y＝kx+b与x轴的交点坐标为B（﹣2，0），又∵当x＜﹣1时，4x+2＜kx+b，当x＞﹣2时，kx+b＜0，∴不等式4x+2＜kx+b＜0的解集为﹣2＜x＜﹣1．故选B．【点睛】本题考查了一次函数与一元一次不等式的关系：从函数的角度看，就是寻求使一次函数y=ax+b的值大于（或小于）0的自变量x的取值范围；从函数图象的角度看，就是确定直线y=kx+b在x轴上（或下）方部分所有的点的横坐标所构成的集合．=-+的图象大致是( ) 20．已知点(k，b)为第二象限内的点，则一次函数y kx bA．B．C．D．【答案】D【解析】【分析】根据已知条件“点（k，b）为第二象限内的点”推知k、b的符号，由它们的符号可以得到一次函数y=-kx+b的图象所经过的象限．【详解】解：∵点（k，b）为第二象限内的点，∴k＜0，b＞0，∴-k＞0．∴一次函数y=-kx+b的图象经过第一、二、三象限，观察选项，D选项符合题意．故选：D．【点睛】本题主要考查一次函数图象在坐标平面内的位置与k、b的关系．解答本题注意理解：直线y=kx+b所在的位置与k、b的符号有直接的关系．k＞0时，直线必经过一、三象限；k＜0时，直线必经过二、四象限；b＞0时，直线与y轴正半轴相交；b=0时，直线过原点；b ＜0时，直线与y轴负半轴相交．。