人教版七年级数学下册第五章平行线的性质复习试题(含答案) (39)

人教版七年级数学下册第五章平行线的性质复习试题（含答案)如图，AB∥CD，∥F=90°，则∥1、∥2、∥3间的关系正确的是（）A．∥2=∥1+∥3 B．∥1+∥2+∥3=90°C．∥2+∥3-∥1=90°D．∥1+∥3-∥2=90°【答案】C【解析】【分析】分别过E、F作EG∥AB、HF∥CD,可得EG∥HF；然后运用平行线线的性质得到一系列相等的角，最后运用等量代换和角的和差解答即可．【详解】解：如图：分别过E、F作EG∥AB、HF∥CD∴EG∥HF∴∠6＝∠5∵EG∥AB∴∠1＝∠4∵CD∥HF∴∠7＝∠3∠∠C FE =90°∠∠6+∠7=90°∠∠6+∠3=90°∠∠6=90°-∠3又∠∠5+∠4=∠2∠∠5+∠1=∠2∠∠5=∠2-∠1又∠∠6＝∠5∠90°-∠3=∠2-∠1∠∠2+∠3-∠1=90°．故答案为C ．【点睛】本题主要考查了平行线的性质，作出辅助线、构造平行线并运用平行线的性质得到一系列相等的角是解答本题的关键．22．如图，直线AD BC ∥，30C ∠=︒，:1:3ADB BDC ∠∠=，则DBC ∠的度数是（ ）A ．35°B ．37.5°C ．45°D ．40°【答案】B【解析】【分析】 根据两直线平行，同旁内角互补，可得出18030015ADC ∠=︒-︒=︒，再结合:1:3ADB BDC ∠∠=即可得出ADB ∠的度数，最后，根据两直线平行，内错角相等即可得出答案．【详解】解：∵//AD BC ，30C ∠=︒∴18030015ADC ∠=︒-︒=︒∵:1:3ADB BDC ∠∠= ∴115037.513ADB ∠=︒⨯=︒+ ∴37.5DBC ADB ∠=∠=︒故选：B ．【点睛】本题考查的知识点是平行线的性质，难度不大，熟记平行线性质的内容是解此题的关键．23．如图，在三角形ABC 中，点D ，E 分别在AB 和AC 上，且DE BC ∥．若BE 平分ABC ∠，20ABE ∠=︒，则BDE ∠的度数为（ ）A ．140°B ．40°C ．120°D ．160°【答案】A【解析】【分析】利用角平分线的性质结合已知条件可知40ABC ∠=︒，再根据两直线平行，同旁内角互补即可得出答案．【详解】解：∵BE 平分ABC ∠，20ABE ∠=︒∴40ABC ∠=︒∵//DE BC∴180BDE ABC ∠+∠=︒∴140BDE ∠=︒故选：A ．【点睛】本题考查的知识点是平行线的性质以及角平分线，解此题的关键是利用角平分线的性质得出40ABC ∠=︒，牢记平行线的性质是解此题的关键．24．如图，AB CD ∥，CE 平分AED ∠，80EDC ∠=︒则ECD ∠=（ ）A ．40︒B ．45︒C ．50︒D ．55︒【答案】C【解析】【分析】根据平行线的性质和角平分线的定义即可得到结论．【详解】解：∵AB∥CD，∴∠AED=180°-∠EDC=100°，∵CE平分∠AED，∴∠AEC=12∠AED=50°，∵AB∥CD，∴∠ECD=∠AEC=50°，故选：C．【点睛】本题考查了平行线的性质，角平分线的定义，熟练掌握平行线的性质是解题的关键．25．如图，现将一块含有60︒角的三角板的顶点放在直尺的一边上，若12∠=∠，那么1∠的度数为（）A．50︒B．60︒C．70︒D．80︒【答案】B【解析】【分析】先根据两直线平行的性质得到∠3=∠2，再根据平角的定义列方程即可得解．【详解】∵AB ∥CD ，∴∠3=∠2，∵∠1=∠2，∴∠1=∠3，∴2∠3+60°=180°，∴∠3=60°，∴∠1=60°，故选：B ．【点睛】此题考查平行线的性质，三角板的知识，熟记性质是解题的关键．26．如图，12180∠+∠=︒，3100∠=︒，则4∠=（ ）A ．60︒B ．70︒C ．80︒D ．100︒【答案】C【解析】【分析】 首先证明a ∥b ，再根据两直线平行同位角相等可得∠3=∠6，再根据对顶角相等可得∠4．【详解】解：∵∠1+∠5=180°，∠1+∠2=180°，∴∠2=∠5，∴a ∥b ，∴∠3=∠6=100°，∴∠4=180°-100°=80°．故选：C ．【点睛】此题考查平行线的判定与性质，解题关键是掌握两直线平行同位角相等．27．如图，已知160∠=︒，260∠=︒，368∠=︒，则4∠等于（ ）A ．68︒B ．60︒C ．102︒D ．112︒【答案】D【解析】【分析】 根据∠1=∠2，得a ∥b ，进而得到∠5=3∠，结合平角的定义，即可求解．【详解】∵160∠=︒，260∠=︒，∴∠1=∠2，∴a ∥b ，∴∠5=368∠=︒，∴∠4=180°-∠5=112︒．故选D ．【点睛】本题主要考查平行线的判定和性质定理以及平角的定义，掌握“同位角相等两直线平行”，“两直线平行，同位角相等”，是解题的关键．28．一把直尺和一块三角板ABC （含30°，60°角）的摆放位置如图，直尺一边与三角板的两直角边分别交于点D 、点E ，另一边与三角板的两直角边分别交于点F 、点A ，且∠CED ＝50°，那么∠BAF ＝（ ）A ．10°B ．50°C ．45°D ．40°【答案】A【解析】【分析】先根据∠CED＝50°，DE∥AF，即可得到∠CAF＝50°，最后根据∠BAC ＝60°，即可得出∠BAF的大小．【详解】∵DE∥AF，∠CED＝50°，∴∠CAF＝∠CED＝50°，∵∠BAC＝60°，∴∠BAF＝60°﹣50°＝10°，故选：A．【点睛】此题考查平行线的性质，几何图形中角的和差关系，掌握平行线的性质是解题的关键.∠=︒，则2∠的度29．如图所示是一架梯子，它的各条横档互相平行，198数是（）A．72°B．82°C．92°D．98°【答案】B【解析】【分析】本题考查“两直线平行，同位角相等”以及邻补角，结合邻补角互补即可解答．【详解】如下图所示∵1∠=98°∴∠3=180°-98°=82°又因为两直线平行所以∠2=∠3=82°故答案为B 选项．【点睛】两直线平行，同位角相等、内错角相等、同旁内角互补要熟练记忆，求解几何图形角度时，利用邻补角互补解题也极为常见．二、解答题30．完成下列的推理说明：已知：如图，BE//CF ，BE 、CF 分别平分ABC ∠和BCD ∠．求证：AB//CD ．证明：BE 、CF 分别平分ABC ∠和BCD ∠（已知）112∴∠=∠________．122∠=∠________（________） BE//CF （________）12∠∠∴=（________）1122ABC BCD ∴∠=∠（________） ABC BCD ∴∠=∠（等式的性质）AB//CD （________）【答案】ABC ；BCD ；角平分线的定义；已知；两直线平行，内错角相等；等量代换；内错角相等，两直线平行．【解析】【分析】先根据角平分线的定义得出∠1与∠ABC 、∠2与∠BCD 的关系，然后根据平行线的性质可得∠1=∠2，进而可得∠ABC 与∠BCD 的关系，再根据平行线的判定即得结论．【详解】证明：BE 、CF 分别平分ABC ∠和BCD ∠（已知），112ABC ∴∠=∠，122BCD ∠=∠（角平分线的定义）， //BE CF （已知），12∠∠∴=（两直线平行，内错角相等），1122ABC BCD ∴∠=∠（等量代换）， ABC BCD ∴∠=∠（等式的性质），//AB CD ∴（内错角相等，两直线平行）．故答案为：ABC；BCD；角平分线的定义；已知；两直线平行，内错角相等；等量代换；内错角相等，两直线平行．【点睛】本题考查了角平分线的定义以及平行线的判定与性质，属于常见题型，熟练掌握平行线的判定和性质是解题关键．。

人教版七年级数学下册第五章平行线的性质作业练习题（含答案)如图，已知,DAF F B D ∠=∠∠=∠求证：AB DC .【答案】见解析【解析】【分析】根据平行线的判定推出AD//BC ，根据平行线的性质得出∠D=∠DCF ，求出∠DCF=∠B ，根据平行线的判定得出即可。

【详解】证明：∵∠DAF=∠F ，∴AD//BC ，∴∠D=∠DCF ，∵∠B=∠D ，∴∠DCF=∠B ，∴AB ∥DC.【点睛】本题考查了平行线的性质和判定的应用，能综合运用性质和判定进行推理是解此题的关键.42．如图所示，已知∠1+∠2=180°，∠B=∠3，求证：∠ACB=∠AED．【答案】见解析.【解析】【分析】根据平行线的判定和性质定理证明即可．【详解】证明：∵∠1+∠2=180°，∠1+∠4=180°∴∠2=∠4，∴BD∥EF（内错角相等、两直线平行）∴∠3=∠ADE（两直线平行，内错角相等）∵∠B=∠3∴∠ADE=∠B∴DE∥BC（同位角相等、两直线平行）∴∠ACB=∠AED（两直线平行，同位角相等）．【点睛】本题考查的是平行线的判定和性质，掌握平行线的判定定理和性质定理是解题的关键．43．已知：如图（1），如果AB∥CD∥EF. 那么∠BAC+∠ACE+∠CEF=360°.老师要求学生在完成这道教材上的题目后，尝试对图形进行变式，继续做拓展探究，看看有什么新发现？（1）小华首先完成了对这道题的证明，在证明过程中她用到了平行线的一条性质，小华用到的平行线性质可能是______________.（2）接下来，小华用《几何画板》对图形进行了变式，她先画了两条平行线AB，EF，然后在平行线间画了一点C，连接AC，EC后，用鼠标拖动点C，分别得到了图（2）（3）（4），小华发现图（3）正是上面题目的原型，于是她由上题的结论猜想到图（2）和（4）中的∠BAC，∠ACE与∠CEF之间也可能存在着某种数量关系．然后，她利用《几何画板》的度量与计算功能，找到了这三个角之间的数量关系.请你在小华操作探究的基础上，继续完成下面的问题：①猜想：图（2）中∠BAC，∠ACE与∠CEF之间的数量关系： .②补全图（4），并直接写出图中∠BAC，∠ACE与∠CEF之间的数量关系： . （3）小华继续探究：如图（5），若直线AB与直线EF不平行，点G，H分别在直线AB、直线EF上，点C在两直线外，连接CG，CH，GH，且GH同时平分∠BGC和∠FHC，请探索∠AGC，∠GCH与∠CHE之间的数量关系？并说明理由.【答案】（1）两直线平行，同旁内角互补.（2）①∠ACE=∠BAC+∠FEC.②∠ACE=∠FEC-∠BAC．（3）2∠GCH=∠AGC+∠CHE．【解析】【分析】（1）根据两直线平行同旁内角互补即可解决问题；（2）①猜想∠ACE=∠BAC+∠FEC．过点C作CD∥AB．利用平行线的性质即可解决问题；②∠BAC，∠ACE与∠CEF之间的数量关系是∠ACE=∠FEC-∠BAC．利用平行线的性质以及三角形的外角的性质即可解决问题；（3）延长AB，EF，交于点P，依据∠CGP=180°-∠AGC，∠CHP=180°-∠CHE，即可得到∠CGP+∠CHP=360°-（∠AGC+∠CHE），再根据四边形内角和，即可得到四边形GCHP中，∠C+∠P=360°-（∠CGP+∠CH）=∠AGC+∠CHE，进而得出结论．【详解】(1)如图，∵AB∥CD∥EF∴∠BAC+∠ACD=180°,（两直线平行，同旁内角互补）∠DCE+∠CEF=180°,（两直线平行，同旁内角互补）∴∠BAC+∠ACD+∠DCE+∠CEF=∠BAC+∠ACE+∠CEF=360°.故答案为：两直线平行，同旁内角互补.（2）①图（2）中∠BAC，∠ACE与∠CEF之间的数量关系：∠ACE=∠BAC+∠FEC.证明：过点C作CD∥AB，如图，∴∠BAC=∠ACD，∵AB∥EF，∴EF∥CD，∴∠DCE=∠CEF∴∠ACD+∠DCE=∠BAC+∠CEF，即∠ACE=∠BAC+∠FEC.②连接AC，CE交AB于点D，如图，∵AB∥EF∴∠BDC=∠CEF，∵∠BDC=∠BAC+∠ACE∴∠CEF=∠BAC+∠ACE，即∠ACE=∠FEC-∠BAC．(3) 延长AB，EF，交于点P，如图，∵GH同时平分∠BGC和∠FHC，∴∠CGH=∠BGH，∠CHG=∠FHG，∴∠C=∠P，∵∠CGP=180°-∠AGC，∠CHP=180°-∠CHE，∴∠CGP+∠CHP=360°-（∠AGC+∠CHE），∵四边形GCHP中，∠C+∠P=360°-（∠CGP+∠CH）=360°-[360°-（∠AGC+∠CHE）]= ∠AGC+∠CHE，即2∠GCH=∠AGC+∠CHE．【点睛】本题主要考查了平行线的性质，解决问题的关键是作平行线构造内错角，利用两直线平行，内错角相等得出结论．44．如图，已知AB∥CD，点E在BC的延长线上，AE与CD交于点F，∠1=∠2，∠3=∠4，试判断AD与BE的位置关系，并说明为什么．【答案】AD∥BE，理由见解析.【解析】【分析】根据平行线的性质推出∠1=∠ACD，求出∠2=∠ACD，根据∠2+∠CAF=∠ACD+∠CAF推出∠DAC=∠4，求出∠DAC=∠3，根据平行线的判定得出即可．【详解】AD∥BE，理由：∵AB∥CD，∴∠1=∠ACD，∵∠1=∠2，∴∠2=∠ACD，∴∠2+∠CAE=∠ACD+∠CAE，∴∠DAC=∠4，∵∠3=∠4，∴∠DAC=∠3，∴AD∥BE．【点睛】本题考查了平行线的性质和判定，三角形的外角性质的应用，能推出∠4=∠DAC=∠3是解此题的关键，注意：平行线的性质有：①两直线平行，同位角相等，②两直线平行，内错角相等，③两直线平行，同旁内角互补，反之亦然．45．如图，AB∥CD，BO与CD交于点O，OE⊥BO，OF平分∠BOD．若∠ABO=50°，求∠EOF的度数．【答案】115°．【解析】【分析】先根据平行线的性质求出∠BOD的度数，再根据OF平分∠BOD求出∠BOF的度数，再根据∠EOF=∠EOB+∠BOF即可得出结论．【详解】∵AB∥CD，∠ABO=50°，∴∠BOD=∠ABO=50°，∵OF平分∠BOD，∴∠BOF=12∠BOD=25°，∵OE⊥BO，∴∠EOB=90°，∴∠EOF=∠EOB+∠BOF=90°+25°=115°．【点睛】本题考查的是平行线的性质，用到的知识点为：两直线平行，内错角相等．46．如图，已知∠1＋∠2＝180o, ∠3＝∠B，试说明∠DEC＋∠C＝180o.请完成下列填空：解：∵∠1＋∠2＝180o(已知)又∵∠1＋∠4＝180o(平角定义)∴∠2＝∠4(________)∴______∥______(_________)∴∠3 ＝∠ADE(__________)又∵∠3＝∠B(已知)∴∠ADE＝∠B(等量代换)∴BC∥_____(_________)∴∠DEC＋∠C＝180o(__________)【答案】同角的补角相等；AB；EF；内错角相等，两直线平行；两直线平行，内错角相等；BE；同位角相等，两直线平行；两直线平行，同旁内角互补【解析】【分析】根据补角的性质，平行线的性质与判定方法即可解答．【详解】解：∵∠1＋∠2＝180°(已知)，又∵∠1＋∠4＝180°(平角定义)，∴∠2＝∠4(同角的补角相等)，∴AB∥EF(内错角相等，两直线平行)，∴∠3＝∠ADE(两直线平行，内错角相等)，又∵∠3＝∠B(已知)，∴∠ADE＝∠B(等量代换)，∴BC∥DE(同位角相等，两直线平行)，∴∠DEC＋∠C＝180°(两直线平行，同旁内角互补)，【点睛】本题考查了平行线的性质定理以及判定定理，理解定理是关键．47．完成下面的证明．如图，已知AB∥CD，∠B=∠C，求证：∠1=∠2．证明：∵AB∥CD（已知）∴∠B= （）．∵∠B=∠C（已知）∴∠BFD=∠C（等量代换）∴EC∥（）∴∠2= （两直线平行，同位角相等）∵∠1= （）∴∠1=∠2（等量代换）．【答案】∠BFD，两直线平行，内错角相等；BF（或FG），同位角相等，两直线平行；∠CHD（或∠CHG）；∠CHD（或∠CHG），对顶角相等；【解析】【分析】根据题目过程，结合平行的性质与判定即可完成.【详解】证明：∵AB∥CD（已知）∴∠B= ∠BFD （两直线平行，内错角相等）．∵∠B=∠C（已知）∴∠BFD=∠C（等量代换）∴EC∥BF（或FG）（同位角相等，两直线平行）∴∠2= ∠CHD（或∠CHG）（两直线平行，同位角相等）∵∠1= ∠CHD（或∠CHG）（对顶角相等）∴∠1=∠2（等量代换）．【点睛】本题考查平行线的性质和判定，难度较低，熟练掌握平行线的相关性质定理是解题关键.48．如图，已知12l l //，且3l 与1l ，2l 分别交于A ，B 两点，点P 在直线AB上.（1）当点P 在A ，B 两点之间运动时，求1∠，2∠，3∠之间的数量关系，并说明理由.（2）如果点P 在A ，B 两点外侧运动，试探究1∠，2∠，3∠之间的数量关系（点P 与A ，B 不重合），并说明理由.【答案】（1）123∠+∠=∠，见解析；（2）123∠-∠=∠或213∠-∠=∠，见解析.【解析】【分析】（1）过点P 作l 1的平行线，根据平行线的性质进行解题；（2）当点P 在下侧时，过点P 作l 1的平行线PQ ，由平行线的性质可得出l 1∥l 2∥PQ ，由此即可得出结论．【详解】（1）123∠+∠=∠.理由如下：如图所示，过点P 作1//PQ l .12//l l ，12////l l PQ ∴，14∴∠=∠，25∠=∠.453∠+∠=∠，123∴∠+∠=∠.（2）123∠-∠=∠或213∠-∠=∠.理由如下：如图所示，当点P 在下侧时，过点P 作1l 的平行线PQ.12//l l ，12////l l PQ ∴，24∴∠=∠，134∠=∠+∠，123∴∠-∠=∠.当点P 在上侧时，同理可得213∠-∠=∠.【点睛】本题考查的是平行线的性质，根据题意作出辅助线是解答此题的关键．49．如图, ∠B 、∠D 的两边分别平行。

小专题（一）平行线中的“拐点”问题模型1 M型【例1】如图，已知AB∥CD，则∠B，∠BED，∠D之间有何数量关系？请说明理由．【思路点拨】由已知条件知，AB∥CD，但图形中没有截这两条平行线的第三条直线，因而不能直接用平行线的性质解决．为此可构造第三条直线，即过点E 作EF∥AB，于是BE，DE就可以作为第三条直线了．变式当点E运动到平行线的外侧1．已知AB∥CD，点E为AB，CD之外任意一点．(1)如图1，探究∠BED与∠B，∠D的数量关系，并说明理由；(2)如图2，探究∠CDE与∠B，∠BED的数量关系，并说明理由．2．(1)如图1中，AB∥CD，则∠E＋∠G与∠B＋∠F＋∠D有何关系？(2)在图2中，若AB∥CD，又能得到什么结论？如果出现多个拐点时，可以作多条平行线，从而将多拐点问题转化为一个拐点问题来处理．M型最终的结论为：朝左的角之和等于朝右的角之和．模型2 铅笔型【例2】如图，直线AB∥CD，∠B，∠BED，∠D之间有什么关系呢？为什么？3．(1)①如图1，MA1∥NA2，则∠A1＋∠A2＝度；②如图2，MA1∥NA3，则∠A1＋∠A2＋∠A3＝度；③如图3，MA1∥NA4，则∠A1＋∠A2＋∠A3＋∠A4＝度；④图4，MA1∥NA5，则∠A1＋∠A2＋∠A3＋∠A4＋∠A5＝度；从上述结论中你发现了什么规律？(2)如图5，MA1∥NAn，则∠A1＋∠A2＋∠A3＋…＋∠An＝度．小专题(二) 利用平行线的性质求角的度数类型1 直接利用平行线的性质与判定求角度1．如图，OC是∠AOB的平分线，l∥OB.若∠1＝52°，则∠2的度数为( ) A．52° B．54° C．64° D．69°2．如图，CD∥AB，点O在AB上，OE平分∠BOD，OF⊥OE，∠D＝110°，则∠AOF 的度数是( )A．20° B．25° C．30° D．35°3．如图，AB∥CD，CB∥DE，∠B＝50°，则∠D＝．4．如图，已知EF∥AD，∠1＝∠2，∠BAC＝80°，求∠AGD的度数．类型2 借助学具的特征求角度5．如图，将直尺与30°角的三角尺叠放在一起．若∠1＝40°，则∠2的大小是( )A．40° B．60° C．70° D．80°6．如图，一块直角三角板的两锐角的顶点刚好落在平行线l1，l2上，已知∠C是直角，则∠1＋∠2的度数等于( )A．75° B．90° C．105° D．120°类型3 折叠问题中求角度7．将一个长方形纸片折叠成如图所示的图形．若∠ABC＝26°，则∠ACD＝．8．如图，一个四边形纸片ABCD，∠B＝∠D＝90°，∠C＝130°.把纸片按如图所示折叠，使点B落在AD边上的B′点，AE是折痕，则∠AEB的度数是．类型4 抽象出平行线模型求角度(建模思想)9．如图，∠AOB的一边OA为平面镜，∠AOB＝38°，一束光线(与水平线OB平行)从点C射入经平面镜反射后，反射光线落在OB上的点E处，已知∠ADC＝∠ODE.则∠DEB的度数是度．10．如图1是我们常用的折叠式小刀，图2中刀柄外形是一个梯形挖去一个小半圆，其中刀片的两条边缘线可看成两条平行的线段，转动刀片时会形成如图2所示的∠1与∠2，则∠1与∠2的度数和是．小专题(三) 平行线的性质与判定的综合运用——教材P37T13的变式与应用教材母题(教材P37T13)：完成下面的证明．(1)如图1，点D，E，F分别是三角形ABC的边BC，CA，AB上的点，DE∥BA，DF ∥CA.求证：∠FDE＝∠A.证明：∵DE∥BA，∴∠FDE＝．∵DF∥CA，∴∠A＝．∴∠FDE＝∠A.(2)如图2，AB和CD相交于点O，∠C＝∠COA，∠D＝∠BOD.求证AC∥BD.证明：∵∠C＝∠COA，∠D＝∠BOD，又∠COA＝∠BOD( )，∴∠C＝．∴AC∥BD(内错角相等，两直线平行)．(1)判定两直线平行的方法有五种：①平行线的定义；②平行公理的推论；③同位角相等，两直线平行；④内错角相等，两直线平行；⑤同旁内角互补，两直线平行．(2)判定两直线平行时，定义一般不常用，其他四种方法要灵活运用，推理时要注意书写格式．(3)由两条直线平行得到同位角相等、内错角相等或同旁内角互补，解题时应结合图形先确认所成的角是不是两平行线被第三条直线所截得的同位角或内错角或同旁内角，同时要学会简单的几何说理，做到每一步有理有据．1．如图，已知AD⊥BC，EF⊥BC，垂足分别为D，F，∠2＋∠3＝180°.试说明：∠GDC＝∠B.下面是不完整的说理过程，请你将横线上的过程和括号里的理由补充完整．解：因为AD⊥BC，EF⊥BC(已知)，①所以∠ADB＝∠EFB＝ (垂直的定义)．②所以 (同位角相等，两直线平行)．③所以∠1＋∠2＝ (两直线平行，同旁内角互补)．④又因为∠2＋∠3＝180°( )，⑤所以∠1＝∠3( )．⑥所以AB∥DG( )．⑦所以∠GDC＝∠B( )．2．如图，点G在射线BC上，射线DE与AB，AG分别交于点H，M.若DF∥AB，∠B＝75°，∠D＝105°，求证：∠AME＝∠AGC.3．如图，AB∥CD，AE平分∠BAD，CD与AE相交于点F，∠CFE＝∠E.求证：AD ∥BC.4．如图，∠E＝∠1，∠3＋∠ABC＝180°，BE是∠ABC的平分线．你能判断DF 与AB的位置关系吗？请说明理由．5．如图，AB⊥BD于点B，点E是BD上的点，AE平分∠BAC，CE平分∠ACD，且∠1＋∠2＝90°.求证：CD⊥BD.6．如图，把一张长方形ABCD的纸片沿EF折叠后，ED与BC的交点为G，点D，C分别落在D′，C′的位置上．若∠EFG＝55°，求∠1，∠2的度数．7．如图，已知BC∥GE，∠AFG＝∠1＝50°.(1)求证：AF∥DE；(2)若AQ平分∠FAC，交BC于点Q，且∠Q＝15°，求∠ACQ的度数．参考答案：小专题（一）平行线中的“拐点”问题模型1 M型【例1】如图，已知AB∥CD，则∠B，∠BED，∠D之间有何数量关系？请说明理由．【思路点拨】由已知条件知，AB∥CD，但图形中没有截这两条平行线的第三条直线，因而不能直接用平行线的性质解决．为此可构造第三条直线，即过点E 作EF∥AB，于是BE，DE就可以作为第三条直线了．【解答】∠BED＝∠B＋∠D.理由：过点E作EF∥AB，则EF∥CD.∴∠B＝∠BEF，∠D＝∠DEF.∴∠BED＝∠BEF＋∠DEF＝∠B＋∠D.变式当点E运动到平行线的外侧1．已知AB∥CD，点E为AB，CD之外任意一点．(1)如图1，探究∠BED与∠B，∠D的数量关系，并说明理由；(2)如图2，探究∠CDE与∠B，∠BED的数量关系，并说明理由．解：(1)∠B＝∠BED＋∠D.理由如下：过点E作EF∥AB，则AB∥CD∥EF.∴∠BEF＝∠B，∠D＝∠DEF.∵∠BEF＝∠BED＋∠DEF，∴∠B＝∠BED＋∠D.(2)∠CDE＝∠B＋∠BED.理由如下：过点E作EF∥AB，则AB∥CD∥EF.∴∠B＋∠BEF＝180°，∠CDE＋∠DEF＝180°.又∵∠DEF＝∠BEF－∠BED，∴∠CDE＋∠BEF－∠BED＝∠B＋∠BEF，即∠CDE＝∠B＋∠BED.拓展平行线间有多个拐点2．(1)如图1中，AB∥CD，则∠E＋∠G与∠B＋∠F＋∠D有何关系？(2)在图2中，若AB∥CD，又能得到什么结论？解：(1)∠BEF＋∠FGD＝∠B＋∠EFG＋∠D.理由：过点E，F，G分别作EM∥AB，FN∥AB，GH∥AB，由AB∥CD，得AB∥EM∥FN∥GH∥CD.∴∠BEM＝∠B，∠MEF＝∠EFN，∠NFG＝∠FGH，∠HGD＝∠D.∴∠BEF＋∠FGD＝∠BEM＋∠MEF＋∠FGH＋∠HGD＝∠B＋∠EFN＋∠NFG＋∠D＝∠B＋∠EFG＋∠D.(2)在图2中，有∠E1＋∠E2＋∠E3＋…＋∠En＝∠B＋∠F1＋∠F2＋…＋∠Fn－1＋∠D.如果出现多个拐点时，可以作多条平行线，从而将多拐点问题转化为一个拐点问题来处理．M型最终的结论为：朝左的角之和等于朝右的角之和．模型2 铅笔型【例2】如图，直线AB∥CD，∠B，∠BED，∠D之间有什么关系呢？为什么？【解答】∠B＋∠BED＋∠D＝360°.理由：过点E作EF∥AB.∵AB∥CD，∴AB∥CD∥EF.∴∠B＋∠BEF＝180°，∠D＋∠DEF＝180°. ∴∠B＋∠BEF＋∠D＋∠DEF＝360°，即∠B＋∠BED＋∠D＝360°.拓展平行线间有多个拐点3．(1)①如图1，MA1∥NA2，则∠A1＋∠A2＝180度；②如图2，MA1∥NA3，则∠A1＋∠A2＋∠A3＝360度；③如图3，MA1∥NA4，则∠A1＋∠A2＋∠A3＋∠A4＝540度；④图4，MA1∥NA5，则∠A1＋∠A2＋∠A3＋∠A4＋∠A5＝720度；从上述结论中你发现了什么规律？(2)如图5，MA1∥NAn，则∠A1＋∠A2＋∠A3＋…＋∠An＝180(n－1)度．解：每增加一个角，度数增加180°.小专题(二) 利用平行线的性质求角的度数类型1 直接利用平行线的性质与判定求角度1．如图，OC是∠AOB的平分线，l∥OB.若∠1＝52°，则∠2的度数为( C ) A．52° B．54° C．64° D．69°2．如图，CD∥AB，点O在AB上，OE平分∠BOD，OF⊥OE，∠D＝110°，则∠AOF 的度数是( D )A．20° B．25° C．30°D．35°3．如图，AB∥CD，CB∥DE，∠B＝50°，则∠D＝130°．4．如图，已知EF∥AD，∠1＝∠2，∠BAC＝80°，求∠AGD的度数．解：∵EF∥AD，∴∠2＝∠3(两直线平行，同位角相等)．∵∠1＝∠2，∴∠1＝∠3(等量代换)．∴AB∥DG(内错角相等，两直线平行)．∴∠BAC＋∠AGD＝180°(两直线平行，同旁内角互补)．∵∠BAC＝80°，∴∠AGD＝100°.类型2 借助学具的特征求角度5．如图，将直尺与30°角的三角尺叠放在一起．若∠1＝40°，则∠2的大小是( D )A．40° B．60° C．70° D．80°6．如图，一块直角三角板的两锐角的顶点刚好落在平行线l1，l2上，已知∠C是直角，则∠1＋∠2的度数等于( B )A．75° B．90° C．105° D．120°类型3 折叠问题中求角度7．将一个长方形纸片折叠成如图所示的图形．若∠ABC＝26°，则∠ACD＝128°．8．如图，一个四边形纸片ABCD，∠B＝∠D＝90°，∠C＝130°.把纸片按如图所示折叠，使点B落在AD边上的B′点，AE是折痕，则∠AEB的度数是65°．类型4 抽象出平行线模型求角度(建模思想)9．如图，∠AOB的一边OA为平面镜，∠AOB＝38°，一束光线(与水平线OB平行)从点C射入经平面镜反射后，反射光线落在OB上的点E处，已知∠ADC＝∠ODE.则∠DEB的度数是76度．10．如图1是我们常用的折叠式小刀，图2中刀柄外形是一个梯形挖去一个小半圆，其中刀片的两条边缘线可看成两条平行的线段，转动刀片时会形成如图2所示的∠1与∠2，则∠1与∠2的度数和是90°．小专题(三) 平行线的性质与判定的综合运用——教材P37T13的变式与应用教材母题(教材P37T13)：完成下面的证明．(1)如图1，点D，E，F分别是三角形ABC的边BC，CA，AB上的点，DE∥BA，DF ∥CA.求证：∠FDE＝∠A.证明：∵DE∥BA，∴∠FDE＝∠BFD(两直线平行，内错角相等)．∵DF∥CA，∴∠A＝∠BFD(两直线平行，同位角相等)．∴∠FDE＝∠A.(2)如图2，AB和CD相交于点O，∠C＝∠COA，∠D＝∠BOD.求证AC∥BD.证明：∵∠C＝∠COA，∠D＝∠BOD，又∠COA＝∠BOD(对顶角相等)，∴∠C＝∠D．∴AC∥BD(内错角相等，两直线平行)．(1)判定两直线平行的方法有五种：①平行线的定义；②平行公理的推论；③同位角相等，两直线平行；④内错角相等，两直线平行；⑤同旁内角互补，两直线平行．(2)判定两直线平行时，定义一般不常用，其他四种方法要灵活运用，推理时要注意书写格式．(3)由两条直线平行得到同位角相等、内错角相等或同旁内角互补，解题时应结合图形先确认所成的角是不是两平行线被第三条直线所截得的同位角或内错角或同旁内角，同时要学会简单的几何说理，做到每一步有理有据．1．如图，已知AD⊥BC，EF⊥BC，垂足分别为D，F，∠2＋∠3＝180°.试说明：∠GDC＝∠B.下面是不完整的说理过程，请你将横线上的过程和括号里的理由补充完整．解：因为AD⊥BC，EF⊥BC(已知)，①所以∠ADB＝∠EFB＝90°(垂直的定义)．②所以AD∥EF(同位角相等，两直线平行)．③所以∠1＋∠2＝180°(两直线平行，同旁内角互补)．④又因为∠2＋∠3＝180°(已知)，⑤所以∠1＝∠3(同角的补角相等)．⑥所以AB∥DG(内错角相等，两直线平行)．⑦所以∠GDC＝∠B(两直线平行，同位角相等)．2．如图，点G在射线BC上，射线DE与AB，AG分别交于点H，M.若DF∥AB，∠B＝75°，∠D＝105°，求证：∠AME＝∠AGC.证明：∵DF∥AB(已知)，∴∠D＝∠BHM(两直线平行，同位角相等)．又∵∠B＝75°，∠D＝105°(已知)，∴∠B＋∠BHM＝75°＋105°＝180°.∴DE∥BC(同旁内角互补，两直线平行)．∴∠AME＝∠AGC(两直线平行，同位角相等)．3．如图，AB∥CD，AE平分∠BAD，CD与AE相交于点F，∠CFE＝∠E.求证：AD ∥BC.证明：∵AE平分∠BAD(已知)，∴∠1＝∠2(角平分线的定义)．∵AB∥CD(已知)，∴∠1＝∠CFE(两直线平行，同位角相等)．又∵∠1＝∠2(已证)，∠CFE＝∠E(已知)，∴∠2＝∠E(等量代换)．∴AD∥BC(内错角相等，两直线平行)．4．如图，∠E＝∠1，∠3＋∠ABC＝180°，BE是∠ABC的平分线．你能判断DF 与AB的位置关系吗？请说明理由．解：DF∥AB.理由：∵BE是∠ABC的平分线，∴∠1＝∠2(角平分线的定义)．∵∠E＝∠1(已知)，∴∠E＝∠2(等量代换)．∴AE∥BC(内错角相等，两直线平行)．∴∠A＋∠ABC＝180°(两直线平行，同旁内角互补)．∵∠3＋∠ABC＝180°(已知)，∴∠A＝∠3(等量代换)．∴DF∥AB(同位角相等，两直线平行)．5．如图，AB⊥BD于点B，点E是BD上的点，AE平分∠BAC，CE平分∠ACD，且∠1＋∠2＝90°.求证：CD⊥BD.证明：∵AE平分∠BAC，CE平分∠ACD(已知)，∴∠BAC＝2∠1，∠ACD＝2∠2(角平分线的性质)．∴∠BAC＋∠ACD＝2∠1＋2∠2＝2(∠1＋∠2)．∵∠1＋∠2＝90°(已知)，∴∠BAC＋∠ACD＝180°.∴AB∥CD(同旁内角互补，两直线平行)．∴∠B＋∠D＝180°(两直线平行，同旁内角互补)．∴∠D＝180°－∠B(等式的性质)．∵AB⊥BD(已知)，∴∠B＝90°(垂直的定义)．∴∠D＝90°，即CD⊥BD.6．如图，把一张长方形ABCD的纸片沿EF折叠后，ED与BC的交点为G，点D，C分别落在D′，C′的位置上．若∠EFG＝55°，求∠1，∠2的度数．解：∵AD∥BC，∠EFG＝55°，∴∠2＝∠GED，∠DEF＝∠EFG＝55°(两直线平行，内错角相等)．由折叠，知∠GEF＝∠DEF＝55°.∴∠GED＝110°.∴∠2＝110°.∴∠1＝180°－∠2＝70°(两直线平行，同旁内角互补)．7．如图，已知BC∥GE，∠AFG＝∠1＝50°.(1)求证：AF∥DE；(2)若AQ平分∠FAC，交BC于点Q，且∠Q＝15°，求∠ACQ的度数．解：(1)证明：∵BC∥GE，∴∠E＝∠1＝50°.∵∠AFG＝∠1＝50°，∴∠E＝∠AFG＝50°.∴AF∥DE.(2)过点A作AP∥GE，∵BC∥GE，∴AP∥GE∥BC.∴∠FAP＝∠AFG＝50°，∠PAQ＝∠Q＝15°.∴∠FAQ＝∠FAP＋∠PAQ＝65°.∵AQ平分∠FAC，∴∠CAQ＝∠FAQ＝65°.∴∠CAP＝80°.∴∠ACQ＝180°－∠CAP＝100°.。

人教版七年级数学下册第五章平行线的性质复习试题（含答案)如图，已知A C ∠=∠，E F ∠=∠，试说明：//AD BC ，【答案】见解析【解析】【分析】由∠E ＝∠F ，根据内错角相等，两直线平行得AE ∥CF ，根据平行线的性质得∠A ＝∠ADF ，利用等量代换得到∠ADF ＝∠C ，然后根据同位角相等，两直线平行可判定AD ∥BC ．【详解】证明：∵E F ∠=∠，∵//AE CF ，∵A ADF ∠=∠，∵A C ∠=∠，∵ADF C =∠∠，∵//AD BC ，【点睛】本题考查了平行线的判定与性质：同位角相等，两直线平行；内错角相等，两直线平行；两直线平行，内错角相等．62．如图，在四边形ABCD中，∠A+∠ABC＝180°，BD⊥CD于点D，EF⊥CD于点F，则∠1＝∠2吗？请说明理由？【答案】∠1＝∠2，理由见解析【解析】【分析】由∠A+∠ABC＝180°，可以判断AD∥BC，进而得到∠1＝∠DBC，由BD⊥CD，EF⊥CD，可得BD∥EF，进而得到∠DBC＝∠2，于是得出结论．【详解】解：∠1＝∠2，理由：∵∠A+∠ABC＝180°，∴AD∥BC，∴∠1＝∠DBC，∵BD⊥CD，EF⊥CD，∴BD∥EF，∴∠DBC＝∠2，∴∠1＝∠2．【点睛】本题考查平行线的性质和判定，掌握平行线的性质和判定是正确得出结论的前提．∠=∠，1∠与2∠互补．63．如图所示，AD与BE相交于点F，A C(1)试说明//AB CE ；(2)若295∠=︒，59C ∠=︒，求E ∠的度数．【答案】（1）见解析；（2）∠E ＝26°【解析】【分析】（1）先由∠1＝∠BFD 得出∠BFD ＋∠2＝180°，故可得出AD ∥BC ，故可得出∠ADE ＝∠C ，据此可得出∠A ＝∠ADE ，进而得出结论；（2）直接根据三角形内角和的性质即可得出结论．【详解】（1）∵∠1＝∠BFD ，∠1＋∠2＝180°，∴∠BFD ＋∠2＝180°，∴AD ∥BC ，∴∠ADE ＝∠C ，∴∠A ＝∠ADE ，∴AB ∥CE ；（2）∵∠2＝95°，∠C ＝59°，∠E ＋∠2＋∠C ＝180°∴∠E ＝180°−95°−59°＝26°．【点睛】本题考查的是平行线的判定与性质，熟知平行线的判定定理是解答此题的关键．64．如图，已知EF ∥AB ，1B ∠=∠，求证：EDC DCB ∠=∠．【答案】见解析【解析】【分析】证明∠EDC=∠DCB ，只需具备DE ∥BC 即可，可以考虑证得∠ADE=∠B ，而∠1与这两个角都相等．【详解】证明：∵EF ∥AB ，∴∠1=∠ADE ，∵∠1=∠B ，∴∠ADE=∠B ，∴DE ∥BC ，∴∠EDC=∠DCB ．【点睛】本题主要考查了平行线的性质与判定，平行线的判定是由角的数量关系判断两直线的位置关系，平行线的性质是由平行关系来寻找角的数量关系．65． 如图，EF ∥AD ，AD ∥BC ，CE 平分∠BCF ，∠DAC=3∠BCF ，∠ACF=20°．（1）求∠FEC的度数；（2）若∠BAC=3∠B，求证：AB⊥AC；（3）当∠DAB=______度时，∠BAC=∠AEC．（请直接填出结果，不用证明）【答案】（1）20°；（2）详见解析；（3）50【解析】【分析】（1）先根据CE平分∠BCF，设∠BCE=∠ECF=12∠BCF=x．由∠DAC=3∠BCF可得出∠DAC=6x．根据AD∥EF，AD∥BC，得出EF∥BC，由平行线的性质即可得出x的值，进而得出结论；（2）根据AD∥BC可知∠DAB=∠B，再由∠BAC=3∠B得出∠DAC=4∠B=120°，故∠B=30°，∠BAC=90°，由此可得出结论；（3）根据（1）可得出∠BCF的度数，设∠BAD=∠B=α，由∠BAC=∠AEC 即可得出结论．【详解】解：（1）∵CE平分∠BCF，∴设∠BCE=∠ECF=12∠BCF=x．∵∠DAC=3∠BCF，∴∠DAC=6x．∵AD∥BC，∴∠DAC+∠ACB=180°，∴6x+2x+20°=180°，∴x=20°，即∠BCE=20°，∵EF∥AD，AD∥BC，∴EF∥BC，∴∠BCE=∠FEC=20°；（2）证明：∵AD∥BC，∴∠DAB=∠B，又∵∠BAC=3∠B，∴∠DAC=4∠B，由（1）可得∠BCA=20°×3=60°，∴∠DAC=4∠B=120°，∴∠B=30°，∴∠BAC=30°×3=90°，∴AB⊥AC；（3）由（1）知∠BCE=20°，∴∠BCF=40°．∴∠DAC=3×40°=120°，∵AD∥BC，∴可设∠BAD=∠B=α，∴∠AEC=∠B+∠BCE=α+20°，∠BAC=∠DAC-∠DAB=120°-α，∴当∠BAC=∠AEC时，α+20°=120°-α，解得α=50°，∴∠DAB=50°．故答案为：50．【点睛】本题考查的是平行线的性质，用到的知识点为：两直线平行，同旁内角互补，难度一般.66．如图，已知AB∥CD，C在D的右侧，BM平分∠ABC，DN平分∠ADC，BM，DN所在直线交于点E，∠ADC=70°.（1）求∠EDC的度数；（2）若∠ABC=n°，求∠BED的度数（用含n的代数式表示）；（3）将线段BC沿DC方向平移，使得点B在点A的右侧，其他条件不变，画出图形并判断∠BED的度数是否改变，若改变，求出它的度数（用含n的式子表示）；若不改变，请说明理由.n°＋35°；（3）见解析.【答案】(1) 35°；（2）12【解析】【分析】（1）根据角平分线的定义即可求∠EDC的度数；（2）过点E作EF∥AB，然后根据两直线平行内错角相等，即可求∠BED的度数；（3）∠BED的度数改变．分三种情况讨论，分别过点E作EF∥AB，先由角平分线的定义可得：∠ABE＝12∠ABC＝12n°，∠CDE＝12∠ADC＝35°，然后根据平行线的性质即可得到∠BED的度数．【详解】解：（1）∵DE平分∠ADC，∠ADC＝70°，∴∠EDC＝12ADC＝12×70°＝35°；（2）过点E作EF∥AB，∵AB∥CD，∴AB∥CD∥EF，∴∠ABE＝∠BEF，∠CDE＝∠DEF，∵BE平分∠ABC，DE平分∠ADC，∠ABC＝n°，∠ADC＝70°，∴∠ABE＝12∠ABC＝12n°，∠CDE＝12∠ADC＝35°，∴∠BED＝∠BEF＋∠DEF＝12n°＋35°；（3）分三种情况：①如图所示，过点E作EF∥AB，∵BE平分∠ABC，DE平分∠ADC，∠ABC＝n°，∠ADC＝70°，∴∠ABE＝2∠ABC＝2n°，∠CDG＝2∠ADC＝35°，∵AB∥CD，∴AB∥CD∥EF，∴∠BEF＝∠ABE＝12n°，∠CDG＝∠DEF＝35°，∴∠BED＝∠BEF−∠DEF＝12n°−35°．②如图所示，过点E作EF∥AB，∵BE平分∠ABC，DE平分∠ADC，∠ABC＝n°，∠ADC＝70°，∴∠ABE＝12∠ABC＝12n°，∠CDE＝12∠ADC＝35°，∵AB∥CD，∴AB∥CD∥EF，∴∠BEF＝180°−∠ABE＝180°−12n°，∠CDE＝∠DEF＝35°，∴∠BED＝∠BEF＋∠DEF＝180°−12n°＋35°＝215°−12n°．③如图所示，过点E作EF∥AB，∵BE平分∠ABC，DE平分∠ADC，∠ABC＝n°，∠ADC＝70°，∴∠ABG＝2∠ABC＝2n°，∠CDE＝2∠ADC＝35°，∵AB∥CD，∴AB∥CD∥EF，∴∠BEF＝∠ABG＝12n°，∠CDE＝∠DEF＝35°，∴∠BED＝∠BEF−∠DEF＝12n°−35°．综上所述答案为：∠BED角度改变，其度数为12n°−35°或215°−12n°．【点睛】此题考查了平行线的判定与性质，解题的关键是：正确添加辅助线，利用平行线的性质进行推算．三、填空题67．如果一张长方形的纸条，如图所示折叠，那么∠α等于____．【答案】70°．【解析】【分析】依据平行线的性质，可得∠BAE=∠DCE=140°，依据折叠即可得到∠α=70°．【详解】解：如图，∵AB ∥CD ，∴∠BAE =∠DCE =140°， 由折叠可得：12DCF DCE ∠=∠，∴∠α=70°．故答案为：70°．【点睛】本题主要考查了平行线的性质，解题时注意：两直线平行，同位角相等．68．如图，将一个宽度相等的纸条按图所示折叠一下，如果∠1＝145°，那么∠2＝_____．【答案】107.5°【解析】【分析】根据折叠的性质得到∠3=∠4，由a ∥b ，根据平行线的性质得到∠1=∠3+∠4，∠2+∠3=180°，可计算出∠3=72.5°，则∠2=180°-72.5°=107.5°．【详解】由折叠可得∠3＝∠4，∵a∥b，∴∠1＝∠3+∠4，∠2+∠3＝180°，∴2∠3＝145°，∴∠3＝72.5°，∴∠2＝180°﹣72.5°＝107.5°．故答案为：107.5°．【点睛】本题主要考查了平行线的性质：两直线平行，内错角相等；两直线平行，同旁内角互补，比较简单.，∠1=∠2，则∠DFE的度数是_______．69．如图已知CD AD【答案】90°【解析】【分析】根据同位角相等两直线平行判定EF∥CD，再根据平行线的性质及垂直的定义得出∥DFE的度数．【详解】解：∥∥1=∥2，∥EF∥CD，∥∥DFE+∥D=180°，又∥CD∥AD，∥∥D=90°，∥∥DFE=180°-90°=90°．故答案为90°．【点睛】本题主要考查了平行线的判定与性质，平行线的判定是由角的数量关系判断两直线的位置关系，平行线的性质是由平行关系来寻找角的数量关系．70．如图，AB∥CD，AD⊥BD，∠A=60°，则∠BDC的度数为__．【答案】30°．【解析】【分析】先根据AB∥CD，∠A=60°，求出∠ADC的度数，再由AD⊥BD得出∠ADB=90°，进而可得出结论．【详解】解：∵AB∥CD，∠A=60°，∴∠BDC=180°﹣60°=120°,∵AD⊥BD，∴∠ADB=90°，∴∠BDC=∠ADC﹣∠ADB=120°﹣90°=30°．故答案为：30°．【点睛】本题考查的是平行线的性质，用到的知识点为：两直线平行，同旁内角互补．。

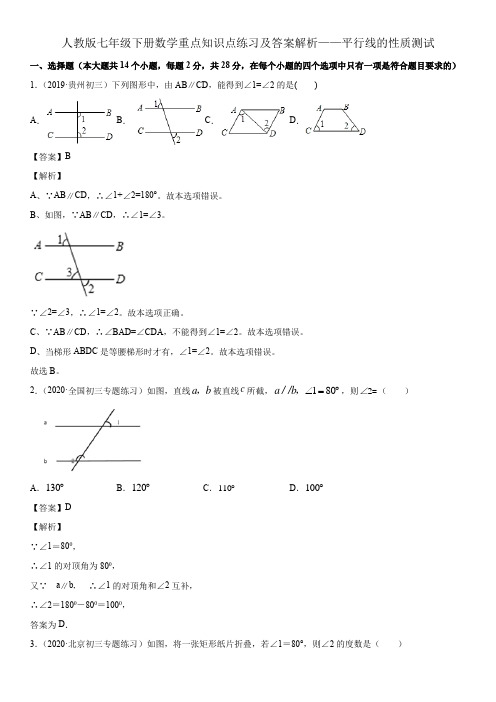
人教版七年级下册数学重点知识点练习及答案解析——平行线的性质测试一、选择题（本大题共14个小题，每题2分，共28分，在每个小题的四个选项中只有一项是符合题目要求的） 1．（2019·贵州初三）下列图形中，由AB ∥CD ，能得到∠1=∠2的是( )A ．B ．C ．D ．【答案】B【解析】A 、∵AB ∥CD ，∴∠1+∠2=180°。

故本选项错误。

B 、如图，∵AB ∥CD ，∴∠1=∠3。

∵∠2=∠3，∴∠1=∠2。

故本选项正确。

C 、∵AB ∥CD ，∴∠BAD=∠CDA ，不能得到∠1=∠2。

故本选项错误。

D 、当梯形ABDC 是等腰梯形时才有，∠1=∠2。

故本选项错误。

故选B 。

2．（2020·全国初三专题练习）如图，直线a b ，被直线c 所截，180a //b ∠=︒，，则2∠=（）A ．130︒B ．120︒C ．110︒D ．100︒【答案】D【解析】∵∠1＝800，∴∠1的对顶角为800，又∵ a ∥b, ∴∠1的对顶角和∠2互补，∴∠2＝1800－800＝1000，答案为D ．3．（2020·北京初三专题练习）如图，将一张矩形纸片折叠，若∠1＝80°，则∠2的度数是（ ）A．50°B．60°C．70°D．80°【答案】A【解析】如图，∵a∥b，∴∠1＝∠3＝80°，（180°﹣80°）＝50°，由翻折不变性可知：∠2＝∠4＝12故选A．4．（2020·全国初三专题练习）如图，要修建一条公路，从A村沿北偏东75°方向到B村，从B村沿北偏西25°方向到C村．若要保持公路CE与AB的方向一致，则∠ECB的度数为（）A．80°B．90°C．100°D．105°【答案】A【解析】解：由题意可得：AN∥FB，EC∥BD，∴∠NAB=∠FBD=75°，∵∠CBF=25°，∴∠CBD=100°，则∠ECB=180°-100°=80°．故选：A．5．（2020·全国初三专题练习）如图，将一块含有30°的直角三角板的顶点放在直尺的一边上，若∠1＝48°，那么∠2的度数是（）A．48°B．78°C．92°D．102°【答案】D【解析】解：如图：∵将一块含有30°的直角三角板的顶点放在直尺的一边上，∠1＝48°，∴∠2＝∠3＝180°﹣48°﹣30°＝102°故选：D．6．（2020·全国初三专题练习）如图，直线a∥b，∠1＝50°，∠2＝40°，则∠3的度数为（）A．40°B．90°C．50°D．100°【答案】B【解析】∵a∥b，∴∠4＝∠1＝50°，∵∠2＝40°，∴∠3＝180°-40°-50°=90°，故选B.7．（2019·海南初三）如图，直线a∥b，AC⊥AB，AC交直线b于点C，∠1＝60°，则∠2的度数是（）A．50°B．45°C．35°D．30°【答案】D【解析】如图，，∵直线a∥b，∴∠3=∠1=60°．∵AC⊥AB，∴∠3+∠2=90°，∴∠2=90°-∠3=90°-60°=30°，故选D．8．（2019·广东初三）如图，五边形ABCDE中，AB∥CD，∠1、∠2、∠3分别是∠BAE、∠AED、∠EDC的外角，则∠1+∠2+∠3等于( )A．90°B．180°C．210°D．270°【答案】B【解析】如图，如图，过点E作EF∥AB，∵AB∥CD，∴EF∥AB∥CD，∴∠1=∠4，∠3=∠5，∴∠1+∠2+∠3=∠2+∠4+∠5=180°，故选B9．（2019·河南初三）如图所示，直线a∥b，∠1＝38°，∠2＝90°，则∠3的度数为（）A．125°B．138°C．148°D．128°【答案】D【解析】解：如图，反向延长∠2的边与a交于一点，由三角形外角性质，可得∠4＝∠2﹣∠1＝52°，∴∠5＝180°﹣∠4＝128°，∵a∥b，∴∠3＝∠5＝128°．故选：D．10．（2018·江苏初一期末）下列说法：①对顶角相等；②若AB＝BC，则点B是AC的中点；③若一个角的两边与另一个角的两边分别平行，则这两个角相等；④同角的补角相等．其中正确的个数是（）A．1个B．2个C．3个D．4个【答案】B【解析】解：①对顶角相等，正确；②若AB＝BC，则点B不一定是AC的中点，错误；③若一个角的两边与另一个角的两边分别平行，则这两个角相等或互补，错误；④同角的补角相等，正确．故选：B．11．（2018·全国初一月考）在公路上骑自行车，若第一次向左拐15°，则第二次向右拐15°就能回到原来的行车方向，这是直接根据（）A．同位角相等，两直线平行B．两直线平行，同位角相等C．两直线平行，同旁内角互补D．平行于同一直线的两直线互相平行【答案】A【解析】解：两次拐弯角度相同后，行驶方向与原来方向是平行的．则根据平行线依据的判定是：同位角相等，两直线平行故选A.12．（2019·安徽雪枫中学初二期中）如果一个角的两边分别平行于另一个角的两边，那么这两个角( )A．相等B．互补C．相等或互补D．不能确定【答案】C【解析】解：如图所示，∠1和∠2，∠1和∠3两对角符合条件．根据平行线的性质，得到∠1=∠2；结合邻补角的定义，得∠1+∠3=∠2+∠3=180°；故选：C．13．（2019·哈尔滨市第一一三中学校初一期中）如图,AB∥CD,BF平分∠ABE,且BF∥DE,则∠ABE与∠D的关系是（）A．∠ABE=3∠D B．∠ABE+∠D=90°C．∠ABE+3∠D=180°D．∠ABE=2∠D【答案】D【解析】延长CD和BF交于点G，∵AB∥CD∴∠CGB=∠ABG，∵BF∥DE∴∠CGB=∠CDE，∴∠CDE=∠ABG，∠，又∵BF平分ABE∠=2∠ABG，∴ABE∠=2∠CDE，∴ABE故选D.14．（2019·全国初一月考）如图，放置在水平操场上的篮球架的横梁EF始终平行于AB，EF与上拉杆CF形成的∠F=150°，主柱AD垂直于地面，通过调整CF和后拉杆BC的位置来调整篮筐的高度．当∠CDB=35°时，点H，D，B在同一直线上，则∠H的度数是（）A．120°B．110°C．115°D．100°【答案】C【解析】解：过D点作DI∥EF，∵∠F=150°，∴∠FDI=30°，∴∠ADB=180°-90°-30°-35°=25°，∴∠ABH=90°-25°=65°．∵GH∥AB，∴∠H=180°-65°=115°．故选C．二、填空题（本题共4个小题；每个小题3分，共12分，把正确答案填在横线上）15．（2019·长沙市开福区青竹湖湘一外国语学校初二月考）如图，AB∥CD，EF∥CD，∠B=40°，∠C=105°，则∠CGB=__________度．【答案】35【解析】∵AB∥CD∥EF，∠B=40°，∠C=105°，∴∠BGF=∠B=40°，∠C+∠CGF=180°，∴∠CGF=75°，∴∠CGB=∠CGF-∠BGF=35°，故答案为：35．16．（2019·沙雅县英买力镇中学初一月考）若AB∥CD，AB∥EF，则CD_______EF，其理由是_______________________。

人教版七年级数学下册第五章平行线的性质作业练习题（含答案)如图，DE BC DF BE ∥，、分别平分ADE ABC ∠、∠，求证：FDE DEB =∠∠.【答案】证明见解析.【解析】【分析】根据平行线的性质与判定，结合角平分线的定义作答．【详解】∵DE ∥BC ，∴∠ADE=∠ABC （两直线平行，同位角相等）．又∵DF 、BE 分别平分∠ADE 和∠ABC ， ∴1122ADF ADE ABE ABC ∠=∠∠=∠，， ∴ADF ABE =∠∠，∴DF ∥BE （同位角相等，两直线平行），∴∠FDE=∠DEB （两直线平行，内错角相等）．【点睛】本题考查平行线的判定与性质，正确识别“三线八角”中的同位角、内错角、同旁内角是正确答题的关键．42．如图，∠1+∠2＝180°，EF ∥BC ，求证：∠3＝∠B ．【答案】见解析.【解析】【分析】依据∠1+∠2=180°，∠2=∠4，即可得出AB ∥FD ，进而得到∠3=∠AEF ，再根据EF ∥BC ，即可得到∠B=∠AEF ，即可得到∠3=∠B ．【详解】∵∠1+∠2＝180°，∠2＝∠4，∴∠1+∠4＝180°，∴AB ∥FD ，∴∠3＝∠AEF ，∵EF ∥BC ，∴∠B ＝∠AEF ，∴∠3＝∠B ．【点睛】本题主要考查了平行线的判定与性质，能运用平行线的性质和判定进行推理是解此题的关键，注意：①两直线平行，同位角相等，②两直线平行，内错角相等，③两直线平行，同旁内角互补，反之亦然．43．（1）如图//AB CD ，试判断BEF ∠、EFG 、FGD ∠之间的关系．并说明理由．（2）如图//AB CD ，150AEF ∠=︒，60DGF ∠=︒．试判断EF 和GF 的位置关系，并说明理由．【答案】（1）EFG FGD BEF ∠=∠+∠，证明见解析；（2）EF FG ⊥，证明见解析.【解析】【分析】（1）过点F 作AB 的平行线FH ，由平行线的性质可得AB ∥FH ∥CD ，由两直线平行，内错角相等，得到∠BEF=∠EFH ，∠FGD=∠HFG ，所以∠BEF+∠FGD=∠EFH+∠HFG ，即∠EFG=∠FGD+∠BEF ．（2）思路同（1）根据∠EFG=∠FGD+∠BEF ，求出∠EFG=90°从而得出EF ⊥FG ．【详解】（1）解：EFG FGD BEF ∠=∠+∠证明：过点F 作AB 的平行线FH//AB CD ，//AB FH//CD FH ∴（平行于同一条直线的两条直线互相平行）AB FH（已作）//∴∠=∠（两直线平行，内错角相等）BEF EFHCD FH（已证）//∴∠=∠（两直线平行，内错角相等FGD HFG∴∠+∠=∠+∠（等量代换）BEF FGD EFH HFG∠+∠=∠即：BEF FGD EFG∴∠=∠+∠EFG FGD BEF⊥（2）EF FG证明：过点F作AB的平行线FHAB FHAB CD，////CD FH∴（平行于同一条直线的两条直线互相平行）//∠+∠=︒（平角的定义）AEF BEF180BEF AEF∴∠=︒-∠=︒-︒=︒180********AB FH（已作）//∴∠=∠（两直线平行，内错角相等）BEF EFHCD FH（已证）//FGD HFG∴∠=∠（两直线平行，内错角相等）∴∠+∠=∠+∠（等量代换）BEF FGD EFH HFG∠+∠=∠即：BEF FGD EFG∴∠=∠+∠=︒+︒=︒603090EFG FGD BEF∴⊥（垂直的定义）EF FG【点睛】本题主要考查的是平行线的性质：两直线平行，内错角相等．44．如图，已知BD⊥AC，EF⊥AC，垂足分别为D、F，∠1＝∠2，请将证明∠ADG＝∠C过程填写完整．证明：BD⊥AC，EF⊥AC（已知）∴∠BDC＝∠EFC＝90°∴BD∥∠2＝∠3又∵∠1＝∠2（已知）∴∠1＝∠3（等量代换）∴DG∥∴∠ADG＝∠C【答案】垂直的定义；EF；两直线平行，同位角相等；BC；两直线平行，同位角相等.【解析】【分析】根据垂直求出∠BDC=∠EFC=90°，根据平行线的判定得出BD∥EF，根据平行线的性质得出∠2=∠3，求出∠1=∠3，根据平行线的判定得出DG∥BC 即可．【详解】证明：∵BD⊥AC，EF⊥AC，∴∠BDC=∠EFC=90°，垂直的定义∴BD∥EF，∴∠2=∠3（两直线平行，同位角相等），又∵∠1＝∠2（已知）∴∠1＝∠3（等量代换）∴DG∥BC，∴∠ADG=∠C．两直线平行，同位角相等【点睛】本题考查了平行线的性质和判定，能熟练地运用定理进行推理是解此题的关键，注意：平行线的性质有：①两直线平行，同位角相等，②两直线平行，内错角相等，③两直线平行，同旁内角互补，反之亦然．45．已知：如图，BE∥CF，且BE＝CF，若BE、CF分别平分∠ABC和∠BCD．（1）请判断AB与CD是否平行？并说明你的理由．（2）CE、BF相等吗？为什么？【答案】（1）AB∥CD．理由见解析；（2）CE、BF相等．理由见解析.【解析】【分析】根据角平分线的定义，得出∠ABC＝2∠1，∠BCD＝2∠2，而由BE∥CF 得出∠1＝∠2，再根据等量代换得出∠ABC＝∠BCD，即可证明AB∥CD；求出∠1=∠2，根据平行线的判定推出即可．【详解】（1）AB∥CD．理由：∵BE、CF分别平分∠ABC和∠BCD，∴∠ABC＝2∠1，∠BCD＝2∠2，∵BE∥CF，∴∠1＝∠2，∴∠ABC＝∠BCD，∴AB∥CD；（2）CE、BF相等．理由：∵BE＝CF，∠1＝∠2，BC＝CB，∴△BCE≌△CBF（SAS），∴CE＝BF．【点睛】本题考查角平分线的定义，根据平分线的性质证明出∠1=∠2是解题关键.46．如图：∠1＝∠2，∠3＝108°.求∠4的度数【答案】72°．【解析】【分析】由∠1=∠2，根据同位角相等，两直线平行，即可求得AB∥CD，又由两直线平行，同旁内角互补，即可求得∠4的度数．【详解】解：∵∠1=∠2，∴AB∥CD．∴∠3+∠4=180°，∵∠3=108°，∴∠4=72°．【点睛】此题考查了平行线的判定与性质．注意同位角相等，两直线平行与两直线平行，同旁内角互补．47．如图，射线AB∥CD，P为一动点，∠BAP与∠DCP的平分线AE与CE交于点E.(1)当P在线段AC上运动时（如图1）,即∠APC=180∘,则∠AEC＝______；(2)当P运动到图2的位置时，猜想∠AEC与∠APC 的关系，并说明理由；(3)当P运动到图3的位置时,（2）中的结论还成立吗?(不要求说明理由)【答案】（1）90°；（2）∠AEC=12∠APC；（3）∠AEC=180°-12∠APC．.【解析】【分析】（1）根据∠BAP与∠DCP的平分线AE与CE交于点E，即可得出∠BAE=∠EAC，∠DCE=∠ACE，再利用平行线的性质求出即可；（2）作EM∥BA，PN∥BA，根据平行的传递性，再根据两直线平行内错角相等的性质可求；（3）根据平行的传递性，再根据两直线平行内错角相等的性质以及平角性质即可求出．【详解】解：（1）过E作EF∥AB，∵AB∥CD，∴∠BAC+∠DCA=180°，∵∠BAP与∠DCP的平分线AE与CE交于点E，∴∠BAE=∠EAC，∠DCE=∠ACE，∴∠BAE+∠CEF=90°；∴∠AEC=180°，此时∠AEC为90度；（2）作EM∥BA，PN∥BA，∴∠BAE=∠AEM，∠MEC=∠ECD，∠APN=∠BAP，∠NPC=∠PCD，∵∠BAE=∠EAP，∠PCE=∠ECD，又∵∠AEC=∠AEM+∠MEC，∠APC=∠APN+∠NPC，∴∠AEC=12∠APC；（3）作EW∥AB，EP∥AB，同理即可得出：2∠AEC=360°-∠APC，∴∠AEC=180°-12∠APC．【点睛】此题主要考查了平行线的性质以及平行线的传递性等知识，解题的关键是正确作出辅助线，然后根据两直线平行内错角相等的性质解此类题．48．如图,已知∠BDG+∠EFG=180°,∠DEF=∠B,试判断∠AED与∠C的大小关系,并加以说明.解:∠AED=∠C．理由:∠∠EFD+∠EFG=180°( ),∠BDG+∠EFG=180°(已知)∠∠BDG =∠EFD ( ),∠BD∠EF( ),∠∠BDE+∠DEF =180°( ).又∠∠DEF=∠B( ),∠∠BDE+∠B =180°( ),∠DE∠BC( ),∠∠AED=∠C( ).【答案】见详解.【解析】【分析】做此题的关键是找出图中角与角的关系，即同位角，内错角，同旁内角等．利用平行线的性质和判定填空．【详解】】解：∠AED=∠C．理由如下：∵∠EFD+∠EFG=180°，（邻补角的定义）∠BDG+∠EFG=180°，（已知）∴∠BDG=∠EFD．（同角的补角相等）∴BD∥EF．（内错角相等，两直线平行）∴∠BDE+∠DEF=180°．（两直线平行，同旁内角互补）又∵∠DEF=∠B，（已知）∴∠BDE+∠B=180°．（等量代换）∴DE∥BC．（同旁内角互补，两直线平行）∴∠AED=∠C．（两直线平行，同位角相等）【点睛】本题主要考查了平行线的判定和性质，熟记定理是解题的关键．49．如图，直线CD与直线AB相交于C，根据下列语句画图，并填空.(1)过点P作PQ∥CD，交AB于点Q(尺规作图)；(2)过点P作PR⊥CD，垂足为R.(3)在(1)(2)的条件下，若∠ACD＝65°，则∠PQB＝____度，∠RPQ＝____度.【答案】(1)见详解；（2）见详解；（3）故答案为115，90．【解析】【分析】（1）平移CD使它经过点P即可得到PQ；（2）过点P作PR⊥DC于R；（3）先根据平行线的性质得∠PQA=∠ACD=65°，则利用邻补角计算∠PQB，根据垂直定义得∠PRC=90°，然后利用平行线的性质求∠RPQ=90°．【详解】解：（1）如图，PQ为所作；（2）如图，PR为所作；（3）在图中，∵PQ∥CD，∴∠PQA=∠ACD=65°，∴∠PQB=180°-65°=115°，∵PR⊥CD，∴∠PRC=90°，∵PQ∥CD，∴∠RPQ+∠PRC=180°，∴∠RPQ=90°．故答案为115，90．【点睛】本题考查了作图-复杂作图：复杂作图是在五种基本作图的基础上进行作图，一般是结合了几何图形的性质和基本作图方法．解决此类题目的关键是熟悉基本几何图形的性质，结合几何图形的基本性质把复杂作图拆解成基本作图，逐步操作．50．如图，已知12180∠+∠=︒，B DEF ∠=∠；那么DE 与BC 平行吗？试说明理由．请将下面的推理过程补充完整．解：DE BC ∥，理由如下：12180∠+∠=︒(已知)2180DHE ∠+∠=︒(平角的定义)1DHE ∴∠=∠( )∴ ( )B ∴∠= (两直线平行，同位角相等)B DEF ∠=∠(已知)DEF ∴∠= ( )DE BC ∴∥(内错角相等，两直线平行)【答案】见解析.【解析】【分析】由于∠1＋∠2＝180°，2180DHE ∠+∠=︒，则1DHE ∠=∠，根据内错角相等，∠，由于∠B＝两直线平行得到AB∥EF，则利用平行线的性质得∠B＝EFC∠，于是根据平行线的判定得到DE∥BC．∠DEF，所以∠DEF＝EFC【详解】证明：12180∠+∠=︒(已知)2180∠+∠=︒(平角的定义)DHE∴∠=∠(同角的补角相等)1DHE∴AB EF (内错角相等，两直线平行)∠(两直线平行，同位角相等)∴∠=EFCB∠=∠(已知)B DEF∠( 等量代换)DEF∴∠=EFC∴∥(内错角相等，两直线平行)DE BC∠；故答案为：同角的补角相等；AB；EF；内错角相等，两直线平行；EFC ∠；等量代换．EFC【点睛】本题考查了平行线的判定与性质：内错角相等，两直线平行；同旁内角互补，两直线平行；两直线平行，同位角相等．。

人教版七年级数学下册第5章同步课时练习5.3.1 平行线的性质★基础练习★【知识点1】平行线的性质11．如图，直线a，b被直线m所截，若a∥b，∠2＝62°，则∠1＝（）A．62°B．108°C．118°D．128°2.已知如图DC∥EG，∠C＝40°，∠A＝70°，则∠AFE的度数为（）A．140°B．110°C．90°D．30°【知识点2】平行线的性质23.如图，已知AB∥CD，直线AB，CD被BC所截，E点在BC上，若∠1＝45°，∠2＝35°，则∠3＝（）A．65°B．70°C．75°D．80°4．如图，已知直线a∥b，∠1＝40°，∠2＝60°，则∠3等于（）A．100°B．90°C．70°D．50°第1页（共7页）2【知识点3】平行线的性质35.如图，点E在AC的延长线上，AB∥CD，下列结论错误的是（）A．∠3＝∠4 B．∠A＝∠DCEC．∠1＝∠2 D．∠A+∠2+∠3＝180°6.如图，AB∥CD，∠1＝56°，FG平分∠EFD，则∠FGB的度数等于（）A．122°B．152°C．116°D．124°★提升练习★7.如图，将三角板与直尺贴在一起，使三角板的直角顶点C（∠ACB＝90°）在直尺的一边上，若∠2＝65°，则∠1的度数是（）A．15°B．25°C．35°D．65°8.如图所示，将含有30°角的三角板（∠A＝30°）的直角顶点放在相互平行的两条直线其中一条上，若∠1＝38°，则∠2的度数（）A．28°B．22°C．32°D．38°9.如图，∠BCD＝95°，AB∥DE，则∠α与∠β满足（）第3页（共7页）A ．∠α+∠β＝95°B ．∠β﹣∠α＝95°C ．∠α+∠β＝85°D ．∠β﹣∠α＝85°10. 如图，将一张长方形纸片沿EF 折叠后，使得点A 、B 分别落在点A 、B 的位置，如果∠2＝56°，那么∠1＝（）A ．56°B ．58°C ．62°D ．68°11. 如图，将一张含有30°角的三角形纸片的两个顶点叠放在矩形的两条对边上，若∠2＝46°，则∠1的大小为（）A ．14°B ．16°C ．90°﹣αD ．α﹣44°12. 如图，直线l 1∥l 2，点A 在直线l 1上，以点A 为圆心，适当长为半径画弧，分别交直线l 1、l 2于B 、C 两点，连接AC 、BC ．若∠ABC ＝54°，则∠1的度数为（）A ．36°B ．54°C ．60°D ．72°13．如图，l 1∥l 2，l 4∥l 3，若∠1＝50°，则∠2＝．14. 如图，三角板直角顶点落在长方形纸片的一边上，∠1＝35°，则∠2＝ °．15.如图，将一张长方形的纸片沿折痕EF翻折，使点C、D分别落在点M、N的位置，且∠BFM= 1∠EFM，则∠AEN的度数为．216.如图所示，已知AD∥BC，BE平分∠ABC，∠A＝110°．求∠ADB的度数．17．如图，AB∥CD，∠CEF＝60°，∠ECD＝125°，求∠A的度数．18.如图，AB∥CD，AC交BD于点O，∠A＝40°，∠D＝45°．求∠1和∠2的度数．★拓展探究突破练习★19.如图，已知AM∥BN，∠A＝64°．点P是射线AM上一动点（与点A不重合），BC、BD分别平分∠ABP和∠PBN，分别交射线AM于点C，D．（1）①∠ABN的度数是；②∵AM∥BN，∴∠ACB＝∠；（2）求∠CBD的度数；（3）当点P运动时，∠APB与∠ADB之间的数量关系是否随之发生变化？若不变化，请写出它们之间的关系，并说明理由：若变化，请写出变化规律；（4）当点P运动到使∠ACB＝∠ABD时，∠ABC的度数是．第5页（共7页）参考答案1．C ．2．B ．3．D ．4．A ．5．A ．6．B ．7．B ．8．B ．9．D ．10．C ．11．B ． 12．D ．13．50°．14．55．15．36°．16. 解：如图所示：∵AD ∥BC ，∴∠A +∠ABC ＝180°，∠ADB ＝∠CBD ， 又∵∠A ＝110°，∴∠ABC ＝180°﹣110°＝70°， 又∵BE 平分∠ABC ， ∴∠CBD = 1²A 捸ᗂ2∴∠CBD = 1 × 11ᗂ° = 捸捸°，2 ∴∠ADB ＝55°．17. 解：如图，过点E 作EG ∥AB ， ∵AB ∥CD ， ∴EG ∥CD ， ∴∠GEC +∠C ＝180°∴∠GEC ＝180°﹣125°＝55° ∵EG ∥AB∴∠A ＝∠FEG ＝∠FEC +∠CEG ＝60°+55°＝115°． 答：∠A 的度数为115°．18. 解：∵AB ∥CD ，∴∠1＝∠A ， ∵∠A ＝40°， ∴∠1＝40°，又∵∠2＝∠D +∠1，∠D ＝45°， ∴∠2＝85°，由上可得，∠1的度数是40°，∠2的度数是85°． 19．解：（1）①∵AM ∥BN ，∠A ＝64°， ∴∠ABN ＝180°﹣∠A ＝116°， 故答案为：116°； ②∵AM ∥BN ， ∴∠ACB ＝∠CBN ，故答案为：CBN；（2）∵AM∥BN，∴∠ABN+∠A＝180°，∴∠ABN＝180°﹣64°＝116°，∴∠ABP+∠PBN＝116°，∵BC平分∠ABP，BD平分∠PBN，∴∠ABP＝2∠CBP，∠PBN＝2∠DBP，∴2∠CBP+2∠DBP＝116°，∴∠CBD＝∠CBP+∠DBP＝58°；（3）不变，∠APB：∠ADB＝2：1，∵AM∥BN，∴∠APB＝∠PBN，∠ADB＝∠DBN，∵BD平分∠PBN，∴∠PBN＝2∠DBN，∴∠APB：∠ADB＝2：1；（4）∵AM∥BN，∴∠ACB＝∠CBN，当∠ACB＝∠ABD时，则有∠CBN＝∠ABD，∴∠ABC+∠CBD＝∠CBD+∠DBN∴∠ABC＝∠DBN，由（1）∠ABN＝116°，∴∠CBD＝58°，∴∠ABC+∠DBN＝58°，∴∠ABC＝29°，故答案为：29°．第7页（共7页）。

人教版七年级下册数学平行线的判定及性质证明题训练（含答案）1．如图，三角形ABC 中，点D 在AB 上，点E 在BC 上，点F ，G 在AG 上，连接,,DG BG EF ．己知12∠=∠，3180ABC ∠+∠=︒，求证：∥BG EF ．将证明过程补充完整，并在括号内填写推理依据．证明：∵_____________（已知）∴∥DG BC （_______________________）∴．CBG ∠=________（____________________）∵12∠=∠（已知）∴2∠=________（等量代换）∴∥BG EF （___________________）2．如图，已知12∠=∠，A F ∠=∠，试说明C D ∠=∠的理由．解：把1∠的对顶角记作3∠，所以13∠=∠（对顶角相等）．因为12∠=∠（已知），所以23∠∠=（ ），所以 ∥ （ ）．（请继续完成接下去的说理过程）3．如图，CD ∥AB ，点O 在直线AB 上，OE 平分∠BOD ，OF ⊥OE ，∠D ＝110°，求∠DOF 的度数．4．如图，DH 交BF 于点E ，CH 交BF 于点G ，12∠=∠，34∠=∠，5B ∠=∠．试判断CH 和DF 的位置关系并说明理由．5．已知：如图，直线DE//AB．求证：∠B+∠D=∠BCD．6．如图，已知AB CD∥，BE平分ABC∠，CE平分BCD∠，求证1290∠+∠=︒．证明：∵BE平分ABC∠（已知），∴2∠=（），同理1∠=，∴1122∠+∠=，又∵AB CD∥（已知）∴ABC BCD∠+∠=（），∴1290∠+∠=︒．7．请把下列证明过程及理由补充完整（填在横线上）：已知：如图，BC，AF是直线，AD∥BC，∠1＝∠2，∠3＝∠4．求证：AB∥CD．证明：∵AD∥BC（已知），∴∠3＝（）．∵∠3＝∠4（已知），∴∠4＝（）．∵∠1＝∠2（已知），∴∠1+∠CAF＝∠2+∠CAF（）．即∠BAF＝．∴∠4＝∠BAF．（）．∴AB∥CD（）．8．如图，已知∠A＝120°，∠FEC＝120°，∠1＝∠2，试说明∠FDG＝∠EFD．请补全证明过程，即在下列括号内填上结论或理由．解：∵∠A＝120°，∠FEC＝120°（已知），∴∠A＝（）．∴AB∥（）．又∵∠1＝∠2（已知），∴EF ∥ （ ）．∴∠FDG ＝∠EFD （ ）．9．在三角形ABC 中，CD AB ⊥于D ，F 是BC 上一点，FH AB ⊥于H ，E 在AC 上，EDC BFH ∠=∠．(1)如图1，求证：∥DE BC ；(2)如图2，若90ACB ∠=︒，请直接写出图中与ECD ∠互余的角，不需要证明．10．已知：如图，直线MN HQ ∥，直线MN 交EF ，PO 于点A ，B ，直线HQ 交EF ，PO 于点D ，C ，DG 与OP 交于点G ，若1103∠=︒，277∠=︒，396∠=︒．（1）求证：EF OP ∥；（2）请直接写出CDG ∠的度数．11．如图直线a b ∥，直线EF 与,a b 分别和交于点,,A B AC AB AC ⊥、交直线b 于点C ．（1）若160∠=︒，直接写出2∠= ；（2）若3,4,5AC AB BC ===，则点B 到直线AC 的距离是 ；（3）在图中直接画出并求出点A 到直线BC 的距离．12．如图，已知AB CD ，BE 平分∠ABC ，∠CDE = 150°，求∠C 的度数．13．如图，在ABC 中，CD 平分ACB ∠交AB 于D ，EF 平分AED ∠交AB 于F ，已知ADE B ∠=∠，求证：EF CD ∥．14．已知：如图，AB ∥CD ∥EF ，点G 、H 、M 分别在AB 、CD 、EF 上．求证：GHM AGH EMH ∠∠∠=+．15．如图所示，点B 、E 分别在AC 、DF 上，BD 、CE 均与AF 相交，A F ∠=∠，C D ∠=∠，求证：12∠=∠．16．如图，在ABC 中，DE ∥AC ，DF ∥AB ．（1）判断∠A 与∠EDF 之间的大小关系，并说明理由．（2）求∠A +∠B +∠C 的度数．17．已知：如图，ABC 中，点D 、E 分别在AB 、AC 上，EF 交DC 于点F ，32180∠+∠=︒ ，1B ∠=∠．（1）求证：∥DE BC ；（2）若DE 平分ADC ∠，33B ∠=∠，求2∠的度数．18．如图，AB ∥DG ，∠1+∠2＝180°．（1）试说明：AD ∥EF ；（2）若DG 是∠ADC 的平分线，∠2＝142°，求∠B 的度数．19．问题情境：如图1，AB CD ∥，130PAB ∠=︒，120PCD ∠=︒，求APC ∠的度数．小明的思路是：如图2，过P 作PE AB ∥，通过平行线性质，可得APC ∠=______．问题迁移：如图3，AD BC ∥，点P 在射线OM 上运动，ADP α∠=∠，BCP β∠=∠．（1）当点P 在A 、B 两点之间运动时，CPD ∠、α∠、β∠之间有何数量关系？请说明理由．（2）如果点P 在A 、B 两点外侧运动时（点P 与点A 、B 、O 三点不重合），请你直接写出CPD ∠、α∠、β∠之间有何数量关系．20．直线AB CD∠．∥，直线EF分别交AB、CD于点M、N，NP平分MND（1）如图1，若MR平分EMB∠，则MR与NP的位置关系是．∠，则MR与NP有怎样的位置关系？请说明理由．（2）如图2，若MR平分AMN（3）如图3，若MR平分BMN∠，则MR与NP有怎样的位置关系？请说明理由．参考答案：1．解：证明：∵3180ABC ∠+∠=︒（已知）∴∥DG BC （同旁内角互补，两直线平行）∴．1CBG ∠=∠（两直线平行，内错角相等）∵12∠=∠（已知）∴2CBG ∠=∠（等量代换）∴∥BG EF （同位角相等，两直线平行）2．解：把1∠的对顶角记作3∠，所以13∠=∠（对顶角相等）．因为12∠=∠（已知），所以23∠∠=（等量代换），所以//BD CE （同位角相等，两直线平行），所以4C ∠=∠（两直线平行，同位角相等），又因为A F ∠=∠，所以//DF AC （同位角相等，两直线平行），所以4D ∠=∠（两直线平行，内错角相等），所以C D ∠=∠（等量代换）．故答案为：等量代换；BD ；CE ；同位角相等，两直线平行．3．解：∵CD AB ∥∴110DOB D ∠=∠=︒∵OE 平分∠BOD ∴1552DOE DOB ∠=∠=︒ 又∵OF ⊥OE∴90EOF ∠=︒∴905535DOF EOF DOE ∠=∠-∠=︒-︒=︒故答案为：35︒4．解：CH DF，理由如下：∵34∠=∠，∴CD BF，∴5180BED∠+∠=︒，∵5B∠=∠，∴180B BED∠+∠=︒，∴BC DH，∴2H∠=∠，∵12∠=∠，∴1H∠=∠，∴CH DF．5．证明：过点C作CF∥AB，∴∠B=∠BCF，∵DE//AB．CF∥AB，∴CF∥DE，∴∠D=∠DCF，∴∠BCD=∠BCF+∠DCF=∠B+∠D．6．证明：∵BE平分∠ABC（已知），∴∠2=12∠ABC（角平分线的定义），同理∠1=12∠BCD，∴∠1+∠2=12(∠ABC+∠BCD)，又∵AB∥CD（已知）∴∠ABC +∠BCD =180°（两直线平行，同旁内角互补 ），∴∠1+∠2=90°． 故答案为：12∠ABC ；角平分线的定义；12∠BCD ；(∠ABC +∠BCD )；180°；两直线平行，同旁内角互补．7．证明：∵AD ∥BC （已知），∴∠3＝∠CAD （两直线平行，内错角相等）．∵∠3＝∠4（已知），∴∠4＝∠CAD （等量代换）．∵∠1＝∠2（已知），∴∠1+∠CAF ＝∠2+∠CAF （等式的性质）．即∠BAF ＝∠CAD ．∴∠4＝∠BAF ．（等量代换）．∴AB ∥CD （同位角相等，两直线平行）．8．解：∵∠A =120°，∠FEC =120°（已知），∴∠A =∠FEC （等量代换），∴AB ∥EF （同位角相等，两直线平行），又∵∠1=∠2（已知），∴AB ∥CD （内错角相等，两直线平行），∴EF ∥CD （平行于同一条直线的两直线互相平行），∴∠FDG =∠EFD （两直线平行，内错角相等），故答案为：∠FEC ；等量代换；EF ；同位角相等，两直线平行；内错角相等，两直线平行；CD ；平行于同一条直线的两直线互相平行；两直线平行，内错角相等．9．证明：∵CD AB ⊥，FH AB ⊥，∴//CD FH ，∴BCD BFH ∠=∠．∵EDC BFH ∠=∠，∴BCD EDC ∠=∠，∴//ED BC ．(2)与ECD ∠互余的角有：EDC BCD BFH A ∠∠∠∠，，，．证明：∵//ED BC ，∴90DEC ACB ∠=∠=︒，EDC BCD ∠=∠，∴90ECD EDC ∠+∠=︒，90ECD BCD ∠+∠=︒．∵//CD FH ，∴BCD BFH ∠=∠，∴90ECD BFH ∠+∠=︒．∵CD AB ⊥，∴90ACD A ∠+∠=︒，即90ECD A ∠+∠=︒．综上，可知与ECD ∠互余的角有：EDC BCD BFH A ∠∠∠∠，，，．10．解：（1）∵1103∠=︒，∴77∠=︒ABC ，∵277∠=︒，∴2ABC ∠=∠，∴EF OP ∥；（2）∵MN HQ ∥，EF OP ∥，∴1103∠=∠=∠=︒FDC FAB ，3180∠+∠=︒FDG ，∵396∠=︒，∴180********∠=︒-∠=︒-︒=︒FDG ，∴1038419∠=∠-∠=︒-︒=︒CDG FDC FDG ．11．解：（1）∵a b ∥，∴12180BAC ∠+∠+∠=︒，∵AC AB ⊥，160∠=︒，∴230∠=︒，故答案为：30︒；（2）∵AC AB⊥，∴点B到直线AC的距离为线段4AB=，故答案为：4；（3）如图所示：过点A作AD BC⊥，点A到直线BC的距离为线段AD的长度，∵AC AB⊥，∴ABC∆为直角三角形，∴1122ABCS AC AB BC AD∆=⨯⨯=⨯⨯，即1134522AD ⨯⨯=⨯⨯，解得：125 AD=，∴点A到直线BC的距离为125．12．解：∵∠CDE=150°，∴∠CDB=180°-∠CDE=30°，又∵AB CD，∴∠ABD=∠CDB=30°，∵BE平分∠ABC，∴∠ABC=2∠ABD=60°，∵AB CD，∴∠C=180°-∠ABC=120°．13．证明：ADE B∠=∠（已知），DE//BC∴（同位角相等，两直线平行），ACB AED∴∠=∠（两直线平行，同位角相等），CD 平分ACB ∠，EF 平分AED ∠（已知），12ACD ACB ∴∠=∠，12AEF AED ∠=∠（角平分线的定义）， ACD AEF ∴∠=∠（等量代换）.EF //CD ∴（同位角相等，两直线平行）.14．证明：∵AB ∥CD （已知）∴1AGH ∠=∠（两直线平行，内错角相等） 又 ∵CD ∥EF （已知）∴2EMH ∠=∠，（两直线平行，内错角相等） ∵12GHM ∠∠∠=+（已知）∴GHM AGH EMH ∠∠∠=+（等式性质）15．证明：∵A F ∠=∠，∴AC DF ∥，∴ABD D ∠=∠，又∵C D ∠=∠，∴ABD C ∠=∠，∴DB CE ∥，∴13∠=∠，∵23∠∠=，∴12∠=∠．16．（1）两角相等，理由如下：∵DE ∥AC ，∴∠A =∠BED (两直线平行，同位角相等).∵DF ∥AB ，∴∠EDF =∠BED (两直线平行，内错角相等)， ∴∠A =∠EDF (等量代换).（2）∵DE ∥AC ，∴∠C =∠EDB (两直线平行，同位角相等).∵DF ∥AB ，∴∠B =∠FDC (两直线平行，同位角相等).∵∠EDB +∠EDF +∠FDC =180°，∴∠A +∠B +∠C =180°(等量代换).17．解：（1）∵32180∠+∠=︒，∠2+∠DFE ＝180°， ∴∠3＝∠DFE ，∴EF //AB ，∴∠ADE ＝∠1，又∵1B ∠=∠，∴∠ADE ＝∠B ，∴DE //BC ，（2）∵DE 平分ADC ∠，∴∠ADE ＝∠EDC ，∵DE //BC ，∴∠ADE ＝∠B ，∵33B ∠=∠∴∠5+∠ADE +∠EDC ＝3B B B ∠+∠+∠＝180°， 解得：36B ∠=︒，∴∠ADC ＝2∠B ＝72°，∵EF //AB ，∴∠2＝∠ADC ＝180°－108°＝72°，18．（1）∵AB ∥DG ，∴∠BAD ＝∠1，∵∠1+∠2＝180°，∴∠BAD +∠2＝180°.∵AD ∥EF .（2）∵∠1+∠2＝180°且∠2＝142°，∴∠1＝38°，∵DG 是∠ADC 的平分线，∴∠CDG ＝∠1＝38°，∵AB ∥DG ，∴∠B ＝∠CDG ＝38°．19．解：问题情境：∵AB ∥CD ，PE ∥AB ，∴PE ∥AB ∥CD ，∴∠A +∠APE =180°，∠C +∠CPE =180°，∵∠P AB =130°，∠PCD =120°，∴∠APE =50°，∠CPE =60°，∴∠APC =∠APE +∠CPE =50°+60°=110°；（1）CPD αβ∠=∠+∠；过点P 作PQ AD ∥，又因为AD BC ∥，所以PQ AD BC ∥∥，则ADP DPE ∠=∠，BCP CPE ∠=∠，所以CPD DPE CPE ADP BCP ∠=∠+∠=∠+∠；（2）情况1：如图所示，当点P 在B 、O 两点之间时，过P 作PE ∥AD ，交ON 于E ，∵AD ∥BC ，∴AD ∥BC ∥PE ，∴∠DPE =∠ADP =∠α，∠CPE =∠BCP =∠β， ∴∠CPD =∠DPE -∠CPE =∠α-∠β，情况2：如图所示，点P 在射线AM 上时，过P 作PE ∥AD ，交ON 于E ，∵AD ∥BC ，∴AD ∥BC ∥PE ，∴∠DPE =∠ADP =∠α，∠CPE =∠BCP =∠β， ∴∠CPD =∠CPE -∠DPE =∠β-∠α20．（1）如题图1，AB CD ∥EMB END ∴∠=∠MR 平分EMB ∠，NP 平分MND ∠．11,22EMR EMB ENP END ∴∠=∠∠=∠ EMR ENP ∴∠=∠∴MR ∥NP ；（2）如题图2，AB CD ∥AMN END ∴∠=∠MR 平分AMN ∠，NP 平分MND ∠．11,22RMN AMN ENP END ∴∠=∠∠=∠ RMN ENP ∴∠=∠∴MR ∥NP ；（3）如图，设,MR PN 交于点Q ，过点Q 作QG AB ∥AB CD ∥180BMN END ∴∠+∠=︒，QG CD ∥ ,MQG BMR GQN PND ∴∠=∠∠=∠ MR 平分BMN ∠，NP 平分MND ∠．11,22BMR BMN PND END ∴∠=∠∠=∠ 90BMR PND ∴∠+∠=︒90MQN MQG NQG ∴∠=∠+∠=︒ ∴MR ⊥NP ；。

2.3 平行线的性质一、选择题1．如图，如果︒=∠601,//,//GH EF CD AB ，那么下列结论不成立的是（ ）A ．︒=∠602B ．︒=∠603C ．︒=∠604D ．︒=∠6052．如图：若CD AB //，则下列结论中（ ）①21∠=∠ ②43∠=∠ ③︒=∠+∠+∠18031D ④︒=∠+∠+∠18042BA ．都正确B ．都不正确C ．只有一个正确D ．只有一个不正确3．如图：AC BC AD CD EF AB ,//,////平分BAD ∠，则图中与AOE ∠相等的角有（ ）个．A ．2B ．3C ．4D ．5二、填空题1．如图，因为21//l l ，所以21∠=∠，理由是_________；2．如图，因为21//l l ，所以____32=∠+∠，理由___________；3．如图，41∠=∠，理由是__________________；4．如图，已知____2,603,1201,////=∠︒=∠︒=∠c b a ．5．如图：AE CD AB ,//平分CE BAC ,∠平分ACD ∠，则____=∠E ．6．在AB 两地间修一条公路，从A 地测得公路的走向为北偏东50°，如果A 、B 两地同时开工，那么在B 地按____=∠α方向施工，才能使公路准确接通．7．已知：如图：︒=∠50,//,//A BC AD CD AB ，则_______=∠C8．如图BD BC AD ,//平分1:2:,=∠∠∠ABC a ABC ，则____=∠DBC9．已知α∠的两边分别与β∠的两边互相平行，当︒=∠40α时，____=∠β10．一条公路经过两次拐弯后和原来平行，已知第一次拐的角是100°，则第二次拐的角可能是_________度．三、解答题1．已知：如图，NH EF BC MN DE AB ////,////，写出图中所有与B ∠相等的角．2．如图，已知CD++∠∠的值．∠32AB//，求4+1∠3．如图，已知CO=50︒∠︒=∠分别是ABC,BO60ACBABC、,∠的∠和ACB平分线，EF过点O且BC∠的度数．EF//，求BOC4．如图，这是一块钢板，EFAB//，工人师傅想用它来做一种产品，需要知道E,这三个角的度数的和，你能帮工人师傅第算一下吗？∠,ACE∠A∠参考答案一、选择题1．A 2．D 3．D二、填空题1．二、两直线平行同位角相等2．180°、两直线平行，同旁内角互补3．对顶角相等 4．120° 5．90° 6．130° 7．50°8．30° 9．40°或140° 10．80°三、解答题1．ERN BPE MNH MRF E DPC ∠∠∠∠∠∠,,、、、2．540°（提示：过E 、F 分别作AB 的平行线，根据两直线平行，同旁内角互补可计算出︒=∠+∠+∠+∠5404321．3．125°（提示：F O E O B B O C ∠-∠-︒=∠180，且︒=∠=∠=∠2521ABC OBC EOB ，︒=∠=∠=∠3021ACB OCB FOC ，︒=∠125BOC ）4．︒=∠+∠+∠360E ACE A （提示：过C 作AB CD //）。