matlab 圆周率的近似计算 实验报告

400000 315925 VC++ 3.159250
500000 395497 VC++ 3.163976
第四部分 级数方法
所用级数 计算项数 精确位数 所用工具 圆周率值 10000 3 MATLAB 3.14149265
第五部分 蒙特卡洛方法的应用
（填写所计算 的积分） （填写该积分 积分结果 的准确结果） （填写总的循 循环次数 环次数） （填写满足条 满足的次数 件次数） （填使用的软 所用工具 件） （用蒙特卡洛 积分的估计 方法估计的 值 值） 计算积分 （
第二部分 数值积分
所用函数
1/ 1 x2 1/ 1 x2 1/ 1 x2 1/ 1 x2 1/ 1 x2
积分方法 矩形公式 分割程度 100 所用工具 VC++ 圆周率值 3.131576
矩形方式 1000 VC++
3.140592
矩形方式 矩形方式 10000 100000 VC++ VC++
3.141494 3.141523
矩形方式 100000 VC++
3.141348
第三部分 蒙特卡洛方法
实验报告 ----计算科学实验室
所用函数 循环次数 满足的次数 所用工具 圆周率值
100000 79037 VC++ 3.141680
200000 158411 VC++ 3.168220
300000 237748 VC++ 3.169973
实验报告 ----计算科学实验室
实验名称： 圆周率的计算
姓名 实验类型 所用知识 魏萱 综合 设计 11112228 实验地点 学号 实验要求 选修 学时量 数学建模 数学软 运筹学 T5-207 6

数学实验报告一、 实验问题人们很早就发现圆的周长和直径的比是个常数，也就是我们都熟悉的圆周率π，那么这个常数的值究竟是多少哪？我国的伟大数学家祖冲之将π精确到3.1415926-3.1415927之间，西方的数学研究者也从来没有停止过对π的计算，那么在今天计算机技术如此发达的情况下，我们如何将π的近似值精确到更多位数哪？二、问题的分析π的精确度问题困扰大家已久，所以我们不妨在MATLAB 中采用循环来实现对π的更高位数的精确。

不妨以精确到小数点后9位为例。

我们知道 31arctan 21arctan 1arctan 4+==π 因此可以利用）（π）（321-1-2n 1-2n 1n 1-n 111-2n 431arctan 21arctan 4+=⎪⎭⎫ ⎝⎛+=∑∞=三、实验内容在MATLAB 中键入以下程序clear;n=0;r=1;p=0;k=-1;a=1;b=1;while r>=1.0e-9n=n+1;k=k*(-1);a=4*a;b=9*b;pl=p+k/(2*n-1)*(2/a+3/b);r=abs(4*(pl-p));fprintf('n=%.0f,p=%.10f\n',n,4*pl);p=pl;end四、问题求解结果和结论n=1,p=3.3333333333n=2,p=3.1172839506n=3,p=3.1455761317n=4,p=3.1408505618n=5,p=3.1417411974n=6,p=3.1415615879n=7,p=3.1415993410n=8,p=3.1415911844n=9,p=3.1415929813n=10,p=3.1415925796n=11,p=3.1415926705n=12,p=3.1415926497n=13,p=3.1415926545n=14,p=3.1415926534n=15,p=3.1415926536对泰勒级数，当｜x ｜越小时级数收敛速度越快，这启示我们另外构造相关级数来逼近π。

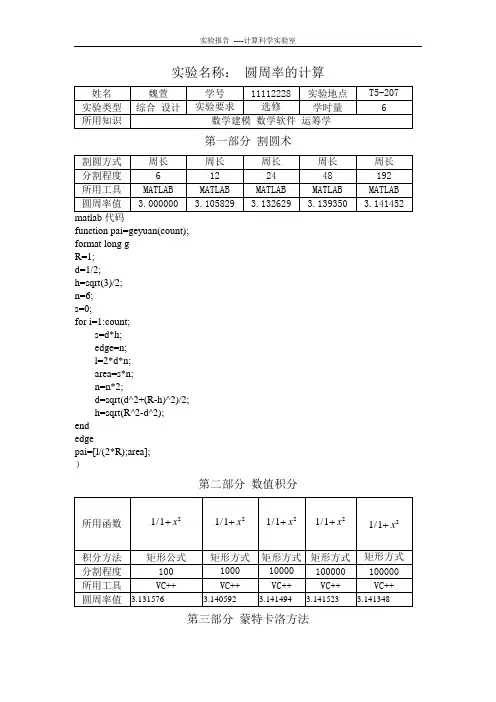
实验三 圆周率的计算学号： 姓名：XX一、 实验目的1. 本实验涉及概率论、定积分、三角函数等有关知识，要求掌握计算π的三种方法及其原理。

2. 学习和掌握数学软件MATLAB 的使用方法。

二、 实验内容圆周率是一个极其驰名的数。

从有文字记载的历史开始，这个数就引起了外行人和学者们的兴趣。

作为一个非常重要的常数，圆周率最早是出于解决有关圆的计算问题。

仅凭这一点，求出它的尽量准确的近似值，就是一个极其迫切的问题了。

事实也是如此，几千年来作为数学家们的奋斗目标，古今中外一代又一代数学家为此献出了自己的智慧和劳动。

回顾历史，人们对π的认识过程，反映了数学和计算技术发展情形的一个侧面。

π的研究，在一定程度上反映这个地区或时代的数学水平。

德国数学家康托说：“历史上一个国家所算的圆周率的准确程度，可以作为衡量这个国家当时数学发展水平的指标。

”直到19世纪初，求圆周率的值还是数学中的头号难题。

1. 圆周率的计算方法古人计算圆周率，一般是用割圆法。

即用圆的内接或外切多边形来逼近圆的周长。

Archomedes 用正96边形得到35位精度；刘徽用正3072边形得到5位精度；Ludolph V an Ceulen 用正2^62边形得到了35位精度。

这种基于几何的算法计算量大，速度慢，吃力不讨好。

随着数学的发展，数学家们在进行数学研究时有意无意得发现了许多计算圆周率的公式。

下面挑选一些经典的常用公式加以介绍。

除了这些经典公式外，还有很多其他公式和由这些经典公式衍生出来的公式，就不一一列举了。

1) Machin 公式2391a r c t a n451a r c t a n 16-=π ()121...753arctan 121753--++-+-=--n x x x x x x n n 这个公式由英国天文学教授John Machin 于1706年发现。

他利用这个公式计算到100位的圆周率。

Machin 公式每计算一项可以得到1.4位的十进制精度。

实验二π 的近似计算一.实验目的1.了解π 的计算历程2.理解和掌握近似计算π的数值积分法、蒙特卡罗（Monte Carlo ）法、韦达公式、级数法、拉马努金公式、迭代法等方法的原理和过程。

3.学习、掌握Mathematica 和MATLAB 的应用环境及其基本功能，通过一些练习掌握其基本的操作及相关命令。

二.实验内容1.运用数值积分法来近似计算π的值。

2.利用蒙特卡罗（Monte Carlo ）法来近似计算π的值。

3.利用韦达（VieTa ）公式近似计算π4.利用级数来近似计算π：（1） 莱布尼茨级数 ∑∞=+-=1212)1(4n nn π （2） 欧拉级数∑∞==12216n n π 和∑∞=+=022)12(18n n π 5.利用拉玛努金（Ranmaunujan ）公式来近似逼近计算π值n n n n n 396263901103)!()!4(980122104+=∑∞=π 三.实验准备及过程π 是人们经常使用的数字常数，对π的研究已经持续了2500多年，同时今天人们还在不断的探索研究进行中。

一般有以下几种近似计算方法。

1.数值积分法 半径为1的圆称为单位圆，它的面积等于π，只要计算出它的面积，计算出了π。

以单位圆的圆心为原点建立直角坐标系，则单位圆在第一象限内的部分是一个扇形，由曲线y= (x ∈[0,1])及两条坐标轴围成，它的面积S=π/4。

算出了S 的近似值，它的4倍就是π的近似值。

（1）梯形公式设分点x 1,…,x n-1将积分区间[a,b]分成n 等份，即x i =a+i(b-a)/n,0≤i ≤n 所有的曲边梯形的宽度都是h=(b-a)/n 。

记y i =f(x i )。

则第i 个曲边梯形的面积S i 近似地等于梯形面积(y i-1+y i )h/2，将所有这些梯形的面积加起来就得到S ≈(b-a)[y 1+y 2+…+y n-1+(y 0+y n )/2]/n这就是梯形公式。

上海电力学院高级程序设计（C）课程设计报告题目：用MATLAB编程求π院系：计算机科学与技术学院专业年级：信息安全2012级学生姓名：涂桂花学号：20123333指导教师：魏为民2015年3月14日目录一、实验目的 (1)二、实验内容和步骤 (1)1. 操作环境 (1)2. 系统配置 (1)3. 操作步骤 (1)4. 程序源代码 (3)三、实验结果 (3)四．实验小结 (4)上 海 电 力 学 院实 验 报 告课程名称 实验项目 姓名 学号 班级 专业 同组人姓名 指导教师 魏为民 实验日期注意：报告文件名格式：学号_姓名_实验项目.doc ，电子版发邮件到afoe@ ，打印版按要求黑白打印。

一、实验目的1.了解MATLAB 编译器的功能并学会使用；2.学会使用MATLAB 语言编写简单的程序；3.用下列公式 求π值，并了解π的其他公式。

二、实验内容和步骤1.操作环境电脑型号 华硕 X550EP 笔记本电脑操作系统 Windows 7 旗舰版 64位 SP1 ( DirectX 11 ) 2.系统配置处理器 AMD E1-2100 APU with Radeon HD Graphics 双核 主板 华硕 X550EP ( AMD 未知(1536h) ) 内存4 GB ( DDR3 1600MHz )主硬盘 日立 HGST HTS545050A7E680 ( 500 GB / 5400 转/分 )显卡ATI Radeon HD 8210 ( 512 MB / 华硕 )显示器 奇美 CMO15A7 ( 15.7 英寸 ) 光驱 松下 DVD-RAM UJ8C2 S DVD 刻录机 声卡 瑞昱 High Definition Audio @网卡 瑞昱 RTL8168/8111/8112 Gigabit Ethernet Controller / 华硕3.操作步骤3.1打开MATLAB 编辑器，如图1-1所示。

nl n 2 , 特别取针的长度 l d / 2 时， md m
本实验涉及的方法
3、蒙特卡罗法——蒲丰(Buffon)掷针法
x表示针的中点与最近的一条平行线间的距离, 为针与平行线 的夹角.则0 x d 2 ,0 , 确定x 平面内一个矩形 .如图：
平面内一个矩形确定的夹角为针与平行线一条平行线间的距离表示针的中点与最近的针与平行线相交本实验涉及的方法3蒙特卡罗法蒲丰buffon掷针法针与平行线相交时针在平行线矩形区域内所组成的区域面积与矩形区域面积比即为针与直线相交的概率
实验三
圆周率的求法
问
题
• 设半径为1的圆的周长与圆的直径比为A; • 设半径为2的圆的周长与圆的直径比为B. • 请问A与B哪个大?
计算历程的几个阶段
3.分析方法时期 17世纪出现了数学分析，这锐利的工具 使得许多初等数学束手无策的问题迎刃 而解。 π 的计算历史也随之进入了一 个新的阶段。
计算历程的几个阶段
1593年，韦达给出
1671年，苏格兰数学家詹姆斯.格雷戈里 公开了他发现的公式： 3 5 7
arctan x x x3 x5 x7 (1 x 1)

故
2 nl md
本实验涉及的方法
3、蒙特卡罗法——蒲丰(Buffon)掷针法
• 随机生成一个针的中点与最近一条平行直线间的 距离x,满足0≤x≤d/2; • 随机生成针与平行线的夹角a,满足0≤a≤ ； • 判断x≤L/2*sin[a],若成立，则针与直线相交， 否则不相交。
本实验涉及的方法
计算历程的几个阶段
圆周长大于内接正四边形而小于外切正四边形
计算历程的几个阶段
在我国，首先是由数学家刘徽得出较精确的 圆周率。他采用割圆术。

3
5
7
2 n 1
并利用这个公式计算到了圆周率的100位.
1914年，印度数学家Srinivasa Ramanujan 表了下面的公式：
9801 ( 4 n )! ( 1103 26390 n ) 22 4 n 4 4 n 4 ( n ! ) 99 n 0
发
在1985年，Gosper用这个公式计算到了圆周率 的17500000位．
在中国
• 祖冲之: 在刘徽研究的基础上，进一步地发展， 经过既漫长又烦琐的计算，一直算到圆内接正 24576边形，而得到一个结论： • 3.1415926 ＜ π ＜ 3.1415927 同时得到π 的两个近似分数：约率为22／7； 密率为355／113。
• 他算出的 π 的8位可靠数字，不但在当时是最精 密的圆周率，而且保持世界记录九百多年。以致 于有数学史家提议将这一结果命名为“祖率”。
1 .圆周率 的幂级数计算方法
例1
利用 arctan x 的 Maclaurin 展开式 ， 计算 的近似值 .
解
1 2 4 n 12 n 1 x x (1 ) x . 2 1 x
xx ( 1 )x arctan x x . 35 2 n 1
1989年，David 和 Gregory Chudnovsky 发表 了下面的公式
n 1 ( 1 ) ( 6 n )! 13591409 5451401 n 12 , 3 3 3 n n ( 3 n )! ( n ! ) 2 0 640320
并在1994年计算到了4044000000位．它的另一 种形式是
在中国
• 刘徽：公元263年前后，刘徽提出著名的 “割圆 术”求出了比较精确的圆周率。他发现：当圆内 接正多边形的边数不断增加后，多边形的周长会 越来越逼近圆周长，而多边形的面积也会越来越 逼近圆面积。于是，刘徽利用正多边形面积和圆 面积之间的关系，从正六边形开始，逐步把边数 加倍：正十二边形、正二十四边形，正四十八边 形……，一直到正三○七二边形，算出圆周率等 于三点一四一六，将圆周率的精度提高到小数点 后第四位。

数学实验报告一、实验目的1.学会用软件对矩阵进行一些数值运算。

2.学会用软件解线性方程组。

3.掌握逆矩阵的一种应用：整数逆矩阵加密、解密方法。

4.熟悉三维空间中的线性变换，加深对正交变换保持距离不变性的理解。

5.掌握泰勒级数在近似计算中的应用，从而理解数值逼近思想。

6.了解无理数e和欧拉常数C的由来历史。

7.了解圆周率π的计算历史，掌握计算圆周率π近似值的多种方法。

8.利用幂级数展开式计算无理数e和欧拉常数C的近似值。

9.学会根据实际问题建立线性规划模型。

10.掌握用软件求解线性函数极值问题。

11.学会建立0-1规划模型，掌握用软件求解0-1规划问题。

二、实验内容1.实验五：练习1：1．（1）程序代码[2,11,1;32,13;1,43,5][1;42][]()结果显示特解：（0.8571，-0.7143，0，0）基础解系：ξ1=（0.1429，-1.2857，1，0），ξ2=（0.1429，0.7143，0，1）通解：0.1429 0.1429 0.8571-1.2857 0.7143 -0.7143k1 1 + k2 0 + 0 12єR0 10感想与反思：A．通过解这道题，熟练掌握了用软件解线性方程组的方法B．手工解线性方程组非常繁琐，通过这道题，进一步认识到的强大2.实验五.练习2.24*4的加密锁：程序代码[3 7 15 22;2 5 11 17;3 6 13 21;9 18 36 46](q)(q)[68 105 108 105 103 101 110 99 101 32 105 115 116 32 116 104 101 32 109 111 116 104 101 114 32 111 102 32 115 117 99 99 101 115 115 32](w,4,9)(q)*b结果显示6*6的加密锁代码[2 3 4 2 1 6;7 7 11 9 2 17;4 6 9 5 2 12;8 7 12 9 2 17;3 3 4 2 1 6;6 4 6 6 1 2](q)(q)[68 105 108 105 103 101 110 99 101 32 105 115 116 32 116 104 101 32 109 111 116 104 101 114 32 111 102 32 115 117 99 99 101 115 115 32](w,6,6)*a(q)*b感想与反思：A．通过解这道题，熟练掌握了逆矩阵的一种应用：整数逆矩阵加密、解密方法B．用矩阵就可以完成对于信息的加密和解密，体会到了矩阵和的神奇C．在选择密码锁矩阵时可以对于一个单位矩阵进行多次初等变换，便于找到3.实验七，练习2.1程序代码单数阶导数在0处的值为零。

Page 10
谢谢观赏
Page 11
matlab计算时间matlab并行计算提高matlab计算精度matlab实验心得matlab计算圆周率matlab实验答案matlab计算积分精通matlab金融计算
本次实验内容为利用级数计算π， 要求不少于5种方法，，并比较 每种方法的收敛速度和误差。
谢志强
1206012005 填实验报告
汤晓峰 1206012010
tic; clear; digits(160); syms('x','a1','a2') x=sym(2)*sym(2)^sym(0.5)/sym(9801)*sym(1103); for i=1:10 i a1=sym(1);a2=sym(1); for j=1:i a1=a1*sym(j); end for j算的近似值
2 1 = 8 n 1 2n 12
计
tic; clear; x=0; for i=1:2000 x=vpa(x+1/(2*i-1)^2,30); pai(i)=vpa(sqrt(8*x),22); error(i)=vpa(pi-sqrt(8*x),22); end for i=1:10 i*200 pai(i*200) error(i*200) end toc; Elapsed time is 9.765762 seconds.
a2=a2*sym(j); end x=x+sym(2)*sym(2)^sym(0.5)/sym(9801)*a2/a1^sym(4) *(sym(1103)+sym(26390)*sym(i))/(sym(396)^(sym(4)*sy m(i))); vpa(1/x,40) vpa((sym(pi)-sym(1/x)),100) end toc; Elapsed time is 0.848219 seconds.

实验九π的近似计算【实验目的】1.了解圆周率π的计算历程。

2.了解计算π的割圆术、韦达公式、级数法、拉马努金公式、迭代法。

3.学习、掌握MATLAB软件有关的命令。

【实验内容】利用韦达（VieTa）公式2=π计算π的近似值。

【实验准备】1.割圆术2.韦达（VieTa）公式3.利用级数计算π4.拉马努金（Ranmaunujan）公式5.迭代方法6.π的两百位近似值【实验重点】1. 圆周率的计算历程【实验难点】1. 圆周率的各种计算公式【实验方法与步骤】练习1 用刘徽的迭代公式1162062626224,32,1n n n n x x s x x ++=--== 计算π的近似值。

相应的MATLAB 代码为>>clear;>>x=1;>>for i=1:30>>x=vpa (sqrt(2-sqrt(4-x^2)),15)%计算精度为15位有效数字 >>S=vpa(3*2^i*x,10)>>end计算可得x = .517638********* S = 3.105828541x = .261052384440103 S = 3.132628613x = .130806258460286 S = 3.139350203x = .654381656435522e-1 S = 3.141031951x = .327234632529735e-1 S = 3.141452472x = .163622792078742e-1 S = 3.141557608x = .818120805246955e-2 S = 3.141583892x = .409061258232818e-2 S = 3.141590463x = .204530736067660e-2 S = 3.141592106x = .102265381402739e-2 S = 3.141592517x = .511326923724832e-3 S = 3.141592619x = .255663463951308e-3 S = 3.141592645x = .127831732236766e-3 S = 3.141592651 x = .639158661510219e-4 S = 3.141592653 x = .319579330795908e-4 S = 3.141592653 x = .159789665403054e-4 S = 3.141592654 x = .798948327021645e-5 S = 3.141592654 x = .399474163511619e-5 S = 3.141592654 x = .199737081755909e-5 S = 3.141592654 x = .998685408779670e-6 S = 3.141592654 x = .499342704389851e-6 S = 3.141592654 x = .249671352194927e-6 S = 3.141592654 x = .124835676097464e-6 S = 3.141592654 x = .624178380487320e-7 S = 3.141592654 x = .312089190243660e-7 S = 3.141592654 x = .156044595121830e-7 S = 3.141592654 x = .780222975609150e-8 S = 3.141592654 x = .390111487804575e-8 S = 3.141592654 x = .195055743902288e-8 S = 3.141592654 x = .975278719511453e-9 S = 3.141592654练习2 用韦达公式2=π计算π的近似值。

matlab 蒙特卡罗法圆周率蒙特卡罗法是一种通过使用随机数来近似计算数学问题的方法。

它基于蒙特卡罗模拟，其中随机样本被用来估计问题的解。

蒙特卡罗法在各个领域都有广泛的应用，其中一个重要的应用就是计算圆周率。

圆周率（π）是数学中一个非常重要的常数，它的值约等于3.14159。

在传统的方法中，计算π的方法比较复杂，而使用蒙特卡罗法可以得到一个相对精确的近似值。

要使用蒙特卡罗法计算圆周率，我们可以考虑一个单位正方形，并在其中绘制一个半径为1的单位圆。

通过生成大量的点，并判断这些点是否在单位圆内，我们可以估计圆的面积与正方形的面积之间的比例。

由于圆的面积为πr^2，而正方形的面积为边长的平方（即1^2=1），我们可以利用这个比例来估计圆周率。

具体而言，我们可以生成一组随机的点，然后判断每个点是否位于单位圆内。

对于一个给定的点（x，y），如果它满足x^2 + y^2 <=1的条件，则它在单位圆内。

我们可以计算在单位圆内的点的数量，并将其除以总的点的数量，得到一个比例。

由于单位圆半径为1，正方形边长为1，我们可以利用这个比例来估计圆周率。

例如，我们生成1000个点，并发现有800个点位于单位圆内。

那么我们可以估计圆周率为800/1000=0.8。

当我们生成更多的点时，使用相同的方法计算比例并得到更准确的估计值。

为了更好的近似值，我们可以增加生成的点的数量。

当我们生成更多的点时，得到的估计值将越来越接近真实值。

这是因为随着点的数量的增加，我们对单位圆内的点的分布有更好的覆盖，并且减少对随机性的依赖。

使用MATLAB编程语言，我们可以很容易地实现蒙特卡罗法来计算圆周率。

下面是一个简单的MATLAB代码示例：```matlabnumPoints = 10000; %生成的点的数量countPointsInsideCircle = 0; %圆内点的数量for i = 1:numPointsx = rand(); %生成一个随机的x坐标y = rand(); %生成一个随机的y坐标if x^2 + y^2 <= 1countPointsInsideCircle = countPointsInsideCircle + 1;endendestimatedPi = 4 * countPointsInsideCircle / numPoints; %估计的圆周率disp(['估计的圆周率为：', num2str(estimatedPi)]);```在这个例子中，我们生成了10000个点，并统计了有多少个点位于单位圆内。

Matlab是一种功能强大的数学软件，它可以用于数值计算、数据分析、图形绘制等各种数学和工程应用。

而蒙特卡罗法是一种基于随机抽样的计算方法，适用于各种数值计算问题。

在本文中，我们将探讨如何利用Matlab来使用蒙特卡罗法来计算圆周率。

1. 蒙特卡罗法的原理蒙特卡罗法是一种基于随机抽样的计算方法，其原理是通过大量的随机抽样来逼近一个问题的解。

具体来说，对于一个给定的概率分布函数，我们可以利用随机数生成器来产生服从该分布的随机数，然后利用这些随机数来估计该分布的各种性质。

在计算圆周率的问题中，我们可以利用蒙特卡罗法来估计圆的面积与正方形的面积的比值，从而得到圆周率的近似值。

2. 利用Matlab实现蒙特卡罗法计算圆周率在Matlab中，我们可以利用内置的随机数生成器来产生均匀分布的随机数。

假设我们要计算一个半径为1的单位圆的面积，则我们可以在一个边长为2的正方形内生成大量的均匀分布的随机点，然后统计落在圆内的随机点的个数。

具体的算法如下：```matlab定义随机点的个数N = 1e6;生成均匀分布的随机点x = rand(N,1)*2-1;y = rand(N,1)*2-1;统计落在圆内的随机点的个数count = sum(x.^2 + y.^2 <= 1);计算圆周率的近似值pi_approx = 4 * count / N;```在上述代码中，我们首先定义了随机点的个数N，并利用rand函数生成了N个服从均匀分布的随机点x和y。

然后我们统计了落在单位圆内的随机点的个数count，并利用count和N的比值来估计圆周率的近似值。

3. 结果分析与讨论通过运行上述代码，我们可以得到一个近似值pi_approx。

我们可以通过多次运行这个算法，并取多次结果的平均值来得到一个更加稳定的近似值。

另外，我们也可以通过增加随机点的个数N来提高近似值的精度。

事实上，蒙特卡罗法的收敛速度是随着N的增大而逐渐减小的，因此要想得到一个较高精度的近似值，需要投入更多的计算资源。

实
验
过
程
及
结
果
1、数值积分法
n=1000
n=10000
n=1000
n=10000
2、泰勒级数法
练习1、
练习2、
3、蒙特卡罗法
n=1000
n=10000
n=50000
实验结果分析
1、数值积分法中s1使用梯形公式计算出的积分的近似值，s2使用辛普森公式计算出的积分的近似值，计算出的积分值与π的值十分接近；
（5）同时按Shift和Enter键运行。
（6）n=10000时，只需将上面两个程序中的第一行“n=1000”改为“n=10000”.即可。
2、泰勒积分法计算Π
练习1、将x=1代入反正切函数的泰勒级数得到 ，在此级数中取n=20000计算 的近似值。观察所得的结果和所花的时间。
(1)在计算机程序中打开Mathematica4.0系统；
取n=1000,10000,用梯形公式和辛普森公式计算 和 的近似值（取二十位有效数字）。将所得的结果与 的准确值相比较。
（1）在计算机程序中打开Mathematica4.0系统；
（2）点击鼠标进入工作区后，输入以下语句：
（3）同时按Shift和Enter键运行。
（4）点击鼠标进入工作区后，输入以下语句：
2、泰勒级数法可以较为精确的计算出π的值；
3、蒙特卡罗法可以近似的计算出π的值，但是精度很低，随着n的增大精度有所提高，但是仍比数值积分法与泰勒级数法计算出的π的值精度低；
以上三种方法中将n的值取得更大，算出的积分的值将更加接近π的值。
（3）同时按Shift和Enter键运行。
3、蒙特卡罗法计算Π
取n=1000，10000，50000，用蒙特卡罗法计算 的近似值。

利用Matlab近似计算圆周率的若干方法作者：叶提芳来源：《科教导刊》2012年第09期摘要本文分别采取幂级数展开式的方法、随机数的方法、数值积分的方法和公式法结合Matlab程序实现对圆周率的近似计算，分析实验结果，比较每种方法的近似程度的高低，实现了Matlab实验和数学理论的很好结合。

关键词 Matlab实验圆周率幂级数随机数数值积分中图分类号：TP312 文献标识码：ASome Methods of Approximatively Calculating Using Matlab ExperimentsYE Tifang(Industrial and Commercial College, Wuhan Polytechnic University, Wuhan, Hubei 430065)Abstract In this paper, we used expanding power series, random number, numerical integration and formula methods combining matlab experiments to achieve the approximate value of . Then, we analyzed the experiments results, and compared the degree approximation of every method. It achieved the satisfying results of combination withMatlab experiment and mathematics theory.Key words Matlab experiments; ; power series; random number; numerical integration古今中外，历史上有许多人积极致力于圆周率的研究与计算。

Matlab圆周率1. 引言圆周率（π）是数学中的一个重要常数，表示圆的周长与直径之间的比值。

圆周率的精确值是一个无限不循环的小数，被广泛应用于数学、物理和工程等领域。

在本文中，我们将使用Matlab来计算圆周率，并探讨一些与圆周率相关的数值计算方法和应用。

2. 圆周率的定义与计算方法2.1 定义圆周率可以通过圆的周长与直径的比值来定义，即π = C/d，其中C表示圆的周长，d表示圆的直径。

2.2 常用计算方法2.2.1 几何法几何法是最直观的计算圆周率的方法之一。

它基于圆的定义，将一个正方形内切于一个圆，并通过计算正方形的边长与圆的直径的比值来逼近圆周率。

几何法的思想简单易懂，但精度较低，随着划分的正方形数量增加，计算结果会逼近真实值。

2.2.2 随机法随机法是一种通过生成随机点，并统计这些点落在圆内的比例来估计圆周率的方法。

随机法利用概率统计的思想，通过大量的随机模拟来逼近圆周率。

使用Matlab可以方便地生成随机数，并进行统计计算，从而得到较为准确的圆周率估计值。

2.2.3 数列法数列法是通过一些特定公式或数列来逼近圆周率的方法。

其中最著名的数列是莱布尼兹级数和无穷乘积法。

莱布尼兹级数是一个交替级数，通过逐项相加可以逼近圆周率的值。

无穷乘积法则是使用无穷乘积的形式来逼近圆周率，其中最著名的是狄利克雷（Dirichlet）级数。

这些数列法适用于在计算机中进行快速近似计算，但对于精确值的计算效果较差。

3. Matlab中的圆周率计算函数Matlab提供了多种计算圆周率的函数，方便了用户进行圆周率的计算和应用。

下面介绍几个常用的Matlab函数。

### 3.1 pi pi是Matlab内置的常量，表示圆周率的值。

使用pi函数可以直接获得圆周率的近似值，具有较高的精度。

3.2 montecarlo_pimontecarlo_pi是一个基于随机法的圆周率计算函数。

它通过生成随机点，并统计这些点落在圆内的比例来估计圆周率。

开放性数学实验报告（2016 / 2017学年第 2学期）题目：基于MATLAB的圆周率近似计算专业通信工程学生姓名杨坤冯著豪周李鑫班级学号 B******** B******** B********指导教师赵礼峰指导单位南京邮电大学理学院日期 2017/5/20MATLAB圆周率的近似计算B16011115 杨坤 B16011110 冯著豪 B16011124周李鑫摘要：圆周率（Pi）是圆的周长与直径的比值，一般用希腊字母π表示，是一个在数学及物理学中普遍存在的数学常数。

π也等于圆形之面积与半径平方之比。

是精确计算圆周长、圆面积、球体积等几何形状的关键值。

在分析学里，π可以严格地定义为满足sin x = 0的最小正实数x。

计算圆周率一直是很多人的追求。

在电子计算机还没有发明的时候就有很多先贤用各种方法计算了圆周率的近似值最著名的应该是祖冲之，他计算出了圆周率的位数达到了小数点后七位。

该记录在世界范围内保持了八百年。

之后圆周率的计算进入了分析法时期，这一时期人们开始利用无穷级数或无穷连乘积求π，摆脱可割圆术的繁复计算。

无穷乘积式、无穷连分数、无穷级数等各种π值表达式纷纷出现，使得π值计算精度迅速增加。

在分析法的基础上，电子计算机的出现使得圆周率的计算精度大幅提高。

计算圆周率已经成为评判超级计算机的性能指标的项目之一。

如今个人计算机的性能也达到了一个极高的程度。

学习使用计算机计算圆周率可以帮助我们更好地学习matlab同时对数学也会有更深的理解。

关键词：圆周率计算；投点法；定积分计分法；幂级数；韦达公式一、问题分析计算圆周率有很多方法，不同方法之间自然也有好坏之分。

在强大的计算机性能的支持下，我们能使用不同的方法计算圆周率并且感受不同方法孰优孰劣。

首先我们需要了解不同的计算方法是怎么计算圆周率的，然后使用matlab编写代码帮助我们实现算法，计算出圆周率。

二、实验方法1.投点法：投点法，顾名思义就是通过投点计算圆周率。

西安交通大学数学实验报告实验题目：圆周率的近似计算填写报告日期：2013年6月3日一、实验目的1.学会用MATLAB 软件对圆周率进行数值积分计算，求出近似值；2.学会用蒙特卡罗法求解几何体体积；二、实验任务1.对P89页示例4，利用矩形、和抛物线形方法求近似值，并与书上的方法进行比较，看哪种方法收敛速度快？2.完成P92页练习5第2题.三、问题分析与求解分析：（1）梯形公式：依次取每个极小区间中点为i ξ，利用积分式∑⎰=→=+ni i f dx x xi 10max102)(11lim ξ i x ∆计算圆周率π的近似值 （2）矩形公式：依次取每个区间某一端点i x ，利用计算圆周率π的近似值。

(3)抛物线公式：利用计算圆周率π的近似值。

1()d ()Δ,nbi i ai f x x f x x =≈∑⎰2221()d ()d i i nbx ax i f x x f x x-==∑⎰⎰2. 蒙特卡罗法求解冰淇淋体积：在区域{(x,y,z)｜x 2 + y 2 ≤ 1,0 ≤x,0≤y, 0≤ z ≤2}内随机取点，对落在冰淇淋体第一卦限内的点进行计数，则落在冰淇淋内的点数m 与落在长方体区域内的点数n 的比值等于体积的比值.故V （冰淇淋）= nm8。

（1）圆周率的数值积分计算矩形方法程序： n=5000 i=0:1/n:1; s=0;for k=1:length(i)s=s+(1/(1+i(k)^2))*1/n; end 4*s 运行结果：抛物线方法程序：n=5000;i=0:1/n:1;s=0;for k=2:length(i)/2s=s+((1/(1+i(2*k-2)^2))+(4/(1+i(2*k-1)^2))+(1/(1+i(2*k)^2))); end8/(6*n)*s运行结果：与书中方法对比，易得抛物线形公式收敛速度最快。

（2）蒙特卡罗法求冰淇淋体积程序：cs=0n=500000for i=1:na=rand(1,3);if a(1)^2+a(2)^2<=4*a(3)-(2*a(3))^2&a(1)^2+a(2)^2<=(2*a(3))^2;cs=cs+1;endendV=8*cs/n运行结果：评论：使用蒙特卡罗法计算冰淇淋的体积，存在较大的随机性，实验结果与理论值相差较大。