初中数学八年级上册《71谁的包裹多》

北师大版初中数学八年级上册《7.1谁的包裹多》精品教案【教学目标】【知识目标】了解二元一次方程、二元一次方程组及其解等有关概念，并会判断一组数是不是某个二元一次方程组的解。

【能力目标】通过讨论和练习，进一步培养学生的观察、比较、分析的能力。

【情感目标】通过对实际问题的分析，使学生进一步体会方程是刻画现实世界的有效数学模型，培养学生良好的数学应用意识。

【重点】二元一次方程组的含义【难点】判断一组数是不是某个二元一次方程组的解，培养学生良好的数学应用意识。

【教学过程】一、引入1、师：在一望无际呼伦贝尔大草原上，一头老牛和一匹小马驮着包裹吃力地行走着，老牛喘着气吃力地说：“累死我了”，小马说：“你还累，这么大的个，才比我多驮2个”老牛气不过地说：“哼，我从你背上拿来一个，我的包裹就是你的2倍！”，小马天真而不信地说：“真的？！”同学们，你们能否用数学知识帮助小马解决问题呢？2、请每个学习小组讨论（讨论2分钟，然后发言）这个问题由于涉及到老牛和小马的驮包裹的两个未知数，我们设老牛驮x个包裹，小马驮y个包裹，老牛的包裹数比小马多2个，由此得方程x-y=2，若老牛从小马背上拿来1个包裹，这时老牛的包裹是小马的2倍， 得方程：x+1=2(y-1)师：同学们能用方程的方法来发现、解决问题这很好，上面所列方程有几个未知数？含未知数的项的次数是多少？ （含有两个未知数，并且所含未知数项的次数是1）师：含有两个未知数，并且含未知数项的次数都是1的方程叫做二元一次方程注意：这个定义有两个地方要注意①、含有两个未知数，②、含未知数的次数是一次练习：（投影）下列方程有哪些是二元一次方程x 1+2y=1 xy+x=1 3x-2y =5 x 2-2=3x xy=1 2x(y+1)=c 2x-y=1 x+y=0二、 议一议、星期天，我们8个人去温州动物园玩，买门票花了34元。

每张成人票5元，每张儿童票3元。

他们到底去了几个成人、几个儿童呢？若设他们中有x 个成人,y 个儿童.由此你能得到怎样的方程?x+y=85x+3y=34师：上面的方程中x+y=8, 5x+3y=34的x 含义相同吗？y 呢？（两个方程中x 表示成人数，y 表示儿童数，x 、y 的含义分别相同。

谁的包裹多学习目标:1．通过实例了解二元一次方程、二元一次方程组及其解等概念．2．会判断一组数是不是某个二元一次方程组的解．3．会依如实际问题列简单的二元一次方程或二元一次方程组．问题与题例:一、导入（讲义215面图片中的问题）设小马驮了x 个包裹，那么老牛驮了________个包裹．假设老牛从小马背上拿来 1 个包裹，这时老牛驮的包裹数是_______________个？小马又是______________个？那么依照题意列一元一次方程为________________________．设老牛驮x 个包裹，小马驮y 个包裹，老牛的包裹数比小马多2个，由此得方程____________________，假设老牛从小马背上拿来1个包裹，这时老牛的包裹是小马的2倍，得方程______________________，像这种方程叫做什么方程呢?二、概念1．二元一次方程的概念：2．二元一次方程组的概念：3．二元一次方程的解的概念：4．二元一次方程组的解的概念：三、例题与练习1．举出一个二元一次方程和一个二元一次方程组：2．说出下面的方程是几元几回方程：（1）022=-+z y x ；（2）0232=-x x ；（3）032322=+-y x ；（4）02=m ． 3．试探：（1）x ＝6，y ＝2适合方程x ＋y ＝8吗？x ＝5，y ＝3呢？x ＝4，y ＝4呢？你还能找到其他x ，y 值适合x ＋y ＝8方程吗？（2） x ＝5, y ＝3适合方程5x ＋3 y ＝34吗？x ＝2, y ＝8呢？（3）你能找到一组值x , y 同时适合方程x ＋ y ＝8和5x ＋3y ＝34吗？4．假设,x a y b =⎧⎨=⎩是方程2x ＋y ＝1的解，求6a ＋3b ＋2的值目标检测：1．以下方程有哪些是二元一次方程：（1）093=-+y x ，（2）012232=+-y x ， （3）743=-b a ， （4）113=-y x ， （5）()523=-y x x ， （6）152=-n m ． 2．若是方程13221=-+-n m m y x 是二元一次方程，那么m ＝ ，n ＝ ．3．判定以下方程组是不是是二元一次方程组：（1）⎩⎨⎧=+=-;1253,12y x y x （2）⎩⎨⎧=-=+;53,12y x y x （3）⎩⎨⎧=+=-;153,37z y y x （4）⎩⎨⎧==;2,1y x （5）⎪⎩⎪⎨⎧=+=-;1283,52y x y x （6）⎩⎨⎧=+=-.325,132b ab b a 4．教材P218《随堂练习》1，2，3．配餐练习：A 组 巩固基础教材P218《习题7．1》“知识技术”1，2，3．B 组 强化训练2．二元一次方程6=+y x 的正整数解为 ．3．若是⎩⎨⎧==2,1y x 是⎩⎨⎧=-=+n y x m y x 3,2的解，那么m ＝ ，n ＝ ． 4．写出一个以⎩⎨⎧-==3,2y x 为解的二元一次方程组为 ． 5．当y ＝－3时，二元一次方程3x ＋5y ＝－3和3y －2ax ＝a ＋2（关于x ，y 的方程）有相同的解，那么a ＝_______．C 组 延伸拓广1．教材P218《习题7．1》“数学明白得”4，5．2．已知2,3,16x mx y y x ny =-=⎧⎧⎨⎨=-=⎩⎩是方程组的解，求m 和n 的值．。

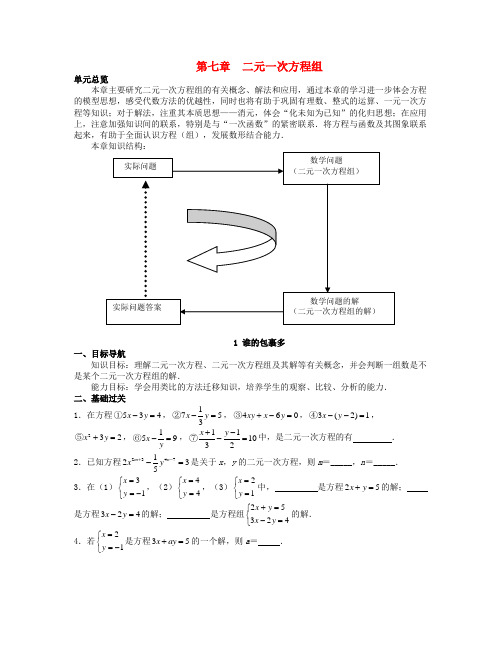
第七章 二元一次方程组单元总览本章主要研究二元一次方程组的有关概念、解法和应用，通过本章的学习进一步体会方程的模型思想，感受代数方法的优越性，同时也将有助于巩固有理数、整式的运算、一元一次方程等知识；对于解法，注重其本质思想——消元，体会“化未知为已知”的化归思想；在应用上，注意加强知识间的联系，特别是与“一次函数”的紧密联系．将方程与函数及其图象联系起来，有助于全面认识方程（组），发展数形结合能力． 本章知识结构：1 谁的包裹多一、目标导航知识目标：理解二元一次方程、二元一次方程组及其解等有关概念，并会判断一组数是不是某个二元一次方程组的解．能力目标：学会用类比的方法迁移知识，培养学生的观察、比较、分析的能力．二、基础过关1．在方程534x y -=①，1753x y -=②，460xy x y +-=③，3(2)1x y --=④，232x y +=⑤，159x y -=⑥，111032x y +--=⑦中，是二元一次方程的有 ． 2．已知方程23471235m n x y +--=是关于x ，y 的二元一次方程，则m ＝_____，n ＝_____． 3．在（1）31x y =⎧⎨=-⎩，（2）44x y =⎧⎨=⎩，（3）21x y =⎧⎨=⎩中， 是方程25x y +=的解； 是方程324x y -=的解； 是方程组25324x y x y +=⎧⎨-=⎩的解． 4．若21x y =⎧⎨=-⎩是方程35x ay +=的一个解，则a ＝ ． 实际问题 数学问题（二元一次方程组）实际问题答案 数学问题的解（二元一次方程组的解）5．若121x y ⎧=⎪⎨⎪=⎩是方程组322ax y x by -=⎧⎨+=⎩的解，则b －a ＝ ． 6．关于x ，y 的二元一次方程4x ＋3y ＝20的所有非负整数解是 ．7．若一个二元一次方程的一个解为21x y =⎧⎨=-⎩，则这个方程可以是 ．（只要求写出一个）8．把方程5x －3y ＝6变形，用x 表示y 应为 ，用y 表示x 应为 ．9．下列方程组属于二元一次方程组的是（ ）A ．6230x y x z +=⎧⎨-=⎩B ．21537x y y ⎧+=⎪⎨⎪=⎩C ．23m n mn +=⎧⎨=-⎩D ．920138a b b a-=⎧⎪⎨+=⎪⎩ 10．若方程ax －3y ＝4x ＋5是二元一次方程，则a 的取值范围是（ ）A ．0a ≠B ．3a ≠C ．4a ≠D ．5a ≠11．以下各组中，是方程组34x y x y =⎧⎨-=⎩的解的是（ ） A ．62x y =⎧⎨=⎩ B ． 26x y =⎧⎨=⎩ C ． 31x y =⎧⎨=⎩ D ．13x y =⎧⎨=⎩12．小丽只带了2元和5元两种人民币，买了一件物品只付了27元，则付款的方法有（ ）A ．一种B ．两种C ．三种D ．四种三、能力提升13．已知2x ＋5y －3＝0，则代数式9－4x －10y ＝____________．14．若3a -与21a b +-()互为相反数，则3a b += ．15．现有1角、5角、1元硬币各10枚，从中取出15枚，共值7元．1角、5角、1元硬币分别取______枚，______枚，______枚．16．若x m y n =⎧⎨=⎩是方程5x ＋9y ＝0的解，且0m ≠，则（ ） A ．m ，n 同号 B ．m ，n 异号 C ．m ，n 可能同号也可能异号 D ．无法确定17、方程x ＋2y ＝7在自然数范围内的解有（ ）A ．一个B ．二个C ．三个D ．四个 18．某校初二（3）班40名同学为“希望工程”捐款，共捐款100元，捐款情况如下表：捐款（元） 1 2 3 4人数 6 7表格中捐款2元和3元的人数不小心被墨水污染已看不清楚，若设捐款2元的有x 名，捐款3元的有y 名同学，根据题意，可得方程组（ ）A ．2272366x y x y +=⎧⎨+=⎩B ．2723100x y x y +=⎧⎨+=⎩C ．2732266x y x +=⎧⎨+=⎩D ．2732100x y x y +=⎧⎨+=⎩19．已知方程218(3)(2)6b a a x b y cxy --+--+=是关于x ，y 的二元一次方程，求a ，b ，c 的值．20．甲、乙两人共同解方程组51641x ay bx y -=⎧⎨+=⎩①②由于甲同学看错了方程①中的a ，得到方程组的解为434x y =-⎧⎪⎨=-⎪⎩，乙看错了方程②中的b ，得到方程组的解为59x y =⎧⎨=-⎩．请计算代数式20072008a b 的值．四、聚沙成塔读诗词解题大江东去浪淘尽，千古风流数人物．而立之年督东吴，早逝英年两位数．十位恰小个位三，个位六倍与寿符．哪位学子算得快，多少年华属周瑜？1 谁的包裹多1．5x－3y＝4，1753(2)13x y x y-=--=；，111032x y+--= 2．m＝－1，n＝23．（1）（3）；（2）（3）；（3） 4．1 5．－7 6．24xy=⎧⎨=⎩；5xy=⎧⎨=⎩7．x－y＝3（答案不唯一） 8．5362;355x y-+ 9．B 10．C 11．A 12．C 13．314．－3 15．5，7，3 16．B 17．D 18．A 19．a＝3，b＝－2，c＝0 20．－1．。

《谁的包裹多》导学案学校 年级 学科 使用人一、学习目标1.能根据题意列出方程或方程组，并判断是所学过的哪种方程（组），能举出二元一次方程及二元一次方程组的例子；2.能列举二元一次方程的解，会判断一组数是不是二元一次方程（组）的解二、学习重点 重点：会列二元一次方程（组）；会用代入法判断是不是方程（组）的解 难点：二元一次方程及二元一次方程组的概念三、学习准备一元一次方程的概念，一元一次方程的解的概念，多项式的次数.四、学习过程（一）课前先学（3分钟）1.你从上图中获得了哪些数学信息？2.请利用上述信息列出方程，并说出你列的是不是一元一次方程。

如果不是一元一次方程，它可以叫什么方程？（二）课中先学活动（1）（4分钟）累死我了 它们各驮了多少包裹呢？1. 如果设去了x 名成人，去了y 名儿童，根据题意请列出方程？你列的是不是二元一次方程？2.请你总结一下满足什么条件的方程是二元一次方程.请举个二元一次方程的例子.小试牛刀（1）：下列方程中是二元一次方程的是（ ）A 1=xyB 201=+yx C 1-=x y D 032=+-y x （三）课中先学活动（2）看课本216页“议一议”，回答下列问题（5分钟）1.在所给的两个方程中，x 都是表示什么？y 呢？2.方程组⎩⎨⎧=+=-3113y x 是不是二元一次方程组？能不能把二元一次方程组的定义说成由两个二元一次方程组成的方程组，这种说法与课本定义有什么不同之处？3.二元一次方程组的特征是什么？小试牛刀（2）：下列方程组中是二元一次方程组的是（ ）A B C D （四）课中先学（3）看课本217页“做一做” 到课本218页上面.思考下列问题（4分钟）：1.你用什么方法找二元一次方程的解？二元一次方程组的解呢？2.你用什么方法判断一个数或一组数是不是方程（组）的解？⎩⎨⎧==+3282y y x ⎩⎨⎧+=-+=-.)1(325y x y x y x ⎪⎩⎪⎨⎧=-=+5211y x y x ⎩⎨⎧=-=+.82,4z x y x小试牛刀（3）下列四组数值中哪些是方程①的解？哪些是方程②的解？哪一组是方程组的解？（五）学习小结（2分钟）：1.你学到了哪些新知识？哪些数学思想方法？2.你还有哪些疑问？五、大试牛刀（6分钟）（一）（60分）基础达标：课本218页随堂练习第1、2、3题各20分.（二）（20分）能力过关：课本219页数学理解第4题.（三）（20分）创新应用：课本219页数学理解第5题.六、反思总结⎩⎨⎧-=-=+182y x y x ① ② ⎩⎨⎧==.32y x ⎩⎨⎧==21y x ⎩⎨⎧==.24y x ⎩⎨⎧==43y x A B C D。

八年级数学上册《7.1 谁的包裹多》学案北师大版7、1 谁的包裹多》学案导入语：（一）问题化：创设核心问题情景，感受数学思考；谁的负担重？这个问题最早出现《希腊文选》。

驴和骡肩并肩地在街上走，各自驮着几个包裹。

驴抱怨主人给他压的担子太重，骡却说：“老兄，你的负担并不算重！你瞧，假如从你背上拿走一个包裹给我，我的负担就是你的两倍；而假如你从我背上取走一个包裹，你的负担也不过和我相同”。

假如每个包裹重量相等，试问驴和骡各驮着几个包裹？教学目标：知识与技能：1、理解二元一次方程（组）及其解的概念。

2、能判别一组数是否是二元一次方程（组）的解。

过程与方法：从丰富的问题情境出发，引入二元一次方程（组）的有关概念。

二元一次方程与一元一次方程有很多类似的地方，学习时可运用类比的思想方法。

比较二元一次方程与一元一次方程有关概念的相同点和不同点。

情感态度与价值观：通过对方程的解的理解，了解变与不变的辩证统一的思想。

教学重点：正确理解二元一次方程的解和二元一次方程组的解的含义。

教学难点：根据实际问题列简单的二元一次方程或二元一次方程组。

教法：先学后教；学法：自主合作、一、课前探究谁的包裹多二、预习交流教材P215-217---做一做三、互助提升自学提纲：（二）探究化：经历新知形成过程，体验探究方法；师：还有没有其他方法呢？你能谈谈你的想法吗？（只要学生的回答有道理，都要予以肯定；若有错，可友善地指出不合理的地方。

若学生能用两个未知数，列出二元一次方程组，就请该生上台讲解。

）师：设老牛驮了X个包裹，小马驮了y个包裹。

则你能列出怎样的方程，试试吧。

三、第二幅图怎样设未知数，把方程列出来。

四、二元一次方程（组）的有关概念类似于，一元一次方程的解一样。

我们有（l）二元一次方程的概念想一想：就方程x＋y ＝8和5X＋3y＝34各含有几个未知数？含未知数的项的次数是多少？含有两个未知数，且未知数项的最高次数是1的整式方程，称为二元一次方程什么叫做二元一次方程？什么叫做二元一次方程组？什么叫做二元一次方程的解？什么叫做二元一次方程组的解？四、体验成功当堂检测及时矫正，实现新课高效、1、在方程2x−3y =6里，若用含x的代数式表示y，则y =错；将2x−3y =6，变形为3y =2x−6，所以y =2、方程组的解是方程x−2y =7的解，反之方程x−2y =7的解也是方程组的解3、随堂练习 P218—1、2、3。

第七章二元一次方程组总课时：8课时执笔人：刘丽娟使用人：备课时间：第九周上课时间：第十三周第1课时：7、1谁的包裹多教学目标知识与技能了解二元一次方程、二元一次方程组及其解等有关概念，并会判断一组数是不是某个二元一次方程组的解.过程与方法通过对实际问题的分析，使学生进一步体会方程是刻画现实世界的有效数学模型，培养学生良好的数学应用意识.情感态度与价值观教学重点二元一次方程组的含义。

教学难点教学准备多媒体课件教学过程第一环节：情境引入（10分钟，学生理解题意，思考解决问题的手段，小组讨论）内容：（一）情境1实物投影，并呈现问题：在一望无际的呼伦贝尔大草原上，一头老牛和一匹小马驮着包裹吃力地行走着，老牛喘着气吃力地说：“累死我了”，小马说：“你还累，这么大的个，才比我多驮2个.”老牛气不过地说：“哼，我从你背上拿来一个，我的包裹就是你的2倍！”，小马天真而不信地说：“真的？！”同学们，你们能否用数学知识帮助小马解决问题呢？请每个学习小组讨论（讨论2分钟，然后发言）。

教师注意引导学生设两个未知数，从而得出二元一次方程。

这个问题由于涉及到老牛和小马的驮包裹的两个未知数，我们设老牛驮x个包裹，小马驮y个包裹，老牛的包裹数比小马多2个，由此得方程x-y=2，若老牛从小马背上拿来1个包裹，这时老牛的包裹是小马的2倍，得方程：x+1=2(y-1)实物投影，并呈现问题：昨天，有8个人去红山公园玩，他们买门票共花了34元.每张成人票5元，每张儿童票3元.那么他们到底去了几个成人、几个儿童呢？同学们，你们能否用所学的方程知识解决呢？仍请每个学习小组讨论（讨论2分钟，然后发言），老师注意引导学生分析其中有几个未知量，如果分别设未知数，将得到什么样的关系式？这个问题由于涉及到有几个成年人和几个儿童两个未知数，我们设他们中有x 个成年人，有y 个儿童，在题目的条件中，我们可以找到的等量关系为：成人人数＋儿童人数＝8，成人票款＋儿童票款＝34.由此我们可以得到方程x +y =8和5x +3y =34.第二环节：新课讲解，练习提高（25分钟，教师引导学生利用方程解决问题的方法，学生理解识记，小组讨论与全班交流想结合掌握方法）内容：（一） 二元一次方程概念的概括提请学生思考：上面所列方程有几个未知数？所含未知数的项的次数是多少？从而归纳出二元一次方程的概念：含有两个未知数，并且所含未知数的项的次数都是1的方程。