编译原理文法与语言
- 格式：ppt
- 大小：113.00 KB
- 文档页数：50
下载文档原格式
合集下载
编译原理清华大学第3章 文法和语言
<句子> => <主语><谓语> => the <形容词><名词><谓语> => the big <名词> <谓语> => the big elephant <谓语>
<主语>::=<冠词><形容词><名词> <冠词> ::=the <形容词>::=big <谓语>::=<动词><宾语> <动词>::=ate <宾语>::=<冠词><名词>
“我是大学生”。是汉语的一个句子 用语法来描述：
〈句子〉∷=〈主语〉〈谓语〉 〈主语〉∷=〈代词〉｜〈名词〉 〈代词〉∷=我｜你｜他 〈名词〉∷=王明｜大学生｜工人｜英语 〈谓语〉∷=〈动词〉〈直接宾语〉 〈动词〉∷=是｜学习 〈直接宾语〉∷=〈代词〉｜〈名词〉
有了一组规则以后，按照如下方式用它们导出句子：开始去找∷= 左端的带有〈句子〉的规则并把它由∷=右端的符号串代替，这个动作表 示成： 〈句子〉 〈主语〉〈谓语〉，然后在得到的串〈主语〉〈谓 语〉中，选取〈主语〉或〈谓语〉，再用相应规则的∷=右端代替之。比 如，选取了〈主语〉，并采用规则〈主语〉∷=〈代词〉， 那么得到：〈主语〉〈谓语〉 〈代词〉〈谓语〉， 重复做下去， 句子：“我是大学生”的全部动作过程是： 〈句子〉 〈主语〉〈谓语〉 〈代词〉〈谓语〉 我〈谓语〉 我〈动词〉〈直接宾语〉 我是〈直接宾语〉 我是〈名词〉 我是大学生 “我是大学生”的构成符合上述规则，而“我大学生是”不符合上 述规则，我们说它不是句子。这些规则成为我们判别句子结构合法与否 的依据，换句话说，这些规则看成是一种元语言，用它描述汉语。这里 仅仅涉及汉语句子的结构描述。其中一种描述元语言称为文法。
<主语>::=<冠词><形容词><名词> <冠词> ::=the <形容词>::=big <谓语>::=<动词><宾语> <动词>::=ate <宾语>::=<冠词><名词>
“我是大学生”。是汉语的一个句子 用语法来描述：
〈句子〉∷=〈主语〉〈谓语〉 〈主语〉∷=〈代词〉｜〈名词〉 〈代词〉∷=我｜你｜他 〈名词〉∷=王明｜大学生｜工人｜英语 〈谓语〉∷=〈动词〉〈直接宾语〉 〈动词〉∷=是｜学习 〈直接宾语〉∷=〈代词〉｜〈名词〉
有了一组规则以后，按照如下方式用它们导出句子：开始去找∷= 左端的带有〈句子〉的规则并把它由∷=右端的符号串代替，这个动作表 示成： 〈句子〉 〈主语〉〈谓语〉，然后在得到的串〈主语〉〈谓 语〉中，选取〈主语〉或〈谓语〉，再用相应规则的∷=右端代替之。比 如，选取了〈主语〉，并采用规则〈主语〉∷=〈代词〉， 那么得到：〈主语〉〈谓语〉 〈代词〉〈谓语〉， 重复做下去， 句子：“我是大学生”的全部动作过程是： 〈句子〉 〈主语〉〈谓语〉 〈代词〉〈谓语〉 我〈谓语〉 我〈动词〉〈直接宾语〉 我是〈直接宾语〉 我是〈名词〉 我是大学生 “我是大学生”的构成符合上述规则，而“我大学生是”不符合上 述规则，我们说它不是句子。这些规则成为我们判别句子结构合法与否 的依据，换句话说，这些规则看成是一种元语言，用它描述汉语。这里 仅仅涉及汉语句子的结构描述。其中一种描述元语言称为文法。
第2章 文法和语言的基本知识
例如， ∑′={0，1}是一个字母表，由0 和1两个元素组成。 不同的语言有不同的字母表，如英文的字 母表是26个字母、数字和标点符号的集合，C语 言的字母表是由字母、数字和若干专用符号组 成。 2. 符号（字符） 字母表中的元素称为符号，或称为字符。 例如，前述例子中，a，b，c是字母中∑ 中的符号；0和1是字母表∑′中的符号。
例如：用A表示∑ + ，用式子A→0表示符号串 0∈A或A生成符号串0，符号“→”读做“生成”或 “由……组成”。则集合A可表示成 A→0 A→1 A→A0 A→A1 显然，由A生成的符号串属于∑+，这就是用文 法描述语言。
编译原理授课教案
2.2.2 文法的形式定义
1. 规则 规则也称产生式，它是一个符号与一个符号 串的有序对(A，β)，通常写做 A→β(或A::=β) 其中，A是规则左部，它是一个符号；β是 规则右部，它是一个符号串；“→”和“::=”表 示“定义为”或”生成”，意思是左部符号用右 部的符号串定义或左部符号生成右部是集合， 而｛ε｝表示由空符号串ε所组成的集合，但 这样的集合不是集合φ＝｛｝。 ３. 符号串的幂运算 设x是符号串，则x的幂运算定义为 x0=ε X1= x x2 = xx ………… xn = xxxx……xx=xxn-1 ( n > 0)
编译原理授课教案
编译原理授课教案
试设计一个表示所有标识符的文法。 例2.2 ：
分析 题意是用文法定义标识符，必须确 定P中规则。为了设计出一组规则，首先应搞清 楚集合中符号串的结构特征。标识符的定义是 字母或以字母开头的字母数字串，结构如图：
字母 字母或数字串
用I代表标识符，L代表字母，D代表数字， 则定义标识符的方法为 G = (VN ,VT, P , S)
编译原理第3章文法和语言
第3章文法和语言第1题文法G＝({A,B,S},{a,b,c},P,S)其中P为：S→Ac|aBA→abB→bc写出L(G[S])的全部元素。
答案：L(G[S])={abc}第2题文法G[N]为：N→D|NDD→0|1|2|3|4|5|6|7|8|9G[N]的语言是什么？答案:G[N]的语言是V+。
V={0,1,2,3,4,5,6,7,8,9}N=>ND=>NDD....=>NDDDD...D=>D......D或者：允许0开头的非负整数？第３题为只包含数字、加号和减号的表达式，例如9-2＋5，3-1，７等构造一个文法。
答案：G[S]:S->S+D|S-D|DD->0|1|2|3|4|5|6|7|8|9第4题已知文法G[Z]：Z→aZb|ab写出L(G[Z])的全部元素。
答案：Z=>aZb=>aaZbb=>aaa..Z...bbb=>aaa..ab...bbbL(G[Z])={anbn|n>=1}第5题写一文法，使其语言是偶正整数的集合。
要求：(1)允许0打头；(2)不允许0打头。
答案：(1)允许0开头的偶正整数集合的文法E→NT|DT→NT|DN→D|1|3|5|7|9D→0|2|4|6|8(2)不允许0开头的偶正整数集合的文法E→NT|DT→FT|GN→D|1|3|5|7|9D→2|4|6|8F→N|0G→D|0第6题已知文法G：<表达式>::=<项>｜<表达式>＋<项> <项>::=<因子>｜<项>*<因子><因子>::=（<表达式>）｜i试给出下述表达式的推导及语法树。
（５）i+(i+i)（６）i+i*i答案：(5)<表达式>=><表达式>＋<项>=><表达式>＋<因子>=><表达式>＋（<表达式>）=><表达式>＋（<表达式>＋<项>）=><表达式>＋（<表达式>＋<因子>）=><表达式>＋（<表达式>＋i）=><表达式>＋（<项>＋i）=><表达式>＋（<因子>＋i）=><表达式>＋（i＋i）=><项>＋（i＋i）=><因子>＋（i＋i）=>i＋（i＋i）(6)<表达式>=><表达式>＋<项>=><表达式>＋<项>*<因子>=><表达式>＋<项>*i=><表达式>＋<因子>*i=><表达式>＋i*i=><项>＋i*i=><因子>＋i*i=>i＋i*i<表达式><表达式>+<项><因子><表达式><表达式>+<项><因子>i<项><因子>i<项><因子>i（)<表达式><表达式>+<项><项>*<因子><因子>i<项><因子>ii第7题证明下述文法G[〈表达式〉]是二义的。
编译原理第二版作业答案_第2章
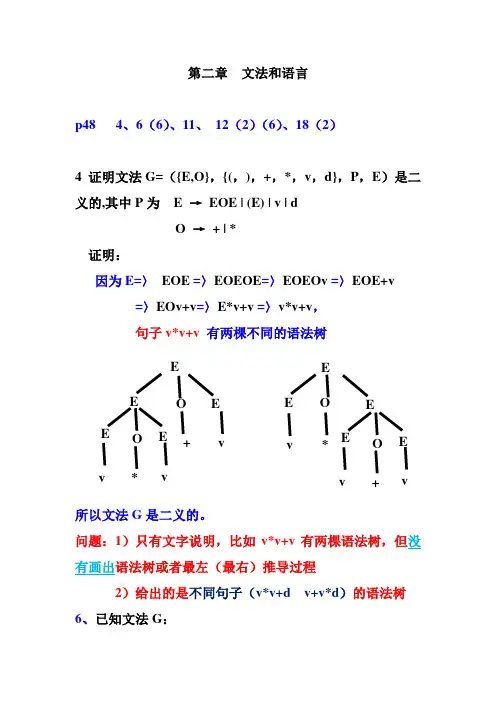
第二章 文法和语言p48 4、6（6）、11、 12（2）（6）、18（2）4 证明文法G=（{E,O}，{(，)，+，*，v ，d}，P ，E ）是二义的,其中P 为 E → EOE | (E) | v | d O → + | * 证明：因为E=〉 EOE =〉EOEOE =〉EOEOv =〉EOE+v=〉EOv+v =〉E*v+v =〉v*v+v ， 句子v*v+v 有两棵不同的语法树所以文法G 是二义的。
问题：1）只有文字说明，比如v*v+v 有两棵语法树，但没有画出语法树或者最左（最右）推导过程2）给出的是不同句子（v*v+d v+v*d ）的语法树 6、已知文法G ：EEEE OO v*v+ vE EE E O O v+v* v〈表达式〉∷=〈项〉|〈表达式〉+〈项〉〈项〉∷=〈因子〉|〈项〉*〈因子〉〈因子〉∷=（〈表达式〉）| i试给出下述表达式的推导及语法树（6）i+i*i推导过程：〈表达式〉=〉〈表达式〉+〈项〉E=〉E+T =〉〈表达式〉+〈项〉*〈因子〉=〉E+ T*F=〉〈表达式〉+〈项〉* i =〉E+ T*i=〉〈表达式〉+ 〈因子〉* i =〉E+F*i=〉〈表达式〉+ i* i =〉E+i*i=〉〈项〉+ i* i =〉T +i*i=〉〈因子〉+ i* i =〉F +i*i=〉i +i*i =〉i +i*i 共8步推导语法树：〈表达式〉+〈因子〉〈项〉i 〈因子〉i〈项〉〈项〉〈因子〉i*11、一个上下文无关文法生成句子abbaa的推导树如下：（1）给出该句子相应的最左推导和最右推导（2）该文法的产生式集合P可能有哪些元素？（3）找出该句子的所有短语、简单短语、句柄。
（1）最左推导：S=〉ABS=〉aBS=〉aSBBS=〉aBBS=〉abBS=〉abbS =〉abbAa=〉abbaa最右推导：S =〉ABS=〉ABAa=〉ABaa=〉ASBBaa=〉ASBbaa=〉ASbbaa=〉Abbaa=〉abbaa（2）该文法的产生式集合P可能有下列元素：S→ABS | Aa|εA→a B→SBB|b（3）因为字符串中的各字符有相对的位置关系，为了能相互区别，给相同的字符标上不同的数字。
编译原理(清华)第三章文法和语言
例 文法G： S→0S1，S→01 有直接推导： 0S1 00S11 （ S→0S1 ） 00S11 000S111 （ S→0S1 ） 000S111 00001111 （ S→01 ） S 0S1 （ S→0S1 ）
推导和归约 若存在v=w0 w1 ... wn=w ,(n>0) 则称v推导出w，或w归约到v,记为v=+>w 若有v =+>w，或v=w，则记作v=*>w
2. 符号串 – 定义:由字母表中的符号组成的任何有穷序列 – 例： 0,00,10是字母表∑={0‚1}上的符号串 a,ab,aaca是Α={a‚b，c}上的符号串 – 在符号串中，符号是有顺序的，顺序不同,代 表不同的符号串，如:ab和ba不同 – 不含任何符号的符号串称为空串，用ε表示 注意:{ε}并不等于空集合{ } – 符号串长度: 符号串中含有符号的个数 如: |abc|=3 | ε|=0
3.3 文法和语言的形式定义
1．文法的定义 2．文法的简化表示法 3．推导与归约 4．句型、句子、语言的定义 5．文法的等价
1．文法的定义
产生式（规则） 产生式是一个有序对(α,β)，通常写作 α→β（或α::=β ） 文法定义: 文法G(Grammar)定义为四元组（VN，VT，P，S） VN (Nonternimal)：非终结符集 VT (Terminal)：终结符集 P (Production)： 产生式（规则）集合 S： 开始符号或识别符号
第三章
文法和语言
学习目标: 掌握：自上而下与自下而上的分析方法 理解：文法的形式定义，推导，归约，句 型，句子，语言，上下文无关文法，规范 句型，语法树，短语，直接短语，句柄 了解：文法的类型，文法使用中的限制， 文法的二义性
编译原理(第二版)第3章 文法和语法
〈动词〉::= 是 | 学习
〈直接宾语〉::=〈代词〉|〈名词〉
“我是大学生”是否是该语言的句子？
〈句子〉::=〈主语〉〈谓语〉 〈主语〉::=〈代词〉|〈名词〉 〈代词〉::= 你 | 我 | 他 〈名词〉::= 王明 | 大学生 | 工人 | 英语 〈谓语〉::=〈动词〉〈直接宾语〉 〈动词〉::= 是 | 学习 〈直接宾语〉::=〈代词〉|〈名词〉 〈句子〉
}的文法。
分析：n≧1，所以必须用递归规则。a和b的 个数 一样多，但c的个数不同，所以将生成 含 a,b的部分与生成含e的部分分开，A生成 ab，B生成e. G[Z]:Z→AB
A→aAb|ab
B→eB|ε
4)文法的等价
• 若L（G1）=L（G2），则称文法G1和G2是等价的。
如文法G1[A]：A→0R 与 G2[S]：S→0S1 等价
设 z = abc, 那么 z 的头是： ε ,a ,ab , abc（除 abc 外都是固有头） z 的尾是： ε ,c ,bc , abc（除 abc 外都是固有尾）
4、符号串的运算
符号串的长度：符号串中符号的个数.符号串s的长度 记为|s|。 ε的长度为0 符号串的连接：符号串x、y的连接,是把y的符号写在 x的符号之后得到的符号串xy 例 x=ST,y=abu 则 xy=STabu
|x|=2,|y|=3,|xy|=5
εx = xε= x
方幂：符号串x自身连接n次得到的符号串 xx…xx(n个x)定义为 xn x0=ε , x1=x, x2=xx, x3=xxx x=AB, 则 x0=ε , x1=AB, x2=ABAB, x3=ABABAB 对于 n>0, xn = xxn-1 = xn-1x
例如： 汉语的字母表中包括汉字、数字及标点符号等。 C语言的字母表是由字母、数字、若干专用符号及IF、 FOR之类的保留字组成。
编译原理语法分析(1)
例如, 考虑句子 i+i*i 按文法G[E]的推导 最左推导: EE+Ei+Ei+E*E i+i*E i+i*i 最右推导: EE+EE+E*EE+E*i E+i*ii+i*i 注意: 推导过程不唯一, 通常只考虑最左 推导或最右推导。 最右推导又称为规范推导。 规范推导的逆过程称为规范归约。
+ 。 * 意味着或 = , 或 即1 n 1 n 1 n
例如,考虑算术表达式文法G[E]： E→E+E∣E*E∣(E)│i 非终结符E代表一类算术表达式, 从E出发可进行一系列推导, 表达式 i+i*i 的推导如下： E E+E E+E*E E+E*i E+i*i i+i*I 注意: 在每一步推 导中,只能对其中一个 非终结符用其对应的产生式右部的 一个候选式来替换。
文法可表示为 VN为非空非终结符集,且VT∩VN=Φ; (3) S为文法开始符, S∈VN; (4)ξ是产生式的非空有限集, 其中每个 产生式(规则)记作 → 或 ::= 左部∈(VT∪VN)+至少含一非终结符, 右部∈(VT∪VN)*。
B
3.1.3 正规式与上下文无关文法 1. 正规式到上下文无关文法的转换 由正规式构造CFG的一种方法： (1)构造正规式的NFA； (2)若0为初始状态, 则A0为开始符； (3)若存在映射关系f(i,a)=j, 则定义产生式Ai →aAj； (4)若存在映射关系f(i,ε)=j， 则定义产生式Ai →Aj； (5) 若i为终态, 则定义产生式Ai →ε。
产生式 (也称产生式规则或规则) 是 定义语法实体的一种书写规则。一个语 法实体的相关规则可能不止一个, 如: P→1, P→2 , P→n 相同左部的产生式可合并为一个: P→ 1| 2|„| n 其中, i(i=1,2,„,n)称为P的候选式。
编译原理第二章 文法和语言资料
第二章文法和语言本章讲述目前广泛使用的上下文无关文法。
即用上下文无关文法作为程序设计语言语法的描述工具。
阐明语法的一个工具是文法。
本章将介绍文法和语言的概念。
本章重点：上下文无关文法及其句型分析中的有关问题。
第一节文法的直观概念当我们表述一种语言时，无非是说明这种语言的句子，如果语言只含有有穷多个句子，则只需列出句子的有穷集就行了，但对于有无穷句子的语言来讲，存在着如何给出它的有穷表示的问题。
以自然语言为例，人们无法列出全部句子，但是人们可以给出一些规则，用这些规则来说明（或者定义）句子的组成结构，比如：“我是大学生”。
是汉语的一个句子。
汉语句子可以是由主语后随谓语而成，构成谓语的是动词和直接宾语，我们采用EBNF来表示这种句子的构成规则：〈句子〉∷＝〈主语〉〈谓语〉〈主语〉∷＝〈代词〉|〈名词〉〈代词〉∷＝我|你|他〈名词〉∷＝王明|大学生|工人|英语〈谓语〉∷＝〈动词〉〈直接宾语〉〈动词〉∷＝是|学习〈直接宾语〉∷＝〈代词〉|〈名词〉“我是大学生”的构成符合上述规则，而“我大学生是”不符合上述规则，我们说它不是句子。
这些规则成为我们判别句子结构合法与否的依据。
一旦有了一组规则以后，我们可以按照如下方式用它们去推导或产生句子。
我们开始去找∷＝左端的带有〈句子〉的规则并把它表示成∷＝右端的符号串，这个动作表示成：〈句子〉⇒〈主语〉〈谓语〉，然后在得到的串〈主语〉〈谓语〉中，选取〈主语〉或〈谓语〉，再用相应的规则∷＝右端代替之。
比如，选取了〈主语〉,并采用规则〈主语〉∷＝〈代词〉，那么得到：〈主语〉〈谓语〉⇒〈代词〉〈谓语〉，重复做下去，我们得到句子：“我是大学生”的全部动作过程是：〈句子〉⇒〈主语〉〈谓语〉⇒〈代词〉〈谓语〉⇒我〈谓语〉⇒我〈动词〉〈直接宾语〉⇒我是〈直接宾语〉⇒我是〈名词〉⇒我是大学生符号⇒的含义是，使用一条规则，代替⇒左边的某个符号，产生⇒右端的符号串。
显然，按照上述办法，不仅生成“我是大学生”这样的句子，还可以生成“王明是大学生”，“王明学习英语”，“我学习英语”，“他学习英语”，“你是工人”，“你学习王明”等几十个句子。
计算机编译原理
本课程的目的
构造编译器基本知识
编译的阶段和相关的活动 相关数据结构和算法
计算机科学中相关的基础理论
形式语言与自动机
进一步加深对软件开发的认识
第一章 概述
【课前思考】 ◇ 什么是编译程序？ ◇ 编译过程和编译程序的结构？ 【学习目标】 介绍语言翻译的基本概念
程序和语言 翻译和解释
介绍翻译的步骤和相关的活动 介绍编译器的开发方法
输入字符串（即源程序） 输出单词符号（最基本的语法单位） 。
词法分析举例
一个C源程序片段：
int a; a=a+2; 词法分析后返回(如右 图)：
单词类型 保留字 标识符 界符 标识符 算符(赋值) 标识符 算符(加) 整数 界符 单词值 int a ; a = a + 2 ；
(2) 语法分析（Syntax analysis）
程序的执行方式
高级语言程序通常采用两种方式执行：解释方 式和翻译方式 解释方式：逐个语句地分析和执行，如Basic， Prolog
优点：易于查错 缺点：效率低，运行速度慢
翻译方式：对整个程序进行分析，翻译成等价 机器语言程序后执行，如Pascal，Fortran，C
优点：只需分析和翻译一次， 缺点：在运行中发现的错误必须在源程序中查找
编译程序的功能
从功能上看，一个 编译程序就是一个 语言翻译程序。 源语言通常是一个 高级语言，如 FORTRAN，C 或 Pascal。 目标语言通常是一 个低级语言,如汇编 或机器语言。
出错和警告信息
编译程序
源语言程序
目标语言程序
T形图
常用T形图来表示编译程序涉及的三个语言： S I 其中： S:源语言(程序)，Source language(program) O:目标语言(程序), target/object language(program) I:实现语言, implementation language O
编译原理 第三章 文法和语言
8
3.2 符号和符号串
四. 符号串集合(语言）的运算
设L和M是两个符号串集合，则 1.合并：L∪M＝｛s|s∈L or s∈M} 2.连接：LM＝｛ st|s∈L and t∈M} 3.方幂： L0={ε}， L1＝L， L2＝LL, ..., Ln＝Ln-1L 4. 语言L的闭包，记作L*， L*＝∪Li(i>=0) =L0∪L1∪L2∪L3 ∪… 5．语言L的正闭包，记作L+（L+＝L L*） L+＝∪Li(i >=1) =L1∪L2∪L3∪L4∪…
16
推导的定义
例： <程序><分程序>. (<程序> → <分程序>. ) <分程序>. <变量说明部分> <语句>. (<分程序> → <变量说明部分> <语句>) VAR<标识符>;BEGIN READ(<标识符>)END. VAR A;BEGIN READ(<标识符> ) END. (<标识符> →A) VAR A;BEGIN READ(<标识符> ) END. VAR A;BEGIN READ( A) END. (<标识符> →A)
22
文法G[S]： 例 文法 ： （1）S→aSBE ） → （2）S→aBE ） → （3）EB→BE ） → （4）aB→ab ） → （5）bB→bb ） → （6）bE→be ） → （7）eE→ee ） → L(G)={ anbnen | n≥1 } ≥ G生成的每个串都在 生成的每个串都在L(G)中 生成的每个串都在 中 L(G)中的每个串确实能被 生成 中的每个串确实能被G生成 中的每个串确实能被 分析参见课本P37. 分析参见课本P37.
四种文法的类型(编译原理)
四种文法的类型（编译原理）在编译原理中，文法是描述一种语言的形式规则的形式化规范。
根据规则的定义方式和特点，可以将文法分为四类类型，分别是正规文法、上下文无关文法、上下文有关文法和无限制文法。
下面将对这四种文法类型进行详细介绍。
1. 正规文法（Regular Grammar）：正规文法是一种最简单的文法类型，也是最严格的限制。
它的产生式右部只能是终结符或一个终结符紧跟一个非终结符，不允许使用任何其它的形式。
正规文法通常用于描述正则语言，而正则语言可以用有限自动机（如DFA、NFA）来识别和生成。
正规文法常用于词法分析中的正则表达式的产生。
2. 上下文无关文法（Context-Free Grammar）：上下文无关文法是一种描述语言结构的文法，它具有比正规文法更高的表达能力。
这种文法的产生式右部可以是终结符或非终结符的任意组合顺序。
上下文无关文法通常用于描述上下文无关语言，而上下文无关语言可以用上下文无关文法来生成和识别。
上下文无关文法是编译器设计和分析的主要方法之一，包括语法分析和语法制导翻译等。
3. 上下文有关文法（Context-Sensitive Grammar）：上下文有关文法是一种更加灵活的文法，它的产生式右部除了可以是终结符和非终结符的任意组合外，还可以根据上下文条件改变生成式。
产生式的左部和右部可以有相同数量的非终结符，但右部至少有一个符号。
上下文有关文法常用于描述上下文有关语言，也被用于描述自然语言处理等。
4. 无限制文法（Unrestricted Grammar）：无限制文法是一种最灵活的文法类型。
它的产生式左部和右部可以是任意长度的终结符和非终结符的组合，没有任何限制和约束条件。
无限制文法通常用于描述递归可枚举语言，递归可枚举语言是图灵机可以识别的语言。
无限制文法被广泛应用于编译器的各个阶段，包括语法制导翻译和语义分析等。
综上所述，正规文法、上下文无关文法、上下文有关文法和无限制文法是编译原理中常用的四种文法类型。
《编译原理》第2章文法和语言的形式定义
《编译原理》第2章文法和语言的形式定义编译原理是计算机科学中的一门重要课程，它研究的是将高级程序语言翻译成机器语言的方法和技术。
在编译原理中，文法和语言的形式定义是非常重要的概念，本文将围绕这个主题展开详细的讨论。
第2章《文法和语言的形式定义》主要介绍文法和语言的概念、应用及其形式定义的方法。
文法是描述语言结构和语法规则的形式化产物，而语言则是文法所描述的符号集合。
在编译原理中，我们需要通过形式定义的方式来描述和理解程序语言的结构和规则。
下面将对文法和语言的形式定义进行详细解释。
1.文法的定义文法是由产生式（Production）组成的四元组(G,N,P,S)，其中：-G：表示文法-N：表示非终结符集合，即一组可以推导出或展开的符号。
-T：表示终结符集合，即不再进行推导或展开的符号。
-P：表示产生式规则集合，是一组指定如何生成目标符号串的规则。
-S：表示一个特殊的非终结符，称为开始符号或起始符号，表示文法的初始状态。
文法的定义可以采用两种形式：巴科斯-诺尔范式（Backus-Naur Form，BNF）和扩充背景文法表达式（Extended Backus-Naur Form，EBNF）。
BNF是最常用的文法定义方法，它使用产生式规则来描述语言的结构和规则。
2.产生式的定义产生式规定了如何用一个符号串替换或展开另一个符号串。
一个产生式由一个非终结符和一个由非终结符和终结符组成的字符串组成。
例如，产生式A->BC，表示用符号串BC替换非终结符A。
产生式可以有多个产生式体，每个产生式体之间使用“，”符号分隔。
例如，产生式A->B，C，表示非终结符A可以被替换成非终结符B或C。
产生式体中可以使用如下符号：-终结符：表示语法中不再与其他符号进行推导的符号，如数字、运算符、关键字等。
-非终结符：表示语法中可以被进一步推导的符号。
-空串：表示不产生任何字符的特殊终结符。
-ε：表示空串。
3.语言的定义语言是符合一些特定文法规则的所有符号串的集合。
编译原理第二章_文法与语言
表示A上所有有穷长串的集合 例如：A={ab，c}，AA={…… }， AAA={…… } A+ = A* A = AA*
（8）符号串集合的自反闭包
设符号串集合为A，则A的自反闭包记为A* ，定义为： A* = A0 ∪ A1 ∪ A2∪… ∪ An
即A* = A0 ∪ A+ = {ε} ∪ A+ 例如： A= {a,b}，则 A*={ε, a, b, aa, ab, ba, bb, aaa, …… }
AB={xy|x∈A,y∈B} 如：若A={ab,c}, B={d,efg},则AB={abd,abefg,cd,cefg} 特别地，有：{ε}A=A{ε}=A
• 空集φ 表示不含任何元素的空集{ }。 有： φA=A φ= φ
<注>请区别： ε，{}，{ε}三种表示方法的含义
12
（5） 符号串的方幂
a1 an 表示：从a1出发经过一步或若干步，可推导出an 。
定义2.5 长度为n（n≥0）的推导 a1 an 表示：从a1出发经过0步（ a1 ＝an ）或若干步，可推导
出an 。
22
2.2.3 句型、句子、语言
1.句型：设G[S]是一个文法，S是它的开始符号，若S α , 则称α是文法G[S]的句型。
5
（1） <句子>::= <主语> <谓语>
推导过程(3/5)
（2） <主语>::= <代词> | <名词> （3） <代词>::= 我 | 你 | 他 （4） <名词>::=王明| 大学生|工人|英语
（5） <谓语>::=<动词> <直接宾语>
（8）符号串集合的自反闭包
设符号串集合为A，则A的自反闭包记为A* ，定义为： A* = A0 ∪ A1 ∪ A2∪… ∪ An
即A* = A0 ∪ A+ = {ε} ∪ A+ 例如： A= {a,b}，则 A*={ε, a, b, aa, ab, ba, bb, aaa, …… }
AB={xy|x∈A,y∈B} 如：若A={ab,c}, B={d,efg},则AB={abd,abefg,cd,cefg} 特别地，有：{ε}A=A{ε}=A
• 空集φ 表示不含任何元素的空集{ }。 有： φA=A φ= φ
<注>请区别： ε，{}，{ε}三种表示方法的含义
12
（5） 符号串的方幂
a1 an 表示：从a1出发经过一步或若干步，可推导出an 。
定义2.5 长度为n（n≥0）的推导 a1 an 表示：从a1出发经过0步（ a1 ＝an ）或若干步，可推导
出an 。
22
2.2.3 句型、句子、语言
1.句型：设G[S]是一个文法，S是它的开始符号，若S α , 则称α是文法G[S]的句型。
5
（1） <句子>::= <主语> <谓语>
推导过程(3/5)
（2） <主语>::= <代词> | <名词> （3） <代词>::= 我 | 你 | 他 （4） <名词>::=王明| 大学生|工人|英语
（5） <谓语>::=<动词> <直接宾语>
编译原理讲义(第二章文法与语言)
语言的定义（短语，简单短语）
• 短语：对于文法G[Z]，如果Z =>* xUy， U=>+ u。显然，w=xuy是一个句型。我 们称u是句型w中相对于U的短语。 • 简单短语：在上面的定义中，如果U ::= u是G的一个规则，那么，u是句型w中相 对于U的简单短语。 • 例子：P22页例2.13。
语言的定义（短语，句柄）
• 注意：在寻找一个句型的短语（或简单 短语）时，必须要求将这个短语规约为 相应的非终结符号后所得到的符号串仍 然是句型。 • 句柄：一个句型的最左简单短语称为该 句型的句柄。 • 定义句柄的原因：在自底向上识别一个 符号串时，总是规约这个句柄。
语言的定义（文法的语言）
• 文法的语言：一个文法G[Z]的语言，用 L(G[Z])表示，定义如下： L(G[Z]) = {x | Z=>* x 并且 x VT+} • 一个文法的语言就是该文法的所有的句子的 集合。 • 文法的语言是所有终结符号串所组成的集合 的子集，一般是真子集。
• 定理2.7 对于CFG，如果存在句型 x=x1x2…xn且x=>*y，必然存在y1,y2,…,yn 使得: xi=>*yi且y= y1y2…yn。 • 定理2.8 如果:x=>*y，如果x的首符号是 终结符号，则y的首符号也是终结符号； 反之，如果y的首符号是非终结符号，那 么x的首符号也是非终结符号。
形式语言与程序设计语言
• 虽然程序设计语言的语法都使用上下文 无关文法来描述，但是通常语言都是上 下文相关的。 • 使用上下文无关文法描述语言的原因是： 存在高效处理上下文无关文法的技术。
关于CFG的进一步讨论
• Chomsky范式：所有的上下文无关语言 都可以用如下形式的文法产生：所有的 规则都形如：U ::= VW 或者 U::=T，其 中U,V,W为非终结符号，T为终结符号。 • Greibach范式：所有上下文无关语言都能 由这样的文法产生：U::=Tu，这里U为非 终结符号，T为终结符号。
编译原理课件CHAPTER2(GrammarandLanguage)
例如： Σ={a,b} a, b, aa, ab, aabba…都是Σ上的符号串 ε是任何Σ上的符号串
在语言理论中，符号串又称为: 句子（sentence）、字（word）
4
2019/2/24
2.1 串和语言
符号串的长度
符号串中包含符号的个数
符号串 s 的长度记为 |s|
例，对于字母表{a,b,c}，aab 是其上的一个符号 串， | aab |=3
2019/2/24 1
Chapter2 Grammar and Language
三．教学内容 串和语言（Strings and Languages ） 文法和语言的定义 （Definitions of Grammar and Language） 文法和语言的分类 （Classification of Grammar and Language） 分析树与句型 （Parse Tree and Sentential form）
Chapter2 Grammar and Language
一．教学目的 掌握文法、语法树、推导、归约、句子、语言、规范推导与归 约、短语、简单短语、句柄、二义性定义，了解文法的分析过程、 文法实用限制、语言分类等。 二．教学重点和难点 重点掌握： 1．串和语言的概念。 2．文法和语言的定义。 3．文法和语言的分类。 4．分析树与句型。 难点： 1．文法和语言的分类。 2．分析树与句型。
2019/2/24
2
2.1 串和语言
字母表（alphabet）：
字母表是符号（symbols）的非空有穷集合，
用∑表示
符号：可以相互区别的记号（元素）
不同的语言有不同的字母表
计算机程序编译原理 第2章 形式语言概论
文法举例
例2.6 1型文法G6=（VN ，VT ，P，S），其中VN={S，X，Y，Z}， VT={x ， y ， z} ， P={S→xSYZ|xYZ, xY→xy, yY→yy, yZ→yz, ZY→YZ, zZ→zz} 例2.7 2型文法G7=（VN，VT，P，S），其中VN={S，T}，VT={a， b，c, d}，P={S→aTd, T→bT|cT|b|c } 例2.8 2型文法G8=（VN，VT，P，B），其中VN={B}，VT={(，) }， P={B→(B)|BB|( )} 例2.9 2型文法G9=（VN，VT，P，S），其中VN={S}，VT={0，1 }， P={S→0S1, S→01} 例2.10 正规文法G10=（VN，VT，P，A），其中VN={A, B, C, D}， VT={x, y, z }，P={A→xB|yC, B→zB|y|yC, C→xD, D→yD|x }
文法和语言的几点说明
(1) 文法中某些非终结符不在任何规则的右部出现，该非 终结符称为不可到达的； (2) 文法中某些非终结符，由它不能推出终结符号串来， 称为不可终止的（无用非终结符）； (3)可空终结符,可以用于消除左递归； (4)一个文法，如果它的一个句子有两棵或两棵以上的语法 树，则称该句子具有二义性。如果一个文法含有二义性的 句子，则该文法具有二义性。形如U→U的产生式。会引起 文法的二义性。
推导
定 义 2.3 G= （ VN, VT, P, S ） ， α→β 是 文 法 G 的 产 生 式 ， γ,δ∈V* ， 若 有 v, w 满 足 ： v=γαδ, w= γβδ, 则 说 ： v （应用规则α→β）直接产生w 或说：w是v的直接推导 或说：w 直接归约到v 记作 v ⇒w。 例 G[S]：S→0S1， S→01 直接推导： 0S1⇒0011 （v=0S1，w=0011，使用规则S→01，γ=0，δ=1） S ⇒0S1 （v=S，w=0S1，使用规则S→0S1，γ=ε，δ= ε ） 0S1⇒00S11 （v=0S1，w=00S11，使用规则S→0S1，γ=0，δ=1） 定义2 定义2.4 v⇒+u 若存在v =α0 =>α1=>…=>αn=u, (n>0) 则称u为u的一个推导，记为v⇒+u。 定义2 定义2.5 v⇒*u 表示v⇒+u 或 v=u
《编译原理》第2章 文法和语言的基本知识
第2章
文法和语言的基本知识
教学目标
1. 本章是编译原理课程的理论基础，要求掌握形 式语言的基本术语和概念,重点掌握短语、直接 短语、句柄、素短语、规范推导、规范归约。 2. 掌握文法和语言的定义，文法的二义性与递归 性的判断方法及句型的分析方法，文法分类。 3. 熟练使用文法定义程序设计语言的单词和语法 成分。 4. 对形式语言的理论有一个初步认识。
2013年8月16日
符号串集合的闭包运算
设A是符号串集合，定义 A＋＝ A1 ∪ A2 ∪ A3 ∪……∪ An ∪…… 称为集合A的正闭包。 A*＝ A0 ∪A＋ 称为集合A的闭包。 例：A={x,y} A＋＝？ {x,y, xx,xy,yx,yy , xxx,xxy,xyx,xyy, ……}
A1 A A A2 A A3 A
2013年8月16日
文法的直观概念：以汉语中的“我是大学生”为例。
①一组终结符号 采用BNF来表示汉语句子的构成规则为： （语言的基本符号） 〈句子〉：：=〈主语〉〈谓语〉 ②一组非终结符号 〈主语〉：：=〈代词〉|〈名词〉 （语法单位） ③一个开始符号 〈代词〉：：=我|你|他 文法的四部分 （一个特殊的非终结 〈名词〉：：=王明|大学生|工人|英语 符号，最感兴趣的语 〈谓语〉：：=〈动词〉〈直接宾语〉 法单位） 〈动词〉：：=是|学习 ④一组规则（也称产 生式或产生规则） 〈直接宾语〉：：=〈代词〉|〈名词〉 根据上述规则，“我是大学生”的构成符合上述规则，而“我 大学生是”不符合，我们说它不是句子。这些规则成为我们判别 句子结构合法与否的依据。换句话说，这些规则看成是一种元语 言，用它描述汉语。这种的语言描述成为文法。
说明： (1) 有若干语法成分同时存在时，我们总是从最左的语法成 分进行推导，这称之为最左推导，类似的有最右推导（一般推 导）。 (2) 从一组规则可推出不同的句子，如以上规则还可推出 “大象吃象”、“大花生吃象”、“大花生吃花生”等句子， 它们 在语法上都正确，但在语义上都不正确。
文法和语言的基本知识
教学目标
1. 本章是编译原理课程的理论基础，要求掌握形 式语言的基本术语和概念,重点掌握短语、直接 短语、句柄、素短语、规范推导、规范归约。 2. 掌握文法和语言的定义，文法的二义性与递归 性的判断方法及句型的分析方法，文法分类。 3. 熟练使用文法定义程序设计语言的单词和语法 成分。 4. 对形式语言的理论有一个初步认识。
2013年8月16日
符号串集合的闭包运算
设A是符号串集合，定义 A＋＝ A1 ∪ A2 ∪ A3 ∪……∪ An ∪…… 称为集合A的正闭包。 A*＝ A0 ∪A＋ 称为集合A的闭包。 例：A={x,y} A＋＝？ {x,y, xx,xy,yx,yy , xxx,xxy,xyx,xyy, ……}
A1 A A A2 A A3 A
2013年8月16日
文法的直观概念：以汉语中的“我是大学生”为例。
①一组终结符号 采用BNF来表示汉语句子的构成规则为： （语言的基本符号） 〈句子〉：：=〈主语〉〈谓语〉 ②一组非终结符号 〈主语〉：：=〈代词〉|〈名词〉 （语法单位） ③一个开始符号 〈代词〉：：=我|你|他 文法的四部分 （一个特殊的非终结 〈名词〉：：=王明|大学生|工人|英语 符号，最感兴趣的语 〈谓语〉：：=〈动词〉〈直接宾语〉 法单位） 〈动词〉：：=是|学习 ④一组规则（也称产 生式或产生规则） 〈直接宾语〉：：=〈代词〉|〈名词〉 根据上述规则，“我是大学生”的构成符合上述规则，而“我 大学生是”不符合，我们说它不是句子。这些规则成为我们判别 句子结构合法与否的依据。换句话说，这些规则看成是一种元语 言，用它描述汉语。这种的语言描述成为文法。
说明： (1) 有若干语法成分同时存在时，我们总是从最左的语法成 分进行推导，这称之为最左推导，类似的有最右推导（一般推 导）。 (2) 从一组规则可推出不同的句子，如以上规则还可推出 “大象吃象”、“大花生吃象”、“大花生吃花生”等句子， 它们 在语法上都正确，但在语义上都不正确。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
• VT∩ VN＝Φ， VT∪ VN为该语言的字母表
文法的定义
• Chomcky文法的定义：
G=(VN,VT,P,S) 其中：VN —非空有限的非终结符号集
VT —非空有限的终结符号集 P — 产生式集 S — 开始符号/识别符号，S∈ VN • 文法被用来精确而无歧义地描述语言的句子的 构成方式。 文法描述语言的时候不考虑语言的含义。
• 字母表：元素的非空有穷集合。记为∑。 字母表包含了语言中所允许出现的一切符号。 例如： ∑= {0，1}
• 符号串(字)：字母表中的符号所组成的有穷序列。 一个语言的句子总是它的字母表的符号串。这个 符号串的组成必须是按照文法规则组合而成的。
• 语法分析的一个重要任务就是：判断一个符号串 的组成是否满足某个文法的规定。
字母表和符号串的基本概念
• 空串：不包含任何符号的串，记为ε。 • Σ*：表示Σ上所有符号串的全体。 • 空集：φ，不包含任何元素。
在本课程中，语言被认为是句子的集合。 所以，一个语言就是对应于它的字母表上 的一个符号串集合。
关于符号串的运算
• 符号串的长度：指符号串x中所含符号的个数，记为 |x|。
例：按文法形式定义表示上例文法。
解：根据文法的形式定义， 文法
G1=（ VN， VT，P，S） • VN={句子，主语，谓语，
冠词，名词，动词，直接 宾语}
• VT={ the，ate，banana， monkey }
• 产生式集合P由右面8条规 则组成
• 开始符号S= <句子>
<句子> → <主语> <谓语> <主语> → <冠词> <名词> <冠词> → the <谓语> → <动词> <直接宾语> <动词> →ate <直接宾语>→<冠词> <名词> <名词>→banana <名词>→monkey
• 符号串相等：若x、y是字母表∑上的两个符号串， 那么当且仅当组成x的各符号与组成y的各符号依次 相等时，则符号串x与符号串y相等，记作x=y。
• 符号串的前缀：指从符号串x的末尾删除0或多个符 号后得到的符号串。
• 符号串的后缀：指从符号串x的开头删除0或多个符 号后得到的符号串。
关于符号串的运算
• 符号串的子串：指从符号串x的开头和末尾删除0或 多个符号后得到的符号串。 符号串的前缀、后缀都 是它的子串。
• 连接(并置)：若x、y是两个符号串，则xy表示连接， 是将符号串y连接在符号串x的后面。若x、y是字母 表∑上的两个符号串，则xy也是字母表∑上的符号串。
注意：连接没有交换率，即 xy ≠ yx 而对于空串ε有 εx=xε=x
内容回顾
• 什么是编译程序 • 编译的过程
– 词法分析 – 语法分析 – 语义分析及中间代码生成 – 优化 – 目标代码生成
• 编译程序的结构与组织
文法和语言
• 字母表和符号串的基本概念 • 文法和语言的形式定义 • 递归规则与递归文法 • 语法树与文法的二义性 • 文法的分类
字母表和符号串的基本概念
符号串集合的运算
• 集合的正则闭包和集合的闭包： 设A为一个集合，则集合A的正则闭包用A+表示，定 义为： A+ =A1 ∪ A2 ∪ …. ∪ A n ∪… 表示A上的所有的非空符号串的集合。 集合A的闭包用A*表示，定义为： A* =A 0 ∪ A+ 表示A上的所有符号串（包括空字符串）的集合。 例如：A ={a，b}， 则A+ ={a,b,aa,ab,ba,bb,aaa,aab,…} A* ={ε ,a,b,aa,ab,ba,bb,aaa,aab,…}
文法的形式定义（产生式/规则）
• 产生式：一个产生式是一个有序对(α,β)，通常写 作α→β 或α ::=β 。其中α为左部； β为右部。 产生式意味着能将一个符号串用另外一个符号串 替换。因而又被称为重写规则。一组规则规定了 一个语言的语法结构。
• 规则中的符号分为两类：终结符号、非终结符号
终结符与非终结符
• 方幂：x的n次方幂即将n个x连接。
x0 = ε, x1 = x, x2 = xx,… xn=xx…x=xx n-1=x n-1 x
符号串集合的运算
• 乘积：令A、B为两个符号串集合，A和B的乘积AB 定义为：AB = {xy | xA且y B} {ε}A=A {ε}=A ΦA= AΦ =Φ
• 方幂：A的n次方幂就是将n个A相乘。 A0={ε} A1=A A2=AA … An=AA…A=AA n-1 =A n-1 A
产生式的简写：A → B , A → C 可以简化为：
A→B|C
1.<无符号整数>→<数字串>
2.<数字串>→<数字串><数字>
3.<数字串>→<数字>
4.<数字>→0
5.<数字>→1
6.<数字>→2
7.<数字>→3
8.<数字&glt;数字>→6
11.<数字>→7
12.<数字>→8
文法和语言的形式定义
• 形式语言描述的两种方法
枚举方法 使用文法来描述
• 文法是一种工具，它可用于严格定义句子的结构。 例如，能够描述句子“the monkey ate the banana” 的文法如下：
<句子> → <主语> <谓语> <主语> → <冠词> <名词> <冠词> → the <谓语> → <动词> <直接宾语> <动词> →ate <直接宾语>→<冠词> <名词> <名词>→banana <名词>→monkey
• 终结符：VT 组成语言的基本符号。在程序设计语言中就是以前 屡次提到的单词符号。如：基本字，标识符，常数， 算符，界符等。从语法分析的角度看，终结符是一 个语言的不可再分的基本符号。
• 非终结符：VN 也称语法变量，用来代表语法单位。如“算术表达 式”、“布尔表达式”、“赋值句”、“子程序”、 “函数”等。一个非终结符代表一个一定的语法概 念，是一个类（集合）记号，而不是一个个体记号。
13.<数字>→9
1.<无符号整数>→<数字串> 2.<数字串>→<数字串><数字> | <数字> 3.<数字>→0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9
文法举例
• G1=(VN,VT,P,S) 其中:VN={E} VT= { i, +, *, (, ) } P= {E→E+E， E →E *E， E →(E) ， E → i} S=E
文法的定义
• Chomcky文法的定义：
G=(VN,VT,P,S) 其中：VN —非空有限的非终结符号集
VT —非空有限的终结符号集 P — 产生式集 S — 开始符号/识别符号，S∈ VN • 文法被用来精确而无歧义地描述语言的句子的 构成方式。 文法描述语言的时候不考虑语言的含义。
• 字母表：元素的非空有穷集合。记为∑。 字母表包含了语言中所允许出现的一切符号。 例如： ∑= {0，1}
• 符号串(字)：字母表中的符号所组成的有穷序列。 一个语言的句子总是它的字母表的符号串。这个 符号串的组成必须是按照文法规则组合而成的。
• 语法分析的一个重要任务就是：判断一个符号串 的组成是否满足某个文法的规定。
字母表和符号串的基本概念
• 空串：不包含任何符号的串，记为ε。 • Σ*：表示Σ上所有符号串的全体。 • 空集：φ，不包含任何元素。
在本课程中，语言被认为是句子的集合。 所以，一个语言就是对应于它的字母表上 的一个符号串集合。
关于符号串的运算
• 符号串的长度：指符号串x中所含符号的个数，记为 |x|。
例：按文法形式定义表示上例文法。
解：根据文法的形式定义， 文法
G1=（ VN， VT，P，S） • VN={句子，主语，谓语，
冠词，名词，动词，直接 宾语}
• VT={ the，ate，banana， monkey }
• 产生式集合P由右面8条规 则组成
• 开始符号S= <句子>
<句子> → <主语> <谓语> <主语> → <冠词> <名词> <冠词> → the <谓语> → <动词> <直接宾语> <动词> →ate <直接宾语>→<冠词> <名词> <名词>→banana <名词>→monkey
• 符号串相等：若x、y是字母表∑上的两个符号串， 那么当且仅当组成x的各符号与组成y的各符号依次 相等时，则符号串x与符号串y相等，记作x=y。
• 符号串的前缀：指从符号串x的末尾删除0或多个符 号后得到的符号串。
• 符号串的后缀：指从符号串x的开头删除0或多个符 号后得到的符号串。
关于符号串的运算
• 符号串的子串：指从符号串x的开头和末尾删除0或 多个符号后得到的符号串。 符号串的前缀、后缀都 是它的子串。
• 连接(并置)：若x、y是两个符号串，则xy表示连接， 是将符号串y连接在符号串x的后面。若x、y是字母 表∑上的两个符号串，则xy也是字母表∑上的符号串。
注意：连接没有交换率，即 xy ≠ yx 而对于空串ε有 εx=xε=x
内容回顾
• 什么是编译程序 • 编译的过程
– 词法分析 – 语法分析 – 语义分析及中间代码生成 – 优化 – 目标代码生成
• 编译程序的结构与组织
文法和语言
• 字母表和符号串的基本概念 • 文法和语言的形式定义 • 递归规则与递归文法 • 语法树与文法的二义性 • 文法的分类
字母表和符号串的基本概念
符号串集合的运算
• 集合的正则闭包和集合的闭包： 设A为一个集合，则集合A的正则闭包用A+表示，定 义为： A+ =A1 ∪ A2 ∪ …. ∪ A n ∪… 表示A上的所有的非空符号串的集合。 集合A的闭包用A*表示，定义为： A* =A 0 ∪ A+ 表示A上的所有符号串（包括空字符串）的集合。 例如：A ={a，b}， 则A+ ={a,b,aa,ab,ba,bb,aaa,aab,…} A* ={ε ,a,b,aa,ab,ba,bb,aaa,aab,…}
文法的形式定义（产生式/规则）
• 产生式：一个产生式是一个有序对(α,β)，通常写 作α→β 或α ::=β 。其中α为左部； β为右部。 产生式意味着能将一个符号串用另外一个符号串 替换。因而又被称为重写规则。一组规则规定了 一个语言的语法结构。
• 规则中的符号分为两类：终结符号、非终结符号
终结符与非终结符
• 方幂：x的n次方幂即将n个x连接。
x0 = ε, x1 = x, x2 = xx,… xn=xx…x=xx n-1=x n-1 x
符号串集合的运算
• 乘积：令A、B为两个符号串集合，A和B的乘积AB 定义为：AB = {xy | xA且y B} {ε}A=A {ε}=A ΦA= AΦ =Φ
• 方幂：A的n次方幂就是将n个A相乘。 A0={ε} A1=A A2=AA … An=AA…A=AA n-1 =A n-1 A
产生式的简写：A → B , A → C 可以简化为：
A→B|C
1.<无符号整数>→<数字串>
2.<数字串>→<数字串><数字>
3.<数字串>→<数字>
4.<数字>→0
5.<数字>→1
6.<数字>→2
7.<数字>→3
8.<数字&glt;数字>→6
11.<数字>→7
12.<数字>→8
文法和语言的形式定义
• 形式语言描述的两种方法
枚举方法 使用文法来描述
• 文法是一种工具，它可用于严格定义句子的结构。 例如，能够描述句子“the monkey ate the banana” 的文法如下：
<句子> → <主语> <谓语> <主语> → <冠词> <名词> <冠词> → the <谓语> → <动词> <直接宾语> <动词> →ate <直接宾语>→<冠词> <名词> <名词>→banana <名词>→monkey
• 终结符：VT 组成语言的基本符号。在程序设计语言中就是以前 屡次提到的单词符号。如：基本字，标识符，常数， 算符，界符等。从语法分析的角度看，终结符是一 个语言的不可再分的基本符号。
• 非终结符：VN 也称语法变量，用来代表语法单位。如“算术表达 式”、“布尔表达式”、“赋值句”、“子程序”、 “函数”等。一个非终结符代表一个一定的语法概 念，是一个类（集合）记号，而不是一个个体记号。
13.<数字>→9
1.<无符号整数>→<数字串> 2.<数字串>→<数字串><数字> | <数字> 3.<数字>→0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9
文法举例
• G1=(VN,VT,P,S) 其中:VN={E} VT= { i, +, *, (, ) } P= {E→E+E， E →E *E， E →(E) ， E → i} S=E