基于传热学原理的高温作业专用服设计

高温作业专用服装设计高温作业专用服装是为了保护人们在高温环境下工作时的身体健康而设计的一种特殊服装。

随着现代工业的发展和人们对工作环境安全和员工健康的重视，高温作业专用服装的研发和设计变得越来越重要。

本文将探讨高温作业专用服装的设计原理和要点，并且提出一种创新的高温作业专用服装设计方案。

高温作业专用服装的设计需要考虑到以下几个方面：透气性、防护性、舒适性和功能性。

透气性是指服装的材料能够让空气和水蒸气自由地通过，以保持人体正常的温度和湿度。

在高温环境下工作时，人体会大量出汗，如果没有透气性良好的服装来排汗，就容易出现中暑和热射病等健康问题。

高温作业专用服装的材料应该选择具有良好透气性的纤维，如棉、麻和透气膜等。

高温作业专用服装的设计要考虑到防护性。

高温环境下，人体容易受到高温和热辐射的伤害，因此服装需要具备一定的防护功能。

服装的外层材料可以选择具有较低的热导率和较高的热稳定性的纤维材料，如聚酰亚胺纤维和耐热纤维等，以减少热辐射的伤害。

服装的设计还要考虑到防火和防烫的功能，以保护人体免受火焰和热源的伤害。

高温作业专用服装的设计还需要考虑到舒适性。

舒适性是指服装对人体穿着时的舒适感和适应性。

在高温环境下工作时，人体会感到热和不适，因此服装需要具备良好的湿气调节性和吸湿性，使人体保持相对干燥的状态。

服装的设计还应该考虑到人体运动的自由度和舒适度，避免过于紧身和束缚，以免影响工作效率。

高温作业专用服装的设计还需要具备一定的功能性。

功能性是指服装能够满足特定工作环境和工作任务的需求。

在高温环境下工作时，人们需要面对的工作任务和工作环境各有不同，因此服装的设计应该根据具体情况进行调整和改进。

一些高温作业需要人体频繁移动和弯曲，因此服装需要具备较好的伸缩性和耐磨性；而一些高温作业可能需要人体长时间保持相对静止，因此服装需要具备较好的保温性和保护性。

高温作业专用服装的设计需要考虑到透气性、防护性、舒适性和功能性等要点。

工业技术科技创新导报 Science and Technology Innovation Herald82DOI：10.16660/ki.1674-098X.2019.15.082高温作业专用服装设计①邱秀亮 俞青清 杨位乾 陈旭(集美大学诚毅学院 福建厦门 361000)摘 要：本文基于傅立叶定律结合多层平壁热传递模型和干燥热传递模型，构造时间—位置—温度的热传递偏微分方程来解决热防护服装厚度的合理设计问题，然后将偏微分方程进行离散化处理，通过数据预处理发现皮肤表层超过1646s 以后温度不再增长，我们认为自此系统处于动态热平衡状态。

利用有限差分法在MATLAB上算出动态热平衡之前的温度分布，得到动态热平衡状态时各层交界处的温度。

关键词：热防护服 干燥热传递模型 有限差分法中图分类号：TS941.2 文献标识码：A 文章编号：1674-098X(2019)05(c)-0082-02①基金项目：本文是2018年“创新创业训练计划”中的项目《高温作业专用服装设计》（项目编号：201813471003 ）的阶段性成果。

作者简介：邱秀亮（1983，1—），男，汉族，江西赣州人，硕士研究生，讲师，研究方向：图论、复杂网络、偏微分方程。

现如今人们从事各种高温作业下的安全隐患有增加的趋势，在高温条件下热防护服具备对人体进行安全防护的功能而显得十分重要。

比如消防员在火场环境灭火救援时常处于高温高辐射的环境，如果防护服太厚重，经常会导致热应激反应，因此在高温作业时保护人体皮肤不受伤害的前提下，如何减少防护服厚度，是本文讨论的根本问题。

目前急需要解决的问题有：(1)根据已知的服装材料的参数值以及在条件为75℃环境温度、II层厚度为6mm、IV 层厚度为5mm、工作时间为90min的情形下，计算温度的分布；(2)当环境温度为65℃时，IV层厚度为5.5mm时，在确保工作60min时，假人皮肤外侧温度不超过47℃，且超过44℃的时间不超过5min的条件下确定II层最优厚度；(3)当环境温度为80℃时，在保证工作30min时，其余条件与上述相同以此来确定II层和IV层的最优厚度。

基于傅里叶热传导定律[1]关于高温工作服装的设计高艺倩（三峡大学电气与新能源学院，湖北宜昌443000）随着科技的发展，人们生活水平的提高离不开各个岗位的工作人员的付出。

再艰巨的环境都要完成任务，比如在高温环境中工作时，人体会出现一系列的生理功能改变，这些功能在一定范围内可有幅变化，但若超过限度就会产生不良影响，所以热防护服就成为了防护高温的重要方法之一。

热防护服是指在高温中穿的促进人体散发热量的、防止热中暑、烧灼伤等的具有防护功能的服装，除了要有较好的阻燃性，而且要有较高的隔热性能。

其原理是减缓热量的转移速度，使热量在人体皮肤上尽少积聚，以保证不被烧灼伤。

1基于傅里叶热传导定律的算法在dt 时间内，沿着某面积元ds 的外法线的方向流过的热量dq ⭢和这个面积元两侧的温度的变化率∂u/∂n 成正比，两者的比例系数为W 。

由于在自然条件下的温度是处于减少的趋势，故在等式的右边有个负号，如下所示：在上述式子中间的W 为导热系数（单位为W/m 2），e ⭢n 是该面积元的外法向量。

在对于一个封闭的体积元Ω的时候，dt 时间内它内部的热量变化为dQ 通过对体积元的闭合面积分，得到以下式子：得到上述式子之后，再进一步地对时间进行积分，这样就可以得到从t 1到t 2时刻流入体积元内部的热量Q 1，再由高斯公式可以的得到以下式子：我们在初中的时候学过类似的热力学公式，为某一物体吸收的热量等于这个物体的质量、比热容和温度增量的乘积。

根据上述热力学公式我们可以得到以下公式：变形得到上述式子之后可以根据热量守恒得到化简以后的式子：如果在物体的内部是存在热源的，那么在dt 的时间内，在（x ，y ，z ）地方的体积元内所产生的热量就是F （x ，y ，z ，t ），所以同样地，我们很容易地就得到了含有热源的热传导的Poisson 方程，如下所示：但却存在一种情况，就是在边界绝热的条件下，如果内部有不灭的热源是没有办法达到热平衡的。

2019第2期中（总第291期）此问题，属于数据预测类问题。

首先构建一个皮肤内侧等效热导层，并建立一维多层平壁导热模型。

发现同一介质内部温度随距离成一次函数关系，建立一个关于各层平壁边界温度的四元方程组，求得稳定状态时温度随位置分布Tmax （x ）。

通过MATLAB 的cftool 工具箱，拟合得到高温条件下某位置温度变化的单一位置参数函数，分析得到参数值和各位置温度变化T （x,t ）,以位置x 步长0.1mm 、时间t 步长1s ，得到温度分布。

对非稳定状态下导热公式（4）离散化，使用差分方法求x=δ5的近似解，与拟合的函数比较，验证函数准确可靠。

最后对本文所建立的高温作业服装模型进行了客观的评价，提出了改进的建议，结合整个模型特点进行推广，提高此模型的实际生产意义。

一、模型假设假设服装各层的热导率等理化因子不随温度变化，且各材料具有各向同性；假设多层平壁紧密结合，结合面的温度相同，不存在热突变；假设热量传递仅依靠热传导，不涉及热辐射和热对流；假设温度不会发生突变，皮肤外侧温度为紧靠近皮肤处温度，皮肤内侧存在小距离温度变化层。

二、模型的建立与求解第一部分：问题1的模型（一）热稳定时材料内部温度分布高温作业服装有I 、II 、III 三层织物材料，其中I 层与外界环境接触，III 层与皮肤之间还存在空隙为IV 层，为了处理假人体内温度恒为37℃，而皮肤表面温度随时间变化，则构建一个皮肤等效热导层v 层存在于体表内侧，其等效热传导率与Ⅳ层相同。

图1皮肤的等效热传导的模型T5为假人的体内温度，即Ⅴ层下限边界温度；T0为服装外界高温环境温度，即Ⅰ层上限边界温度。

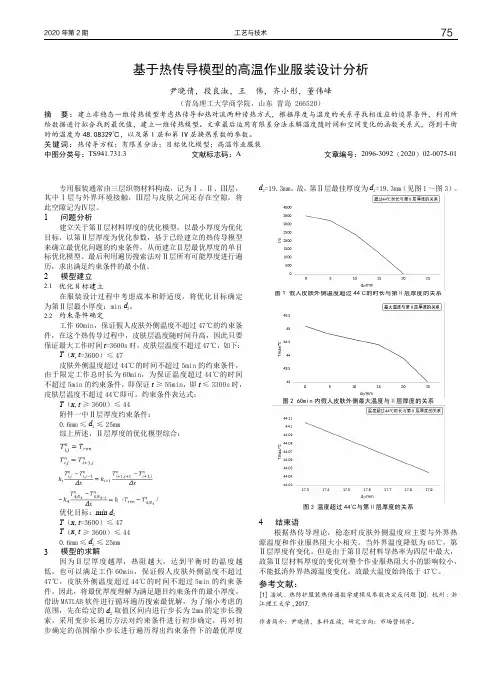
将体内温度为37oC 的假人放置在高温环境中，测量假人皮肤外侧的温度，根据题目所给附件二的具体数值通过程序2画出图2。

由图2可知，将假人放置在高温条件1625秒时，体表外侧服装内侧达到最大值48.08℃。

由于各层的长、宽都远远大于其厚度，因此假设我们的研究对象是无限大平壁。

高温作业专用服装设计数学建模引言高温作业条件下工作人员需要穿着专用的服装，以保护身体免受高温的伤害。

本文将通过数学建模的方法，探讨高温作业专用服装的设计问题。

通过分析热传导理论、热耗散原理和人体工程学等知识，以及使用数学模型和计算机仿真，设计出一款适合高温作业的专用服装。

背景知识热传导理论热传导是指热量通过材料的传递现象。

根据傅里叶热传导定律，热量的传导速率与温度梯度成正比。

在高温作业环境中，人体会产生大量的热量，若无法及时散热，可能导致中暑等严重后果。

热耗散原理热耗散是指热量通过热辐射、对流和传导等形式散发到周围环境的过程。

在高温作业中，热耗散是消耗热量的主要方式。

通过合理设计服装的热耗散特性，可以提高服装的散热能力，保护工作人员的身体。

人体工程学人体工程学是研究人体与工作环境之间的相互关系的学科。

通过了解人体特性，合理设计服装的结构和尺寸，可以使工作人员感到舒适，提高工作效率。

设计目标根据上述背景知识，我们的设计目标是设计一款高温作业专用服装，要求具有以下特点：•热传导小：降低热量对人体的传递，减轻体感温度。

•散热快：提高服装的热耗散能力，加速热量的散发。

•舒适性好：根据人体工程学原理，设计服装的结构和尺寸，使工作人员感到舒适。

数学建模为了实现上述设计目标，我们将使用数学建模的方法进行分析和设计。

下面是我们设计过程中使用的数学模型：热传导模型根据热传导理论，我们可以建立服装材料内部热传导的数学模型。

通过对材料的热传导特性进行数学描述，可以计算出热传导速率，从而评估服装材料的热传导性能。

热耗散模型热耗散是指热量通过热辐射、对流和传导等形式散发到周围环境的过程。

我们可以建立服装的热耗散模型，计算出服装的散热能力，并通过改变服装结构和材料来提高散热效果。

人体工程学模型人体工程学模型可以帮助我们了解人体的尺寸和特性，通过数学计算和计算机仿真，我们可以获得人体在不同环境下的舒适度评估。

根据评估结果，我们可以调整服装的尺寸和结构，使其更符合人体工程学原理。

工艺与技术2020年第2期75基于热传导模型的高温作业服装设计分析尹晓倩，段良淑，王 伟，齐小彤，董伟峰（青岛理工大学商学院，山东 青岛 266520）摘　要：建立非稳态一维传热模型考虑热传导和热对流两种传热方式，根据厚度与温度的关系寻找相适应的边界条件，利用所给数据进行拟合找到最优值，建立一维传热模型。

文章最后运用有限差分法求解温度随时间和空间变化的函数关系式，得到平衡时的温度为48.08329℃，以及第I 层和第IV 层换热系数的参数。

关键词：热传导方程；有限差分法；目标优化模型；高温作业服装中图分类号：TS941.731.3 文献标志码：A 文章编号：2096-3092（2020）02-0075-01专用服装通常由三层织物材料构成，记为Ⅰ、Ⅱ、Ⅲ层，其中Ⅰ层与外界环境接触，Ⅲ层与皮肤之间还存在空隙，将此空隙记为Ⅳ层。

1 问题分析建立关于第Ⅱ层材料厚度的优化模型，以最小厚度为优化目标，以第Ⅱ层厚度为优化参数，基于已经建立的热传导模型来确立最优化问题的约束条件，从而建立Ⅱ层最优厚度的单目标优化模型。

最后利用遍历搜索法对Ⅱ层所有可能厚度进行遍历，求出满足约束条件的最小值。

2 模型建立2.1 优化目标建立在服装设计过程中考虑成本和舒适度，将优化目标确定为第Ⅱ层最小厚度：min d 2。

2.2 约束条件确定47℃的约束条皮肤层温度不超过47℃，如下：T （x ,t =3600）≤475min 的约束条件，由于限定工作总时长为60min，为保证温度超过44℃的时间不超过5min 的约束条件，即保证t ≥55min，即t ≤3300s 时，皮肤层温度不超过44℃即可。

约束条件表达式：T （x ,t ≥3600）≤44附件一中Ⅱ层厚度约束条件：0.6mm ≤d 2≤25mm综上所述，Ⅱ层厚度的优化模型综合：优化目标：min d 2T （x ,t =3600）≤47T （x ,t ≥3600）≤440.6mm ≤d 2≤25mm3 模型的求解因为Ⅱ层厚度越厚，热阻越大，达到平衡时的温度越低，也可以满足工作60min，保证假人皮肤外侧温度不超过47℃，皮肤外侧温度超过44℃的时间不超过5min 的约束条件。

高温作业专用服装设计摘要本文对高温作业的热防护服进行研究，通过建立数学模型，运用遗传算法、热阻分析法对热防护服的材料进行热传递研究，并求出合理的解。

针对问题一，首先对热防护服进行微元法分析，可以将防护服看成多块平板拼接而成。

再假设热传递是沿垂直于皮肤方向进行的，并忽略了热辐射和热对流，只考虑热传导。

进而我们可以使用一维多层平板的热阻分析法。

求得第i层右壁的温度为：T i(t)=T i+1(t)+r i+1q(t)。

再由附件给出的假人皮肤外侧温度随时间分布表我们就可以计算出各个接面的温度，并存于“problem1.xlsx”。

并绘制“各接面温度随时间变化分布图”和“模型（1-1）热防护服内部温度的曲面图”。

针对问题二，首先对热防护服同样做了微元法分析，可以将热防护服看成多块平板拼接而成。

然后对问题进行假设：热传递为垂直皮肤方向进行，故可视为一维的；热防护服的织物是各项同性的。

从而建立热传递模型，因为第II层材料数值变量的不确定性，具有一定的离散特征，且所建立的偏微分方程要得出满足条件的解析表达式比较困难，因此采用在可接受的时间和在可接受的精度范围内求出数值函数近似最优解的方法，即利用遗传算法。

将适应度函数代入MATLAB算法工具箱使用遗传算法求解，设置变量上下界为[0.0006,0.025]。

求出以F tem21为目标函数的适应度函数结果为4.768。

求出以F tem22为目标函数的适应度函数结果为2.708mm。

为确保环境温度为65ºC时，工作60分钟，假人皮肤外侧温度不超过47ºC，且超过44ºC的时间不超过5分钟。

取较大值4.768mm。

针对问题三，与第二问相似，建立偏微分方程使用差分法求数值解，相对第二问的偏微分方程多出用于表示第IV层变量，利用遗传算法进行多参数优化。

利用热传递方程求出适应度函数，再将适应度函数代入MATLAB算法工具箱使用遗传算法求解，设置变量1上下界为[0.0006,0.0064]，变量2上下界为[0.0006,0.0025]。

基于热传导模型的高温作业专用服装设计作者：王婧琦乔梦雪刘艺航肖亚美来源：《无线互联科技》2019年第11期摘; ;要：高温作业专用服装不仅适用于消防人员在火场的火焰区进行抢险救援，也可适用于玻璃、水泥、陶瓷等行业中的高温抢修时穿着。

文章针对提供隔热保护专用服装的设计问题，结合相应数据建立环境温度随时间变化的热传导模型，利用偏微分方程边界值问题差分法对所建模型进行求解，进而确定高温作业专用服装厚度的最优设计。

關键词：高温作业服装;热传导;偏微分方程1; ; 问题分析首先，利用Matlab仿真对附件数据进行处理得出皮肤温度随时间变化的曲线图。

其次，通过对数据进行三阶拟合可得到假人皮肤温度与时间变化的函数关系为：y=（9.1e−0.9）x3−（3e−0.5）x2+0.033x+37再次，以第I层接触空气的点为原点，沿 II，III，IV，皮肤层方向为x轴建立坐标系，进而确定环境温度随时间变化的热传导数学模型，此模型分为高温作业下专用服装中的热传递模型与空气层中的热传递模型。

最后，利用偏微分方程边界值问题差分法对所建模型进行求解。

2; ; 模型假设（1）热防护服装的织物材料是各项同性的。

（2）系统热传递仅考虑热辐射、热传导的传热，忽略水汽、汗液的影响，即不考虑湿传递。

（3）厚度的测量的数值为精确值。

（4）假设假人都为成年男性，身高大约为170 cm。

3; ; 模型建立与求解3.1; 数据预处理首先，利用Matlab仿真得出皮肤的温度与时间的拟合关系，从而建立起外界温度到假人皮肤之间所要经过的热传导模型。

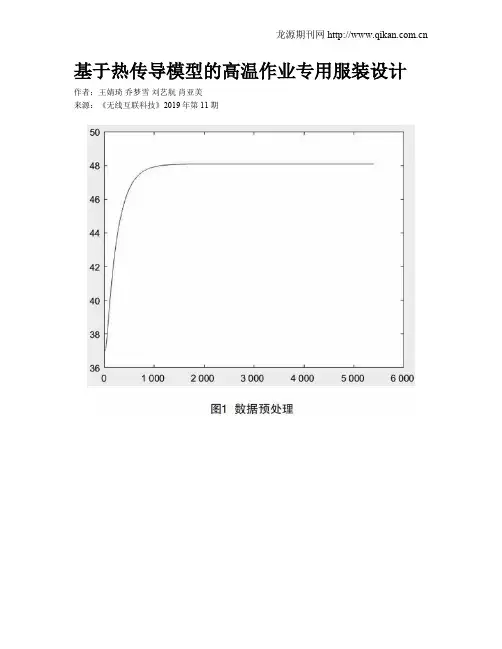
已知环境温度为75 ℃，90 min内实验数据的变化情况，且假人皮肤的初始温度为37 ℃，利用Matlab对数据进行描点绘图，数据预处理如图1所示。

通过观察图1可知在，1 736 s之后曲线平滑，没有明显上升趋势。

之后对0 s和1 745 s之间的数据使用Matlab进行三阶拟合，得出拟合方程为：y=9.1e−0.3×x3−3e−0.5×x2+0.033×x+37此方程可表明皮肤温度与时间的函数关系。

高温作业专用服装设计在高温环境下工作时，穿戴适合的专用服装是非常重要的。

高温环境下的工作，例如高温车间、锅炉房、矿山、油田等，工人们面临高温、高湿和高辐射的压力，所以需要具备一定的防护性能的服装。

高温作业专用服装应选用透气性好的材料，以便及时排出体内的汗液和水分。

透气性好的材料可以帮助身体散发热量，保持适宜的体温，减少对人体的热压力。

常用材料有涤纶、尼龙、棉麻等。

这些材料具有较好的透气性，能够满足身体散热的需求。

高温作业专用服装应具备防辐射功能，以保护身体免受高温炉火和辐射的伤害。

高温作业场所通常存在辐射源，例如高温炉火或放射性物质，所以服装需要具备辐射防护功能。

一些特殊防辐射材料可以有效地阻挡热辐射和电磁辐射，减少对人体的伤害。

高温作业专用服装还应具备防火功能。

高温作业场所往往面临着火灾的风险，因此服装需要具备较好的防火性能，以减少火灾对工人的伤害。

防火材料可以有效地阻燃，减缓火焰传播的速度，增加逃生的时间窗口。

高温作业专用服装还应具备耐磨性和耐高温性。

高温作业场所通常地面温度较高，工人们需要长时间地站立，所以服装需要具备耐磨性，以延长使用寿命。

高温作业场所的温度往往接近或超过了普通材料的极限温度，所以服装需要具备耐高温性，以确保工人的安全。

高温作业专用服装应注重舒适性和人体工学设计。

在高温环境下工作往往引起工人们的不适，所以服装需要有良好的舒适性，以提高工人的工作效率。

服装的设计应考虑到工人的活动范围和姿势，以提供更好的工作体验。

设计高温作业专用服装需要考虑透气性、防辐射功能、防火功能、耐磨性、耐高温性、舒适性和人体工学设计等因素，以满足工人在高温环境下的工作需求。

这样的专用服装可以帮助工人们保持舒适和安全，提高工作效率，减少工伤事故的发生。

高温作业专用服装设计的数学建模
高温作业专用服装设计是一项非常具有挑战性的任务，需要考虑到人体在高温环境下
的生理特点以及热传导、蒸发和辐射等因素对热交换的影响。

本文将通过数学建模的方法，对高温作业专用服装的设计进行研究和优化。

我们需要了解人体在高温环境下的散热机制。

根据生理学研究，人体散热的主要机制
有三种：传导、对流和辐射。

传导是通过物质的直接接触和分子的传递来传导热量；对流
是通过流体的对流运动来带走热量；辐射是通过电磁波的辐射来传递热量。

在高温环境下，由于空气温度较高，传导和对流成为主要的散热机制。

接下来，我们将考虑到高温作业专用服装的主要功能是帮助人体散热并保持舒适。

根
据这个目标，我们可以建立如下的数学模型：
1. 传导的数学模型：
传导是服装和人体之间的直接接触，可以通过传热学的基本原理来描述。

传热学
中的一个经典模型是傅里叶热传导定律，可以使用如下的方程描述：
q = - k * A * (dT / dx)
q 是通过传导传递的热量，k 是传导系数，A 是传热面积，dT/dx 是温度梯度。

在高温环境下，通过选择合适的材料和设计合理的传热面积，可以最大限度地减
小传热损失。

通过数学建模的方法可以对高温作业专用服装的设计进行研究和优化。

通过建立传导
和对流的数学模型，并将其结合起来，可以得到一个全面考虑热传导和对流效果的热传导
模型，进一步优化服装的设计参数，提高穿着者在高温环境下的舒适度和安全性。

基于热传导理论对高温专用服装设计问题的研究摘要本文针对高温作业专用服装设计问题，运用了热传导理论、抛物型微分方程、差分法近似求解、多目标最优化、遗传算法等方法，建立了热防护服－空气层－皮肤模型、第Ⅱ层厚度最优模型和第Ⅱ层第IV层厚度最优模型，综合运用了Matlab等软件编程求解。

在问题一的条件下，得到了每层材料的温度，在问题二的约束条件下，第Ⅱ层的最优厚度为5.998mm，在问题三的条件下，第Ⅱ层和第IV层的最优厚度分别为12.03425mm和6.4mm等结论。

针对问题一，要求计算温度分布的问题。

首先运用热传导理论、抛物型微分方程和差分近似求解法建立了热防护服－空气层－皮肤模型，然后运用了Matlab 编程求解，得到温度在各个材料层的分布。

针对问题二，要求在题目条件下，求解第Ⅱ层的最优厚度。

首先，采用了最优化理论和遗传算法建立了第Ⅱ层厚度最优模型，然后运用了Matlab编程求解，最后得出第Ⅱ层的最优厚度为5.998mm。

针对问题三，在题目给定条件下，求解第Ⅱ层和第IV层的最优厚度。

首先，采用了多目标优化和遗传算法建立了第Ⅱ层第IV层厚度最优模型，然后运用了Matlab编程求解，最后得出第Ⅱ层和第IV层的最优厚度分别为12.0345mm和6.4mm。

本文最后还对模型进行了误差分析，对模型的优缺点进行了客观的评价，基于热湿耦合理论对本文未考虑湿热传递进行了改进。

本文的创新点在于用差分法求解模型近似解，避免了求解模型解析解过于复杂难以求解的情况，节省了时间，提高了模型精度。

关键词：抛物型微分差分法遗传算法热防护服－空气层－皮肤模型一、问题重述在高温环境下工作时，人们需要穿着专用服装以避免灼伤。

高温专用服装通常由三层织物材料构成，记为I、II、III层，其中I层与外界环境接触，第IV层为III层与皮肤之间存在的空隙。

将体内温度控制在37ºC的假人放置在实验室的高温环境中，测量假人皮肤外侧的温度。

高温作业专用服装设计一、设计背景高温作业是指在高温环境下进行的工作，例如炼钢、冶炼、玻璃制造、炼油等行业。

在这些行业中，工人需要长时间在高温下工作，容易受到高温热辐射的影响，容易出现中暑、热射病等健康问题。

设计一款适合高温作业环境的专用服装对于保护工人的健康和安全至关重要。

二、设计原则1. 防火防热：服装面料需要具有较高的防火防热性能，能够有效隔离热辐射和高温气体，降低工人受到热辐射的影响。

2. 透气舒适：由于高温作业环境下工人易出汗，所以服装需要具有良好的透气性能，减少汗液在身体表面停留的时间，保持皮肤干爽。

3. 耐磨耐烧：由于高温环境中工作条件较为恶劣，服装需要具有较高的耐磨耐烧性能，保证长时间使用不易磨损和破损。

4. 设计合理：服装设计应考虑工人的工作姿势和动作，确保穿着舒适并且不影响工作的灵活性。

5. 显眼安全：在设计服装时需要考虑在高温环境下工人的安全性，例如增加反光条等安全元素，提高工人在高温环境中的可见度。

三、设计要点1. 面料选择：选择具有良好耐磨、防火、透气性能的面料，例如阻燃涤纶面料、阻燃棉面料等。

2. 结构设计：采用宽松的设计，保证透气性能的同时还能保持舒适性，增加通风口和散热口，加强通风效果。

3. 功能细节：设计口袋时应放置于工作服正面上，便于工人放置工具和物品；增加安全反光条，提高工人在高温环境中的可见度。

4. 防护细节：在领口、袖口和裤腿处设计防火防热的细节，保护工人的身体部位免受高温热辐射侵害。

四、设计示意图[图片]五、设计材料1. 面料：阻燃涤纶面料2. 配件：反光条、拉链、纽扣3. 辅料：纺织标签、洗水标签、尺码标签、吊牌七、成本估算面料成本：500元/米配件成本：50元/套辅料成本：10元/套高温作业专用服装的设计，不仅要具有防火防热、透气舒适、耐磨耐烧等功能性能，还要考虑到工人的工作姿势和动作，确保穿着舒适和不影响工作的灵活性。

在设计服装时需要综合考虑面料、结构、功能细节和防护细节等因素，以确保工人在高温环境下的健康和安全。

高温作业专业服装的设计摘要：本文以Matlab为工具，利用有限容积法求解二维热传导方程从而对高温作业专业服装各层的导热性能进行研究，并结合附件中的相关数据解得各层的温度随厚度、时间的变化关系函数。

问题一、首先对高温作业专业服装的各层模型做简化处理，将热传导看成在简单的二维平面内沿厚度x方向进行。

将每层的材料视为无数“有限体积单元”的叠加；再对每个“有限体积单元”进行研究并得到温度T关于时间t、厚度x的偏微分方程。

运用有限容积法对该偏微分方程进行求解。

问题二、利用以上模型在给定的条件下，首先确保在60min时假人皮肤外侧的温度低于47℃。

随后将Ⅱ层厚度划分为从0mm-1mm……24mm-25mm的25个区间，并在这25个区间内分别进行数值分析与试探,求得符合条件的14个厚度区间，再对符合条件的厚度区间进一步划分并重复以上操作以求得厚度的最优解为8.7mm。

问题三、基于问题一的模型在给定条件下可得到以II层，IV层厚度为自变量，皮肤外侧温度为因变量的非线性二元函数。

采用随机搜索法确定最优解的近似值，用牛顿法对函数进行求解，得出厚度的最佳值为II层为18.4mm，IV层为6.2mm。

关键词：一维传热方程、有限容积法、牛顿迭代法、Matlab一、问题重述高温作业专用服装为高温从业者提供人身安全保障，通过对高温作业专用服装的相关参数的确定完成以下问题的解答：问题一：结合附件1给出的数值，对当环境温度为75oC、II层厚度为6 mm、IV层厚度为5 mm、工作时间为90分钟的情形开展实验，测量得到假人皮肤外侧的温度。

建立合适的数学模型，分析并计算假人皮肤外侧的温度随时间及厚度在各层的分布规律，并生成温度分布的相关Excel文件。

问题二：当环境温度为65oC、IV层的厚度为5.5 mm时，确定II层的最优厚度，确保工作60分钟时，假人皮肤外侧温度不超过47oC，且超过44oC的时间不超过5分钟。

问题三：当环境温度为80℃时，确定II层和IV层的最优厚度，确保工作30分钟时，假人皮肤外侧温度不超过47oC，且超过44oC的时间不超过5分钟。

高温作业专用服装设计原理高温作业专用服装设计原理1. 引言随着经济的发展和科技的进步，高温作业已经成为现代工业生产中的一个重要环节。

高温环境对工人的身体健康和生产效率都具有极大的影响。

为了保护工人的安全和提高生产效率，高温作业专用服装的设计变得非常重要。

本文将围绕高温作业专用服装的设计原理展开探讨，旨在为高温作业专用服装的研发和生产提供参考。

2. 高温作业环境分析高温作业环境通常被定义为环境温度超过30摄氏度的工作环境。

在这种环境下，高温会加速人体流汗和水分蒸发的速度，导致身体脱水、血液黏稠度增加，易引发中暑等健康问题。

因此，高温作业专用服装设计必须能够有效地防止高温对工人身体的伤害。

3. 高温作业专用服装设计原理3.1 透气性高温作业专用服装必须具备良好的透气性，以保证工人在高温环境下的舒适度和健康。

透气性是指材料在一定条件下对空气和水汽的渗透性能。

优秀的透气性能有助于排汗和蒸发，避免过度脱水，降低体温快速上升的风险。

在设计过程中，可以选择透气性好的材料，或者采用特殊的织物结构来增强透气性。

3.2 吸湿性吸湿性是指材料吸收水分的能力。

高温环境下，工人大量流汗，必须有一种材料能够迅速吸收汗水，并快速蒸发释放出来，以保持衣物的干燥和工人的舒适度。

通常使用具有较好吸湿性的纤维材料来制作高温作业专用服装。

3.3 耐高温性高温环境下，高温作业专用服装必须具备一定的耐高温性。

材料应具有较高的熔点和耐热性，能够承受较高的温度而不融化或变形。

为了提高耐高温性，可以使用具有良好热稳定性的高温纤维材料或者采用多层结构来隔断高温热量。

3.4 耐磨性在高温作业环境中，工人的服装往往要接触到各种尖锐物体、粗糙表面或者物品的摩擦摩擦，因此高温作业专用服装必须具备较好的耐磨性。

通过材料的选择和处理，可以增强高温作业专用服装的耐磨性能。

3.5 舒适度高温作业专用服装的舒适度是指在高温环境下，工人能够感受到适度的舒适感。

为了提高舒适度，设计人员可以考虑服装的质地、版型和重量等因素。

创新论坛科技创新导报 Science and Technology Innovation Herald255DOI：10.16660/ki.1674-098X.2019.09.255高温作业服装的设计郭经峰 毛敏捷 齐丹辰 刘兴迪(青岛理工大学 山东青岛 266520)摘 要：本文针对高温专用服装的设计展开研究，依托MATLAB、LINGO、EXCEL等软件对专用服装各层材料的温度分布进行了详尽的分析，并对不同高温工作环境下服装织物材料厚度进行优化设计。

为确定服装的最优厚度，建立以热量传递的长度为x轴，热量传递的时间为y轴，假人皮肤外层温度热量z轴的温度分布空间三维坐标系，建立以热传导为主的热传递偏微分方程模型，利用MATLAB软件编程得到专用服装（空气层）—皮肤外侧系统温度分布函数，以此函数作为目标约束建立目标规划模型，以皮肤外侧温度不超过47℃且超过44℃的时间不超过5min为刚性约束，以皮肤外层温度不超过45℃为柔性约束（当皮肤外层温度达到45℃时会有灼烧感），构建目标规划数学表达式。

最后，我们对模型进行灵敏度检验和鲁棒性分析，验证模型的可行性，并对模型进行客观的评价和适当的推广。

关键词：高温作业 热传递偏微分方程 多目标规划中图分类号：TD79 3 文献标识码：A 文章编号：1674-098X(2019)03(c)-0255-021 基本假设(1)假设专用服装的初始温度与假人皮肤外侧的初始温度相同，均为37℃。

(2)假设外界环境恒为某一定值。

(3)假设专用服装的各层之间接触良好，中间没有附加热阻。

(4)假设专用服装材料的各项参数不随温度、时间的变化而变化。

(5)假设热传递是垂直于皮肤方向进行，故可视为一维的。

(6)假设高温作业环境的热传递以热传导为主，不考虑热辐射以及热对流。

空气层厚度小于8mm，热对流影响小，可忽略。

(7)假设专用服装织物之间，织物与空气层之间，空气层与皮肤外侧之间的温度变化是连续的，温度梯度是跳跃的。

高温作业专用服装设计一、问题重述1、1问题背景高温作业专用服装属于个体劳动保护专用服装类,广泛适用于冶金、电力、矿山、消防、国防等高温作业场所个人防暑降温,可保障安全与健康。

由于环境温度过高导致人体表面温度升高就是损害工作人员身体健康得主要原因.近年来由于生产制造业得飞速发展，新工艺、新设备得大量采用,劳动群体也日渐庞大.因此，研制一种适合高温作业人员使用专用服装就是我们得首要任务.１、2问题得提出问题一：已知专用服装材料得某些参数值并且当环境温度为75ºC、ＩI层厚度为6 mm、IＶ层厚度为5 mm、工作时间为90分钟时，假人皮肤外侧得温度数据表已知。

通过建立数学模型,计算假人皮肤外侧温度分布，并生成温度分布得E ｘcel文件。

问题二:当环境温度为６5ºC、IＶ层得厚度为5、５mm,工作6０分钟时，假人皮肤外侧温度不超过47ºC,且超过44ºC得时间不超过5分钟。

求解IＩ层得最优厚度。

问题三:当环境温度为80时，工作30分钟时，假人皮肤外侧温度不超过47ºC，且超过4４ºC得时间不超过５分钟,求解II层与IＶ层得最优厚度。

二、问题分析所谓高温作业, 就就是指操作场所得热源(炉子、明火、发热设备、灼热原料与大量蒸汽得设备），发出强烈得热辐射及对流热。

为设计专用服装,将体内温度控制在37ºＣ得假人放置在实验室得高温环境中,测量假人皮肤外侧得温度。

问题一得分析：分析题意，可知由于就是在两个坐标方向上存在温度梯度，分别就是厚度与时间，传热虽然只发生在厚度这个方向上,但就是温度得变化就是随厚度与时间同时发生改变。

假设系统在沿材料厚度变化得方向就是无热源稳态热传导，沿厚度与时间两个方向建立微分方程模型，高温作业服装得温度分布可通过求解带有正确边界条件得导热方程来确定，借助傅里叶定律与热传导公式确定传热速率，从而得到温度分布，最后利用mａtlab软件求解方程，得到得结果导入eｘceｌ表格。