《圆心角、圆周角的性质》的中考题集锦(一)

初三数学圆周角和圆心角的关系试题1.已知,如图,∠BAC的对角∠BAD=100°,则∠BOC=_______度.【答案】160°【解析】由∠BAD=100°可得∠BAC的度数，再根据圆周角定理即可求得结果.∵∠BAD=100°∴∠BAC=80°∴∠BOC=160°.【考点】邻补角定理，圆周角定理点评：本题是圆周角定理的基础应用题，在中考中比较常见，一般以选择题、填空题形式出现，属于基础题，难度不大.2.如图,AB是⊙O的直径, ,∠A=25°,则∠BOD的度数为________.【答案】50°【解析】圆周角定理：同弧或等弧所对的圆周角相等，均等于所对圆心角的一半.∵,∠A=25°∴∠BOD=50°.【考点】圆周角定理点评：本题是圆周角定理的基础应用题，在中考中比较常见，一般以选择题、填空题形式出现，属于基础题，难度不大.3.如图,AB是半圆O的直径,AC="AD,OC=2,∠CAB=30°," 则点O到CD的距离OE=____.【答案】【解析】由AC=AD，∠CAB=30°可得∠CDO的度数，即可得到∠EOD、∠COE的度数，判断出△COE的形状再结合勾股定理即可求得结果.∵AC=AD，∠CAB=30°，OA=OC∴∠CDO=75°，∠COD=60°∴∠EOD=15°∴∠COE=45°∴△COE为等腰直角三角形∵OC=2∴OE=.【考点】三角形内角和定理，勾股定理点评：特殊三角形的性质的应用是初中数学平面图形中极为重要的知识点，与各个知识点结合极为容易，是中考中的热点，在各种题型中均有出现，需多加关注.4.如图,A、B、C、D四个点在同一个圆上,四边形ABCD的对角线把四个内角分成的八个角中,相等的角有( )A.2对B.3对C.4对D.5对【答案】C【解析】圆周角定理：同弧或等弧所对的圆周角相等，均等于所对圆心角的一半.相等的角有∠ADB=∠ACB，∠BAC=∠BDC，∠CAD=∠CBD，∠ACD=∠ABC4对，故选C.【考点】圆周角定理点评：本题是圆周角定理的基础应用题，在中考中比较常见，一般以选择题、填空题形式出现，属于基础题，难度不大.5.如图,D是弧AC的中点,则图中与∠ABD相等的角的个数是( )A．4个B．3个C．2个D．1个【答案】B【解析】圆周角定理：同弧或等弧所对的圆周角相等，均等于所对圆心角的一半.∵D是弧AC的中点∴∠ABD=∠ACD=∠CBD=∠CAD故选B.【考点】圆周角定理点评：本题是圆周角定理的基础应用题，在中考中比较常见，一般以选择题、填空题形式出现，属于基础题，难度不大.6.如图, ,则∠A+∠B等于( )A．100°B．80°C．50°D．40°【答案】C【解析】连接CO并延长交圆于点D，根据圆周角定理即可得到结果.连接CO并延长交圆于点D由图可得∠A+∠B=∠AOD+∠BOD=∠AOB=50°故选C.【考点】圆周角定理点评：辅助线问题是初中数学学习中的难点，能否根据具体情况正确作出恰当的辅助线往往能够体现一个学生对图形的理解能力，因而这类问题在中考中比较常见，在各种题型中均有出现，一般难度较大，需多加关注.7.在半径为R的圆中有一条长度为R的弦,则该弦所对的圆周角的度数是( )A．30°B．30°或150°C．60°D．60°或120°【答案】B【解析】根据圆的性质可得这条弦与半径围成的三角形为等边三角形，再根据圆周角定理即可求得结果.由题意得这条弦与半径围成的三角形为等边三角形则该弦所对的圆周角的度数是30°或150°故选B.【考点】圆周角定理点评：特殊三角形的性质的应用是初中数学平面图形中极为重要的知识点，与各个知识点结合极为容易，是中考中的热点，在各种题型中均有出现，需多加关注.8.如图,⊙O的直径AB=8cm,∠CBD=30°,求弦DC的长.【答案】4cm【解析】连接OC、OD，根据圆周角定理可得∠COD=60°，即可得到△COD是等边三角形，根据等边三角形的性质即可求得结果.连接OC、OD,则OC=OD=4cm,∠COD=60°,故△COD是等边三角形,从而CD=4cm.【考点】圆周角定理，等边三角形的判定和性质点评：辅助线问题是初中数学学习中的难点，能否根据具体情况正确作出恰当的辅助线往往能够体现一个学生对图形的理解能力，因而这类问题在中考中比较常见，在各种题型中均有出现，一般难度较大，需多加关注.9.如图,AB为半圆O的直径,弦AD、BC相交于点P,若CD=3,AB=4,求tan∠BPD的值【答案】【解析】连接BD, 根据圆周角定理可得∠ADB=90°，证得△PCD ∽△PAB,根据相似三角形的性质结合余弦的定义可得∠BPD的余弦值，再结合勾股定理即可求得结果.连接BD,∵AB是直径,∴∠ADB=90°.∵∠C=∠A,∠D=∠B,∴△PCD ∽△PAB,∴.在Rt△PBD中,cos∠BPD==,设PD=3x,PB=4x,则BD=,∴tan∠BPD=.【考点】圆周角定理，相似三角形的判定和性质，勾股定理，三角函数点评：本题综合性强，知识点较多，因而这类问题在中考中比较常见，在各种题型中均有出现，一般难度较大，需多加关注.10.在足球比赛场上,甲、乙两名队员互相配合向对方球门MN进攻.当甲带球部到A点时,乙随后冲到B点,如图所示,此时甲是自己直接射门好,还是迅速将球回传给乙,让乙射门好呢?为什么?(不考虑其他因素)【答案】让乙射门较好【解析】根据圆周角定理结合三角形外角的性质分析即可得到结论.迅速回传乙,让乙射门较好,在不考虑其他因素的情况下, 如果两个点到球门的距离相差不大,要确定较好的射门位置,关键看这两个点各自对球门MN的张角的大小,当张角越大时,射中的机会就越大,如图所示,则∠A<MCN=∠B,即∠B>∠A, 从而B处对MN的张角较大,在B处射门射中的机会大些.【考点】圆周角定理，三角形外角的性质点评：本题是圆周角定理的基础应用题，在中考中比较常见，一般以选择题、填空题形式出现，属于基础题，难度不大.。

圆周角的练习题初三圆周角是指以圆心为顶点的角，它的度数等于所对弧的度数。

在初三的几何学中，圆周角是一个重要的概念，掌握圆周角的计算方法对于解决几何题目至关重要。

本文将为大家提供一些圆周角的练习题，帮助初三学生巩固和掌握这一知识点。

练习题一：已知直径AB的圆上一点C，连结AC和BC两条弦。

求∠ACB的度数。

解析：根据圆的性质可知，在圆上以弦为底的两个圆周角是等角，所以∠ACB = ∠AEB。

而直径AB是圆上的一条直径，它对应的圆周角为180度。

因此，∠ACB = ∠AEB = 180度。

练习题二：已知弧AC与弧BC分别是圆上的两个等分弧，且∠ACB = 20度。

求弧AC的度数。

解析：根据题目可知，∠ACB为圆周角，而弧AC和弧BC是等分弧，所以它们所对应的圆周角也相等，即∠ACB = ∠AEB。

而∠ACB 已知为20度，所以∠AEB = 20度。

而直径AB上的圆周角为180度，所以弧AC的度数为180度减去∠AEB的度数，即弧AC = 180度 - 20度 = 160度。

练习题三：已知直径AB的圆上一点C与D，连结AC和BD两条弦，交于点E。

若∠AEB = 70度，求证：∠ACD = 35度。

解析：要证明∠ACD = 35度，可以利用等角的性质。

根据题目已知，∠AEB = ∠AED = 70度。

而由圆周角的性质可知，∠ACD =∠AEB = 70度。

又∠ACD和∠ACB是同弦内角和对应的圆周角，所以有∠ACD = 180度 - ∠ACB。

将已知条件带入，∠ACD = 180度 - 70度= 110度。

由此可知，∠ACD的度数为35度。

练习题四：已知弦AB的长为8cm，圆心角∠AOB的度数为60度，求弦AB所对应的弧长。

解析：弦AB所对应的弧可以通过圆心角的度数与圆周长的比例来求解。

已知圆心角∠AOB的度数为60度，而整个圆的圆心角为360度，所以∠AOB所对应的弧所占圆周长的比例为60度/360度= 1/6。

圆心角圆周角练习题圆心角和圆周角是圆内角的一种特殊形式，它们在几何学中具有重要的地位。

本文将介绍关于圆心角和圆周角的一些练习题，帮助读者加深对这一概念的理解。

一、选择题1. 在同一个圆中，圆心角和对应的圆周角的关系是：A. 圆心角大于对应的圆周角B. 圆心角等于对应的圆周角C. 圆心角小于对应的圆周角2. 已知在同一个圆中，圆心角的度数为56°，则对应的圆周角的度数为：A. 56°B. 112°C. 224°3. 在圆O中，∠ACB是圆心角，则它所对应的圆周角的度数为：A. 30°B. 60°C. 120°4. 若∠ACD是圆O中的圆心角，且其度数为72°，则弧AB所对应的圆周角的度数为：A. 72°B. 144°C. 288°5. 在同一个圆中，圆心角和对应的弧所对应的圆周角之间的关系是：A. 圆心角小于对应的圆周角B. 圆心角等于对应的圆周角C. 圆心角大于对应的圆周角二、填空题1. 在同一圆中，一条弧的度数等于其所对应的圆周角的度数，则这条弧所对应的圆心角的度数为________。

2. 在圆O中，已知∠ACB是圆心角，则它所对应的圆周角的度数为________。

3. 在同一个圆中，圆心角的度数等于所对应的弧所对应的圆周角的度数，则该弧所对应的圆周角的度数为________。

三、解答题1. 在同一个圆中，圆心角和对应的圆周角的关系是什么？为什么？2. 已知在同一个圆中，圆心角的度数为60°，则对应的圆周角的度数是多少？并通过计算或推理进行解答。

3. 在圆O中，∠ACB是圆心角，则它所对应的圆周角的度数是多少？并通过计算或推理进行解答。

4. 若∠ACD是圆O中的圆心角，且其度数为90°，则弧AB所对应的圆周角的度数是多少？并通过计算或推理进行解答。

总结：本文通过选择题、填空题和解答题的形式，对圆心角和圆周角的概念进行了练习和探讨。

初三数学上册圆心角与圆周角训练题初三数学上册圆心角与圆周角的训练积累越多，学会越熟练。

下面是我们为大家带来的关于初三数学上册圆心角与圆周角的训练题，期望会给大家带来协助。

初三数学上册圆心角与圆周角训练题目一、选择题1.在同圆中，同弦所对的圆周角 A.相等 B.互补 C.相等或互补D.互余2.3-63所示，A，B，C，D在同一个圆上，四边形ABCD的两条对角线把四个内角分成的8个角中，相等的角共有 A.2对 B.3对 C.4对 D.5对3.3-64所示，⊙O的半径为5，弦AB，C是圆上一点，则ACB的度数是.4.四边形 ABCD内接于⊙O，若BOD=100，则DAB的度数为A.50B.80C.100D.1305.是中国共产主义年轻人团团旗上的案，点A、B、C、D、E五等分圆，则A+B+C+D+E的度数是A.180B.15 0C.135D.1206.下列命题中，正确的命题个数是①顶点在圆周上的角是圆周角;②圆周角度数等于圆心角度数的一半;③900的圆周角所对的弦是直径;④圆周角相等，则它们所对的弧也相等。

A、1个B、2个C、3个D、4个二、填空题7.3-65所示，在⊙O中，AOB=100，C为优弧ACB的中点，则CAB=8.3-66所示，AB为⊙O的直径，AB=6，CAD=30，则弦DC= .9.3-67所示，AB是⊙O的直径，BOC=120，CDAB，求ABD的度数.10.已知AB是⊙O的直径，AD ∥ OC弧AD的度数为80，则BOC=_________11.⊙O内接四边形ABCD中，AB=CD则中和1相等的角有______。

12.弦AB的长等于⊙O的半径，点C在AB上，则C的度数是________-.三、解答题13.3-68所示，在△ABC中，AB=AC，C=70，以AB为直径的半圆分别交AC，BC于D，E，O为圆心，求DOE的度数.14.已知⊙O的直径为10，点A，点B，点C在⊙O上，CAB的平分线交⊙O于点D.①，若BC为⊙O的直径，AB=6，求AC，BD，CD的长;②，若CAB=60，求BD的长.15.3-70所示，在⊙O中，AB是直径，弦AC=12 cm，BC=16 cm，ACB的平分线交⊙O于点D，求AD的长.16.3-71所示，AB是半圆O的直径，C是半圆上一点，D是AC的中点，DHAB，H是垂足，AC分别交BD，DH于E，F，试说明DF=EF.初三数学上册圆心角与圆周角训练题答案1.C2.C3.60[提示：3-72所示，作ODAB，垂足为D，则BDsinBODBOD=60，BOA=120，BCABOA=60.故填60.]4.剖析：由于BOD=100，所以C=50，所以A=130，由于圆内接四边形的对角互补。

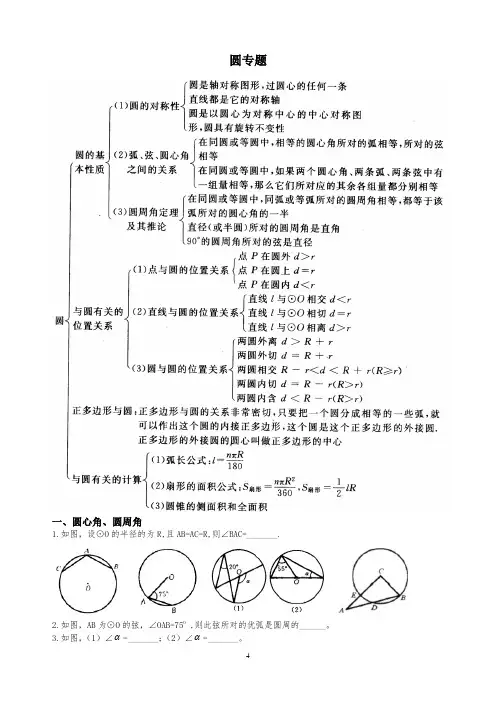
圆专题一、圆心角、圆周角1.如图，设⊙O的半径的为R,且AB=AC=R,则∠BAC=_______.2.如图，AB为⊙O的弦，∠OAB=75O ,则此弦所对的优弧是圆周的______。

4.如图，在△ABC 中，∠C 是直角，∠A=32O 18’ ，以点C 为圆心、BC 为半径作圆，交AB 于点D,交AC 于点E,则⋂BD 的度数是______。

5.如图，点O 是△ABC 的外心，已知∠ACB=100O ,则劣弧⋂AB 所对的∠AOB=______度。

6.如图，AB 是⊙O 的直径，CD 与AB 相交于点E, ∠ACD=60O , ∠ADC=50O ,则∠AEC=______度。

7.如图，以等腰△ABC 的边AB 为直径的半圆，分别交AC 、BC 于点D 、E,若AB=10, ∠OAE=30O,则DE=______。

8.在锐角△ABC 中，∠A=50O ,若点O 为外心，则∠BOC=_____;若点I 为内心，则∠BIC=______；若点H 为垂心，则∠BHC=________.9.若△ABC 内接于⊙O ，∠A=n O,则∠BOC=_______.10.如图，已知AB 和CD 是⊙O 相交的两条直径，连AD 、CB ，那么α和β的关系是（ ） A.α=β B.β>21α C.β<21α D.β=2α 11.如图，在⊙O 中，弦AC 、BD 交于点E ，且⋂⋂⋂==CDBC AB ，若∠BEC=130O ,则∠ACD 的度数为（ ）A.15OB.30OC.80OD.105O12.如图，AB 为半圆的直径，AD ⊥AB,点C 为半圆上一点，CD ⊥AD,若CD=2,AD=3,求AB 的长。

13.如图，AO ⊥BO,AO 交⊙O 于点D ，AB 交⊙O 于点C, ∠A=27O,试用多种方法求⋂DC 、⋂BC 的度数。

14.求证：如果AB 和CD 为⊙O 内互相垂直的两条弦，那么∠AOC 和∠BOD 互补。

初三圆周角练习题圆周角在初三数学中是一个重要的概念，理解和掌握圆周角的性质及计算方法对解题非常关键。

下面给出一系列的圆周角练习题，帮助初三学生加深对这一概念的理解和应用。

题目一：已知半径为5cm的圆上的一条弧所对圆心角的度数是120°，求此弧的长度。

解析：根据圆周角的性质，圆周角的度数等于所对弧的度数，因此所求弧的度数也是120°。

由于圆周角的度数等于所对弧的弧长与半径的比值，设所求弧的弧长为L，则有120/360 = L/(2π×5)。

解方程可得L ≈ 10π/3 cm。

题目二：在半径为8cm的圆中，两条弦长分别为12cm和16cm，求这两条弦所对的圆周角的度数。

解析：根据圆周角的性质，圆周角的度数等于所对弦所对应的弧的度数，而弧长等于弦的长度。

设所求圆周角的度数为x°，根据等式关系12/8 = x/360 和16/8 = x/360，解这两个方程可得x ≈ 180° 和x ≈ 240°。

因此，一条弦所对圆周角的度数为180°，另一条弦所对圆周角的度数为240°。

题目三：一个扇形的圆心角是64°，对应的弧长为10π cm，求此扇形的面积。

解析：根据扇形面积公式，扇形的面积等于扇形所在圆的面积乘以圆心角的度数与360°的比值。

设扇形的面积为S，圆的面积为A，则有S/A = 64°/360° = 64/360。

解方程可得S = (64/360) × π × r^2，代入已知条件，可得S ≈ (64/360) × π × (10/2)^2 = 16π/9 cm^2。

题目四：在半径为3cm的圆中，一条弦的弦长为4cm，这条弦与半径所夹的圆周角的弧度数为1/6π rad，求该弦所对的弧长。

解析：根据圆周角的性质，弧度数等于所对弧的弧长与半径的比值。

圆---圆心角、圆周角1. 如图，已知AB是⊙O的直径，C.D是上的三等分点，∠AOE＝60°，则∠COE是( )A.40°B.60°C.80°D.120°2.如图，已知在⊙O中，点C为的中点，∠A＝40°，则∠BOC等于( )A.40°B.50°C.70°D.80°3. 下面四个图中的角，是圆心角的是( )4. 下列说法正确的是( )A.相等的圆心角所对的弦相等B.相等的圆心角所对的弧相等C.等弧所对的弦相等D.度数相等的弧的长度相等5. 如图，在⊙O中，弦AB.CD相交于点E，且AB＝CD，连接AD.BC，则下列给出的结论中，正确的有( )①②AD＝BC ③∠CBD＝∠ADB ④∠A＝∠C ⑤AE＝CEA.5个B.4个C.3个D.2个6. 如图，在⊙O中，AC∥OB，∠BAO＝25°，则∠BOC的度数为( )A.25°B.50°C.60°D.80°7. 如图，已知经过原点的⊙P与x、y轴分别交于A.B两点，点C是劣弧OB上一点，则∠ACB＝( )A.80°B.90°C.100°D.无法确定8. 圆内接四边形ABCD中，已知∠A＝70°，则∠C＝( )A.20°B.30°C.70°D.110°9. 如图，四边形ABCD为⊙O的内接四边形，已知∠BOD＝100°，则∠BCD的度数为( )A.50°B.80°C.100°D.130°10. 顶点在圆心，两边与圆相交的角叫做_________.在同圆或等圆中，相等的圆心角所对的弧_____，所对的弦也______；在同圆或等圆中，如果两条弧相等，那么它们所对的圆心角______，所对的弦_________；在同圆或等圆中，如果两条弦相等，那么它们所对的圆心角_____，所对的弦_______-.11. 顶点在_________，两边都和圆_______的角叫圆周角.一条弧所对的圆周角等于它所对的圆心角的_______.在__________(或相等的圆)中，同弧或等弧所对的圆周角_______；反之，相等的圆周角所对的弧_________.12. 半圆(或直径)所对的圆周角是_______；90°的圆周角所对的弦是________.13.如果一个多边形的所有顶点都在同一个圆上，这个多边形叫做__________，这个圆叫做___________；圆内接四边形对角_________-.14. 已知圆O的半径为5cm，弦AB的长为5cm，则弦AB所对的圆心角∠AOB＝__________.15. 如图，已知AB为⊙O的直径，点D为半圆周上的一点，且所对圆心角的度数是所对圆心角度数的两倍，则圆心角∠BOD的度数为_____.16. 下列四个图中，∠x是圆周角的是________.17. 如图，AB.CD是⊙O的两条互相垂直的弦，圆心角∠AOC＝130°，AD.CB的延长线相交于P，则∠P＝_______-.18. 如图所示，A.B.C.D是⊙O上顺次四点.若∠AOC＝160°，则∠D＝_______________ ，∠B＝____________.19. 如图，已知A.B.C.D是⊙O上四点，若AC＝BD，求证：AB＝CD.20. 如图，在△AOB中，AO＝AB，以点O为圆心，OB为半径的圆交AB于D，交AO于点E，AD＝BO.试说明，并求∠A的度数.21. 如图，A.B.C在圆上，弦AE平分∠BAC交BC于D.求证：BE2＝ED·EA.22. 如图所示，AB是⊙O的直径，AB＝8cm，∠ADE＝60°，DC平分∠ADE，求AC.BC的长.23. 如图，△ABC内接于⊙O，过C作CD∥AB与⊙O相交于D点，E是上一点，且满足AD＝DE，连接BD 与AE相交于点F.求证：△ADF∽△ABC.24. 如图，四边形ABCD内接于⊙O，点E在对角线AC上，EC＝BC＝DC.(1)若∠CBD＝39°，求∠BAD的度数；(2)求证：∠1＝∠2.25. 如图，已知△ABC是等边三角形，⊙O经过点A.B.C，点P是BC上任一点.(1)图中与∠PBC相等的角为________；(2)试猜想三条线段PA.PB.PC之间的数量关系，并证明.26. 如图，以△ABC的一边AB为直径的半圆与其它两边AC.BC的交点分别为D.E，且.(1)试判断△ABC的形状，并说明理由；(2)已知半圆的半径为5，BC＝12，求sin∠ABD的值.参考答案：1—9 CBDCA BBDD10. 圆心角相等相等相等相等相等相等11. 圆上相交一半同一圆相等相等12. 90°直径13. 圆的内接多边形多边形的外接圆互补14. 60°15. 60°16. ③17. 40°18. 80° 100°19.20. 解：设∠A ＝x°.∵AD ＝BO ，又OB ＝OD ，∴OD ＝AD ，∴∠AOD ＝∠A ＝x°，∴∠ABO ＝∠ODB ＝∠AOD ＋∠A ＝2x°.∵AO ＝AB ，∴∠AOB ＝∠ABO ＝2x°.从而∠BOD ＝2x°－x°＝x°，即∠BOD ＝∠AOD ，∴由三角形的内角和为180°，有2x°＋2x°＋x°＝180°，x°＝36°，即∠A ＝36°.21. 证明：∵AE 平分∠BAC ，∴∠EAB ＝∠EAC ，又∵∠EBC ＝∠EAC ，∴∠EBC ＝∠EAB ，又∵∠E 公用，∴△EBD ∽△EAB ，∴EB EA ＝ED EB，∴EB2＝EA·ED. 22. 解：∵∠ADE ＝60°，DC 平分∠ADE ，∴∠ADC ＝12∠ADE ＝30°＝∠ABC.又∵AB 为⊙O 的直径，∴∠ACB ＝90°，∴AC ＝12AB ＝4cm.BC ＝AB2－AC2＝82－42＝43(cm). 23. 证明：∵AB ∥CD ，∴∠BAC ＝∠ACD ，∵AD ＝DE ，∴∠DAE ＝∠AED ，∴∠DAE ＝∠AED ＝∠ACD ＝∠BAC ，∵∠ADF ＝∠ACB ，∠DAE ＝∠BAC ，∴△ADF ∽△ABC.24. (1)解：∵BC ＝DC ，∴∠CBD ＝∠CDB ＝39°，∵∠BAC ＝∠CDB ＝39°，∠CAD ＝∠CBD ＝39°，∴∠BAD ＝∠BAC ＋∠CAD ＝39°＋39°＝78°；(2)证明：∵EC ＝BC ，∴∠CEB ＝∠CBE ，而∠CEB ＝∠2＋∠BAE ，∠CBE ＝∠1＋∠CBD ，∴∠2＋∠BAE ＝∠1＋∠CBD ，∵∠BAE ＝∠CBD ，∴∠1＝∠2.25. 解：(1)∠PAC ；(2)PA ＝PB ＋PC.在AP 上截取PD ＝PC ，连接CD 可证△PCD 是等边三角形，△ACD ≌△BCP.26. 解：(1)△ABC 为等边三角形.理由如下：连接AE ，如图，∵，∴∠DAE ＝∠BAE ，即AE 平分∠BAC ，∵AB 为直径，∴∠AEB ＝90°，∴AE ⊥BC ，∴△ABC 为等腰三角形；(2)∵△ABC 为等腰三角形，AE ⊥BC ，∴BE ＝CE ＝12BC ＝12×12＝6，在Rt △ABE 中，∵AB ＝10，BE ＝6，∴AE ＝102－62＝8，∵AB 为直径，∴∠ADB ＝90°，∴12AE·BC＝12BD·AC，∴BD ＝8×1210＝485，在Rt △ABD 中，∵AB ＝10，BD ＝485，∴AD ＝AB2－BD2＝145，∴sin ∠ABD ＝AD AB ＝14510＝725.。

初三数学圆心角试题1.在同一个圆中，同弧所对的圆周角和圆心角的关系是．【答案】圆周角度数等于圆心角度数的一半【解析】直接根据圆周角定理填空即可.在同一个圆中，同弧所对的圆周角和圆心角的关系是圆周角度数等于圆心角度数的一半.【考点】圆周角定理点评：本题是圆周角定理的基础应用题，在中考中比较常见，一般以选择题、填空题形式出现，难度一般.2.如图，直径垂直于弦，垂足为，，则的度数为，的度数为，的度数为，的度数为．【答案】，，，【解析】根据垂径定理及圆周角定理依次分析即可得到结果.∵直径垂直于弦，∴弧AD的度数等于弧AC的度数等于∴弧CBD的度数等于∴=，的=.【考点】垂径定理，圆周角定理点评：垂径定理是圆中极为重要的知识点，一般与勾股定理结合使用，因而是中考的热点，在各种题型中均有出现，一般难度不大，需特别注意.3.如图，是半圆的直径，为圆心，是半圆上一点，且，是延长线上一点，与半圆相交于点，如果，则，，．【答案】，，【解析】设∠A=x，由AB=OC，得到∠BOA=x，根据三角形外角性质得到∠EBO=2x，而OB=OE，得∠AEO=2x，则x+2x=93°，得到x=31°，再根据三角形的内角和定理即可求得∠EOB、∠ODE．设∠A=x，∵AB=OC，∴∠BOA=x，∴∠EBO=2x，而OB=OE，∴∠AEO=2x，∴∠EOD=∠A+∠AEO，而∠EOD=93°，∴x+2x=93°，∴x=31°，∴∠EOB=180°-4x=180°-124°=56°，∴∠ODE=（180°-93°）÷2=．【考点】圆的基本性质，等腰三角形的性质，三角形内角和定理，三角形的外角性质点评：本题知识点多，综合性强，在中考中比较常见，在各种题型中均有出现，一般难度不大，需特别注意.4.如图，，则，，，．【答案】，，，【解析】在同一个圆中，同弧或等弧所对的圆周角度数等于圆心角度数的一半.∵弧ACB:弧ADB=5:4，弧ACB+弧ADB=360°∴弧ACB=200°，弧ADB=160°∴，，，.【考点】圆周角定理点评：本题是圆周角定理的基础应用题，在中考中比较常见，一般以选择题、填空题形式出现，难度一般.5.如图，△内接于，，点，分别在和上，若，则，．【答案】，【解析】由可得弧AC的度数，由可得弧AB的度数，即可得到弧BFC的度数，从而求得结果.∵，∴弧AC的度数等于弧AB的度数等于100°∴弧BFC的度数等于160°，弧BAC的度数等于200°∴，.【考点】圆周角定理点评：圆周角定理是圆中极为重要的知识点，在中考中比较常见，在各种题型中均有出现，一般难度不大，需熟练掌握.6.在同圆中，同弦所对的两个圆周角（）A．相等B．互补C．相等或互补D．互余【答案】C【解析】根据圆周角定理及圆的基本性质即可判断.在同圆中，同弦所对的两个圆周角相等或互补，故选C.【考点】圆周角定理，圆的基本性质点评：圆周角定理是圆中极为重要的知识点，在中考中比较常见，在各种题型中均有出现，一般难度不大，需熟练掌握.7.在中，弦所对的劣弧为圆的，有以下结论：①为，②，③，④△为等边三角形，⑤弦的长等于这个圆的半径．其中正确的是（）A．①②③④⑤B．①②④⑤C．①②D．②④⑤【答案】B【解析】根据圆周角定理及圆的基本性质依次分析各小题即可判断.∵弦所对的劣弧为圆的∴弧AB为60°，，△为等边三角形，弦的长等于这个圆的半径故选B.【考点】圆周角定理，圆的基本性质点评：圆周角定理是圆中极为重要的知识点，在中考中比较常见，在各种题型中均有出现，一般难度不大，需熟练掌握.8.，，，，依次是上的四个点，，弦，的延长线交于点，若，则等于（）A．B．C．D．【答案】C【解析】根据圆周角的度数等于它所对的弧的度数的一半得到弧AD的度数，从而得到弧ABCD的度数，根据弧AB=弧CB=弧CD，即可求得弧BC的度数，从而求得结果．如图：∵∠ABD=60°，∴弧AD的度数=2×60°=120°，∴弧ABCD的度数=360°-120°=240°，又∵弧AB=弧CB=弧CD，∴弧BC的度数=×240°=80°，∴∠BDC=40°，而∠ABD=∠P+∠BDP，∴∠P=60°-40°=20°．故选C．【考点】圆的基本性质，等腰三角形的性质，三角形内角和定理，三角形的外角性质点评：本题知识点多，综合性强，在中考中比较常见，在各种题型中均有出现，一般难度不大，需特别注意.9.如图，△为锐角三角形，△内接于圆，，是△的垂心，是的直径．求证：．【答案】见解析【解析】易得△BCD为含30°的直角三角形，则CD=BD，利用H是垂心及直径所对的圆周角是直角可得四边形AHCD是平行四边形，则AH=CD，可得所证．连接AD，CD，CH∵BD是⊙O直径，∴∠BAD=∠BCD=90°，又∠BAC=60°，∴∠CAD=30°，∠DBC=∠CAD=30°，在Rt△BCD中，CD=BD，H是△ABC的垂心，AH⊥BC，CH⊥AB，又DC⊥BC，DA⊥AB，∴四边形AHCD为平行四边形，∵AH=CD，∴．【考点】与圆有关的证明点评：辅助线问题是初中数学的难点，能否根据题意准确作出适当的辅助线很能反映一个学生的对图形的理解能力，因而是中考的热点，尤其在压轴题中比较常见，需特别注意.10.如图，已知是外任意一点，过点作直线，，分别交于点，，，．求证：（的度数的度数）．【答案】见解析【解析】先由三角形外角的性质得∠BCD=∠P+∠ABC，再由圆周角定理即可得出结论．∵的度数等于弧BD的度数，的度数等于弧AC的度数（弧BD的度数-弧AC的度数）．【考点】三角形外角的性质，圆周角定理点评：辅助线问题是初中数学的难点，能否根据题意准确作出适当的辅助线很能反映一个学生的对图形的理解能力，因而是中考的热点，尤其在压轴题中比较常见，需特别注意.。

垂径定理圆心角圆周角定理一选择题：1、如图，⊙O是△ABC的外接圆，∠OBC=42°，则∠A的度数是（）A．42°B．48°C．52°D．58°2.如图，A、B、C、D四个点均在⊙O上，∠AOD=50°，AO∥DC，则∠B的度数为( )A．50° B．55° C．60° D．65°3.如图，点B、D、C是⊙O上的点，∠BDC=130°，则∠BOC是（）A．100° B．110° C．120°D．130°4.如图，⊙O的半径为5，弦AB的长为8，点M在线段AB（包括端点A，B）上移动，则OM取值范围是（）A.3≤OM≤5B.3≤OM＜5C.4≤OM≤5 D.4≤OM＜55、如图所示，AB是⊙O的直径，AD=DE，AE与BD交于点C，则图中与∠BCE相等的角有（）A．2个 B．3个 C．4个 D．5个6.将量角器按如图所示的方式放置在三角形纸板上，使点C在半圆上．点A、B 的读数分别为86°、30°，则∠ACB的大小为( )A．15°B．28° C.29°D．34°7.如图，C为⊙O直径AB上一动点,过点C的直线交⊙O于D、E两点,且∠ACD=45°,DF⊥AB于点F,EG⊥AB于点G,当点C在AB上运动时,设AF=x,DE=y,下列中图象中,能表示y与x的函数关系式的图象大致是( )8.如图.⊙O 中，AB、AC是弦，O在∠ABO的内部，，，，则下列关系中，正确的是（）A. B. C． D.9.如图，四边形ABCD内接于⊙O，BC是直径，AD=DC，∠ADB=20º，则∠ACB，∠DBC分别为（）A．15º与30º B．20º与35º C．20º与40º D．30º与35º10.图中∠BOD的度数是（）A．55° B．110° C．125° D．150°11.如图，点I为△ABC的内心，点O为△ABC的外心，∠O=140°，则∠I为（）（A）140°（B）125°（C）130°（D）110°12.如图,弦AB∥CD，E为上一点，AE平分，则图中与相等（不包括）的角共有（）A．3个 B．4个 C．5个 D．6个13、如图，已知的半径为1，锐角内接于，于点，于点，则的值等于（）A．的长 B．的长 C．的长 D．的长14.如图，在直角∠O的内部有一滑动杆AB，当端点A沿直线AO向下滑动时，端点B会随之自动地沿直线OB向左滑动，如果滑动杆从图中AB处滑动到A′B′处，那么滑动杆的中点C所经过的路径是（）A.直线的一部分B.圆的一部分C.双曲线的一部分 D.抛物线的一部分15.如图，AB是⊙O的直径，弦BC=2cm，∠ABC=60°.若动点P以2cm/s的速度从B点出发沿着B→A的方向运动，点Q从A点出发沿着A→C的方向运动，当点P到达点A时，点Q也随之停止运动．设运动时间为t(s)，当△APQ是直角三角形时，t的值为（）A. B. C.或 D.或或16.如图，，在以为直径的半圆上，，在上，为正方形，若正方形边长为1，，，则下列式子中，不正确的是（）A. B. C. D.17.如图，AB是⊙O的直径，AB=8，点M在⊙O上，∠MAB=20°，N是弧MB的中点，P是直径AB上的一动点．若MN=1，则△PMN周长的最小值为（）A．4 B．5 C．6 D．718.如图，在△ABC中，AD是高，AE是直径，AE交BC于G，有下列四个结论：•①AD2=BD·CD；②BE2=EG·AE；③AE·AD=AB·AC；④AG·EG=BG·CG．其中正确结论的有（）A．1个 B．2个 C．3个 D．4个19.如图，C是以AB为直径的半圆O上一点，连结AC，BC，分别以AC，BC为边向外作正方形ACDE，BCFG，DE，FG，，的中点分别是M，N，P，Q。

知识点三：弧、弦、圆心角与圆周角1、圆心角定义：顶点在的角叫做圆心角2. 在同圆或等圆中，弧、弦、圆心角之间的关系：两个圆心角相等圆心角所对的弧(都是优弧或都是劣弧)相等圆心角所对的弦相等3、一个角是圆周角必须满足两个条件：（1）角的顶点在________;(2)角的两边都是与圆有除顶点外的交点。

4. 同一条弧所对的圆周角有__________个5.圆周角定理：1=2圆周角圆心角6.圆周角定理推论：（1）同弧或等弧所对的圆周角相等（2）半圆或直径所对的圆周角相等（3）90°的圆周角所对的弦是直径。

注意：“同弧或等弧”改为“同弦或等弦”结论就不一定成立了，因为一条弦所对的圆周角有两类，它们是相等或互补关系。

7. 圆内接四边形：定义：如果一个多边形的所有顶点都在圆上，这个多边形叫做，这个圆叫做。

性质：圆内接四边形的对角夯实基础1．如果两个圆心角相等，那么（ ）A ．这两个圆心角所对的弦相等;B ．这两个圆心角所对的弧相等C ．这两个圆心角所对的弦的弦心距相等;D ．以上说法都不对2.下列语句中不正确的有（ ）①相等的圆心角所对的弧相等 ②平分弦的直径垂直于弦 ③圆是轴对称图形，任何一条直径所在直线都是它的对称轴 ④长度相等的两条弧是等弧A.3个B.2个C.1个D.以上都不对3. 在同圆或等圆中，下列说法错误的是（ ）A ．相等弦所对的弧相等B ．相等弦所对的圆心角相等C ．相等圆心角所对的弧相等D ．相等圆心角所对的弦相等4、如图，在⊙O 中，AB AC ，∠B =70°，则∠A 等于 ．5、如图，在⊙O 中，若C 是BD 的中点，则图中与∠BAC 相等的角有（ ）A.1个B.2 个C.3个D.4个6、如图，若AB 是⊙O 的直径，AB=10cm ，∠CAB=30°，则BC= cm ．7、如图，已知OA ，OB 均为⊙O 上一点，若∠AOB=80°，则∠ACB=（ ）A ．80°B ．70°C ．60°D ．40°8、圆内接四边形ABCD ，∠A ，∠B ，∠C 的度数之比为3：4：6，则∠D 的度数为（ ）A ．60B ．80C ．100D ．1209、已知如图，四边形ABCD 内接于⊙O ，若∠A ＝60°，则∠DCE ＝ .题型一：利用圆心角圆周角定理求角度1、如图，AB 是 ⊙O 的直径，C ，D 是BE 上的三等分点，∠AOE=60°，则∠COE 是（ ）A ． 40° B. 60° C. 80° D. 120 °2、如图，AB 是 ⊙O 的直径，BC⌒ =BD ⌒ ,∠A=25°， 则∠BOD= .3、已知圆O 的半径为5,弦AB 的长为5,则弦AB 所对的圆心角∠AOB = .4、在⊙O 中，弦AB 所对的劣弧为圆周的41，圆的半径等于12，则圆心角∠AOB ＝ ；弦AB 的长为 .5、如图，AB 是⊙O 的直径，点C 在⊙O 上，若∠A=40 º，则∠B 的度数为（ ）A ．80 ºB ．60 ºC ．50 ºD ．40 º6、如图，在△ABC 中，AB 为⊙O 的直径，∠B=60°，∠BOD=100°，则∠C 的度数为（ ） OED C B A OD CBAA．50°B．60°C．70°D．80°7、如图，AB、CD是⊙O的两条弦，连接AD、BC，若∠BAD=60°，则∠BCD的度数为（）A.40°B.50°C.60°D.70°9、如图，点A、B、C、D在⊙O上，OB⊥AC，若∠BOC=56°，则∠ADB=度．10、如图，⊙O的弦CD与直径AB相交，若∠BAD＝50°，则∠ACD＝..11、如图，AB是⊙O的直径，点C是圆上一点，∠BAC=70°，则∠OCB=．12、如图，在Rt △ABC 中，∠C=90°，∠A=26°，以点C 为圆心，BC 为半径的圆分别交AB 、AC 于点D 、点E ，则弧BD 的度数为（ ）A ．26°B ．64°C ．52°D ．128°题型二：利用圆心角圆周角的性质定理求线段1、在⊙O 中，圆心角∠AOB =90°,点O 到弦AB 的距离为4,则⊙O 的直径的长为( )A.4B.82C.24D.162、如图，⊙O 是△ABC 的外接圆，∠B=60°，OP ⊥AC 于点P ，，则⊙O 的半径为（）A ．B ．C ．8D ．123、如图，△ABC 内接于⊙O ，∠BAC=120°，AB=AC ，BD 为⊙O 的直径，AD=6，则DC= ．题型三：利用弧、弦、圆心角、圆周角之间的关系证明弧相等，线段相等，角度相等1、如图，在⊙O 中 ,AB =AC ,∠ACB=60°，求证∠AOB ＝∠BOC ＝∠AOC .B2．如图，在⊙O 中，C 、D 是直径AB 上两点，且AC=BD ，MC ⊥AB ，ND ⊥AB ，M 、N •在⊙O 上．（1）求证：AM =BN ；（2）若C 、D 分别为OA 、OB 中点，则AM MN NB ==成立吗？3、如图，以⊙O 的直径BC 为一边作等边△ABC,AB 、AC 交⊙O 于D 、E,求证：BD=DE=EC4、如图，⊙O 的直径AB 为10cm ，弦AC 为6cm ，∠ACB 的平分线交⊙O 于D ，求BC ，AD ，BD 的长.5、如图，AB 是⊙O 的直径，C 是BD 的中点，CE ⊥AB 于 E ，BD 交CE 于点F ．（1）求证：CF ﹦BF ；（2）若CD ﹦6， AC ﹦8，则⊙O 的半径为 ，CE 的长是 ．BA作业1、如图，AB 是⊙O 的直径，==，∠COD=34°，则∠AEO 的度数是（ ）A ．51°B ．56°C ．68°D ．78°2、圆中有两条等弦AB=AE ，夹角∠A=88°，延长AE 到C ，使EC=BE ，连接BC ，如图．则∠ABC 的度数是（ ）A ．90°B ．80°C ．69°D ．65°3. 如图所示⊙O 中，已知∠BAC=∠CDA=20°，则∠ABO 的度数为 ．B4. 如图，A，P，B，C是半径为8的⊙O上的四点，且满足∠BAC=∠APC=60°，（1）求证：△ABC是等边三角形；（2）求圆心O到BC的距离OD．5、如图，⊙O是△ABC的外接圆，AB是⊙O的直径，D为⊙O上一点，OD⊥AC，垂足为E，连接BD（1）求证：BD平分∠ABC；（2）当∠ODB=30°时，求证：BC=OD．。

完整版)圆心角圆周角练习题知识点三：弧、弦、圆心角与圆周角1.定义圆心角为顶点在圆心的角。

2.在同圆或等圆中，弧、弦、圆心角之间的关系：两个圆心角相等，圆心角所对的弧相等（无论是优弧还是劣弧），圆心角所对的弦相等。

3.一个角是圆周角必须满足两个条件：（1）角的顶点在圆上；（2）角的两边都与圆有除顶点外的交点。

4.同一条弧所对的圆周角有两个。

5.圆周角定理：圆周角等于圆心角的一半。

6.圆周角定理的推论：（1）同弦或等弦所对的圆周角相等；（2）半圆或直径所对的圆周角相等；（3）90°的圆周角所对的弦是直径。

需要注意的是，“同弦或等弦”改为“同弧或等弧”结论就不一定成立了，因为一条弦所对的圆周角有两类，它们是相等或互补关系。

7.圆内接四边形定义为所有顶点都在圆上的多边形，圆心即为这个圆内接四边形的交点。

圆内接四边形的对角线相互垂直，且交点为对角线的中点。

夯实基础1.如果两个圆心角相等，则它们所对的弧相等，选项B正确。

2.不正确的语句为③，因为圆不一定是轴对称图形，只有圆上的任何一条直径所在直线才是它的对称轴。

3.错误的说法是D，相等圆心角所对的弦不一定相等。

4.根据圆心角的性质，∠A=2∠B，所以∠A=140°。

5.∠BAC与∠BCD互补，∠BCD与∠CBD相等，所以与∠BAC相等的角有2个，即∠CBD和∠ABD。

6.因为∠CAB为30°，所以∠ABC为60°，由正弦定理可得BC=5√3.7.根据圆周角定理，∠ACB=40°。

8.设∠A=3x，∠B=4x，∠C=6x，则∠D=360°-3x-4x-6x=120°。

9.∠DCE=∠A。

1、如图，AB是⊙O的直径，C，D是BE上的三等分点，∠AOE=60°，求证∠COE=80°。

证明：由三等分点的性质可知，BC=CD=DE，又∠AOE=60°，所以∠AOC=120°。

中考数学复习----《圆周角定理》知识点总结与专项练习题（含答案）知识点总结1.圆心角、弦以及弧之间的关系：①定理：在同圆和等圆中，相等的圆心角所对的弧相等，所对的弦也相等。

②推论：在同圆或等圆中，如果两个圆心角、两条弧、两条弦中有一组量相等，那么它们所对应的其余各组量都分别相等。

说明：同一条弦对应两条弧，其中一条是优弧，一条是劣弧，而在本定理和推论中的“弧”是指同为优弧或劣弧。

2.圆周角的定义：顶点在圆上，并且两边都与圆相交的角叫做圆周角。

3.圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半。

4.圆周角定理的推论：半圆（或直径）所对的圆周角是直角，90°的圆周角所对的弦是直径。

5.圆的内接四边形：①定义：四个顶点都在圆上的四边形叫做圆的内接四边形。

②性质：I：圆内接四边形的对角互补。

II：圆内接四边形的任意一个外角等于它的内对角。

练习题1、（2022•襄阳）已知⊙O的直径AB长为2，弦AC长为2，那么弦AC所对的圆周角的度数等于．【分析】首先利用勾股定理逆定理得∠AOC＝90°，再根据一条弦对着两种圆周角可得答案．【解答】解：如图，∵OA＝OC＝1，AC＝，∴OA2+OC2＝AC2，∴∠AOC＝90°，∴∠ADC＝45°，∴∠AD'C＝135°，故答案为：45°或135°．2、（2022•日照）一圆形玻璃镜面损坏了一部分，为得到同样大小的镜面，工人师傅用直角尺作如图所示的测量，测得AB＝12cm，BC＝5cm，则圆形镜面的半径为．【分析】连接AC，根据∠ABC＝90°得出AC是圆形镜面的直径，再根据勾股定理求出AC 即可．【解答】解：连接AC，∵∠ABC＝90°，且∠ABC是圆周角，∴AC是圆形镜面的直径，由勾股定理得：AC＝＝＝13（cm），所以圆形镜面的半径为cm，故答案为：cm．3、（2022•永州）如图，AB是⊙O的直径，点C、D在⊙O上，∠ADC＝30°，则∠BOC＝度．【分析】根据在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半求出∠AOC的度数，根据平角的定义即可得到∠BOC＝180°﹣∠AOC的度数．【解答】解：∵∠ADC是所对的圆周角，∴∠AOC＝2∠ADC＝2×30°＝60°，∴∠BOC＝180°﹣∠AOC＝180°﹣60°＝120°．故答案为：120．4、（2022•苏州）如图，AB是⊙O的直径，弦CD交AB于点E，连接AC，AD．若∠BAC＝28°，则∠D＝°．【分析】如图，连接BC，证明∠ACB＝90°，求出∠ABC，可得结论．【解答】解：如图，连接BC．∵AB是直径，∴∠ACB＝90°，∴∠ABC＝90°﹣∠CAB＝62°，∴∠D＝∠ABC＝62°，故答案为：62．5、（2022•湖州）如图，已知AB 是⊙O 的弦，∠AOB ＝120°，OC ⊥AB ，垂足为C ，OC 的延长线交⊙O 于点D ．若∠APD 是AB ⌒所对的圆周角，则∠APD 的度数是 ．【分析】由垂径定理得出，由圆心角、弧、弦的关系定理得出∠AOD ＝∠BOD ，进而得出∠AOD ＝60°，由圆周角定理得出∠APD ＝∠AOD ＝30°，得出答案．【解答】解：∵OC ⊥AB ，∴，∴∠AOD ＝∠BOD ，∵∠AOB ＝120°，∴∠AOD ＝∠BOD ＝∠AOB ＝60°，∴∠APD ＝∠AOD ＝×60°＝30°，故答案为：30°．6、（2022•徐州）如图，A 、B 、C 点在圆O 上，若∠ACB ＝36°，则∠AOB ＝ ．【分析】利用一条弧所对的圆周角等于它所对的圆心角的一半即可得出结论．【解答】解：∵∠ACB ＝∠AOB ，∠ACB ＝36°，∴∠AOB ＝2×∠ACB ＝72°．故答案为：72°．7、（2022•锦州）如图，四边形ABCD内接于⊙O，AB为⊙O的直径，∠ADC＝130°，连接AC，则∠BAC的度数为．【分析】利用圆内接四边形的性质和∠ADC的度数求得∠B的度数，利用直径所对的圆周角是直角得到∠ACB＝90°，然后利用直角三角形的两个锐角互余计算即可．【解答】解：∵四边形ABCD内接于⊙O，∠ADC＝130°，∴∠B＝180°﹣∠ADC＝180°﹣130°＝50°，∵AB为⊙O的直径，∴∠ACB＝90°，∴∠CAB＝90°﹣∠B＝90°﹣50°＝40°，故答案为：40°．8、（2022•雅安）如图，∠DCE是⊙O内接四边形ABCD的一个外角，若∠DCE＝72°，那么∠BOD的度数为．【分析】根据邻补角的概念求出∠BCD，根据圆内接四边形的性质求出∠A，根据圆周角定理解答即可．【解答】解：∵∠DCE＝72°，∴∠BCD＝180°﹣∠DCE＝108°，∵四边形ABCD内接于⊙O，∴∠A＝180°﹣∠BCD＝72°，由圆周角定理，得∠BOD＝2∠A＝144°，故答案为：144°．9、（2022•甘肃）如图，⊙O是四边形ABCD的外接圆，若∠ABC＝110°，则∠ADC＝°．【分析】根据圆内接四边形的对角互补即可得到结论．【解答】解：∵四边形ABCD内接于⊙O，∠ABC＝110°，∴∠ADC＝180°﹣∠ABC＝180°﹣110°＝70°，故答案为：70．。

北师大版九年级下册 3.4 圆周角与圆心角的关系中考试题精选（含答案）一．选择题（共20小题）1．（2019•营口）如图，BC是⊙O的直径，A，D是⊙O上的两点，连接AB，AD，BD，若∠ADB＝70°，则∠ABC的度数是（）A．20°B．70°C．30°D．90°2．（2019•陕西）如图，AB是⊙O的直径，EF，EB是⊙O的弦，且EF＝EB，EF与AB交于点C，连接OF，若∠AOF＝40°，则∠F的度数是（）A．20°B．35°C．40°D．55°3．（2019•沈阳）如图，AB是⊙O的直径，点C和点D是⊙O上位于直径AB两侧的点，连接AC，AD，BD，CD，若⊙O的半径是13，BD＝24，则sin∠ACD的值是（）A．B．C．D．4．（2019•广元）如图，AB，AC分别是⊙O的直径和弦，OD⊥AC于点D，连接BD，BC，且AB＝10，AC＝8，则BD的长为（）A．2B．4 C．2D．4.8 5．（2019•吉林）如图，在⊙O中，所对的圆周角∠ACB＝50°，若P为上一点，∠AOP＝55°，则∠POB的度数为（）A．30°B．45°C．55°D．60°6．（2019•柳州）如图，A，B，C，D是⊙O上的点，则图中与∠A相等的角是（）A．∠B B．∠C C．∠DEB D．∠D 7．（2019•镇江）如图，四边形ABCD是半圆的内接四边形，AB是直径，＝．若∠C ＝110°，则∠ABC的度数等于（）A．55°B．60°C．65°D．70°8．（2019•十堰）如图，四边形ABCD内接于⊙O，AE⊥CB交CB的延长线于点E，若BA 平分∠DBE，AD＝5，CE＝，则AE＝（）A．3 B．3C．4D．2 9．（2019•贵港）如图，AD是⊙O的直径，＝，若∠AOB＝40°，则圆周角∠BPC的度数是（）A．40°B．50°C．60°D．70°10．（2019•宜昌）如图，点A，B，C均在⊙O上，当∠OBC＝40°时，∠A的度数是（）A．50°B．55°C．60°D．65°11．（2019•眉山）如图，⊙O的直径AB垂直于弦CD，垂足是点E，∠CAO＝22.5°，OC ＝6，则CD的长为（）A．6B．3C．6 D．12 12．（2019•安顺）如图，半径为3的⊙A经过原点O和点C（0，2），B是y轴左侧⊙A优弧上一点，则tan∠OBC为（）A．B．2C．D．13．（2019•襄阳）如图，AD是⊙O的直径，BC是弦，四边形OBCD是平行四边形，AC与OB相交于点P，下列结论错误的是（）A．AP＝2OP B．CD＝2OP C．OB⊥AC D．AC平分OB 14．（2019•兰州）如图，四边形ABCD内接于⊙O，若∠A＝40°，则∠C＝（）A．110°B．120°C．135°D．140°15．（2019•天水）如图，四边形ABCD是菱形，⊙O经过点A、C、D，与BC相交于点E，连接AC、AE．若∠D＝80°，则∠EAC的度数为（）A．20°B．25°C．30°D．35°16．（2019•威海）如图，⊙P与x轴交于点A（﹣5，0），B（1，0），与y轴的正半轴交于点C．若∠ACB＝60°，则点C的纵坐标为（）A．+B．2+C．4D．2+2 17．（2019•菏泽）如图，AB是⊙O的直径，C，D是⊙O上的两点，且BC平分∠ABD，AD 分别与BC，OC相交于点E，F，则下列结论不一定成立的是（）A．OC∥BD B．AD⊥OC C．△CEF≌△BED D．AF＝FD 18．（2019•聊城）如图，BC是半圆O的直径，D，E是上两点，连接BD，CE并延长交于点A，连接OD，OE．如果∠A＝70°，那么∠DOE的度数为（）A．35°B．38°C．40°D．42°19．（2019•白银）如图，点A，B，S在圆上，若弦AB的长度等于圆半径的倍，则∠ASB 的度数是（）A．22.5°B．30°C．45°D．60°20．（2019•潍坊）如图，四边形ABCD内接于⊙O，AB为直径，AD＝CD，过点D作DE⊥AB于点E，连接AC交DE于点F．若sin∠CAB＝，DF＝5，则BC的长为（）A．8 B．10 C．12 D．16二．填空题（共20小题）21．（2019•辽阳）如图，A，B，C，D是⊙O上的四点，且点B是的中点，BD交OC于点E，∠AOC＝100°，∠OCD＝35°，那么∠OED＝．22．（2019•娄底）如图，C、D两点在以AB为直径的圆上，AB＝2，∠ACD＝30°，则AD ＝．23．（2019•常州）如图，AB是⊙O的直径，C、D是⊙O上的两点，∠AOC＝120°，则∠CDB＝°．24．（2019•东营）如图，AC是⊙O的弦，AC＝5，点B是⊙O上的一个动点，且∠ABC＝45°，若点M、N分别是AC、BC的中点，则MN的最大值是．25．（2019•宜宾）如图，⊙O的两条相交弦AC、BD，∠ACB＝∠CDB＝60°，AC＝2，则⊙O的面积是．26．（2019•连云港）如图，点A、B、C在⊙O上，BC＝6，∠BAC＝30°，则⊙O的半径为．27．（2019•台州）如图，AC是圆内接四边形ABCD的一条对角线，点D关于AC的对称点E在边BC上，连接AE．若∠ABC＝64°，则∠BAE的度数为．28．（2019•株洲）如图所示，AB为⊙O的直径，点C在⊙O上，且OC⊥AB，过点C的弦CD与线段OB相交于点E，满足∠AEC＝65°，连接AD，则∠BAD＝度．29．（2019•盐城）如图，点A、B、C、D、E在⊙O上，且为50°，则∠E+∠C＝°．30．（2019•凉山州）如图所示，AB是⊙O的直径，弦CD⊥AB于H，∠A＝30°，CD＝2，则⊙O的半径是．31．（2019•湖州）已知一条弧所对的圆周角的度数是15°，则它所对的圆心角的度数是．32．（2018•朝阳）如图，点A，B，C在⊙O上，AC∥OB，∠BAO＝20°，则∠BOC的度数为．33．（2018•辽阳）如图，AB是半圆O的直径，E是半圆上一点，且OE⊥AB，点C为的中点，则∠A＝°．34．（2018•黑龙江）如图，AC为⊙O的直径，点B在圆上，OD⊥AC交⊙O于点D，连接BD，∠BDO＝15°，则∠ACB＝．35．（2018•镇江）如图，AD为△ABC的外接圆⊙O的直径，若∠BAD＝50°，则∠ACB ＝°．36．（2018•北京）如图，点A，B，C，D在⊙O上，＝，∠CAD＝30°，∠ACD＝50°，则∠ADB＝．37．（2018•东莞市）同圆中，已知所对的圆心角是100°，则所对的圆周角是．38．（2018•杭州）如图，AB是⊙O的直径，点C是半径OA的中点，过点C作DE⊥AB，交⊙O于D，E两点，过点D作直径DF，连结AF，则∠DF A＝．39．（2018•无锡）如图，点A、B、C都在⊙O上，OC⊥OB，点A在劣弧上，且OA＝AB，则∠ABC＝．40．（2018•青海）如图，A、B、C是⊙O上的三个点，若∠AOC＝110°，则∠ABC＝．三．解答题（共10小题）41．（2019•南通）如图，在Rt△ABC中，∠ACB＝90°，∠A＝30°，BC＝1，以边AC上一点O为圆心，OA为半径的⊙O经过点B．（1）求⊙O的半径；（2）点P为劣弧AB中点，作PQ⊥AC，垂足为Q，求OQ的长；（3）在（2）的条件下，连接PC，求tan∠PCA的值．42．如图，在⊙O中，B是⊙O上的一点，∠ABC＝120°，弦AC＝2，弦BM平分∠ABC 交AC于点D，连接MA，MC．（1）求⊙O半径的长；（2）求证：AB+BC＝BM．43．（2019•南京）如图，⊙O的弦AB、CD的延长线相交于点P，且AB＝CD．求证：P A ＝PC．44．（2018•鞍山）如图，四边形ABCD内接于⊙O，AC与BD为对角线，∠BCA＝∠BAD，过点A作AE∥BC交CD的延长线于点E．（1）求证：EC＝AC．（2）若cos∠ADB＝，BC＝10，求DE的长．45．（2018•宜昌）如图，在△ABC中，AB＝AC，以AB为直径的圆交AC于点D，交BC于点E，延长AE至点F，使EF＝AE，连接FB，FC．（1）求证：四边形ABFC是菱形；（2）若AD＝7，BE＝2，求半圆和菱形ABFC的面积．46．（2018•无锡）如图，四边形ABCD内接于⊙O，AB＝17，CD＝10，∠A＝90°，cos B ＝，求AD的长．47．（2017•济南）如图，AB是⊙O的直径，∠ACD＝25°，求∠BAD的度数．48．（2016•温州）如图，在△ABC中，∠C＝90°，D是BC边上一点，以DB为直径的⊙O 经过AB的中点E，交AD的延长线于点F，连结EF．（1）求证：∠1＝∠F．（2）若sin B＝，EF＝2，求CD的长．49．（2016•宁夏）已知△ABC，以AB为直径的⊙O分别交AC于D，BC于E，连接ED，若ED＝EC．（1）求证：AB＝AC；（2）若AB＝4，BC＝2，求CD的长．50．（2016•株洲）已知AB是半径为1的圆O直径，C是圆上一点，D是BC延长线上一点，过点D的直线交AC于E点，且△AEF为等边三角形（1）求证：△DFB是等腰三角形；（2）若DA＝AF，求证：CF⊥AB．3.4 圆周角与圆心角的关系参考答案与试题解析一．选择题（共20小题）1．（2019•营口）如图，BC是⊙O的直径，A，D是⊙O上的两点，连接AB，AD，BD，若∠ADB＝70°，则∠ABC的度数是（）A．20°B．70°C．30°D．90°解：连接AC，如图，∵BC是⊙O的直径，∴∠BAC＝90°，∵∠ACB＝∠ADB＝70°，∴∠ABC＝90°﹣70°＝20°．故答案为20°．故选A．2．（2019•陕西）如图，AB是⊙O的直径，EF，EB是⊙O的弦，且EF＝EB，EF与AB交于点C，连接OF，若∠AOF＝40°，则∠F的度数是（）A．20°B．35°C．40°D．55°解：连接FB．∵∠AOF＝40°，∴∠FOB＝180°﹣40°＝140°，∴∠FEB＝∠FOB＝70°∵EF＝EB∴∠EFB＝∠EBF＝55°，∵FO＝BO，∴∠OFB＝∠OBF＝20°，∴∠EFO＝∠EBO，∠EFO＝∠EFB﹣∠OFB＝35°，故选B．3．（2019•沈阳）如图，AB是⊙O的直径，点C和点D是⊙O上位于直径AB两侧的点，连接AC，AD，BD，CD，若⊙O的半径是13，BD＝24，则sin∠ACD的值是（）A．B．C．D．解：∵AB是直径，∴∠ADB＝90°，∵⊙O的半径是13，∴AB＝2×13＝26，由勾股定理得AD＝10，∴sin∠B＝＝＝，∵∠ACD＝∠B，∴sin∠ACD＝sin∠B＝，故选D．4．（2019•广元）如图，AB，AC分别是⊙O的直径和弦，OD⊥AC于点D，连接BD，BC，且AB＝10，AC＝8，则BD的长为（）A．2B．4 C．2D．4.8解：∵AB为直径，∴∠ACB＝90°，∴BC＝＝＝6，∵OD⊥AC，∴CD＝AD＝AC＝4，在Rt△CBD中，BD＝＝2．故选C．5．（2019•吉林）如图，在⊙O中，所对的圆周角∠ACB＝50°，若P为上一点，∠AOP＝55°，则∠POB的度数为（）A．30°B．45°C．55°D．60°解：∵∠ACB＝50°，∴∠AOB＝2∠ACB＝100°，∵∠AOP＝55°，∴∠POB＝45°，故选B．6．（2019•柳州）如图，A，B，C，D是⊙O上的点，则图中与∠A相等的角是（）A．∠B B．∠C C．∠DEB D．∠D解：∵∠A与∠D都是所对的圆周角，∴∠D＝∠A．故选D．7．（2019•镇江）如图，四边形ABCD是半圆的内接四边形，AB是直径，＝．若∠C ＝110°，则∠ABC的度数等于（）A．55°B．60°C．65°D．70°解：连接AC，∵四边形ABCD是半圆的内接四边形，∴∠DAB＝180°﹣∠C＝70°，∵＝，∴∠CAB＝∠DAB＝35°，∵AB是直径，∴∠ACB＝90°，∴∠ABC＝90°﹣∠CAB＝55°，故选A．8．（2019•十堰）如图，四边形ABCD内接于⊙O，AE⊥CB交CB的延长线于点E，若BA 平分∠DBE，AD＝5，CE＝，则AE＝（）A．3 B．3C．4D．2解：连接AC，如图，∵BA平分∠DBE，∴∠1＝∠2，∵∠1＝∠CDA，∠2＝∠3，∴∠3＝∠CDA，∴AC＝AD＝5，∵AE⊥CB，∴∠AEC＝90°，∴AE＝＝＝2．故选D．9．（2019•贵港）如图，AD是⊙O的直径，＝，若∠AOB＝40°，则圆周角∠BPC的度数是（）A．40°B．50°C．60°D．70°解：∵＝，∠AOB＝40°，∴∠COD＝∠AOB＝40°，∵∠AOB+∠BOC+∠COD＝180°，∴∠BOC＝100°，∴∠BPC＝∠BOC＝50°，故选B．10．（2019•宜昌）如图，点A，B，C均在⊙O上，当∠OBC＝40°时，∠A的度数是（）A．50°B．55°C．60°D．65°解：∵OB＝OC，∴∠OCB＝∠OBC＝40°，∴∠BOC＝180°﹣40°﹣40°＝100°，∴∠A＝∠BOC＝50°．故选A．11．（2019•眉山）如图，⊙O的直径AB垂直于弦CD，垂足是点E，∠CAO＝22.5°，OC ＝6，则CD的长为（）A．6B．3C．6 D．12解：∵CD⊥AB，∴CE＝DE，∵∠BOC＝2∠A＝2×22.5°＝45°，∴△OCE为等腰直角三角形，∴CE＝OC＝×6＝3，∴CD＝2CE＝6．故选A．12．（2019•安顺）如图，半径为3的⊙A经过原点O和点C（0，2），B是y轴左侧⊙A优弧上一点，则tan∠OBC为（）A．B．2C．D．解：作直径CD，在Rt△OCD中，CD＝6，OC＝2，则OD＝＝4，tan∠CDO＝＝，由圆周角定理得，∠OBC＝∠CDO，则tan∠OBC＝，故选D．13．（2019•襄阳）如图，AD是⊙O的直径，BC是弦，四边形OBCD是平行四边形，AC与OB相交于点P，下列结论错误的是（）A．AP＝2OP B．CD＝2OP C．OB⊥AC D．AC平分OB 解：∵AD为直径，∴∠ACD＝90°，∵四边形OBCD为平行四边形，∴CD∥OB，CD＝OB，在Rt△ACD中，sin A＝＝，∴∠A＝30°，在Rt△AOP中，AP＝OP，所以A选项的结论错误；∵OP∥CD，CD⊥AC，∴OP⊥AC，所以C选项的结论正确；∴AP＝CP，∴OP为△ACD的中位线，∴CD＝2OP，所以B选项的结论正确；∴OB＝2OP，∴AC平分OB，所以D选项的结论正确．故选A．14．（2019•兰州）如图，四边形ABCD内接于⊙O，若∠A＝40°，则∠C＝（）A．110°B．120°C．135°D．140°解：∵四边形ABCD内接于⊙O，∴∠C+∠A＝180°，∴∠C＝180°﹣40°＝140°．故选D．15．（2019•天水）如图，四边形ABCD是菱形，⊙O经过点A、C、D，与BC相交于点E，连接AC、AE．若∠D＝80°，则∠EAC的度数为（）A．20°B．25°C．30°D．35°解：∵四边形ABCD是菱形，∠D＝80°，∴∠ACB＝∠DCB＝（180°﹣∠D）＝50°，∵四边形AECD是圆内接四边形，∴∠AEB＝∠D＝80°，∴∠EAC＝∠AEB﹣∠ACE＝30°，故选C．16．（2019•威海）如图，⊙P与x轴交于点A（﹣5，0），B（1，0），与y轴的正半轴交于点C．若∠ACB＝60°，则点C的纵坐标为（）A．+B．2+C．4D．2+2解：连接P A，PB，PC，过P作PD⊥AB于D，PE⊥OC于E，∵∠ACB＝60°，∴∠APB＝120°，∵P A＝PB，∴∠P AB＝∠PBA＝30°，∵A（﹣5，0），B（1，0），∴AB＝6，∴AD＝BD＝3，∴PD＝，P A＝PB＝PC＝2，∵PD⊥AB，PE⊥OC，∠AOC＝90°，∴四边形PEOD是矩形，∴OE＝PD＝，PE＝OD＝2，∴CE＝＝＝2，∴OC＝CE+OE＝2+，∴点C的纵坐标为2+，故选B．17．（2019•菏泽）如图，AB是⊙O的直径，C，D是⊙O上的两点，且BC平分∠ABD，AD 分别与BC，OC相交于点E，F，则下列结论不一定成立的是（）A．OC∥BD B．AD⊥OC C．△CEF≌△BED D．AF＝FD解：∵AB是⊙O的直径，BC平分∠ABD，∴∠ADB＝90°，∠OBC＝∠DBC，∴AD⊥BD，∵OB＝OC，∴∠OCB＝∠OBC，∴∠DBC＝∠OCB，∴OC∥BD，选项A成立；∴AD⊥OC，选项B成立；∴AF＝FD，选项D成立；∵△CEF和△BED中，没有相等的边，∴△CEF与△BED不全等，选项C不成立；故选C．18．（2019•聊城）如图，BC是半圆O的直径，D，E是上两点，连接BD，CE并延长交于点A，连接OD，OE．如果∠A＝70°，那么∠DOE的度数为（）A．35°B．38°C．40°D．42°解：连接CD，如图所示：∵BC是半圆O的直径，∴∠BDC＝90°，∴∠ADC＝90°，∴∠ACD＝90°﹣∠A＝20°，∴∠DOE＝2∠ACD＝40°，故选C．19．（2019•白银）如图，点A，B，S在圆上，若弦AB的长度等于圆半径的倍，则∠ASB 的度数是（）A．22.5°B．30°C．45°D．60°解：设圆心为O，连接OA、OB，如图，∵弦AB的长度等于圆半径的倍，即AB＝OA，∴OA2+OB2＝AB2，∴△OAB为等腰直角三角形，∠AOB＝90°，∴∠ASB＝∠AOB＝45°．故选C．20．（2019•潍坊）如图，四边形ABCD内接于⊙O，AB为直径，AD＝CD，过点D作DE⊥AB于点E，连接AC交DE于点F．若sin∠CAB＝，DF＝5，则BC的长为（）A．8 B．10 C．12 D．16解：连接BD，如图，∵AB为直径，∴∠ADB＝∠ACB＝90°，∵AD＝CD，∴∠DAC＝∠DCA，而∠DCA＝∠ABD，∴∠DAC＝∠ABD，∵DE⊥AB，∴∠ABD+∠BDE＝90°，而∠ADE+∠BDE＝90°，∴∠ABD＝∠ADE，∴∠ADE＝∠DAC，∴FD＝F A＝5，在Rt△AEF中，∵sin∠CAB＝＝，∴EF＝3，∴AE＝＝4，DE＝5+3＝8，∵∠ADE＝∠DBE，∠AED＝∠BED，∴△ADE∽△DBE，∴DE：BE＝AE：DE，即8：BE＝4：8，∴BE＝16，∴AB＝4+16＝20，在Rt△ABC中，∵sin∠CAB＝＝，∴BC＝20×＝12．故选C．二．填空题（共20小题）21．（2019•辽阳）如图，A，B，C，D是⊙O上的四点，且点B是的中点，BD交OC于点E，∠AOC＝100°，∠OCD＝35°，那么∠OED＝60°．解：连接OB．∵＝，∴∠AOB＝∠BOC＝50°，∴∠BDC＝∠BOC＝25°，∵∠OED＝∠ECD+∠CDB，∠ECD＝35°，∴∠OED＝60°，故答案为60°．22．（2019•娄底）如图，C、D两点在以AB为直径的圆上，AB＝2，∠ACD＝30°，则AD ＝1．解：∵AB为直径，∴∠ADB＝90°，∵∠B＝∠ACD＝30°，∴AD＝AB＝×2＝1．故答案为1．23．（2019•常州）如图，AB是⊙O的直径，C、D是⊙O上的两点，∠AOC＝120°，则∠CDB＝30°．解：∵∠BOC＝180°﹣∠AOC＝180°﹣120°＝60°，∴∠CDB＝∠BOC＝30°．故答案为30．24．（2019•东营）如图，AC是⊙O的弦，AC＝5，点B是⊙O上的一个动点，且∠ABC＝45°，若点M、N分别是AC、BC的中点，则MN的最大值是．解：∵点M，N分别是BC，AC的中点，∴MN＝AB，∴当AB取得最大值时，MN就取得最大值，当AB是直径时，AB最大，连接AO并延长交⊙O于点B′，连接CB′，∵AB′是⊙O的直径，∴∠ACB′＝90°．∵∠ABC＝45°，AC＝5，∴∠AB′C＝45°，∴AB′＝＝＝5，∴MN最大＝．故答案为．25．（2019•宜宾）如图，⊙O的两条相交弦AC、BD，∠ACB＝∠CDB＝60°，AC＝2，则⊙O的面积是4π．解：∵∠A＝∠BDC，而∠ACB＝∠CDB＝60°，∴∠A＝∠ACB＝60°，∴△ACB为等边三角形，∵AC＝2，∴圆的半径为2，∴⊙O的面积是4π，故答案为4π．26．（2019•连云港）如图，点A、B、C在⊙O上，BC＝6，∠BAC＝30°，则⊙O的半径为6．解：∵∠BOC＝2∠BAC＝60°，又OB＝OC，∴△BOC是等边三角形∴OB＝BC＝6，故答案为6．27．（2019•台州）如图，AC是圆内接四边形ABCD的一条对角线，点D关于AC的对称点E在边BC上，连接AE．若∠ABC＝64°，则∠BAE的度数为52°．解：∵圆内接四边形ABCD，∴∠D＝180°﹣∠ABC＝116°，∵点D关于AC的对称点E在边BC上，∴∠D＝∠AEC＝116°，∴∠BAE＝116°﹣64°＝52°．故答案为52°．28．（2019•株洲）如图所示，AB为⊙O的直径，点C在⊙O上，且OC⊥AB，过点C的弦CD与线段OB相交于点E，满足∠AEC＝65°，连接AD，则∠BAD＝20度．解：连接OD，如图：∵OC⊥AB，∴∠COE＝90°，∵∠AEC＝65°，∴∠OCE＝90°﹣65°＝25°，∵OC＝OD，∴∠ODC＝∠OCE＝25°，∴∠DOC＝180°﹣25°﹣25°＝130°，∴∠BOD＝∠DOC﹣∠COE＝40°，∴∠BAD＝∠BOD＝20°，故答案为20．29．（2019•盐城）如图，点A、B、C、D、E在⊙O上，且为50°，则∠E+∠C＝155°．解：连接EA，∵为50°，∴∠BEA＝25°，∵四边形DCAE为⊙O的内接四边形，∴∠DEA+∠C＝180°，∴∠DEB+∠C＝180°﹣25°＝155°，故答案为155．30．（2019•凉山州）如图所示，AB是⊙O的直径，弦CD⊥AB于H，∠A＝30°，CD＝2，则⊙O的半径是2．解：连接BC，如图所示：∵AB是⊙O的直径，弦CD⊥AB于H，∴∠ACB＝90°，CH＝DH＝CD＝，∵∠A＝30°，∴AC＝2CH＝2，在Rt△ABC中，∠A＝30°，∴AC＝BC＝2，AB＝2BC，∴BC＝2，AB＝4，∴OA＝2，即⊙O的半径是2；故答案为2．31．（2019•湖州）已知一条弧所对的圆周角的度数是15°，则它所对的圆心角的度数是30°．解：∵一条弧所对的圆周角的度数是15°，∴它所对的圆心角的度数为2×15°＝30°．故答案为30°．32．（2018•朝阳）如图，点A，B，C在⊙O上，AC∥OB，∠BAO＝20°，则∠BOC的度数为40°．解：∵OA＝OB，∴∠BAO＝∠B＝20°，∵AC∥OB，∴∠CAB＝∠B＝20°，∴∠OAC＝40°，∵OA＝OC，∴∠C＝∠OAC＝40°，∴∠BOC＝∠C＝40°，故答案为40°．33．（2018•辽阳）如图，AB是半圆O的直径，E是半圆上一点，且OE⊥AB，点C为的中点，则∠A＝22.5°．解：连接OC，∵OE⊥AB，∴∠EOB＝90°，∵点C为的中点，∴∠BOC＝45°，∵OA＝OC，∴∠A＝∠ACO＝×45°＝22.5°，故答案为22.5°．34．（2018•黑龙江）如图，AC为⊙O的直径，点B在圆上，OD⊥AC交⊙O于点D，连接BD，∠BDO＝15°，则∠ACB＝60°．解：连接DC，∵AC为⊙O的直径，OD⊥AC，∴∠DOC＝90°，∠ABC＝90°，∵OD＝OC，∴∠ODC＝45°，∵∠BDO＝15°，∴∠BDC＝30°，∴∠A＝30°，∴∠ACB＝60°，故答案为60°．35．（2018•镇江）如图，AD为△ABC的外接圆⊙O的直径，若∠BAD＝50°，则∠ACB＝40°．解：连接BD，如图，∵AD为△ABC的外接圆⊙O的直径，∴∠ABD＝90°，∴∠D＝90°﹣∠BAD＝90°﹣50°＝40°，∴∠ACB＝∠D＝40°．故答案为40．36．（2018•北京）如图，点A，B，C，D在⊙O上，＝，∠CAD＝30°，∠ACD＝50°，则∠ADB＝70°．解：∵＝，∠CAD＝30°，∴∠CAD＝∠CAB＝30°，∴∠DBC＝∠DAC＝30°，∵∠ACD＝50°，∴∠ABD＝50°，∴∠ACB＝∠ADB＝180°﹣∠CAB﹣∠ABC＝180°﹣50°﹣30°﹣30°＝70°．故答案为70°．37．（2018•东莞市）同圆中，已知所对的圆心角是100°，则所对的圆周角是50°．解：弧AB所对的圆心角是100°，则弧AB所对的圆周角为50°．故答案为50°．38．（2018•杭州）如图，AB是⊙O的直径，点C是半径OA的中点，过点C作DE⊥AB，交⊙O于D，E两点，过点D作直径DF，连结AF，则∠DF A＝30°．解：∵点C是半径OA的中点，∴OC＝OD，∵DE⊥AB，∴∠CDO＝30°，∴∠DOA＝60°，∴∠DF A＝30°，故答案为30°39．（2018•无锡）如图，点A、B、C都在⊙O上，OC⊥OB，点A在劣弧上，且OA＝AB，则∠ABC＝15°．解：∵OA＝OB，OA＝AB，∴OA＝OB＝AB，即△OAB是等边三角形，∴∠AOB＝60°，∵OC⊥OB，∴∠COB＝90°，∴∠COA＝90°﹣60°＝30°，∴∠ABC＝15°，故答案为15°40．（2018•青海）如图，A、B、C是⊙O上的三个点，若∠AOC＝110°，则∠ABC＝125°．解：如图，在优弧AC上取点D，连接AD，CD，∵∠AOC＝100°，∴∠ADC＝∠AOC＝55°，∴∠ABC＝180°﹣∠ADC＝125°．故答案为125°．三．解答题（共10小题）41．（2019•南通）如图，在Rt△ABC中，∠ACB＝90°，∠A＝30°，BC＝1，以边AC上一点O为圆心，OA为半径的⊙O经过点B．（1）求⊙O的半径；（2）点P为劣弧AB中点，作PQ⊥AC，垂足为Q，求OQ的长；（3）在（2）的条件下，连接PC，求tan∠PCA的值．解：（1）作OH⊥AB于H．在Rt△ACB中，∵∠C＝90°，∠A＝30°，BC＝1，∴AB＝2BC＝2，∵OH⊥AB，∴AH＝HB＝1，∴OA＝AH÷cos30°＝．（2）如图2中，连接OP，P A．设OP交AB于H．∵＝，∴OP⊥AB，∴∠AHO＝90°，∵∠OAH＝30°，∴∠AOP＝60°，∵OA＝OP，∴△AOP是等边三角形，∵PQ⊥OA，∴OQ＝QA＝OA＝．（3）连接PC．在Rt△ABC中，AC＝BC＝，∵AQ＝QO＝AO＝．∴QC＝AC﹣AQ＝﹣＝，∵△AOP是等边三角形，PQ⊥OA，∴PQ＝1，∴tan∠ACP＝＝＝．42．如图，在⊙O中，B是⊙O上的一点，∠ABC＝120°，弦AC＝2，弦BM平分∠ABC 交AC于点D，连接MA，MC．（1）求⊙O半径的长；（2）求证：AB+BC＝BM．解：（1）连接OA、OC，过O作OH⊥AC于点H，如图1，∵∠ABC＝120°，∴∠AMC＝180°﹣∠ABC＝60°，∴∠AOC＝2∠AMC＝120°，∴∠AOH＝∠AOC＝60°，∵AH＝AC＝，∴OA＝，故⊙O的半径为2．（2）证明：在BM上截取BE＝BC，连接CE，如图2，∵∠MBC＝60°，BE＝BC，∴△EBC是等边三角形，∴CE＝CB＝BE，∠BCE＝60°，∴∠BCD+∠DCE＝60°，∵∠ACM＝60°，∴∠ECM+∠DCE＝60°，∴∠ECM＝∠BCD，∵∠ABC＝120°，BM平分∠ABC，∴∠ABM＝∠CBM＝60°，∴∠CAM＝∠CBM＝60°，∠ACM＝∠ABM＝60°，∴△ACM是等边三角形，∴AC＝CM，∴△ACB≌△MCE，∴AB＝ME，∵ME+EB＝BM，∴AB+BC＝BM．43．（2019•南京）如图，⊙O的弦AB、CD的延长线相交于点P，且AB＝CD．求证：P A ＝PC．证明：连接AC，∵AB＝CD，∴＝，∴+＝+，即＝，∴∠C＝∠A，∴P A＝PC．44．（2018•鞍山）如图，四边形ABCD内接于⊙O，AC与BD为对角线，∠BCA＝∠BAD，过点A作AE∥BC交CD的延长线于点E．（1）求证：EC＝AC．（2）若cos∠ADB＝，BC＝10，求DE的长．（1）证明：∵BC∥AE，∴∠ACB＝∠EAC，∵∠ACB＝∠BAD，∴∠EAC＝∠BAD，∴∠EAD＝∠CAB，∵∠ADE+∠ADC＝180°，∠ADC+∠ABC＝180°，∴∠ADE＝∠ABC，∵∠EAD+∠ADE+∠E＝180°，∠BAC+∠ABC+∠ACB＝180°，∴∠E＝∠ACB＝∠EAC，∴CE＝CA．（2）解：设AE交⊙O于M，连接DM，作MH⊥DE于H．∵∠EAD＝∠CAB，∴＝，∴DM＝BC＝10，∵∠MDE+∠MDC＝180°，∠MDC+∠MAC＝180°，∴∠MDE＝∠CAM，∵∠E＝∠CAE，∴∠E＝∠MDE，∴MD＝ME＝10，∵MH⊥DE，∴EH＝DH，∵∠ADB＝∠ACB＝∠BAD＝∠E，∴cos∠E＝＝，∴EH＝4，∴DE＝2EH＝8．45．（2018•宜昌）如图，在△ABC中，AB＝AC，以AB为直径的圆交AC于点D，交BC于点E，延长AE至点F，使EF＝AE，连接FB，FC．（1）求证：四边形ABFC是菱形；（2）若AD＝7，BE＝2，求半圆和菱形ABFC的面积．（1）证明：∵AB是直径，∴∠AEB＝90°，∴AE⊥BC，∵AB＝AC，∴BE＝CE，∵AE＝EF，∴四边形ABFC是平行四边形，∵AC＝AB，∴四边形ABFC是菱形．（2）设CD＝x．连接BD．∵AB是直径，∴∠ADB＝∠BDC＝90°，∴AB2﹣AD2＝CB2﹣CD2，∴（7+x）2﹣72＝42﹣x2，解得x＝1或﹣8（舍弃）∴AC＝8，BD＝＝，∴S菱形ABFC＝8．∴S半圆＝•π•42＝8π．46．（2018•无锡）如图，四边形ABCD内接于⊙O，AB＝17，CD＝10，∠A＝90°，cos B ＝，求AD的长．解：∵四边形ABCD内接于⊙O，∠A＝90°，∴∠C＝180°﹣∠A＝90°，∠ABC+∠ADC＝180°．作AE⊥BC于E，DF⊥AE于F，则CDFE是矩形，EF＝CD＝10．在Rt△AEB中，∵∠AEB＝90°，AB＝17，cos∠ABC＝，∴BE＝AB•cos∠ABE＝，∴AE＝＝，∴AF＝AE﹣EF＝﹣10＝．∵∠ABC+∠ADC＝180°，∠CDF＝90°，∴∠ABC+∠ADF＝90°，∵cos∠ABC＝，∴sin∠ADF＝cos∠ABC＝．在Rt△ADF中，∵∠AFD＝90°，sin∠ADF＝，∴AD＝＝＝6．47．（2017•济南）如图，AB是⊙O的直径，∠ACD＝25°，求∠BAD的度数．解：∵AB为⊙O直径∴∠ADB＝90°∵相同的弧所对应的圆周角相等，且∠ACD＝25°∴∠B＝25°∴∠BAD＝90°﹣∠B＝65°．48．（2016•温州）如图，在△ABC中，∠C＝90°，D是BC边上一点，以DB为直径的⊙O 经过AB的中点E，交AD的延长线于点F，连结EF．（1）求证：∠1＝∠F．（2）若sin B＝，EF＝2，求CD的长．解：（1）证明：连接DE，∵BD是⊙O的直径，∴∠DEB＝90°，∵E是AB的中点，∴DA＝DB，∵∠B＝∠F，∴∠1＝∠F；（2）∵∠1＝∠F，∴AE＝EF＝2，∴AB＝2AE＝4，在Rt△ABC中，AC＝AB•sin B＝4，∴BC＝＝8，设CD＝x，则AD＝BD＝8﹣x，∵AC2+CD2＝AD2，即42+x2＝（8﹣x）2，∴x＝3，即CD＝3．49．（2016•宁夏）已知△ABC，以AB为直径的⊙O分别交AC于D，BC于E，连接ED，若ED＝EC．（1）求证：AB＝AC；（2）若AB＝4，BC＝2，求CD的长．（1）证明：∵ED＝EC，∴∠EDC＝∠C，∵∠EDC＝∠B，（∵∠EDC+∠ADE＝180°，∠B+∠ADE＝180°，∴∠EDC＝∠B）∴∠B＝∠C，（2）方法一：解：连接AE，∵AB为直径，∴AE⊥BC，由（1）知AB＝AC，∴BE＝CE＝BC＝，∵△CDE∽△CBA，∴，∴CE•CB＝CD•CA，AC＝AB＝4，∴•2＝4CD，∴CD＝．方法二：解：连接BD，∵AB为直径，∴BD⊥AC，设CD＝a，由（1）知AC＝AB＝4，则AD＝4﹣a，在Rt△ABD中，由勾股定理可得BD2＝AB2﹣AD2＝42﹣（4﹣a）2在Rt△CBD中，由勾股定理可得BD2＝BC2﹣CD2＝（2）2﹣a2∴42﹣（4﹣a）2＝（2）2﹣a2整理得a＝，即：CD＝．50．（2016•株洲）已知AB是半径为1的圆O直径，C是圆上一点，D是BC延长线上一点，过点D的直线交AC于E点，且△AEF为等边三角形（1）求证：△DFB是等腰三角形；（2）若DA＝AF，求证：CF⊥AB．解：（1）∵AB是⊙O直径，∴∠ACB＝90°，∵△AEF为等边三角形，∴∠CAB＝∠EF A＝60°∴∠B＝30°，∵∠EF A＝∠B+∠FDB，∴∠B＝∠FDB＝30°，∴△DFB是等腰三角形；（2）过点A作AM⊥DF于点M，设AF＝2a，∵△AEF是等边三角形，∴FM＝EM＝a，AM＝a，在Rt△DAM中，AD＝AF＝2a，AM＝，∴DM＝5a，∴DF＝BF＝6a，∴AB＝AF+BF＝8a，在Rt△ABC中，∠B＝30°，∠ACB＝90°，∴AC＝4a，∵AE＝EF＝AF＝2a，∴CE＝AC﹣AE＝2a，∴∠ECF＝∠EFC，∵∠AEF＝∠ECF+∠EFC＝60°，∴∠CFE＝30°，∴∠AFC＝∠AFE+∠EFC＝60°+30°＝90°，∴CF⊥AB．。

2021年中考真题圆周角（1－41题）圆内接四边形（42－48题）一．试题（共48小题）1．（2021•巴中）如图，AB 是⊙O 的弦，且AB ＝6，点C 是弧AB 中点，点D 是优弧AB 上的一点，∠ADC ＝30°，则圆心O 到弦AB 的距离等于（ ）A ．3√3B ．32C ．√3D ．√322．（2021•鞍山）如图，AB 为⊙O 的直径，C ，D 为⊙O 上的两点，若∠ABD ＝54°，则∠C 的度数为（ ）A ．34°B ．36°C ．46°D ．54°3．（2021•抚顺）如图，在⊙O 中，弦CD 与直径AB 相交于点E ，连接OC ，BD ．若∠ABD＝20°，∠AED ＝80°，则∠COB 的度数为（ ）A ．80°B ．100°C ．120°D ．140°4．（2021•阜新）如图，A ，B ，C 是⊙O 上的三点，若∠O ＝70°，则∠C 的度数是（ ）A ．40°B ．35°C ．30°D ．25° 5．（2021•牡丹江）如图，点A ，B ，C 为⊙O 上的三点，∠AOB =13∠BOC ，∠BAC ＝30°，则∠AOC 的度数为（ ）A ．100°B ．90°C ．80°D ．60°6．（2021•遵义）如图，点C 是以点O 为圆心，AB 为直径的半圆上一点，连接AC ，BC ，OC ．若AC ＝4，BC ＝3，则sin ∠BOC 的值是（ ）A ．1B ．2425C ．1625D ．9257．（2021•桂林）如图，AB 是⊙O 的直径，点C 是⊙O 上一点，连接AC ，BC ，则∠C 的度数是（ ）A ．60°B ．90°C ．120°D ．150°8．（2021•营口）如图，⊙O 中，点C 为弦AB 中点，连接OC ，OB ，∠COB ＝56°，点D是AB̂上任意一点，则∠ADB 度数为（ ）A．112°B．124°C．122°D．134°̂上9．（2021•赤峰）如图，点C，D在以AB为直径的半圆上，且∠ADC＝120°，点E是AD任意一点，连接BE、CE．则∠BEC的度数为（）A．20°B．30°C．40°D．60°10．（2021•常州）如图，BC是⊙O的直径，AB是⊙O的弦，若∠AOC＝60°，则∠OAB的度数是（）A．20°B．25°C．30°D．35°̂的中点，点11．（2021•贵港）如图，点A，B，C，D均在⊙O上，直径AB＝4，点C是BDD关于AB对称的点为E，若∠DCE＝100°，则弦CE的长是（）A．2√3B．2C．√3D．112．（2021•黄石）如图，A、B是⊙O上的两点，∠AOB＝60°，OF⊥AB交⊙O于点F，则∠BAF等于（）A．20°B．22.5°C．15°D．12.5°13．（2021•荆州）如图，矩形OABC的边OA，OC分别在x轴、y轴的正半轴上，点D在OA的延长线上，若A（2，0），D（4，0），以O为圆心、OD长为半径的弧经过点B，交y轴正半轴于点E，连接DE，BE，则∠BED的度数是（）A．15°B．22.5°C．30°D．45°14．（2021•宜昌）如图，C，D是⊙O上直径AB两侧的两点，设∠ABC＝25°，则∠BDC ＝（）A．85°B．75°C．70°D．65°15．（2021•聊城）如图，A，B，C是半径为1的⊙O上的三个点，若AB=√2，∠CAB＝30°，则∠ABC的度数为（）A．95°B．100°C．105°D．110°16．（2021•长沙）如图，点A，B，C在⊙O上，∠BAC＝54°，则∠BOC的度数为（）A．27°B．108°C．116°D．128°̂沿BC翻折交AB于点17．（2021•武汉）如图，AB是⊙O的直径，BC是⊙O的弦，先将BĈ沿AB翻折交BC于点E．若BÊ=DÊ，设∠ABC＝α，则α所在的范围是（）D，再将BDA．21.9°＜α＜22.3°B．22.3°＜α＜22.7°C．22.7°＜α＜23.1°D．23.1°＜α＜23.5°18．（2021•邵阳）如图，点A，B，C是⊙O上的三点．若∠AOC＝90°，∠BAC＝30°，则∠AOB的大小为（）A．25°B．30°C．35°D．40°19．（2021•嘉峪关）如图，点A，B，C，D，E在⊙O上，AB＝CD，∠AOB＝42°，则∠CED＝（）A．48°B．24°C．22°D．21°20．（2021•南充）如图，AB是⊙O的直径，弦CD⊥AB于点E，CD＝2OE，则∠BCD的度数为（）A．15°B．22.5°C．30°D．45°̂=3AĈ，弦CD 21．（2021•眉山）如图，在以AB为直径的⊙O中，点C为圆上的一点，BC⊥AB于点E，弦AF交CE于点H，交BC于点G．若点H是AG的中点，则∠CBF的度数为（）A．18°B．21°C．22.5°D．30°22．（2021•重庆）如图，AB是⊙O的直径，AC，BC是⊙O的弦，若∠A＝20°，则∠B的度数为（）A ．70°B ．90°C ．40°D ．60°23．（2021•朝阳）已知⊙O 的半径是7，AB 是⊙O 的弦，且AB 的长为7√3，则弦AB 所对的圆周角的度数为 ．24．（2021•盘锦）如图，在平面直角坐标系xOy 中，点A 在x 轴负半轴上，点B 在y 轴正半轴上，⊙D 经过A ，B ，O ，C 四点，∠ACO ＝120°，AB ＝4，则圆心点D 的坐标是 ．25．（2021•德阳）在锐角三角形ABC 中，∠A ＝30°，BC ＝2，设BC 边上的高为h ，则h的取值范围是 ．26．（2021•淮安）如图，AB 是⊙O 的直径，CD 是⊙O 的弦，∠CAB ＝55°，则∠D 的度数是 ．27．（2021•南通）如图，在△ABC 中，AC ＝BC ，∠ACB ＝90°，以点A 为圆心，AB 长为半径画弧，交AC 延长线于点D ，过点C 作CE ∥AB ，交BD̂于点E ，连接BE ，则CE BE 的值为 ．28．（2021•徐州）如图，AB是⊙O的直径，点C、D在⊙O上，若∠ADC＝58°，则∠BAC ＝°．29．（2021•本溪）如图，由边长为1的小正方形组成的网格中，点A，B，C都在格点上，以AB为直径的圆经过点C和点D，则tan∠ADC＝．30．（2021•黑龙江）如图，在⊙O中，AB是直径，弦AC的长为5cm，点D在圆上且∠ADC ＝30°，则⊙O的半径为cm．31．（2021•黑龙江）如图，在Rt△AOB中，∠AOB＝90°，OA＝4，OB＝6，以点O为圆心，3为半径的⊙O，与OB交于点C，过点C作CD⊥OB交AB于点D，点P是边OA 上的动点，则PC+PD的最小值为．32．（2021•广元）如图，在4×4的正方形网格图中，已知点A、B、C、D、O均在格点上，其中A、B、D又在⊙O上，点E是线段CD与⊙O的交点．则∠BAE的正切值为．33．（2021•宿迁）如图，在Rt△ABC中，∠ABC＝90°，∠A＝32°，点B、C在⊙O上，̂的中点，则∠ABE＝．边AB、AC分别交⊙O于D、E两点，点B是CD34．（2021•长沙）如图，在⊙O中，弦AB的长为4，圆心到弦AB的距离为2，则∠AOC的度数为．35．（2021•天津）如图，在每个小正方形的边长为1的网格中，△ABC的顶点A，C均落在格点上，点B在网格线上．（Ⅰ）线段AC的长等于；（Ⅱ）以AB为直径的半圆的圆心为O，在线段AB上有一点P，满足AP＝AC．请用无刻度的直尺，在如图所示的网格中，画出点P，并简要说明点P的位置是如何找到的（不要求证明）．36．（2021•徐州）如图，AB为⊙O的直径，点C、D在⊙O上，AC与OD交于点E，AE＝EC，OE＝ED．连接BC、CD．求证：（1）△AOE≌△CDE；（2）四边形OBCD是菱形．37．（2021•包头）如图，在锐角三角形ABC中，AD是BC边上的高，以AD为直径的⊙Ô于点G，交AD于点交AB于点E，交AC于点F，过点F作FG⊥AB，垂足为H，交AEM，连接AG，DE，DF．（1）求证：∠GAD+∠EDF＝180°；（2）若∠ACB＝45°，AD＝4，tan∠ABC＝2，求HF的长．̂的三等分点，AC∥BE．38．（2021•深圳）如图，AB为⊙O的弦，D，C为ACB（1）求证：∠A＝∠E；（2）若BC＝3，BE＝5，求CE的长．̂=BĈ=CD̂，OC与AD相交于点E．39．（2021•临沂）如图，已知在⊙O中，AB求证：（1）AD∥BC；（2）四边形BCDE为菱形．40．（2021•安徽）如图，圆O中两条互相垂直的弦AB，CD交于点E．（1）M是CD的中点，OM＝3，CD＝12，求圆O的半径长；（2）点F在CD上，且CE＝EF，求证：AF⊥BD．̂所对的圆周角，∠ACD＝30°．41．（2021•湖州）如图，已知AB是⊙O的直径，∠ACD是AD（1）求∠DAB的度数；（2）过点D作DE⊥AB，垂足为E，DE的延长线交⊙O于点F．若AB＝4，求DF的长．42．（2021•吉林）如图，四边形ABCD内接于⊙O，点P为边AD上任意一点（点P不与点A，D重合）连接CP．若∠B＝120°，则∠APC的度数可能为（）A．30°B．45°C．50°D．65°43．（2021•海南）如图，四边形ABCD是⊙O的内接四边形，BE是⊙O的直径，连接AE．若∠BCD＝2∠BAD，则∠DAE的度数是（）A．30°B．35°C．45°D．60°44．（2021•泰安）如图，四边形ABCD是⊙O的内接四边形，∠B＝90°，∠BCD＝120°，AB＝2，CD＝1，则AD的长为（）A．2√3−2B．3−√3C．4−√3D．2 45．（2021•重庆）如图，四边形ABCD内接于⊙O，若∠A＝80°，则∠C的度数是（）A．80°B．100°C．110°D．120°46．（2021•盐城）如图，在⊙O内接四边形ABCD中，若∠ABC＝100°，则∠ADC＝°．47．（2021•常德）如图，已知四边形ABCD是圆O的内接四边形，∠BOD＝80°，则∠BCD ＝．48．（2021•苏州）如图，四边形ABCD内接于⊙O，∠1＝∠2，延长BC到点E，使得CE ＝AB，连接ED．（1）求证：BD＝ED；（2）若AB＝4，BC＝6，∠ABC＝60°，求tan∠DCB的值．2021年中考真题圆周角（1－41题）圆内接四边形（42－48题）参考答案与试题解析一．试题（共48小题）1．（2021•巴中）如图，AB 是⊙O 的弦，且AB ＝6，点C 是弧AB 中点，点D 是优弧AB 上的一点，∠ADC ＝30°，则圆心O 到弦AB 的距离等于（ ）A ．3√3B ．32C ．√3D ．√32【解答】解：如图，连接OA 、OC ，OC 交AB 于点E ， ∵点C 是弧AB 中点，AB ＝6， ∴OC ⊥AB ，且AE ＝BE ＝3， ∵∠ADC ＝30°，∴∠AOC ＝2∠ADC ＝60°， ∴OE =1√3AE =√3， 故圆心O 到弦AB 的距离为√3． 故选：C ．2．（2021•鞍山）如图，AB 为⊙O 的直径，C ，D 为⊙O 上的两点，若∠ABD ＝54°，则∠C 的度数为（ ）A．34°B．36°C．46°D．54°【解答】解：连接AD，如图，∵AB为⊙O的直径，∴∠ADB＝90°，∴∠A＝90°﹣∠ABD＝90°﹣54°＝36°，∴∠C＝∠A＝36°．故选：B．3．（2021•抚顺）如图，在⊙O中，弦CD与直径AB相交于点E，连接OC，BD．若∠ABD ＝20°，∠AED＝80°，则∠COB的度数为（）A．80°B．100°C．120°D．140°【解答】解：∵∠ABD＝20°，∠AED＝80°，∴∠D＝∠AED﹣∠ABD＝80°﹣20°＝60°，∴∠COB＝2∠D＝120°，故选：C．4．（2021•阜新）如图，A，B，C是⊙O上的三点，若∠O＝70°，则∠C的度数是（）A ．40°B ．35°C ．30°D ．25°【解答】解：∵∠AOB 和∠C 都对AB ̂， ∴∠C =12∠AOB =12×70°＝35°． 故选：B ．5．（2021•牡丹江）如图，点A ，B ，C 为⊙O 上的三点，∠AOB =13∠BOC ，∠BAC ＝30°，则∠AOC 的度数为（ ）A ．100°B ．90°C ．80°D ．60°【解答】解：∵∠BOC ＝2∠BAC ＝60°，OB ＝OC ， ∴△BOC 是等边三角形， ∵∠AOB =13∠BOC ＝20°，∴∠AOC ＝∠BOC +∠AOB ＝60°+20°＝80°， 故选：C ．6．（2021•遵义）如图，点C 是以点O 为圆心，AB 为直径的半圆上一点，连接AC ，BC ，OC ．若AC ＝4，BC ＝3，则sin ∠BOC 的值是（ ）A ．1B ．2425C ．1625D ．925【解答】解：如图，过点C 作CH ⊥AB 于H ．∵AB是直径，∴∠ACB＝90°，∵AC＝4，BC＝3，∴AB=√AC2+BC2=√42+32=5，∴OC=12AB=52，∵S△ABC=12•AB•CH=12•AC•BC，∴CH=3×45=125，∴sin∠BOC=CHOC=12552=2425，故选：B．7．（2021•桂林）如图，AB是⊙O的直径，点C是⊙O上一点，连接AC，BC，则∠C的度数是（）A．60°B．90°C．120°D．150°【解答】解：∵AB为⊙O的直径，∴∠C＝90°，故选：B．8．（2021•营口）如图，⊙O中，点C为弦AB中点，连接OC，OB，∠COB＝56°，点D 是AB̂上任意一点，则∠ADB度数为（）A．112°B．124°C．122°D．134°【解答】解：作AB̂所对的圆周角∠APB，如图，∵OC⊥AB，OA＝OB，∴OC平分∠AOB，∴∠AOC＝∠BOC＝56°，∴∠APB=12∠AOB＝56°，∵∠APB+∠ADB＝180°，∴∠ADB＝180°﹣56°＝124°．故选：B．9．（2021•赤峰）如图，点C，D在以AB为直径的半圆上，且∠ADC＝120°，点E是AD̂上任意一点，连接BE、CE．则∠BEC的度数为（）A．20°B．30°C．40°D．60°【解答】解：连接AC，如图，∵四边形ABCD为⊙O的内接四边形，∴∠ADC+∠ABC＝180°，∴∠ABC＝180°﹣120°＝60°，∵AB为直径，∴∠ACB＝90°，∴∠BAC＝90°﹣60°＝30°，∴∠BEC＝∠BAC＝30°．故选：B．10．（2021•常州）如图，BC是⊙O的直径，AB是⊙O的弦，若∠AOC＝60°，则∠OAB 的度数是（）A．20°B．25°C．30°D．35°【解答】解：∵∠AOC＝60°，∴∠B=12∠AOC＝30°，∵OA＝OB，∴∠OAB＝∠B＝30°，故选：C．11．（2021•贵港）如图，点A，B，C，D均在⊙O上，直径AB＝4，点C是BD̂的中点，点D关于AB对称的点为E，若∠DCE＝100°，则弦CE的长是（）A．2√3B．2C．√3D．1【解答】解：连接AD、AE、OD、OC、OE，过点O作OH⊥CE于点H，∵∠DCE＝100°，∴∠DAE＝180°﹣∠DCE＝80°，∵点D关于AB对称的点为E，∴∠BAD＝∠BAE＝40°，∴∠BOD＝∠BOE＝80°，̂的中点，∵点C是BD∴∠BOC＝∠COD＝40°，∴∠COE＝∠BOC+∠BOE＝120°，∵OE＝OC，OH⊥CE，∴EH＝CH，∠OEC＝∠OCE＝30°，∵直径AB＝4，∴OE＝OC＝2，∴EH＝CH=√3，∴CE＝2√3．故选：A．12．（2021•黄石）如图，A、B是⊙O上的两点，∠AOB＝60°，OF⊥AB交⊙O于点F，则∠BAF等于（）A．20°B．22.5°C．15°D．12.5°【解答】解：∵OF⊥AB，̂=BF̂，∴AF∴∠AOF＝∠BOF=12∠AOB=12×60°＝30°，∴∠BAF=12∠BOF=12×30°＝15°．故选：C．13．（2021•荆州）如图，矩形OABC的边OA，OC分别在x轴、y轴的正半轴上，点D在OA的延长线上，若A（2，0），D（4，0），以O为圆心、OD长为半径的弧经过点B，交y轴正半轴于点E，连接DE，BE，则∠BED的度数是（）A．15°B．22.5°C．30°D．45°【解答】解：如图，连接OB，∵A（2，0），D（4，0），矩形OABC，∴OA＝2，OD＝4＝OB，∴∠OBA＝30°，∴∠BOD＝90°﹣30°＝60°，∴∠BED=12∠BOD=12×60°＝30°，故选：C．14．（2021•宜昌）如图，C，D是⊙O上直径AB两侧的两点，设∠ABC＝25°，则∠BDC ＝（）A．85°B．75°C．70°D．65°【解答】解：连接OC，如图，∵∠ABC＝25°，∴∠AOC＝2∠ABC＝2×25°＝50°，∴∠BOC＝180°﹣∠AOC＝180°﹣50°＝130°，∴∠BDC=12∠BOC=12×130°=65°．解法二：因为AB是直径，所以∠ACB＝90°所以∠BDC＝∠CAB＝90°﹣∠ABC＝65°．故选：D．15．（2021•聊城）如图，A，B，C是半径为1的⊙O上的三个点，若AB=√2，∠CAB＝30°，则∠ABC的度数为（）A．95°B．100°C．105°D．110°【解答】解：如图，连接OB 、OC ，过点O 作OD ⊥AB ，垂足为D ，则有：OA ＝OB ＝OC ＝1，AD ＝BD =12AB =√22，在Rt △OAD 中，OD 2＝OA 2﹣AD 2，∴OD =12−(√22)2=√22，∴△OAD 是等腰直角三角形，∴∠OAD ＝45°，∴∠OBA ＝∠OAD ＝45°，∵∠BAC ＝30°，∴∠COB ＝2∠BAC ＝60°，∴△OBC 是等边三角形，∠OBC ＝60°，∴∠ABC ＝∠OBA +∠OBC ＝45°+60°＝105°，故选：C ．16．（2021•长沙）如图，点A ，B ，C 在⊙O 上，∠BAC ＝54°，则∠BOC 的度数为（ ）A ．27°B ．108°C ．116°D ．128°【解答】解：∵∠A ＝54°，∴∠BOC ＝2∠A ＝108°，故选：B ．17．（2021•武汉）如图，AB 是⊙O 的直径，BC 是⊙O 的弦，先将BĈ沿BC 翻折交AB 于点D ，再将BD ̂沿AB 翻折交BC 于点E ．若BE ̂=DE ̂，设∠ABC ＝α，则α所在的范围是（ ）A．21.9°＜α＜22.3°B．22.3°＜α＜22.7°C．22.7°＜α＜23.1°D．23.1°＜α＜23.5°【解答】解：如图，连接AC，CD，DE．̂=EB̂，∵ED∴ED＝EB，∴∠EDB＝∠EBD＝α，̂=CD̂=DÊ，∵AC∴AC＝CD＝DE，∴∠DCE＝∠DEC＝∠EDB+∠EBD＝2α，∴∠CAD＝∠CDA＝∠DCE+∠EBD＝3α，∵AB是直径，∴∠ACB＝90°，∴∠CAB+∠ABC＝90°，∴4α＝90°，∴α＝22.5°，故选：B．18．（2021•邵阳）如图，点A，B，C是⊙O上的三点．若∠AOC＝90°，∠BAC＝30°，则∠AOB的大小为（）A．25°B．30°C．35°D．40°̂，【解答】解：∵∠BAC与∠BOC所对弧为BC由圆周角定理可知：∠BOC＝2∠BAC＝60°，又∠AOC＝90°，∴∠AOB＝∠AOC﹣∠BOC＝90°﹣60°＝30°．故选：B．19．（2021•嘉峪关）如图，点A，B，C，D，E在⊙O上，AB＝CD，∠AOB＝42°，则∠CED＝（）A．48°B．24°C．22°D．21°【解答】解：连接OC、OD，∵AB＝CD，∠AOB＝42°，∴∠AOB＝∠COD＝42°，∴∠CED=12∠COD＝21°．故选：D．20．（2021•南充）如图，AB是⊙O的直径，弦CD⊥AB于点E，CD＝2OE，则∠BCD的度数为（）A．15°B．22.5°C．30°D．45°【解答】解：连接OD，∵AB是⊙O的直径，弦CD⊥AB于点E，∴CD＝2ED＝2CE，∵CD＝2OE，∴DE＝OE，∵CD⊥AB，∴∠DOE＝∠ODE＝45°，∴∠BCD=12∠DOE＝22.5°．故选：B．21．（2021•眉山）如图，在以AB为直径的⊙O中，点C为圆上的一点，BĈ=3AĈ，弦CD ⊥AB于点E，弦AF交CE于点H，交BC于点G．若点H是AG的中点，则∠CBF的度数为（）A．18°B．21°C．22.5°D．30°【解答】解：∵AB是直径，∴∠ACB＝90°，∴∠ABC+∠CAB＝90°，̂=3AĈ，∵BC∴∠CAB＝3∠ABC，∴∠ABC＝22.5°，∠CAB＝67.5°，∵CD⊥AB，∴∠ACE＝22.5°，∵点H是AG的中点，∠ACB＝90°，∴AH＝CH＝HG，∴∠CAH＝∠ACE＝22.5°，∵∠CAF＝∠CBF，∴∠CBF＝22.5°，故选：C．22．（2021•重庆）如图，AB是⊙O的直径，AC，BC是⊙O的弦，若∠A＝20°，则∠B的度数为（）A．70°B．90°C．40°D．60°【解答】解：∵AB是⊙O的直径，∴∠C＝90°，∵∠A＝20°，∴∠B＝90°﹣∠A＝70°，故选：A．23．（2021•朝阳）已知⊙O的半径是7，AB是⊙O的弦，且AB的长为7√3，则弦AB所对的圆周角的度数为60°或120°．【解答】解：∠ACB和∠ADB为弦AB所对的圆周角，连接OA、OB，如图，过O点作OH⊥AB于H，则AH＝BH=12AB=7√32，在Rt△OAH中，∵cos∠OAH=AHOA=7√327=√32，∴∠OAH＝30°，∵OA＝OB，∴∠OBH＝∠OAH＝30°，∴∠AOB＝120°，∴∠ACB=12∠AOB＝60°，∵∠ADB+∠ACB＝180°，∴∠ADB＝180°﹣60°＝120°，即弦AB所对的圆周角的度数为60°或120°．故答案为60°或120°．24．（2021•盘锦）如图，在平面直角坐标系xOy中，点A在x轴负半轴上，点B在y轴正半轴上，⊙D经过A，B，O，C四点，∠ACO＝120°，AB＝4，则圆心点D的坐标是（−√3，1）．【解答】解：∵四边形ABOC为圆的内接四边形，∴∠ABO+∠ACO＝180°，∴∠ABO＝180°﹣120°＝60°，∵∠AOB＝90°，∴AB为⊙D的直径，∴D点为AB的中点，在Rt△ABO中，∵∠ABO＝60°，∴OB=12AB＝2，∴OA=√3OB＝2√3，∴A（﹣2√3，0），B（0，2），∴D点坐标为（−√3，1）．故答案为（−√3，1）．25．（2021•德阳）在锐角三角形ABC中，∠A＝30°，BC＝2，设BC边上的高为h，则h 的取值范围是2√3＜h≤2+√3．【解答】解：如图，BC为⊙O的弦，OB＝OC＝2，∵BC＝2，∴OB＝OC＝BC，∴△OBC为等边三角形，∴∠BOC＝60°，∴∠BAC=12∠BOC＝30°，作直径BD、CE，连接BE、CD，则∠DCB＝∠EBC＝90°，∴当点A在DÊ上（不含D、E点）时，△ABC为锐角三角形，在Rt△BCD中，∵∠D＝∠BAC＝30°，∴CD=√3BC＝2√3，̂的中点时，A点到BC的距离最大，即h最大，当A点为DE延长AO交BC于H，如图，̂的中点，∵A点为DÊ=AĈ，∴AB∴AH⊥BC，∴BH＝CH＝1，∴OH=√3BH=√3，∴AH＝OA+OH＝2+√3，∴h的范围为2√3＜h≤2+√3．故答案为2√3＜h≤2+√3．26．（2021•淮安）如图，AB是⊙O的直径，CD是⊙O的弦，∠CAB＝55°，则∠D的度数是35°．【解答】解：∵AB是⊙O的直径，∴∠ACB＝90°，∵∠CAB＝55°，∴∠B＝90°﹣∠CAB＝35°，∴∠D＝∠B＝35°．故答案为：35°．27．（2021•南通）如图，在△ABC 中，AC ＝BC ，∠ACB ＝90°，以点A 为圆心，AB 长为半径画弧，交AC 延长线于点D ，过点C 作CE ∥AB ，交BD̂于点E ，连接BE ，则CE BE 的值为 √22 ．【解答】解：如图，过点A 作CE 的垂线交EC 延长线于F ，过E 作EG ⊥AB 交AB 于G ，连AE ，∵AC ＝BC ，∠ACB ＝90°，∴∠CAB ＝45°，∵CE ∥AB ，∴∠F AB ＝90°，∴∠F AC ＝45°，∴△AFC 为等腰直角三角形，设AF ＝x ，则CF ＝x ，∴AC =√AF 2+CF 2=√2x ，∴AB =√AC 2+BC 2=√2AC =2x ，∵AE 、AB 均为⊙的半径，∴AE ＝2x ，∴EF =√AE 2−AF 2=√3x ，∴CE =(√3−1)x ，∵∠F ＝∠F AB ＝∠AGE ＝90°，∴四边形F AGE 为矩形，∴AF ＝EG ＝x ，EF ＝AG =√3x ，∴BG ＝AB ﹣AG ＝（2−√3）x ，∴BE =√EG 2+BG 2=(√6−√2)x ，∴CE BE =√3−1√6−√2=√22． 故答案为：√22． 28．（2021•徐州）如图，AB 是⊙O 的直径，点C 、D 在⊙O 上，若∠ADC ＝58°，则∠BAC＝ 32 °．【解答】解：∵AB 是⊙O 的直径，∴∠ACB ＝90°，∵∠B ＝∠ADC ＝58°，∴∠BAC ＝90°﹣∠B ＝32°．故答案为32．29．（2021•本溪）如图，由边长为1的小正方形组成的网格中，点A ，B ，C 都在格点上，以AB 为直径的圆经过点C 和点D ，则tan ∠ADC ＝ 32 ．【解答】解：∵AB 为直径，∴∠ACB ＝90°，在Rt △ABC 中，tan ∠ABC =AC BC =32，∵∠ADC ＝∠ABC ，∴tan ∠ADC =32．故答案为32． 30．（2021•黑龙江）如图，在⊙O 中，AB 是直径，弦AC 的长为5cm ，点D 在圆上且∠ADC＝30°，则⊙O 的半径为 5 cm ．【解答】解：如图，连接OC ．∵∠AOC ＝2∠ADC ，∠ADC ＝30°，∴∠AOC ＝60°，∵OA ＝OC ，∴△AOC 是等边三角形，∴OA ＝AC ＝5（cm ），∴⊙O 的半径为5cm ．故答案为：5．31．（2021•黑龙江）如图，在Rt △AOB 中，∠AOB ＝90°，OA ＝4，OB ＝6，以点O 为圆心，3为半径的⊙O ，与OB 交于点C ，过点C 作CD ⊥OB 交AB 于点D ，点P 是边OA 上的动点，则PC +PD 的最小值为 2√10 ．【解答】解：延长CO 交⊙O 于点E ，连接ED ，交AO 于点P ，则PC +PD 的值最小，最小值为线段DE 的长．∵CD ⊥OB ，∴∠DCB ＝90°，∵∠AOB ＝90°，∴∠DCB ＝∠AOB ，∴CD ∥AO ，∴CD AO =BC BO ， ∴CD 4=36，∴CD ＝2，在Rt △CDE 中，DE =√CD 2+CE 2=√22+62=2√10，∴PC +PD 的最小值为2√10．故答案为：2√10．32．（2021•广元）如图，在4×4的正方形网格图中，已知点A 、B 、C 、D 、O 均在格点上，其中A 、B 、D 又在⊙O 上，点E 是线段CD 与⊙O 的交点．则∠BAE 的正切值为 12 ．【解答】解：由题意可得，∠BDE ＝∠BAE ，在Rt △BDC 中，∠DBC ＝90°，∴tan ∠BDC =BC BD =24=12，∴tan ∠BAE =12．故答案为：12． 33．（2021•宿迁）如图，在Rt △ABC 中，∠ABC ＝90°，∠A ＝32°，点B 、C 在⊙O 上，边AB 、AC 分别交⊙O 于D 、E 两点，点B 是CD̂的中点，则∠ABE ＝ 13° ．【解答】解：如图，连接DC ，∵∠DBC ＝90°，∴DC 是⊙O 的直径，∵点B 是CD̂的中点， ∴∠BCD ＝∠BDC ＝45°，在Rt △ABC 中，∠ABC ＝90°，∠A ＝32°，∴∠ACB ＝90°﹣32°＝58°，∴∠ACD ＝∠ACB ﹣∠BCD ＝58°﹣45°＝13°＝∠ABE ，故答案为：13°．34．（2021•长沙）如图，在⊙O 中，弦AB 的长为4，圆心到弦AB 的距离为2，则∠AOC的度数为 45° ．【解答】解：∵OC ⊥AB ,∴AC＝BC=12AB=12×4=2,∵OC＝2,∴△AOC为等腰直角三角形，∴∠AOC＝45°，故答案为：45°．35．（2021•天津）如图，在每个小正方形的边长为1的网格中，△ABC的顶点A，C均落在格点上，点B在网格线上．（Ⅰ）线段AC的长等于√5；（Ⅱ）以AB为直径的半圆的圆心为O，在线段AB上有一点P，满足AP＝AC．请用无刻度的直尺，在如图所示的网格中，画出点P，并简要说明点P的位置是如何找到的（不要求证明）取BC与网格线的交点D，连接OD延长OD交⊙O于点E，连接AE交BC于点G，连接BE，延长AC交BE的延长线于F，连接FG延长FG交AB于点P，点P即为所求．【解答】解：（Ⅰ）AC=√22+12=√5．故答案为：√5．（Ⅱ）如图，点P即为所求．故答案为：如图，取BC与网格线的交点D，则点D为BC中点，连接OD并延长OD交⊙O于点E，连接AE交BC于点G，连接BE，延长AC交BE的延长线于F，则OE为△BF A的中位线，则AB＝AF，连接FG延长FG交AB于点P，则BG＝FG，∠AFG＝∠ABG ，即△F AP ≌△BAC ，则点P 即为所求．36．（2021•徐州）如图，AB 为⊙O 的直径，点 C 、D 在⊙O 上，AC 与OD 交于点E ，AE＝EC ，OE ＝ED ．连接BC 、CD ．求证：（1）△AOE ≌△CDE ；（2）四边形OBCD 是菱形．【解答】证明：（1）在△AOE 和△CDE 中，{AE =CE ∠AEO =∠CED OE =DE，∴△AOE ≌△CDE （SAS ）；（2）∵△AOE ≌△CDE ，∴OA ＝CD ，∠AOE ＝∠D ，∴OB ∥CD ，∴四边形OBCD 为平行四边形，∵OB ＝OD ，∴四边形OBCD 是菱形．37．（2021•包头）如图，在锐角三角形ABC 中，AD 是BC 边上的高，以AD 为直径的⊙O交AB 于点E ，交AC 于点F ，过点F 作FG ⊥AB ，垂足为H ，交AÊ于点G ，交AD 于点M ，连接AG ，DE ，DF ．（1）求证：∠GAD +∠EDF ＝180°；（2）若∠ACB ＝45°，AD ＝4，tan ∠ABC ＝2，求HF 的长．【解答】（1）证明：由题可知∠AGF＝∠ADF（同弧所对的圆周角相等），∵GF⊥AB，AD为圆的直径，∴∠AGF+∠GAE＝90°，∠ADF+∠F AD＝90°，∴∠GAE＝∠F AD，∴∠GAE+∠DAE＝∠F AD+∠DAE，即∠GAD＝∠EAF，∵四边形AEDF是圆的内接四边形，∴∠EAF+∠EDF＝180°，∴∠GAD+∠EDF＝180°．（2）解：如图，连接OF，∵AD是圆的直径，且AD是△ABC的高，GF⊥AB，∴∠AED＝∠ADB＝∠AHM＝∠AFD＝90°，∴△AHM∽△ADB，∴AHHM =AD BD，∵tan∠ABC=ADBD=2，∴AHHM=2，∵∠ACB ＝45°，∴∠DAC ＝∠ADF ＝∠AFO ＝45°，∴∠AOF ＝90°，∵在Rt △AHM 与Rt △FOM 中：∠AMH ＝∠FMO （对顶角）， ∴△AHM ∽△FOM ，∴FO OM =AH HM =2，∵AD ＝4，∴OF ＝OA ＝2，∴FO OM =2，解得OM ＝1，AM ＝OA ﹣OM ＝1，设HM ＝x ，则AH ＝2x ，在Rt △AHM 中有：AH 2+HM 2＝AM 2，即（2x ）2+x 2＝1，解得x 1=√55，x 2=−√55（舍去），∴AH =2√55， ∵OF ＝OA ＝2，∴AF ＝2√2，在Rt △AHF 中，有：AH 2+HF 2＝AF 2，即（2√55）2+HF 2＝（2√2）2， 解得HF =6√55，或HF =−6√55（舍去），故HF 的长为6√55． 38．（2021•深圳）如图，AB 为⊙O 的弦，D ，C 为ACB̂的三等分点，AC ∥BE ． （1）求证：∠A ＝∠E ；（2）若BC ＝3，BE ＝5，求CE 的长．【解答】（1）证明：∵AC ∥BE ，∴∠E ═∠ACD ，∵D ，C 为ACB̂的三等分点， ∴BĈ=CD ̂=AD ̂， ∴∠ACD ═∠A ，∴∠E ═∠A ，（2）解：由（1）知BĈ=CD ̂=AD ̂， ∴∠D ═∠CBD ═∠A ═∠E ，∴BE ═BD ═5，BC ═CD ═3，△CBD ∽△BDE ，∴CB BD ═BD DE ，即35=5DE ，解得DE ═253，∴CE ═DE ﹣CD ═253−3═163．39．（2021•临沂）如图，已知在⊙O 中，AB̂=BC ̂=CD ̂，OC 与AD 相交于点E ． 求证：（1）AD ∥BC ；（2）四边形BCDE 为菱形．【解答】证明：（1）连接BD ，∵AB̂=CD ̂， ∴∠ADB ＝∠CBD ，∴AD ∥BC ；（2）连接CD，BD，设OC与BD相交于点F，∵AD∥BC，∴∠EDF＝∠CBF，̂=CD̂，∵BC∴BC＝CD，BF＝DF，又∠DFE＝∠BFC，∴△DEF≌△BCF（ASA），∴DE＝BC，∴四边形BCDE是平行四边形，又BC＝CD，∴四边形BCDE是菱形．40．（2021•安徽）如图，圆O中两条互相垂直的弦AB，CD交于点E．（1）M是CD的中点，OM＝3，CD＝12，求圆O的半径长；（2）点F在CD上，且CE＝EF，求证：AF⊥BD．【解答】解：（1）连接OD，如图：∵M是CD的中点，CD＝12，∴DM=12CD＝6，OM⊥CD，∠OMD＝90°，Rt△OMD中，OD=√OM2+DM2，且OM＝3，∴OD=√32+62=3√5，即圆O的半径长为3√5；（2）连接AC，延长AF交BD于G，如图：∵AB⊥CD，CE＝EF，∴AB是CF的垂直平分线，∴AF＝AC，即△ACF是等腰三角形，∵CE＝EF，∴∠F AE＝∠CAE，∵BĈ=BĈ，∴∠CAE＝∠CDB，∴∠F AE＝∠CDB，Rt△BDE中，∠CDB+∠B＝90°，∴∠F AE+∠B＝90°，∴∠AGB＝90°，∴AG⊥BD，即AF⊥BD．41．（2021•湖州）如图，已知AB是⊙O的直径，∠ACD是AD̂所对的圆周角，∠ACD＝30°．（1）求∠DAB的度数；（2）过点D作DE⊥AB，垂足为E，DE的延长线交⊙O于点F．若AB＝4，求DF的长．【解答】解：（1）如图，连接BD，∵∠ACD＝30°，∴∠B＝∠ACD＝30°，∵AB是⊙O的直径，∴∠ADB＝90°，∴∠DAB＝90°﹣∠B＝60°；（2）∵∠ADB＝90°，∠B＝30°，AB＝4，∴AD=12AB＝2，∵∠DAB＝60°，DE⊥AB，且AB是直径，∴EF＝DE＝AD sin60°=√3，∴DF＝2DE＝2√3．42．（2021•吉林）如图，四边形ABCD内接于⊙O，点P为边AD上任意一点（点P不与点A，D重合）连接CP．若∠B＝120°，则∠APC的度数可能为（）A．30°B．45°C．50°D．65°【解答】解：∵四边形ABCD内接于⊙O，∴∠B+∠D＝180°，∵∠B＝120°，∴∠D＝180°﹣∠B＝60°，∵∠APC为△PCD的外角，∴∠APC＞∠D，只有D满足题意．故选：D．43．（2021•海南）如图，四边形ABCD是⊙O的内接四边形，BE是⊙O的直径，连接AE．若∠BCD＝2∠BAD，则∠DAE的度数是（）A．30°B．35°C．45°D．60°【解答】解：∵四边形ABCD是⊙O的内接四边形，∴∠BCD+∠BAD＝180°，∵∠BCD＝2∠BAD，∴∠BCD＝120°，∠BAD＝60°，∵BE是⊙O的直径，∴∠BAE＝90°，∴∠DAE＝90°﹣∠BAD＝90°﹣60°＝30°，故选：A．44．（2021•泰安）如图，四边形ABCD是⊙O的内接四边形，∠B＝90°，∠BCD＝120°，AB＝2，CD＝1，则AD的长为（）A．2√3−2B．3−√3C．4−√3D．2【解答】解：延长AD、BC交于E，∵∠BCD＝120°，∴∠A＝60°，∵∠B＝90°，∴∠ADC＝90°，∠E＝30°，在Rt△ABE中，AE＝2AB＝4，在Rt△CDE中，DE=CDtan∠E=√3，∴AD＝AE﹣DE＝4−√3，故选：C．45．（2021•重庆）如图，四边形ABCD内接于⊙O，若∠A＝80°，则∠C的度数是（）A．80°B．100°C．110°D．120°【解答】解：∵四边形ABCD内接于⊙O，∴∠A+∠C＝180°，∵∠A＝80°，∴∠C＝100°，故选：B．46．（2021•盐城）如图，在⊙O内接四边形ABCD中，若∠ABC＝100°，则∠ADC＝80°．【解答】解：∵四边形ABCD是⊙O的内接四边形，∴∠ABC+∠ADC＝180°，∴∠ADC＝180°﹣100°＝80°．故答案为：80．47．（2021•常德）如图，已知四边形ABCD是圆O的内接四边形，∠BOD＝80°，则∠BCD ＝140°．【解答】解：∵∠BAD为BD̂所对的圆周角且∠BOD＝80°，∴∠BAD=12∠BOD=12×80°=40°，又∵四边形ABCD是圆O的内接四边形，∴∠BAD+∠BCD＝180°,∴∠BCD＝180°﹣∠BAD＝180°﹣40°＝140°，故答案为：140°．48．（2021•苏州）如图，四边形ABCD内接于⊙O，∠1＝∠2，延长BC到点E，使得CE ＝AB，连接ED．（1）求证：BD＝ED；（2）若AB＝4，BC＝6，∠ABC＝60°，求tan∠DCB的值．【解答】（1）证明：∵四边形ABCD 内接于⊙O ， ∴∠A ＝∠DCE ，∵∠1＝∠2，∴AD̂=DC ̂， ∴AD ＝DC ，在△ABD 和△DCE 中，{AB =CE ∠A =∠DCE AD =DC，∴△ABD ≌△CED （SAS ），∴BD ＝ED ；（2）解：过点D 作DM ⊥BE 于M ，∵AB ＝4，BC ＝6，CE ＝AB ，∴BE ＝BC +EC ＝10，∵BD ＝ED ，DM ⊥BE ，∴BM ＝ME =12BE ＝5，∴CM ＝BC ﹣BM ＝1，∵∠ABC ＝60°，∠1＝∠2，∴∠2＝30°，∴DM ＝BM •tan ∠2＝5×√33=5√33，∴tan ∠DCB =DM CM =5√33．。

垂径定理圆心角圆周角练习1.如图．⊙O中OA⊥BC，∠CDA=25o，则∠AOB的度数为_______．2.如图．AB为⊙O的直径，点C、D在⊙O上，∠BAC=50o．则∠ADC=_______．第1题第2题第3题3.如图，点A、B、C都在⊙O上，连结AB、BC、AC、OA、OB，且∠BAO=25°，则∠ACB的大小为___________.第4题第5题4.已知：如图，四边形ABCD是⊙O的内接四边形，∠BOD=140°，则∠DCE=.5、如图，AB是⊙O的直径，C,D,E都是⊙O上的点，则∠1＋∠2=.6、⊙O中，若弦AB长22cm，弦心距为2cm，则此弦所对的圆周角等于．7、已知AB是⊙O的直径，AC,AD是弦，且AB=2,AC=2，AD=1，则圆周角∠CAD的度数是()A.45°或60°B.60°C.105°D.15°或105°8、如图，AB是⊙的直径，弦CD垂直平分OB，则∠BDC=（）A.20°B.30°C.40°D.50°9、如图，点A、B、C为圆O上的三个点，∠AOB=的度数．13∠BOC,∠BAC=45°，求∠ACB 10、如图，AD是∆ABC的高，AE是∆ABC的外接圆的直径．试说明狐B E CF。

DF11、如图，AB,AC是⊙O的两条弦，且AB=AC．延长CA到点D．使AD=AC，连结DB并延长,交⊙O于点E．求证：CE是⊙O的直径．12、已知：如图，AB为⊙O的直径，AB=AC，B C交⊙O于点D，AC交⊙O于点E，∠BAC=45°．（1）求∠EBC的度数；（2）求证：BD=CD．△13．如图所示，ABC为圆内接三角形，A B＞AC，∠A的平分线AD交圆于D，作D E⊥AB于E，D F⊥AC于F，求证：BE=CFAEB CFD△14．如图所示，在ABC中，∠BAC与∠ABC的平分线AE、BE相交于点E，延长AE交△ABC的外接圆于D点，连接BD、CD、CE，且∠BDA=60°（1）求证△BDE是等边三角形；（2）若∠BDC=120°，猜想BDCE是怎样的四边形，并证明你的猜想。

备战中考数学基础必练（浙教版）圆心角与圆周角（含解析）2019备战中考数学基础必练（浙教版）-圆心角与圆周角（含解析）一、单选题1.如图，AB是⊙0的直径，点C在⊙0上，∠B=65°，则∠A=( )A. 20°B. 25°C. 30°D. 35°2.如图，点C在以AB为直径的半圆上，∠BAC=20°，则∠BOC等于（）A. 20°A. 18°B. 30°C. 36°D. 72°5.如图，已知AB是☉O的直径，D，C是劣弧EB 的三等分点，∠BOC=40°，那么∠AOE=（）A. 40°B. 60°C. 80°D. 120°6.如图，点A、B、C都在⊙O上，若∠AOB=76°，则∠ACB的度数为（）A. 19°B. 30°C. 38°D. 76°7.如图，点A、B、C在⊙O上，若∠ABC=52°，则∠AOC的度数为（）A. 128°B. 104°C. 50°D. 52°8.如图，在⊙O中，∠ABC=60°，则∠AOC等于（）A. 30°B. 60°C. 100°D. 120°9.如图，CD为⊙O的直径，CD⊥EF,垂点为G，∠EOD=40°，则∠DCF （）A. 80°B. 50°C. 40°D. 20°10.已知弧CD是⊙O的一条弧，点A是弧CD的中点，连接AC，CD．则（）A. CD=2ACB. CD＞2ACC. CD＜2ACD. 不能确定．二、填空题11.如图，已知AB,CD是⊙O的直径，CE是弦，且, ，则弧BE的度数________.12. 如图24-1-4-5，OB、OC是⊙O的半径，A 是⊙O上一点，若已知∠B=20°，∠C=30°，则∠A=________.13.已知A、B的坐标分别为（﹣2，0）、（4，0），点P在直线y= x+2上，如果△ABP为直角三角形，这样的P点共有________个．14.如图，BD是⊙O的直径，∠A=65°，则∠DBC 的度数是________15.如图，AB是⊙O的直径，弦CD垂直AB，已知AC=1，BC=，那么sin∠ACD的值是________．16.如图，⊙O的直径CD⊥AB，∠AOC=50°，则∠CDB大小为________．17.如图，AB为△ADC的外接圆⊙O的直径，若∠BAD=50°，则∠ACD=________°．18.将量角器按如图所示的方式放置在三角形纸板上，使点C在半圆上．点A、B的读数分别为86°、30°，则∠ACB的大小为________．三、综合题19.如图：三角形ABC内接于圆O，∠BAC与∠ABC 的角平分线AE，BE相交于点E，延长AE交外接圆O于点D，连接BD，DC，且∠BCA=60°（1）求∠BED的大小；（2）证明：△BED为等边三角形；（3）若∠ADC=30°，圆O的半径为r，求等边三角形BED的边长．20.如图，∠BAC的平分线交△ABC的外接圆于点D，∠ABC的平分线交AD于点E．（1）求证：DE=DB；（2）若∠BAC=90°，BD=4，求△ABC外接圆的半径．21.O为等腰△ABC的底边AB的中点，以点O为圆心，AB为直径的半圆分别交AC，BC于点D，E．（1）求证：∠AOE=∠BOD．（2）求证：22.已知：如图，△ABC内接于⊙O，点D在OC的延长线上，sinB= ，∠CAD=30°．（1）求证：AD是⊙O的切线；（2）若OD⊥AB，BC=5，求AD的长．答案解析部分一、单选题1.【答案】B【考点】圆周角定理【解析】【分析】因为AB是⊙0的直径，所以∠C=90°。

绝密★启用前中考数学圆心角和圆周角的性质题型学霸总结阳光老师：祝你学业有成未命名注意事项：1．答题前填写好自己的姓名、班级、考号等信息2．请将答案正确填写在答题卡上第I 卷（选择题）请点击修改第I 卷的文字说明一、单选题1．如图，ABC 内接于O ，若O 的半径为6，60A ∠=，则BC 的长为（）A．B ．C ．D 2．如图，AB 为O 的切线，切点为A ，OB 交O 于点,D C 为O 上一点，若40,ABO ∠=︒则ACD ∠的度数为（ ）A ．50︒B ．25︒C ．45︒D ．20︒3．如图，PA 、PB 、AB 与圆O 相切，60P ∠=︒，则AOB ∠=（ ）A ．50°B ．60°C ．70°D ．80° 4．如图，PA ，PB 是O 的切线，A ，B 为切点，AC 是O 的直径，若25BAC ∠=︒，则P ∠=（ ）度．A ．30B ．60C ．50D ．755．如图，在平面直角坐标系中，直线AB 经过点A （-4，0），B （0，4），⊙O 的半径为1（O 为坐标原点），点P 在直线AB 上，过点P 作⊙O 的一条切线PQ ，Q 为切点，则切线长PQ 的最小值为（ ）A ．6B ．7C ．2D ．3 6．以坐标原点O 为圆心，作半径为1的圆，若直线y x b =-+与⊙O 相交，则b 的取值范围是（ ）A ．01b ≤<B ．0b ≤≤C ．11b -<<D ．b <7．如图，PA ，PB 为⊙O 的切线，A ，B 为切点，根据图形得出四个结论：①PA=PB ；②∠1=∠2；③∠3=∠4；④AB 被OP 垂直平分． 其中正确结论的个数为（ ）A ．1个B ．2个C ．3个D ．4个8．如图，AB 为⊙O 的切线，A 为切点，BO 的延长线交⊙O 于点C ，∠OAC=35°，则∠B 的度数是（ ）A ．15°B ．20°C ．25°D ．35° 9．如图，不等边ABC 内接于O ，下列结论不成立的是（ ）A ．12∠=∠B ．14∠=∠C ．2AOB ACB ∠=∠D ．23ACB ∠=∠+∠10．如图，在等边ABC 中，点O 在边AB 上，O 过点B 且分别与边AB BC 、相交于点D 、E ，F 是AC 上的点，判断下列说法错误的是（ ）A ．若EF AC ⊥，则EF 是O 的切线B ．若EF 是O 的切线，则EF AC ⊥C ．若2BE EC =，则AC 是O 的切线 D ．若BE EC =，则AC 是O 的切线11．如图，AB 是⊙O 的直径，直线P A 与⊙O 相切于点A ，PO 交⊙O 于点C ，连接BC ，若∠BCO ＝α，则∠P 的度数为（ ）A．2αB．90°﹣2αC．45°﹣2αD．45°+2α第II卷（非选择题）请点击修改第II卷的文字说明二、解答题12．已知，如图，A是⊙O上一点，半径OC的延长线与过点A的直线交于B点，OC＝BC，AC＝12 OB．（1）求证：AB是⊙O的切线；（2）若∠ACD＝45°，OC＝2，求弦AD的长．13．请解答下列各题：（1）如图1，如图，CD所在的直线垂直平分线AB，利用这样的工具，最少使用几次就可以找到圆形工件的圆心；（2）如图2，有一块破碎的圆形残片，请你用直尺和圆规找出它的圆心O．（保留作图痕迹）．14．如图，AB为O的直径，,C D是O上的点，P是O外一点，AC PD⊥于点,E AD平分BAC∠．()1求证：PD 是O 的切线； ()2若60DE BAC =∠=︒，求O 的半径． 15．AB 为O 的直径，C 是O 上的一点，D 在AB 的延长线上，且DCB A ∠=∠，（1）CD 与O 相切吗？如果相切，请你加以证明；如果不相切，请说明理由．（2）若30D ∠=︒，10cm BD =．求O 的半径． 16．如图，圆O 的直径AB ＝12cm ，C 为AB 延长线上一点，点P 为BD 中点，过点B 作弦BD //CP ，连接PD ．（1）求证：CP 与圆O 相切；（2）若∠C ＝∠D ，求四边形BCPD 的面积．17．如图，在Rt △ABC 中，∠ACB=90°，AD 平分∠BAC 交BC 于点D ，且AD=BD ，点O 是AB 边上一点，以O 为圆心作⊙O 且经过A ，D 两点，交AB 于点E ． （1）求证：BC 是⊙O 的切线；（2）求∠B 的度数．18．如图，以点O 为圆心的两个同心圆中，大圆的弦AB 是小圆的切线，点P 为切点．求证：AP=BP ．19．如图，已知AB 是⊙O 的直径，点C 在⊙O 上，CD 是⊙O 的切线，AD ⊥CD 于点D ，E 是AB 延长线上一点，CE 交⊙O 于点F ，连接OC ，AC ．（1）求证：AC 平分∠DAO ；（2）若∠DAO ＝105°，∠E ＝30°，①求∠OCE 的度数；②若⊙O 的半径为，求线段EF 的长．20．如图，在ABC 中，BC AC =，以BC 为直径的O 与边AB 相交于点D ，与边AB 相交于点F ，DE AC ⊥，垂足为点E ，连接OD .（1）求证：DE 与O 相切； （2）若2AE =，O 的半径4R =，求DE 的长.21．已知点A 、B 在半径为2的⊙O 上，直线AC 与⊙O 相切，OC OB ，连接AB 交OC 于点D ．（1）如图①，若60ACO ︒∠=，求B ：（2）如图②，OC 与⊙O 交于点E ，若//BE OA ，求AB 的长．22．对于给定的M 和点P ，若存在边长为1的等边PQR ∆，满足点Q 在M 上，且MP MR≥（当点,R M 重合时，定义0MR =），则称点P 为M 的“等边远点”，此时，等边PQR ∆是点P 关于M 的“关联三角形”，MR 的长度为点P 关于M 的“等边近距”．在平面直角坐标系xOy 中，O（1）试判断点)A 是否是O 的“等边远点”，若是，请画出对应的“关联三角形”；若不是，请说明理由．（2）下列各点：()()(10,3,,,,0,122B C D E ⎛ ⎝⎭中， “等边远点”有（3）已知直线():0FG y b b =+>分别交,x y 轴于点,F G ，且线段FG 上存在O 的“等边远点”，求b 的取值范围；（4）直接写出O 的“等边远点”关于O 的“等边近距”d 的取值范围是23．如图，在Rt △ABC 中，∠C =90°，以BC 为直径的圆O 交AB 于点D ，切线DE 交AC 于点E ．（1）求证：∠A =∠ADE ；（2）若AD =8，DE =5，求BC 的长．24．如图，在ABC 中，45C ∠=︒，以AB 为直径的O 经过BC 的中点D ．（1）求证：AC 是O 的切线；（2）取AD 的中点E ，连接OE ，延长OE 交AC 于点F ，若2EF =，求O 的半径．25．如图，在33⨯的网格中有一个圆，请仅用无刻度直尺作图（保留画图痕迹）．（1）在图1中，圆过格点A ，B ，请作出圆心O ；（2）在图2中，⊙O 的两条弦AB CD =，请作一个45圆周角．26．已知点(,)M p q 在抛物线21y x =-上，若以M 为圆心的圆与x 轴有两个交点,A B ，且,A B 两点的横坐标是关于x 的方程220x px q -+=的两根．（1）当M 在抛物线上运动时，M 在x 轴上截得的弦长是否变化？为什么？ （2）若M 与x 轴的两个交点和抛物线的顶点C 构成一个等腰三角形，试求,p q 的值．三、填空题27．如图，AB 是O 的直径，点Р是BA 延长线上一点，PC 切O 于点C ，若30,6P PB ∠=︒=，则PC 等于____________．28．已知Rt ABC 的两直角边分别是6和8，则其内切圆半径为_________． 29．如图，已知直线334y x =-与x 轴、y 轴分别交于A B 、两点，点P 是以()0,2C 为圆心，2为半径的圆上一动点，连接PA ，PB ，则PAB ∆的面积最大值是______．30．如图，已知直线5512y x =-与x 轴、y 轴分别交于B 、C 两点，点A 是以(0,2)D 为圆心，2为半径的D 上的一个动点，连接AC 、AB ，则ABC 面积的最小值是__________．31．如图，在△ABC 中，AC =6cm ，BC =8cm ，AB =10cm ，则△ABC 内切圆的半径为___________cm ．32．如图，等腰直角△ABC 中，∠BAC=90°，AB=AC=4．平面内的直线l 经过点A ，作CE ⊥l 于点E ，连接BE.则当直线l 绕着点A 转动时，线段BE 长度的最大值是________．33．如图，PA ，PB 是O 的切线，A ，B 为切点，AC 是O 的直径，35BAC ∠=︒，则P ∠的度数为________.34．如图，PA 切⊙O 于,A PO 与⊙O 交于20B P ∠=︒，，则ABO ∠的大小为_______．参考答案1．B【分析】连结半径BO 延长交圆于D ，连结DC ，利用直径所对的圆周角为之角，利用同弧所对圆周角相等∠D=60º，在Rt △BDC 中，利用特殊三角函数值直接计算即可．【详解】连结BO 并延长交圆于D ，连结DC ，∵O 的半径为6，∴OB=OD=6，∴BD=12，∵BD 为直径，∴∠DCB=90º∵60A ∠=，∴∠D=∠A=60º，在Rt △BDC 中，BC=BD•sin60º=12×2故选择：B ．【点睛】本题考查圆内接三角形问题，掌握圆的有关性质，会利用圆的性质构造直径，利用直径构造直角三角形，利用同弧所对圆周角，再利用特殊三角和数值解决问题是关键．2．B【分析】根据切线的性质定理得∠OAB=90°，进而可求得∠AOB=50°，再根据圆周角定理即可求得∠ACD 的度数．【详解】解：∵AB为O的切线，切点为A，∴∠OAB=90°，∵∠ABO=40°，∴∠AOB=90°﹣∠ABO=90°﹣40°=50°，∴∠ACD=12∠AOB=25°，故选：B．【点睛】本题考查了切线的性质定理、直角三角形的两锐角互余、圆周角定理，熟练掌握切线性质和圆周角定理是解答的关键．3．B【分析】设PA、PB、AB分别与⊙O相切于点C、D、E，然后连接OC、OD、OE，则有OC=OD=OE，进而根据切线定理可得∠OCA=∠ODB=∠OEB=90°，然后可得∠COD=120°，OA、OB分别平分∠EOC、∠EOD，最后根据角的和差关系可求解．【详解】解：设PA、PB、AB分别与⊙O相切于点C、D、E，然后连接OC、OD、OE，如图所示：∵PA、PB、AB与圆O相切，∴∠OCA=∠ODB=∠OEB=90°，OC=OD=OE，∴OA、OB分别平分∠EOC、∠EOD，∵∠P=60°，∴∠COD=120°，∴11,22AOE COE BOE EOD，∴1602AOB AOE BOE EOC EOD，故选B．【点睛】本题主要考查切线的性质定理及角平分线的性质定理的逆定理，熟练掌握切线定理及角平分线的性质定理是解题的关键．4．C【分析】根据切线性质得出PA＝PB，∠PAO＝90°，求出∠PAB的度数，得出∠PAB＝∠PBA，根据三角形的内角和定理求出即可．【详解】∵PA、PB是⊙O的切线，A、B为切点，AC是⊙O的直径，∴∠CAP＝90°，PA＝PB，∴∠PAB＝∠PBA，∵∠BAC＝25°，∴∠PBA＝∠PAB＝90°−25°＝65°，∴∠P＝180°−∠PAB−∠PBA＝180°−65°−65°＝50°，故选：C．【点睛】本题考查了切线长定理，切线性质，三角形的内角和定理，等腰三角形的性质的应用，主要考查学生运用定理进行推理和计算的能力，题目具有一定的代表性，难度适中．5．B【分析】连接OP．根据勾股定理知PQ2＝OP2−OQ2，当OP⊥AB时，线段OP最短，即线段PQ最短．【详解】解：如图，连接OP、OQ．∵PQ 是⊙O 的切线，∴OQ ⊥PQ ．根据勾股定理知PQ 2＝OP 2−OQ 2，∵当PO ⊥AB 时，线段PQ 最短，又∵A （−4，0）、B （0，4），∴OA ＝OB ＝4．∴AB ＝∴OP ＝12AB ＝∴PQ ．故答案为：B ．【点睛】本题考查了切线的判定与性质、坐标与图形性质等知识点．运用切线的性质来进行计算或论证，常通过作辅助线连接圆心和切点，利用垂直构造直角来解决有关问题．6．D【分析】求出直线y x b =-+与圆相切，且函数经过一、二、四象限，和当直线y x b =-+与圆相切，且函数经过二、三、四象限b 的值，则相交时b 的值在相切时的两个b 之间．【详解】当直线y x b =-+与圆相切，且函数经过一、二、四象限时如图在y x b =-+中，令x=0,y=b ，则与y 轴的交点为（0,b ）令y=0,x=b ，则与x 轴的交点为（b,0）则OA=OB ，即△AOB 是等腰直角三角形连接圆心O 和切点C ，则OC=1∴△BOC 也是等腰直角三角形∴BC=OC=1∴=同理当直线y x b =-+与圆相切，且函数经过二、三、四象限时，∴直线y x b =-+与⊙O 相交，则b 的取值范围是b <<故选D ．【点睛】此题主要考查直线与圆的关系综合，解题的关键是根据题意找到直线与圆相切时b 的值． 7．D【分析】根据切线的有关性质可以得到解答．【详解】解：根据切线长定理可知：PA=PB ，∠3=∠4，∴①、③正确；由OA=OB 及两点确定一条直线可知OP 是AB 的垂直平分线，∴④正确；根据切线的性质定理可知，∠OAP=∠OBP=90°，∴∠1=∠2，②正确．故选D ．【点睛】本题考查切线的应用，熟练掌握切线的性质定理和切线长定理是解题关键．8．B【分析】根据圆的有关性质及切线定理可以得解．【详解】解：∵OC=OA，∴∠C=∠OAC=35°，∴∠AOB=∠C+∠OAC=70°，∵AB为⊙O的切线，∴△OAB为直角三角形，∴∠B=90°-∠AOB=20°，故选B．【点睛】本题考查圆的应用，熟练掌握同圆半径相等及圆的切线定理是解题关键．9．B【分析】利用OB=OC可对A选项的结论进行判断；由于AB≠BC，则∠BOC≠∠AOB，而∠BOC=180°-2∠1，∠AOB=180°-2∠4，则∠1≠∠4，于是可对B选项的结论进行判断；根据圆周角定理可对C选项的结论进行判断；利用∠OCA=∠3，∠1=∠2可对D选项的结论进行判断．【详解】解：∵OB=OC，∴∠1=∠2，所以A选项的结论成立；∵OA=OB，∴∠4=∠OBA，∴∠AOB=180°-∠4-∠OBA=180°-2∠4，∵△ABC为不等边三角形，∴AB≠BC，∴∠BOC≠∠AOB，而∠BOC=180°-∠1-∠2=180°-2∠1，∴∠1≠∠4，所以B选项的结论不成立；∵∠AOB与∠ACB都对弧AB，∴∠AOB=2∠ACB，所以C选项的结论成立；∵OA=OC，∴∠OCA=∠3，∴∠ACB=∠1+∠OCA=∠2+∠3，所以D选项的结论成立．故选：B．【点睛】本题考查了三角形的外接圆与外心：三角形外接圆的圆心是三角形三条边垂直平分线的交点，叫做三角形的外心．也考查了圆周角定理和等腰三角形的性质．10．D【分析】A、如图1，连接OE，根据同圆的半径相等得到OB=OE，根据等边三角形的性质得到∠BOE=∠BAC，求得OE∥AC，于是得到A选项正确；B、由于EF是⊙O的切线，得到OE⊥EF，根据平行线的性质得到B选项正确；C、根据等边三角形的性质和圆的性质得到AO=OB，如图2，过O作OH⊥AC于H，根据三角函数得到，于是得到C 选项正确；由于C正确，D自然就错误了．【详解】解：A、如图，连接OE，则OB=OE，∵∠B=60°∴∠BOE=60°，∵∠BAC=60°，∴∠BOE=∠BAC，∴OE∥AC，∵EF⊥AC，∴OE⊥EF，∴EF是⊙O的切线∴A选项正确B、∵EF是⊙O的切线，∴OE⊥EF，由A知：OE∥AC，∴AC⊥EF，∴B选项正确；C、如图，∵，∴BE，∵AB=BC，BO=BE，∴OB，，∴OH=2∴AC是⊙O的切线，∴C选项正确．D、∵∠B=60°，OB=OE，∴BE=OB，∵BE=CE，∴BC=AB=2BO，∴AO=OB，如图，过O作OH⊥AC于H，∵∠BAC=60°，，∴OH=2∴D选项错误；故选：D．【点睛】本题考查了切线的判定和性质，等边三角形的性质，正确的作出辅助线是解题的关键．11．B【分析】由圆周角定理可求得∠AOP 的度数，由切线的性质可知∠PAO=90°，则可中求得∠P ．【详解】解：∵OC ＝OB ，∴∠BCO ＝∠ABC ＝α，∴∠AOP ＝2∠ABC ＝2α，∵P A 是⊙O 的切线，∴P A ⊥AB ，∴∠P AO ＝90°，∴∠P ＝90°﹣∠AOP ＝90°﹣2α，故选：B ．【点睛】本题主要考查切线的性质及圆周角定理，根据圆周角定理可切线的性质分别求得∠AOP 和∠PAO 的度数是解题的关键．12．（1）见解析；（2）【分析】（1）连接OA ，由12AC AB =，OC ＝CB ，证明AC OC CB ==，再证明90OAB ∠=︒， 即可得到结论；（2）连接OD ，由45DCA ∠=︒，证明90DOA ∠=︒， 结合2OD OA OC ===， 利用勾股定理可得答案．【详解】（1）证明：如图连接OA ．∵12AC AB =，OC ＝CB ， ∴AC ＝OC ＝CB ，∴∠=∠∠=∠COA CAO CAB CBA,,()∴∠+∠=︒，CAO CAB2180∴∠+∠=︒，90CAO CAB∴∠OAB＝90°，∴AB是⊙O的切线．（2）解：连接OD．∵∠DOA＝2∠DCA，∠DCA＝45°，∴∠DOA＝90°，∵OD＝OA＝OC＝2，∴AD=【点睛】本题考查的是圆周角定理，切线的判定，等腰三角形的定义与性质，三角形的内角和定理，勾股定理的应用，掌握以上知识是解题的关键．13．（1）两次；（2）详见解析．【分析】（1）由垂径定理可得，CD所在直线是直径的位置，再根据两个直径的交点即为圆心即可解答；（2）连接AC、BC，分别作它们的垂直平分线其交点即为圆心．【详解】解：（1）如图所示，根据垂径定理的推论，两个直径的交点即为圆心．（2）在AB上任作一点C，如图所示：1．分别连接AC，BC．2．分别作AC，BC的垂直平分线交于点O，则点O即为所求．【点睛】本题主要考查垂径定理的推论，掌握弦的垂直平分线经过圆心且平分这条弦所对的弧成为解答本题的关键．14．（1）见解析；（2【分析】（1）连接OD，根据角平分线的定义得到∠BAD＝∠DAE，根据等腰三角形的性质得到∠ODA＝∠OAD，由垂直的定义得到∠AEP＝90°，根据切线的判定定理即可得到结论；（2）连接BD，根据角平分线的定义得到∠BAD＝∠DAE＝30°，推出AB＝2BD，设BD ＝x，则AB＝2x，根据勾股定理即可得到结论．【详解】（1）证明：∵AD平分∠BAC，∴∠OAD＝∠DAE．∵OA＝OD，∴∠ODA＝∠OAD．∴∠ODA＝∠DAE．∴OD∥AE．∵AC⊥PD，∴∠AEP＝90°．∴∠ODP＝∠AEP＝90°．∵OD是⊙O的半径，∴PD是⊙O的切线．（2）解：如图，连接BD，∵AD平分∠BAC，∠BAC＝60°，∴∠BAD＝∠DAE＝30°．∵AC⊥PE，DE∴AD＝2DE＝∵AB为⊙O的直径，∴∠ADB＝90°．∴AB＝2BD．设BD＝x，则AB＝2x，∵AD2＋BD2＝AB2，∴x2＋（2＝（2x）2，解得x即BD，AB，∴AO，∴⊙O．【点睛】本题考查了圆的切线的判定及圆的相关计算，解答此题的关键是明确题意，找出所求问题需要的条件，正确的作出辅助线利用勾股定理解答．15．（1）相切，证明见解析；（2）10cm【分析】（1）相切，由已知可证得∠OCD=90°即CD是⊙O的切线；（2）由已知可推出∠A=∠BCD=30°，即BC=BD=10，从而得到AB=20即可得到半径的长．【详解】解：（1）CD与⊙O相切．证明：∵AB为⊙O的直径，C是⊙O上一点，∴∠ACB=90°，即∠ACO+∠OCB=90°；∵∠A=∠OCA，且∠DCB=∠A，∴∠OCA=∠DCB，∴∠OCD=90°，∴CD是⊙O的切线．（2）在Rt△OCD中，∠D=30°；∴∠COD=60°，∴∠A=30°，∴∠BCD=30°，∴BC=BD=10，∴AB=20，∴r=10．【点睛】本题考查的是切线的判定，要证某线是圆的切线，已知此线过圆上某点，连接圆心和这点（即为半径），再证垂直即可．16．（1）见解析；（2）【分析】（1）连接OP，根据垂径定理得到BD⊥OP，根据平行线的性质即可得到结论；（2）根据圆周角定理得到∠POB=2∠D，根据三角形的内角和得到∠C=30°，推出四边形BCPD是平行四边形，计算OE、OP、PC的值，进而得到高PE的值，于是得到结论．【详解】（1）证明：连接OP，交BD于点E，∵点P 为的中BD 点．∴BD ⊥OP ，∵BD ∥CP ，∴∠OEB ＝∠OPC ＝90°∴PC ⊥OP ，∴CP 与⊙O 相切于点P ；（2）解：∵∠POB ＝2∠D ，∠C ＝∠D ，∴∠POB ＝2∠C ，∵∠CPO ＝90°，∴∠C ＝30°，∵BD ∥CP ，∴∠C ＝∠DBA ，∴∠D ＝∠DBA ，∴BC ∥PD ，∴四边形BCPD 是平行四边形，∵PO ＝12AB ＝6，∴PC ＝∵∠ABD ＝∠C ＝30°，∴OE ＝12OB ＝3， ∴PE ＝3，∴四边形BCPD 的面积＝PC •PE ＝3⨯＝【点睛】本题考查了切线的判定，垂径定理，平行四边形的判定和性质，解直角三角形，正确的作出辅助线是解题的关键．17．（1）证明过程见解析；（2）30B ∠=︒【分析】（1）通过已知条件证明90ODB ∠=︒即可证明；（2）根据角平分线的性质和等腰三角形的性质求解即可；【详解】（1）∵OA OD =，∴OAD ODA ∠=∠，∵AD 平分∠BAC ，∴CAD OAD ∠=∠，∴CAD ODA ∠=∠，∴OD ∥AC ，∴ACB ODB ∠=∠，∵90ACB ∠=︒，∴90ODB ∠=︒，∵OD 是半径，∴BC 是⊙O 的切线；（2）∵AD BD =，∴DAB B ∠=∠，∵AD 平分∠BAC ，∴CAD OAD ∠=∠，∵90C ∠=︒，∴90B CAB ∠+∠=︒，∴90B CAD BAD ∠+∠+∠=︒，∴390B =︒∠，∴30B ∠=︒．【点睛】本题主要考查了切线的证明，结合角平分线的性质、直角三角形两锐角互余进行计算是关键． 18．见解析【分析】根据切线的性质得出OP ⊥AB ，根据垂径定理得出即可．【详解】证明：如图，连接OP ，∵大圆的弦AB是小圆的切线，点P为切点，∴OP⊥AB，∵OP过O，∴AP=BP．【点睛】本题考查了切线的性质和垂径定理的应用，主要考查学生的推理能力，题目比较好，难度适中．19．（1）见解析；（2）①45°，②2．【分析】（1）由切线性质知OC⊥CD，结合AD⊥CD得AD∥OC，即可知∠DAC＝∠OCA＝∠OAC，从而得证；（2）①由AD∥OC知∠EOC＝∠DAO＝105°，结合∠E＝30°可得结果；②作OG⊥CE，根据垂径定理及等腰直角三角形性质知CG＝FG＝OG，由OC＝得出CG＝FG＝OG＝2，在Rt△OGE中，由∠E＝30°可得GE＝【详解】（1）证明：∵CD是⊙O的切线，∴OC⊥CD．∵AD⊥CD，∴AD∥OC．∴∠DAC＝∠OCA．∵OC＝OA，∴∠OCA＝∠OAC．∴∠OAC＝∠DAC．∴AC平分∠DAO．（2）①∵AD∥OC，∴∠EOC ＝∠DAO ＝105°．∵∠E ＝30°，∴∠OCE ＝180°－∠EOC －∠E ＝45°．②作OG ⊥CE 于点G ，∵OC ＝OCE ＝45°，∴CG ＝OG ＝2．∴FG ＝2．在Rt △OGE 中，∠E ＝30°，∴GE ＝∴EF ＝GE−FG ＝2．【点睛】本题考查了圆的切线的性质、平行线的判定与性质、垂径定理等知识，熟练掌握切线的性质、平行线的判定与性质、垂径定理是解题的关键．20．（1）见解析；（2）【分析】（1）根据内错角证明两直线平行，再换算角度即可证明DE 与 ⊙O 相切；（2）构造直角三角形根据勾股定理即可求出DE 的长．【详解】（1）证明：连接CD∵BC 为O 的直径，∴90BDC ∠=︒∴CD AB ⊥又∵BC AC =∴12∠=∠∵OD OC =∴13∠=∠∴23∠∠=∴//OD AC∴ODE AED ∠=∠∵DE AC ⊥∴90AED ∠=︒∴90ODE ∠=︒∴DE OD ⊥∴DE 与O 相切（2）过O 作ON CF ⊥于N ，可得四边形ODEN 是矩形，∴4EN OD R ===，ON DE =又∵2AE =，448AC CB ==+=，∴2CN AC AE EN AC AE OD =--=--=，在Rt ONC 中，ON =∴ON =∴DE =【点睛】此题考查圆的相关知识，涉及到切线，平行线的判定，勾股定理等．21．（1）30°；（2）【分析】（1）由切线的性质可知∠OAC=90°，由三角形的内角和定理可知∠AOC=30°，由∠AOB=∠AOC+∠BOC 可得出∠AOB 的度数，结合OA=OB 可得出∠B=30°；（2）过B 作BH AO ⊥交AO 的延长线于H ，由BE ∥OA 可得出ABE OAB ∠=∠，结合等腰直角三角形的性质可得出45OBE ︒∠=，根据勾股定理得出OH BH ==结合勾股定理即可得出结论．【详解】解：（1））∵AC与⊙O相切，∴∠OAC=90°∵∠OCA=60°∴∠AOC=30°∵OC⊥OB，∴∠AOB=∠AOC+∠BOC=120°∵OA=OB，∴180120302B︒︒︒-∴∠==；（2）过B作BH AO⊥交AO的延长线于H//BE OAABE OAB∴∠=∠,90OB OE BOE︒=∠=45OBE︒∴∠=45HO B OAB OBA ABE OBA OBE︒∴∠=∠+∠=∠+∠=∠=2OA OB==OH BH∴==AB∴===【点睛】本题考查了切线的性质，勾股定理，等腰三角形的性质，熟练掌握切线的性质是解本题的关键．22．（1）是，画图见解析；（2）,C D ；（3）12b ≤≤+（41d ≤≤【分析】 （1）根据“等边远点”的定义即可作图，求出“等边远点”到圆心的距离范围，故可进行判断； （2）根据“等边远点”的定义求出点到圆心的距离即可判断；（3）找到O 的所有的“等边远点”构成的图形，即可求解； （4）根据O 的“等边近距”找到最远与最近，即可求解．【详解】（1）如图，根据定义作图，点I 在圆上，作边长为1的等边△IJK,当O 、I 、J 在同一直线上时，J 点为最远的“等边远点”，此时1，当点J 在圆内时，如△LMN 所示，OL ⊥MN ，此时M 或N 为最近的“等边远点”，LM=1,MH=12MN=12=∴∴1=故要判断是否为“等边远点”，只需判断点到圆心的距离，即1∵)A∴2=由1，故点)A 是O 的“等边远点”，对应的“关联三角形”如下：是，“关联三角形”△AFG 如图所示；（2）∵()()(10,3,,,0,12B C D E ⎛ ⎝⎭∴1=，OE=1∴“等边远点”有,C D 故答案为,C D ；（3）如图，O 的所有的“等边远点”构成以O 为圆心，以半径OB=1,OA 为1+外径的圆环，∵直线():0FG y b b =+>分别交,x y 轴于点,F G ，且线段FG 上存在O 的“等边远点”，∴12b ≤≤+（4）如图，当O,C,Q 在同一直线上时，C 点为最近的“等边近距”，此时1;当OD ⊥EF 于G 点时，F 点为最远的“等边近距”，DG= 2=OG=2+2∴故“等边近距”d 1d ≤≤1d ≤≤【点睛】此题主要考查圆的综合运用，解题的关键是根据题意理解“等边远点” 、“等边近距”的定义利用点与圆的关系，垂径定理等性质来解答． 23．（1）证明见解析；（2）152． 【分析】（1）只要证明90A B ∠+∠=︒，90ADE B ∠+∠=︒，即可解决问题； （2）首先证明210AC DE ==，在Rt △ADC 中，6DC =，设BD x =， 在Rt△BDC 中，2226BC x =+，在Rt△ABC 中，()222810BC x =+-，可得()22226810x x +=+-，解方程即可解决问题；【详解】（1）证明：连接OD ， ∵DE 是切线， ∴90ODE ∠=︒，∴90ADE BDO ∠+∠=︒， ∵90ACB ∠=︒， ∴90A B ∠+∠=︒， ∵OD=OB ， ∴B BDO ∠=∠， ∴ADE A ∠=∠； （2）连接CD ， ∵ADE A ∠=∠， ∴AE=DE ，∵BC 为圆O 的直径，90ACB ∠=︒， ∴EC 是O 的切线，∴ED=EC ， ∴AE=EC ， ∵5DE =， ∴210AC DE ==， 在Rt △ADC 中，6DC =，设BD x =，在Rt△BDC 中，222=6BC x +，在Rt△ABC 中，()222810BC x =+-， ∴()22226810x x +=+-， 解得：92x =，∴152BC ==．【点睛】本题主要考查了圆的基本性质，切线的性质，准确分析计算是解题的关键．24．（1）见解析；（22+ 【分析】（1）连接AD ，先由圆周角定理得∠ADB ＝90°，则AD ⊥BC ，再由线段垂直平分线的性质得AB ＝AC ，则∠B ＝∠C ＝45°，求得∠BAC ＝90°，即可得出结论；（2）作EH ⊥OF 交AF 于H ，则EH 是⊙O 的切线，先由垂径定理得OE ⊥AD ，AG ＝DG ，再证出△EFH 是等腰直角三角形，得EH ＝EF FH EF ＝2，然后由切线长定理得AH ＝EH ，则AF ＝AH ＋FH ＋2，最后由等腰直角三角形的性质得OA ＝AF 2即可． 【详解】（1）证明：连接AD ，如图所示：∵AB 是⊙O 的直径，∴∠ADB＝90°，OA是⊙O的半径，∴AD⊥BC，∵D是BC的中点，∴AB＝AC，∴∠B＝∠C＝45°，∴∠BAC＝180°−45°−45°＝90°，∴AC⊥OA，∴AC是⊙O的切线；（2）解：作EH⊥OF交AF于H，如图所示：则EH是⊙O的切线，∵E是AD的中点，∴OE⊥AD，AG＝DG，∵AD⊥BC，∴OF∥BC，∴∠EFH＝∠C＝45°，∵EH⊥OF，∴△EFH是等腰直角三角形，∴EH＝EF，FH EF＝2，∵AC是⊙O的切线，∴AH＝EH，∴AF＝AH＋FH2，由（1）得：∠BAC＝90°，∴△AOF是等腰直角三角形，∴OA＝AF＋2，即⊙O ＋2． 【点睛】本题考查了切线的判定与性质、圆周角定理、垂径定理、线段垂直平分线的性质、等腰三角形的判定与性质等知识；熟练掌握切线的判定与性质、垂径定理和圆周角定理是解题的关键． 25．（1）见解析；（2）见解析. 【分析】（1）如图3，连接AN 、BM ，通过圆内接三角形是直角三角形时，斜边就是直径来确定圆心位置；（2）连接BC 、AD 、BD ，通过同（等）弧所对圆周角相等推出ABD CDB ∠=∠，进而推出45BDC ∠=︒． 【详解】（1）如图3，连接AN 、BM 交点O 即为圆心 ∵9090ABN BAM ∠=︒∠=︒，， ∴AN 、BM 是直径， ∴直径交点O 就是圆心．（2）如图4，连接BC 、AD 、BD ∵AB=CD ， ∴AB CD =， ∴ADB CBD ∠=∠， 又∵AC CA =， ∴ABC CDA ∠=∠， ∴ABD CDB ∠=∠， 又∵90BED ∠=︒，∴45ABD CDB ∠=∠=︒， 故连接BD ，则45BDC ∠=︒．【点睛】本题考查确定圆心和确定圆弧圆周角等问题，解题的关键是圆内接三角形是直角三角形时，斜边就是直径以及同（等）弧所对圆周角相等．26．（1）不变，弦长始终为2，理由见解析；（2）0,1p q ==-或13p q =+=+13p q =-=-1,3p q ==+1,3p q ==-【分析】(1)设A B 、两点的横坐标分别是12x x 、，由韦达定理结合点(,)M p q 在抛物线上求出21212124ABx x x x x x 即可求解；(2)按照等腰三角形顶角不同分成三类讨论，逐个求解即可． 【详解】解：（1）设A B 、两点的横坐标分别是12x x 、，由根与系数的关系知12122,x x p x x q +=⋅=，那么：12AB x x =-===，又因为M 在抛物线21y x =-上，所以21q p =-．故2AB =，故答案为: 弦长AB 不变，始终为2； (2)(0,1)C -，①当C 为等腰三角形顶角时：AC BC =，此时M 点与C 点重合，A 、B 两点关于y 轴对称，即12x x =-，∴0,1p q ==-；②当A 为等腰三角形顶角时:AC AB =，且222211AC OA OC x ，24AB =∴2114x ，解得13x ，当1x =22x =13,323p q ，当1x =22x =13p q =-=-③当B 为等腰三角形顶角时：BC AB =，且222221BC OB OC x ，24AB =∴2214x ，解得13x ，当2x =时，12x =，对应的1,3p q ==+当2x =时，132x ，对应的1,3p q ==-综上所述：0,1p q ==-或13p q =+=+13p q =-=-1,3p q ==+1,3p q ==-【点睛】本题考查了圆中弦长的求法，韦达定理，二次函数上点的坐标特征，等腰三角形的存在性问题等，属于一道综合题，计算过程中细心是解决本题的关键．27．【分析】连接OC ，求出∠PCO=90°，设O 的半径是R ，根据30°角所对的直角边等于斜边的一半求得R=2，由勾股定理得出22+PC 2=（6-2）2，求出即可． 【详解】解：如图，连结CO ， ∵PC 切⊙O 于点C ， ∴∠PCO=90°， ∵30P ∠=，∴PO=2OC， ∵PB=6，∴PO+OB=PO+CO=3CO=6， ∴CO=2， ∴PO=6－2=4，∵===PC故答案为【点睛】本题主要考查了切线的性质和勾股定理的应用，解此题的关键是能根据题意求出PCO △是直角三角形.28．2 【分析】根据勾股定理求出直角三角形的斜边，再根据内切圆的半径的特点进行求解即可； 【详解】 如图，∵8AC =，6BC =， ∴10AB =， 设内切圆的半径为r ， ∴==CE CF r ， ∴8AD AF r ==-，6BD BE r ==-，∴6810r r -+-=， 解得2r．故答案是2． 【点睛】本题主要考查了三角形的内切圆，准确计算是解题的关键． 29．13 【分析】求出A 、B 的坐标，根据勾股定理求出AB ，求出点C 到AB 的距离，即可求出圆C 上点到AB 的最大距离，根据面积公式求出即可． 【详解】解：∵直线334y x =-与x 轴、y 轴分别交于A 、B 两点， ∴A 点的坐标为（4，0），B 点的坐标为（0，-3），3x-4y-12=0， 即OA=4，OB=3，由勾股定理得：AB=5 过C 作CM ⊥AB 于M ，连接AC ， 则由三角形面积公式得：111222AB CM OA OC OA OB =+ ∴5CM 4134=⨯+⨯ ∴16CM 5=∴圆C 上点到直线334y x =-的最大距离是：1626255+= ∴PAB 面积的最大值是12651325⨯⨯= 故答案为：13． 【点睛】本题考查了三角形的面积，点到直线的距离公式的应用，解此题的关键是求出圆上的点到直线AB 的最大距离．30．29【分析】过点D 作DM BC ⊥于点M ，连接BD ，根据三角形面积公式求出DM 的长，可知D 上的点到直线5512y x =-的最小距离是DM 长减半径，就可以算出面积最小值． 【详解】解：如图，过点D 作DM BC ⊥于点M ，连接BD ，令0y =，则12x =，令0x =，则5y =-，∴()12,0B ，()0,5C -，∴12OB =，5OC =，13BC ==， 根据三角形面积公式，1122BC DM OB CD ⋅=⋅， ∴8413DM =， ∴D 上的点到直线5512y x =-的最小距离是845821313-=， ∴ABC 面积的最小值是1581329213⨯⨯=． 故答案是：29．【点睛】本题考查一次函数，圆上一点到定直线的最短距离，解题的关键是求出圆上的点到直线BC 的最小距离．31．2【分析】根据勾股定理逆定理证得△ABC 为直角三角形，又因为OD AC ⊥、OE BC ⊥且OD=OE 得到四边形ODCE 为正方形，再根据切线长定理得到AD=AF ，BE=BF ，代入数值即可求解.【详解】∵2226810+=∴222AB BC AC +=∴△ABC 为直角三角形∵OD AC ⊥、OE BC ⊥且OD=OE∴四边形ODCE 为正方形∴CD=CE=OD=OE∵AD 、AB 、BC 为圆的切线∴AD=AF ，BE=BF ∴6810222AC BC AB CD +-+-=== 故答案为：2．【点睛】本题考查了勾股定理逆定理、正方形的判定和性质以及切线长定理，关键是掌握切线长定理并能熟练应用．32．2+【分析】以AC 为直径作圆O ，连接BO ，并延长交圆O 于点E '，可得BO+O E '＞B E '，从而可得BO+OE ＞B E '，即BE 为最大值，再由勾股定理求出BO 的长即可解决问题．【详解】解：由题意知，CE ⊥l 于点E ，∴以AC 为直径作圆O ，∵CE ⊥AE,∴点E 在圆O 上运动，连接BO ，并延长交圆O 于点E '，如图，∴BO+O E '＞B E '，∵OE=O E '，∴BO+OE ＞B E '，∴BE 的长为最大值，∵AO=OC=OE ，且AB=AC=4， ∴122OE AC == 又∵∠BAC=90°∴222224220BO AO AB =+=+=∴BO =∴BE=2BO OE +=故答案为：2+【点睛】此题主要考查了求线段的最大值，构造出△ACE 的外接贺是解答本题的关键．33．70°【分析】根据题意可以求得∠OAP 和∠OBP 的度数，然后根据∠BAC ＝35°，即可求得∠P 的度数．【详解】解：连接OB ：∵PA 、PB 是⊙O 的两条切线，A 、B 是切点，AC 是⊙O 的直径，∴∠OAP ＝∠OBP ＝90°，∵∠BAC ＝35°，OA ＝OB ，∴∠BAC ＝∠OBA ＝35°，∴∠PAB ＝∠PBA ＝55°，∴∠P ＝180°−∠PAB−∠PBA ＝70°，即∠P 的度数是70°，故答案为：70°．【点睛】本题考查切线的性质，解答此类问题的关键是明确题意，找出所求问题需要的条件，利用切线的性质解答问题．34．55°【分析】由切线可到∠OAP=90°，然后可知70AOP ∠=︒，根据半径相等得到OAB OBA ∠=∠，从而计算即可得到结果．【详解】解：∵PA 切⊙O 于A ，∴OA ⊥AP ，即∠OAP=90°，∵20P ∠=︒，∴902070AOP ∠=︒-︒=︒，∵OA=OB ， ∴()118070552ABO OAB =∠=︒-︒=︒∠， 故答案为：55°．【点睛】本题考查了切线的性质，如果直线与圆相切，则圆心到直线的距离等于半径．。