2007年考研数学一真题及答案

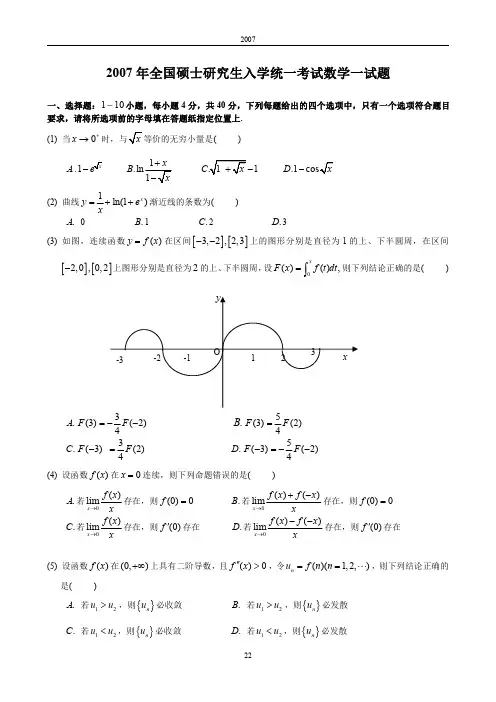
2007年考研数学一真题一、选择题（本题共10小题，每小题4分，满分40分，在每小题给的四个选项中，只有一项符合题目要求，把所选项前的字母填在题后括号内）（1） 当0x +→( )A. 1-B.C. 1D.1-(2) 曲线y=1ln(1x e x++), 渐近线的条数为 ( ) A.0 B.1 C.2 D.3(3)如图，连续函数y=f(x)在区间[-3，-2]，[2，3]上的图形分别是直径为1的上、下半圆周，在区间[-2，0]，[0，2]的图形分别是直径为2的上、下半圆周，设F(x)=0()xf t dt ⎰.则下列结论正确的是 ( )A. F(3)=3(2)4F -- B. F(3)=5(2)4F C. F(3)=3(2)4F + D. F(3)= 5(2)4F -- (4)设函数f （x ）在x=0处连续，下列命题错误的是 ( )A. 若0()limx f x x →存在，则f （0）=0 B. 若0()()lim x f x f x x→+- 存在，则f （0）=0C. 若0()lim x f x x → 存在，则'(0)f =0D. 若0()()lim x f x f x x→-- 存在，则'(0)f =0(5)设函数f （x ）在（0, +∞）上具有二阶导数，且"()f x o >, 令n u =f(n)=1,2,…..n, 则下列结论正确的是 ( ) A.若12u u >，则{n u }必收敛 B. 若12u u >，则{n u }必发散 C. 若12u u <，则{n u }必收敛 D. 若12u u <，则{n u }必发散(6)设曲线L ：f(x, y) = 1 (f(x, y)具有一阶连续偏导数），过第Ⅱ象限内的点M 和第Ⅳ象限内的点N,T 为L 上从点M 到N 的一段弧，则下列小于零的是 ( ) A.(,)rx y dx ⎰ B. (,)rf x y dy ⎰C.(,)rf x y ds ⎰D.'(,)'(,)x y rf x y dx f x y dy +⎰（7）设向量组1α，2α，3α线形无关，则下列向量组线形相关的是： ( ) （A ）,,122331αααααα--- （B ） ,,122331αααααα+++（C ） 1223312,2,2αααααα--- （D ）1223312,2,2αααααα+++（8）设矩阵A=211121112--⎛⎫ ⎪-- ⎪ ⎪--⎝⎭，B=100010000⎛⎫ ⎪⎪ ⎪⎝⎭，则A 于B ( )(A) 合同，且相似(B) 合同，但不相似 (C) 不合同，但相似(D)既不合同，也不相似（9）某人向同一目标独立重复射击，每次射击命中目标的概率为p ()01p <<，则此人第4次射击恰好第2次命中目标的概率为： ( ) （A ）23(1)p p - (B)26(1)p p - (C) 223(1)p p -(D) 226(1)p p -(10) 设随即变量（X ，Y ）服从二维正态分布，且X 与Y 不相关，()X f x ，()Y f y 分别表示X ，Y 的概率密度，则在Y ＝y 的条件下，X 的条件概率密度|(|)X Yf x y 为 ( )（A ）()X f x(B) ()Y f y(C) ()X f x ()Y f y(D)()()X Y f x f y 二．填空题：11－16小题，每小题4分，共24分，请将答案写在答题纸指定位置上 （11）31211x e dx x⎰＝_______. （12）设(,)f u v 为二元可微函数，(,)y xz f x y =，则zx∂∂＝______. (13)二阶常系数非齐次线性方程2''4'32x y y y e -+=的通解为y ＝____________. (14)设曲面∑：||||||1x y z ++=，则(||)x y ds ∑+⎰⎰＝_____________.(15)设矩阵A ＝0100001000010000⎛⎫ ⎪ ⎪ ⎪ ⎪⎝⎭，则3A 的秩为________. （16）在区间（0，1）中随机地取两个数，则这两个数之差的绝对值小于12的概率为________. 三．解答题：17~24小题，共86分.请将解答写在答题纸指定的位置上.解答应写出文字说明、证明过程或演算步骤.222222(,)2{(,)4,0}f x y x y x y D x y x y y =+-=+≤≥(17)（本题满分11分）求函数在区域上的最大值和最小值。

2007年考研数学一真题一、选择题（110小题，每小题4分，共40分。

下列每题给出的四个选项中，只有一个选项是符合题目要求的。

）(1)当时，与等价的无穷小量是(A)(B)(C)(D)【答案】B。

【解析】时几个不同阶的无穷小量的代数和，其阶数由其中阶数最低的项来决定。

综上所述，本题正确答案是B。

【考点】高等数学—函数、极限、连续—无穷小量的性质及无穷小量的比较(2)曲线渐近线的条数为(A)0(B)1(C)2(D)3【答案】D。

【解析】由于，则是曲线的垂直渐近线；又所以是曲线的水平渐近线；斜渐近线：由于一侧有水平渐近线，则斜渐近线只可能出现在一侧。

则曲线有斜渐近线，故该曲线有三条渐近线。

综上所述，本题正确答案是D。

【考点】高等数学—一元函数微分学—函数图形的凹凸性、拐点及渐近线(3)如图，连续函数在区间上的图形分别是直径为1的上、下半圆周，在区间上的图形分别是直径为2的下、上半圆周，设,则下列结论正确的是(A)(B)(C)(D)【答案】C。

【解析】-3-2-10123【方法一】四个选项中出现的在四个点上的函数值可根据定积分的几何意义确定则【方法二】由定积分几何意义知,排除(B)又由的图形可知的奇函数，则为偶函数，从而显然排除(A)和(D),故选(C)。

综上所述，本题正确答案是C。

【考点】高等数学—一元函数积分学—定积分的概念和基本性质，定积分的应用(4)设函数在处连续，下列命题错误．．的是(A)若存在，则(B)若存在，则(C)若存在，则存在(D)若存在，则存在【答案】D。

【解析】(A)：若存在，因为,则,又已知函数在处连续，所以,故,(A)正确；(B)：若存在，则,则，故(B)正确。

(C)存在，知，则则存在，故(C)正确(D)存在，不能说明存在例如在处连续，存在，但是不存在，故命题(D)不正确。

综上所述，本题正确答案是D。

【考点】高等数学—一元函数微分学—导数和微分的概念(5)设函数在内具有二阶导数，且,令,则下列结论正确的是 (A)若,则必收敛(B)若,则必发散 (C)若,则必收敛(D)若,则必发散【答案】D 。

2007年考研数学一真题一、选择题（本题共10小题，每小题4分，满分40分，在每小题给的四个选项中，只有一项符合题目要求，把所选项前的字母填在题后括号内） （1） 当0x +→时，与x 等价的无穷小量是 ( ) A. 1xe- B.1ln1xx+- C. 11x +- D.1cos x -(2) 曲线y=1ln(1x e x++), 渐近线的条数为 ( ) A.0 B.1 C.2 D.3(3)如图，连续函数y=f(x)在区间[-3，-2]，[2，3]上的图形分别是直径为1的上、下半圆周，在区间[-2，0]，[0，2]的图形分别是直径为2的上、下半圆周，设F(x)=0()xf t dt ⎰.则下列结论正确的是 ( ) A. F(3)=3(2)4F -- B. F(3)=5(2)4F C. F(3)=3(2)4F + D. F(3)= 5(2)4F --(4)设函数f （x ）在x=0处连续，下列命题错误的是 ( )A. 若0()limx f x x →存在，则f （0）=0 B. 若0()()lim x f x f x x→+- 存在，则f （0）=0C. 若0()lim x f x x → 存在，则'(0)f =0D. 若0()()lim x f x f x x→-- 存在，则'(0)f =0(5)设函数f （x ）在（0, +∞）上具有二阶导数，且"()f x o >, 令n u =f(n)=1,2,…..n, 则下列结论正确的是 ( )A.若12u u >，则{n u }必收敛B. 若12u u >，则{n u }必发散C. 若12u u <，则{n u }必收敛D. 若12u u <，则{n u }必发散(6)设曲线L ：f(x, y) = 1 (f(x, y)具有一阶连续偏导数），过第Ⅱ象限内的点M 和第Ⅳ象限内的点N,T 为L 上从点M 到N 的一段弧，则下列小于零的是 ( ) A.(,)rx y dx ⎰ B. (,)rf x y dy ⎰C.(,)rf x y ds ⎰D.'(,)'(,)x y rf x y dx f x y dy +⎰（7）设向量组1α，2α，3α线形无关，则下列向量组线形相关的是： ( ) （A ）,,122331αααααα--- （B ） ,,122331αααααα+++（C ） 1223312,2,2αααααα--- （D ）1223312,2,2αααααα+++（8）设矩阵A=211121112--⎛⎫ ⎪-- ⎪ ⎪--⎝⎭，B=100010000⎛⎫ ⎪⎪ ⎪⎝⎭，则A 于B ( )(A) 合同，且相似(B) 合同，但不相似 (C) 不合同，但相似(D)既不合同，也不相似（9）某人向同一目标独立重复射击，每次射击命中目标的概率为p ()01p <<，则此人第4次射击恰好第2次命中目标的概率为： ( ) （A ）23(1)p p - (B)26(1)p p - (C) 223(1)p p -(D) 226(1)p p -(10) 设随即变量（X ，Y ）服从二维正态分布，且X 与Y 不相关，()X f x ，()Y f y 分别表示X ，Y 的概率密度，则在Y ＝y 的条件下，X 的条件概率密度|(|)X Yf x y 为 ( )（A ）()X f x(B) ()Y f y(C) ()X f x ()Y f y(D)()()X Y f x f y 二．填空题：11－16小题，每小题4分，共24分，请将答案写在答题纸指定位置上 （11）31211x e dx x⎰＝_______. （12）设(,)f u v 为二元可微函数，(,)y xz f x y =，则zx∂∂＝______. (13)二阶常系数非齐次线性方程2''4'32x y y y e -+=的通解为y ＝____________. (14)设曲面∑：||||||1x y z ++=，则(||)x y ds ∑+⎰⎰＝_____________.(15)设矩阵A ＝0100001000010000⎛⎫ ⎪⎪ ⎪ ⎪⎝⎭，则3A 的秩为________. （16）在区间（0，1）中随机地取两个数，则这两个数之差的绝对值小于12的概率为________. 三．解答题：17~24小题，共86分.请将解答写在答题纸指定的位置上.解答应写出文字说明、证明过程或演算步骤.222222(,)2{(,)4,0}f x y x y x y D x y x y y =+-=+≤≥(17)（本题满分11分）求函数在区域上的最大值和最小值。

2007年考研数学一真题一、选择题（110小题，每小题4分，共40分。

下列每题给出的四个选项中，只有一个选项是符合题目要求的。

）(1)当时，与等价的无穷小量是(A) (B)(C) (D)【答案】B。

【解析】当时几个不同阶的无穷小量的代数和，其阶数由其中阶数最低的项来决定。

综上所述，本题正确答案是B。

【考点】高等数学—函数、极限、连续—无穷小量的性质及无穷小量的比较(2)曲线渐近线的条数为(A)0 (B)1(C)2 (D)3【答案】D。

【解析】由于∞，则是曲线的垂直渐近线；又∞∞∞∞∞所以是曲线的水平渐近线；斜渐近线：由于∞一侧有水平渐近线，则斜渐近线只可能出现在∞一侧。

∞∞∞∞∞∞∞∞∞则曲线有斜渐近线，故该曲线有三条渐近线。

综上所述，本题正确答案是D。

【考点】高等数学—一元函数微分学—函数图形的凹凸性、拐点及渐近线(3)如图，连续函数在区间上的图形分别是直径为1的上、下半圆周，在区间上的图形分别是直径为2的下、上半圆周，设,则下列结论正确的是(A)(B)(C)(D)【答案】C。

【解析】【方法一】四个选项中出现的在四个点上的函数值可根据定积分的几何意义确定则【方法二】由定积分几何意义知,排除(B)又由的图形可知的奇函数，则为偶函数，从而显然排除(A)和(D),故选(C)。

综上所述，本题正确答案是C。

【考点】高等数学—一元函数积分学—定积分的概念和基本性质，定积分的应用(4)设函数在处连续，下列命题错误．．的是(A)若存在，则(B)若存在，则(C) 若存在，则′存在(D) 若存在，则′存在【答案】D。

【解析】(A)：若存在，因为,则,又已知函数在处连续，所以,故,(A)正确；(B)：若存在，则,则，故(B)正确。

(C)存在，知，则′则′存在，故(C)正确(D)存在，不能说明存在例如在处连续，存在，但是′不存在，故命题(D)不正确。

综上所述，本题正确答案是D。

【考点】高等数学—一元函数微分学—导数和微分的概念(5)设函数在∞内具有二阶导数，且′′,令,则下列结论正确的是(A)若,则必收敛 (B)若,则必发散(C)若,则必收敛 (D)若,则必发散【答案】D。

2007年考研数学一真题一、选择题（本题共10小题，每小题4分，满分40分，在每小题给的四个选项中，只有一项符合题目要求，把所选项前的字母填在题后括号内） （1） 当0x +→( )A. 1-B.C. 1D.1-(2) 曲线y=1ln(1x e x++), 渐近线的条数为 ( ) A.0 B.1 C.2 D.3(3)如图，连续函数y=f(x)在区间[-3，-2]，[2，3]上的图形分别是直径为1的上、下半圆周，在区间[-2，0]，[0，2]的图形分别是直径为2的上、下半圆周，设F(x)=0()xf t dt ⎰.则下列结论正确的是 ( ) A. F(3)=3(2)4F -- B. F(3)=5(2)4F C. F(3)=3(2)4F + D. F(3)= 5(2)4F -- (4)设函数f （x ）在x=0处连续，下列命题错误的是 ( )A. 若0()limx f x x →存在，则f （0）=0 B. 若0()()lim x f x f x x→+- 存在，则f （0）=0C. 若0()lim x f x x → 存在，则'(0)f =0D. 若0()()lim x f x f x x→-- 存在，则'(0)f =0(5)设函数f （x ）在（0, +∞）上具有二阶导数，且"()f x o >, 令n u =f(n)=1,2,…..n, 则下列结论正确的是 ( )A.若12u u >，则{n u }必收敛B. 若12u u >，则{n u }必发散C. 若12u u <，则{n u }必收敛D. 若12u u <，则{n u }必发散(6)设曲线L ：f(x, y) = 1 (f(x, y)具有一阶连续偏导数），过第Ⅱ象限内的点M 和第Ⅳ象限内的点N,T 为L 上从点M 到N 的一段弧，则下列小于零的是 ( ) A.(,)rx y dx ⎰ B. (,)rf x y dy ⎰C.(,)rf x y ds ⎰D.'(,)'(,)x y rf x y dx f x y dy +⎰（7）设向量组1α，2α，3α线形无关，则下列向量组线形相关的是： ( ) （A ）,,122331αααααα--- （B ） ,,122331αααααα+++（C ） 1223312,2,2αααααα--- （D ）1223312,2,2αααααα+++（8）设矩阵A=211121112--⎛⎫ ⎪-- ⎪ ⎪--⎝⎭，B=100010000⎛⎫ ⎪⎪ ⎪⎝⎭，则A 于B ( )(A) 合同，且相似(B) 合同，但不相似 (C) 不合同，但相似(D)既不合同，也不相似（9）某人向同一目标独立重复射击，每次射击命中目标的概率为p ()01p <<，则此人第4次射击恰好第2次命中目标的概率为： ( ) （A ）23(1)p p - (B)26(1)p p - (C) 223(1)p p -(D) 226(1)p p -(10) 设随即变量（X ，Y ）服从二维正态分布，且X 与Y 不相关，()X f x ，()Y f y 分别表示X ，Y 的概率密度，则在Y ＝y 的条件下，X 的条件概率密度|(|)X Yf x y 为 ( )（A ）()X f x(B) ()Y f y(C) ()X f x ()Y f y(D)()()X Y f x f y 二．填空题：11－16小题，每小题4分，共24分，请将答案写在答题纸指定位置上 （11）31211x e dx x⎰＝_______. （12）设(,)f u v 为二元可微函数，(,)y xz f x y =，则zx∂∂＝______. (13)二阶常系数非齐次线性方程2''4'32x y y y e -+=的通解为y ＝____________. (14)设曲面∑：||||||1x y z ++=，则(||)x y ds ∑+⎰⎰＝_____________.(15)设矩阵A ＝0100001000010000⎛⎫ ⎪⎪ ⎪ ⎪⎝⎭，则3A 的秩为________. （16）在区间（0，1）中随机地取两个数，则这两个数之差的绝对值小于12的概率为________. 三．解答题：17~24小题，共86分.请将解答写在答题纸指定的位置上.解答应写出文字说明、证明过程或演算步骤.222222(,)2{(,)4,0}f x y x y x y D x y x y y =+-=+≤≥(17)（本题满分11分）求函数在区域上的最大值和最小值。

2007年全国硕士研究生入学统一考试理工数学一试题详解及评析一、选择题（本题共10小题，每小题4分，满分40分，在每小题给的四个选项中，只有一项符合题目要求，把所选项前的字母填在题后括号内） （1） 当0x +→等价的无穷小量是 ( )A. 1−B.C. 1−D.1−(2) 曲线y=1ln(1x e x++), 渐近线的条数为 ( ) A.0 B.1 C.2 D.3(3)如图，连续函数y=f(x)在区间[-3，-2]，[2，3]上的图形分别是直径为1的上、下半圆周，在区间[-2，0]，[0，2]的图形分别是直径为2的上、下半圆周，设F(x)=0()xf t dt ∫.则下列结论正确的是 ( ) A. F(3)=3(2)4F −− B. F(3)=5(2)4F C. F(3)=3(2)4F + D. F(3)= 5(2)4F −− (4)设函数f （x ）在x=0处连续，下列命题错误的是 ( ) A. 若0()limx f x x →存在，则f （0）=0 B. 若0()()lim x f x f x x→+− 存在，则f （0）=0C. 若0()lim x f x x → 存在，则'(0)f =0D. 若0()()lim x f x f x x→−− 存在，则'(0)f =0(5)设函数f （x ）在（0, +∞）上具有二阶导数，且"()f x o >, 令n u =f(n)=1,2,…..n, 则下列结论正确的是 ( )A.若12u u >，则{n u }必收敛B. 若12u u >，则{n u }必发散C. 若12u u <，则{n u }必收敛D. 若12u u <，则{n u }必发散(6)设曲线L ：f(x, y) = 1 (f(x, y)具有一阶连续偏导数），过第Ⅱ象限内的点M 和第Ⅳ象限内的点N,T 为L 上从点M 到N 的一段弧，则下列小于零的是 ( ) A.(,)rx y dx ∫ B. (,)rf x y dy ∫C.(,)rf x y ds ∫D.'(,)'(,)x y rf x y dx f x y dy +∫（7）设向量组1α，2α，3α线形无关，则下列向量组线形相关的是： ( ) （A ） ,,122331αααααα−−− （B ） ,,122331αααααα+++（C ）1223312,2,2αααααα−−− （D ）1223312,2,2αααααα+++（8）设矩阵A=211121112−−⎛⎞⎜⎟−−⎜⎟⎜⎟−−⎝⎠，B=100010000⎛⎞⎜⎟⎜⎟⎜⎟⎝⎠，则A 于B ()(A) 合同，且相似 (B) 合同，但不相似 (C) 不合同，但相似 (D)既不合同，也不相似（9）某人向同一目标独立重复射击，每次射击命中目标的概率为p ()01p <<，则此人第4次射击恰好第2次命中目标的概率为： ( ) （A ）23(1)p p −(B)26(1)p p −(C) 223(1)p p − (D) 226(1)p p −(10) 设随即变量（X ，Y ）服从二维正态分布，且X 与Y 不相关，()X f x ，()Y f y 分别表示X ，Y 的概率密度，则在Y ＝y 的条件下，X 的条件概率密度|(|)X Yf x y 为 ( )（A ）()X f x(B) ()Y f y(C) ()X f x ()Y f y(D)()()X Y f x f y 二．填空题：11－16小题，每小题4分，共24分，请将答案写在答题纸指定位置上 （11）31211x e dx x∫＝_______. （12）设(,)f u v 为二元可微函数，(,)yxz f x y =，则zx∂∂＝______. (13)二阶常系数非齐次线性方程2''4'32xy y y e −+=的通解为y ＝____________. (14)设曲面∑：||||||1x y z ++=，则(||)x y ds ∑+∫∫Ò＝_____________.(15)设矩阵A ＝0100001000010000⎛⎞⎜⎟⎜⎟⎜⎟⎜⎟⎝⎠，则3A 的秩为________. （16）在区间（0，1）中随机地取两个数，则这两个数之差的绝对值小于12的概率为________. 三．解答题：17~24小题，共86分.请将解答写在答题纸指定的位置上.解答应写出文字说明、证明过程或演算步骤.222222(,)2{(,)4,0}f x y x y x y D x y x y y =+−=+≤≥(17)（本题满分11分）求函数在区域上的最大值和最小值。

2007年考研数学一真题及参考答案一、选择题（本题共10小题，每小题4分，满分40分，在每小题给的四个选项中，只有一项符合题目要求，把所选项前的字母填在题后括号内）（1） 当0x +→时，与x 等价的无穷小量是 (B) A. 1xe- B.1ln1xx+- C. 11x +- D.1cos x -(2) 曲线y=1ln(1x e x++), 渐近线的条数为 (D) A.0 B.1 C.2 D.3(3)如图，连续函数y=f(x)在区间[-3，-2]，[2，3]上的图形分别是直径为1的上、下半圆周，在区间[-2，0]，[0，2]的图形分别是直径为2的上、下半圆周，设F(x)=0()xf t dt ⎰.则下列结论正确的是 (C) A. F(3)=3(2)4F -- B. F(3)=5(2)4F C. F(3)=3(2)4F + D. F(3)= 5(2)4F --(4)设函数f （x ）在x=0处连续，下列命题错误的是 (C)A. 若0()limx f x x →存在，则f （0）=0 B. 若0()()lim x f x f x x→+- 存在，则f （0）=0C. 若0()lim x f x x → 存在，则'(0)f =0D. 若0()()lim x f x f x x→-- 存在，则'(0)f =0(5)设函数f （x ）在（0, +∞）上具有二阶导数，且"()f x o >, 令n u =f(n)=1,2,…..n, 则下列结论正确的是(D)A.若12u u >，则{n u }必收敛B. 若12u u >，则{n u }必发散C. 若12u u <，则{n u }必收敛D. 若12u u <，则{n u }必发散(6)设曲线L ：f(x, y) = 1 (f(x, y)具有一阶连续偏导数），过第Ⅱ象限内的点M 和第Ⅳ象限内的点N,T 为L 上从点M 到N 的一段弧，则下列小于零的是 (B) A.(,)rx y dx ⎰ B. (,)rf x y dy ⎰C.(,)rf x y ds ⎰D.'(,)'(,)x y rf x y dx f x y dy +⎰（7）设向量组1α，2α，3α线形无关，则下列向量组线形相关的是： (A) （A ） ,,122331αααααα--- （B ） ,,122331αααααα+++（C ）1223312,2,2αααααα--- （D ）1223312,2,2αααααα+++（8）设矩阵A=211121112--⎛⎫ ⎪-- ⎪ ⎪--⎝⎭，B=100010000⎛⎫ ⎪⎪ ⎪⎝⎭,则A 于B ， (B)(A) 合同，且相似(B) 合同，但不相似 (C) 不合同，但相似(D)既不合同，也不相似（9）某人向同一目标独立重复射击，每次射击命中目标的概率为p ()01p <<，则此人第4次射击恰好第2次命中目标的概率为： (C) （A ）23(1)p p - (B)26(1)p p - (C) 223(1)p p -(D) 226(1)p p -(10) 设随即变量（X ，Y ）服从二维正态分布，且X 与Y 不相关，()X f x ，()Y f y 分别表示X ，Y 的概率密度，则在Y ＝y 的条件下，X 的条件概率密度|(|)XYf x y 为 (A)（A ）()X f x(B) ()Y f y(C) ()X f x ()Y f y(D)()()X Y f x f y 二．填空题：11－16小题，每小题4分，共24分，请将答案写在答题纸指定位置上。

2007年考研数学一真题一、选择题（本题共10小题，每小题4分，满分40分，在每小题给的四个选项中，只有一项符合题目要求，把所选项前的字母填在题后括号内） （1） 当0x +→时，与x 等价的无穷小量是 ( ) A. 1xe- B.1ln1xx+- C. 11x +- D.1cos x -(2) 曲线y=1ln(1x e x++), 渐近线的条数为 ( ) A.0 B.1 C.2 D.3(3)如图，连续函数y=f(x)在区间[-3，-2]，[2，3]上的图形分别是直径为1的上、下半圆周，在区间[-2，0]，[0，2]的图形分别是直径为2的上、下半圆周，设F(x)=0()xf t dt ⎰.则下列结论正确的是 ( ) A. F(3)=3(2)4F -- B. F(3)=5(2)4F C. F(3)=3(2)4F + D. F(3)= 5(2)4F --(4)设函数f （x ）在x=0处连续，下列命题错误的是 ( )A. 若0()limx f x x →存在，则f （0）=0 B. 若0()()lim x f x f x x→+- 存在，则f （0）=0C. 若0()lim x f x x → 存在，则'(0)f =0D. 若0()()lim x f x f x x→-- 存在，则'(0)f =0(5)设函数f （x ）在（0, +∞）上具有二阶导数，且"()f x o >, 令n u =f(n)=1,2,…..n, 则下列结论正确的是 ( )A.若12u u >，则{n u }必收敛B. 若12u u >，则{n u }必发散C. 若12u u <，则{n u }必收敛D. 若12u u <，则{n u }必发散(6)设曲线L ：f(x, y) = 1 (f(x, y)具有一阶连续偏导数），过第Ⅱ象限内的点M 和第Ⅳ象限内的点N,T 为L 上从点M 到N 的一段弧，则下列小于零的是 ( ) A.(,)rx y dx ⎰ B. (,)rf x y dy ⎰C.(,)rf x y ds ⎰D.'(,)'(,)x y rf x y dx f x y dy +⎰（7）设向量组1α，2α，3α线形无关，则下列向量组线形相关的是： ( ) （A ）,,122331αααααα--- （B ） ,,122331αααααα+++（C ） 1223312,2,2αααααα--- （D ）1223312,2,2αααααα+++（8）设矩阵A=211121112--⎛⎫ ⎪-- ⎪ ⎪--⎝⎭，B=100010000⎛⎫ ⎪⎪ ⎪⎝⎭，则A 于B ( )(A) 合同，且相似(B) 合同，但不相似 (C) 不合同，但相似(D)既不合同，也不相似（9）某人向同一目标独立重复射击，每次射击命中目标的概率为p ()01p <<，则此人第4次射击恰好第2次命中目标的概率为： ( ) （A ）23(1)p p - (B)26(1)p p - (C) 223(1)p p -(D) 226(1)p p -(10) 设随即变量（X ，Y ）服从二维正态分布，且X 与Y 不相关，()X f x ，()Y f y 分别表示X ，Y 的概率密度，则在Y ＝y 的条件下，X 的条件概率密度|(|)X Yf x y 为 ( )（A ）()X f x(B) ()Y f y(C) ()X f x ()Y f y(D)()()X Y f x f y 二．填空题：11－16小题，每小题4分，共24分，请将答案写在答题纸指定位置上 （11）31211x e dx x⎰＝_______. （12）设(,)f u v 为二元可微函数，(,)y xz f x y =，则zx∂∂＝______. (13)二阶常系数非齐次线性方程2''4'32x y y y e -+=的通解为y ＝____________. (14)设曲面∑：||||||1x y z ++=，则(||)x y ds ∑+⎰⎰＝_____________.(15)设矩阵A ＝0100001000010000⎛⎫ ⎪⎪ ⎪ ⎪⎝⎭，则3A 的秩为________. （16）在区间（0，1）中随机地取两个数，则这两个数之差的绝对值小于12的概率为________. 三．解答题：17~24小题，共86分.请将解答写在答题纸指定的位置上.解答应写出文字说明、证明过程或演算步骤.222222(,)2{(,)4,0}f x y x y x y D x y x y y =+-=+≤≥(17)（本题满分11分）求函数在区域上的最大值和最小值。

2007年全国硕士研究生入学统一考试数学(一)试卷一、选择题(本题共10小题,每小题4 分,满分40分,在每小题给的四个选项中,只有一项符合题目要求,把所选项前的字母填在题后括号内)(1)当0x +→时,(A)1−(B)ln1(D)1−【考点分析】：等价无穷小的定义和常用的等价无穷小 【求解过程】：◼ 方法一：利用等价无穷小0x +→时，()11~−=−−()12111~=+−2111~22x −=，(ln 1~=+◼ 方法二：可用洛必达法则和等价无穷小的定义来求解 验证极限,,lim x A B C D +→是否等于1，其中(),,A B C D 表示A ，B ，C ，D 四个选项中的式子。

故选B【基础回顾】：下面，我们就无穷小之比的极限存在或为无穷大时。

来说明两个无穷小之间的比较。

应当注意，下面的α及β都是在同一个自变量的变化过程中的无穷小，且0α≠，lim βα也是在这个变化过程中的极限。

定义：如果lim0βα=就说β是比α高阶的无穷小，记作()o βα=； 如果lim βα=∞，就说β是比α低阶的无穷小。

如果lim 0c βα=≠，就说β与α是同阶无穷小；如果lim 0,0k c k βα=≠>，就说β是关于α的k 阶无穷小。

如果lim1βα=，就说β与α是等价无穷小，记作αβ。

显然，等价无穷小是同阶无穷小的特殊情形，即1c =的情形。

常用等价无穷小，当0x →时，1~ln(1)~sin ~tan ~xe x x x x −+()11~x x αα+−， 211cos ~2x x −(2)曲线()1ln 1x y e x=++,渐近线的条数为 (A)0 (B)1 (C)2 (D)3 【考点分析】：曲线的渐近线（水平、垂直、斜渐近线）的条数 【求解过程】：计算垂直渐近线：求函数在其不连续点0x x =处的极限，若为∞则存在垂直渐近线0x x =函数只有间断点0x =，()001lim lim ln 1x x x y e x →→=++=∞⎪⎝⎭，故存在垂直渐近线0x =计算水平渐近线：求函数在,x x →+∞→−∞时的极限a ，若a 存在，则有水平渐近线y a =()1lim lim ln 10x x x y e x →−∞→−∞⎛⎫=++= ⎪⎝⎭，故存在水平渐近线0y = 计算斜渐近线：求yx在,x x →+∞→−∞时的极限a ，若a 存在，且0a ≠，求出y ax −在相应处的极限b ，则有斜渐近线y ax b =+()2ln 11lim lim 0lim 11x xx x x x e y e x x x e→+∞→+∞→+∞⎛⎫+ ⎪=+=+= ⎪+⎝⎭()()111lim lim ln 1lim ln 0x xx x x x e y x e x x x e →+∞→+∞→+∞⎛⎫⎛⎫+⎛⎫−=++−=+= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭故存在斜渐近线y x = 选D 。

2007年数学一一、选择题：(本题共１0小题，每小题4分,共４0分． 每小题给出的四个选项中,只有一项符合题目要求，把所选项前的字母填在题后的括号内)(１) 当0x +→时,等价的无穷小量是(A ） 1- (B ）(C) 1． (Ｄ) 1- [ B ］ 【分析】 利用已知无穷小量的等价代换公式，尽量将四个选项先转化为其等价无穷小量,再进行比较分析找出正确答案．【详解】 当0x +→时，有1(1)~-=--1~;2111~.22x -= 利用排除法知应选(B). (2） 曲线1ln(1)x y e x=++，渐近线的条数为 (A ） ０. (B ） 1. (C ） 2. (D ） ３. [ D ］【分析】 先找出无定义点，确定其是否为对应垂直渐近线；再考虑水平或斜渐近线。

【详解】 因为01lim[ln(1)]xx e x →++=∞,所以0x =为垂直渐近线; 又 1lim[ln(1)]0xx e x →-∞++=，所以ｙ=０为水平渐近线； 进一步，21ln(1)ln(1)lim lim []lim x x x x x y e e x x x x →+∞→+∞→+∞++=+==lim 11xx x e e→+∞=+, 1lim[1]lim[ln(1)]x x x y x e x x →+∞→+∞-⋅=++-=lim[ln(1)]xx e x →+∞+- =lim[ln (1)]lim ln(1)0x x xx x e e x e --→+∞→+∞+-=+=, 于是有斜渐近线：y = ｘ. 故应选(Ｄ）.(3） 如图，连续函数y =f （x )在区间［−３,−2],［２,3］上的图形分别是直径为1的上、下半圆周,在区间[−2,0］,[０，２]的图形分别是直径为2的上、下半圆周,设0()().x F x f t dt =⎰则下列结论正确的是 (A) 3(3)(2)4F F =--. (Ｂ) 5(3)(2)4F F =． (C ） )2(43)3(F F =-. (D) )2(45)3(--=-F F . [ C ] 【分析】 本题考查定积分的几何意义，应注意ｆ(ｘ)在不同区间段上的符号,从而搞清楚相应积分与面积的关系。